Подмножества множеств примеры: Множества и подмножества, число, мощность, примеры, урок и презентация по алгебре, 9 класс

Подмножество 9 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

С понятием «множество» вы уже знакомы. Подмножество, как можно догадаться из названия, – это определенная часть множества. Например:

 

А – это множество всех учеников в классе.

В – это множество девочек указанного выше класса.

С – множество всех мальчиков класса.

D – множество всех отличников данного класса.

Е – множество всех мальчиков-отличников этого класса.

Таким образом, были перечислены множество (А) и его подмножества (В, С, D, Е). Теперь мы можем дать определение, что такое «подмножество».

 

Определение

 

 

Если каждый элемент множества В является элементом множества А, то множество В называют подмножеством множества А.

 

В ⊂ А

Как пример, девочки класса из примера выше (множество В) являются ученицами класса (множество А). Значит, В входит в А.

Мальчики тоже являются частью класса, значит, С ⊂ А.
Все отличники являются частью класса, D ⊂ A.

Как и мальчики, отличники – это ученики класса, то есть Е ⊂ А.

 

Разница между значками ∈ и ⊂

 

 

Если у нас а ∈ А, то это значит, что а принадлежит А.То есть, это один элемент a принадлежит множеству А.

 

Если же подмножество В входит в А, то мы пишем В ⊂ А.

То есть между значками есть разница.

 

Примеры важных числовых множеств и подмножеств

 

 

N – множество натуральных чисел (с их помощью мы считаем предметы, природу и так далее.)

 

N =

Z – множество целых чисел.

Z =

Ясно, что натуральные числа – это подмножество целых чисел, то есть N ⊂ Z.

Q – множество рациональных чисел.

Q =

Если к множеству рациональных чисел добавить множество иррациональных чисел, то мы получим множество всех действительных чисел.

R – множество действительных чисел.

R =

Запишем правильные включения:

N ⊂ Z ⊂ Q ⊂ R

 

Пример из геометрии

 

 

Пусть множество А – это множество всех четырехугольников: A, B, C, D (рис. 1).

 

Рис. 1. Множество А

Пусть множество В – это множество четырехугольников с парой равных параллельных сторон: A, B, C, D (рис. 2).

BC = AD       BC || AD

      

Рис. 2. Множество В

Множество С – это множество таких четырехугольников, у которых диагонали, пересекаясь, делятся пополам: AB, CD – диагонали, т. О – точка пересечения диагоналей, АО = ОС, BO = OD (рис. 3).

Рис. 3. Множество С

Итак, было рассмотрено 3 множества четырехугольников: множество произвольных четырехугольников; множество четырехугольников, у которых парные стороны равны и параллельны; множество четырехугольников, у которых диагонали, пересекаясь, точкой пересечения делятся пополам.

Рассмотрим еще 2 множества.

Множество D – это множество всех параллелограммов, и множество Е – множество параллелограммов с прямым углом (рис. 4).

Рис. 4. Множества D и Е

Таким образом, мы имеем 5 множеств четырехугольников.

 

Задача

 

 

Написать верное включение (то есть, какое множество является подмножеством другого множества) (рис. 5).

 

Рис. 5. Иллюстрация к задаче

Наиболее богатое – это множество всех четырехугольников. Значит:

B ⊂ A; C ⊂ A; D ⊂ A; E ⊂ A

Множества В, С, D и Е являются подмножествами множества А.

Далее вспомним определение параллелограмма:

Параллелограммом называется такой четырехугольник, у которого противоположные стороны попарно параллельны.

Для того чтобы убедиться, что фигура является параллелограммом, необходимо вспомнить его признаки:

1. Если 2 стороны параллельны и равны, то такой четырехугольник является параллелограммом.

Значит, В – это множество всех параллелограммов.

2. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то эта фигура – параллелограмм.

Значит, С – это множество всех параллелограммов.

Про множество D напрямую было сказано, что это множество всех параллелограммов.

Если будет стоять вопрос, какие множества равны между собой, то можно ответить, что:

В = С = D – это множества всех параллелограммов.

3. Если в параллелограмме хотя бы один угол равен 90⁰, то такой параллелограмм является прямоугольником.

Значит, Е – это множество всех прямоугольников. Множество всех прямоугольников является подмножеством (частным случаем) произвольного четырехугольника и подмножеством параллелограмма. Отсюда имеем:

Е ⊂ А; E ⊂ B; E ⊂ C; E ⊂ D

Мы рассмотрели множества четырехугольников, из которых самое богатое множество – это множество всех четырехугольников, далее по-разному заданы множества параллелограммов и, наконец, Е – это множество всех прямоугольников. Были даны ответы на вопросы, где верные включения, какие множества равны между собой.

 

Вывод

 

 

Итак, мы узнали, что такое подмножество, и привели примеры.

 

 

Список литературы

1. Мордкович А.Г., Семенов П.В. Алгебра 9 класс. – 12-е изд., стер. – М.: 2010. – 224 с.
2. Макарычев Ю.Н., Миндюк Н.Г., Алгебра 9 класс. – 16-е изд., стер. – М.: 2009. – 271 с.

 

Домашнее задание

1. № 3.8, 3.9, 3.10, 3.11 стр. 22. Мордкович А.Г. Алгебра 9 класс. Задачник для учащихся общеобразовательных школ. – 12-е изд. – М.: Мнемозина, 2010. – 273 стр.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Ru.wikipedia.org  (Источник).
2. Интернет-портал Stu.sernam.ru  (Источник).
3. Интернет-портал Scienceland.info  (Источник).

 

Подмножества

Если каждый элемент множества В является в то же время элементом множества А, то говорят, что В – подмножество в А, и пишут . Каждое непустое множество имеет по крайней мере два подмножества: пустое множество Ø и само множество А. Таким образом, пустое множество является подмножеством любого множества.

Приведем примеры подмножеств:

1. числовой отрезок [–1, 3] есть подмножество числового отрезка [–4; 5];

2. множество всех квадратов есть подмножество множества всех прямоугольников;

3. множество Z всех целых чисел есть подмножество множества Q всех рациональных чисел;

4. множество точек треугольника, вписанного в круг, есть подмножество множества точек этого круга;

5. множество точек круга является подмножеством множества точек описанного вокруг него квадрата;

6. множество звезд нашей Галактики является подмножеством множества всех звезд Вселенной;

7. множество учеников восьмого класса данной школы есть подмножество множества всех учеников этой школы. В свою очередь множество учеников этой школы является подмножеством множества всех школьников в Республики Беларусь;

8. множество жителей Москвы является подмножеством множества всех жителей России;

9. множество граждан г. Минск является подмножеством множества всех людей на земном шаре.

Н а рисунке 6 прямые MN и PQ пересекаются в точке R.

Эта точка принадлежит как прямой MN, так и прямой PQ, т.е. является общим элементом двух множеств – множества точек прямой MN и множества точек прямой PQ. Точно так же множество точек прямой MN и множество точек окружности Г (рис. 7) имеют два общих элемента – точку А и точку B. Прямая и окружность пересекаются в двух точках.

Введем теперь общее понятие пересечения нескольких множеств.

Пересечением множеств А и В называют новое множество Х, содержащее те и только те элементы, которые входят и в множество А и в множество В.

Пересечение множеств А и В обозначают или AB. Например, если А – множество мальчиков, обучающихся в данной школе, а В – множество всех учеников из 8 класса, то – множество мальчиков, которые учатся в 8 классе.

С понятием пересечения множеств приходится иметь дело и в арифметике. Пусть А – множество натуральных делителей числа 72:

A ={1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72},

а В – множество натуральных делителей числа 54:

B ={1, 2, 3, 6, 9, 18, 27, 54}.

Тогда множество состоит из чисел 1, 2, 3, 6, 9, 18:

={1, 2, 3, 6, 9, 18}.

Эти числа являются общими делителями для 72 и 54. Наибольший элемент множества равен 18. Это – наибольший общий делитель чисел 54 и 72. Множество делителей числа 72 конечно. А множество кратных этого числа бесконечно:

С = {72, 144, 216, … , 72n, …}.

Бесконечно и множество кратных числа 54:

D = {54, 108, 162, 216, … , 54m, …}.

Пересечением этих множеств является множество общих кратных для чисел 72 и 54:

= {216, 432, …}.

Наименьшее число в , т.е. 216, называется наименьшим общим кратным для 72 и 54.

Иногда приходится пересекать множества геометрических фигур. Например, множество всех квадратов является пересечением множества всех прямоугольников с множеством всех ромбов, т.к. квадрат – это фигура, являющаяся одновременно и прямоугольником, и ромбом. Пересечением множества всех треугольников с множеством всех правильных многоугольников является множество правильных треугольников.

Что означают подмножества в статистике?

В этой статье

1. Что такое подмножество?

2. Типы подмножеств

3. Что такое символы подмножеств?

4. Подмножества и надмножества

5. Сколько подмножеств в наборе?

6. Что такое набор мощности набора?

7. Подмножество часто задаваемых вопросов

Теория множеств лежит в основе математики. Его используют математики, статистики и специалисты по данным, но можете ли вы? Конечно. Любой может изучить основы. Давайте рассмотрим, как множества и подмножества определяют, группируют и организуют математические объекты.

Что такое подмножество?

В статистике набор — это совокупность объектов. Объектами могут быть буквы, цифры, формы, символы или любые другие математические объекты. Когда мы разбираем набор, эти меньшие части являются подмножествами.

Подмножество — это множество, состоящее из элементов другого множества.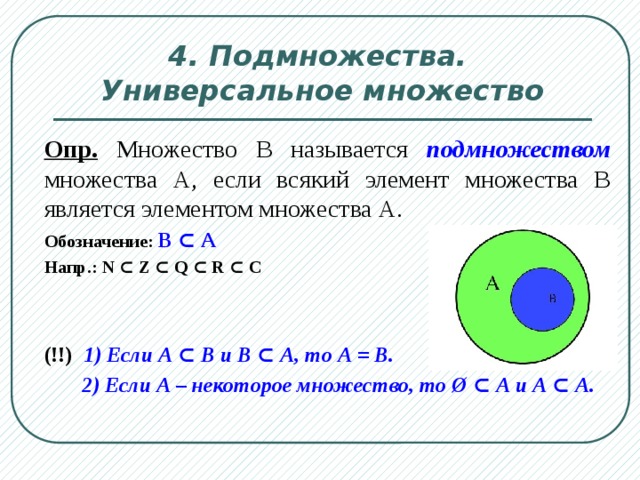 Более формально, множество B является подмножеством другого множества A, если все элементы B также принадлежат A.

Вот несколько примеров:

• Если набор A = {2, 4, 6, 8, 10} и набор B = {2, 6, 8}, набор B является подмножеством набора A. Все элементы набора B входят в набор A.

• Если набор 1 = {a, b, c, d, e} и набор 2 = {a, b, c, z}, набор 2 НЕ является подмножеством набора 1. Хотя некоторые элементы набора 2 находятся в наборе 1, Набор 2 также содержит элемент (букву z), которого нет в наборе 1.

• Если набор A равен результатам подбрасывания монеты, а набор B = {орел}, то набор B является подмножеством набора A.

• Если набор A представляет собой набор целых чисел, а набор B — набор нечетных чисел, набор B является подмножеством набора A.

• Если Набор 1 = {⚫, ⬛,⬟}, Набор 1 является подмножеством самого себя! Это справедливо для всех наборов. Мы рассматриваем множество как собственное подмножество.

• Если множество C = {1, 2, 3, 4, 5}, то пустое множество {} является подмножеством множества C. Мы всегда рассматриваем пустое множество как подмножество любого множества.

Типы подмножеств

Существует два типа подмножеств: правильные подмножества и неправильные подмножества.

• Правильное подмножество — это любое подмножество множества, кроме самого множества.

• Неправильным подмножеством является само множество. Мы также можем определить неправильное подмножество как любое подмножество, которое не является правильным подмножеством. Неправильным подмножеством множества A является множество A. Каждое множество имеет только одно неправильное подмножество.

Вот еще один пример.

Предположим, что множество A представляет собой множество, состоящее из всех букв английского алфавита (26 букв). Каковы некоторые из правильных подмножеств множества A? Что является неправильным подмножеством множества A?

Набор A имеет много собственных подмножеств, включая {a,b,c, d}, {s, u, b}, {c, l, x, y, z}. Множество A имеет только одно неправильное подмножество — множество A!

Что такое символы подмножества?

Мы можем использовать символ ⊂ или ⊆ для обозначения подмножества. ⊂ — это символ, используемый для правильных подмножеств, а ⊆ — символ, который может применяться как для правильных, так и для неправильных подмножеств.

Символ ⊂ означает «…является правильным подмножеством…».

Символ ⊆ означает «…является правильным или неправильным подмножеством…»

Подмножества и надмножества

Мы также можем описать подмножества в терминах их надмножеств. Если все элементы набора B находятся в наборе A, то набор A называется надмножеством набора B. Иными словами, если набор B является подмножеством набора A, то набор A является надмножеством набора B.

Суперсеты также могут быть правильными и неправильными. Надмножество является неправильным надмножеством, если оно является надмножеством самого себя — множество A является неправильным надмножеством множества A.

Если надмножество не является неправильным надмножеством, оно является правильным надмножеством. 93 = 823=8. Это множество будет иметь 7 правильных подмножеств и 1 неправильное подмножество.

Set A = {a, b, c}

Subsets of A

{a, b, c}

{a}

{b}

{c}

{a, b}

{b, c}

{a, c}

{ }

Обратите внимание, что последним подмножеством в списке является пустое множество { }. Пустое множество — это множество, в котором нет элементов. Иногда его называют нулевым множеством, а его символ — ∅. Мы считаем пустое множество подмножеством каждого множества!

Какова мощность набора?

Набор мощностей — это набор, содержащий всех подмножеств набора.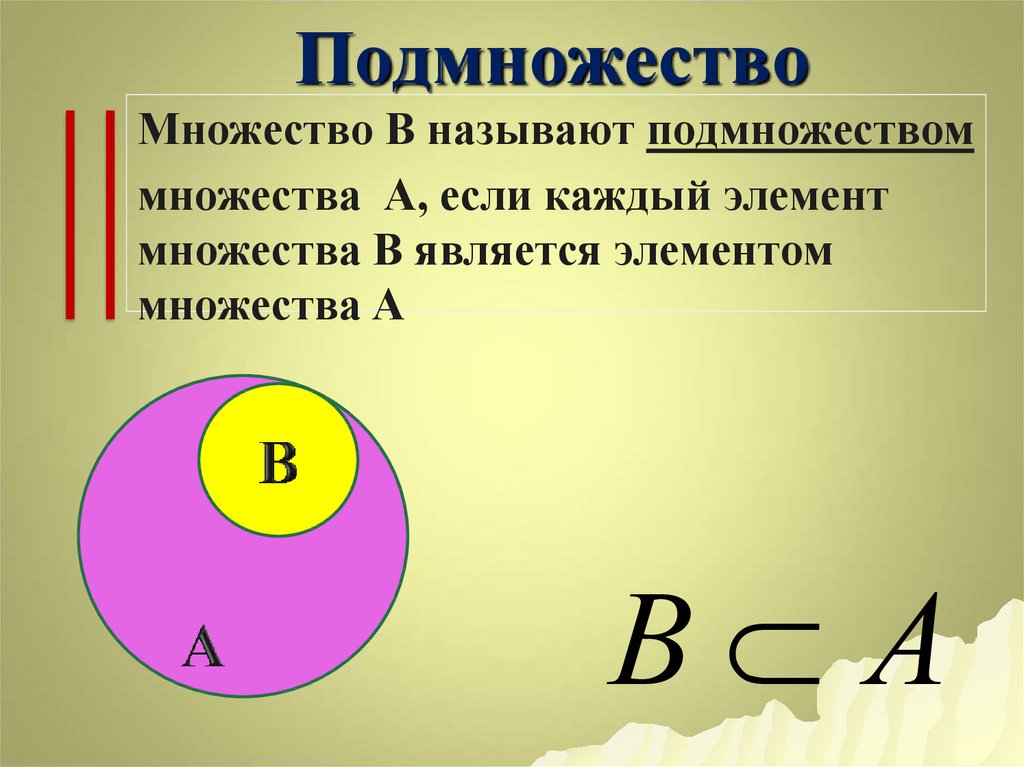 P( ) — его символ. 9н элементов.

P(A) = {{a, b, c}, {a}, {b}, {c}, {a, b}, {b, c}, {a, c} , {} }

Надмножеством A может быть {a, b, c, d, e} или любое другое множество, содержащее элементы a, b и c.

Проверьте, сможете ли вы построить набор мощности для набора, содержащего результаты подбрасывания монеты!

Вы должны получить набор мощности { {головы, хвосты}, {головы}, {решки}, {}}

Часто задаваемые вопросы о подмножестве

Что такое определение подмножества?

Множество B является подмножеством другого множества A, если все элементы B также принадлежат A.

Что такое теория множеств?

Теория множеств — это раздел математики, изучающий логику и отношения между множествами. Набор — это любой набор математических объектов. Чтобы узнать больше о множествах, прочитайте об операциях над множествами.

Может ли множество быть подмножеством самого себя?

Да! Множество всегда является подмножеством самого себя. Когда вы хотите обратиться к множеству как к подмножеству самого множества, вы используете термин «неправильное подмножество». 90 = 120=1.

Какие примеры подмножеств?

Подмножества, как и множества, могут состоять из:

Подмножество может даже содержать другие множества!

Вот несколько примеров:

• Набор {1, 3, 5} является подмножеством {1, 3, 5, 8, 9}

• Набор {like, disklike} является подмножеством набора {нравится, не нравится, нет предпочтения}

• Набор четных чисел является подмножеством множества целых чисел

• Множество натуральных чисел является подмножеством действительных чисел

• Множество {⚫} является подмножеством {⚫, ⬛,⬟}

Как представить подмножество на диаграмме Венна?

Диаграммы Венна — это визуальное представление множеств. Поскольку подмножество c, вы можете представить подмножество в виде круга, нарисованного внутри границ большего круга, представляющего надмножество.

На рисунке ниже набор B является подмножеством набора A.

• Набор A = {1, 2, 3, 5, 7, 8, 9}

• Набор B= {8}

• Набор C = {8, 11, 20}

• Набор D= {30, 50}

Теперь, когда вы знаете, что такое подмножество, вы можете углубиться в такие понятия, как операции с множествами и нотация множеств. В Берлине есть даже первые теоретические часы, которые называются Mengenlehreuhr. Он показывает время с помощью подсвеченных цветных полей вместо цифр. Как вы будете исследовать и расширять свои знания дальше?

Ознакомьтесь с отмеченными наградами курсами For-Credit от Outlier

Outlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов для создания будущего онлайн-колледжа.

Ознакомьтесь с этими связанными курсами:

Введение в статистику

Изучите курс

Введение в статистику

Как данные описывают наш мир.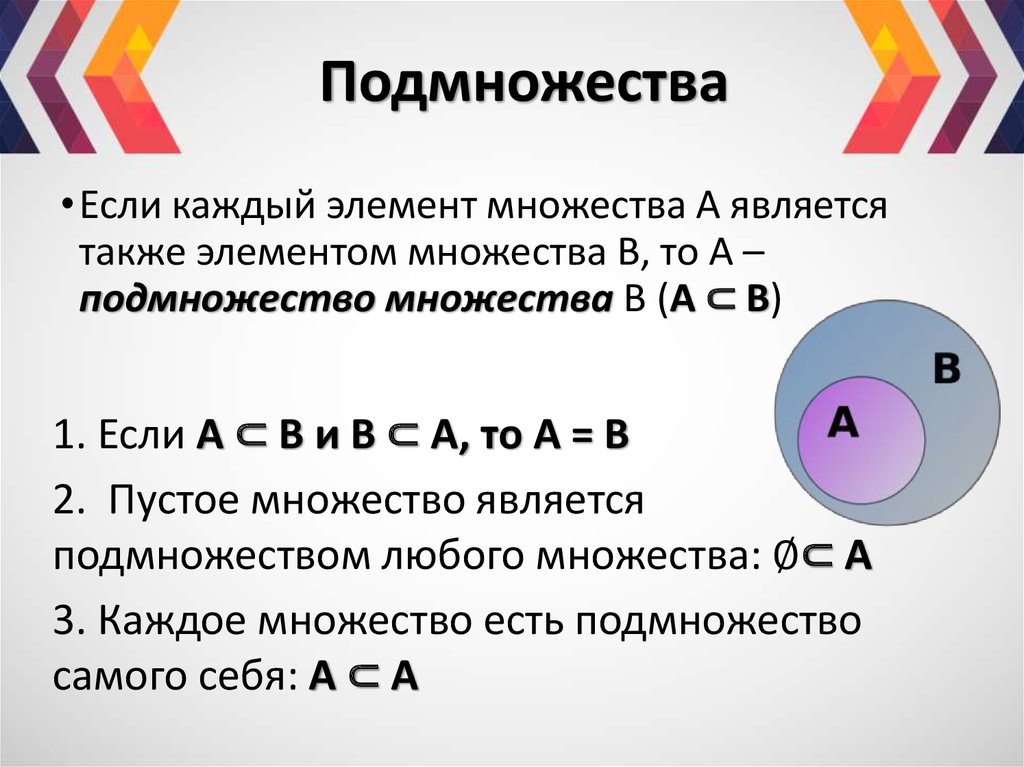

Обзор курса

Введение в микроэкономику

Изучите курс

Введение в микроэкономику

Почему маленькие решения имеют большое значение.

Изучить курс

Введение в макроэкономику

Изучить курс

Введение в макроэкономику

Как деньги движут нашим миром.

Изучить курс

Введение в психологию

Изучить курс

Введение в психологию

Наука о разуме.

Изучите курс

Подмножества, мощные и универсальные наборы

Чтобы правильно понимать вещи и запоминать их на долгое время, люди предпочитают хранить информацию в связках или категориях, однотипная информация помещается в одну категорию, так информация выглядит аккуратнее и ее легче запомнить. Таким же образом определяются множества. Чтобы сохранить элементы, принадлежащие к одной и той же категории, они хранятся в одном наборе, таким образом, в математике данные также могут быть аккуратно организованы. Однако наборы не позволяют упоминать качества элементов. Например, всех девочек 8-го класса можно поместить в один набор, но всех симпатичных девочек 8-го класса нельзя считать примером набора. Давайте узнаем о наборах более подробно.

Наборы

Наборы определяются как хорошо определенный набор данных. Данные, представленные в наборе, известны как элемент, каждый элемент, принадлежащий одному набору, отличается от другого, но категория, к которой они принадлежат, всегда одна и та же, например, мешок с разными видами фруктов, все натуральные числа, и т. д. 

Примеры наборов:

• {1, 2, 3, 4, 5} ⇢ Пример конечного набора.
• {} ⇢ Пример нулевого набора.
• {a: a — нечетное число} ⇢ Пример бесконечного множества.
• {p} ⇢ Пример одноэлементного набора.

Подмножества

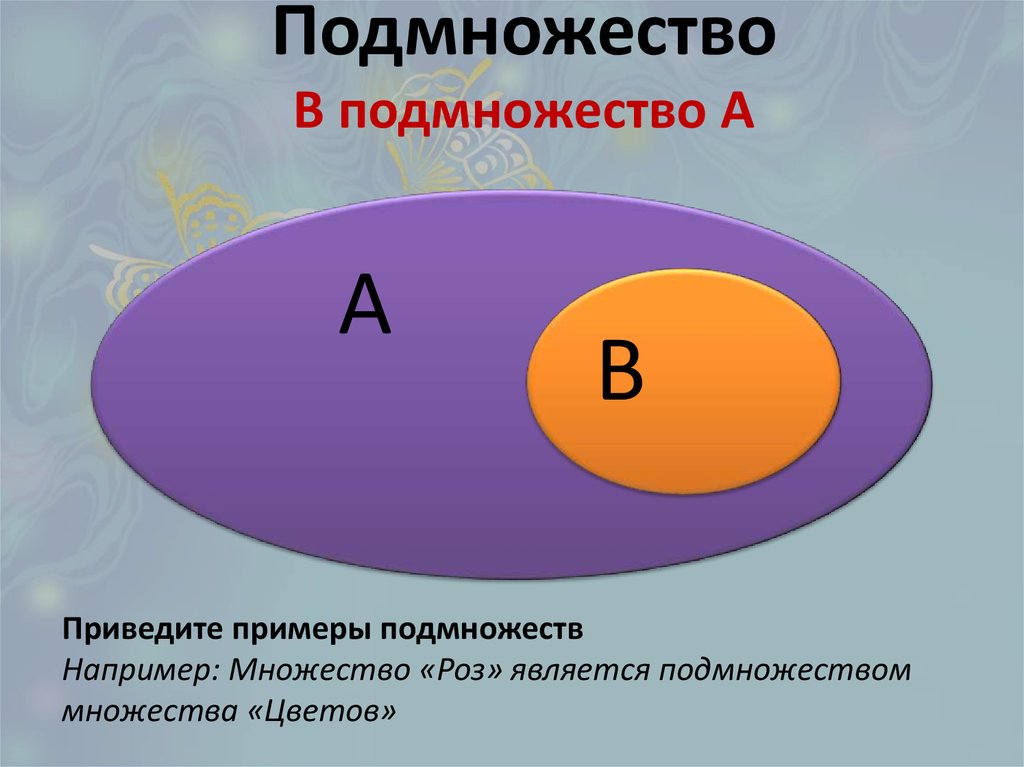
Если в наборе все элементы принадлежат другим наборам, этот набор будет известен как подмножество другого набора. Подмножество обозначается как «⊆». Если множество A является подмножеством множества B, оно представляется как A ⊆ B. 

Пример подмножества,

Множество A= {m, n, o, p, q}

Множество B= { k, l, m, n, o, p, q, r}

Затем, A ⊆ B

Правильный набор

Если в наборе A все элементы присутствуют в наборе B, а в наборе B больше элементов, то набор A является правильным набором набора B. Правильный набор представлен как «⊂»

Два набора, имеющие равное количество элементов никогда не могут быть собственными множествами друг друга, следовательно, множество никогда не является собственным множеством самого себя.

Примечание: Все собственные наборы являются подмножествами, но не все подмножества могут считаться правильными наборами.

Наборы мощности

Набор мощности определяется как набор всех возможных подмножеств данного набора. Определение кажется немного запутанным, но на самом деле наборы мощности очень легко понять. Представьте множество, в котором присутствуют некоторые элементы, теперь напишите все возможные подмножества, которые можно записать для конкретного множества, рассматривайте подмножества как элементы, поместите их в отдельный набор, полученный набор будет называться набором мощности.

Пример набора мощности,

Набор A = {2,3}

Возможные подмножества A = {}, {2}, {3}, {2, 3}

Набор мощности A = P( A)= {{}, {2}, {3}, {2, 3}}

Примечание: 2 ^п .

Универсальный набор

Универсальный набор является мастером всех наборов, то есть содержит все элементы, присутствующие во всех данных наборах. Универсальное множество изображается как U, а на диаграмме Венна оно изображается прямоугольником, все остальные множества нарисованы внутри прямоугольника, это сделано для того, чтобы показать, что универсальное множество содержит все возможные элементы.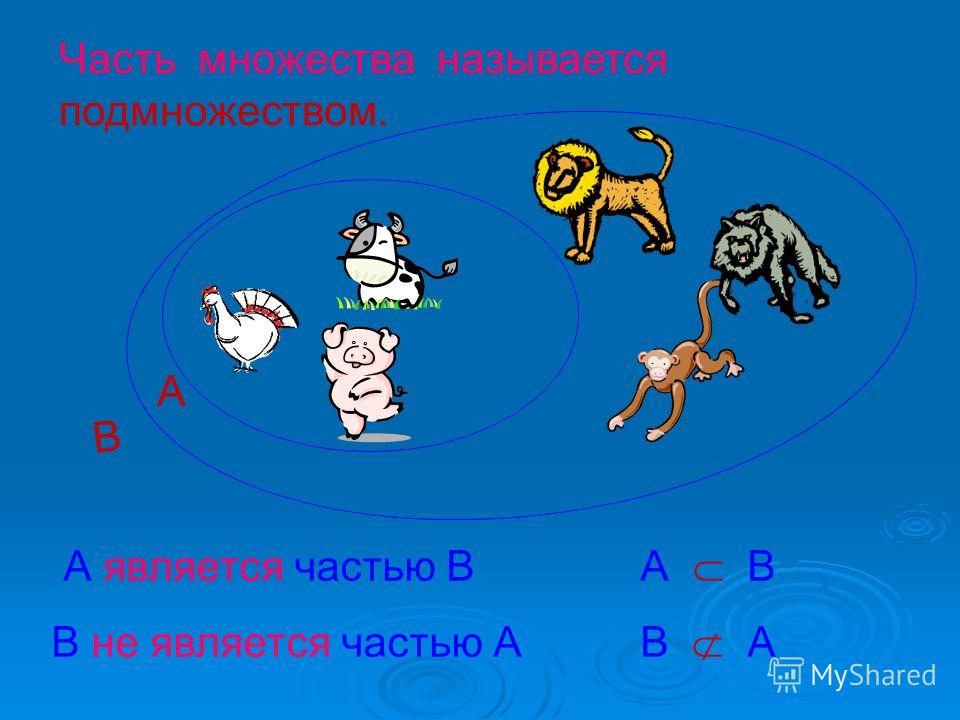

Предположим, что набор A и набор B являются частями универсальных наборов. 2, 3, 4, 5, 6}

Это должно выглядеть примерно так на диаграмме Венна,

Примеры задач

Каждый набор является подмножеством самого себя

Если все элементы набора A присутствуют в наборе B, набор B становится подмножеством набора A.

Универсальное никогда не является подмножеством любого другого множества.

Не все наборы являются подмножествами универсального набора .

Power Set не включает пустой набор.

Ответ:

1. Верно. Каждое множество можно обозначить как подмножество самого себя.
2. Ложь. Верным утверждением должно быть то, что множество A ⊂ множество B.
3. Верно. Универсальный набор содержит все элементы в себе.
4. Ложь. Все множества являются подмножествами U.
5. Ложь. Набор Power включает пустой набор.

Вопрос 2. Объясните, какие из следующих множеств являются подмножествами множества P,

Множество P = {1, 3, 5, 7, 9, 11, 13, 15,17,19}

1. Набор A = {a, 1, 0, 2}
2. Набор B = {3, 7, 9}
3. Набор C = {1, 4, 6, 11}
   8 Набор D = {19,1}
4. Набор E = {9, 13, 15, 17}

Ответ:

1. Множество A содержит элементы a, 1, 0, 2, которых нет в множестве P. Следовательно, множество A не является подмножеством.
2. Набор B содержит элементы, присутствующие в наборе P. Следовательно, набор B ⊆ набор P
3. Набор C содержит 2 дополнительных элемента. Следовательно, ни одно подмножество P
4. Set D не содержит 1, 19 в качестве элемента. Следовательно, множество D ⊆ множество P
5. Все элементы множества E совпадают с элементами множества P. Следовательно, множество E ⊆ множество P.

Вопрос 3: Какие элементы не могут быть включены в Набор?

Ответ:

Все, что говорит о качестве или характеристиках элементов, например о хорошем или плохом, не может быть помещено в набор. Например, «всех хороших футболистов» Это высказывание нельзя поставить в набор, Или «всех учеников, плохо выступивших на уроке» нельзя поставить в набор.

Вопрос 4: В чем разница между подмножеством и собственным набором?

Ответ:

Если множество A имеет все свои элементы, присутствующие в множестве B, то можно сказать, что множество A ⊆ множество B, важно отметить, что оба множества могут быть равны и все же быть подмножества друг друга.

Если множество A содержит все элементы, присутствующие в множестве B, и элементов множества B больше, чем элементов множества A, то можно сказать, что множество A является собственным множеством множества B.

No related posts.