Подобие треугольников. Решение задач
Тема урока: Использование подобия треугольников для решения задач практического содержания
Класс: 9
Цели урока:
Образовательные: повторить признаки подобия треугольников, продолжить вырабатывать умения применять знания на практике.
Оборудование: проектор, карточки с заданиями.
Используемая литература:
Лысенко, Ф. Ф. Математика. Базовый уровень ГИА -2014. Пособие для «чайников». Модуль 3: Реальная математика. / Ф. Ф. Лысенко, С. Ю. Кулабухова. : Легион, 2013 – 128 с.
Открытый банк заданий ОГЭ 2015 (ФИПИ)
Атанасян, Л. С. Геометрия. 7-9 классы : учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. : Просвещение, 2010. – с. 138 – 155.
Перельман, Я. И. Занимательная геометрия / Я. И. Перельман : ГТТИ, 1950. – 206 с.
И. Занимательная геометрия / Я. И. Перельман : ГТТИ, 1950. – 206 с.
Тип урока: урок обобщения и систематизации знаний
План проведения занятия:
Организационный момент. (1 мин)
Формулировка темы урока. (2 мин)
Повторение теоретического материала по теме. (5 мин)
Историческая справка (5 минут)
Групповая работа (18 мин)
Самостоятельная работа (10 мин)
Рефлексия (3 мин)
Домашнее задание (1 мин)
Ход урока:
№ | Время | Действия учителя | Действия ученика | Методы обучения | Средства обучения | Форма организации учебной деятельности |
1. | Учитель заходит в класс, приветствует учащихся. | Встают, приветствуют учителя. | ||||
2. | — Позвольте начать урок со слов Фалеса Милетского: «— Что есть больше всего на свете? – Пространство. — Что быстрее всего? – Ум — Что мудрее всего? – Время. — Что приятнее всего? – Достичь желаемого».(Слайд 1) Вспомните произведение Л. Керолла «Алиса в стране чудес». Какие изменения происходили с главной героиней: то она вырастала до нескольких футов, то уменьшалась до нескольких дюймов, всегда оставаясь, впрочем, сама собой. — О каком преобразовании с точки зрения геометрии идет речь? — А как вы думаете, где нам могут пригодиться знания о подобии фигур? — Какова будет тема нашего урока? (Слайд 2) | — О преобразовании подобия. — Для решения задач «Реальной математики» из ОГЭ и решения задач из жизни. — Использование подобия треугольников для решения задач практического содержания | ||||
3. | Повторим теоретический материал: — Какие фигуры называются подобными? — Признаки и свойства каких геометрических фигур, связанных с подобием, мы с вами изучали? — Какие треугольники называются подобными?(Слайд 3) — Сколько признаков подобия треугольников мы знаем? — Назовите признаки подобия треугольников — А теперь работаем в парах. На каждой парте лежат карточки, возьмите их . Нужно выбрать номера верных утверждений. | — Если они переводятся друг в друга преобразованием подобия. .- Треугольников — Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. — 3 признака — 1 признак: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны(Слайд 4). 2 признак: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то таике треугольники подобны.(Слайд 5) 3 признак: Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.(Слайд 6) Работая в парах с карточкой. — Выберите номера верных утверждений. 1. Отношение площадей подобных треугольников равно квадрату подобия. 2. 4. В подобных треугольниках медианы, биссектрисы, высоты и периметры пропорциональны с тем же коэффициентом. 5. Площадь треугольника равна половине произведения его катетов. Сравнивают ответы со слайдом. | Опрос | Фронтальная | ||
4. | Историческая справка Идея отношения и пропорции зародилась в глубокой древности. Уже в XVI в. нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». | Слайд(8, 9, 10) | ||||
5. | Класс разбивается на 7 групп, каждой группе дается лист А3 с заданием , необходимо оформить решение на листе, прикрепить лист к доске и пояснить решение. 1 группа. Определение высоты тела по зеркалу. Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до зеркала больше, чем расстояние от зеркала до вас. Помните: угол падения равен углу отражения (закон отражения). (Ответ: 13,5м). 3 группа. Определение высоты тела с помощью шеста с вращающейся планкой. Аналог метода – измерение высоты по тени. Что в солнечный день не составляет труда . Необходимо взять предмет (например, палку) известной длины и установить ее перпендикулярно поверхности. Тогда от предмета будет падать тень. Зная высоту палки, длину тени от палки, длину тени от предмета, высоту которого мы измеряем, можно определить высоту предмета. Этот способ был предметно описан у Жюля Верна в романе «Таинственный Остров». Этот способ можно применять, когда нет солнца и не видно тени от предметов. Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от предмета, чтобы лежа можно было видеть верхушку предмета на одной прямой линии с верхней точкой шеста. Тогда высоту предмета можно найти, зная длину линии, проведенной от вашей головы до основания предмета. (Ответ 24 м). 4 и 5 группы. Нахождение расстояния до корабля методом составления подобного треугольника с равными углами. (Ответ: 62,м и 48м). 6 группа. Измерение расстояния с помощью пальца. Если человек идет слева направо, зафиксировать его при закрытом левом глазе, тут же сменить закрытый глаз и зафиксировать человека правым, сосчитав количество шагов, которые он сделает до момента второй фиксации. 7 группа. Измерение расстояния при помощи травинки. Алгоритм изложен в приложении. (Ответ 240 шагов или 180 м). В ходе обсуждения затронуть вопросы техники выполнения необходимых измерений и удобства использования. | Работают сообща в группе. | Решение задач | Групповая | ||
5. | Самостоятельная работа (приложение) | Решают самостоятельно задания на карточках, сдают работы. | Групповая | |||
6. | Чем мы занимались на уроке? Что вам понравилось на уроке, а что нет? Где в жизни нам могут пригодиться знания и умения полученные на уроке? | Отвечают на вопросы в соответствии со своими ощущениями. | Индивидуальная | |||
7. | На доске записано домашнее задание. Дерево высотой 5,4 м стоит на расстоянии 14 шагов от дома, на котором установлен прожектор. Тень от дерева равна трём шагам. Какова высота дома в метрах (см. рис.)? | Открывают тетради и записывают задачу на дом. | Фронтальная |
Приложение №1
Памятка. Работа в паре и в группе. Повернись к соседу лицом. Говори шепотом. Слушай внимательно, молча и не перебивай. Работайте сообща. Вывод делайте вместе. |
Определение высоты дерева с помощью зеркала.
Запишите формулу для нахождения и найдите высоту дерева, если расстояние до дерева от человека 10м, а до зеркала – 1м. Человек этот — вы.
Какие треугольники подобны и почему?
Сделайте необходимые измерения (размер головы равен размеру стопы, глаза располагаются посередине головы).
Вынесите данные на чертеж.
Чему равен коэффициент подобия?
Чему равна высота дерева?
Определение высоты скалы по методу Жюля Верна.
Определите высоту объекта, если высота планки 1м, расстояние от головы до планки – 2м, а до основания скалы – 50м.
Какие треугольники подобны и почему? Обозначьте их буквами.
Вынесите данные на чертеж.
Чему равен коэффициент подобия?
Найдите высоту скалы.
Определение высоты дерева с помощью шеста с вращающейся планкой.
Запишите формулу для нахождения и найдите высоту дерева, если расстояние до дерева от шеста 10м, а до точки В – 1м.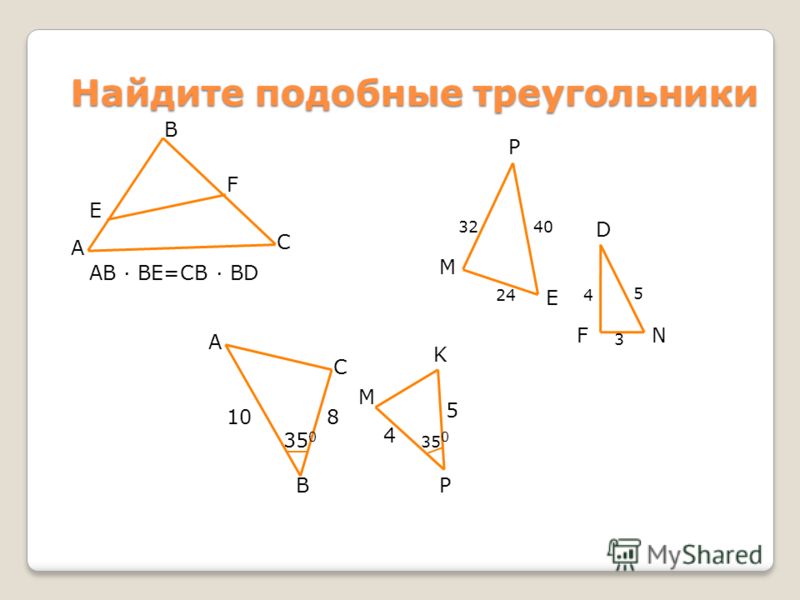 Высота шеста – 1,5 м.
Высота шеста – 1,5 м.
Выполните дополнительное построение.
Какие треугольники подобны и почему?
Вынесите данные на чертеж.
Чему равен коэффициент подобия?
Чему равна высота дерева?
Определение расстояния до недоступного объекта.
Найдите расстояние до корабля, если углы при основании треугольников одинаковы и основания равны 3,2 см и 80м.
Обозначьте треугольники.
Докажите их подобие.
Вынесите данные на чертеж.
Выполните дополнительное построение.
Сделайте дополнительные измерения.
Чему равен коэффициент подобия?
Запишите формулу для нахождения расстояния до корабля.
Найдите это расстояние.
Определение расстояния до недоступного объекта.
Найдите расстояние до корабля, если основания равны 60 м и 3 см, а левый угол при основании большого треугольника равен правому при основании углу малого.
Обозначьте треугольники.
Докажите их подобие.
Вынесите данные на чертеж.
Выполните дополнительное построение.
Сделайте дополнительные измерения.
Чему равен коэффициент подобия?
Выполните дополнительное построение.
Запишите формулу для нахождения расстояния до корабля.
Найдите это расстояние.
Определение расстояния до объекта с помощью пальца.
Обозначения к рисунку: П — правый глаз наблюдателя, Л — левый глаз наблюдателя, Р — вытянутая рука с большим пальцем, А — начальная точка, определяется прямой линией от правого глаза наблюдателя через палец, Б — конечная точка, определяется прямой линией от левого глаза наблюдателя через палец.
Расстояние между глазами – 6 см
Расстояние вытянутой руки – 60 см
Для перевода шагов в метры их количество надо умножить на ¾.
Вынесите данные на чертеж.
Докажите подобие треугольников.
Запишите формулу для нахождения расстояния, пройденного объектом.
Запишите формулу для нахождения расстояния до объекта.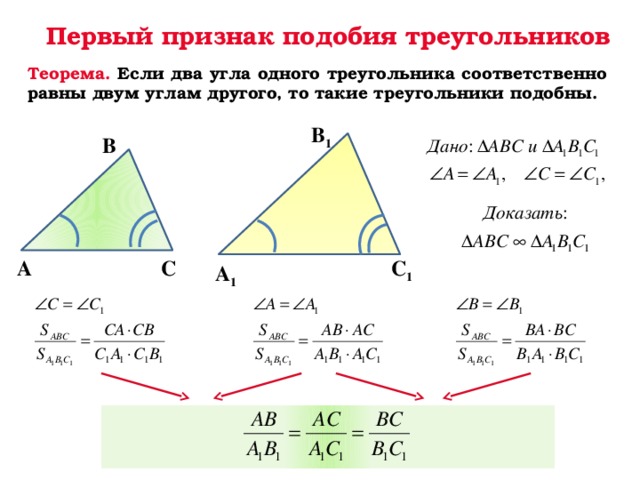
Составьте план действий, для нахождения расстояния.
Чему равно пройденное расстояние, если объект прошел 50 шагов?
Определение расстояния до объекта с помощью травинки.
Алгоритм:
Взять травинку подлиннее, сложить ее вдвое.
Сложенной травинкой визуально закрыть расстояние между двумя выбранными точками, расположенными в области нужного объекта.
Если сложенная травинка закрывает выбранный вами промежуток с излишком, то лучше оторвать лишнюю часть.
Затем нужно развернуть травинку в длину.
Приближайтесь к объекту, двигаясь перпендикулярно к выбранному промежутку. Время от времени следует останавливаться и смотреть на упомянутый отрезок сквозь развернутую травинку.
Остановитесь в тот момент, когда развернутая в длину травинка полностью закроет промежуток АБ. Это значит, что человек находится на полпути от первоначального места, откуда было начато измерение.
Измерить пройденную часть пути. Полученное значение будет равно половине расстояния до объекта. То есть пройдено и оставшееся расстояние до объекта равны.
Объясните алгоритм:
Введите обозначения на чертеже.
Докажите подобие треугольников.
Выполните дополнительное построение.
Выполните дополнительные измерения.
Чему равен коэффициент подобия?
Запишите формулу для нахождения расстояния.
Решение геометрических задач ОГЭ по теме «Подобие треугольников» | Учебно-методический материал по математике (9 класс):
Технологическая карта
Данилина Галина Алексеевна
учитель математики МБОУ СОШ №4 город Льгов
Уровень образования: общеобразовательный класс
Тема: Решение геометрических задач ОГЭ по теме «Подобие треугольников»
Тип урока: урок обобщения и систематизации знаний
Форма проведения урока: фронтальная, индивидуальная, парная.
Время проведения: 14 ноября
Участники: учащиеся 9 класса МБОУ СОШ №4 г. Льгов.
Льгов.
Цель: — образовательные: применение подобия треугольников при проведении измерительных работ на местности, взаимосвязи теории с практикой; ознакомление учащихся с различными способами определения высоты предмета и расстояния до недоступного объекта; формирование умения применять полученные знания при решении разнообразных задач данного вида.
-воспитательные: повышение коммуникативной активности учащихся, создание благоприятных условий для проявления индивидуальности, выбора своей позиции, формирование умения аргументировано отстаивать свою точку зрения.
развивающие:
— Регулятивные УУД: умение оценивать правильность выполнения действия на уровне адекватной оценки; проговаривать последовательность действий на уроке; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
— Коммуникативные УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
— Познавательные УУД: умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;
добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Планируемый результат обучения, в том числе и формирование УУД:
Личностные: уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные: работа над понятием информация-знание; развивать познавательную деятельность учащихся.
Предметные: понимать, что такое подобие, отношение, пропорция,уметь использовать данные понятия при решении стандартных заданий.
Познавательные УУД: умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение.
Коммуникативные УУД: умение находить общее решение и решать конфликты на основе согласования позиций и учета интересов.
Регулятивные УУД: умение адекватно оценивать правильность или ошибочность выполнения учебной задачи.
Личностные УУД: способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Основные понятия: подобие, признаки подобия, пропорция, отношение, площадь треугольника, равновеликие фигуры.
Межпредметные связи: математика
Ресурсы: Геометрия, 8 класс ( базовый учебник – Погорелов А. В., Геометрия 7-9 классы,- М.: Просвещение, 2010)
омпьютер, проектор, презентация подготовленная учителем, ЦОР из Единой коллекции,раздаточный материал, детские игрушки, посуда.
Технологическая карта урока
Содержание учебного материала. Деятельность учителя | Деятельность обучающихся | ФОУД | Формирование УУД |
1-й этап. Организационный. Цель этапа: настроить учащихся к учебной деятельности. | |||
| Активное слушание, взаимодействие с учителем. | Ф | П. Формулирование собственных ожиданий. Р. Проявление эмоционального отношения в учебно-познавательной деятельности. |
2-й этап. Актуализация знаний. Цель этапа: актуализировать мыслительные операции. | |||
Организует устную фронтальную работу, демонстрирует задания с использованием слайдовой презентации. Постановка проблемы: Выявить связь между геометрическими представлениями подобия и алгебраическими вычислениями(ориентированное на ОГЭ) | Взаимодействуют с учителем во время опроса, участвуют в принятии решений. Выявляют место затруднения. Проговаривают причину. Работали активно, все были включены в работу. | Ф И | П. Учатся извлекать информацию из иллюстраций, умение формулировать проблему. К. Учатся слушать, вести диалог в соответствии целями и задачами общения. Р. Умение слушать в соответствии с целевой установкой, дополнять, уточнять высказанные мнения. Л. Осуществляют актуализацию личного жизненного опыта. |
3-й этап. Изучение нового материала. Цель этапа: рассмотреть решение геометрической задачи на подобие треугольников алгебраическим методом. | |||
1. Организует исследование. Вспомним, основную теорию 2.Организует проверку анализа и вывода гипотез | Выполняя задания в соответствии с этим планом, ученики все промежуточные действия и конечные выводы записывают в тетради. Взаимодействуют с учителем, записывают в тетради информацию из лекции. Работали активно, все были включены в работу. | ФИ | П. Самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации, осознанное построение речевого высказывания в устной и письменной форме. К. Планирование учебного сотрудничества с учителем и сверстниками, умение полно и точно выражать свои мысли. Р. Постановка учебной задачи на основе соотнесения того, что уже известно и усвоено, и того, что ещё неизвестно. Прогнозирование, контроль, коррекция, саморегуляция. Л. Постепенное накопление учащимися информации (от простого к сложному), установление связи между целью учебной деятельности и её мотивом. |
4-й этап. Первичная проверка и понимание изученного. Цель этапа: рассмотреть применение алгебраического метода при решении геометрических задач на подобие треугольников | |||
Давайте закрепим полученную информацию на практике. Устно выполнить предложенные задания | Ответы учащихся (устная работа) Работа с учебником. Работали активно, все были включены в работу. | Ф | П. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. К. Планирование учебного сотрудничества с учителем и сверстниками, умение полно и точно выражать свои мысли. Р. Прогнозирование, контроль, коррекция, саморегуляция. |
5-й этап. Физкультминутка. Цель этапа: предупреждение утомляемости учащихся. | |||
Проводит физкультминутку. (презентация) | Выполняют гимнастику. | ||
6-й этап. Закрепления и применения изученного. Цель этапа:при решении задач отработать применение полученных навыков | |||
Организует решение упражнений, выбранных из тестов подготовки к ОГЭ
| Обсуждение задач в группах. Демонстрация решения. Работали активно. | Ф И | П. Выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Осознанное построение речевого высказывания в устной и письменной форме; построение логической цепочки рассуждений. К. Умение с достаточной полнотой и точностью выражать свои мысли. Р. Прогнозирование, контроль, коррекция, саморегуляция. Л. Личностное самоопределение, установление обучающимися связи между целью учебной деятельности и её мотивом (смыслообразование), оценивание усваиваемого содержания. |
7-й этап. Применение знаний в новой ситуации . Цель этапа: умение применить знания в новой ситуации. | |||
Обучающимся предлагаются задания из вариантов ОГЭ для работы в парах. Учитель демонстрирует слайды презентации, координирует работу обучающихся, консультирует их. Решение задач на клетчатой бумаге. | Выстраивают систему аргумен-тов для убеждения, продумыва-ют ответы и обсуждают их с соседом по парте. Сравнивают свое решение с образцом, находят и исправляют ошибки. Все были включены в работу. | П И | П. Развитие и углубление потребностей и мотивов учебно-познавательной деятельности. К. Взаимодействуют с соседом по парте, учитывают позицию собеседника, осуществляют сотрудничество и кооперацию с учителем и одноклассником. Р. Оценивают предложенные варианты, выбирают наиболее точный. Происходит восприятие, осмысление, запоминания материала. |
8-й этап. Итогово-оценочный. Цель этапа: организовать целостное осмысление и обобщение полученной информации, проведение самооценки учениками работы на уроке. | |||
1. Мотивирует обучающихся к самоанализу деятельности и проектированию дальнейшего продвижения в изучении темы. 2. Объявляет свою оценку и обосновывает ее. Делает рекомендации. 3. Предлагает и объясняет домашнего задания. | Участвуют в беседе по обсуждению достижений, отвечая на вопросы учителя, делают выводы. Оценивает каждый сам себя. Записывают задания. | Ф | П. Самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации. К. Умение с достаточной полнотой и точностью выражать свои мысли. Разрешение конфликтов. Р. Прогнозирование, саморегуляция. Л. Личностное самоопределение, смыслообразование. |
9-й этап. Рефлексия учебной деятельности. | |||
Организует рефлексию и самооценку учениками собственной учебной деятельности. Продолжите фразы: «Сегодня на уроке я узнал…» «Мне было труднее всего…» «Самым полезным для меня было…» | Отвечают на вопросы учителя. Делают самооценку Все были включены в работу. | Ф | П. Поиск и выделение необходимой информации, построение речевого высказывания в устной форме. Анализ и синтез информации. К. Умение полно и точно выражать свои мысли. Разрешение конфликтов. Р. Прогнозирование, саморегуляция. Уметь оценивать правильность выполнения действия на уровне адекватной оценки. Л. Нравственно-этическая ориентация, в том числе, и оценивание усваиваемого содержания. Способность к самооценке на основе критерия успешности учебной деятельности. |
ФОУД – форма организации учебной деятельности обучающихся (Ф – фронтальная, И – индивидуальная, П – парная, Г – групповая).
Работа обучающихся на уроке (указать активность, меру занятости): обучающиеся работали активно, все были включены в работу.
Дифференциация и индивидуализация обучения (подчеркнуть): присутствовала/отсутствовала.
Оценка достижения целей урока: урок достиг поставленных целей.
Примечание
Сокращения, используемые в столбце формируемые УУД (универсальные учебные действия):
П – познавательные
Л – личностные
К – коммуникативные
Р – регулятивные
NCERT Solutions for Class 9 Math Chapter 1
- Решения НЦЭРТ
- Класс 9
- Математика
- подобные треугольники
NCERT Solutions for Class 9 Math Глава 1 Подобные треугольники представлены здесь с простыми пошаговыми объяснениями.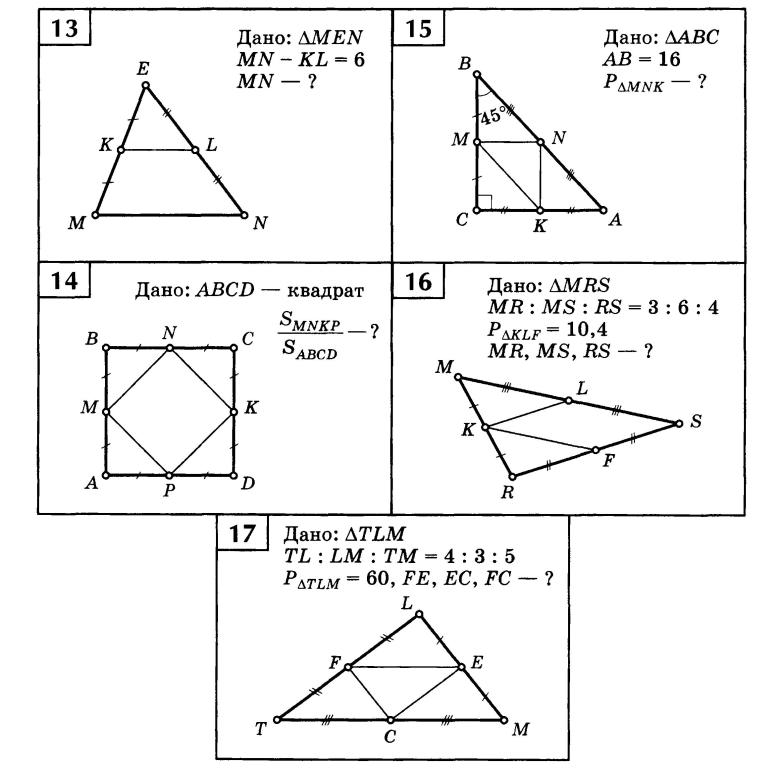 Эти решения для похожих треугольников чрезвычайно популярны среди учащихся 9 класса по математике. Решения для похожих треугольников пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги NCERT по математике для 9-го класса, глава 1, предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы в решениях NCERT от Meritnation. Все решения NCERT для класса Class 9Математика подготовлена экспертами и на 100% точна.
Эти решения для похожих треугольников чрезвычайно популярны среди учащихся 9 класса по математике. Решения для похожих треугольников пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги NCERT по математике для 9-го класса, глава 1, предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы в решениях NCERT от Meritnation. Все решения NCERT для класса Class 9Математика подготовлена экспертами и на 100% точна.
Страница № 133:
Вопрос 1:
В треугольнике проведена линия, параллельная одной стороне, и отрезан маленький треугольник.
Докажите, что отсеченный треугольник подобен исходному треугольнику.
Ответ:
Дано: Δ ABC и, Δ AEF , что отсечено от Δ ABC
Также,
0033 EF параллелен BC .
AS EF является параллельностью BC , AEF AEF = тий ABC и тий AFE = ♂ ACB (ROPECT = RT ACB (ROPECTING = RET (AFE = REM (AFE = секрет . ABC :
ABC :
тий AEF = тий ABC (подтверждено выше)
тий AFE = тий (Доказано выше)
4 (Доказано выше)
4 (доказано.0033 BAC (Общий)
Поскольку все углы треугольника равны углам другого треугольника, оба треугольника подобны.
Таким образом, отрезанный треугольник подобен исходному треугольнику.
Страница № 133:
Вопрос 2:
В первой задаче, если параллельная линия проведена через середину одной стороны, то какая часть площади исходного треугольника составляет площадь треугольника? маленький треугольник?
Ответ:
Дано: Δ ABC и Δ AEF , что отсечено от Δ ABC
Кроме того, EF 3 4 параллельно 9003.
AS EF параллельна до н.э. и Δ ABC :
∠ AEF = тий ABC (подтверждено выше)
тий AFE = тий ACB (Доказано выше)
тий EAF = AND ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( (. треугольника равны углы другого треугольника, оба треугольника подобны.
треугольника равны углы другого треугольника, оба треугольника подобны.
Мы знаем, что если два треугольника подобны, то соответствующие стороны треугольников пропорциональны.
E и F являются средними точками AB и AC соответственно.
⇒ AE = EB и AF = FC
Давайте нарисовать перпендикулярный от A до EF и BC , до , , , , , , , до . соответственно.
Теперь в Δ ADF и Δ AKC :
∠ ADF = ∠ AKC = ∠ AKC =0 ° (по строительству)
тий AFAM = тий ACK (Соответствующие углы)
тий DAF = тий kac (Common)
All Trians углам другого треугольника оба треугольника подобны. Мы знаем, что если два треугольника подобны, то соответствующие стороны треугольников пропорциональны.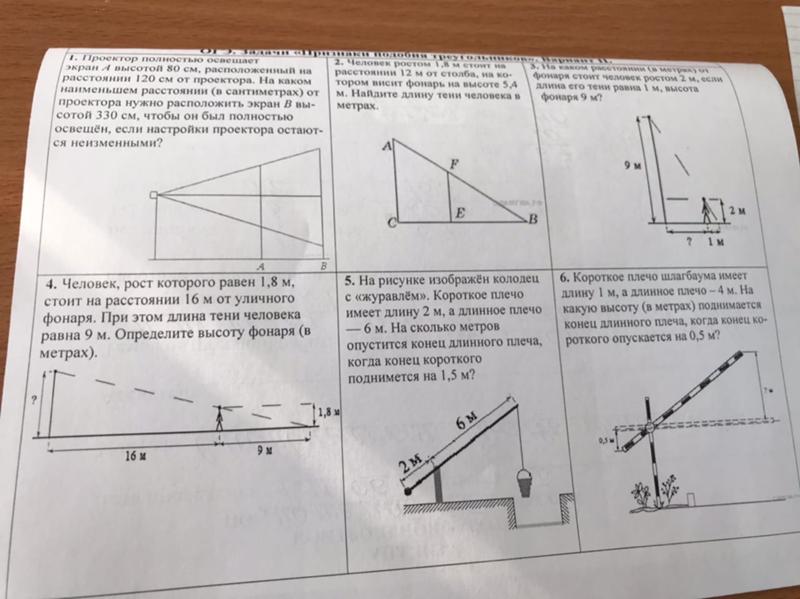
Кроме того, AF = FC (как F is the midpoint of AC )
Area of Δ ABC =
Area of Δ AEF =
∴ Area of Δ ABC = 4 × Area of Δ AEF
Страница № 133:
Вопрос 3:
На рисунке ниже, стороны двух треугольников параллель:
Профилируют, что они являются схожими
.
Дано: Δ ABC и Δ DEF с AB || ДЭ , АС || DF и EF || до н.э.
T ABC = тий DEF , тий BAC = T EDF и секре
и секре и секре . и секре . . ABC и Δ DEF :∠ ABC = ∠ DEF (доказано выше)
тий BAC = ♂ EDF (доказано выше)
тий ACB = ♂ DFE (Доказано выше)
, как All All the All The All the All the All the All the All the All the All Triamles as All All the All the All the Angles другой треугольник, оба треугольника подобны.
Страница № 139:
Вопрос 1:
Окружности, показанные ниже, имеют один и тот же центр O.
Докажите, что ΔΔOAB подобны.
Answer:
In Δ OAB :
OA = OB (Radii of the small circle)
⇒ ∠ OBA = ∠ OAB (Angles opposite to equal sides по меру равны)
Аналогично, OQ = OP (радиусы большего круга)
⇒ тий OPQ = тий OQP
Использование Свойства угла в Δ OQP
. Свойство угла в Δ OQPQ :
. ОКП + тий QPO + тий POQ = 180 °
⇒ om POQ = 180 ° — потряк — Sum — OAB :
T OBA + RT BAO + тий AOB = 180 °
⇒ Dom AOB = 180 ° – − R aob = 180 ° – − R aob = 180 ° – −. = 180 ° – R = 180 ° . )
= 180 ° – R = 180 ° . )
As ∠ AOB = ∠ POQ , из (1) и (2) имеем:
180 ° — тий OQP — тий QPO = 180 ° — тий — тий BAO
⇒ OQP + QP
⇒ OQP + QP + QP + QP + QPP + QP + QP
⇒P OQP
⇒P OQP .
As ∠ OBA = ∠ OAB and ∠ OPQ = ∠ OQP
⇒ 2∠ OQP = 2∠ OBA
⇒ ∠ OQP = ∠ OBA
Аналогично, ∠ OAB = π OPQ
Сейчас в Δ OAB и Δ OPQ :
тий OAB = тий OPQ (Довольно выше)
(Докашено выше) . выше)∠ AOB = ∠ POQ (общий)
Поскольку все углы треугольника равны углам другого треугольника, оба треугольника подобны.
Страница № 139:
Вопрос 2:
Докажите, что четыре треугольника, полученные путем соединения середины треугольника, конгруэнтны и подобны исходному треугольнику.
ОТВЕТ:
Дано: D , E и F — средние точки по бокам BC , CA 44333334. .
∴ BD = DC = , AE = EC = , AF = FB = …(1)
Так как отрезок DE проходит через середины сторон BC и AC , то DE параллелен 3 0 4 DE 4 AB и 4 AB .
⇒ DE = AF = FB … (2)
в CDE и Δ DBF :
DC = 4:
DC = 4 (
DC = 4 (
DC = 4 (
. CDE = ∠ DBF (Соответствующие углы)
BF = DE (Из уравнения (2))
Поскольку сторона, угол и сторона одного треугольника равны соответствующим стороне, углу и стороне другого треугольника, Δ CDE ≅ Δ DBF .
Аналогично, Δ FBD , Δ DEF и Δ AFE конгруэнтны друг другу.
Теперь в Δ DCE и Δ BCA :
∠ CED = ∠ CAB (Corresponding angles)
∠ CDE = ∠ CBA (Corresponding angles)
∠ ECD = ∠ ACB (Common angles)
As all the angles треугольника равны углам другого треугольника, оба треугольника подобны.
Аналогично, Δ BDF , Δ FEA и Δ EFD аналогичны Δ BCA .
Таким образом, четыре треугольника, полученные путем соединения середины треугольника, конгруэнтны и подобны исходному треугольнику.
Страница № 139:
Вопрос 3:
Докажите, что, соединив середины любого четырехугольника, мы получим параллелограмм.
ОТВЕТ:
Дано: a Quadrillatoral ABCD с P , Q , R и S AS , RA и S AS AS , RA и S AS AS , RA и S 333333333333333 годы 333333333.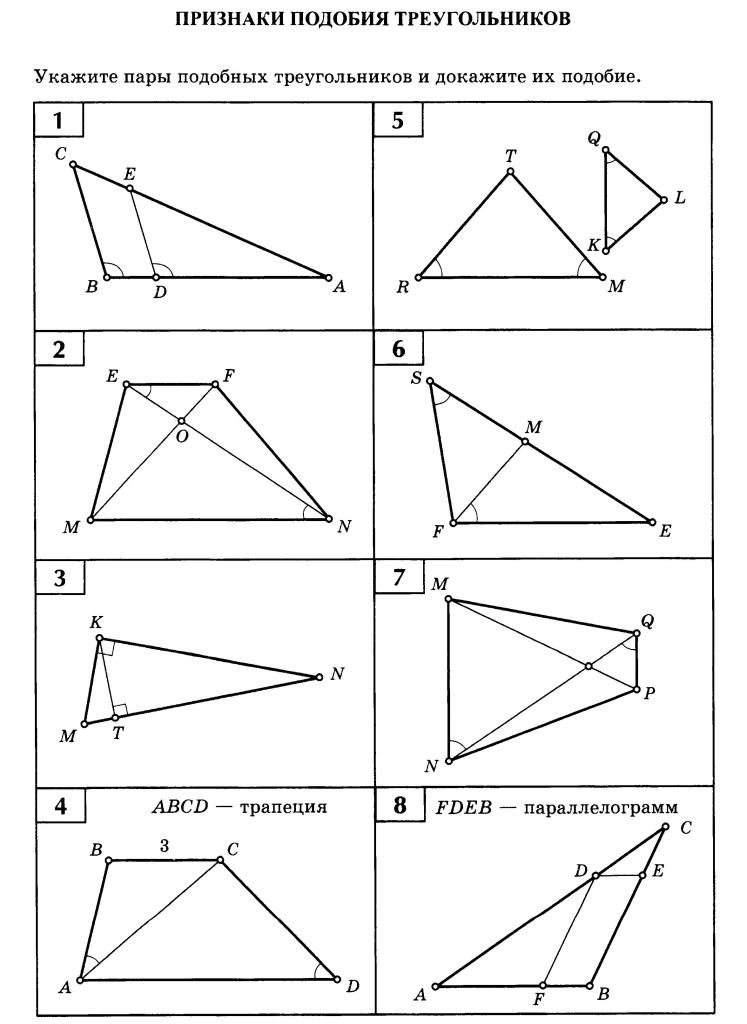 BC и CD
BC и CD
In Δ ABD , P и Q являются серединами сторон AD и AB соответственно.
⇒ PQ || DB и PQ = …(1)
Аналогично, в Δ CBD , R и S являются серединами сторон CB и CD 90 соответственно.
⇒ RS || BD и RS = …(2)
Из уравнения (1) и (2) имеем:
PQ || SR и PQ = SR
Аналогично, PS || QR и PS = QR
Таким образом, противоположные стороны четырехугольника PQRS равны и параллельны.
Следовательно, PQRS является параллелограммом.
Отсюда можно сказать, что, соединив середины сторон любого четырехугольника, мы получим параллелограмм.
Страница № 139:
Вопрос 4:
В последней задаче для какого четырехугольника мы получим прямоугольник, соединив его середины?
Ответ:
Соединив середины сторон ромба, получим прямоугольник.
Страница № 140:
Вопрос 1:
На рисунке ниже G является центром тяжести ΔABC.
Докажите, что треугольники AGB, AGC, BGC имеют одинаковую площадь.
Ответ:
Дано: G является центром тяжести Δ ABC .
Построение: Продолжить AG так, чтобы он пересекал BC в точке D .
в Δ ABD и Δ ACD :
BD = DC (AS AD — это средний из треуульянга),
, а также высота.
∴ Площадь Δ ABD = × Высота × BD
= × Height × DC
= Area of Δ ACD
Area of Δ ABD = Area of Δ ACD …(1)
Now, in ΔGBD and ΔGCD:
BD = DC (Поскольку AD является медианой треугольника)
Кроме того, высота обоих треугольников равна.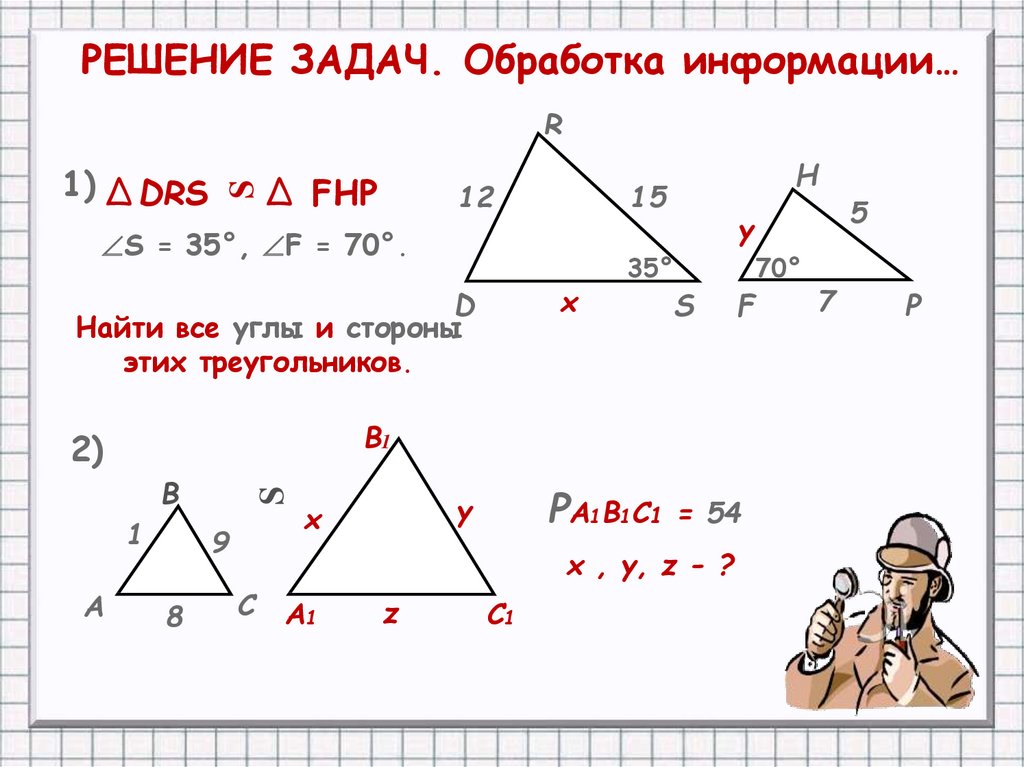
∴ Площадь Δ GBD = × Высота × BD
= × Высота × DC
= Площадь Δ НОД
Площадь Δ ГБД = Площадь Δ НОД …(2)
Вычитание уравнения (2) из уравнения (1):
Площадь Δ 9 ГБД = Площадь Δ ACD — Площадь Δ GCD
⇒ Площадь Δ AGB = Площадь Δ AGC
Аналогично, площадь AGB =
аналогично, площадь AGB =
, Аналогичная область AGB =
, AGB =
, AGB =
.
⇒ Площадь Δ AGB = Площадь Δ GBC = Площадь Δ AGC
Номер страницы 140:
Вопрос 2:
Докажите, что в треугольнике прямая, делящая две стороны пропорционально, параллельна третьей стороне.
Answer:
Given,
⇒
⇒
⇒
⇒
⇒
In Δ ABC and Δ ADE :
∠ A = ∠ A (общий угол)
Если один угол треугольника равен одному углу другого треугольника и стороны, включающие эти углы, пропорциональны, то эти два треугольника подобны.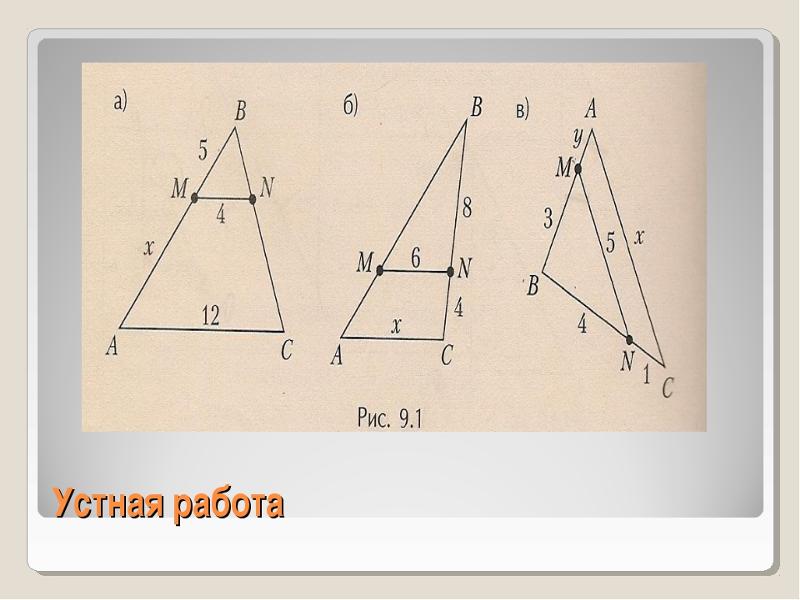
⇒ Δ ABC Δ ADE
∴ тий ABC = ϩ ADE
по конверсу соответствующих угловых аксевых аксов,
по конверсу соответствующих угловых,
. DE
Таким образом, в треугольнике линия, пропорционально делящая две стороны, параллельна третьей стороне.
Куллабс
регистр Логин
Найдите свой запрос
Обзор
\(\треугольник\)ABC и \(\треугольник\)XYZ похожи, т.е. \(\треугольник\)ABC и \(\traingle\)XYZ имеют одинаковую форму, но разные размеры. Если любые два угла равны друг другу, то они подобны.
- Примечание
- То, что нужно запомнить
- Видео
- Упражнение
- Контрольный опрос
Сходство
Условия для сходства треугольников
Существует три условия для сходства треугольных Если два угла одного треугольника соответственно равны двум углам другого треугольника, то два треугольника подобны.
Например:
Здесь ∠B = ∠Y и ∠C = ∠Z. Остальные углы ∠A и ∠X также равны.
∴ \ (\ Triangle \) ABC~ \ (\ ТРЕЙОНГЛИ \) XYZ
II) Сторона, сторона, тест сходства
1111111111111111111111111111111111111111111111111111111111111111111111111111111111111. НЕОБ
Если соответствующие стороны двух треугольников пропорциональны, то треугольники подобны.
Например:
Здесь PQ/XY = QR/YZ = PR/XZ
∴ \(\треугольник\)PQR∼ \(\треугольник\)XYZ
III) Сторона, угол, боковый тест сходства
Рис.: SAS
, а также Andly, Anderse Antrienge Antry. эти стороны равны, то треугольники подобны.
Например:
Здесь XY/AB = YZ/BC и ∠Y =∠B
∴ \(\треугольник\)XYZ∼ \(\треугольник\)ABC
Подобные многоугольники
Два многоугольника подобны при следующих условиях:
i) Когда два или более многоугольника равноугольные, они подобны.
На рисунке, ♂ = Ϫp, ♂ = ♂, ♂ = ♂, ♂ = ♂
∴ Quad ABCD Quad PQRS
II) 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 соответствующие стороны двух многоугольников пропорциональны, они подобны.
На рисунке AB/PQ = BC/QR = CD/RS = DA/SP
∴ четверка ABCD∼ четверка PQRS
iii) Когда соответствующие диагонали многоугольников пропорциональны их соответствующим сеям, они подобны.
На рисунке, AC/PR = BD/QS = AB/PQ
∴ Quad ABCD -Quad PQRS
IV). одинаковое количество подобных треугольников, многоугольники равны.
\(\треугольник\)ABC~ \(\треугольник\)PQR, \(\треугольник\)ACD~ \(\треугольник\)PRS, \(\треугольник\)ADE~ \(\треугольник\) PSV
∴ многоугольник ABCDE∼ многоугольник PQRS
Примечание: Теоремы со знаком ‘*’ в главе о подобии не требуют доказательства или экспериментальной проверки, но связанные с ними задачи включены в учебную программу.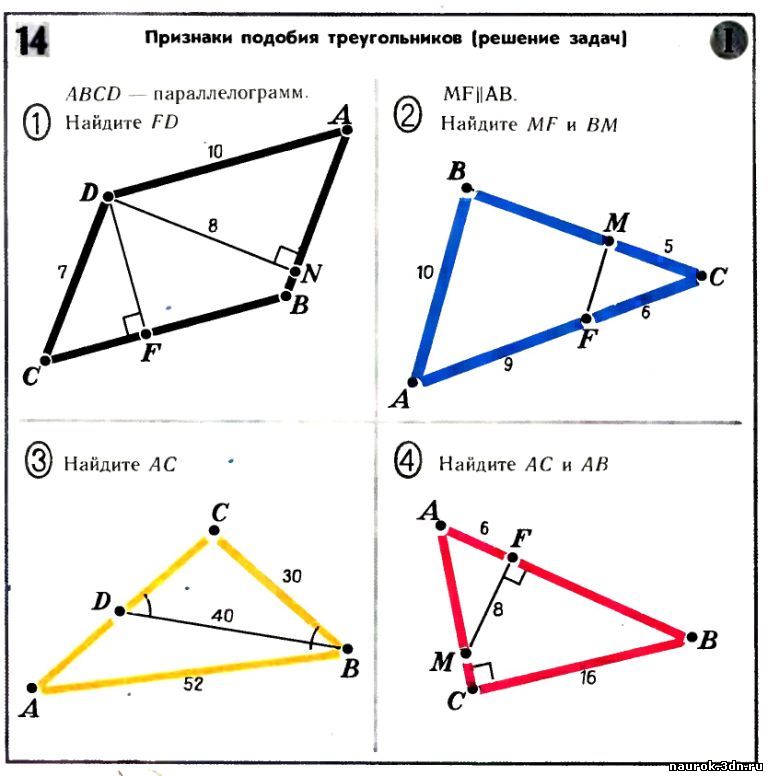
Что следует помнить
- Два геометрических объекта называются подобными, если они оба имеют одинаковую форму или один имеет такую же форму, как зеркальное отражение другого. Точнее, одно можно получить из другого путем равномерного масштабирования (увеличения или уменьшения), возможно, с дополнительным переносом, поворотом и отражением.
- Включает в себя все отношения, установившиеся между людьми.
- В обществе может быть более одного сообщества. Сообщество меньше, чем общество.
- Это сеть социальных отношений, которую нельзя увидеть или потрогать.
- общие интересы и общие цели не нужны обществу.
Видео для сходства
Вопросы и ответы
| Утверждения | Основания |
1. В АВЕ и АКД В АВЕ и АКД (i) АБЭ = АКД (ii) БЕА = АКД (iii) АБЭ ~ АКД | 1; БЫТЬ || CD. (ii) соответствующие углы; БЫТЬ || CD. (iii) По подобию A.A |
| 2. \(\frac{AC}{AB}\) = \(\frac{CD}{BE}\) или , \(\frac{x + 4}{4}\) = \(\frac{3}{2}\) или , 2x + 18 = 12 э.э., 2x = 12 — 8 = 4 \ (\следовательно\) \(\frac{4}{2}\) = 2 см. | 2. В подобных треугольниках ACD и ABE соответствующие стороны пропорциональны. |
| 3. \(\frac{AD}{AE}\) = \(\frac{CD}{BE}\) или , \(\frac{y + 3}{y}\) = \ (\frac{8.1}{5.4}\) или , \(\frac{y + 3}{y}\) = \(\frac{3}{2}\) или , 2y + 6 = 3y или , 6 = 3y — 3y \(\поэтому\) y = 6 см. | 3. Из утверждения (2). |
Здесь, в ОЛН и ЛПМ
| 1. ЛНО = ЛПМ | 1. Из дан. |
| 2. OLN = PLM | 2. Общий угол. Общий угол. |
| 3. OLN ~ LPM | 3. Два равноугольных треугольника подобны. |
| 4. \(\frac{LN}{LP}\)= \(\frac{LO}{LM}\) или , \(\frac{LM + MN}{LP}\) = \ (\frac{LP + PQ}{LM}\) или , \(\frac{5 + MN}{6}\) = \(\frac{6 + 1}{5}\) = \(\frac{7}{5}\) или , 25 + 5MN = 42 или , 5MN = 42 — 25 = 17 \(\следовательно\) MN = \(\frac{17}{5}\) = 3,4 см | Соответствующие стороны подобных треугольников пропорциональны. |
| (i) CEA = CBD | Дано |
| (ii) ACE = BCD | Общий угол |
| (iii) CAE = BDC | Остаточный угол |
| (iv) AEC~BDC | По подобию A.A.A |
| (v) \(\frac{CE(\}{BC})\ frac{CA}{CD}\) или ,\(\frac{ED + 5}{6}\) =\(\frac{3 + 6}{5}\) или ,\(\frac{ED + 5}{6}\) =\(\frac{9}{5}\) или , ED + 5 =\(\frac{54}{5}\) или , ED = 10,8 -5 = 5,8 см | Будучи AEC ~ BDC |
Здесь , DCO и OAB
1. CDO = OBA CDO = OBA | 1. Будучи DC || AB , DB — поперечные и перекрестные углы. |
| 2/ DCO = OAB | 2. Будучи DC || АВ, АС — поперечные и противоположные углы. |
| 3/ DCO ~ OAB | 3. По сходству A.A.A |
| 4. \(\frac{AB}{DC}\) =\(\frac{BO}{OD}\) или \(\frac{x}{3}\) =\(\frac{5}{2}\) или , x =\(\frac{15}{2}\) = 7,5 x = 7,5 см | 4. Соответствующие стороны подобного треугольника пропорциональны |
Здесь р = 7см, b = 5см, h= ? Мы знаем, что sqrt{74}\) = 8,6 см Ans.
Здесь h = 13см, p = 8см, b = ?
We know that ,
p 2 + b 2 = h 2
or , 8 2 + b 2 = 13 2
or , b 2 = 13 2 — 8 2 = 169 — 64 = 105
b = \(\sqrt{105}\) = 10,25 см Анс.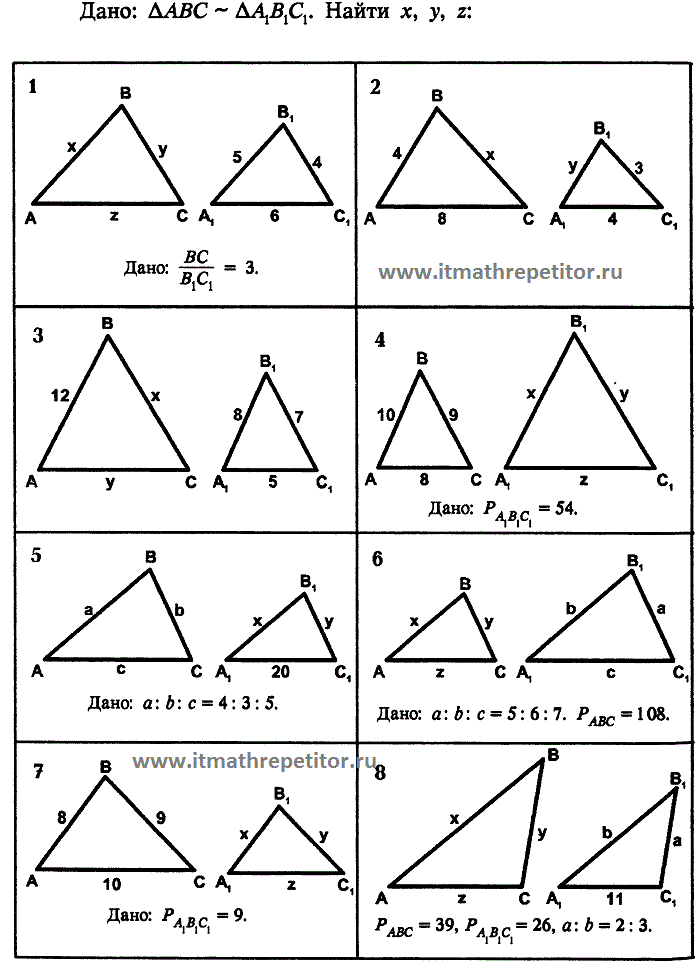
Здесь , GH 2 + HI 2 = GI 2
или , GH 2 + 24 2 = 252
или , GH 21079 = 25 2 — 242
или , GH 2 = 625 — 57
или , GH 2 = 625 — 576
или , GH 2 = 4 = 1 39 }\) = 7 см
В данном прямоугольнике ABCD , AB = 12 см, BC = 8 см, диагональ (AC) = ?
В рт. угловой треугольник ABC
AC 2 = AB 2 + BC 2
или , AC 2 = 12 2 + 8 2 = 144 + 64
= 208
Диагональ AC = \(\sqrt{208}\) = 14,42 см
В квадрате ABCD, BC = 6 см, AB = 6 см, диагональ (AC) =?
В рт. угловой треугольник ABC ,
или , AC2 = 62 + 62 = 36 + 36 = 72
диагональ AC = \(\sqrt{72}\) =\(\sqrt[6]{2}\) = 8,48 см.

В прямоугольнике ABCD, AB = 8 см, диагональ AC = 12 см, BC = ?
В рт. angled triangle ABC
AB 2 + BC 2 = AC 2
or , 8 2 + BC 2 = 12 2
or , BC2 = 12 2 — 8 2 = 144 — 64 = 80
или , BC = \(\sqrt{80}\) = 8,94 см Ans.
Предположим, что АВ — телефонный столб, а СА — провод.
Здесь CB — расстояние по перпендикуляру от веревки, закрепленной на земле C, до стойки AB.
Здесь AB = 7 м и AC = 7,6 м
Теперь в прямоугольном треугольнике ABC
или , 7 2 7 7 9 9 9 0 7 7 7 BC 2
или , BC2 = 7,6 2 — 7 2 = 57,76 — 49 = 8,76
\(\следовательно\) BC = \(\sqrt{8,76}\) = 2,96 м Анс.
В прямоугольнике ABCD ,
Длина (АВ) = 5,1 см, диагональ (АС) = 6,1 см и ширина (ВС) = ?
Здесь , в rt., угловой треугольник ABC ,
(5.1) 2 + (BC) 2 = (6.1) 2
или , BC 2 = (6.1) 9 — (5.079) 2
или , BC 2 = 37,21 — 26,01 = 11,2
\(\следовательно\) BC = \(\sqrt{11,2}\) = 3,35 см
Площадь прямоугольника ABCD = длина \(\times\) ширина = 5,1 \(\раз\) 3,35 см 2
= 17,085 см 2
В DEF, EF = 12 см, DE = 9 см, AD = ?
В рт. Угловой треугольник def, используя теорему Pythagoras,
DF 2 = EF 2 + DE 2
OR, DF 2 = 12 2 + 2

Теперь , в rt. угловой треугольник ADF,
AF = 8 см, DF = 15 см, DA = ?
Здесь, в АПД,
DA 2 = DF 2 + AF 2
или , x 2 = 15 2 + 8 2
или , x 2 = 225 + 64
\(\следовательно\) x = \(\sqrt{289}\) = 17см.
В JHI, HI = 5 см, JI = 2 см, HJ =?
JH 2 = HI 2 + JI 2
OR, JH 2 = 5 2 + 2 2
или, JH 2 9 \ \1313 \1313 \ 23 \ 23 \ 23 \ 23 \ 23 \ 213 \ 2 \ 2
или, JH 2 \ \ \ \ = 29119. \) JH = \(\sqrt{29}\) см.
Опять же,
HG2 = JH 2 + GJ 2
или , HG 2 = (\(\sqrt{29}\) ) 2 + 32
или , HG 2 = 29 + 12 = 138 38 \(\sqrt{38}\) 6,16
\(\следовательно\)x = 6,16 см Ответ.





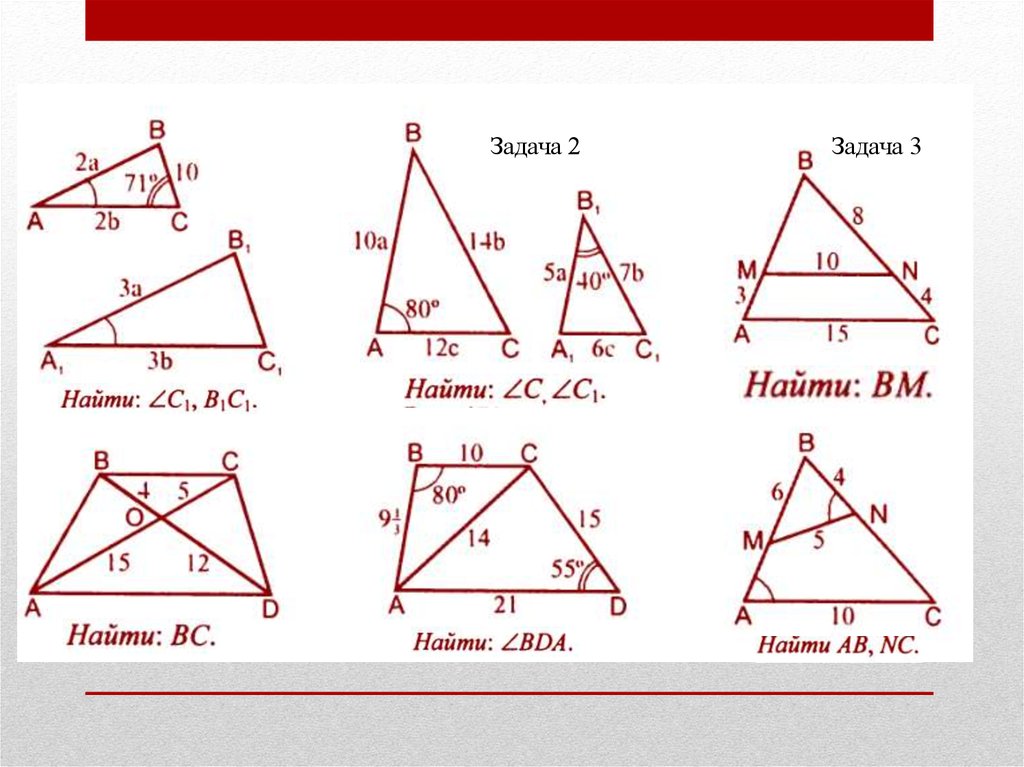
 Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого.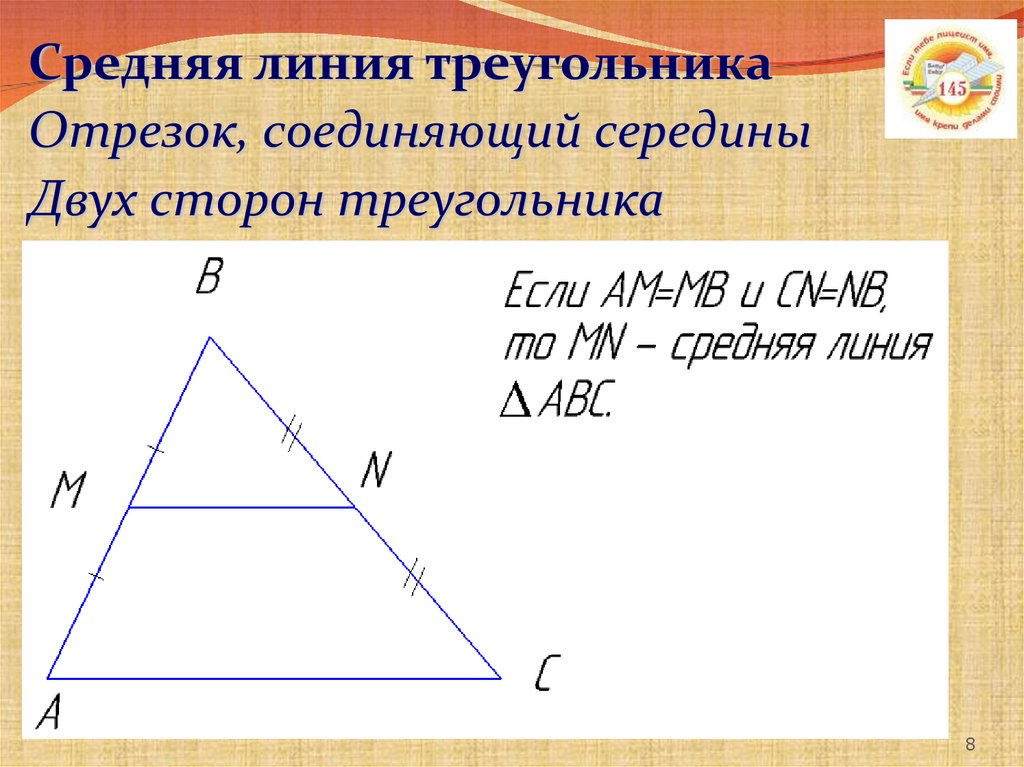 Сохранившаяся копия относится к 1629 г.
Сохранившаяся копия относится к 1629 г. 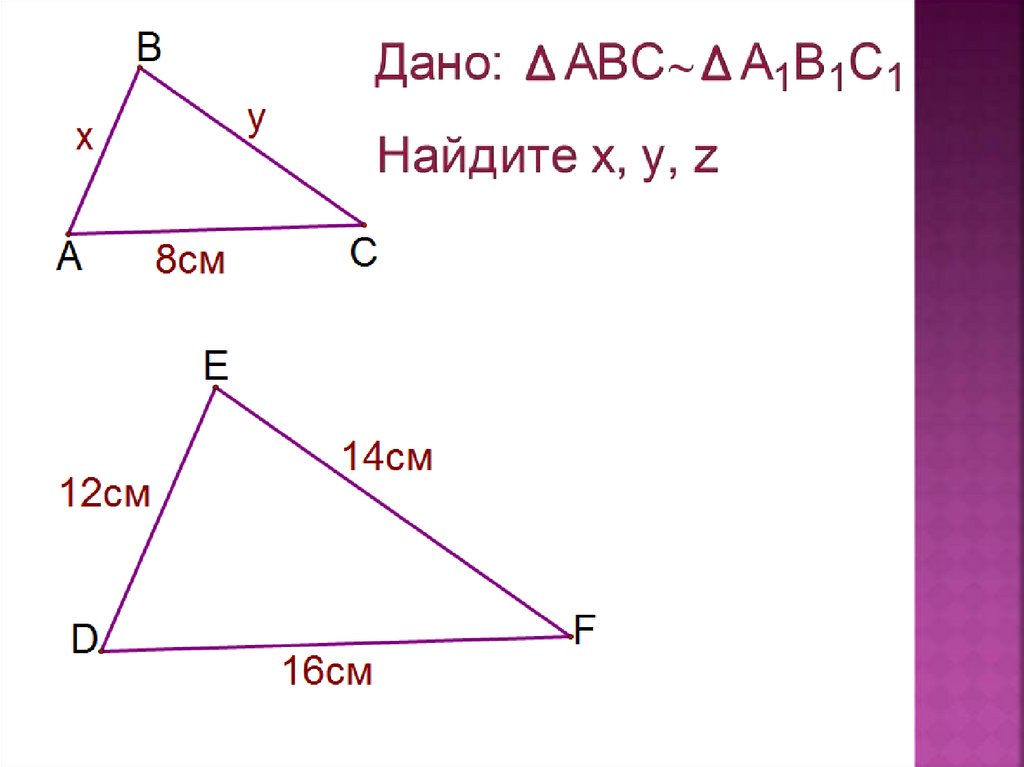
 Для этого нудно рассмотреть подобие двух треугольников. Помните: солнечные лучи падают параллельно друг другу. (Ответ:15м).
Для этого нудно рассмотреть подобие двух треугольников. Помните: солнечные лучи падают параллельно друг другу. (Ответ:15м).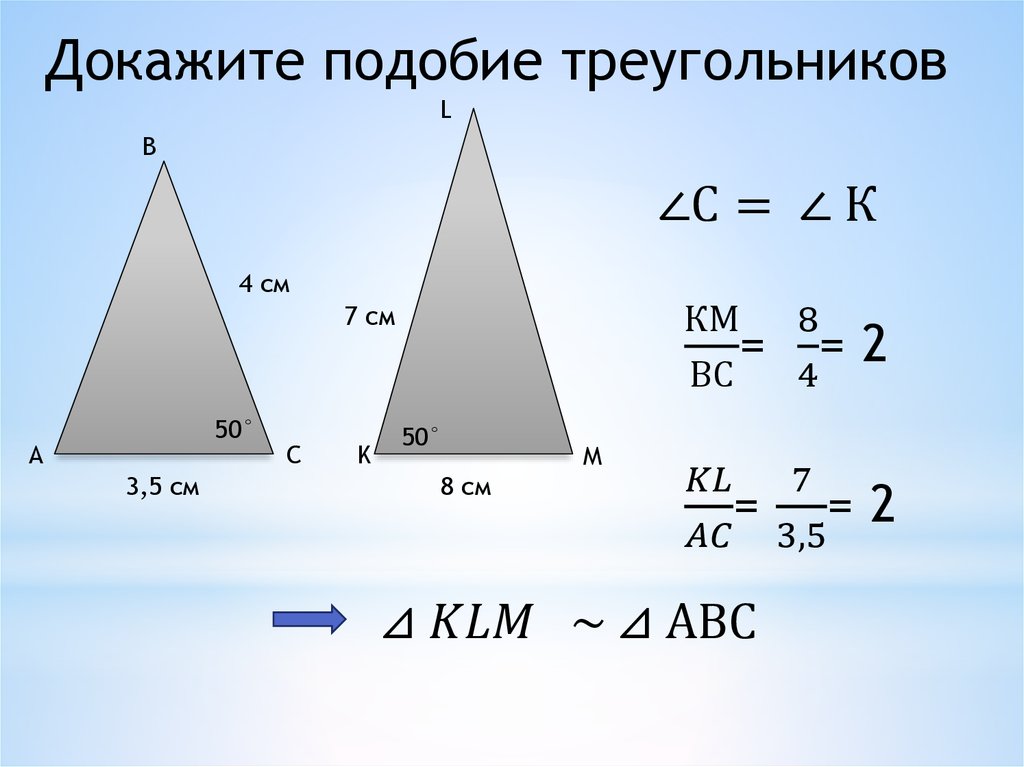 (Ответ: х=3/4*n*10; 375м).
(Ответ: х=3/4*n*10; 375м).
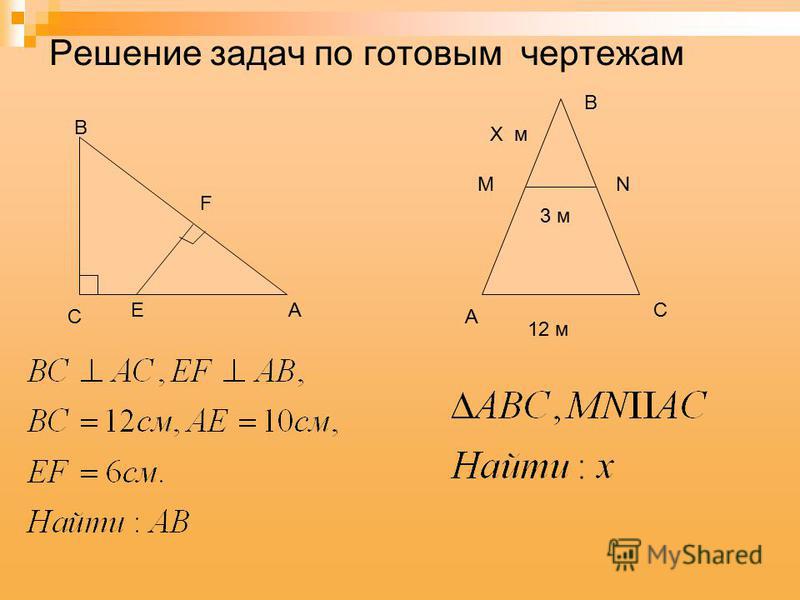

 Анализ и синтез информации. Самостоятельное создание способов решения проблем поискового характера.
Анализ и синтез информации. Самостоятельное создание способов решения проблем поискового характера.


 Организует обсуждение достижений, ставя заранее подготовленные вопросы.
Организует обсуждение достижений, ставя заранее подготовленные вопросы.