Показательное неравенство и его решение: Как решать показательные неравенства. Методы и способы решения

Содержание

11.3.5. Решение показательных неравенств, приводящихся к квадратным неравенствам.

Главная » 11 класс. Алгебра. » 11.3.5. Решение показательных неравенств, приводящихся к квадратным неравенствам

На чтение 2 мин. Просмотров 2.3k.

При решении показательных неравенств, приводящихся к квадратным неравенствам, поступают так же, как в примерах решения показательных уравнений, приводящихся к квадратным уравнениям, т. е. делают замену переменных, получают квадратное неравенство, которое решают, а затем возвращаются к прежней переменной.

Рассмотрим несколько примеров.

Решить неравенство:

Пример 1

1) (0,5)²^x+2 x.

Сделаем замену: пусть (0,5)^х=у. Получаем неравенство:

у²+2 y²-3y+2

Разложим квадратный трехчлен y²-3y+2 на линейные множители по формуле:

ax²+bx+c=a (x-x₁)(x-x₂), где х₁ и х₂– корни квадратного уравнения ax²+bx+c=0.

Находим корни приведенного квадратного уравнения y²—3y+2=0. Дискриминант D=b²-4ac=3²-4∙1∙2=9-8=1=1². Так как дискриминант является полным квадратом, то применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

у₁+у₂=3, у₁∙у₂=2. Отсюда: у₁=1, у₂=2. Значит, y²-3y+2=(у-1)(у-2).

Решаем неравенство: (у-1)(у-2)

Получаем: ує(1; 2), отсюда: (0,5)^хє(1; 2).

(0,5)^х=1 → (0,5)^х=(0,5)⁰ → х=0.

(0,5)^х=2 → (¹/₂)^x=2 → 2^—^x=2¹ → -x=1; x=-1. Значит, хє(-1; 0).

Ответ: (-1; 0).

Пример 2

2) 9^x^-1x^-1+6.

Представим 9^х-1 в виде степени числа 3.

3^{2 (}^x^-1)x^-1+6. Сделаем замену: 3^х-1=у. Тогда получается квадратное неравенство: у²

у²-у-6 . Находим корни приведенного квадратного уравнения у²-у-6=0. Проверим, возможно ли применить теорему Виета, ведь ею пользуются только, если корни являются целыми числами. Гарантией этого будет дискриминант, который должен быть полным квадратом некоторого числа. Находим дискриминант D=b²-4ac=1-4∙(-6)=1+24=25=5². Дискриминант является полным квадратом числа 5, поэтому, подбираем корни, пользуясь теоремой Виета: у₁+у₂=1, у₁∙у₂=-6. Подходят значения: у₁=-2 и у₂=3.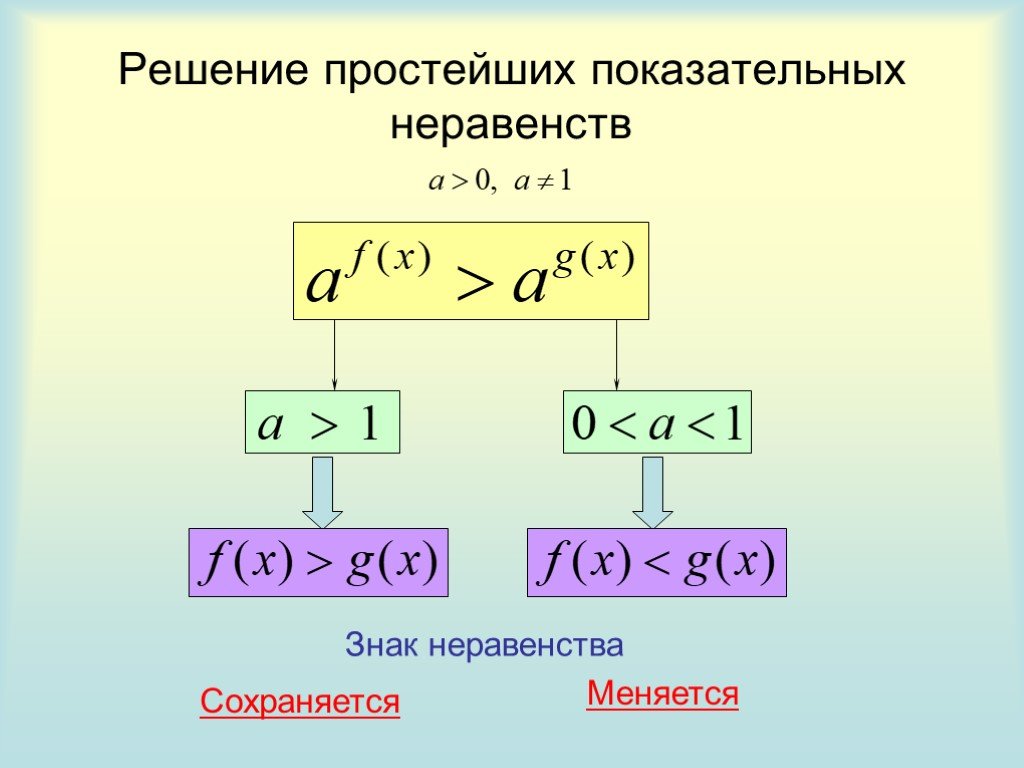

Раскладываем левую часть неравенства на линейные множители, получаем:

(у+2)(у-3)

ує(-2; 3). Возвращаемся к переменной х:

3^х-1є(-2; 3), но так как отрицательных значений степень 3^х-1принимать не может, то запишем: 3^х-1є(0; 3). Определим интервал значений переменной х.

3^х-1→0 при х-1 → -∞, так как число 3 в степени, стремящейся к минус бесконечности, фактически будет равным нулю, значит, х→ -∞.

Далее, 3^х-1=3 → 3^х-1=3¹ → х-1=1 → х=2.

Получили хє(-∞; 2).

Ответ: (-∞; 2).

показательные неравенства

( Пока оценок нет )

Решение показательных неравенств | Логарифмы

Решение показательных неравенств продолжим рассмотрением примеров, приводимых к простейшим с использованием свойств степеней.

Решение показательных неравенств тесно связано с решением соответствующего вида показательных уравнений. Отличие — в переходе от степеней к показателям степеней. В уравнениях из равенства степеней с одинаковыми основаниями следует равенство показателей степеней, в неравенствах же знак либо не изменяется (если основание a>1), либо меняется на противоположный (при 0<a<1).

Рассмотрим решение показательных неравенствах на конкретных примерах.

ОДЗ: x∈R.

Приведём обе части неравенства к степеням с одинаковым основанием. Используем для этого свойства степеней.

Десятичную дробь сначала преобразуем в обыкновенную (как слышим, так и пишем) затем — в степень:

Так как основание 5>1, показательная функция

возрастает, поэтому знак неравенства между показателями степеней не изменяется:

Переносим все слагаемые в левую часть, чтобы справа получить нуль:

Это — квадратичное неравенство. Решим его методом интервалов. Ищем нули функции, стоящей в левой части неравенства, то есть решаем квадратное уравнение:

Полученные корни отметим на числовой прямой. Для проверки знака берём любое число из любого промежутка. Например, нуль:

В промежуток, которому принадлежит нуль, ставим «минус», остальные знаки расставляем в шахматном порядке. Так как левая часть неравенства меньше либо равна нуля, выбираем промежуток со знаком «минус» и записываем ответ.

Ответ:

ОДЗ: x+2≠0; x+4≠0, то есть x — любое число, кроме 2 и 4.
Так как π ≈ 3,14, основание

показательная функция

убывает, поэтому знак неравенства между показателями степеней меняется на противоположный:

Переносим все слагаемые в левую часть, чтобы справа остался нуль, и приводим дроби к наименьшему общему знаменателю:

Это неравенство решаем методом интервалов. Ищем нули функции, то есть решаем уравнение

Его корень — x=0. Так как x ², 0 — кратный корень чётной степени, следовательно, в нём — «петля».
На числовой прямой отмечаем 0 (неравенство нестрогое, точка закрашенная) и -2 и -4 (точки выколотые, так как не входят в ОДЗ).
Для проверки знака берём любое число из любого промежутка, например, 1:

получили положительное число, поэтому в промежутке, которому принадлежит 1, ставим знак «+». Остальные знаки расставляем в шахматном порядке («петля» позволяет это сделать. Знак в петле — «виртуальный», его ставят только для поддержания шахматного порядка).
Отдельно стоящую закрашенную точку включаем в ответ.
Ответ:

ОДЗ: x≠0, то есть x — любое число, кроме нуля.
Приводим обе части неравенства к степеням с одинаковым основанием:

смешанное число переводим в неправильную дробь

Приходим к неравенству

далее —

Так как основание 3/5 меньше единицы, показательная функция

убывает, знак неравенства между показателями степеней меняется на противоположный:

Переносим все слагаемые в левую часть, упрощаем и приводим дроби к общему знаменателю:

Это неравенство решим методом интервалов.

Полученные точки отмечаем на числовой прямой (с учётом ОДЗ). Все они выколотые (так как неравенство строгое).
Для проверки знака возьмем 1. В 1 — «минус». Остальные знаки расставляем в шахматном порядке. Так как в неравенстве левая часть больше нуля, выбираем промежутки со знаком «плюс» и записываем ответ.
Ответ:

Рубрика: Показательные неравенства | Комментарии
Урок Рабочий лист:Экспоненциальные неравенства | Нагва
Начать практику
В этом рабочем листе мы будем практиковаться в решении экспоненциальных неравенств, все основания которых можно привести к одному и тому же значению.
Q1:
Известно, что 16 находится в интервале [0,25,0,5]. В каком интервале лежит 𝑥?

А[−0,25,0,5]
Б[-0,5,-0,25]
С[−0,5,0,5]
Д[0,25,0,5]
Э[−0,5,0,25]
Q2:
Если 13>13, что из следующего должно быть верно относительно 𝑥 и 𝑦?
А𝑥=𝑦
Б𝑥>𝑦
C𝑦>𝑥
Q3:
Найдите значения 𝑥, удовлетворяющие следующему неравенству: 4>8.
А𝑥2
Б𝑥1
C𝑥>2
Д𝑥>1
Э𝑥0
Q4:
Найдите все значения 𝑥, удовлетворяющие следующему неравенству: 2>2.
А𝑥1
B𝑥>3
C𝑥3
Д𝑥0
E𝑥>1
Q5:
Предположим, что 𝑎𝑥𝑏 является решением следующего неравенства: 13>19. Находить 𝑏−𝑎.
Q6:
Найдите все значения 𝑥, которые удовлетворяют следующему неравенству: 1≥4.

А𝑥≤4
B𝑥≥−94
C𝑥≤−94
Д𝑥≥−4
E𝑥≤−4
Q7:
Найдите все значения 𝑥, удовлетворяющие следующему неравенству: (0,01)≥110.
А𝑥≥−5
B𝑥≥−2
C𝑥≤−2
Д𝑥≥5
E𝑥≥−53
Q8:
Найдите все значения 𝑥, удовлетворяющие следующему неравенству: −423≤−9.
А𝑥≤−3
B𝑥≥−3
C𝑥≥1
D𝑥≤1
E𝑥≥3
Q9:
Найдите все значения 𝑥, удовлетворяющие неравенству (0. 01)1.
А𝑥>5
B𝑥>2
C𝑥5
Д𝑥92

E𝑥>92
Q10:
Найдите все значения 𝑥, которые удовлетворяют следующему неравенству: 2≤14.
А𝑥≤2
Б𝑥≥2
C𝑥≤4
D𝑥≤−2
E𝑥≥4
Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.

Экспоненциальное уравнение и неравенства.pptx
Экспоненциальное уравнение и неравенства.pptx
Реклама
1 из 23
Верхний вырезанный слайд
Скачать для чтения в автономном режиме
Образование 90 004
Показательное уравнение и неравенства
Реклама
Реклама
Экспоненциальное уравнение и неравенства.pptx
Роки М. Гонзага, Лпт 10 ноября 2020 г.
Молитва
Уважение (уважать всех в классе) Усилия (показывайте усилия и интерес) Отношение (наблюдайте за своим отношением во время онлайн-занятия) непрерывный) Сотрудничество (сотрудничать и следовать заданным график работы) Честность (честность в выполнении вашей офлайн-задачи будет сделать вас успешным)
Вызов памятки
Деятельность
Направление: Определите, является ли следующее уравнение показательным или показательным неравенства 1. 3x= 32x−1 2. 2𝑥2 ≥ 32 3. 5x−1= 125 5. 3𝑥2 < 27 4. 2𝑥−2 ≥ 1 2 𝑥−3 6. 49 = 7х+1
Направление: Определите, является ли следующее уравнение показательным или показательным Неравенства. 1. 3x = 32x−1 2. 2𝑥2 ≥ 32 3. 5x−1= 125 5. 3𝑥2 < 27 4. 2𝑥−2 ≥ 1 2 𝑥−3 6. 49 = 7х+1 1. Исходя из деятельности, что вы заметили? 2. Что вы заметили из данных символов?

ЭКСПОНЕНЦИАЛЬНЫЙ УРАВНЕНИЕ ЭКСПОНЕНЦИАЛЬНЫЙ НЕРАВЕНСТВА Показательное уравнение — это уравнения показатели которого являются переменными. 1. 3x= 32x−1 2. 5x−1= 125 3. 49 = 7х+1 Экспоненциальные неравенства — это неравенства с показателями, которые можно решить аналогично решению традиционных уравнений. 1. 2х2≥ 32 2. 2х−2 ≥ 1 2 х-3 3. 3х2 < 27
ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ  Показательное уравнение – это уравнение, показатели которого являются переменными. Пример: 1. 3x= 32x−1 2. 5x−1 = 125 3. 49 = 7x+1 Чтобы решить:  Перепишите/выразите обе части уравнения в виде степеней с одинаковым основанием.  Если основанием является число, просто разбейте его с помощью факторного дерева.  Если основание представляет собой дробь, СНАЧАЛА запишите целое число, используя отрицательные показатели.  Решите полученное уравнение.
ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ  Решите набор решений следующего показательного уравнения; 1. 2𝑥 = 8 Решение: 2𝑥 = 8 2𝑥 = 23 𝑥 = 3 выразите обе части уравнения в виде степеней с одним и тем же основанием. Решите полученное уравнение. Проверка: 2𝑥 = 8, так как 𝑥 = 3 23 = 8 8 = 8
ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ  Решите набор решений следующего показательного уравнения; 2. 2𝑥 «=» 1 16 Решение: 2𝑥 = 1 16 2𝑥 = 1 24 2𝑥 = 2−4 𝑥 = −4 выразите обе части уравнения в виде степеней с одним и тем же основанием. Поскольку данное основание является дробью, запишите целое число, используя отрицательные показатели. Проверка: 2𝑥 = 1 16 , так как 𝑥 = −4 2−4 = 1 16 1 16 «=» 1 16 Решите полученное уравнение.
 Решите набор решений следующего показательного уравнения; 1. 102𝑥 = 0,1 2. 4𝑥+2 = 64 3. 32𝑥−1 + 5 = 32
ЭКСПОНЕНЦИАЛЬНЫЕ НЕРАВЕНСТВА  Экспоненциальные неравенства — это неравенства с показателями, которые можно решить аналогично решению традиционных уравнений.  Задействованные символы неравенства. Пример: 1. 2х2≥ 32 2. 2х−2 ≥ 1 2 х-3 3. 3х2 < 27 Примечание:  Неравенства с четными показателями обычно есть 2 решения.  Неравенства с нечетными показателями содержат один решение.
ЭКСПОНЕНЦИАЛЬНЫЕ НЕРАВЕНСТВА Найдите множество решений каждого из следующих показательных неравенств: 1. 2𝑥3 + 14 ≥ 30 Решение: 2𝑥3 + 14 ≥ 30 2𝑥3 + 14 — 14 ≥ 30 — 14 2𝑥3 ≥ 16 2𝑥3 2 ≥ 16 2 𝑥3 ≥ 8 3 𝑥3 ≥ 3 8 𝑥 ≥ 2 Применить свойство вычитания Решите для x, применяя свойство деления Применить раздел имущества Извлеките корни выражения
ЭКСПОНЕНЦИАЛЬНЫЕ НЕРАВЕНСТВА Найдите множество решений каждого из следующих показательных неравенств: 2. 2𝑥2 ≥ 32 Решение: 2𝑥2 ≥ 32 2𝑥2 2 ≥ 32 2 𝑥2 ≥ 16 2 𝑥2 ≥ 2 16 𝑥 ≥ ±4 Решите для x, применяя свойство деления Применить раздел имущества Извлеките корни выражения Так как в данном задании четная степень, то есть 2 решения. 𝑥 ≥ 4 и 𝑥 ≥ −4.
Найдите множество решений каждой из следующих экспоненциальных неравенства: 1.
No related posts.