Лекции по математической физике
Лекции по математической физике
ОглавлениеПРЕДИСЛОВИЕГлава I.  ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ§ 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ 2. Малые поперечные колебания упругой струны 3. Случай многих пространственных переменных § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ 1. Стационарное распределение тепла 2. Задачи электростатики 3. Установившиеся колебания 4. Установившиеся электромагнитные колебания 5. Постановка краевых задач § 4. ОБЩИЕ ЗАМЕЧАНИЯ Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ § 4.  ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ§ 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ 2. Свойства гамма-функции 3. Степенной ряд для функций Бесселя 4. Рекуррентные формулы 5. Функции Бесселя полуцелого порядка 6. Интегральное представление функций Бесселя 7. Функции Ханкеля. Интегральное представление 9. Линейная независимость цилиндрических функций 10. Асимптотика цилиндрических функций 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ 2. Основные свойства классических ортогональных полиномов 3.  Производящая функция классических ортогональных полиномов4. Полиномы Якоби 5. Полиномы Лежандра 6. Полиномы Лагерра 7. Полиномы Эрмита § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА 2. Краевая задача для присоединенных функций Лежандра 3. Полнота и замкнутость системы присоединенных функций Лежандра § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ § 6. ШАРОВЫЕ ФУНКЦИИ § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ 2. Собственные функции цилиндра 3. Собственные функции шара Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА 2. Основные свойства гармонических функций § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА 2. Внутренние вторая и третья краевые задачи § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ 2. Единственность решения внешних задач в трехмерном случае 3. Единственность решения внешних задач для уравнения Лапласа на плоскости § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА 2. Свойства функции Грина задачи Дирихле 3.  Функция Грина внутренней третьей краевой задачи4. Функция Грина внутренней задачи Неймана 5. Функции Грина внешних краевых задач 6. Примеры построения функций Грина 7. Функция Грина задачи Дирихле на плоскости § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ 2. Краевая задача для уравнения Лапласа в прямоугольнике § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА 2. Несобственные интегралы, зависящие от параметра 4. Непрерывность потенциала простого слоя 5. Поверхности Ляпунова 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности 7. Разрыв потенциала двойного слоя 8. Разрыв нормальной производной потенциала простого слоя § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ 2. Интегральное уравнение для внутренней задачи Дирихле 3. Интегральное уравнение для внешней задачи Неймана 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле Глава VI.  УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА§ 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ § 2. ПРИНЦИП МАКСИМУМА § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ 2. Существование классического решения уравнения теплопроводности на отрезке § 5. ФУНКЦИЯ ГРИНА § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ 2. Неоднородное граничное условие § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 2. Теорема единственности 3. Фундаментальное решение. Интеграл Пуассона 4. Свойства фундаментального решения § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ 2. Пример § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ 2. Однородные граничные условия 3. Краевой режим 4.  Неоднородное граничное условие второго рода§ 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ 2. Формула Даламбера 3. Существование, единственность и устойчивость решения задачи Коши 4. Физическая интерпретация решения 5. Колебания струны под действием мгновенного сосредоточенного импульса 6. Существование и единственность решения § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ 2. Формула Кирхгофа 3. Формула Пуассона 4. Метод спуска 5. Локальные начальные условия 6. Установившиеся колебания § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА) § 11. ОБЩАЯ ЗАДАЧА КОШИ.  ФУНКЦИЯ РИМАНА§ 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ 2. Обобщенное решение. Условия на разрыве 3. Уравнение Кортевега — де Фриза и законы сохранения 4. Схема метода обратной задачи 5. Солитонные решения Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА 2. Свойства собственных значений и собственных функций § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА 3. Потенциалы уравнения Гельмгольца 4. Принцип максимума для уравнения … § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ 2. Принцип предельного поглощения ЛИТЕРАТУРА ДОПОЛНЕНИЕ |
9 полных кратких фактов —
Многочлен Эрмита широко используется в приложениях как ортогональная функция.
Многочлен Эрмита является решением ряда дифференциального уравнения Эрмита.
Дифференциальное уравнение второго порядка с конкретными коэффициентами в виде
d2г / дх2 – 2x dy/dx + 2xy = 0
известно как уравнение Эрмита, решая это дифференциальное уравнение, мы получим многочлен, который Многочлен Эрмита.
Найдем решение уравнения
d2г / дх2 – 2x dy/dx + 2ny = 0
с помощью последовательного решения дифференциального уравнения
теперь подставляя все эти значения в уравнение Эрмита, мы имеем
Это уравнение удовлетворяет значению k = 0, и, как мы предположили, значение k не будет отрицательным, теперь для члена самой низкой степени xм-2 возьмем k = 0 в первом уравнении, поскольку второе дает отрицательное значение, поэтому коэффициент xм-2 is
a0м (м-1)=0 ⇒ м=0,м=1
как0 ≠ 0
теперь таким же образом приравнивая коэффициент при xм-1 из второго суммирования
и приравнивая коэффициенты при xм + к к нулю,
aк + 2(м+к+2)(м+к+1)-2аk(м+кн) = 0
мы можем записать это как
aк + 2 = 2(m+kn)/(m+k+2)(m+k+1)k
если m = 0
aк + 2 = 2(kn)/(k+2)(k+1) аk
если m = 1
aк + 2 = 2(k+1-n)/(k+3)(k+2) аk
для этих двух случаев теперь обсудим случаи для k
Когда $m=0,к + 2= 2(kn)/(k+2)(k+1)} аk$
Если $k=0 а2 =-2 н/2 а0=-на0$
$k=1, а3=2(1-n)/6 а1 =-2(n-1)/3 ! а1$
Если $k=2,4 =2(2-n)/12 а2 =2 (2-н)/12 (-на0) = 22 п(п-2)/4 ! а0$
пока m = 0, мы имеем два условия, когда a1= 0, то a3=a5=a7=….
= А2к + 1= 0 и когда a1 не равно нулю тогда
следуя этому положению значений a0,a1,a2,a3,a4 и5 у нас есть
а при m = 1 a1= 0, положив k = 0,1,2,3,… .. получаем
aк + 2 = 2(к+1-п)/(к+3)(к+2)аk
так что решение будет
так что полное решение
где A и B — произвольные постоянные
Многочлен ЭрмитаРешение уравнения Эрмита имеет вид y (x) = Ay1(x) + По2(x) где y1(x) и y2(x) — члены ряда, как обсуждалось выше,
одна из этих серий заканчивается, если n — неотрицательное целое число, если n — четное y1 заканчивается в противном случае y2 если n нечетное, и мы легко можем проверить, что для n = 0,1,2,3,4 …… .. эти многочлены являются
1,х,1-2х2, х-2/3 х3, 1-4x2+4/3x4, х-4/3х3+ 4/15x5
поэтому мы можем сказать здесь, что решение уравнения Эрмита является постоянным кратным этим многочленам, а члены, содержащие наивысшую степень x, имеют вид 2nxn обозначается Hn(x) известен как Эрмитовый полином
Производящая функция полинома ЭрмитаМногочлен Эрмита обычно определяется с помощью отношения, использующего производящую функцию
[n / 2] — наибольшее целое число, меньшее или равное n / 2, поэтому оно следует за значением Hn(Х) as
это показывает, что Hn(Х) является многочленом степени n от x и
Hn(х) = 2nxn + пп-2 (Х)
в котором πп-2 (x) — многочлен степени n-2 от x, и он будет четной функцией x для четного значения n и нечетной функцией x для нечетного значения n, поэтому
Hn(-х) = (-1)n Hn(Х)
некоторые из начальных многочленов Эрмита являются
H0(х) = 1
H1(х) = 2x
H2(х) = 4x2 -2
H3(х) = 8x3-12
H4(х) = 16x4 — 48x2+12
H5(х) = 32x2 — 160x3+ 120x
Производящая функция полинома Эрмита по формуле РодригаМногочлен Эрмита также можно определить с помощью формулы Родрига, используя производящую функцию
так как отношение производящей функции
Используя теорему Маклорена, имеем
or
положив z = xt и
для t = 0, поэтому z = x дает
это мы можем показать по-другому, как
дифференцирующий
по t дает
принимая предел t стремится к нулю
теперь дифференцируя по x
принимая предел t стремится к нулю
из этих двух выражений мы можем написать
таким же образом мы можем написать
дифференцируя n раз, положим t = 0, получим
из этих значений мы можем написать
из них мы можем получить значения
Пример полинома Эрмита- Найдите обычный многочлен от
Решение: используя определение полинома Эрмита и соотношения, которые мы имеем
2.
Найдите многочлен Эрмита обыкновенного многочлена
Решение: данное уравнение мы можем преобразовать в Эрмита как
и из этого уравнения приравнивая тот же коэффициент мощности
следовательно, многочлен Эрмита будет
Ортогональность многочлена Эрмита | Ортогональность полинома ЭрмитаВажной характеристикой полинома Эрмита является его ортогональность, согласно которой
Чтобы доказать эту ортогональность, напомним, что
которая является производящей функцией для полинома Эрмита, и мы знаем
поэтому умножая эти два уравнения, мы получим
умножение и интегрирование в бесконечных пределах
и с тех пор
so
используя это значение в приведенном выше выражении, мы имеем
который дает
теперь приравняем коэффициенты с обеих сторон
что показывает свойство ортогональности многочлена Эрмита.
Результат ортогональности многочлена Эрмита можно показать иным образом, рассмотрев рекуррентное соотношение
Пример ортогональности многочлена Эрмита1.
вычислить интеграл
Решение: Используя свойство ортогональности многочлена Эрмита
поскольку здесь значения m = 3 и n = 2, поэтому
2. Вычислить интеграл
Решение: Используя свойство ортогональности многочлена Эрмита, мы можем написать
Рекуррентные соотношения полинома ЭрмитаЗначение полинома Эрмита легко найти с помощью рекуррентных соотношений
Полиномиальные рекуррентные соотношения ЭрмитаЭти отношения легко получить с помощью определения и свойств.
Доказательства: 1. Мы знаем уравнение Эрмита
y”-2xy’+2ny = 0
и отношение
частично выполняя дифференцирование по x, мы можем записать его как
из этих двух уравнений
теперь замените n на n-1
приравнивая коэффициент при tn
так что требуемый результат
2. Аналогичным образом дифференцируя частично по t уравнение
мы получаем
n = 0 исчезнет, поэтому, положив это значение e
теперь приравняв коэффициенты при tn
таким образом
3.
Для доказательства этого результата исключим Hп-1 от
и
так что мы получаем
таким образом, мы можем записать результат
4. Чтобы доказать этот результат, продифференцируем
мы получаем отношение
подставляя значение
и заменив n на n + 1
который дает
Примеры рекуррентных соотношений многочлена Эрмита1. покажите это
H2n(0) = (-1)n. 22n (1 / 2)n
Решение:
Чтобы показать результат, у нас есть
Н2п(х) =
взяв x = 0, мы получаем
2. Покажите, что
ЧАС’2n + 1(0) = (-1)n 22n + 1 (3 / 2)2
Решение:
Поскольку из рекуррентного соотношения
ЧАС’n(х) = 2нГнп-1(Х)
здесь замените n на 2n + 1, чтобы
ЧАС’2n-1(х) = 2(2n+1) Н2n(Х)
принимая x = 0
3. Найдите значение
H2n + 1(0)
Решения
Поскольку мы знаем
используйте x = 0 здесь
H2n-1(0) = 0
4.
Найдите значение H ‘2n(0).
Решения :
у нас есть рекуррентное соотношение
ЧАС’n(х) = 2нГнп-1(Х)
здесь замените n на 2n
ЧАС’2n(х) = =2(2n)Н2n-1(Х)
положим x = 0
ЧАС’2n(0) = (4n)Н2n-1(0) = 4n*0=0
5. Покажите следующий результат
Решения :
Используя рекуррентное соотношение
ЧАС’n(х) = 2нГнп-1 (Х)
so
и
d3/ дх3 {Hn(х)} = 23п (п-1) (п-2) Нп-3(Х)
дифференцируя это m раз
который дает
6. Покажите, что
Hn(-х) = (-1)n Hn(Х)
Решения :
мы можем написать
от коэффициента tn у нас есть
и для -x
7. Вычислите интеграл и покажите
Решения : Для решения этой интегральной части используйте интеграционные части как
Теперь дифференциация под знаком интеграла дифференцируется с
относительно х
через
ЧАС’n(х) = 2nHп-1 (Х)
и
ЧАС’m(х) = 2 мГнм-1 (Х)
у нас есть
и с тех пор
𝝳 н,м-1 = 𝝳п+1, м
поэтому значение интеграла будет
Вывод:Конкретный многочлен, который часто встречается в приложениях, — это многочлен Эрмита, поэтому здесь вкратце обсуждались основное определение, производящая функция, рекуррентные отношения и примеры, связанные с многочленом Эрмита, если вам требуется дополнительное чтение, пройдите
https://en.
wikipedia.org/wiki/Hermite_polynomials
Чтобы узнать больше о математике, следите за нашими Страница математики
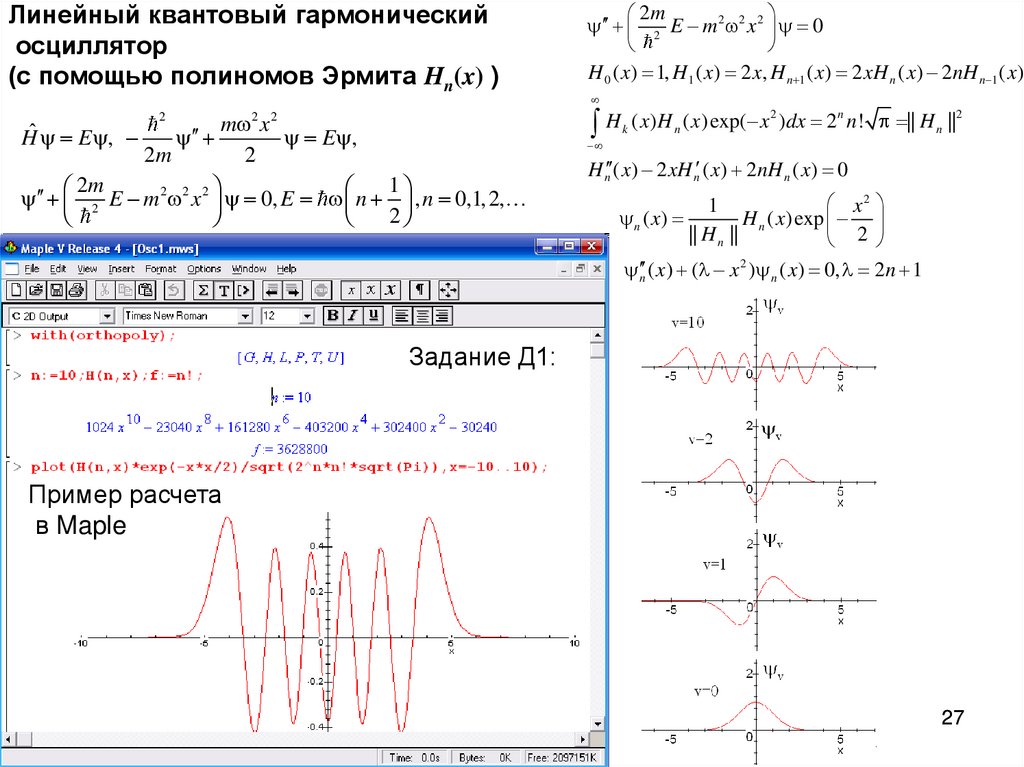
Полином Эрмита
Полином ЭрмитаНабор ортогональных многочленов. Полиномы Эрмита проиллюстрированы выше для и , 2, …, 5.
Производящая функция для полиномов Эрмита:
| (1) |
Использование ряда Тейлора показывает, что
С ,
Теперь определите операторы
| (4) | |||
| (5) |
Следует, что
| (6) | |||
| (7) |
так
| (8) |
и
| (9) |
что означает, что следующие определения эквивалентны:
| (10) | |||
| (11) | |||
| (12) |
Полиномы Эрмита связаны с производной функции ошибок соотношением
| (13) |
Они имеют контурное интегральное представление
| (14) |
Они ортогональны в диапазоне относительно функции взвешивания
| (15) |
Определите связанные функции
| (16) |
Они подчиняются условиям ортогональности
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) |
если четный и , , и .
В противном случае
последний интеграл равен 0 (Szegö 1975, стр. 390). Они также удовлетворяют рекуррентным соотношениям
| (22) |
| (23) |
Дискриминант
| (24) |
(Сего 1975, стр. 143).
Интересная идентичность
| (25) |
Первые несколько многочленов
Класс обобщенных многочленов Эрмита, удовлетворяющих
| (26) |
был изучен Субраманяном (1990).
Класс связанных многочленов, определяемый | (27) |
и с производящей функцией
| (28) |
был изучен Джорджевичем (1996). Они удовлетворяют
| (29) |
Модифицированная версия полинома Эрмита иногда определяется как
| (30) |
См. также Полиномиальная формула Эрмита Мелера, функции Вебера.
Каталожные номера
Абрамовиц М. и Стегун С. А. (ред.). «Ортогональные многочлены.
» Гл. 22 дюйма Справочник по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, стр. 771–802, 1972.
Арфкен, Г. «Функции Эрмита». §13.1 в «Математические методы для физиков», 3-е изд. Орландо, Флорида: Academic Press, стр. 712–721, 1985.
Чебышев П. Л. «О развитии функций по одной переменной». Бюлл. ф.-мат., акад. Имп. наук Санкт-Петербург 1 , 193-200, 1859.
Чебышев П. Л. Oeuvres, Vol. 1. Нью-Йорк: Челси, стр. 49-508, 1987.
Джорджевич Г. «О некоторых свойствах обобщенных многочленов Эрмита». Фиб. кв. 34 , 2-6, 1996.
Hermite, C. «Sur un nouveau développement en série de fonctions». Compt. Ренд. акад. науч. Париж 58 , 93–100 и 266–273, 1864 г. Перепечатано в Hermite, C. Oeuvres complètes, Vol. 2. Париж, стр. 29.3-308, 1908.
Hermite, C. Полные произведения, Vol. 3. Париж, с.
432, 1912.
Иянага С. и Кавада Ю. (ред.). «Полиномы Эрмита». Приложение A, таблица 20.IV в Математический энциклопедический словарь. Кембридж, Массачусетс: MIT Press, стр. 1479-1480, 1980.
Сансоне, Г. «Расширения в рядах Лагерра и Эрмита». Гл. 4 в Orthogonal Functions, rev. английское изд. Нью-Йорк: Довер, стр. 295–385, 1991.
Спаниер, Дж. и Олдхэм, К. Б. «Многочлены Эрмита». Ч. 24 из Атлас функций. Вашингтон, округ Колумбия: Hemisphere, стр. 217-223, 1987.
Субраманян, П. Р. Источники полиномов Эрмита. Фиб. кв. 28 , 156-161, 1990.
Сегё, Г. Ортогональные многочлены, 4-е изд. Провиденс, Род-Айленд: амер. Мат. Соц., 1975.
© 1996-9 Эрик В. Вайсштейн
1999-05-25
9 Полный список кратких фактов —
Полином Эрмита широко используется в приложениях как ортогональная функция. Полином Эрмита представляет собой ряд решений дифференциального уравнения Эрмита.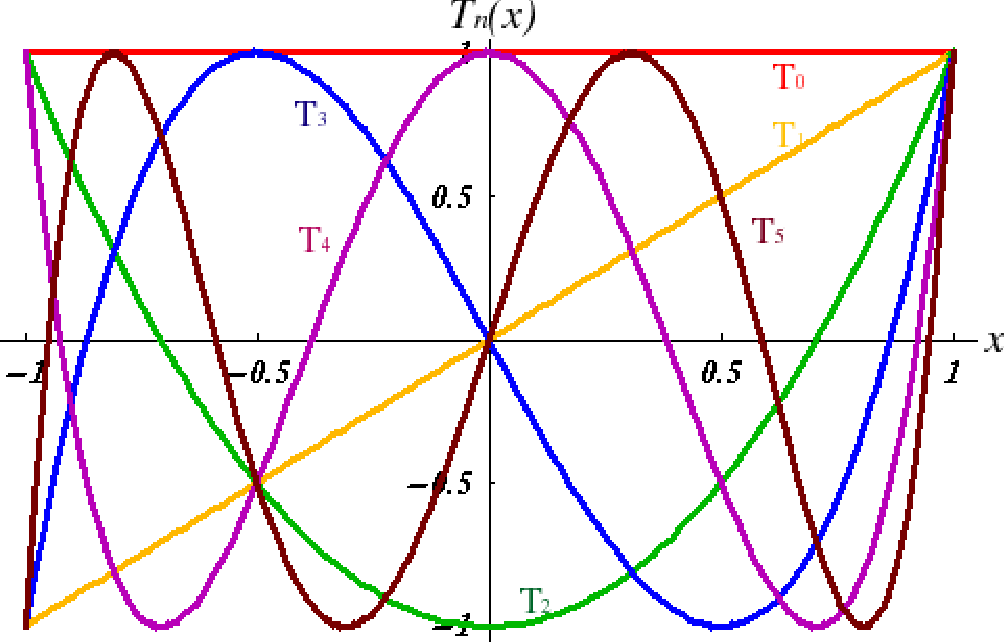
Дифференциальное уравнение второго порядка со специфическими коэффициентами
D 2 Y/DX 2 — 2x DY/DX + 2XY = 0,00009
4044040444441 — 2x DY/DX + 2x = 0
=a 2r+1 =0 и когда 1 не равно нулю, то
4 – 48x 2 +12
Чтобы доказать этот результат, мы исключим H n-1 из
Найдите значение