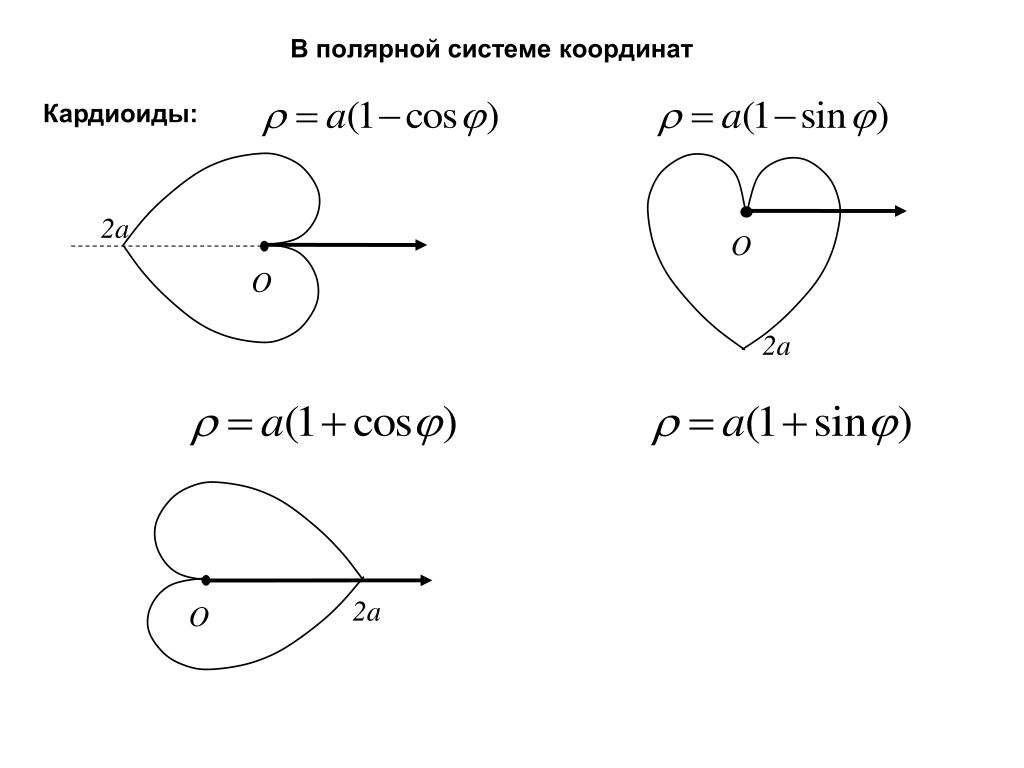
Исследовательская работа «Полярные координаты»
Муниципальное автономное образовательное учреждение
«Средняя общеобразовательная школа №47»
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
на тему:
«ПОЛЯРНЫЕ КООРДИНАТЫ »
Выполнили:
ученики 10 класса
Чугаев Егор Андреевич
Полканов Владислав Алексеевич
Руководитель:
учитель математики
Карнишина Валентина Ивановна
Пермь 2019
Оглавление
Введение. ………………………………………………………………………………………………………3
………………………………………………………………………………………………………3
Полярная система координат 4
Графическое представление……………………………. 4
История создания…………………………………………………………………………………………..5
Прямоугольная система координат на плоскости…………………………………………….6
Связь между декартовыми и полярными координатами 7
Уравнения кривых в полярных координатах7
Решение задач………………………………………………………………………….8
Заключение.10
Использованная литература…………………………………………………………………………..11
Приложения………………………………………………………………………………………………….12
Введение
Точке на плоскости соответствуют ее координаты.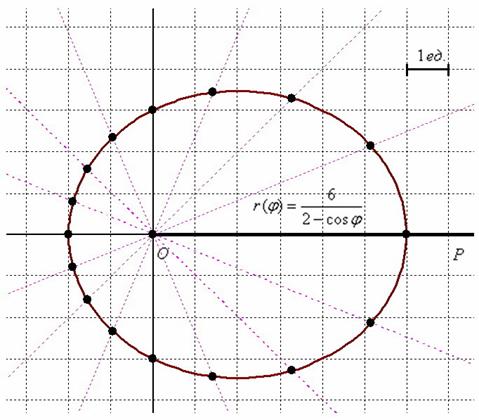 Не
всегда удобно и рационально использовать привычную нам прямоугольную декартовую
систему координат. Существуют и другие системы. Например, полярная. Правильный
выбор системы координат может значительно упростить решение той или иной
задачи, получить желаемую наглядность результата.
Не
всегда удобно и рационально использовать привычную нам прямоугольную декартовую
систему координат. Существуют и другие системы. Например, полярная. Правильный
выбор системы координат может значительно упростить решение той или иной
задачи, получить желаемую наглядность результата.
Именно полярная система координат будет объектом исследования в данной работе. Данная тема актуальна, т.к. не изучается в школьной программе, несмотря на то, что не все графики удобно строить в декартовой системе. Различные кривые, построенные в такой системе, имеют большое применение на практике.
Цель работы: изучение полярной системы координат; ознакомление с некоторыми кривыми, построенными в этой системе; приобретение навыков решения простейших задач в полярной системе координат.
Задачи:
· изучить основную теорию полярной системы координат;
· сравнить полярную систему координат с декартовой;
· рассмотреть основные кривые и их применение в жизни;
·
научиться решать
простейшие задачи в полярной системе координат.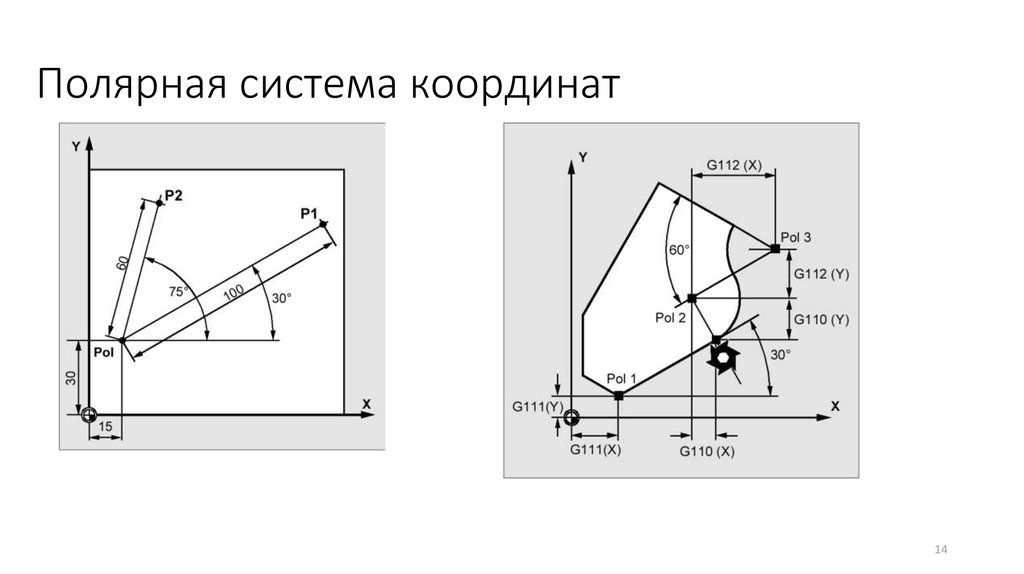
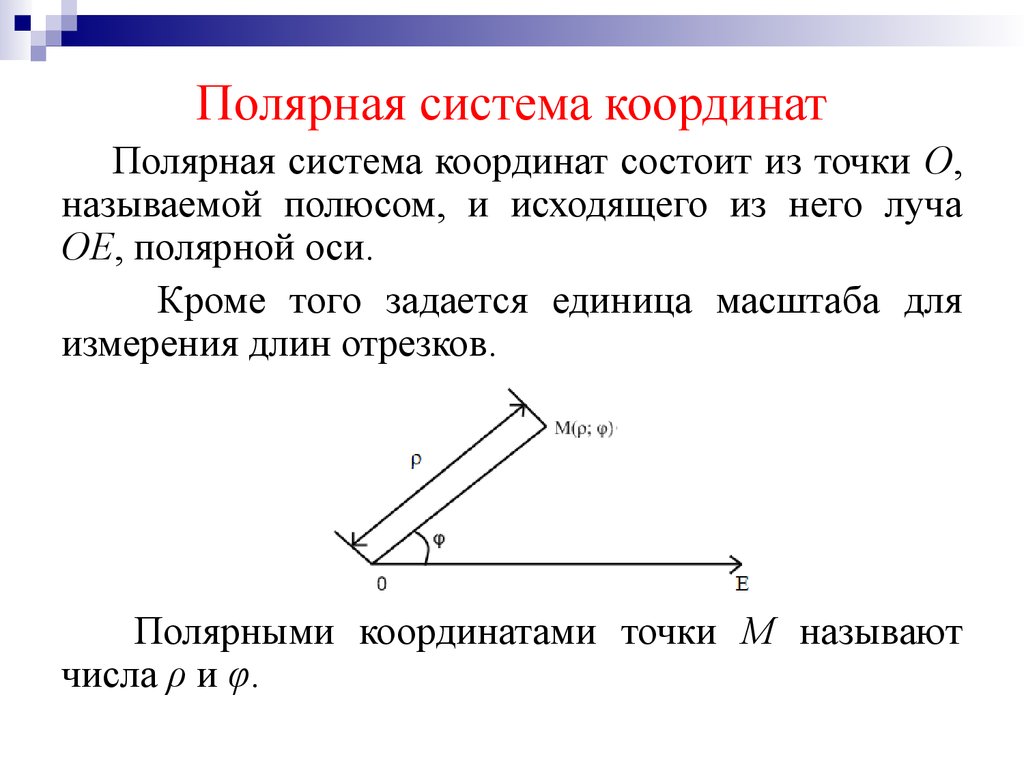
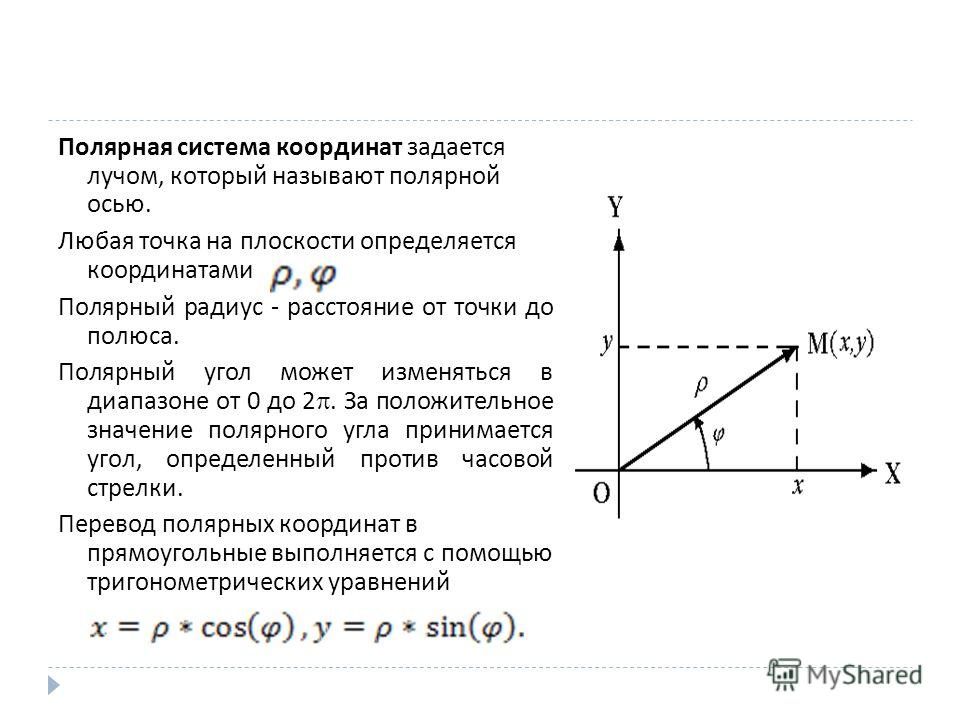
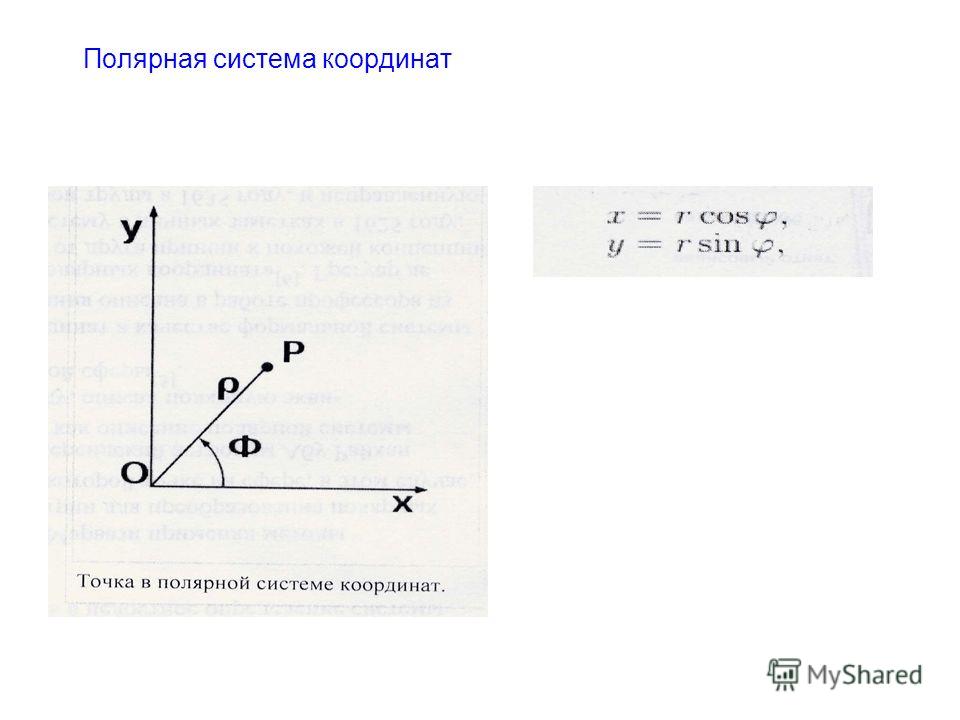
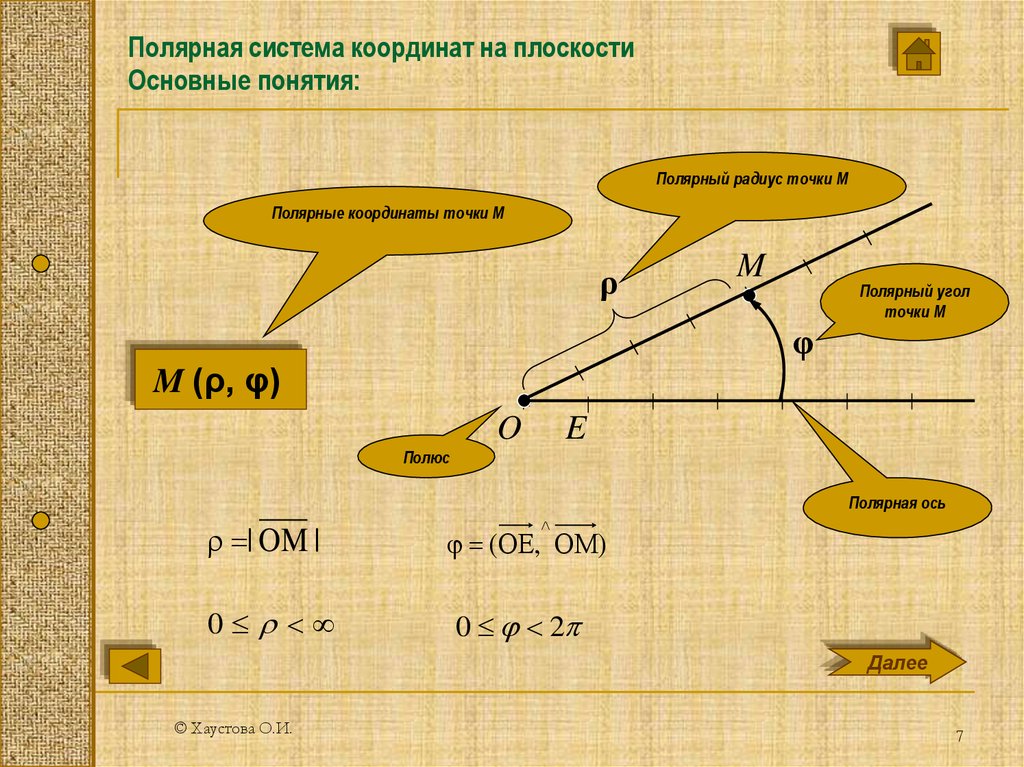
Полярная система координат (рис. 1,2) – двухмерная
система координат, в которой каждая точка на плоскости однозначно определяется
двумя числами – полярным углом и полярным радиусом. Полярная система координат
особенно полезна в случаях, когда отношения между точками проще изобразить в
виде радиусов и углов; в более распространённой декартовой, или прямоугольной,
системе координат, такие отношения можно установить только путём применения
тригонометрических уравнений.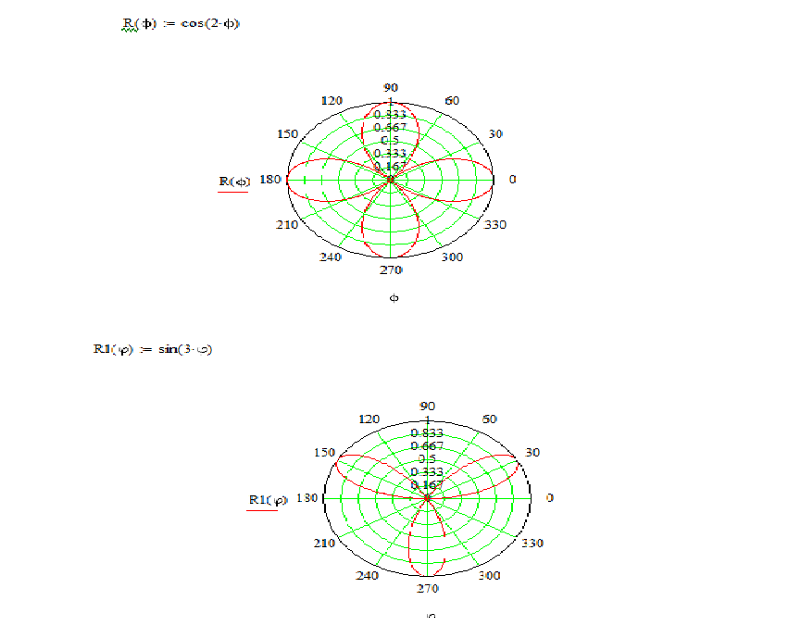
Графическое представление
Каждая точка в полярной системе координат
может быть определена двумя полярными координатами, что обычно называются r и φ.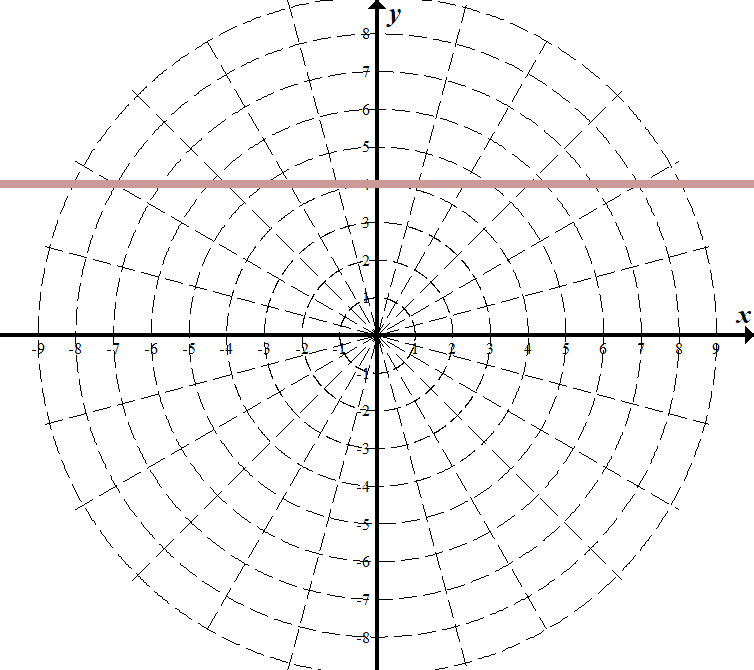 Координата r соответствует расстоянию от точки до центра, или полюса
системы координат, а координата равна углу, отсчитываемого в направлении против
часовой стрелки от луча через 0°.
Координата r соответствует расстоянию от точки до центра, или полюса
системы координат, а координата равна углу, отсчитываемого в направлении против
часовой стрелки от луча через 0°.
Полярный угол измеряется в радианах и отсчитывается от полярной оси:
в положительном направлении (против направления движения часовой стрелки), если значение угла положительное; в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное. Одной из важных особенностей полярной системы координат является то, что одна и та же точка может быть представлена бесконечным количеством способов. Это происходит потому, что для определения азимута точки нужно повернуть полярную ось так, чтобы она указывала на точку. Но направление на точку не изменится, если осуществить произвольное число дополнительных полных оборотов. Углы в полярных координатах задаются либо в градусах, либо в радианах, при этом 2π =360°.
История создания
Существуют разные версии о
введении полярных координат в качестве формальной системы координат.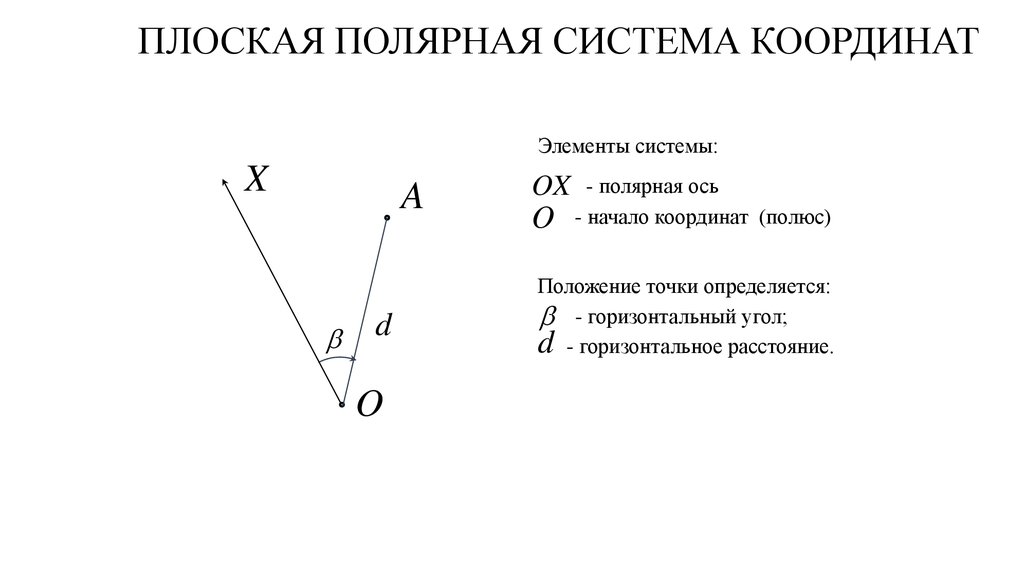 Полная
история возникновения и исследования описана в работе профессора из Гарварда
Джулиан Лоувел Кулидж «Происхождение полярных координат». Грегуар де Сен-Венсан
и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в
середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625
году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635
году, и исправленную версию в 1653 году. Кавальери применял полярные координаты
для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль
впоследствии использовал полярные координаты для вычисления длин параболических
дуг.
Полная
история возникновения и исследования описана в работе профессора из Гарварда
Джулиан Лоувел Кулидж «Происхождение полярных координат». Грегуар де Сен-Венсан
и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в
середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625
году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635
году, и исправленную версию в 1653 году. Кавальери применял полярные координаты
для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль
впоследствии использовал полярные координаты для вычисления длин параболических
дуг.
В книге «Метод флюксий» (англ.
Method of Fluxions, написана в 1671 году, напечатана в 1736 году) сэр Исаак
Ньютон исследовал преобразование между полярными координатами, которые он
обозначал как «Седьмой способ; Для спиралей» («англ. Seventh Manner; For
Spirals»), и девятью другими системами координат. В статье, опубликованной в
1691 году в журнале Acta eruditorum, Якоб Бернулли использовал систему с точкой
на прямой, которые он назвал полюсом и полярной осью соответственно.
Введение термина «полярные координаты» приписывают Грегорио Фонтана. В XVIII веке он входил в лексикон итальянских авторов.
Прямоугольная система координат на плоскости (рис. 3, 4)
Прямоугольная система координат – прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует её широкому применению.
Прямоугольная система координат на
плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y.
Положение точки A на плоскости определяется двумя координатами x и y.
Координата x
равна длине отрезка OB, координата y – длине отрезка OC в
выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X
соответственно. При этом координате x
приписывается знак минус, если точка B лежит
на луче OX’ (а не на луче OX, как на рисунке). Координате y приписывается знак минус, если точка C лежит на луче OY’.
Таким образом, OX’ и OY’
являются отрицательными направлениями осей координат (каждая ось координат
рассматривается как числовая ось). Ось x
называется осью абсцисс, а ось y – осью ординат. Координата x называется абсциссой точки A,
координата y – ординатой точки A. Символически это записывают так: A(x,y)
или A = (x,y) В правосторонней системе координат положительное
направление осей выбирают так, чтобы при направлении оси Y’Y вверх, ось X’X смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y называются координатными углами, четвертями или квадрантами плоскости.
Точки внутри координатного угла I имеют положительные абсциссы и ординаты.
Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты.
Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты
Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.
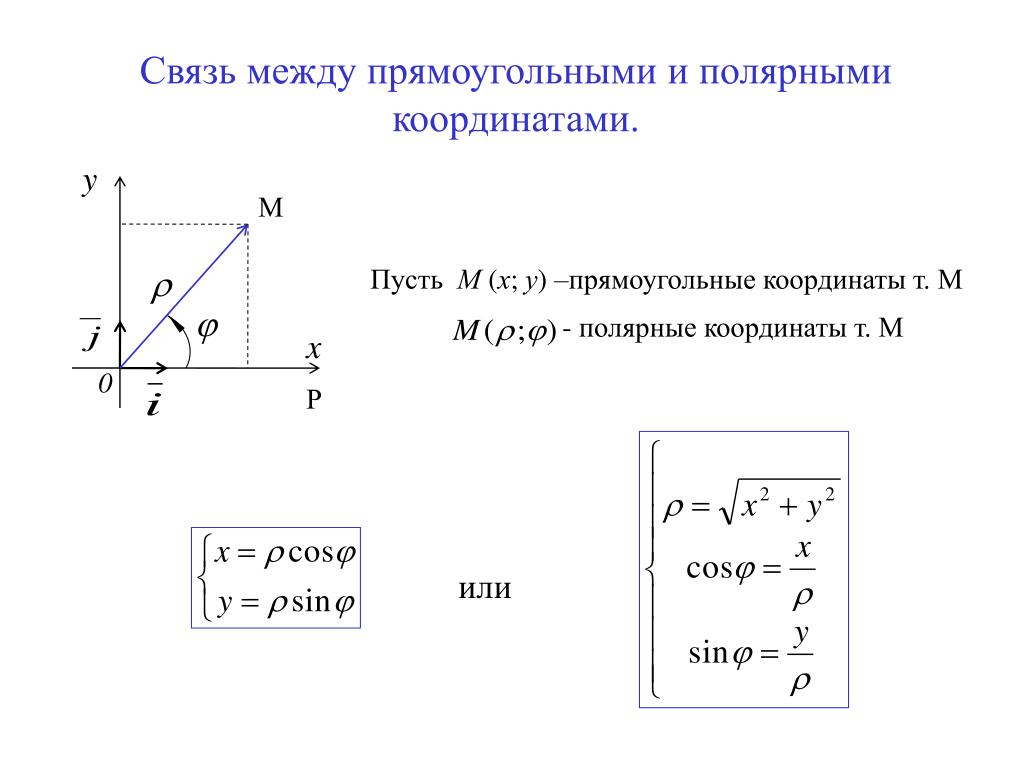
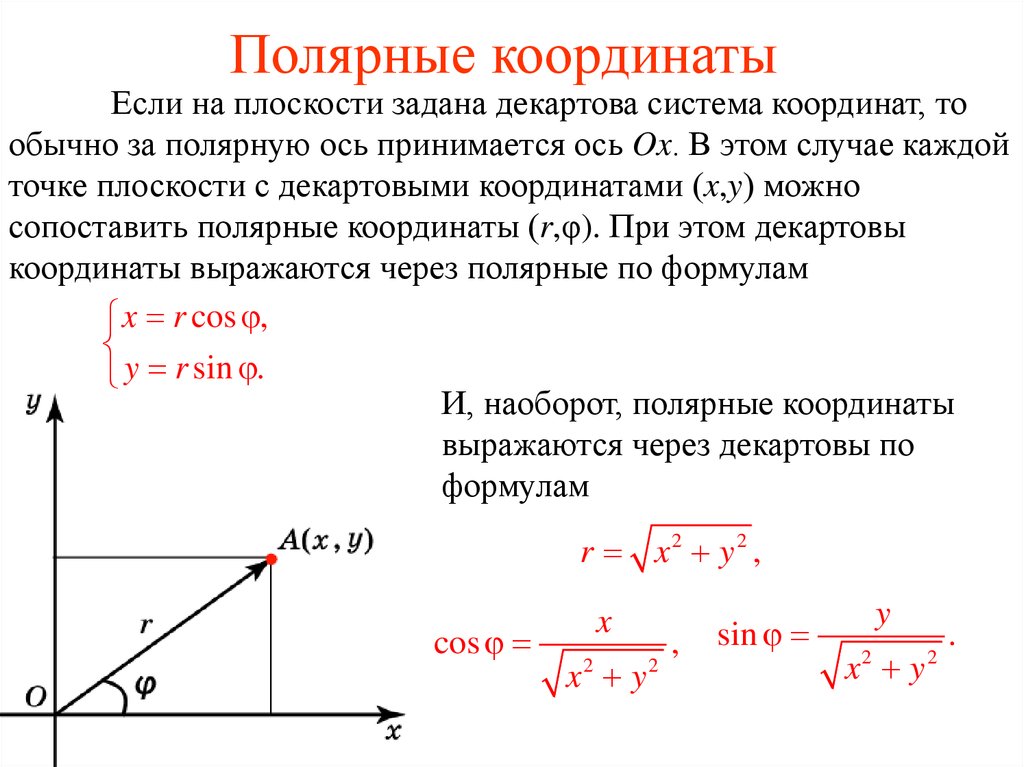
Связь между декартовыми и полярными координатами
Полярные координаты r и φ можно перевести в декартовы координаты x и y путем применения тригонометрических функций синуса и косинуса (при этом предполагается, что нулевой луч полярной системы координат совпадает с осью x декартовой системы):
r² = y² + x²,
φ = arctg y/x; x ≠ 0;
в то время как декартовы координаты x и y могут быть переведены в полярные координаты r и φ следующим образом:
x = r cos φ,
y = r sin φ.
Уравнения кривых в полярных координатах
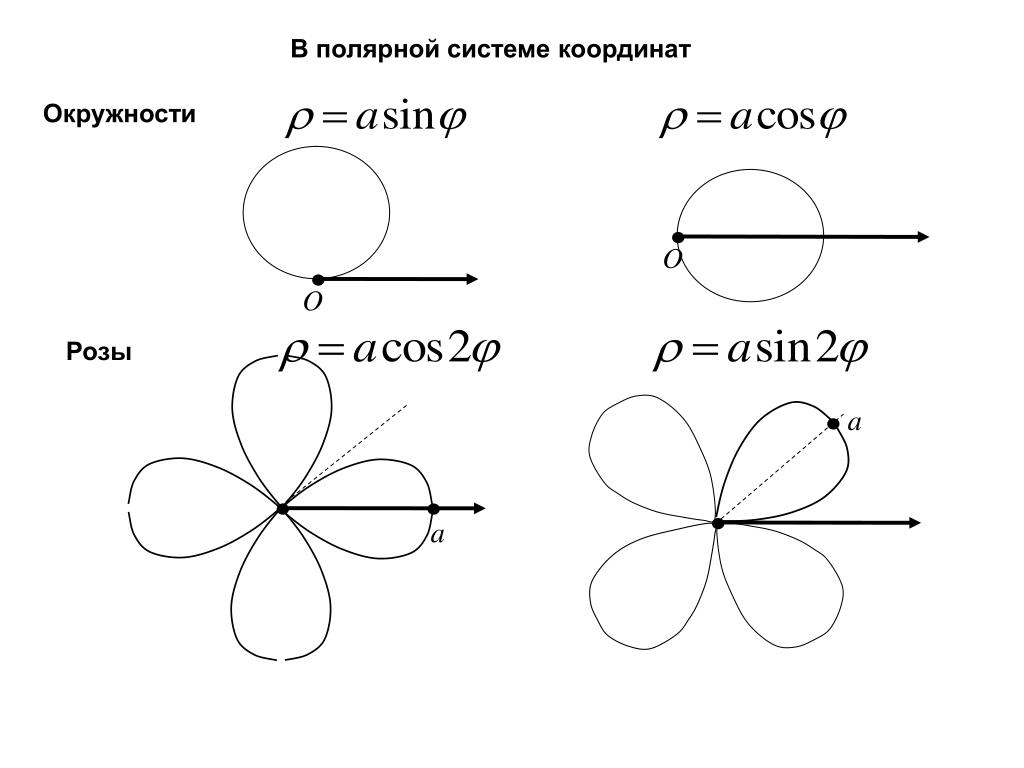
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль.
1. Окружность в полярной системе (рис. 5).
Общее уравнение окружности с центром в (r0, θ) и радиусом a имеет вид:
r2 – 2rr0 cos(φ — θ) + r02 = a2.
Это уравнение может быть упрощено для частных случаев, например: r(φ) = a является уравнением, определяющим окружность с центром в полюсе и радиусом a.
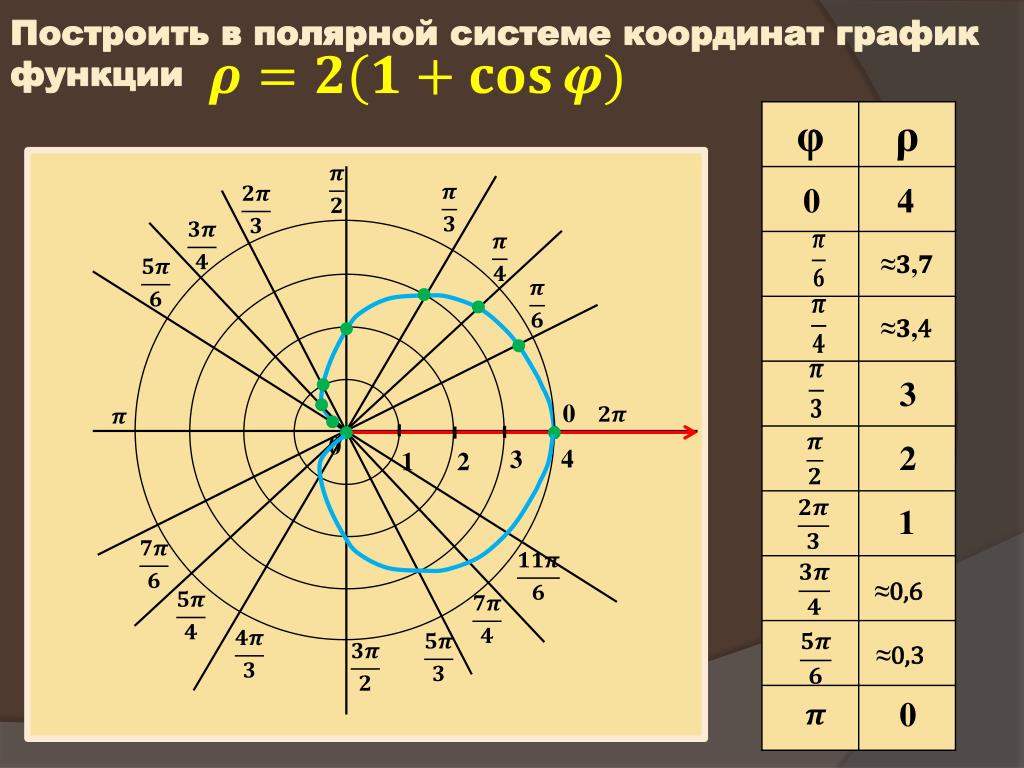
2. Полярная роза (рис. 6).
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
r(φ) = a cos(kφ + θ)
для произвольной постоянной θ (включая 0).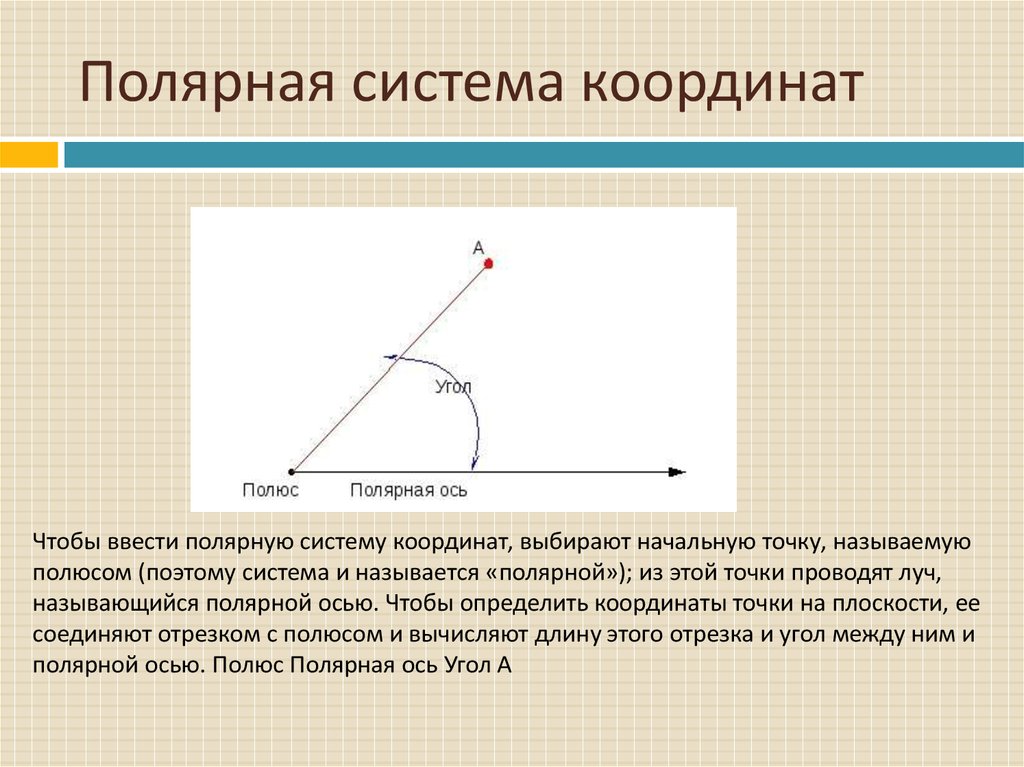 Если k –
целое число, то это уравнение будет определять розу с k лепестками для нечётных k, либо с 2k лепестками для чётных k. Если k – рациональное, но не целое,
график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут
перекрываться.
Если k –
целое число, то это уравнение будет определять розу с k лепестками для нечётных k, либо с 2k лепестками для чётных k. Если k – рациональное, но не целое,
график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут
перекрываться.
Практическое применение розы.
В различных областях науки и техники
Применяется в измерительных лабораториях и цехах предприятий точного приборостроения, машиностроения, микроэлектроники, в инструментальном производстве, а также в лабораториях НИИ (рис. 9).
В математическом дизайне и архитектуре малых форм.
С помощью выращенных цветов, различных кривых в полярных координатах и графических редакторов можно сделать например различные рисунки, рамки-орнаменты, или украсить ими различные предметы (рис. 10).
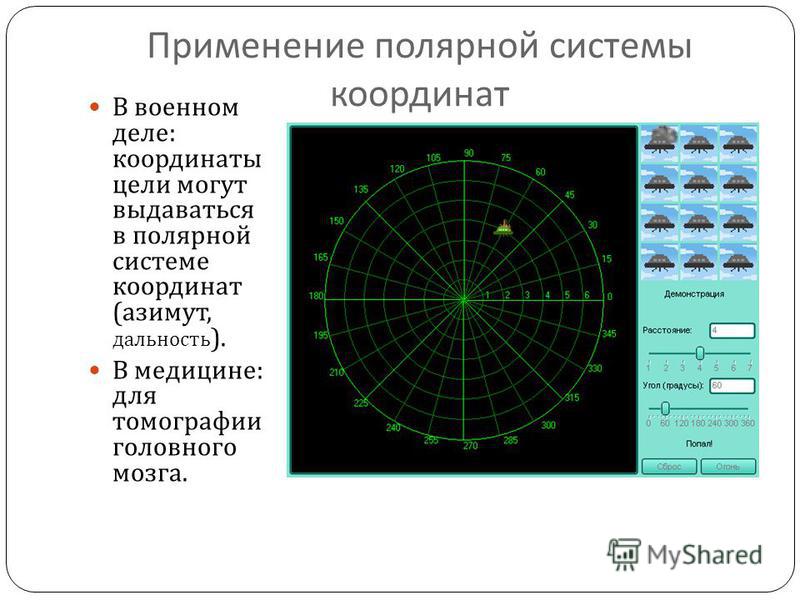
В военном деле.
Координаты цели могут выдаваться в полярной системе координат (азимут, дальность), прямоугольной (X, Y) (рис. 8).
3. Спираль Архимеда (рис. 7).
Архимедова спираль названа в честь
её изобретателя, древнегреческого математика Архимеда.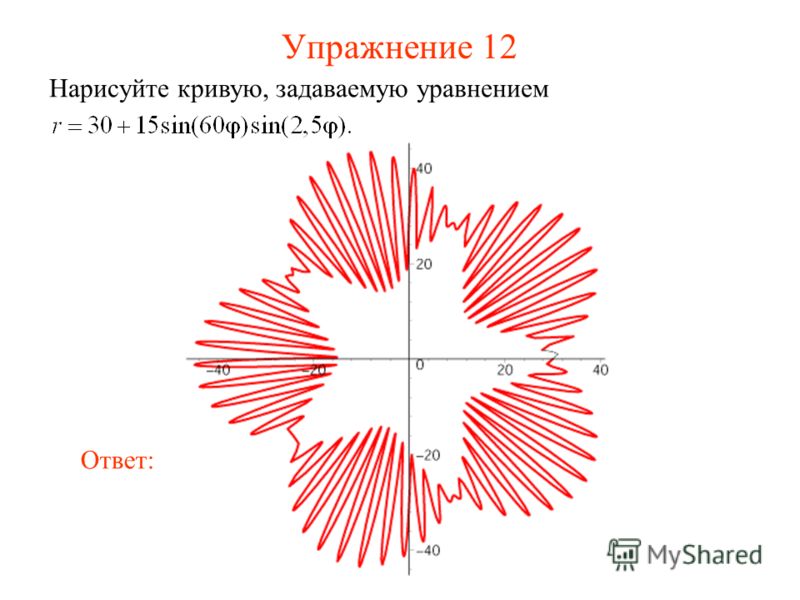 Эту спираль можно
определить с помощью простого полярного уравнения:
Эту спираль можно
определить с помощью простого полярного уравнения:
r(φ) = a + bφ.
Изменения параметра a приводят к повороту спирали, а параметра b – расстояния между витками, которое является константой для конкретной спирали.
Практическое применение спирали
В III веке да нашей эры Архимед на основе своей спирали изобрёл винт, который успешно применяли для передачи воды в оросительные каналы из водоёмов (рис. 11).
В автомобильной технике архимедовы винты могут применяться вместо колес. Принцип движения шнекороторного вездехода прост. При вращении они отталкиваются от кашеобразной или жидкой субстанции, по которой движется вездеход, и продвигают его вперед (рис. 11).
Решение задач
1. Задача на перевод координат из полярной в декартову систему и наоборот.
Возьмём точку в декартовой системе координат A(4;3).
Воспользуемся формулами по переводу в полярную систему координат:
r² = y² + x²,
φ = arctg y/x; x ≠ 0;
И получаем, что r2 = 32 + 42, r=5.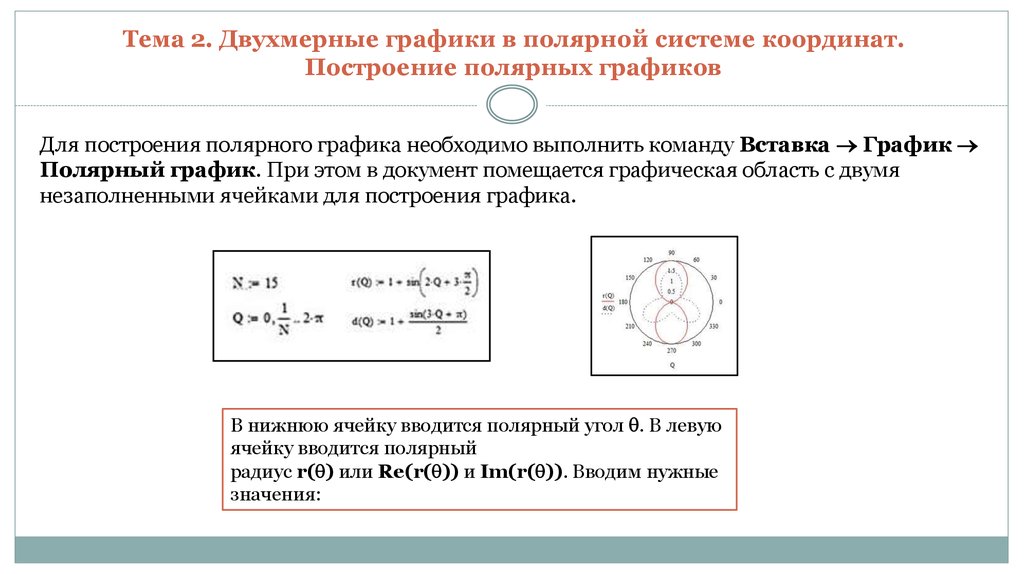
φ = arctg ¾, φ = 0.64 rad
A(5;0.64 )
Теперь переведем из полярной системы в декартову
Возьмем точку M(5; 5/6 π)
x = r cos φ,
y = r sin φ.
С помощью этих формул найдем абсциссу и ординату точки:
x = 5 cos(5/6 π), x ≈ -4,3,
y = 5 sin(5/6 π), y = 2,5.
2. Построение лемнискаты Бернулли
Рассмотрим уравнение кривой в декартовой системе координат:
(x2 + y2)2 = 2c2 (x2 – y2).
Переведем в полярную систему с помощью формул
x = r cos φ,
y = r sin φ.
(r2 cos2 φ + r2 sin2 φ)2 = 2c2 (r2 cos2 φ – r2 sin2 φ).
Получим: r2 = 2c2 cos2φ.
Построим эту кривую.
φ | 0 | π/12 | π/8 | π/6 | π/4 | 3π/4 | 5π/6 | 7π/8 | 11π/12 | π |
r | ≈1,4 | ≈1,3 | ≈1,1 | 1 | 0 | 0 | 1 | ≈1,1 | ≈1,3 | ≈1,4 |
Дальше точки симметричные.
Как мы можем заметить, в уравнении полярной системы происходят более легкие подсчеты, чем в декартовой.
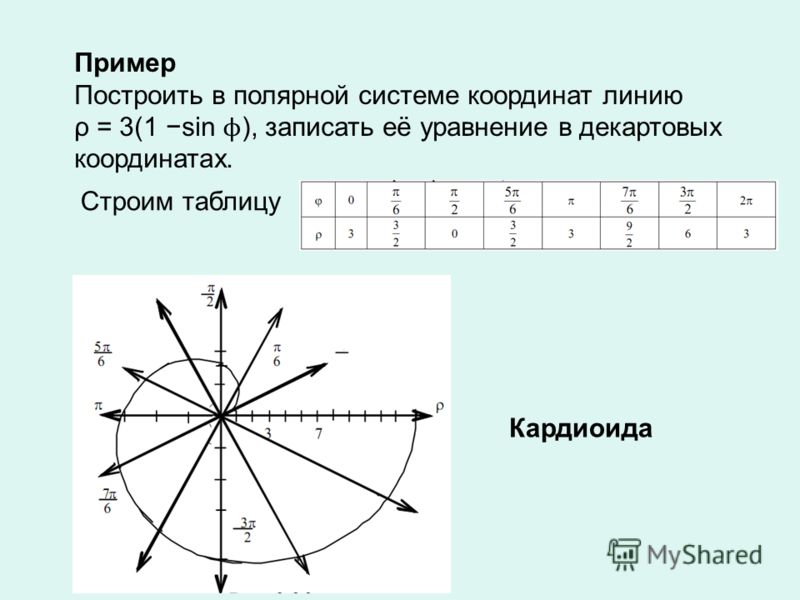
Это уравнение лемнискаты Бернулли. Плоская алгебраическая кривая. По форме напоминает восьмёрку или символ бесконечности (рис. 12).
Заключение
В данной работе мы исследовали полярную систему координат на плоскости.
Рассмотрели связь между декартовыми и полярными координатами, а так же уравнения линий в полярных координатах
Научились: переводить координаты одной системы в другую и наоборот, решать задачи на построение сложных кривых и узнали, как они используются в жизни.
Узнали, что в полярной системе координат, в отличие от прямоугольной, некоторые кривые могут быть достаточно просто описаны полярным уравнением.
Использованная литература
1. https://ru.wikipedia.org/wiki/Лемниската_Бернулли
https://ru.wikipedia.org/wiki/Лемниската_Бернулли
2. http://mathprofi.ru/poljarnye_koordinaty.html
3. https://ru.wikipedia.org/wiki/Полярная_система_координат
4. https://infourok.ru/proekt-na-temu-zamechatelnie-krivie-3010763.html
5. https://ru.wikipedia.org/wiki/Прямоугольная_система_координат
6. https://www.matburo.ru/ex_ag.php?p1=agpsk
Приложения
рис. 1
1
рис. 2 рис. 3
рис. 4 рис. 5 рис. 6
рис. 7
рис. 8 рис. 9
7
рис. 8 рис. 9
рис. 10 рис. 11
рис. 12
5.2. Построение графиков в полярной системе координат при помощи MathCad
Для того чтобы построить график в полярной системе координат при помощи MathCAD, необходимо:
Определить как дискретную переменную (в пределах области определения).
Задать функцию () .
Щелкнуть мышью в свободном месте.
 Выбрать из
меню «Графика» PolarPlot (Полярный график).
Выбрать из
меню «Графика» PolarPlot (Полярный график).В появившемся шаблоне напечатать в нижнем поле, напечатать () в левом поле.
Щелкнуть мышью вне графика.
Пример 2. Построим график функции (спираль Архимеда) при помощиMathCAD.
Решение.
График в полярных координатах можно форматировать.
Чтобы открыть окно форматирования графика поступают также как при форматировании декартово графика. Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.
5.3. Задания для самостоятельного решения
1. Построить (в тетради) в полярной системе координат линию по точкам, придавая значения от 0 до с шагом (для вычисления значений можно использовать возможности MathCAD):
1. | ,, | 11. | , , |
2. | , , | 12. | , , |
3. | , , | 13. | , , |
4. | , , | 14. | , , |
5. | , , | 15. | ,, |
6. | , , | 16. | , , |
7. | , , | 17. | , , |
8. | , , | 18. | , , |
9. | , , | 19. | , , |
10. | , , | 20. | , , |
2. При помощи MathCAD построить кривые в полярной системе координат, придавая различные значения параметру а:
1. | 11. | ||
2. | 12. | ||
3. | 13. | ||
4. | 14. | ||
5. | 15. | ||
6. | 16. | ||
7. | 17. | ||
8. | 18. | ||
9. | 19. | ||
10. | 20. |
Лабораторная работа № 6 Тема: Символьные вычисления
Цель работы: Научиться производить символьные вычисления: преобразовывать выражения, вычислять пределы.
MathCAD позволяет получить значение некоторого выражения в численном виде (при помощи обычного знака равенства) или в символьном виде (при помощи знака символьного равенства, о котором будет рассказано ниже). В первом случае после знака равенства появляется одно или несколько чисел. Во втором случае результатом вычислений является некоторое выражение.
Прежде, чем производить символьные вычисления, необходимо убедиться, что символьный процессор включен в работу: в меню «Math» должны быть отмечены команды «Live Symbolics» («Использовать символику») и «Automatic Mode» («Автоматический режим»).
Знак
символьного равенства
представляет собой стрелку вправо ()
и набирается сочетанием клавиш [Ctrl]
и [. ],
либо с палитры «Преобразования».
],
либо с палитры «Преобразования».
Чтобы произвести символьные вычисления, необходимо:
Ввести выражение, которое надо вычислить или преобразовать.
Выделить выражение синей выделительной рамкой и набрать знак символьного равенства.
Щелкнуть мышью вне выражения.
Проиллюстрируем разницу между численным и символьным результатом на простом примере. Вычислим двумя способами:
Следует отметить, что для одних выражений можно произвести как численные, так и символьные вычисления, для других – только численные, для третьих – только символьные.
При помощи символьных вычислений можно вычислять пределы, решать неопределенные системы уравнений (т.е. системы, которые имеют множество решений), преобразовывать выражения, находить производные и т.д.
8.3 Полярные координаты — предварительное вычисление 2e
Цели обучения
В этом разделе вы:
- Нанесение точек с использованием полярных координат.

- Преобразовать полярные координаты в прямоугольные.
- Преобразовать прямоугольные координаты в полярные.
- Преобразование уравнений между полярной и прямоугольной формами.
- Определите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.
На расстоянии более 12 км от порта парусник попадает в непогоду и сбивается с курса ветром со скоростью 16 узлов (см. рис. 1). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
Рисунок 1
Нанесение точек с использованием полярных координат
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах (x,y)(x,y) в декартовой координатной плоскости. Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные (r, θ) (r, θ) и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.
Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.
Полярная сетка масштабируется как единичный круг с положительной осью x-, которая теперь рассматривается как полярная ось, а начало координат — как полюс. Первая координата rr — это радиус или длина направленного отрезка прямой от полюса. Угол θ, θ, измеренный в радианах, указывает направление r.r. Сдвинемся против часовой стрелки от полярной оси на угол θ, θ и отмерим направленный отрезок длиной rr в направлении θ.θ. Несмотря на то, что сначала мы измеряем θθ, а затем r, r, полярная точка записывается с помощью r -координата первая. Например, чтобы нанести точку (2,π4),(2,π4), мы должны переместиться на π4π4 единицы против часовой стрелки, а затем на длину, равную 2, от полюса. Эта точка нанесена на сетку на рисунке 2.
Рисунок 2
Пример 1
Нанесение точки на полярную сетку
Нанесение точки (3,π2)(3,π2) на полярную сетку.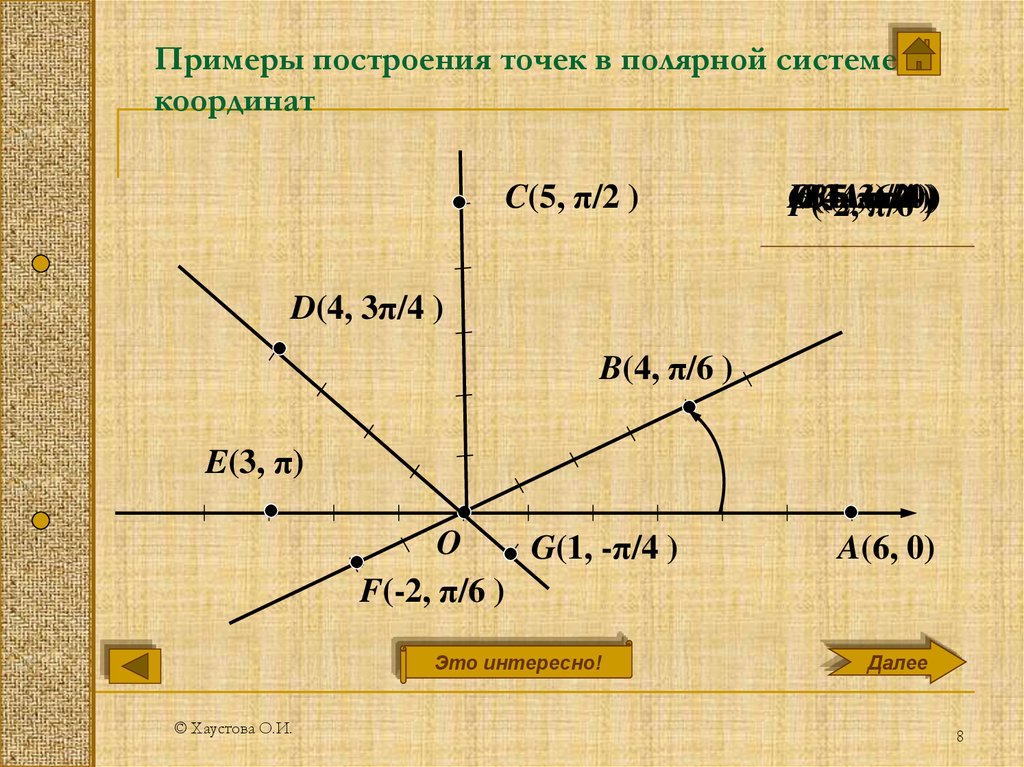
Решение
Угол π2π2 находится путем пролистывания против часовой стрелки 90° от полярной оси. Точка расположена на расстоянии 3 единиц от полюса в направлении π2π2, как показано на рисунке 3.
Рисунок 3
Попытайся #1
Нанесите точку (2,π3)(2,π3) на полярную сетку.
Пример 2
Нанесение точки в полярной системе координат с отрицательной составляющей
Нанесение точки (−2,π6)(−2,π6) на полярную сетку.
Решение
Мы знаем, что π6π6 находится в первом квадранте. Однако r=-2.r=-2. Мы можем подойти к построению точки с отрицательным значением rr двумя способами:
- Постройте точку (2,π6)(2,π6), переместив π6π6 против часовой стрелки и продлив направленный отрезок на 2 единицы в первый квадрант. Затем проследите направленный отрезок обратно через полюс и продолжайте движение на 2 единицы в третий квадрант;
- Переместите π6π6 против часовой стрелки и проведите отрезок, направленный от полюса, на 2 единицы в отрицательном направлении, в третий квадрант.

См. рис. 4(а). Сравните это с графиком полярной координаты (2,π6)(2,π6), показанным на рисунке 4(b).
Рисунок 4
Попытайся #2
Нанесите точки (3,−π6)(3,−π6) и (2,9π4)(2,9π4) на одну и ту же полярную сетку.
Преобразование полярных координат в прямоугольные координаты
Когда задан набор полярных координат, нам может потребоваться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными x, y, r, x, y, r и θ.θ.
cosθ=xr→x=rcosθsinθ=yr→y=rsinθcosθ=xr→x=rcosθsinθ=yr→y=rsinθ
Если опустить перпендикуляр из точки плоскости на ось x-, получится прямоугольный треугольник, как показано на рис. 5. Простой способ запомнить приведенные выше уравнения — представить cosθcosθ как прилежащую сторону к гипотенузе и sinθsinθ как противоположная сторона относительно гипотенузы.
Рисунок 5
Преобразование полярных координат в прямоугольные координаты
Чтобы преобразовать полярные координаты (r, θ) (r, θ) в прямоугольные координаты (x, y), (x, y), пусть
cosθ=xr→x=rcosθcosθ=xr→x=rcosθ
sinθ=yr→y=rsinθsinθ=yr→y=rsinθ
Как
Учитывая полярные координаты, преобразовать в прямоугольные координаты.
- Учитывая полярную координату (r,θ),(r,θ), напишите x=rcosθx=rcosθ и y=rsinθ.y=rsinθ.
- Оценить cosθcosθ и sinθ.sinθ.
- Умножьте cosθcosθ на rr, чтобы найти координату x- прямоугольной формы.
- Умножьте sinθsinθ на rr, чтобы найти y- координата прямоугольной формы.
Пример 3
Запись полярных координат в виде прямоугольных координат
Запись полярных координат (3,π2)(3,π2) в виде прямоугольных координат.
Решение
Использовать эквивалентные отношения.
x=rcosθx=3cosπ2=0y=rsinθy=3sinπ2=3x=rcosθx=3cosπ2=0y=rsinθy=3sinπ2=3
Прямоугольные координаты (0,3).(0,3). См. рис. 6.
Рис. 6
Пример 4
Запись полярных координат в виде прямоугольных координат
Запись полярных координат (−2,0)(−2,0) в виде прямоугольных координат.
Решение
См. рис. 7. Записав полярные координаты в виде прямоугольника, мы получим rsinθy=−2sin(0)=0
Прямоугольные координаты также равны (−2,0).(−2,0).
Рисунок 7
Попытайся #3
Запишите полярные координаты (−1,2π3)(−1,2π3) в виде прямоугольных координат.
Преобразование прямоугольных координат в полярные координаты
Чтобы преобразовать прямоугольные координаты в полярные координаты, мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки.
Преобразование прямоугольных координат в полярные координаты
Преобразование прямоугольных координат в полярные требует использования одного или нескольких соотношений, показанных на рис. 8.
cosθ=xrx=rcosθsinθ=yrory=rsinθr2=x2+y2tanθ=yxcosθ=xrx=rcosθsinθ=yrory=rsinθr2=x2+y2tanθ=yx
Рисунок 8
Пример 5
Запись прямоугольных координат в виде полярных координат
Преобразование прямоугольных координат (3,3)(3,3) в полярные координаты.
Решение
Мы видим, что исходная точка (3,3)(3,3) находится в первом квадранте. Чтобы найти θ,θ, используйте формулу tanθ=yx.tanθ=yx. Это дает
tanθ=33tanθ=1θ=tan−1(1)θ=π4tanθ=33tanθ=1θ=tan−1(1)θ=π4
Чтобы найти r,r, подставляем значения xx и yy в формулу r=x2+y2.r=x2+y2. Мы знаем, что rr должно быть положительным, так как π4π4 находится в первом квадранте. Таким образом,
r=32+32r=9+9r=18=32r=32+32r=9+9r=18=32
Итак, r=32r=32 и θ=π4,θ=π4, что дает нам полярную точка (32,π4).(32,π4). См. рис. 9.
Рис. 9
Анализ
Существуют и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки (−32,5π4)(−32,5π4) и (32,−7π4)(32,−7π4) совпадут с исходным решением (32,π4).(32,π4). Точка (−32,5π4)(−32,5π4) указывает на дальнейшее движение против часовой стрелки на π,π, что прямо противоположно π4.π4. Радиус выражается как -32.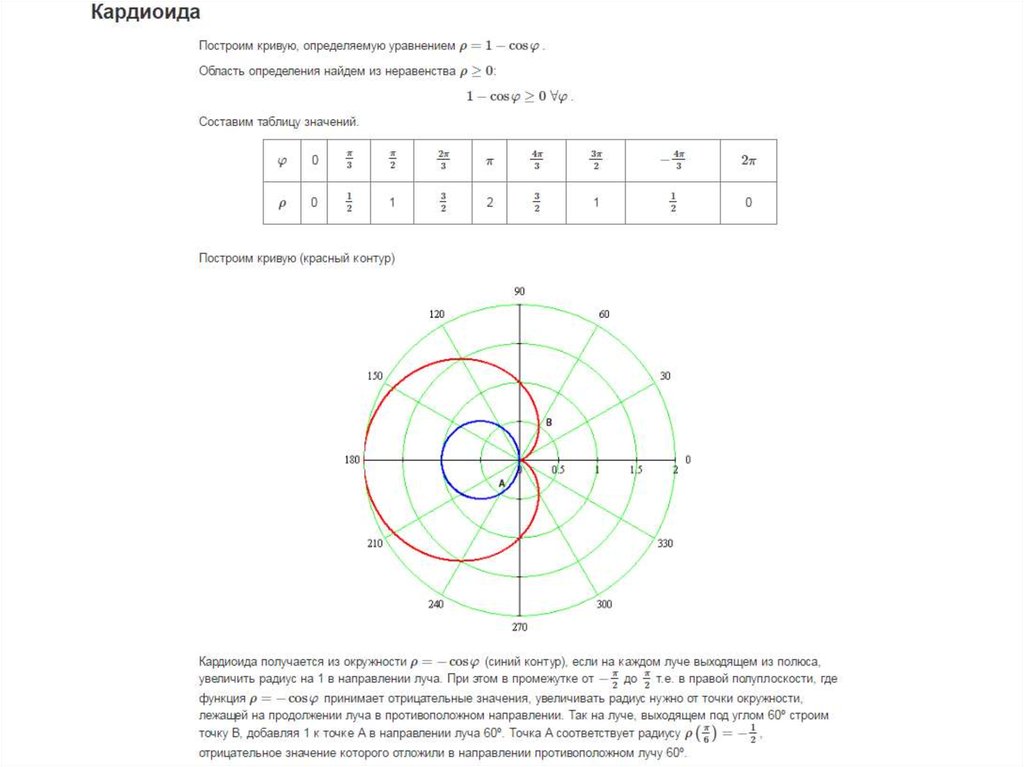 -32. Однако угол 5π45π4 расположен в третьем квадранте, и, поскольку rr отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант. Это та же точка, что и (32,π4).(32,π4). Точка (32,−7π4)(32,−7π4) находится дальше по часовой стрелке на −7π4,−7π4 от точки π4.π4. Радиус 32,32 такой же.
-32. Однако угол 5π45π4 расположен в третьем квадранте, и, поскольку rr отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант. Это та же точка, что и (32,π4).(32,π4). Точка (32,−7π4)(32,−7π4) находится дальше по часовой стрелке на −7π4,−7π4 от точки π4.π4. Радиус 32,32 такой же.
Преобразование уравнений между полярными и прямоугольными формами
Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами. Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, что и для преобразования точек между системами координат. Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.
Как
Имея уравнение в полярной форме, постройте его график с помощью графического калькулятора.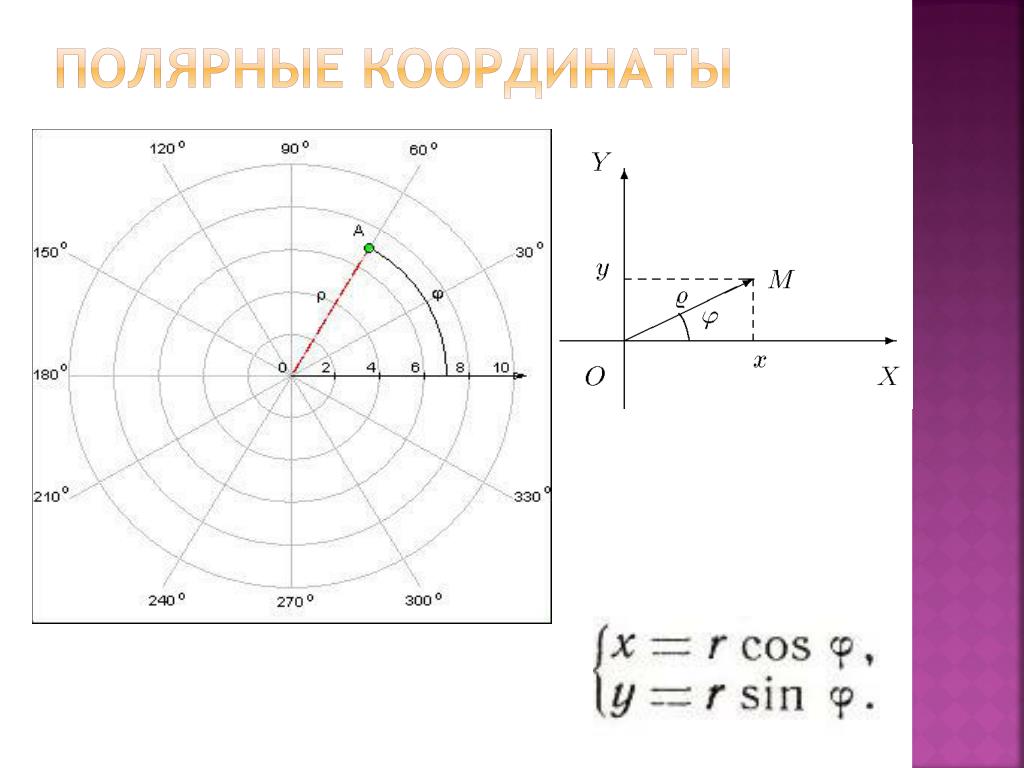
- Измените MODE на POL , представляя полярную форму.
- Нажмите кнопку Y= , чтобы вызвать экран, позволяющий ввести шесть уравнений: r1,r2,…,r6.r1,r2,…,r6.
- Введите полярное уравнение, установите равным r.r.
- Нажмите ГРАФИК .
Пример 6
Написание декартова уравнения в полярной форме
Напишите декартово уравнение x2+y2=9×2+y2=9 в полярной форме.
Решение
Цель состоит в том, чтобы исключить xx и yy из уравнения и ввести rr и θ.θ. В идеале мы запишем уравнение rr как функцию θ.θ. Чтобы получить полярную форму, мы будем использовать соотношения между (x,y)(x,y) и (r,θ).(r,θ). Поскольку x=rcosθx=rcosθ и y=rsinθ,y=rsinθ, мы можем подставить и решить для r.r.
(rcosθ)2+(rsinθ)2=9r2cos2θ+r2sin2θ=9r2(cos2θ+sin2θ)=9r2(1)=9Замените cos2θ+sin2θ=1.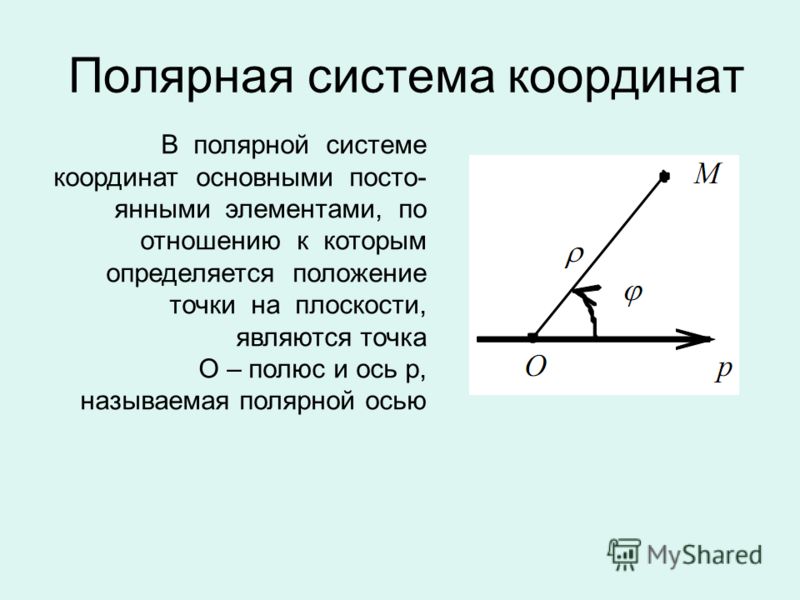 r=±3Используйте свойство квадратного корня. (rcosθ)2+(rsinθ)2=9 r2cos2θ+r2sin2θ=9r2(cos2θ+sin2θ)=9r2(1)=9Замените cos2θ+sin2θ=1. r=±3Используйте свойство квадратного корня.
r=±3Используйте свойство квадратного корня. (rcosθ)2+(rsinθ)2=9 r2cos2θ+r2sin2θ=9r2(cos2θ+sin2θ)=9r2(1)=9Замените cos2θ+sin2θ=1. r=±3Используйте свойство квадратного корня.
Таким образом, x2+y2=9,r=3,x2+y2=9,r=3 и r=-3r=-3 должны генерировать один и тот же граф. См. рис. 10.
Рис. 10 (a) Декартова форма x2+y2=9×2+y2=9 (b) Полярная форма r=3r=3
Чтобы нарисовать окружность в прямоугольной форме, мы должны сначала найти y.y.
x2+y2=9 y2=9−x2 y=±9−x2x2+y2=9 y2=9−x2 y=±9−x2
Обратите внимание, что это две отдельные функции, поскольку окружность не совпадает с вертикальной линией тест. Поэтому нам нужно ввести в калькулятор положительные и отрицательные квадратные корни отдельно, как два уравнения вида Y1=9−x2Y1=9−x2 и Y2=−9−x2.Y2=−9−x2. Нажмите ГРАФИК.
Пример 7
Преобразование декартова уравнения в полярное уравнение
Преобразование декартова уравнения x2+y2=6yx2+y2=6y в полярное уравнение.
Решение
Это уравнение похоже на предыдущий пример, но для преобразования уравнения требуются другие шаги.
Мы все еще можем следовать тем же процедурам, которые мы уже изучили, и сделать следующие замены: )=0Фактор и решение.r=0Мы отклоняем r=0, так как он представляет только одну точку, (0,0).r=6sinθr2=6yUse x2+y2=r2.r2=6rsinθSubstitutey=rsinθ.r2−6rsinθ=0Установить равным к 0.r(r−6sinθ)=0Factor и решить.r=0Мы отвергаем r=0, так как он представляет только одну точку, (0,0).r=6sinθ
Следовательно, уравнения x2+y2=6yx2+y2=6y и r=6sinθr=6sinθ должны дать нам один и тот же график. См. рис. 11.
Рис. 11 (a) Декартова форма x2+y2=6yx2+y2=6y (b) Полярная форма r=6sinθr=6sinθ
Декартово или прямоугольное уравнение наносится на прямоугольную сетку, а полярное уравнение наносится на полярную сетку. Ясно, что графики идентичны.
Пример 8
Переписывание декартова уравнения в полярной форме
Перепишите декартово уравнение y=3x+2y=3x+2 как полярное уравнение.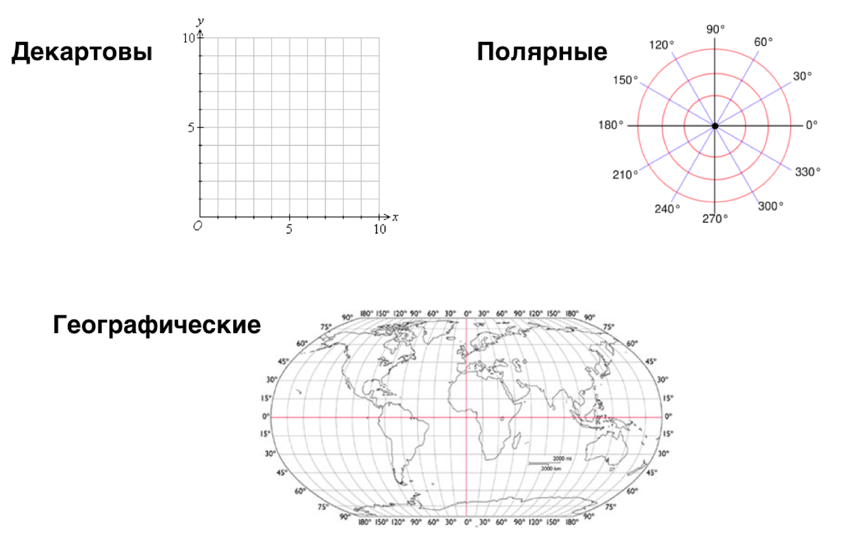
Решение
Мы будем использовать соотношения x=rcosθx=rcosθ и y=rsinθ.y=rsinθ.
y=3x+2 rsinθ=3rcosθ+2rsinθ−3rcosθ=2r(sinθ−3cosθ)=2Изолировать r.r=2sinθ−3cosθ. Решить для r y=3x+2 rsinθ=3rcosθ+2rsinθ−3rcosθ=2r(sinθ−3cosθ)=2Изолировать r.r=2sinθ−3cosθНайти r.
Попытайся #4
Перепишите декартово уравнение y2=3−x2y2=3−x2 в полярной форме.
Определение и построение полярных уравнений путем преобразования в уравнения прямоугольной формы
Мы научились преобразовывать прямоугольные координаты в полярные и увидели, что точки действительно совпадают. Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Пример 9
График полярного уравнения путем преобразования в прямоугольное уравнение
Превратите полярное уравнение r=2secθr=2secθ в прямоугольное уравнение и нарисуйте соответствующий график.
Решение
Преобразование
r=2secθr=2cosθrcosθ=2x=2r=2secθr=2cosθrcosθ=2x=2
Обратите внимание, что уравнение r=2secθr=2secθ, нарисованное на полярной сетке, явно совпадает с вертикальной линией x=2x =2 на прямоугольной сетке (см. рис. 12). Точно так же, как x=cx=c является стандартной формой для вертикальной линии в прямоугольной форме, r=csecθr=csecθ является стандартной формой для вертикальной линии в полярной форме.
Рисунок 12 (a) Полярная сетка (b) Прямоугольная система координат
Аналогичное обсуждение покажет, что графиком функции r=2cscθr=2cscθ будет горизонтальная линия y=2.y=2. Фактически, r=ccscθr=ccscθ является стандартной формой горизонтальной линии в полярной форме, соответствующей прямоугольной форме y=c.y=c.
Пример 10
Переписать полярное уравнение в декартовой форме
Переписать полярное уравнение r=31−2cosθr=31−2cosθ как декартово уравнение.
Решение
Цель состоит в том, чтобы исключить θθ и r,r и ввести xx и y.y. Очищаем дробь, а затем используем подстановку. Чтобы заменить rr на xx и y,y, мы должны использовать выражение x2+y2=r2.x2+y2=r2.
r=31-2cosθr(1-2(xr))=3r-2x=3Usecosθ=xrtoeliminateθr-2x=3r=3+2xIsoloterr2=(3+2x)2Квадрат с обеих сторонx2+y2=(3+2x)2Usex2+y2= r2r=31-2cosθr(1-2(xr))=3r-2x=3Usecosθ=xrчтобы исключить θr-2x=3r=3+2xIsolaterr2=(3+2x)2Квадратобе стороныx2+y2=(3+2x)2Usex2+y2=r2
Декартово уравнение: x2+y2=(3+2x)2.x2+y2=(3+2x)2. Однако для его построения, особенно с помощью графического калькулятора или компьютерной программы, мы хотим выделить y.y.
x2+y2=(3+2x)2 y2=(3+2x)2−x2 y=±(3+2x)2−x2x2+y2=(3+2x)2 y2=(3+2x)2 −x2 y=±(3+2x)2−x2
Когда все наше уравнение было изменено с rr и θθ на xx и y, y, мы можем остановиться, если только нас не попросят найти yy или упростить. См. рис. 13.
Рис.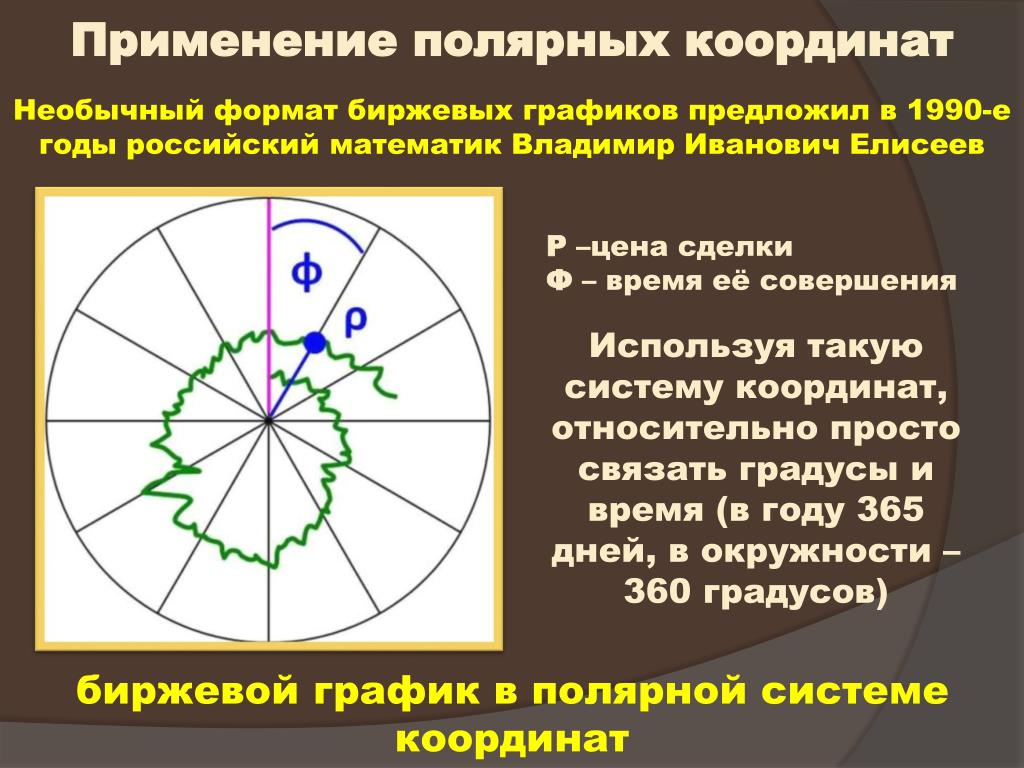 13
13
Форма графика в виде песочных часов называется гипербола . Гиперболы имеют много интересных геометрических свойств и приложений, которые мы будем исследовать далее в разделе «Аналитическая геометрия».
Анализ
В этом примере правая часть уравнения может быть расширена, а уравнение еще больше упрощено, как показано выше. Однако уравнение нельзя записать в виде одной функции в декартовой форме. Мы можем захотеть записать прямоугольное уравнение в стандартной форме гиперболы. Для этого мы можем начать с исходного уравнения.
x2+y2=(3+2x)2×2+y2-(3+2x)2=0x2+y2-(9+12x+4×2)=0x2+y2-9-12x-4×2=0-3×2-12x+ y2=9Умножить на-13×2+12x-y2=-93(x2+4x+)-y2=-93(x2+4x+4)-y2=-9+12 Организовать термины, чтобы заполнить квадрат дляx3(x+2)2-y2=3(x+2) )2-y23=1×2+y2=(3+2x)2×2+y2-(3+2x)2=0x2+y2-(9+12x+4×2)=0x2+y2-9-12x-4×2=0-3×2 -12x+y2=9Умножить на-13×2+12x-y2=-93(x2+4x+)-y2=-93(x2+4x+4)-y2=-9+12 Организуйте члены, чтобы заполнить квадрат для x3(x+2)2-y2=3( х+2)2-у23=1
Попытайся #5
Перепишите полярное уравнение r=2sinθr=2sinθ в декартовой форме.
Пример 11
Переписать полярное уравнение в декартовой форме
Переписать полярное уравнение r=sin(2θ)r=sin(2θ) в декартовой форме.
Решение
r=sin(2θ)Используйте тождество двойного угла для синуса. r=2sinθcosθИспользуйте cosθ=xr и sinθ=yr. r=2(xr)(yr) Упростить. r=2xyr2 Умножьте обе части на r2. r3=2xy(x2+y2)3=2xyAsx2+y2=r2,r=x2+y2. r=sin(2θ)Используйте тождество двойного угла для синуса. r=2sinθcosθИспользуйте cosθ=xr и sinθ=yr. r=2(xr)(yr) Упростить. r=2xyr2 Умножьте обе части на r2. r3=2xy(x2+y2)3=2xyAsx2+y2=r2,r=x2+y2.
Это уравнение также можно записать в виде
(x2+y2)32=2xyorx2+y2=(2xy)23(x2+y2)32=2xyorx2+y2=(2xy)23
8.3 Секционные упражнения
Устный
1.
Чем полярные координаты отличаются от прямоугольных?
2.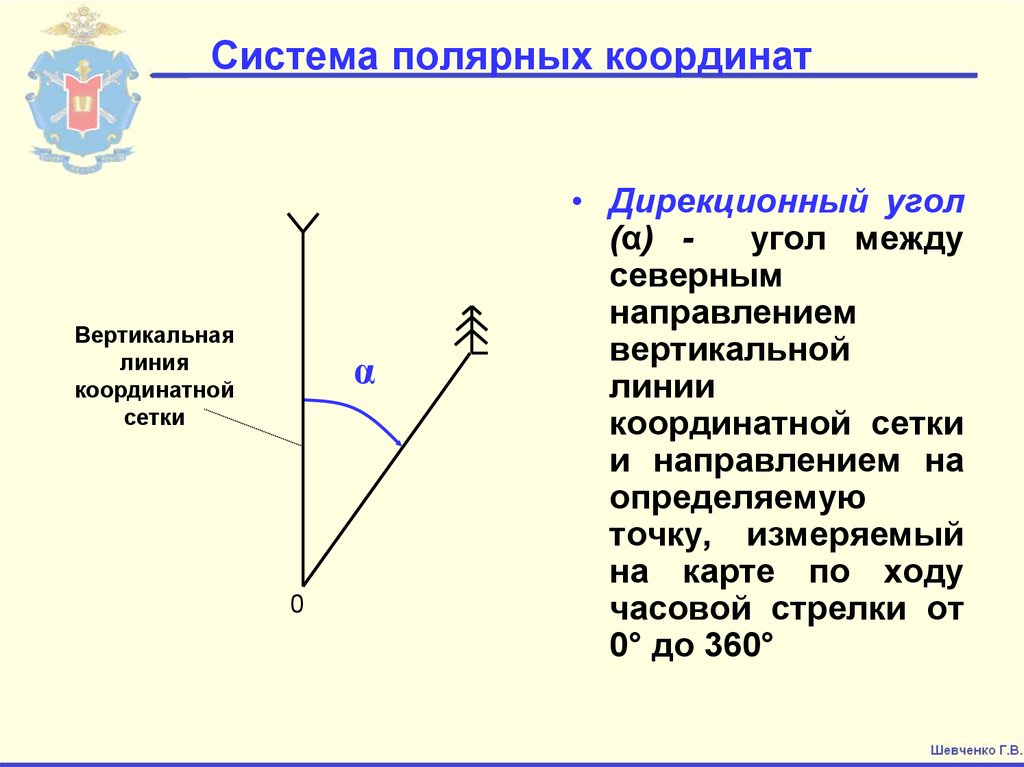
Чем полярные оси отличаются от осей x и y декартовой плоскости?
3.
Объясните, как изображаются полярные координаты.
4.
Как связаны точки (3,π2)(3,π2) и (−3,π2)(−3,π2)?
5.
Объясните, почему точки (−3,π2)(−3,π2) и (3,−π2)(3,−π2) совпадают.
Алгебраический
Для следующих упражнений преобразуйте заданные полярные координаты в декартовы координаты. Не забудьте учитывать квадрант, в котором находится данная точка, при определении θθ для точки.
6.
(7,7π6)(7,7π6)
7.
(5,π)(5,π)
8.
(6,−π4)(6,−π4)
9.
(−3,π6)(−3,π6)
10.
(4,7π4)(4,7π4)
Для следующих упражнений преобразуйте заданные декартовы координаты в полярные координаты с r>0,0≤θ<2π.r>0,0≤θ<2π. Не забудьте рассмотреть квадрант, в котором находится данная точка.
11.
(4,2)(4,2)
12.
(−4,6)(−4,6)
13.
(3,−5)(3,−5)
14.
(-10,-13)(-10,-13)
15.
(8,8)(8,8)
Для следующих упражнений преобразуйте данное декартово уравнение в полярное уравнение.
16.
х=3х=3
17.
у=4у=4
18.
у=4х2у=4х2
19.
у=2х4у=2х4
20.
х2+у2=4ух2+у2=4у
21.
х2+у2=3хх2+у2=3х
22.
х2-у2=хх2-у2=х
23.
х2-у2=3ух2-у2=3у
24.
х2+у2=9х2+у2=9
25.
х2=9ух2=9у
26.
у2=9ху2=9х
27.
9xy=19xy=1
Для следующих упражнений преобразуйте данное полярное уравнение в декартово уравнение. Если возможно, напишите в стандартной форме коники и определите представленное коническое сечение.
28.
r=3sinθr=3sinθ
29.
r=4cosθr=4cosθ
30.
r=4sinθ+7cosθr=4sinθ+7cosθ
31.
r=6cosθ+3sinθr=6cosθ+3sinθ
32.
r=2сек θr=2секθ
33.
r=3cscθr=3cscθ
34.
r=rcosθ+2r=rcosθ+2
35.
r2=4секθcscθr2=4секθcscθ
36.
р=4р=4
37.
г2=4р2=4
38.
r=14cosθ−3sinθr=14cosθ−3sinθ
39.
r=3cosθ−5sinθr=3cosθ−5sinθ
Графический
Для следующих упражнений найдите полярные координаты точки.
40.
41.
42.
43.
44.
Для следующих упражнений отметьте точки.
45.
(−2,π3)(−2,π3)
46.
(−1,−π2)(−1,−π2)
47.
(3,5,7π4)(3,5,7π4)
48.
(−4,π3)(−4,π3)
49.
(5,π2)(5,π2)
50.
(4,−5π4)(4,−5π4)
51.
(3,5π6)(3,5π6)
52.
(−1,5,7π6)(−1,5,7π6)
53.
(−2,π4)(−2,π4)
54.
(1,3π2)(1,3π2)
Для следующих упражнений преобразуйте уравнение из прямоугольной в полярную форму и постройте график на полярной оси.
55.
5х-у=65х-у=6
56.
2x+7y=-32x+7y=-3
57.
х2+(у-1)2=1х2+(у-1)2=1
58.
(х+2)2+(у+3)2=13(х+2)2+(у+3)2=13
59.
х=2х=2
60.
х2+у2=5ух2+у2=5у
61.
х2+у2=3хх2+у2=3х
Для следующих упражнений преобразуйте уравнение из полярной формы в прямоугольную и начертите график на прямоугольной плоскости.
62.
г=6р=6
63.
r=-4r=-4
64.
θ=−2π3θ=−2π3
65.
θ=π4θ=π4
66.
r=секθr=секθ
67.
r=-10sinθr=-10sinθ
68.
r=3cosθr=3cosθ
Технология
69.
Используйте графический калькулятор, чтобы найти прямоугольные координаты (2,−π5).(2,−π5). Округлить до тысячных.
70.
Используйте графический калькулятор, чтобы найти прямоугольные координаты (−3,3π7).(−3,3π7). Округлить до тысячных.
71.
Используйте графический калькулятор, чтобы найти полярные координаты (−7,8)(−7,8) в градусах. Округлить до тысячных.
72.
Используйте графический калькулятор, чтобы найти полярные координаты (3,−4)(3,−4) в градусах. Округлить до сотых.
73.
Используйте графический калькулятор, чтобы найти полярные координаты (−2,0)(−2,0) в радианах. Округлить до сотых.
Расширения
74.
Опишите график зависимости r=asecθ;a>0.r=asecθ;a>0.
75.
Опишите график зависимости r=asecθ;a<0.r=asecθ;a<0.
76.
Опишите график зависимости r=acscθ;a>0.r=acscθ;a>0.
77.
Опишите график зависимости r=acscθ;a<0.r=acscθ;a<0.
78.
Какие полярные уравнения дадут косую линию?
Для следующего упражнения постройте график полярного неравенства.
79.
р<4р<4
80.
0≤θ≤π40≤θ≤π4
81.
θ=π4,r≥2θ=π4,r≥2
82.
θ=π4,r≥−3θ=π4,r≥−3
83.
0≤θ≤π3,r<20≤θ≤π3,r<2
84.
−π6<θ≤π3,−3 Калькулятор уравнения прямоугольной формы в полярную имеет дело с двумя системами координат: прямоугольной или декартовой системой координат и полярной системой координат. Эти две системы используются для определения положения точки на 2D-плоскости. Калькулятор уравнения прямоугольной формы в полярную используется для определения положения точки P(x,y) путем нахождения полярных координат (r,θ). Калькулятор уравнения прямоугольной формы в полярную представляет собой онлайн-калькулятор, который преобразует двумерные прямоугольные координаты в полярные координаты. Этот калькулятор принимает прямоугольные компоненты x и y в качестве входных данных, где x — расстояние точки P от начала координат (0,0) по оси x, а y — расстояние точки P от начала координат по оси y. -ось. Полярные координаты r и θ задают положение точки P, где r — радиус окружности или расстояние, пройденное от центра окружности до точки P. θ — угол от положительного x- ось в 9009{ι. Получается из уравнения прямоугольных координат (x+ιy). Ниже приведены шаги, необходимые для использования калькулятора уравнения прямоугольной формы в полярную. Рис. 2 Пошаговый метод преобразования Введите значения координат x и y в блоках с заголовками x и y соответственно. Нажмите кнопку отправки, чтобы калькулятор обработал полярные координаты r и θ. Вывод покажет четыре окна следующим образом: Калькулятор показывает интерпретированные значения координат x и y, для которых определены полярные координаты. Значения по умолчанию для координат x и y равны 3 и -2 соответственно. Блок результатов показывает значения r и θ. Значение r получается путем подстановки значений x и y в следующее уравнение: Калькулятор уравнения прямоугольной формы в полярную + онлайн-решатель с бесплатными шагами
 θ} \]
θ} \] Как использовать калькулятор уравнения прямоугольной формы в полярную
Шаг 1:
Шаг 2:
Вывод:
Интерпретация ввода:
Результат:
Значение r показывает длину вектора или величину результирующего вектора, который всегда является положительным значением.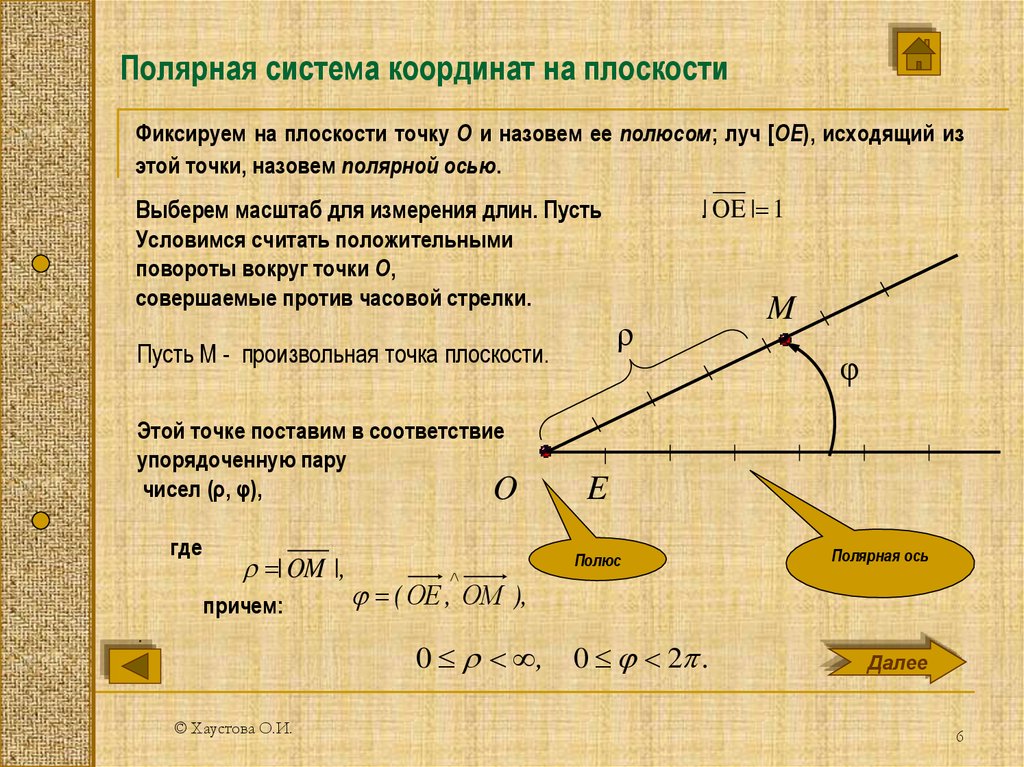
Кроме того, значение θ получается путем подстановки значений x и y в следующее уравнение:
\[ \theta = \arctan (\frac{y}{x}) \]
Положительное значение θ показывает направление против часовой стрелки от оси x, а отрицательное значение показывает направление по часовой стрелке от оси x.
Векторный график:
Векторный график показывает двумерный график с положительными и отрицательными прямоугольными осями координат x и y.
Результирующий вектор рисуется выходными полярными векторами (r, θ) с величиной r, взятой из начала координат, и углом θ, взятым из положительной оси x. Квадрант результирующего вектора определяется координатами (x, y), отображаемыми на графике.
Длина вектора:
Длина вектора показывает величину r результирующего вектора.
Примеры
Вот несколько примеров, которые решаются с помощью калькулятора уравнений прямоугольного и полярного типов . 92 } \]
\[ r = \sqrt{ 4 + 12 } \]
\[ r = \sqrt{ 16 } \]
r = 4
\[ \theta = \arctan (\ frac{y}{x}) \]
\[ \theta = \arctan (\frac{2(\sqrt{3})}{2}) \]
\[ \theta = \arctan ( \sqrt {3} ) \]
$\theta$ = 60°
На рис.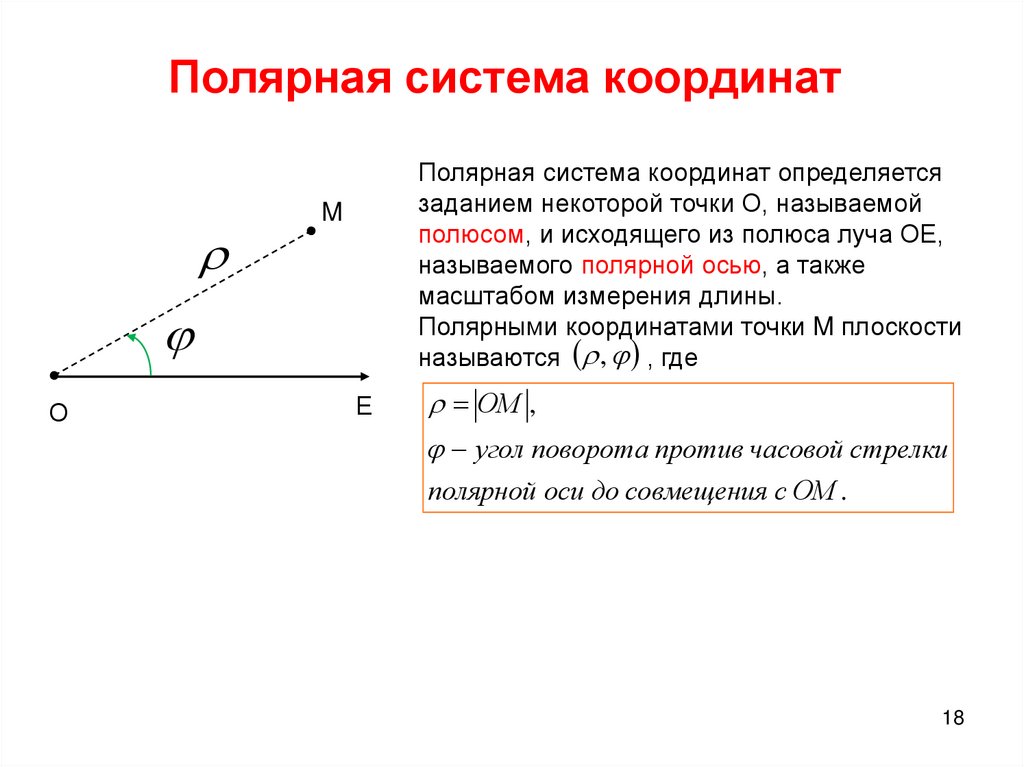

 Выбрать из
меню «Графика» PolarPlot (Полярный график).
Выбрать из
меню «Графика» PolarPlot (Полярный график).