Функция РАНГ — Служба поддержки Майкрософт
Excel
Формулы и функции
Другие функции
Другие функции
Функция РАНГ
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции РАНГ в Microsoft Excel.
Описание
Возвращает ранг числа в списке чисел. Ранг числа — это его величина относительно других значений в списке. (Если отсортировать список, то ранг числа будет его позицией.)
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение.
Дополнительные сведения о новых функциях см. в разделах Функция РАНГ.СР и Функция РАНГ.РВ.
Синтаксис
РАНГ(число;ссылка;[порядок])
Аргументы функции РАНГ описаны ниже.
-
Число Обязательный. Число, для которого определяется ранг.
-
Ссылка Обязательный. Массив или ссылка на список чисел. Нечисловые значения в ссылке игнорируются.
org/ListItem»>
Порядок Необязательный. Число, определяющее способ упорядочения.
Если значение аргумента «порядок» равно 0 или опущено, ранг числа определяется в Microsoft Excel так, как если бы ссылка была списком, отсортированным в порядке убывания.
Если значение аргумента «порядок» — любое число, кроме нуля, то ранг числа определяется в Microsoft Excel так, как если бы ссылка была списком, отсортированным в порядке возрастания.
Замечания
-
Функция РАНГ присваивает повторяющимся числам одинаковые значения ранга. Однако наличие повторяющихся чисел влияет на ранги последующих чисел. Например, если в списке целых чисел, отсортированных по возрастанию, дважды встречается число 10, имеющее ранг 5, число 11 будет иметь ранг 7 (ни одно из чисел не будет иметь ранга 6).

-
В некоторых случаях может потребоваться определить ранг, учитывая при этом связь. В предыдущем примере можно было бы получить измененный ранг числа 5,5 для числа 10. Для этого добавьте следующий коэффициент исправления к значению, возвращаемом функцией РАНГ. Этот коэффициент исправления подходит как для случая, когда ранг вычисляется в порядке убывания (порядок = 0 или опущен) или в порядке возрастания (порядок = нелиценз).
Поправочный коэффициент для связанных рангов = [СЧЕТ(ссылка) + 1 – РАНГ(число, ссылка, 0) – РАНГ(число, ссылка, 1)]/2.
В следующем примере РАНГ(A2,A1:A5,1) равен 3. Поправочный коэффициент равен (5 + 1 – 2 – 3)/2 = 0,5, а ранг, пересмотренный с учетом связей в учетной записи, равен 3 + 0,5 = 3,5. Если то или иное число появляется в ссылке только один раз, поправочный коэффициент будет равен 0, поскольку РАНГ для связи не будет изменяться.

Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
7 |
||
|
3,5 |
||
|
3,5 |
||
|
1 |
||
|
2 |
||
| Формула |
Описание (результат) |
Результат |
|
=РАНГ(A3;A2:A6;1) |
Ранг числа 3,5 в приведенном выше списке (3) |
3 |
|
=РАНГ(A2;A2:A6;1) |
Ранг числа 7 в приведенном выше списке (5) |
|
4.
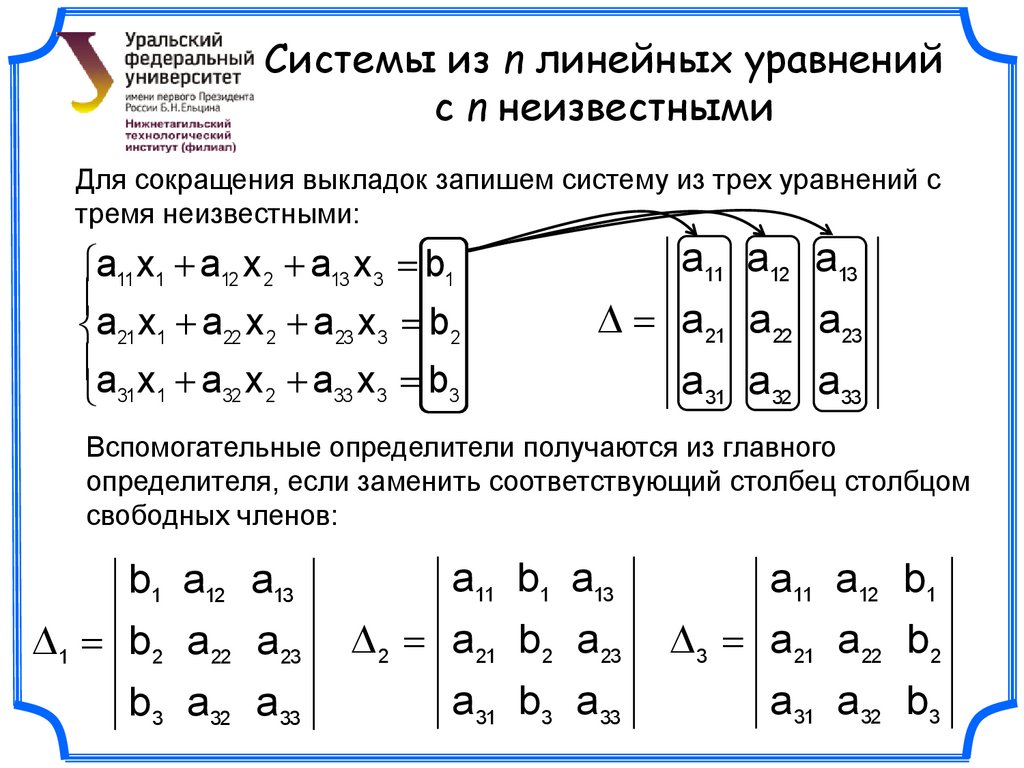
 1.5 Линейная зависимость между столбцами матрицы. Понятие о ранге матрицы
1.5 Линейная зависимость между столбцами матрицы. Понятие о ранге матрицыПусть даны две числовые матрицы, состоящие из одного столбца и . Операции сложения столбцов и умножения столбцов на число определяются следующим образом:
, .
Матрицу называют линейной комбинацией столбцов .
Определение. Совокупность столбцов называется линейно зависимой, если найдутся такие числа , среди которых хотя бы одно не равно нулю, что
(*)
(здесь 0 – нуль-столбец, т. е. столбец, все элементы которого равны нулю). Если равенство (*) возможно только в случае, когда все , то столбцы называются линейно независимыми. (Сравните с аналогичным определением для совокупности векторов).
Справедливы теоремы о линейной зависимости между столбцами, аналогичные соответствующим теоремам для векторов.
Определение. Пусть дана матрица размера . Выделим в этой матрице какие-либо строк и столбцов. На их пересечении получится квадратная матрица -го порядка.
(Не путайте понятия «минора данного элемента» и «минор -го порядка»).
Определение. Число называется рангом матрицы , если:
1) в матрице есть минор порядка , отличный от нуля;
2) все миноры порядка и выше, если они существуют, равны нулю.
Иначе, ранг матрицы – это наивысший порядок минора, отличного от нуля.
Обозначения: , , или .
Из определения следует, что – целое положительное число. Для нуль-матрицы считают ранг равным нулю.
Определение. Пусть дана матрица ранга . Любой минор матрицы, отличный от нуля и имеющий порядок , называется базисным, а строки и столбцы его составляющие – базисными строками и столбцами.
Согласно этому определению, матрица может иметь несколько базисных миноров.
Пример 14. Даны две матрицы , и их миноры , . Какой из них можно принять в качестве базисного?
Решение. Минор , поэтому он не может быть базисным ни для одной из матриц. Минор и имеет порядок 2, значит его можно принять в качестве базисного матриц или / и при условии, что они имеют ранги, равные 2. Поскольку (как определитель с двумя пропорциональными столбцами), то и можно взять за базисный минор матрицы . Ранг матрицы равен 3, в силу того, что и, следовательно, порядок базисного минора этой матрицы должен равняться 3, то есть не является базисным для матрицы . Отметим, что у матрицы единственный базисный минор, равный определителю матрицы .
Минор и имеет порядок 2, значит его можно принять в качестве базисного матриц или / и при условии, что они имеют ранги, равные 2. Поскольку (как определитель с двумя пропорциональными столбцами), то и можно взять за базисный минор матрицы . Ранг матрицы равен 3, в силу того, что и, следовательно, порядок базисного минора этой матрицы должен равняться 3, то есть не является базисным для матрицы . Отметим, что у матрицы единственный базисный минор, равный определителю матрицы .
Теорема (о базисном миноре). Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).
Следствия из теоремы.
1. Всякие столбцов (строк) матрицы ранга r линейно зависимы.
2. Если ранг матрицы меньше числа ее строк (столбцов), то ее строки (столбцы) линейно зависимы. Если равен числу ее строк (столбцов), то строки (столбцы) линейно независимы.
3. Определитель матрицы равен нулю тогда и только тогда, когда ее строки (столбцы) линейно зависимы.
4. Если к строке (столбцу) матрицы прибавить другую строку, (столбец) умноженную на любое число, отличное от нуля, то ранг матрицы не изменится.
5. Если в матрице зачеркнуть строку (столбец), являющуюся линейной комбинацией других строк (столбцов), то ранг матрицы не изменится.
6. Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).
7. Максимальное число линейно независимых строк совпадает с максимальным числом линейно независимых столбцов.
Пример 15. Найти ранг матрицы
.
Решение. Исходя из определения ранга матрицы, будем искать минор наивысшего порядка, отличный от нуля. Сначала преобразуем матрицу к более простому виду. Для этого первую строку матрицы умножим на и прибавим ко второй, затем ее же умножим на и прибавим к третьей:
.
Поскольку вторая и третья строки пропорциональны, то одну из них можно вычеркнуть, что не изменит ранг. Получаем , так как в матрице есть минор второго порядка, отличный от нуля, а миноры более высокого порядка отсутствуют.
Пример 16. Найти ранг матрицы
.
Решение. Получим нули в первом столбце, оперируя первой строкой .
Третью строку вычеркиваем, поскольку она получается умножением второй строки на 2, а в последней строке отбросим общий множитель:
.
Для самостоятельного решения.
1. Найти ранг матрицы .
Ответ: .
2. При каких ранг матрицы Равен 2? равен 3?
Ответ: при ранг равен 2, при ранг равен 3.
3. Столбцы матрицы порядка связаны соотношением , где . Входят ли столбцы 1, 2, 3, 4 в базисный минор?
4. Дана матрица . Каков ее ранг?
5. Матрица порядка 3 составлена из трех ненулевых попарно неколлинеарных компланарных векторов. Укажите ранг матрицы.
6. Даны три матрицы:
Числа – максимально возможные порядки базисных миноров соответствующих матриц. Укажите наибольшее из этих чисел.
| < Предыдущая | Следующая > |
|---|
Калькулятор матрицы рангов заболеваемости
✖Количество узлов определяется как количество узлов, в которых соединены два или более элементов. |
✖Ранг матрицы относится к количеству линейно независимых строк или столбцов в матрице.ⓘ Ранг матрицы заболеваемости [ρ] | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Ранг решения матрицы заболеваемости
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Количество узлов: 4 —> Преобразование не требуется
ШАГ 2: Оценка формулы
ШАГ 3: Преобразование результата в единицу вывода
3 —> Преобразование не требуется
< 5 Калькуляторы по теории цепейФормула матрицы ранга заболеваемости
Ранг матрицы = количество узлов-1
р = N-1
Определить матрицу заболеваемости
Матрица инцидентности — это та матрица, которая представляет график таким образом, что с помощью этой матрицы мы можем нарисовать график. Если из заданной матрицы инцидентности [AC] удалить любую произвольную строку, то образовавшаяся новая матрица будет редуцированной матрицей инцидентности.
Если из заданной матрицы инцидентности [AC] удалить любую произвольную строку, то образовавшаяся новая матрица будет редуцированной матрицей инцидентности.
Как рассчитать ранг матрицы заболеваемости?
Калькулятор матрицы ранга инцидентности использует Ранг матрицы = количество узлов-1 для расчета ранга матрицы. Ранг матрицы инцидентности равен (n-1), где n — количество узлов графа. Порядок матрицы инцидентности равен (n × b), где b — количество ветвей графа. Ранг матрицы обозначается символом ρ .
Как рассчитать матрицу рангов заболеваемости с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для матрицы рангов заболеваемости, введите число узлов 9.0074 (N) и нажмите кнопку расчета. Вот как можно объяснить расчет матрицы рангов заболеваемости с заданными входными значениями -> 3 = 4-1 .
Часто задаваемые вопросы
Что такое матрица рангов заболеваемости?
Ранг матрицы инцидентности (n-1), где n — количество узлов графа. Матрица инцидентности имеет порядок (n × b), где b — количество ветвей графа и представляется как ρ = N-1 или Ранг матрицы = количество узлов-1 . Количество узлов определяется как соединения, в которых соединены два или более элемента.
Матрица инцидентности имеет порядок (n × b), где b — количество ветвей графа и представляется как ρ = N-1 или Ранг матрицы = количество узлов-1 . Количество узлов определяется как соединения, в которых соединены два или более элемента.
Как рассчитать ранг матрицы заболеваемости?
Ранг матрицы инцидентности (n-1), где n — количество узлов графа. Порядок матрицы инцидентности равен (n × b), где b — количество ветвей графа, рассчитанное с использованием . Ранг матрицы = количество узлов-1 . Чтобы рассчитать ранг матрицы заболеваемости, вам нужно количество узлов (Н) . С помощью нашего инструмента вам нужно ввести соответствующее значение для количества узлов и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов вычисления ранга матрицы?
В этой формуле Ранг матрицы использует количество узлов. Мы можем использовать 1 другой способ (способы) для вычисления того же самого, который выглядит следующим образом:
- Скопировано!
Редукция ранга Расчет многомерной разреженной матрицы на основе теории сетевой управляемости .
 Наборы данных, генерируемые Интернетом, часто соответствуют анализу разреженных матриц большой размерности. Несмотря на недавние успехи в продвижении традиционной сингулярной декомпозиции (SVD), по-прежнему отсутствует эффективный алгоритм оценки ранга разреженной матрицы большой размерности. Вдохновленные теорией управляемости сложных сетей, мы преобразовали ранг матрицы в вычисление максимального совпадения. Затем мы создали алгоритм быстрой оценки ранга, используя метод резонатора, мощный приближенный метод вычисления максимального паросочетания, для оценки ранга разреженной матрицы. В силу естественной малой сложности метода резонаторов мы показали, что ранг разреженной матрицы большой размерности можно оценить гораздо быстрее, чем SVD, с высокой точностью. Наш метод предлагает эффективный способ быстрой оценки ранга многомерной разреженной матрицы, когда временные затраты на вычисление ранга с помощью SVD неприемлемы.
Наборы данных, генерируемые Интернетом, часто соответствуют анализу разреженных матриц большой размерности. Несмотря на недавние успехи в продвижении традиционной сингулярной декомпозиции (SVD), по-прежнему отсутствует эффективный алгоритм оценки ранга разреженной матрицы большой размерности. Вдохновленные теорией управляемости сложных сетей, мы преобразовали ранг матрицы в вычисление максимального совпадения. Затем мы создали алгоритм быстрой оценки ранга, используя метод резонатора, мощный приближенный метод вычисления максимального паросочетания, для оценки ранга разреженной матрицы. В силу естественной малой сложности метода резонаторов мы показали, что ранг разреженной матрицы большой размерности можно оценить гораздо быстрее, чем SVD, с высокой точностью. Наш метод предлагает эффективный способ быстрой оценки ранга многомерной разреженной матрицы, когда временные затраты на вычисление ранга с помощью SVD неприемлемы.1. Введение
С развитием онлайновых социальных сетей исследователи часто сталкиваются со сложными сетями, состоящими из огромного количества людей и множественных отношений между ними.
 Для анализа этих больших сложных сетей нам необходимо преобразовать сеть в соответствующую ей матрицу и получить некоторые характеристики исходной сети из ее матрицы на основе традиционной матричной теории, такой как метод ранжирования страниц [1], метод обнаружения сообществ [ 2] и некоторые динамические задачи [3, 4]. Ранг — одна из важнейших числовых характеристик матрицы. В настоящее время большое количество исследователей сосредотачивается на ранге специальной матрицы [5], задаче низкого ранга [6–9], проблема максимального ранга [10], отсутствие графов [11, 12] и применение в робастном анализе главных компонент [13–15]. Наиболее успешным методом вычисления ранга является традиционное разложение по сингулярным числам (SVD), при котором ранг вычисляется путем разложения исходной матрицы на сингулярные значения и вычисления статистических свойств разложенной матрицы. Однако сложность SVD равна кубу размера матрицы (обозначается как ), что затрудняет численное вычисление SVD в многомерных ситуациях.
Для анализа этих больших сложных сетей нам необходимо преобразовать сеть в соответствующую ей матрицу и получить некоторые характеристики исходной сети из ее матрицы на основе традиционной матричной теории, такой как метод ранжирования страниц [1], метод обнаружения сообществ [ 2] и некоторые динамические задачи [3, 4]. Ранг — одна из важнейших числовых характеристик матрицы. В настоящее время большое количество исследователей сосредотачивается на ранге специальной матрицы [5], задаче низкого ранга [6–9], проблема максимального ранга [10], отсутствие графов [11, 12] и применение в робастном анализе главных компонент [13–15]. Наиболее успешным методом вычисления ранга является традиционное разложение по сингулярным числам (SVD), при котором ранг вычисляется путем разложения исходной матрицы на сингулярные значения и вычисления статистических свойств разложенной матрицы. Однако сложность SVD равна кубу размера матрицы (обозначается как ), что затрудняет численное вычисление SVD в многомерных ситуациях. Поэтому было разработано несколько методов для решения проблемы сложности, основанных на новой матричной декомпозиции [16, 17], моделировании Монте-Карло [18] и мультикомпьютерных технологиях [19].–23]. Однако все эти методы не могут значительно улучшить временную сложность.
Поэтому было разработано несколько методов для решения проблемы сложности, основанных на новой матричной декомпозиции [16, 17], моделировании Монте-Карло [18] и мультикомпьютерных технологиях [19].–23]. Однако все эти методы не могут значительно улучшить временную сложность.Благодаря развитию теории управления сложными сетями мы знаем, что ранг матрицы связи отражает точную управляемость разреженных сложных сетей. С другой стороны, структурная управляемость может быть измерена максимальным согласованием разреженных сложных сетей. Для разреженных сложных сетей точная управляемость эквивалентна структурной управляемости [24, 25]. Метод полостей, мощный метод аппроксимации, разработанный в статистической механике [26, 27], может быть разработан для расчета максимального согласования сложных сетей. Таким образом, управляемость разреженных сложных сетей является связующим звеном между методом резонатора и ранговым вычислением.
Другими словами, для -мерной разреженной матрицы мы можем преобразовать ее в -узловую сложную сеть и вычислить ее структурную управляемость с помощью метода полости.
 Благодаря своей разреженности структурная управляемость равна точной управляемости, и можно приближенно оценить ранг входной -мерной разреженной матрицы. Этот процесс, который представляет собой метод быстрой оценки ранга разреженной матрицы, называемый FER, может оценить ранг разреженной матрицы высокой размерности намного быстрее, чем SVD. Поэтому мы применили FER к случайно обобщенным разреженным матрицам и систематически сравнивали FER с SVD с точки зрения эффективности, точности и применимости в двух типичных распределениях ненулевых элементов каждой строки (обозначенных как ). Мы обнаружили, что временные затраты FER существенно не увеличиваются при выращивании с постоянным , а результаты, оцененные FER, сохраняют высокую точность, что подтверждает, что FER является эффективным инструментом для оценки ранга матриц большой размерности. Мы также изучили влияние на временные затраты и точность FER, и производительность FER осталась очень хорошей. Наконец, мы применили FER к матрицам с единицей ненулевых элементов.
Благодаря своей разреженности структурная управляемость равна точной управляемости, и можно приближенно оценить ранг входной -мерной разреженной матрицы. Этот процесс, который представляет собой метод быстрой оценки ранга разреженной матрицы, называемый FER, может оценить ранг разреженной матрицы высокой размерности намного быстрее, чем SVD. Поэтому мы применили FER к случайно обобщенным разреженным матрицам и систематически сравнивали FER с SVD с точки зрения эффективности, точности и применимости в двух типичных распределениях ненулевых элементов каждой строки (обозначенных как ). Мы обнаружили, что временные затраты FER существенно не увеличиваются при выращивании с постоянным , а результаты, оцененные FER, сохраняют высокую точность, что подтверждает, что FER является эффективным инструментом для оценки ранга матриц большой размерности. Мы также изучили влияние на временные затраты и точность FER, и производительность FER осталась очень хорошей. Наконец, мы применили FER к матрицам с единицей ненулевых элементов. Эффективность и точность ФЭР по-прежнему оставались очень высокими. Все результаты показывают, что FER является допустимым доступом для оценки ранга разреженной матрицы, особенно для оценки ранга разреженной матрицы высокой размерности, что практически неприемлемо для вычисления ранга с помощью SVD с учетом временных затрат.
Эффективность и точность ФЭР по-прежнему оставались очень высокими. Все результаты показывают, что FER является допустимым доступом для оценки ранга разреженной матрицы, особенно для оценки ранга разреженной матрицы высокой размерности, что практически неприемлемо для вычисления ранга с помощью SVD с учетом временных затрат.2. Материалы и методы
ТЭР основан на развитии теории управляемости сложных сетей. Двумя существующими теоретическими основами для количественной оценки управляемости сложной сети являются теория структурной управляемости (SCT) и теория точной управляемости (ECT) [28]. SCT утверждает, что структурная управляемость любой направленной сети определяется максимальным соответствием. Максимальное согласование может быть решено резонаторным методом, когда сеть ориентирована со структурной матрицей. Точная управляемость, получаемая с помощью ЭХО, определяется максимальной кратностью собственных значений матрицы связи. В разреженной ситуации ECT является эффективным инструментом для получения управляемости сетей путем вычисления ранга матрицы связи.
 Когда сеть разрежена и веса связей слабо коррелированы, структурная управляемость и точная управляемость теоретически эквивалентны [24]. Следовательно, вычисление ранга разреженной матрицы можно преобразовать в задачу максимального соответствия; тогда мы можем оценить ранг, эффективно решая соответствующие уравнения связи резонаторного метода. Это ядро ФЭР.
Когда сеть разрежена и веса связей слабо коррелированы, структурная управляемость и точная управляемость теоретически эквивалентны [24]. Следовательно, вычисление ранга разреженной матрицы можно преобразовать в задачу максимального соответствия; тогда мы можем оценить ранг, эффективно решая соответствующие уравнения связи резонаторного метода. Это ядро ФЭР.Без ограничения общности рассмотрим произвольную разреженную входную матрицу со слабо коррелированными ненулевыми элементами, как показано на рис. 1(а), где только белые сетки представляют нулевые элементы, а более темный цвет представляет большее значение ненулевых элементов . Затем мы применяем FER к входной матрице, и процедура FER может быть описана как следующие пять шагов:
Шаг 1. Преобразование входной матрицы в структурную матрицу, в которой элементы могут быть только 0 или 1,0 s представляют нулевые элементы, обозначенные как белые сетки, а 1 представляют ненулевые элементы, обозначенные как черные сетки, как показано на рисунке 1(a) и 1(b);
Шаг 2.
 Рассмотрим структурную матрицу как матрицу связи сложной сети и построим направленную сеть, как показано на рисунках 1(b)–1(c);
Рассмотрим структурную матрицу как матрицу связи сложной сети и построим направленную сеть, как показано на рисунках 1(b)–1(c);Шаг 3. Получите распределения степени входа и выхода направленной сети, где . — количество узлов со значением степени входа (выхода) во всей сети, как показано на рисунках 1 (c)–1 (d);
Шаг 4. Расчет структурной управляемости направленной сети по распределению степеней методом полости [25], который проиллюстрирован на рис. 1(г)–1(д), где и упорядочены следующим образом уравнения: и являются решениями следующих уравнений связи: В приведенных выше уравнениях функции и показаны как согласно (4), и могут быть рассчитаны по распределению степеней ( и ). В большинстве случаев распределение степеней, основное статистическое свойство, может быть легко получено из эмпирических данных, как описано в шаге 3. Приведенные выше уравнения связи являются трансцендентными уравнениями, а решения , , и могут быть получены путем численного решения уравнения (3).
 Наконец, из уравнения (1) получаем структурную управляемость.
Наконец, из уравнения (1) получаем структурную управляемость.Шаг 5. Поскольку SCT и ECT эквивалентны, когда входная матрица разрежена, структурная управляемость равна точной управляемости . Таким образом, мы можем оценить ранг входной разреженной матрицы, как показано на рисунках 1(e)–1(f): Стоит отметить, что, во-первых, он может быть напрямую рассчитан методом максимального сопоставления на основе SCT [28]. Метод резонаторов является эффективным инструментом, основанным на статистической физике, для оценки максимального соответствия, которое может быть получено только по распределению степеней. То есть сложность метода FER определяется сложностью статистики распределения степеней и точностью численного решения. Во-вторых, если матрица содержит совершенно нерелевантные значения элементов (каждый ненулевой элемент является реальным случайным числом), теоретически она равна на основе SCT и ECT. Однако это предположение слишком строго для общих случаев, а это означает, что результат FER является всего лишь инструментом оценки ранга входной матрицы.
 Сила корреляции ненулевых элементов во входной матрице действительно влияет на точность FER.
Сила корреляции ненулевых элементов во входной матрице действительно влияет на точность FER.3. Результаты
Некоторые сравнения между FER и SVD показаны с точки зрения эффективности и точности в некоторых типичных ситуациях. Чтобы проанализировать влияние размера матрицы, мы генерируем некоторые матрицы случайным образом с фиксированной разреженностью, т. е. средним числом ненулевых элементов в каждой строке. Ненулевые элементы генерируются в соответствии с двумя типичными распределениями: случайным распределением и степенным распределением. Затем к сгенерированным матрицам применяем FER и SVD, и результаты сравнения эффективности и точности показаны на рис. 2. Эффективность алгоритма определяется временными затратами на решение задачи, обозначенными как . Как показано на рисунках 2(a) и 2(c), при увеличении SVD увеличивается в соответствии с его теоретической вычислительной сложностью. Хотя мы можем использовать GPU для ускорения, скорость SVD увеличивается по мере увеличения.
 Напротив, FER очень мало увеличивается при увеличении, что позволяет предположить, что его вычислительная сложность определяется размером матрицы и средним числом ненулевых элементов в каждой строке вместе взятых.
Напротив, FER очень мало увеличивается при увеличении, что позволяет предположить, что его вычислительная сложность определяется размером матрицы и средним числом ненулевых элементов в каждой строке вместе взятых.Ранг, оцененный с помощью FER (обозначенного как ) и SVD (обозначенного как ), почти перекрывается, как показано на рисунках 2 (b) и 2 (d), что означает, что эти два метода дают одинаковый результат независимо от того, насколько увеличивается. Чтобы объяснить высокую точность FER более подробно, мы рассматриваем ранг, вычисленный SVD, как основную истину и определяем относительную ошибку как:
С другой стороны, чтобы сравнить точность FER при увеличении, мы определяем нормализованный ранг ( обозначается как ) в виде следующего уравнения:
Цифры-врезки на рисунках 2(b) и 2(d) показывают относительную ошибку при случайном распределении и степенном законе соответственно. довольно мала с флуктуациями по мере увеличения и остается ниже 0,003 и 0,001 в случайных и степенных ситуациях соответственно.
 Результаты показывают, что FER имеет хорошую производительность в обоих типичных сценариях. Когда увеличивается, имеет тенденцию к снижению в обоих распределениях, что означает, что относительная ошибка между FER и SVD должна быть очень маленькой, когда она достаточно велика. Таким образом, для многомерной разреженной матрицы мы можем использовать FER для эффективного получения точной оценки ранга с той же точностью, что и SVD, независимо от случайного или степенного распределения.
Результаты показывают, что FER имеет хорошую производительность в обоих типичных сценариях. Когда увеличивается, имеет тенденцию к снижению в обоих распределениях, что означает, что относительная ошибка между FER и SVD должна быть очень маленькой, когда она достаточно велика. Таким образом, для многомерной разреженной матрицы мы можем использовать FER для эффективного получения точной оценки ранга с той же точностью, что и SVD, независимо от случайного или степенного распределения.Как показано на рисунке 3, мы проверили, как разреженность входной матрицы, измеряемая , влияет на эффективность и точность FER, когда размер матрицы фиксирован как . Показано, что и являются функциями в случайных ситуациях (рис. 3(а)) и степенных ситуациях (рис. 3(в)). намного меньше, чем в каждой ситуации. На рисунках 3(b) и 3(d) мы проанализировали увеличение точности FER. Различий между результатами ФЭР и СВД практически нет, а разбросы основных цифр почти перекрываются. Затем мы рассматриваем относительную ошибку FER, как показано на вставках рисунков 3(b) и 3(d).

Если увеличивается, то оба значения намного меньше в двух ситуациях, что явно колеблется в случайных ситуациях. остается почти постоянным и меньше, чем в степенной ситуации. Таким образом, мы находим, что FER намного эффективнее, чем SVD, независимо от того, когда увеличивается, и влияние FER на эффективность и точность FER довольно мало в обеих ситуациях.
FER работает, только если все ненулевые элементы в разреженной матрице некоррелированы. Однако в реальных данных есть много релевантных элементов, а это означает, что ошибки неизбежны, если ненулевые элементы коррелированы. Таким образом, мы обсудим, является ли приемлемым результат, полученный приближенно с помощью FER, когда ненулевые элементы входной матрицы коррелированы. На рисунке 4 мы рассматриваем крайний случай, когда все ненулевые элементы во входной матрице идентичны (установлены как 1), что означает, что все ненулевые элементы сильно коррелированы. Сильная корреляция оказывает негативное влияние как в случайных ситуациях (рис.
 4(а)) так и в степенных ситуациях (рис. 4(в)). по-прежнему намного меньше, чем . Однако результаты, показанные на рисунках 4(b) и 4(d), показывают, что точность FER значительно снижается по сравнению с рисунками 3(b) и 3(d). Это означает, что корреляция входной матрицы действительно влияет на точность FER, что согласуется с ограничением структурной управляемости, а также с резонаторным методом. Хотя точность FER уменьшилась, мы также можем узнать из вложенных рисунков, что относительная ошибка FER все еще очень мала в обеих ситуациях. Особенно при увеличении более 4 имеет очевидный спуск. Другими словами, даже несмотря на то, что ненулевые элементы в разреженной матрице сильно коррелированы, производительность FER также приемлема с точки зрения эффективности и точности. Надежность FER предполагает его эффективность при оценке ранга более общей матрицы, извлеченной из набора эмпирических данных.
4(а)) так и в степенных ситуациях (рис. 4(в)). по-прежнему намного меньше, чем . Однако результаты, показанные на рисунках 4(b) и 4(d), показывают, что точность FER значительно снижается по сравнению с рисунками 3(b) и 3(d). Это означает, что корреляция входной матрицы действительно влияет на точность FER, что согласуется с ограничением структурной управляемости, а также с резонаторным методом. Хотя точность FER уменьшилась, мы также можем узнать из вложенных рисунков, что относительная ошибка FER все еще очень мала в обеих ситуациях. Особенно при увеличении более 4 имеет очевидный спуск. Другими словами, даже несмотря на то, что ненулевые элементы в разреженной матрице сильно коррелированы, производительность FER также приемлема с точки зрения эффективности и точности. Надежность FER предполагает его эффективность при оценке ранга более общей матрицы, извлеченной из набора эмпирических данных.4. Обсуждение
Таким образом, мы использовали метод резонатора для оценки максимального совпадения.
 Опираясь на теорию управляемости сложных сетей, мы знаем, что ранг матрицы теоретически равен максимальному паросочетанию сети, когда сеть разреженная и веса связей слабо коррелированы. Затем мы создали эффективный инструмент оценки для анализа ранга многомерной разреженной матрицы методом полости, который называется FER. Мы обсудили влияние размера входной матрицы , разреженности матрицы (измеряемой ) и корреляции ненулевых элементов на эффективность (измеряемую ) и точность (измеряемую ) FER в случайных ситуациях и степенных ситуациях. Мы обнаружили, что FER имеет замечательную производительность с точки зрения как эффективности, так и точности в случайном распределении и распределении по степенному закону. Хотя характеристики ненулевых элементов влияют на результаты, FER все еще может применяться к большинству разреженных матриц для оценки их ранга с высокой скоростью и высокой точностью. Он может значительно превосходить СВД по затратам времени и имеет аналогичную с СВД точность. Следовательно, FER обеспечивает эффективный и точный метод оценки ранга разреженной матрицы.
Опираясь на теорию управляемости сложных сетей, мы знаем, что ранг матрицы теоретически равен максимальному паросочетанию сети, когда сеть разреженная и веса связей слабо коррелированы. Затем мы создали эффективный инструмент оценки для анализа ранга многомерной разреженной матрицы методом полости, который называется FER. Мы обсудили влияние размера входной матрицы , разреженности матрицы (измеряемой ) и корреляции ненулевых элементов на эффективность (измеряемую ) и точность (измеряемую ) FER в случайных ситуациях и степенных ситуациях. Мы обнаружили, что FER имеет замечательную производительность с точки зрения как эффективности, так и точности в случайном распределении и распределении по степенному закону. Хотя характеристики ненулевых элементов влияют на результаты, FER все еще может применяться к большинству разреженных матриц для оценки их ранга с высокой скоростью и высокой точностью. Он может значительно превосходить СВД по затратам времени и имеет аналогичную с СВД точность. Следовательно, FER обеспечивает эффективный и точный метод оценки ранга разреженной матрицы. Специально для работы с большой реальной сетью с помощью некоторых алгоритмов с ее матричным рангом FER может хорошо оценить ранг непосредственно по распределению степеней, полученному из необработанных данных, в то время как SVD неприменим из-за его чрезмерных временных затрат. Кроме того, в некоторых особых ситуациях, когда может быть обнаружена только структурная информация социальной сети, например распределение степеней или частично отсутствующее распределение степеней, FER по-прежнему применим для оценки ранга соответствующей матрицы. Это означает, что FER потенциально может использоваться в некоторых алгоритмах, предназначенных для неполных данных или данных, загрязненных интерференционным шумом.
Специально для работы с большой реальной сетью с помощью некоторых алгоритмов с ее матричным рангом FER может хорошо оценить ранг непосредственно по распределению степеней, полученному из необработанных данных, в то время как SVD неприменим из-за его чрезмерных временных затрат. Кроме того, в некоторых особых ситуациях, когда может быть обнаружена только структурная информация социальной сети, например распределение степеней или частично отсутствующее распределение степеней, FER по-прежнему применим для оценки ранга соответствующей матрицы. Это означает, что FER потенциально может использоваться в некоторых алгоритмах, предназначенных для неполных данных или данных, загрязненных интерференционным шумом.Доступность данных
Данные не использовались для поддержки этого исследования.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Авторы благодарят профессора Wen-Xu Wang за ценные предложения. Эта работа поддерживается Национальным фондом естественных наук Китая (гранты № 61703136 и 61672206), Фондом естественных наук провинции Хэбэй (гранты № F2020205012 и F2017205064) и проектом «Выдающиеся таланты молодежи» Департамента образования провинции Хэбэй (грант № BJ2020035).
 .
.Ссылки
А. Н. Лэнгвилл и К. Д. Мейер, Рейтинг страниц Google и выше: наука о ранжировании в поисковых системах , Princeton University Press, Принстон, Нью-Джерси, 2011.
, G. A. Rio T. Cantwell,
M. Reinert и M.E.J. Newman, «Эффективный метод оценки количества сообществ в сети», Physical Review , vol. 96, ID статьи 032310, 2017.
Посмотреть по адресу:
Сайт издателя | Академия Google
Л. М. Пекора и Т. Л. Кэрролл, «Основные функции стабильности для синхронизированных связанных систем», Physical Review Letters , vol. 80, 1998.
Посмотреть по адресу:
Сайт издателя | Google Scholar
К. Кастеллано и Р. Пастор-Саторрас, «Пороги распространения эпидемии в сетях», Physical Review Letters , vol. 105, ID статьи 218701, 2010.
Посмотреть по адресу:
Сайт издателя | Академия Google
А.
 Дакс, «Числовой ранг матриц Крылова», Линейная алгебра и ее приложения , том. 528, 2017.
Дакс, «Числовой ранг матриц Крылова», Линейная алгебра и ее приложения , том. 528, 2017.Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Б. Сюй и Д. Се, «Преследование аппроксимации низкого ранга для завершения матрицы», , Механические системы и обработка сигналов, , том. 95, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Парех и И. В. Селесник, «Улучшенная оценка разреженной низкоранговой матрицы», Обработка сигналов , том. 139, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Накацукаса, Т. Сома и А. Ушмаев, «Поиск базиса низкого ранга в матричном подпространстве», , Математическое программирование, , том. 162, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
X.
 D. Feng и X. M. He, «Надежные аппроксимации матриц данных низкого ранга», Science China Mathematics , vol. 60, 2017.
D. Feng и X. M. He, «Надежные аппроксимации матриц данных низкого ранга», Science China Mathematics , vol. 60, 2017.Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Мешулам, «Максимальный ранг в матричных пространствах с помощью сопоставлений графов», Linear Algebra and its Applications , vol. 529, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. М. Цветкович и И. Гутман, Избранные темы по приложениям спектров графов , Математический институт САНУ, Белград, 2011.
Л. Хогбен и Б. Шейдер, », Линейная алгебра и ее приложения , том. 432, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Z. Hu, F. Nie, R. Wang, R.
 Wang, and X Li, «Регуляризация низкого ранга: обзор», Neural Networks: The Official Journal of the International Neural Network Society , об. 136, стр. 218–232, 2021.
Wang, and X Li, «Регуляризация низкого ранга: обзор», Neural Networks: The Official Journal of the International Neural Network Society , об. 136, стр. 218–232, 2021.Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Чи, Завершение матрицы низкого ранга , Журнал обработки сигналов IEEE, август 2018 г.
Н. Васвани, Т. Боуманс, С. Джавед и П. Нараянамурти, «Надежный анализ подпространства анализа главных компонентов и отслеживание», Журнал обработки сигналов IEEE , том . 35 июля 2018 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. К. Ядав, Р. Синха и П. К. Бора, «Эффективное сокращение SVD для оценки ранга», IEEE Signal Processing Letters , vol. 22, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Л.
 Де Латаувер, Б. Де Мур и Дж. Вандевалле, «Многолинейное разложение по сингулярным числам», SIAM Journal on Matrix Analysis and Applications , vol. 21, 2000.
Де Латаувер, Б. Де Мур и Дж. Вандевалле, «Многолинейное разложение по сингулярным числам», SIAM Journal on Matrix Analysis and Applications , vol. 21, 2000.Посмотреть по адресу:
Сайт издателя | Google Scholar
П. А. Карран, Анализ ошибок методом Монте-Карло рангового теста Спирмена , с. 3816, 2014 г., http://arxiv.org/abs/1411.3816.
М. Аарон, М. Элад и А. М. Брукштейн, «K-svd и его неотрицательный вариант для разработки словаря», Proceedings of Spie the International Society for Optical Engineering , vol. 5914, 2005.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Л. Марчеллино и Г. Наварра, «Алгоритм SVD с ускорением на графическом процессоре, основанный на QR-факторизации и заданных вращениях для шумоподавления DWI», в Трудах 12-й Международной конференции по технологии сигналов и изображений и Интернету.
 Базовые системы , SITIS, Неаполь, Италия, ноябрь 2016 г.
Базовые системы , SITIS, Неаполь, Италия, ноябрь 2016 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
Т. Донг, А. Хайдар, С. Томов и Дж. Донгарра, «Ускорение двудиагонализации svd пакета небольших матриц с использованием графического процессора», Journal of Computational ence , vol. 26, 2018.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Гейтс, С. Томов и Дж. Донгарра, «Ускорение двухступенчатого двудиагонального сокращения svd и разделяй и властвуй с помощью графических процессоров», Параллельные вычисления , том. 74, 2018.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Куомо, Л. Марчеллино и Г. Наварра, «Параллельная реализация одностороннего метода Хестенеса-Якоби с использованием GPU-CUDA», в Трудах 26-й международной конференции Euromicro по параллельным вычислениям , Распределенная и сетевая обработка , Кембридж, Великобритания, март 3018 г.

Посмотреть по адресу:
Google Scholar
Z. Yuan, C. Zhao, Z. Di, W. X. Wang и YC Lai, «Точная управляемость сложных сетей», Nature Communications , vol. 4, с. 2447, 2013.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Ю. Лю, Дж. Дж. Слотин и А. Л. Барабаси, «Управляемость сложных сетей», Nature , vol. 473, стр. 167–73, 2011.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Чжоу и З. Оу-Янг, «Максимальное совпадение на случайных графах», 2003 г., http://arxiv.org/abs/cond-mat/0309348.
Посмотреть по адресу:
Google Scholar
Ю. Ю. Лю, Э. Чока, Х. Чжоу и М. Посфай, «Проникновение ядра в сложных сетях», Physical Review Letters , vol.




 Наборы данных, генерируемые Интернетом, часто соответствуют анализу разреженных матриц большой размерности. Несмотря на недавние успехи в продвижении традиционной сингулярной декомпозиции (SVD), по-прежнему отсутствует эффективный алгоритм оценки ранга разреженной матрицы большой размерности. Вдохновленные теорией управляемости сложных сетей, мы преобразовали ранг матрицы в вычисление максимального совпадения. Затем мы создали алгоритм быстрой оценки ранга, используя метод резонатора, мощный приближенный метод вычисления максимального паросочетания, для оценки ранга разреженной матрицы. В силу естественной малой сложности метода резонаторов мы показали, что ранг разреженной матрицы большой размерности можно оценить гораздо быстрее, чем SVD, с высокой точностью. Наш метод предлагает эффективный способ быстрой оценки ранга многомерной разреженной матрицы, когда временные затраты на вычисление ранга с помощью SVD неприемлемы.
Наборы данных, генерируемые Интернетом, часто соответствуют анализу разреженных матриц большой размерности. Несмотря на недавние успехи в продвижении традиционной сингулярной декомпозиции (SVD), по-прежнему отсутствует эффективный алгоритм оценки ранга разреженной матрицы большой размерности. Вдохновленные теорией управляемости сложных сетей, мы преобразовали ранг матрицы в вычисление максимального совпадения. Затем мы создали алгоритм быстрой оценки ранга, используя метод резонатора, мощный приближенный метод вычисления максимального паросочетания, для оценки ранга разреженной матрицы. В силу естественной малой сложности метода резонаторов мы показали, что ранг разреженной матрицы большой размерности можно оценить гораздо быстрее, чем SVD, с высокой точностью. Наш метод предлагает эффективный способ быстрой оценки ранга многомерной разреженной матрицы, когда временные затраты на вычисление ранга с помощью SVD неприемлемы. Для анализа этих больших сложных сетей нам необходимо преобразовать сеть в соответствующую ей матрицу и получить некоторые характеристики исходной сети из ее матрицы на основе традиционной матричной теории, такой как метод ранжирования страниц [1], метод обнаружения сообществ [ 2] и некоторые динамические задачи [3, 4]. Ранг — одна из важнейших числовых характеристик матрицы. В настоящее время большое количество исследователей сосредотачивается на ранге специальной матрицы [5], задаче низкого ранга [6–9], проблема максимального ранга [10], отсутствие графов [11, 12] и применение в робастном анализе главных компонент [13–15]. Наиболее успешным методом вычисления ранга является традиционное разложение по сингулярным числам (SVD), при котором ранг вычисляется путем разложения исходной матрицы на сингулярные значения и вычисления статистических свойств разложенной матрицы. Однако сложность SVD равна кубу размера матрицы (обозначается как ), что затрудняет численное вычисление SVD в многомерных ситуациях.
Для анализа этих больших сложных сетей нам необходимо преобразовать сеть в соответствующую ей матрицу и получить некоторые характеристики исходной сети из ее матрицы на основе традиционной матричной теории, такой как метод ранжирования страниц [1], метод обнаружения сообществ [ 2] и некоторые динамические задачи [3, 4]. Ранг — одна из важнейших числовых характеристик матрицы. В настоящее время большое количество исследователей сосредотачивается на ранге специальной матрицы [5], задаче низкого ранга [6–9], проблема максимального ранга [10], отсутствие графов [11, 12] и применение в робастном анализе главных компонент [13–15]. Наиболее успешным методом вычисления ранга является традиционное разложение по сингулярным числам (SVD), при котором ранг вычисляется путем разложения исходной матрицы на сингулярные значения и вычисления статистических свойств разложенной матрицы. Однако сложность SVD равна кубу размера матрицы (обозначается как ), что затрудняет численное вычисление SVD в многомерных ситуациях. Поэтому было разработано несколько методов для решения проблемы сложности, основанных на новой матричной декомпозиции [16, 17], моделировании Монте-Карло [18] и мультикомпьютерных технологиях [19].–23]. Однако все эти методы не могут значительно улучшить временную сложность.
Поэтому было разработано несколько методов для решения проблемы сложности, основанных на новой матричной декомпозиции [16, 17], моделировании Монте-Карло [18] и мультикомпьютерных технологиях [19].–23]. Однако все эти методы не могут значительно улучшить временную сложность. Благодаря своей разреженности структурная управляемость равна точной управляемости, и можно приближенно оценить ранг входной -мерной разреженной матрицы. Этот процесс, который представляет собой метод быстрой оценки ранга разреженной матрицы, называемый FER, может оценить ранг разреженной матрицы высокой размерности намного быстрее, чем SVD. Поэтому мы применили FER к случайно обобщенным разреженным матрицам и систематически сравнивали FER с SVD с точки зрения эффективности, точности и применимости в двух типичных распределениях ненулевых элементов каждой строки (обозначенных как ). Мы обнаружили, что временные затраты FER существенно не увеличиваются при выращивании с постоянным , а результаты, оцененные FER, сохраняют высокую точность, что подтверждает, что FER является эффективным инструментом для оценки ранга матриц большой размерности. Мы также изучили влияние на временные затраты и точность FER, и производительность FER осталась очень хорошей. Наконец, мы применили FER к матрицам с единицей ненулевых элементов.
Благодаря своей разреженности структурная управляемость равна точной управляемости, и можно приближенно оценить ранг входной -мерной разреженной матрицы. Этот процесс, который представляет собой метод быстрой оценки ранга разреженной матрицы, называемый FER, может оценить ранг разреженной матрицы высокой размерности намного быстрее, чем SVD. Поэтому мы применили FER к случайно обобщенным разреженным матрицам и систематически сравнивали FER с SVD с точки зрения эффективности, точности и применимости в двух типичных распределениях ненулевых элементов каждой строки (обозначенных как ). Мы обнаружили, что временные затраты FER существенно не увеличиваются при выращивании с постоянным , а результаты, оцененные FER, сохраняют высокую точность, что подтверждает, что FER является эффективным инструментом для оценки ранга матриц большой размерности. Мы также изучили влияние на временные затраты и точность FER, и производительность FER осталась очень хорошей. Наконец, мы применили FER к матрицам с единицей ненулевых элементов. Эффективность и точность ФЭР по-прежнему оставались очень высокими. Все результаты показывают, что FER является допустимым доступом для оценки ранга разреженной матрицы, особенно для оценки ранга разреженной матрицы высокой размерности, что практически неприемлемо для вычисления ранга с помощью SVD с учетом временных затрат.
Эффективность и точность ФЭР по-прежнему оставались очень высокими. Все результаты показывают, что FER является допустимым доступом для оценки ранга разреженной матрицы, особенно для оценки ранга разреженной матрицы высокой размерности, что практически неприемлемо для вычисления ранга с помощью SVD с учетом временных затрат.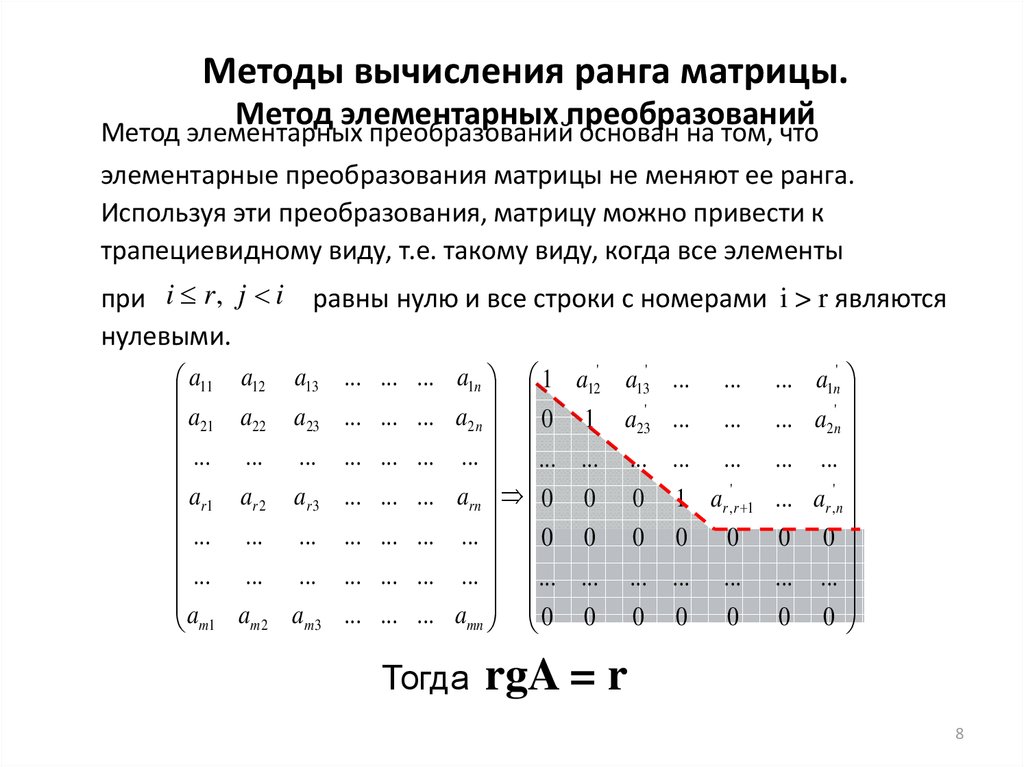 Когда сеть разрежена и веса связей слабо коррелированы, структурная управляемость и точная управляемость теоретически эквивалентны [24]. Следовательно, вычисление ранга разреженной матрицы можно преобразовать в задачу максимального соответствия; тогда мы можем оценить ранг, эффективно решая соответствующие уравнения связи резонаторного метода. Это ядро ФЭР.
Когда сеть разрежена и веса связей слабо коррелированы, структурная управляемость и точная управляемость теоретически эквивалентны [24]. Следовательно, вычисление ранга разреженной матрицы можно преобразовать в задачу максимального соответствия; тогда мы можем оценить ранг, эффективно решая соответствующие уравнения связи резонаторного метода. Это ядро ФЭР. Рассмотрим структурную матрицу как матрицу связи сложной сети и построим направленную сеть, как показано на рисунках 1(b)–1(c);
Рассмотрим структурную матрицу как матрицу связи сложной сети и построим направленную сеть, как показано на рисунках 1(b)–1(c); Наконец, из уравнения (1) получаем структурную управляемость.
Наконец, из уравнения (1) получаем структурную управляемость. Сила корреляции ненулевых элементов во входной матрице действительно влияет на точность FER.
Сила корреляции ненулевых элементов во входной матрице действительно влияет на точность FER. Напротив, FER очень мало увеличивается при увеличении, что позволяет предположить, что его вычислительная сложность определяется размером матрицы и средним числом ненулевых элементов в каждой строке вместе взятых.
Напротив, FER очень мало увеличивается при увеличении, что позволяет предположить, что его вычислительная сложность определяется размером матрицы и средним числом ненулевых элементов в каждой строке вместе взятых. Результаты показывают, что FER имеет хорошую производительность в обоих типичных сценариях. Когда увеличивается, имеет тенденцию к снижению в обоих распределениях, что означает, что относительная ошибка между FER и SVD должна быть очень маленькой, когда она достаточно велика. Таким образом, для многомерной разреженной матрицы мы можем использовать FER для эффективного получения точной оценки ранга с той же точностью, что и SVD, независимо от случайного или степенного распределения.
Результаты показывают, что FER имеет хорошую производительность в обоих типичных сценариях. Когда увеличивается, имеет тенденцию к снижению в обоих распределениях, что означает, что относительная ошибка между FER и SVD должна быть очень маленькой, когда она достаточно велика. Таким образом, для многомерной разреженной матрицы мы можем использовать FER для эффективного получения точной оценки ранга с той же точностью, что и SVD, независимо от случайного или степенного распределения.
 4(а)) так и в степенных ситуациях (рис. 4(в)). по-прежнему намного меньше, чем . Однако результаты, показанные на рисунках 4(b) и 4(d), показывают, что точность FER значительно снижается по сравнению с рисунками 3(b) и 3(d). Это означает, что корреляция входной матрицы действительно влияет на точность FER, что согласуется с ограничением структурной управляемости, а также с резонаторным методом. Хотя точность FER уменьшилась, мы также можем узнать из вложенных рисунков, что относительная ошибка FER все еще очень мала в обеих ситуациях. Особенно при увеличении более 4 имеет очевидный спуск. Другими словами, даже несмотря на то, что ненулевые элементы в разреженной матрице сильно коррелированы, производительность FER также приемлема с точки зрения эффективности и точности. Надежность FER предполагает его эффективность при оценке ранга более общей матрицы, извлеченной из набора эмпирических данных.
4(а)) так и в степенных ситуациях (рис. 4(в)). по-прежнему намного меньше, чем . Однако результаты, показанные на рисунках 4(b) и 4(d), показывают, что точность FER значительно снижается по сравнению с рисунками 3(b) и 3(d). Это означает, что корреляция входной матрицы действительно влияет на точность FER, что согласуется с ограничением структурной управляемости, а также с резонаторным методом. Хотя точность FER уменьшилась, мы также можем узнать из вложенных рисунков, что относительная ошибка FER все еще очень мала в обеих ситуациях. Особенно при увеличении более 4 имеет очевидный спуск. Другими словами, даже несмотря на то, что ненулевые элементы в разреженной матрице сильно коррелированы, производительность FER также приемлема с точки зрения эффективности и точности. Надежность FER предполагает его эффективность при оценке ранга более общей матрицы, извлеченной из набора эмпирических данных. Опираясь на теорию управляемости сложных сетей, мы знаем, что ранг матрицы теоретически равен максимальному паросочетанию сети, когда сеть разреженная и веса связей слабо коррелированы. Затем мы создали эффективный инструмент оценки для анализа ранга многомерной разреженной матрицы методом полости, который называется FER. Мы обсудили влияние размера входной матрицы , разреженности матрицы (измеряемой ) и корреляции ненулевых элементов на эффективность (измеряемую ) и точность (измеряемую ) FER в случайных ситуациях и степенных ситуациях. Мы обнаружили, что FER имеет замечательную производительность с точки зрения как эффективности, так и точности в случайном распределении и распределении по степенному закону. Хотя характеристики ненулевых элементов влияют на результаты, FER все еще может применяться к большинству разреженных матриц для оценки их ранга с высокой скоростью и высокой точностью. Он может значительно превосходить СВД по затратам времени и имеет аналогичную с СВД точность. Следовательно, FER обеспечивает эффективный и точный метод оценки ранга разреженной матрицы.
Опираясь на теорию управляемости сложных сетей, мы знаем, что ранг матрицы теоретически равен максимальному паросочетанию сети, когда сеть разреженная и веса связей слабо коррелированы. Затем мы создали эффективный инструмент оценки для анализа ранга многомерной разреженной матрицы методом полости, который называется FER. Мы обсудили влияние размера входной матрицы , разреженности матрицы (измеряемой ) и корреляции ненулевых элементов на эффективность (измеряемую ) и точность (измеряемую ) FER в случайных ситуациях и степенных ситуациях. Мы обнаружили, что FER имеет замечательную производительность с точки зрения как эффективности, так и точности в случайном распределении и распределении по степенному закону. Хотя характеристики ненулевых элементов влияют на результаты, FER все еще может применяться к большинству разреженных матриц для оценки их ранга с высокой скоростью и высокой точностью. Он может значительно превосходить СВД по затратам времени и имеет аналогичную с СВД точность. Следовательно, FER обеспечивает эффективный и точный метод оценки ранга разреженной матрицы. Специально для работы с большой реальной сетью с помощью некоторых алгоритмов с ее матричным рангом FER может хорошо оценить ранг непосредственно по распределению степеней, полученному из необработанных данных, в то время как SVD неприменим из-за его чрезмерных временных затрат. Кроме того, в некоторых особых ситуациях, когда может быть обнаружена только структурная информация социальной сети, например распределение степеней или частично отсутствующее распределение степеней, FER по-прежнему применим для оценки ранга соответствующей матрицы. Это означает, что FER потенциально может использоваться в некоторых алгоритмах, предназначенных для неполных данных или данных, загрязненных интерференционным шумом.
Специально для работы с большой реальной сетью с помощью некоторых алгоритмов с ее матричным рангом FER может хорошо оценить ранг непосредственно по распределению степеней, полученному из необработанных данных, в то время как SVD неприменим из-за его чрезмерных временных затрат. Кроме того, в некоторых особых ситуациях, когда может быть обнаружена только структурная информация социальной сети, например распределение степеней или частично отсутствующее распределение степеней, FER по-прежнему применим для оценки ранга соответствующей матрицы. Это означает, что FER потенциально может использоваться в некоторых алгоритмах, предназначенных для неполных данных или данных, загрязненных интерференционным шумом. .
. Дакс, «Числовой ранг матриц Крылова», Линейная алгебра и ее приложения , том. 528, 2017.
Дакс, «Числовой ранг матриц Крылова», Линейная алгебра и ее приложения , том. 528, 2017. D. Feng и X. M. He, «Надежные аппроксимации матриц данных низкого ранга», Science China Mathematics , vol. 60, 2017.
D. Feng и X. M. He, «Надежные аппроксимации матриц данных низкого ранга», Science China Mathematics , vol. 60, 2017. Wang, and X Li, «Регуляризация низкого ранга: обзор», Neural Networks: The Official Journal of the International Neural Network Society , об. 136, стр. 218–232, 2021.
Wang, and X Li, «Регуляризация низкого ранга: обзор», Neural Networks: The Official Journal of the International Neural Network Society , об. 136, стр. 218–232, 2021. Де Латаувер, Б. Де Мур и Дж. Вандевалле, «Многолинейное разложение по сингулярным числам», SIAM Journal on Matrix Analysis and Applications , vol. 21, 2000.
Де Латаувер, Б. Де Мур и Дж. Вандевалле, «Многолинейное разложение по сингулярным числам», SIAM Journal on Matrix Analysis and Applications , vol. 21, 2000. Базовые системы , SITIS, Неаполь, Италия, ноябрь 2016 г.
Базовые системы , SITIS, Неаполь, Италия, ноябрь 2016 г.
