Как построить график функции y=f(kx), если известен график функции y=f(x). Примеры построения 10 класс онлайн-подготовка
Тема: Тригонометрические функции
Урок: Как построить график функции y=f(kx) если известен график функции y=f(x). Примеры построения
1. Тема урока, введение
На предыдущем уроке мы вывели правило построения графика функции по известному графику для Точку пересечения с осью y мы оставляли без изменения, остальные точки кривой сжимали или растягивали в k раз вдоль оси x. Приведем пример и распространим правило на случай
2. Построение графика функции y=f(kx), k>0
Задача 1. Построить график функции если известен график функции
Решение:
Рис. 1.
Происходит сжатие кривой к оси y в 2 раза. Если на участке исходная функция укладывается ровно в одну полную волну, то новая функция, имеющая период , уложится 2 раза.
Если на участке исходная функция укладывается ровно в одну полную волну, то новая функция, имеющая период , уложится 2 раза.
График функции можно построить и другим способом. Возьмем участок графика на промежутке и произведем сжатие к оси y в 2 раза. Получим точки которые ограничивают полуволну новой кривой (рис. 2).
С помощью полученной полуволны несложно построить график функции на всей области определения.
3. Построение графика функции y=f(-x)
Мы привели пример построения графика функции при
Получим кривую из кривой
Возьмем точку на графике, и противоположную ей точку В точке значение функции равно
Таким образом, точка A переходит в точку B:
(рис. 3).
Графики функций и симметричны относительно оси y.
4. Построение графика функции y=f(kx), k<0
Перейдем к построению графика функции
Если то
Необходимо сделать следующее:
1. Сжать исходную кривую к оси y с коэффициентом Получим кривую
Сжать исходную кривую к оси y с коэффициентом Получим кривую
2. Отобразить симметрично кривую относительно оси y. Получаем искомую кривую
Пример: Построить график функции
Решение.
Функция косинус – четная, значит, выполняется равенство:
Нам необходимо построить график функции
Построим одну полуволну графика (рис. 4):
a)
b) растяжение в 3 раза вдоль оси y.
c) симметричное отображение относительно оси x.
d) сжатие к оси y в 2 раза.
Мы получили одну полуволну графика, с ее помощью строим график функции на всей области определения (рис. 5).
5. Вывод, заключение
Мы рассмотрели правило получения графика функции по известному графику Преобразования графиков будут использованы на следующем уроке при изучении гармонических колебаний.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. . Г. Мордковича. –М.: Мнемозина, 2007.
№№ 17.7 – 17.9, 18.7.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
Преобразование графиков тригонометрических функций, 10 класс
Конспект урока по алгебре в 10 классе
Васильева Екатерина Сергеевна,
учитель математики
ОГБОУ «Смоленская специальная (коррекционная)
общеобразовательная школа I и II видов»
Смоленск
Тема урока: «Преобразование графиков тригонометрических функций».
Название модуля: преобразование графиков тригонометрических функций.
Интегрирующая дидактическая цель: отработать навыки построения графиков тригонометрических функций.
Целевой план действий для учащихся:
повторить основные свойства тригонометрических функций;
отработать навык преобразования графиков тригонометрических функций;
способствовать развитию логического мышления;
воспитывать интерес к изучению предмета.
Банк информации.
Входной контроль.
Назовите свойства функций y = sin x (рис. 1).
Рис. 1
Свойства:
D(y)=R
E(y)=[-1;1], функция ограничена
sin(-x)=-sinx, функция нечётная
Наименьший положительный период: 2π
sin (x+2πn)= sin x, n Є Z, x Є R.
sin x=0 при x=πk, kЄ Z
sin x>0, x Є (2πk;2π+2πk), k Є Z
sin x
Наибольшее значение, равное 1, y=sin x принимает в точках x=π/2+ 2πk, k Є Z.
Наименьшее значение, равное -1, y=sin x принимает в точках x=3π/2+ 2πk, k Є Z.
Рассмотрим график фукции y= cos x (рис. 2).
Рис. 2
Свойства:
D (y)=R
E (y)=[-1;1], функция ограничена
cos(-x)= cos x, функция чётная
Наименьший положительный период: 2π
cos (x+2πn)=cos x, n Є Z, x Є Rcos x=0 при x=π/2+πk, kЄZ
cos x>0, x Є (-π/2+2πk; π/2+2πk), k Є Z
cos x
Наибольшее значение, равное 1, y=cos x принимает в точках x= 2πk, k Є Z.
Наименьшее значение, равное -1, y=cos x принимает в точках x=π+ 2πk, k Є Z.
Cледующий график функции y=tg x (рис. 3)
3)
Риc. 3
Свойства:
D(y)-множество всех действительных чисел, кроме чисел вида x=π/2 +πk, k Є Z
E(y)=(-∞;+ ∞), функция неограниченная
tg(-x)=-tg x, функция нечётная
наименьший положительный период: π
tg(x+π)= tg xtgx= 0 при x=πk, k Є Z
tg x> 0, x Є ( πk; π/2+πk), k Є Z
tg x
Следующий график функции y=ctg x (рис. 4)
Рис. 4
Свойства:
D(y)-множество всех действительных чисел, кроме чисел вида x=πk, k Є Z
E(y)= (-∞;+ ∞), функция неограниченная
ctg(-x)=-ctg x, функция нечётная
Наименьший положительный период: π
ctg(x+π)=tg xctg x = 0 при x=π/2+πk, k Є Z
ctg x>0, x Є( πk; π/2+πk), k Є Z
ctg x
Объяснение материала.
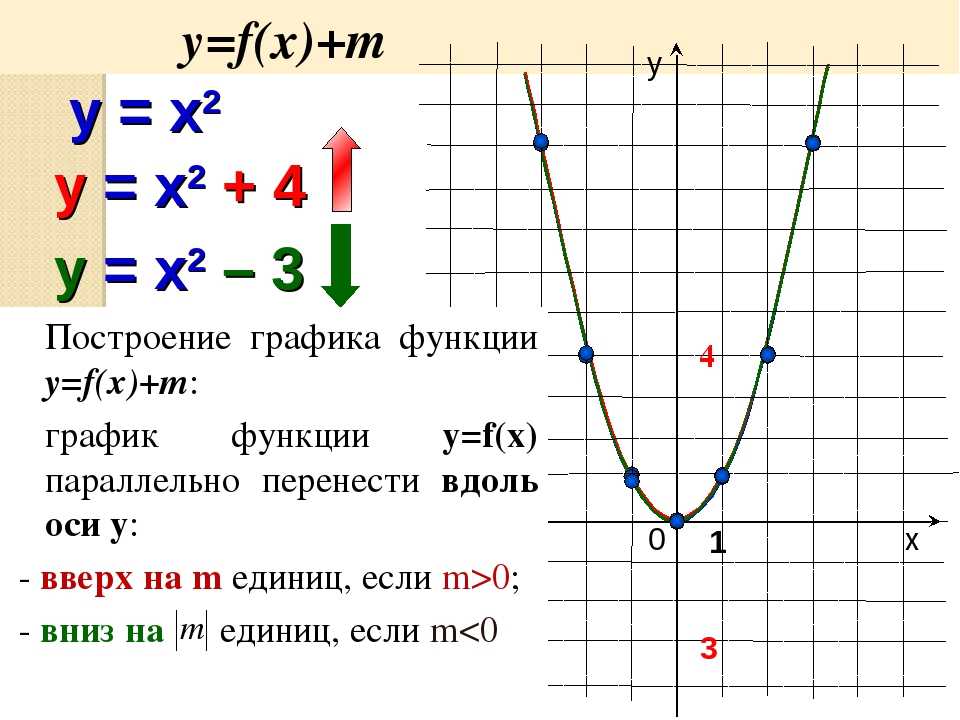
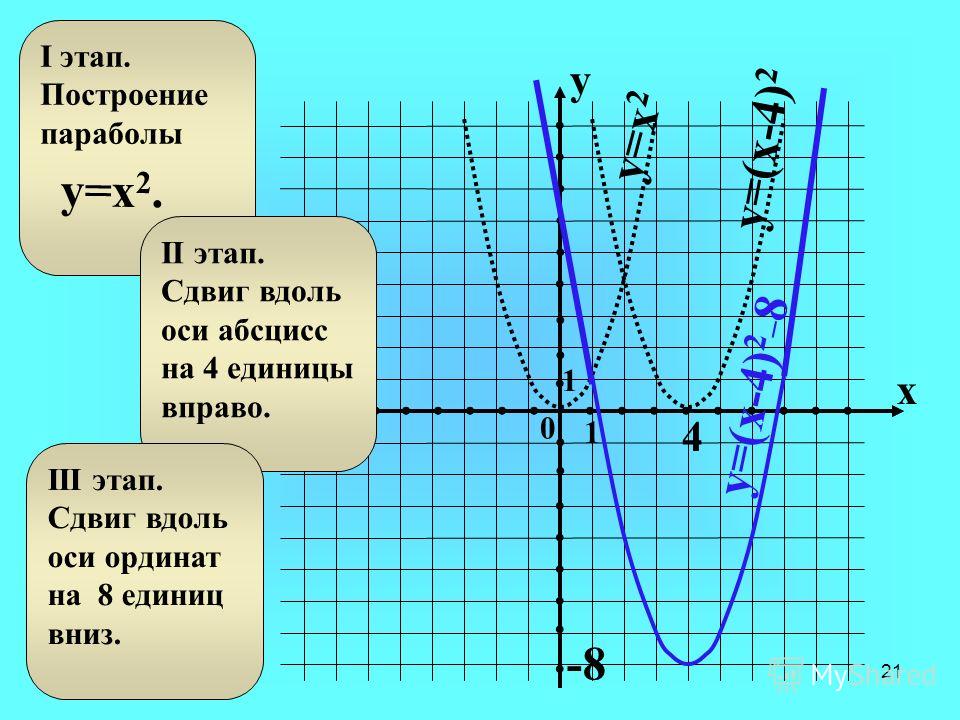
Для построения графика функции y=f(x)+a, где a — постоянное число, надо перенести график y=f(x) вдоль оси ординат. Если a>0, то график переносим параллельно самому себе вверх, если a
Для построения графика функции y=kf(x) надо растянуть график функции y=f(x) в k раз вдоль оси ординат. Если |k|>1, то происходит растяжение графика вдоль оси OY, если 0k|, то – сжатие.
График функции y=f(x+b) получается из графика y=f(x) путем параллельного переноса вдоль оси абсцисс. Если b>0 , то график перемещается влево, если b
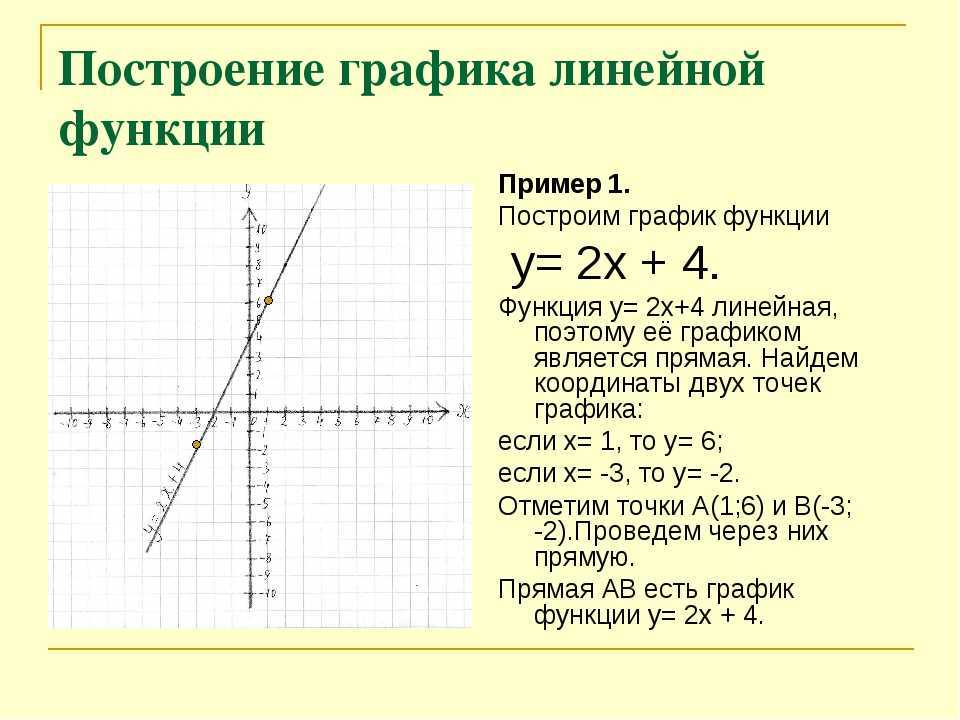
Для построения графика функции y=f(kx) надо растянуть график y=f(x) вдоль оси абсцисс.
 Если |k|>1, то происходит сжатие графика вдоль оси OХ, если 0
Если |k|>1, то происходит сжатие графика вдоль оси OХ, если 0
Закрепление материала.
Уровень А
Частная дидактическая цель: отработать навык построения тригонометрических функций путем преобразований.
Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.
1.
График функции получается из графика путем растяжения вдоль оси Ox в 3 раза.
2.
График функции получается из графика путем растяжения вдоль оси Oy в 2 раза.
3.
График функции получается из графика путем параллельного переноса на 2 единицы вверх вдоль оси Oy.
График функции получается из графика путем параллельного переноса вдоль оси абсцисс на единиц влево.
Г
рафик функции получается из графика путем сжатия вдоль оси Oy в 4 раза.
Уровень В.
Частная дидактическая цель: отработать навык построения графиков тригонометрических функций путем последовательного применения преобразований.
Методический комментарий для учащихся: постройте графики функций, выполнив преобразования.
График функции получается из графика путем параллельного переноса вдоль оси абсцисс на единиц вправо.
График функции получается из графика функции путем последовательного выполнения следующих преобразований:
1) параллельный перенос на единицы влево вдоль оси абсцисс
2) сжатие вдоль оси Оy в 4 раза.
3.
График функции получается из графика функции , каждая ордината которого изменяется в -2 раза. Для этого выполняем следующие преобразования:
1) отображаем симметрично относительно оси Ox,
2) растягиваем в 2 раза вдоль оси Oy.
4.
График функции получается из графика функции последовательного выполнения следующих преобразований:
1) сжатие вдоль оси абсцисс в 2 раза;
2) растяжение в 3 раза вдоль оси Oy;
3) параллельный перенос на 1 единицу вверх вдоль оси ординат.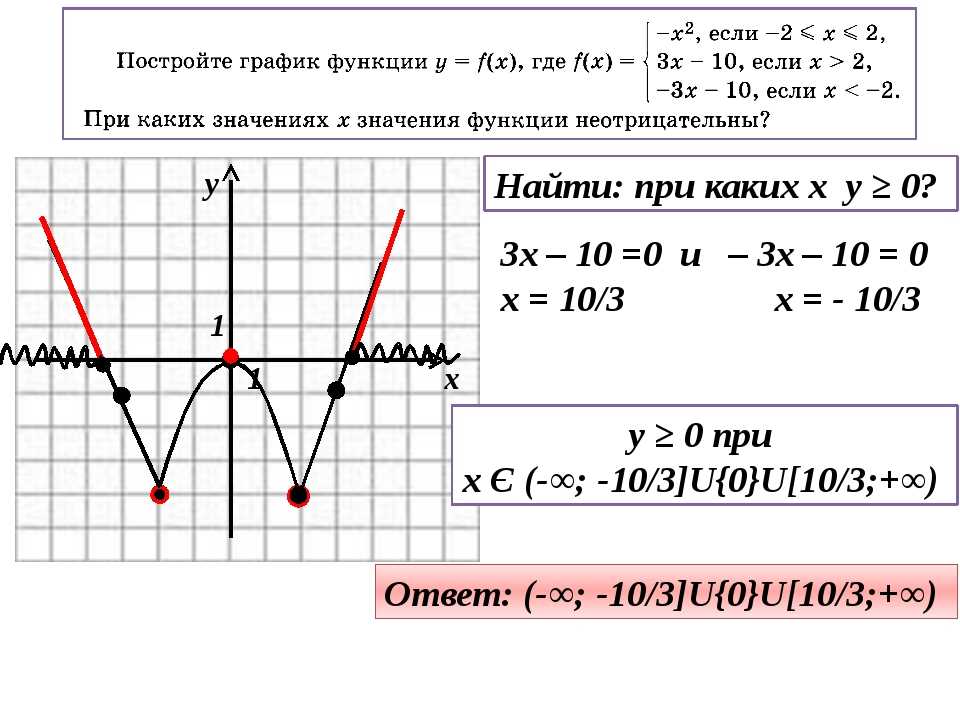
Уровень С.
Частная дидактическая цель: отработать навык построения графиков тригонометрических функций путем последовательного применения преобразований.
Методический комментарий для учащихся: укажите, какие преобразования нужно выполнить для построения графиков. Постройте графики.
1.
График функции получается из графика функциипутем последовательного выполнения следующих преобразований:
1) отображение симметрично относительно оси Ox,
2) сжатие в 2 раза вдоль оси Oy;
3) параллельный перенос на 2 единицы вниз вдоль оси Оy.
2.
График функции получается из графика функции последовательного выполнения следующих преобразований:
1) параллельный перенос вдоль оси абсцисс на единиц влево,
2) растяжение в 5 раза вдоль оси Oy.
3
.
График функции получается из графика функции последовательного выполнения следующих преобразований:
1) растяжение вдоль оси абсцисс в 2 раза;
2) параллельный перенос на единиц влево вдоль оси абсцисс.
3) растяжение в 2 раза вдоль оси Oy.
4.
Так как cos (-x)=cos x, следовательно, y= cos x — чётная функция, значит, график функции тот же, что и график функции y= cos x.
5.
График функции получается из графика функции .Части графика функции , расположенные ниже оси абсцисс, зеркально отразятся и будут распо
ложены в верхней полуплоскости.
Использованные ресурсы:
http://tvsh2004.narod.ru/alg07.html
http://www.aiportal.ru/services/graph.html
6.7 Интерпретация графиков | Функции
Предыдущий 6.6 Тригонометрические функции | Следующий 6.8 Краткое содержание главы |
6.
 {2}+q \\
\поэтому q& = 1
\конец{выравнивание*}
9{2}+1\).
{2}+q \\
\поэтому q& = 1
\конец{выравнивание*}
9{2}+1\).Рабочий пример 23: Определение уравнения гиперболы
Используйте рисунок ниже, чтобы определить значения \(a\) и \(q\) для гиперболы форма \(y=\frac{a}{x}+q\).
Изучите эскиз
Две кривые гиперболы лежат во втором и четвертом квадранте, поэтому \(а<0\). Мы также видим, что график смещен вертикально вверх, поэтому \(q>
Подставить данные точки в уравнение и решить
Подставить точку \((-1;2)\):
\начать{выравнивать*} y& = \frac{a}{x}+q \\ 2& = \frac{a}{-1}+q \\ \поэтому 2& = -a+q \конец{выравнивание*}
Подставить точку \((1;0)\):
\начать{выравнивать*} y& = \frac{a}{x}+q \\ 0& = \frac{a}{1}+q \\ \поэтому а& = -q \конец{выравнивание*}
Решите уравнения одновременно, используя подстановку
\начать{выравнивать*} 2& = -а+д \\ & = д + д \\ &=2q\\ \поэтому q& = 1 \\ \поэтому а& = -q \\ & = -1 \end{выравнивание*} 9{2}+4\) и \(y=x-2\). Рассчитайте следующее:
Рассчитайте следующее:координаты \(A\), \(B\), \(C\), \(D\)
координаты \(E\)
- 9{2}-4& = 0 \\
(х+2)(х-2)& = 0 \\
\поэтому x& = ±2
\конец{выравнивание*}
Это дает точки \(A(-2;0)\) и \(B(2;0)\).
Для прямой линии, чтобы вычислить точку пересечения \(y\), пусть \(x=0\):
\начать{выравнивать*} у& = х-2 \\ & = 0-2 \\ & = -2 \конец{выравнивание*} 9{2}+x-6& = 0 \\ \поэтому (x-2)(x+3)& = 0 \\ \поэтому x& = 2 \text{ или } -3 \конец{выравнивание*}
В \(E\), \(x=-3\), поэтому \(y=x-2=-3-2=-5\).
 Это дает точку \(E(-3;-5)\).
Это дает точку \(E(-3;-5)\).Расчет расстояния \(CD\)
\начать{выравнивать*} CD& = CO+OD \\ & = 4+2 \\ & = 6 \конец{выравнивание*}
Расстояние \(CD\) составляет \(\text{6}\) единиц.
Напишите окончательный ответ
координаты \(A(-2;0)\), \(B(2;0)\), \(C(0;4)\), \(D(0;-2)\)
координаты \(E(-3;-5)\)
расстояние \(CD = 6\) единиц
Рабочий пример 25: Интерпретация тригонометрических графиков
С помощью эскиза определите уравнение тригонометрической функции \(f\) форма \(y=a f(\theta)+q\).

Осмотрите эскиз
Из скетча мы видим, что график представляет собой график синусоиды, который был сдвинут вертикально вверх. Общая форма уравнения: \(y=a\sin\theta +q\).
Подставить данные точки в уравнение и решить
При \(N\), \(\theta =210°\) и \(y=0\):
\начать{выравнивать*} y& = a\sin\theta +q \\ 0& = а\sin 210°+q \\ & = a\left(-\frac{1}{2}\right)+q \\ \поэтому q& = \frac{a}{2} \конец{выравнивание*}
При \(M\), \(\theta = 90°\) и \(y=\frac{3}{2}\):
\начать{выравнивать*} \frac{3}{2}& = a\sin90°+q \\ & = а + д \конец{выравнивание*}
Решите уравнения одновременно, используя подстановку
\начать{выравнивать*} \frac{3}{2}& = a+q \\ & = а+\фракция {а}{2} \\ 3& = 2а+а \\ 3а& = 3 \\ \поэтому а& = 1 \\ \поэтому q& = \frac{a}{2} \\ & = \фракция{1}{2} \end{выравнивание*} 90 и = 1 \конец{выровнено}\)Это также единственная точка пересечения.

Для обоих графов нет \(x\)-перехвата.
\(y = x\) и \(y = \dfrac{2}{x}\)
\(y = x\) представляет собой простой линейный граф. Для тебя =\frac{2}{x}\) нет \(y\)-перехвата и нет \(x\)-перехват. Заметим, что это гиперболический граф который был растянут на 2 единицы. 92 — 2 & = 0\\ (х — \sqrt{2})(х + \sqrt{2}) & = 0\\ х = \sqrt{2} &\text{ или } х = -\sqrt{2} \\ y = \sqrt{2} &\text{ или } y = -\sqrt{2} \конец{выравнивание*}
Графики пересекаются в \(\left(\sqrt{2};\sqrt{2}\right)\) и \(\left(-\sqrt{2};-\sqrt{2}\right)\).
 2 — 3 &= 0 \\
(х — \sqrt{3})(х + \sqrt{3}) & = 0\\
х = \sqrt{3} &\text{ или } х = -\sqrt{3} \\
у = 6
\конец{выравнивание*}
9{2}\) — парабола, отраженная относительно
ось \(х\). Для \(y =\frac{8}{x}\) нет
\(y\)-перехват и нет \(x\)-перехвата. Из
значения \(a\) мы видим, что это основная гипербола
который был растянут на 8 единиц. 93 &= — 8 \\
х & = -2\\
y &= \frac{8}{-2} \\
у &= -4
\конец{выравнивание*}
2 — 3 &= 0 \\
(х — \sqrt{3})(х + \sqrt{3}) & = 0\\
х = \sqrt{3} &\text{ или } х = -\sqrt{3} \\
у = 6
\конец{выравнивание*}
9{2}\) — парабола, отраженная относительно
ось \(х\). Для \(y =\frac{8}{x}\) нет
\(y\)-перехват и нет \(x\)-перехвата. Из
значения \(a\) мы видим, что это основная гипербола
который был растянут на 8 единиц. 93 &= — 8 \\
х & = -2\\
y &= \frac{8}{-2} \\
у &= -4
\конец{выравнивание*}Графики пересекаются в точке \(\left(-2;-4\right)\).

Для прямолинейного графика имеем \(x\) и \(y\)-перехваты. \(y\)-перехват дает \(c = 2\). Теперь мы можем вычислить градиент прямой линии график:
\начать{выравнивать*} у &= тх + 2 \\ m &= \frac{2 — 0}{0 — (-2)} \\ &= 1 \конец{выравнивание*}
Следовательно, уравнение прямолинейного графика имеет вид \(y = x + 2\). 92 + 2\)
Для линейного графика заметим, что он проходит через \((0;0)\) и, следовательно, \(c = 0\).

У нас есть две точки на графике прямой, поэтому мы можем вычислить градиент, \(м\):
\начать{выравнивать*} у &= тх + 0 \\ m &= \frac{8 — (-8)}{1 — (- 1)} \\ м &= 8 \конец{выравнивание*}
Уравнение прямолинейного графика: \(y = 8x\).
Для гиперболы заметим, что график не сдвинут либо вверх, либо вниз. Поэтому \(q = 0\). Сейчас мы может вычислить \(a\):
\начать{выравнивать*} y &= \frac{a}{x} \\ 8 &= \frac{a}{1} \\ а &= 8 \конец{выравнивание*}
Следовательно, уравнение гиперболы имеет вид \(y = \ гидроразрыва {8} {x} \).

Уравнения для двух графиков: \(y = 8x\) и \(y = \ гидроразрыва {8} {x} \).
Диапазон \(y = 2 \sin{\theta} + 1\):
- \(1 \ле \тета \ле 2\)
- \(-2 \le \тета \le 2\)
- \(-1 \ле \тета \ле 3\)
- \(-2 \ле \тета \ле 3\)
3
Диапазон \(y = 2 \cos{\theta} — 4\):
- \(-6 \le \тета \le 2\)
- \(-4 \le \тета \le -2\)
- \(-6 \le \тета \le 1\)
- \(-6 \le \тета \le -2\)
9х + 1\) равно:
- \(3\)
- \(1\)
- \(2\)
- \(0\)
3
Что из следующего проходит через \((1;7)\)?
- \(y = \frac{7}{x}\)
- \(у = 2х + 3\)
- \(y = \frac{4}{x}\) 92 + 1\)
1
Предыдущий
6.
 6 Тригонометрические функции
6 Тригонометрические функцииОглавление Следующий
6.8 Краткое содержание главы
10 класс – Блог Джошуа
joshuas2015 на
- Следите за выполнением упражнений в классе и будьте внимательны.
- Выполняйте домашнее задание каждый день.
- Исследование для тестов, а не только прошлой ночью.
- Делайте каждую запись в блоге подробно и усердно.
- При необходимости обратитесь за помощью или обратитесь к учебникам.
Все эти пять вещей имеют решающее значение для Math 10, если вы хотите добиться успеха в курсе. Потратив время и усилия на эти пять вещей, вы сможете добиться хороших результатов на всех математических курсах.
Категории: 10 класс, Математика 10 Оставить комментарий
joshuas2015 на
Изображение:
Категории: 10 класс, 10 класс Оставить комментарий Биномиал — это алгебраическое выражение, состоящее из двух терминов, например: . Чтобы умножить три бинома, в игру вступает FOIL. Вместо того, чтобы использовать FOIL один раз, после того, как вы получите свой ответ со средним биномом, с вашим новым ответом, сделайте это снова с оставшимся биномом, чтобы получить полное расширение.

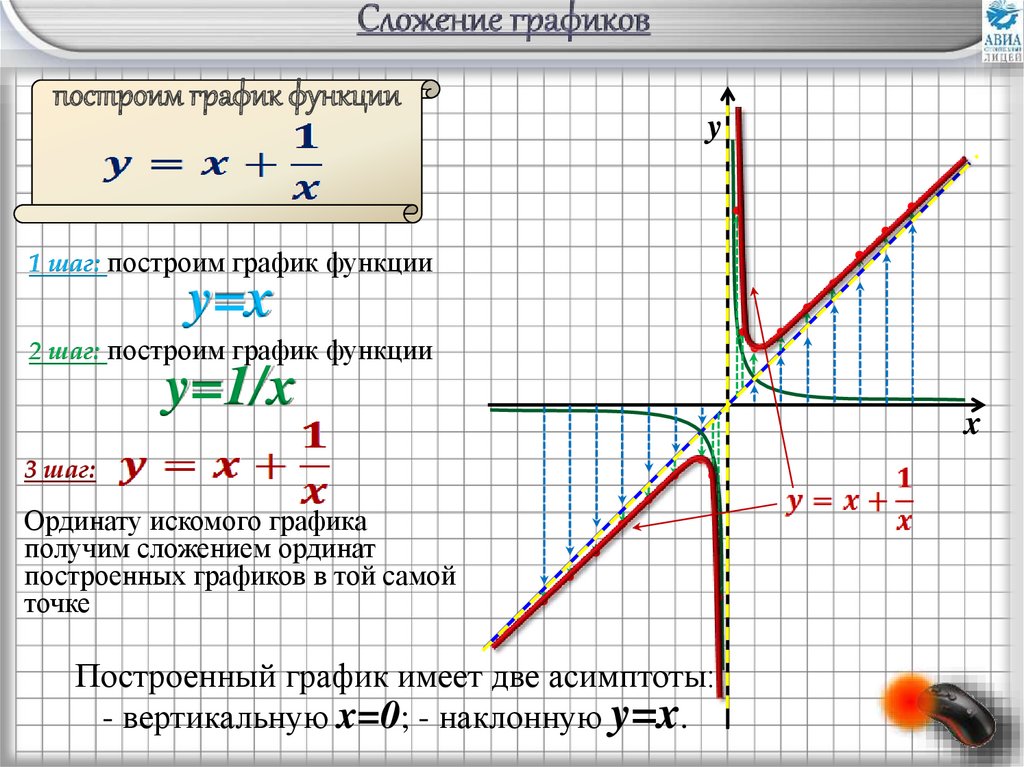
 Если |k|>1, то происходит сжатие графика вдоль оси OХ, если 0
Если |k|>1, то происходит сжатие графика вдоль оси OХ, если 0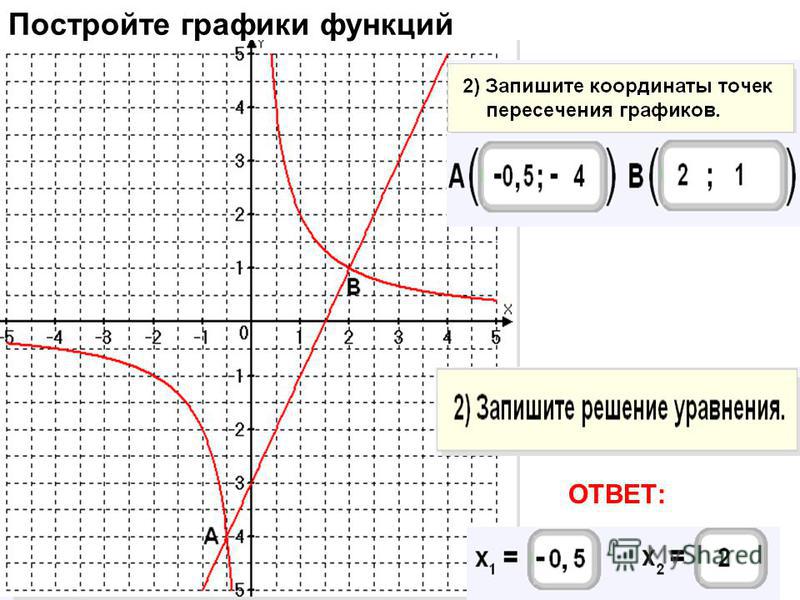 Это дает точку \(E(-3;-5)\).
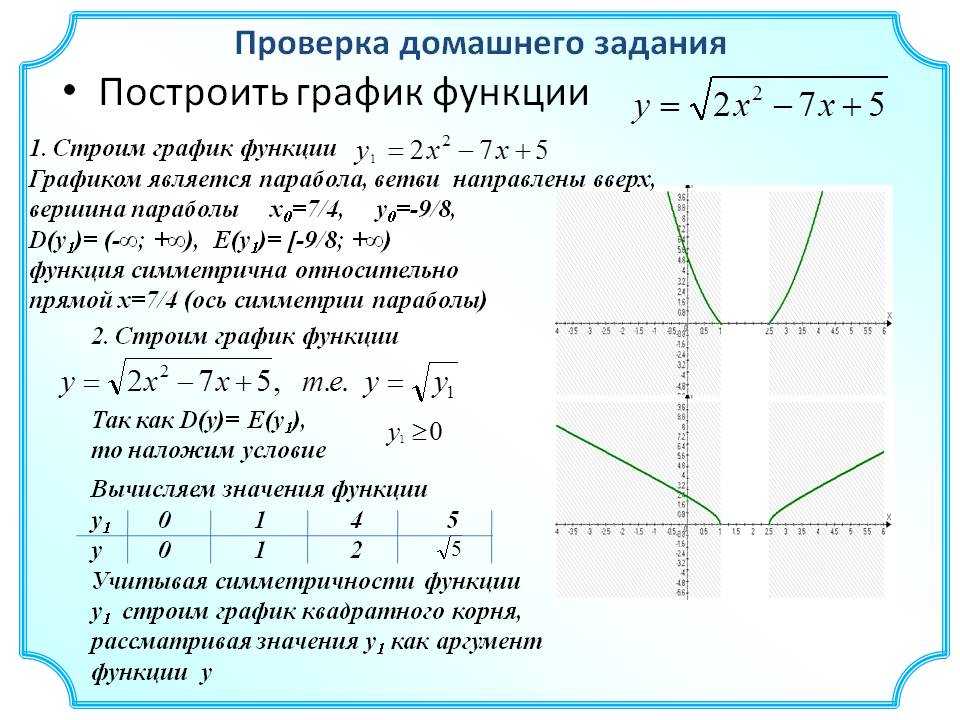
Это дает точку \(E(-3;-5)\).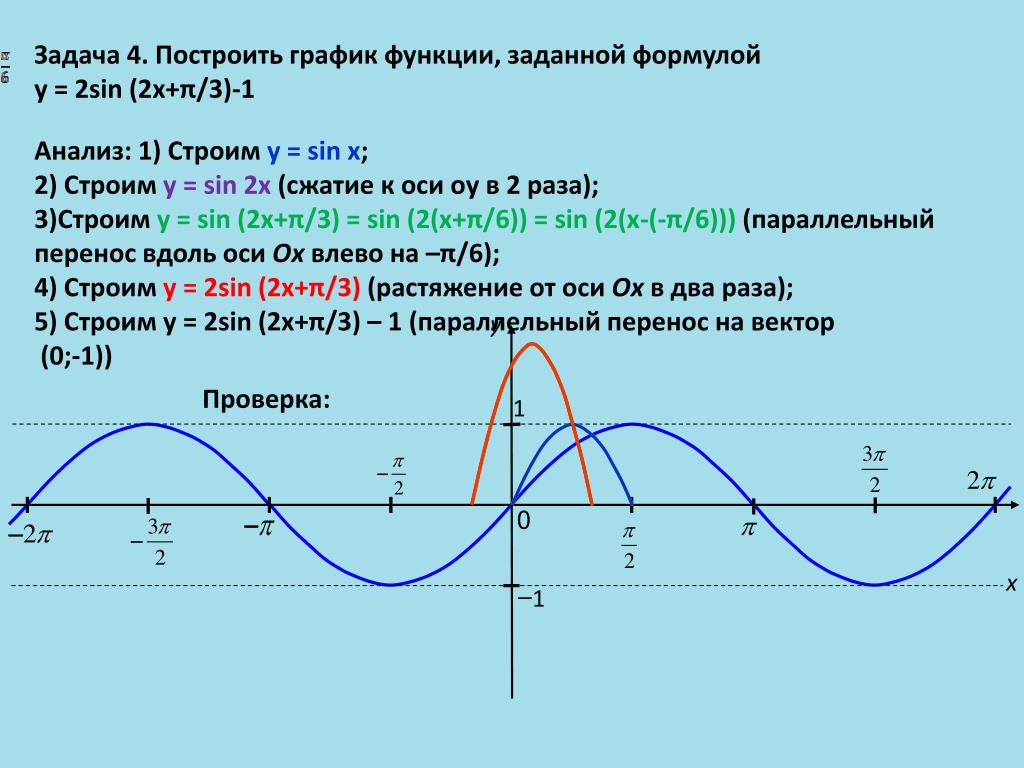
 2 — 3 &= 0 \\
(х — \sqrt{3})(х + \sqrt{3}) & = 0\\
х = \sqrt{3} &\text{ или } х = -\sqrt{3} \\
у = 6
\конец{выравнивание*}
9{2}\) — парабола, отраженная относительно
ось \(х\). Для \(y =\frac{8}{x}\) нет
\(y\)-перехват и нет \(x\)-перехвата. Из
значения \(a\) мы видим, что это основная гипербола
который был растянут на 8 единиц. 93 &= — 8 \\
х & = -2\\
y &= \frac{8}{-2} \\
у &= -4
\конец{выравнивание*}
2 — 3 &= 0 \\
(х — \sqrt{3})(х + \sqrt{3}) & = 0\\
х = \sqrt{3} &\text{ или } х = -\sqrt{3} \\
у = 6
\конец{выравнивание*}
9{2}\) — парабола, отраженная относительно
ось \(х\). Для \(y =\frac{8}{x}\) нет
\(y\)-перехват и нет \(x\)-перехвата. Из
значения \(a\) мы видим, что это основная гипербола
который был растянут на 8 единиц. 93 &= — 8 \\
х & = -2\\
y &= \frac{8}{-2} \\
у &= -4
\конец{выравнивание*}


 6 Тригонометрические функции
6 Тригонометрические функции