Построение графиков функций с модулем | Презентация к уроку по алгебре (9 класс) по теме:
Слайд 6
График функции у = |x+a| получается параллельным переносом графика y=|x| в отрицательном направлении от оси х на |а| при а>0 и в положительном направлении на |a| при a
Слайд 7
Построить график функции у = х ² — 4 | х | + 3. 1 способ. Раскрываем | х | = х при х≥0, получаем график у = х² — 4х + 3. При х
Слайд 9
2 способ. Если рассмотрим график у = х² — 4х + 3 при х≥0 и отобразить его относительно оси ОУ мы получим тот же самый график.
Слайд 10
Для построения графика функции у = |f(х) | достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
Слайд 11
Построить график функции у = | х ² — х -6 | 1.Построим график функции у =х ² — х -6 2 . Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.
Слайд 12
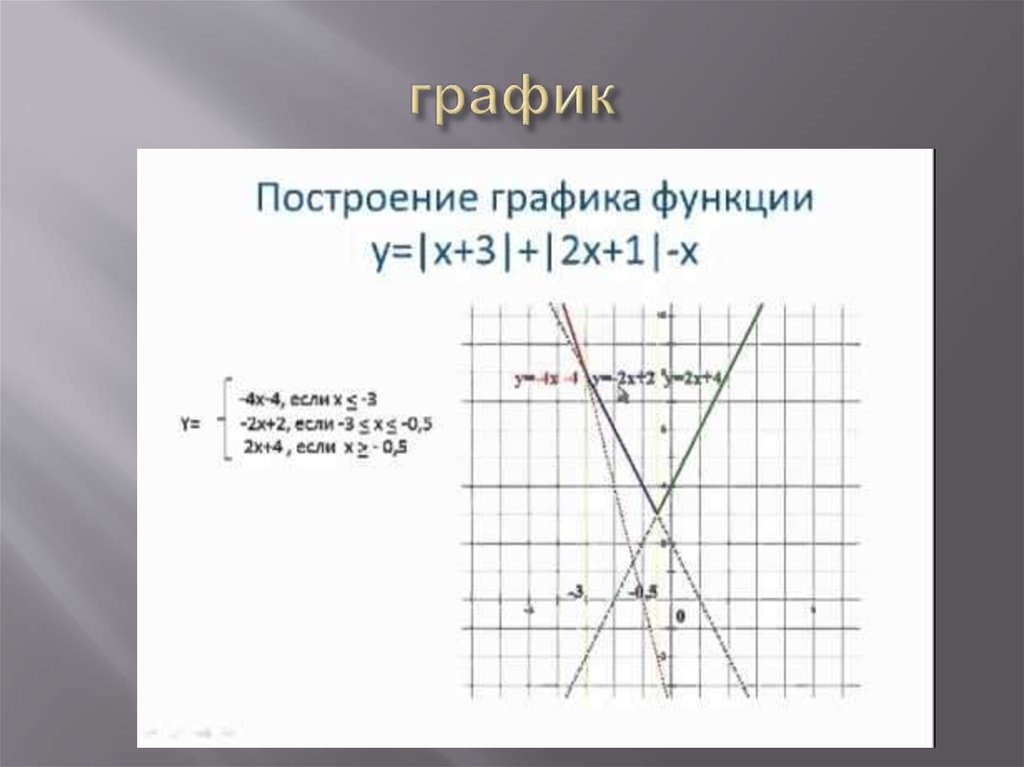
Построить график функции у = | х + 3 | + |2x + 1| — x Строить график будем с помощью раскрытия модуля. Алгоритм построения: Приравняем каждое подмодульное выражение к нулю и находим точки, в которых подмодульные выражения, входящие в уравнение функции меняют знак. Наносим эти точки на ось х и выделяем промежутки, в которых подмодульные выражения сохраняют знак. Раскрываем модуль на каждом промежутке и получаем соответствующие уравнения функции. Строим график на каждом промежутке.
Алгоритм построения: Приравняем каждое подмодульное выражение к нулю и находим точки, в которых подмодульные выражения, входящие в уравнение функции меняют знак. Наносим эти точки на ось х и выделяем промежутки, в которых подмодульные выражения сохраняют знак. Раскрываем модуль на каждом промежутке и получаем соответствующие уравнения функции. Строим график на каждом промежутке.
Слайд 13
у = | х + 3 | + |2x + 1| — x Приравниваем каждое подмодульное выражение к нулю и находим точки, в которых происходит смена знака: Наносим точки на ось х:
Слайд 14
3. При
Слайд 16
у = | х + 3 | + |2x + 1| — x
Слайд 17
Построить график функции у = | 2|х | — 3| 1. Построить у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х | >1,5 т.е. х 1,5 а) у = 2х — 3 , для х > 0 б) для х 0 б) для х
Слайд 18
у = | 2|х | — 3| 1) Построить у = 2х-3, для х>0. 2) Построить прямую, симметричную построенной относительно оси ОУ. 3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.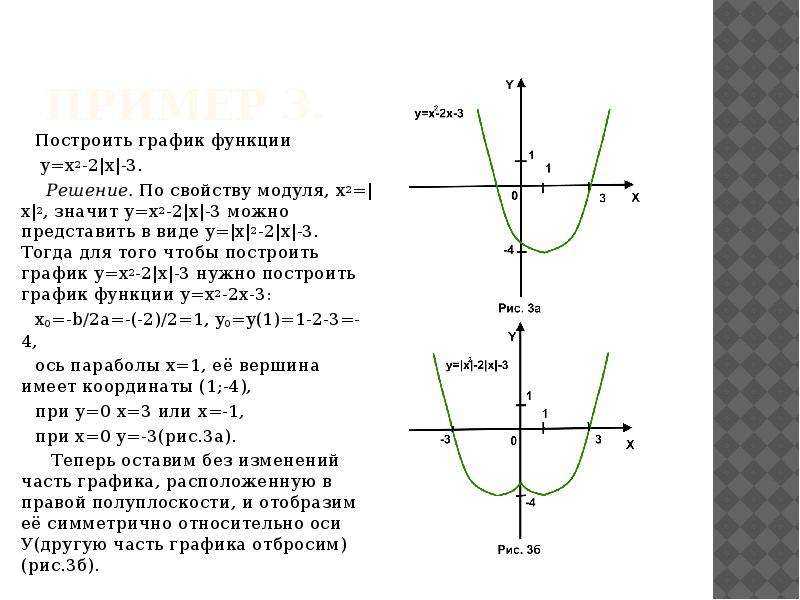 Сравнивая оба графика, видим что они одинаковые.
Сравнивая оба графика, видим что они одинаковые.
Слайд 19
у = | х ² – 5|х| | Построим у = х ² – 5 х, для х>0. Вершина параболы в (2,5; -6,25) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. 3. Для х
Слайд 20
Найти корни уравнения ||x-2|-5| = 3. Выполняем построение первого (внутреннего) модуля y = |x-2| Параллельно переносим линии вниз на 5 , чтобы получить график функции y = |x-2|- 5 Отражаем все что находится ниже оси абсцисс. Это и будет искомая функция y=||x-2|-5| . Также выполняем построение прямой у=3
Слайд 21
Найти корни уравнения ||x-2|-5|=3. Нетрудно определить по графику, что решениями уравнения с модулями будут значения x = — 6; x = 0; x = 4; x = 10 .
Слайд 22
Построить график функции у = | (|х| — 2) 2 – 3 | Строим график функции у = (х — 2) 2 – 3 Совершаем преобразование: для этого часть графика, расположенную левее оси оу стираем.
Слайд 23
Построить график функции у = | (|х| — 2) 2 – 3 | Часть графика, расположенную правее оси оу достраиваем симметрично относительно этой оси. Получаем график функции у = (|х| — 2) 2 – 3
Получаем график функции у = (|х| — 2) 2 – 3
Слайд 24
Построить график функции у = | (|х| — 2) 2 – 3 | Часть графика, расположенную ниже оси ох отображаем симметрично относительно этой оси.
Слайд 25
График неравенства | у — 2х -1| + 2|х| ≤ 3 Задача. Изобразите на координатной плоскости множество решений неравенства. Раскроем модули. Для этого каждое подмодульное выражение приравняем к нулю: у – 2х – 1 = 0; у = 2х + 1 х = 0 Подмодульные выражения меняют знак при переходе через прямые у = 2х + 1 и х = 0.
Слайд 26
Выводы: Для построения графика функции у = f |(х)|: 1.Построить график функции у = f (х) для х>0; 2.Построить для х0. 2. Строим вторую часть графика, т. е. построенный график симметрично отражаем относительно ОУ 3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Слайд 27
у = f |(х)| у = | f (х)| у = | f |(х)| | у = f (х), х>0 Построить часть для х0
Построение графиков онлайн x y.
 Функции и графики
Функции и графики«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.

- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).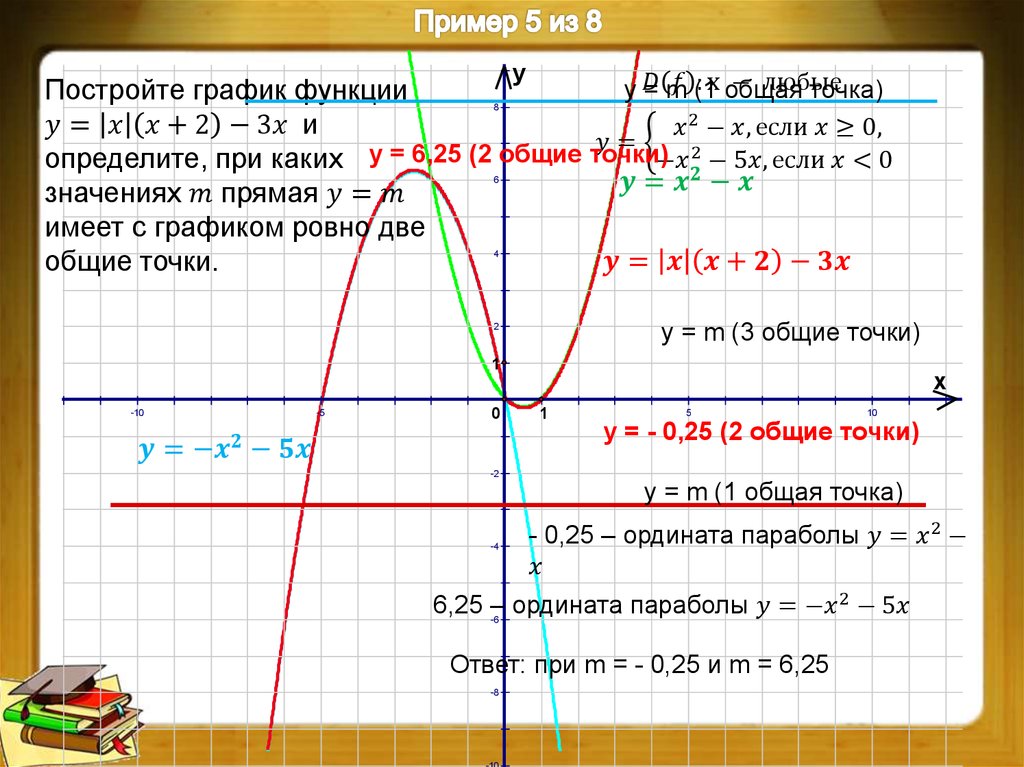
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому.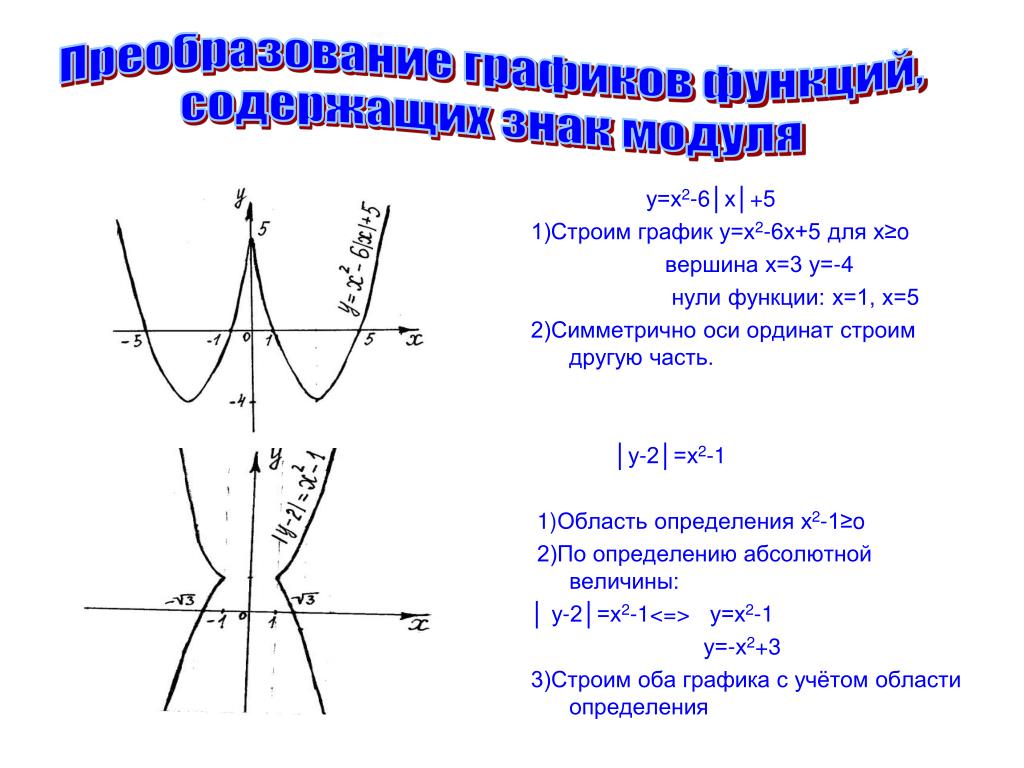 Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т.
 д.
д. - Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции.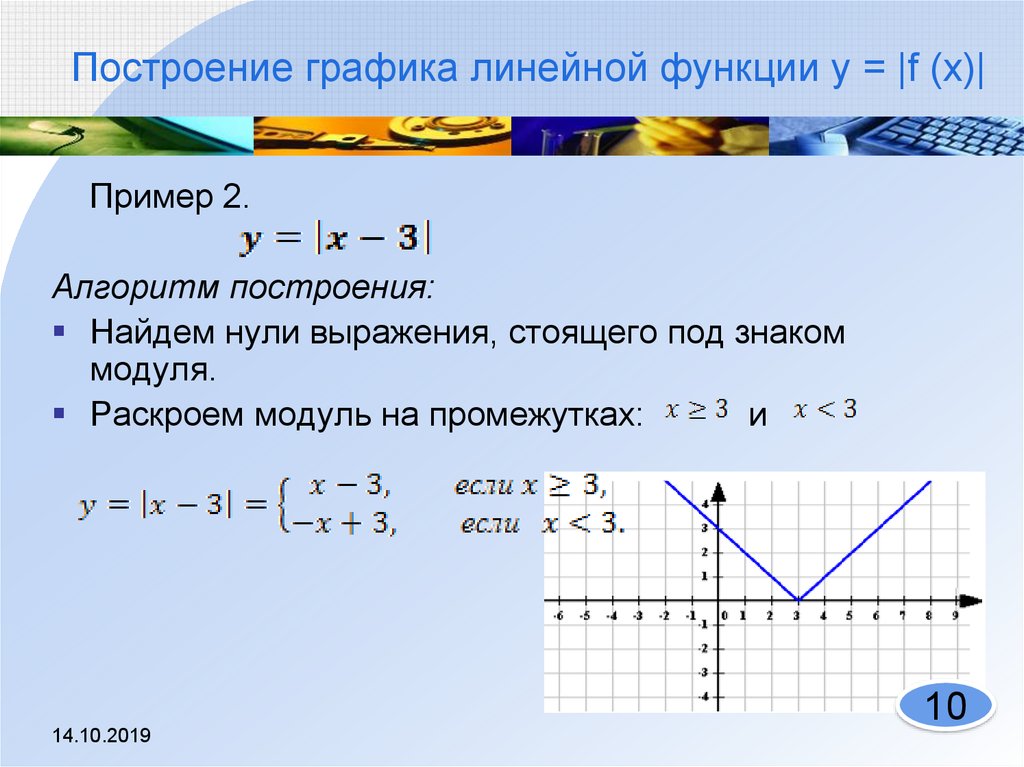 Давайте разберемся, что же это за алгоритмы.
Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
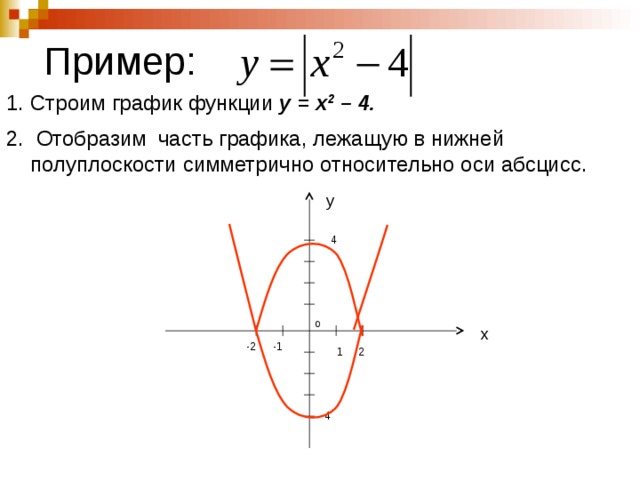
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y.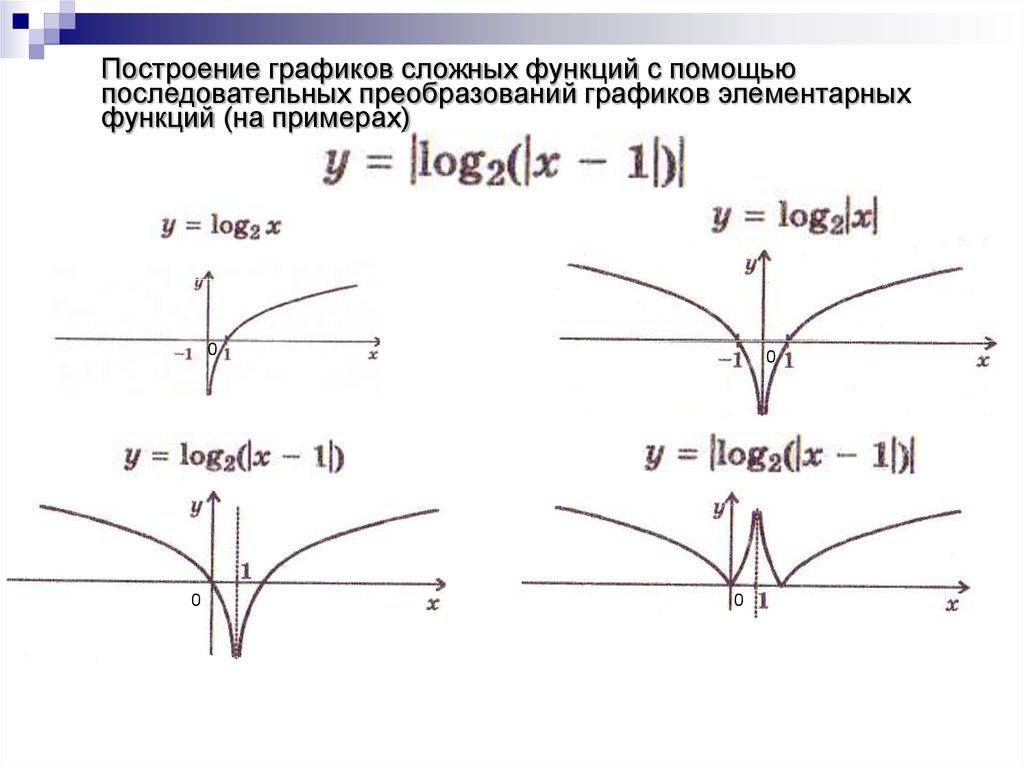
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.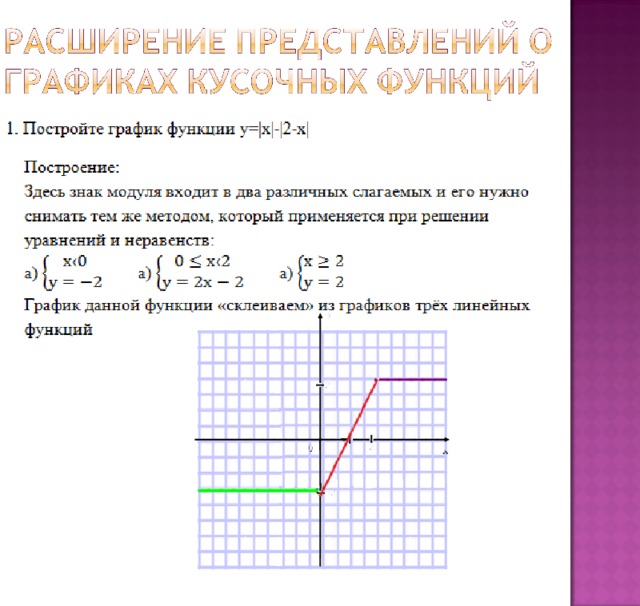 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Сюжетный экспресс на Python
Питон > Основы > Сюжетный экспресс
Предложить редактирование этой страницыPlotly Express — это краткий, согласованный высокоуровневый API для создания фигур.
Новичок в сюжете?
Plotly — бесплатная графическая библиотека с открытым исходным кодом для Python. Мы рекомендуем вам прочитать наше руководство по началу работы, чтобы получить последние инструкции по установке или обновлению, а затем перейти к нашим учебным пособиям по основам Plotly или погрузиться прямо в некоторые учебные пособия по базовым диаграммам.
Обзор¶
Модуль plotly.express (обычно импортируется как px ) содержит функции, которые могут создавать целые фигуры сразу, и называется Plotly Express или PX. Plotly Express является встроенной частью plotly и является рекомендуемой отправной точкой для создания наиболее распространенных фигур. Каждая функция Plotly Express использует графические объекты внутри и возвращает экземпляр plotly.graph_objects.Figure . В документации plotly вы найдете способ построения рисунков Plotly Express в верхней части любой применимой страницы, за которым следует раздел о том, как использовать графические объекты для построения подобных рисунков. Любая фигура, созданная с помощью одного вызова функции с помощью Plotly Express, может быть создана с использованием только графических объектов, но с использованием в 5–100 раз большего количества кода.
Plotly Express предоставляет более 30 функций для создания различных типов фигур.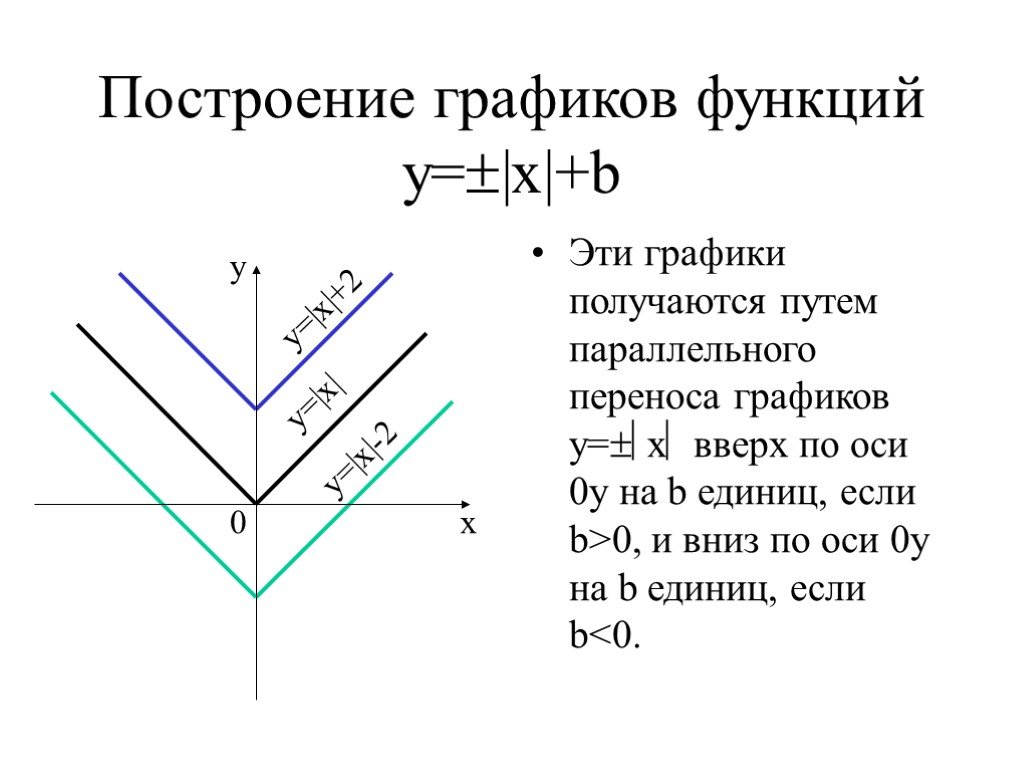 API для этих функций был тщательно разработан, чтобы быть как можно более последовательным и простым в освоении, что позволяет легко переключаться с точечной диаграммы на гистограмму, гистограмму и диаграмму солнечных лучей во время сеанса исследования данных. Прокрутите вниз, чтобы увидеть галерею графиков Plotly Express, каждый из которых создается с помощью одного вызова функции.
API для этих функций был тщательно разработан, чтобы быть как можно более последовательным и простым в освоении, что позволяет легко переключаться с точечной диаграммы на гистограмму, гистограмму и диаграмму солнечных лучей во время сеанса исследования данных. Прокрутите вниз, чтобы увидеть галерею графиков Plotly Express, каждый из которых создается с помощью одного вызова функции.
Вот доклад с конференции SciPy 2021, в котором дается хорошее введение в Plotly Express и Dash:
Plotly Express в настоящее время включает в себя следующие функции:
- Основы :
разброс,линия,область,бар,воронка 90 013 ,временная шкала - Часть Целого :
круг,солнечные лучи,карта дерева,сосулька,funnel_area - Одномерные распределения :
гистограмма,поле,скрипка,полоса,ecdf - 2D-распределения :
density_heatmap,density_contour - Ввод матрицы или изображения :
imshow - Трехмерный :
scatter_3d,line_3d - Многомерный :
scatter_matrix,parallel_coordinates,parallel_categories - Тайловые карты :
scatter_mapbox,line_mapbox,choropleth_mapbox,density_mapbox - Контурные карты :
scatter_geo,line_geo,choropleth - Полярные карты :
scatter_polar,line_polar,bar_polar - Троичные диаграммы :
scatter_ternary,line_ternary
Функции высокого уровня¶
API Plotly Express в целом предлагает следующие функции:
- Единая точка входа в
plotly: простоимпортируйте plotly.и получите доступ ко всем функциям построения графиков, а также встроенную демонстрацию наборы данных под express как px
express как px px.dataи встроенные цветовые шкалы и последовательности подpx.color. Каждая функция PX возвращает объектplotly.graph_objects.Рисунок, поэтому вы можете редактировать его, используя все те же методы, что и 9.0012 update_layout иadd_trace. - Разумные, переопределяемые значения по умолчанию : Функции PX будут выводить разумные значения по умолчанию везде, где это возможно, и всегда позволят вам переопределить их.
- Гибкие форматы ввода : функции PX принимают ввод в различных форматах, от
lists иdictдо длинных или широких форм PandasDataFrames доnumpyмассивов иxarraysв GeoPandasGeoDataFrames. - Конфигурация автоматической трассировки и макета : Функции PX будут создавать одну трассировку на кадр анимации для каждой уникальной комбинации значений данных, сопоставленных с дискретным цветом, символом, линией-тире, строкой-фасетом и/или гранью-столбцом.
 Атрибуты traces
Атрибуты traces legendgroupиshowlegendустановлены таким образом, что только один элемент легенды появляется на уникальную комбинацию дискретного цвета, символа и/или линии-тире. Трассировки автоматически связываются с правильно сконфигурированным подграфиком соответствующего типа. - Автоматическая маркировка рисунков : функции PX маркируют оси, легенды и цветные полосы на основе входных данных
DataFrameилиxarrayи обеспечивают дополнительный контроль с помощью аргументаlabels. - Автоматические метки при наведении : функции PX заполняют метку при наведении с помощью меток, упомянутых выше, и обеспечивают дополнительный контроль с помощью аргументов
hover_nameиhover_data. - Управление стилем : функции PX считывают информацию о стиле из шаблона фигуры по умолчанию и поддерживают часто необходимые косметические элементы управления, такие как
category_ordersиcolor_discrete_mapдля точного управления категориальными переменными.
- Единая обработка цвета : Функции PX автоматически переключаются между непрерывным и категоричным цветом в зависимости от типа ввода.
- Facet : функции двумерного декартова графика поддерживают фасетирование строк, столбцов и обернутых фасетов с аргументами
facet_row,facet_colиfacet_col_wrap. - Маргинальные участки : функции двумерного декартова графика поддерживают графики предельного распределения с аргументами
marginal,marginal_xиmarginal_y. - Серверная часть Pandas : функции 2D-декартова графика доступны как серверная часть графика Pandas, поэтому вы можете вызывать их через
df.plot(). - Линии тренда :
px.scatterподдерживает встроенные линии тренда с доступными выходными данными модели. - Анимации : многие функции PX поддерживают простую поддержку анимации с помощью аргументов
animation_frameиanimation_group.
- Автоматическое переключение WebGL : для достаточно больших точечных диаграмм PX будет автоматически использовать WebGL для рендеринга с аппаратным ускорением.
Plotly Express в Dash¶
Dash — лучший способ создавать аналитические приложения на Python с использованием рисунков Plotly. Чтобы запустить приложение ниже, запустите pip install dash , нажмите «Загрузить», чтобы получить код, и запустите питон app.py .
Начните с официальной документации Dash, и узнайте, как без особых усилий создавать и развертывать подобные приложения с помощью Dash Enterprise.
Выход[2]:
Галерея¶
Следующий набор рисунков — это всего лишь пример того, что можно сделать с помощью Plotly Express.
Точечная, линейная, площадная и гистограмма¶
Узнайте больше о диаграммах рассеяния и дискретном цвете.
В [3]:
импортировать plotly.express как px df = px.data.iris() рис = px.scatter(df, x="sepal_width", y="sepal_length", color="species") рис.шоу()
В [4]:
импортируйте plotly.express как px.
df = px.data.iris()
рис = px.scatter(df, x="sepal_width", y="sepal_length", color="species", marginal_y="скрипка",
marginal_x="box", trendline="ols", template="simple_white")
рис.шоу()
Подробнее о планках погрешностей.
В [5]:
импортировать plotly.express как px df = px.data.iris() df["e"] = df["sepal_width"]/100 рис = px.scatter(df, x="sepal_width", y="sepal_length", color="species", error_x="e", error_y="e") рис.шоу()
Подробнее о гистограммах.
В [6]:
импортировать plotly.express как px df = px.data.tips() fig = px.bar(df, x="sex", y="total_bill", color="smoker", barmode="group") рис.шоу()
В [7]:
импортируйте plotly.express как px. df = px.data.medals_long() рис = px.bar(df, x="медаль", y="количество", цвет="нация", pattern_shape="нация", pattern_shape_sequence=[".", "x", "+"]) рис.шоу()
Подробнее о фасетных графиках.
В [8]:
импортируйте plotly.express как px.
df = px.data.tips()
fig = px.bar(df, x="sex", y="total_bill", color="smoker", barmode="group", facet_row="time", facet_col="day",
category_orders={"день": ["Чт", "Пт", "Сб", "Вс"], "время": ["Обед", "Ужин"]})
рис.шоу()
Подробнее о матрицах диаграмм рассеяния (SPLOM).
В [9]:
импортируйте plotly.express как px. df = px.data.iris() рис = px.scatter_matrix (df, размеры = ["sepal_width", "sepal_length", "petal_width", "petal_length"], color="species") рис.шоу()
Подробнее о параллельных координатах и параллельных категориях, а также о непрерывном цвете.
В [10]:
импортировать plotly.express как px df = px.data.iris() рис = px.parallel_coordinates(df, color="species_id", labels={"species_id": "Виды", "sepal_width": "Ширина чашелистика", "sepal_length": "Длина чашелистика", "petal_width": "Ширина лепестка", "petal_length": "Длина лепестка", }, color_continuous_scale=px.colors.diverging.Tealrose, color_continuous_midpoint=2) рис.шоу()
В [11]:
импортировать plotly.express как px df = px.data.tips() рис = px.parallel_categories(df, color="size", color_continuous_scale=px.colors.sequential.Inferno) рис.шоу()
Подробнее о метках при наведении.
В [12]:
импортируйте plotly.express как px.
df = px.data.gapminder()
fig = px.scatter(df.query("year==2007"), x="gdpPercap", y="lifeExp", size="pop", color="continent",
hover_name="страна", log_x=True, size_max=60)
рис.шоу()
Подробнее об анимации.
В [13]:
импортировать plotly.express как px df = px.data.gapminder() рис = px.scatter(df, x="gdpPercap", y="lifeExp", анимация_frame="год", анимация_группа="страна", размер = "поп", цвет = "континент", hover_name = "страна", facet_col = "континент", log_x=Истина, size_max=45, range_x=[100,100000], range_y=[25,90]) рис.шоу()
Узнайте больше о линейных графиках.
В [14]:
импортировать plotly.express как px
df = px.data.gapminder()
fig = px.line(df, x="год", y="lifeExp", color="континент", line_group="country", hover_name="country",
line_shape="сплайн", render_mode="svg")
рис.шоу()
Подробнее о диаграммах с областями.
В [15]:
импортируйте plotly.express как px. df = px.data.gapminder() fig = px.area(df, x="год", y="население", color="континент", line_group="страна") рис.шоу()
Подробнее о временной шкале/диаграммах Ганта.
В [16]:
импортируйте plotly.express как px.импортировать панд как pd df = pd.DataFrame([ dict(Task="Job A", Start='2009-01-01', Finish='2009-02-28', Resource="Alex"), dict(Task="Job B", Start='2009-03-05', Finish='2009-04-15', Resource="Alex"), dict(Task="Job C", Start='2009-02-20', Finish='2009-05-30', Resource="Max") ]) fig = px.timeline(df, x_start="Начало", x_end="Готово", y="Ресурс", color="Ресурс") рис.шоу()
Подробнее о воронкообразных диаграммах.
В [17]:
импортируйте plotly.express как px.
данные = дикт(
число=[39, 27,4, 20,6, 11, 2],
stage=["Посещение сайта", "Загрузки", "Потенциальные клиенты", "Запрашиваемая цена", "Счет отправлен"])
рис = px.funnel (данные, x = 'число', y = 'этап')
рис.шоу()
Диаграммы от части к целому¶
Узнайте больше о круговых диаграммах.
В [18]:
импортируйте plotly.express как px.
df = px.data.gapminder().query("год == 2007").query("континент == 'Европа'")
df.loc[df['pop'] < 2. e6, 'country'] = 'Другие страны' # Представляет только большие страны
fig = px.pie(df, values='pop', names='country', title='Население европейского континента')
рис.шоу()
e6, 'country'] = 'Другие страны' # Представляет только большие страны
fig = px.pie(df, values='pop', names='country', title='Население европейского континента')
рис.шоу()
Узнайте больше о диаграммах солнечных лучей.
В [19]:
импортируйте plotly.express как px.
df = px.data.gapminder().query("год == 2007")
fig = px.sunburst(df, path=['континент', 'страна'], values='pop',
color='lifeExp', hover_data=['iso_alpha'])
рис.шоу()
Подробнее о древовидных картах.
В [20]:
импортируйте plotly.express как px.
импортировать numpy как np
df = px.data.gapminder().query("год == 2007")
fig = px.treemap(df, path=[px.Constant('мир'), 'континент', 'страна'], values='pop',
color='lifeExp', hover_data=['iso_alpha'])
рис.шоу()
Узнайте больше о картах сосулек.
В [21]:
импортировать plotly.express как px импортировать numpy как np df = px.data.gapminder().query("год == 2007") fig = px.icicle(df, path=[px.Constant('мир'), 'континент', 'страна'], values='pop', color='lifeExp', hover_data=['iso_alpha']) рис.шоу()
Распределения¶
Подробнее о гистограммах.
В [22]:
импортируйте plotly.express как px. df = px.data.tips() fig = px.histogram(df, x="total_bill", y="tip", color="sex", marginal="коврик", hover_data=df.columns) рис.шоу()
Узнайте больше о ящичковых диаграммах.
В [23]:
импортируйте plotly.express как px. df = px.data.tips() fig = px.box(df, x="day", y="total_bill", color="курильщик", notched=True) рис.шоу()
Подробнее о скрипичных сюжетах.
В [24]:
импортировать plotly.express как px df = px.data.tips() fig = px.violin(df, y="tip", x="курильщик", color="sex", box=True, points="all", hover_data=df.columns) рис.шоу()
В [25]:
импортировать plotly.express как px df = px.data.tips() рис = px.ecdf(df, x="total_bill", color="sex") рис.шоу()
В [26]:
импортировать plotly.express как px df = px.data.tips() рис = px.strip(df, x="общий_счет", y="время", ориентация="ч", цвет="курильщик") рис.шоу()
Узнайте больше о контурах плотности, также известных как контуры двумерной гистограммы.
В [27]:
импортируйте plotly.express как px. df = px.data.iris() рис = px.density_contour(df, x="sepal_width", y="sepal_length") рис.шоу()
Узнайте больше о тепловых картах плотности, также известных как двумерные гистограммы.
В [28]:
импортировать plotly.express как px df = px.data.iris() fig = px.density_heatmap(df, x="sepal_width", y="sepal_length", marginal_x="коврик", marginal_y="гистограмма") рис.шоу()
Изображения и тепловые карты¶
Узнайте больше о тепловых картах и изображениях.
В [29]:
импортируйте plotly.express как px. данные = [[1, 25, 30, 50, 1], [20, 1, 60, 80, 30], [30, 60, 1, 5, 20]] рис = px.imshow (данные, labels=dict(x="День недели", y="Время дня", color="Производительность"), x=['Понедельник', 'Вторник', 'Среда', 'Четверг', 'Пятница'], y=['Утро', 'День', 'Вечер'] ) fig.update_xaxes (сторона = "сверху") рис.шоу()
В [30]:
импортировать plotly.express как px
из skimage import io
img = io.imread('https://upload.wikimedia.org/wikipedia/commons/thumb/0/00/Crab_Nebula.jpg/240px-Crab_Nebula.jpg')
рис = px.imshow (изображение)
рис.шоу()
Тайловые карты¶
Узнайте больше о тайловых картах и точках на тайловых картах.
В [31]:
импортировать plotly.express как px
df = px.data.carshare()
рис = px.scatter_mapbox(df, lat="centroid_lat", lon="centroid_lon", color="peak_hour", size="car_hours",
color_continuous_scale=px.colors.cyclical. IceFire, size_max=15, масштаб=10,
mapbox_style="карто-позитрон")
рис.шоу()
IceFire, size_max=15, масштаб=10,
mapbox_style="карто-позитрон")
рис.шоу()
Подробнее о тайловой карте Картограммы GeoJSON.
В [32]:
импортировать plotly.express как px
df = px.data.election()
геоджсон = px.data.election_geojson()
рис = px.choropleth_mapbox(df, geojson=geojson, color="Bergeron",
местоположения = "район", featureidkey = "properties.district",
центр = {"широта": 45,5517, "долгота": -73,7073},
mapbox_style="карто-позитрон", zoom=9)
рис.шоу()
Контурные карты¶
Узнайте больше о контурных картах символов.
В [33]:
импортировать plotly.express как px
df = px.data.gapminder()
рис = px.scatter_geo(df, location="iso_alpha", color="continent", hover_name="country", size="pop",
animation_frame="год", проекция="природная земля")
рис.шоу()
Подробнее о картограммах.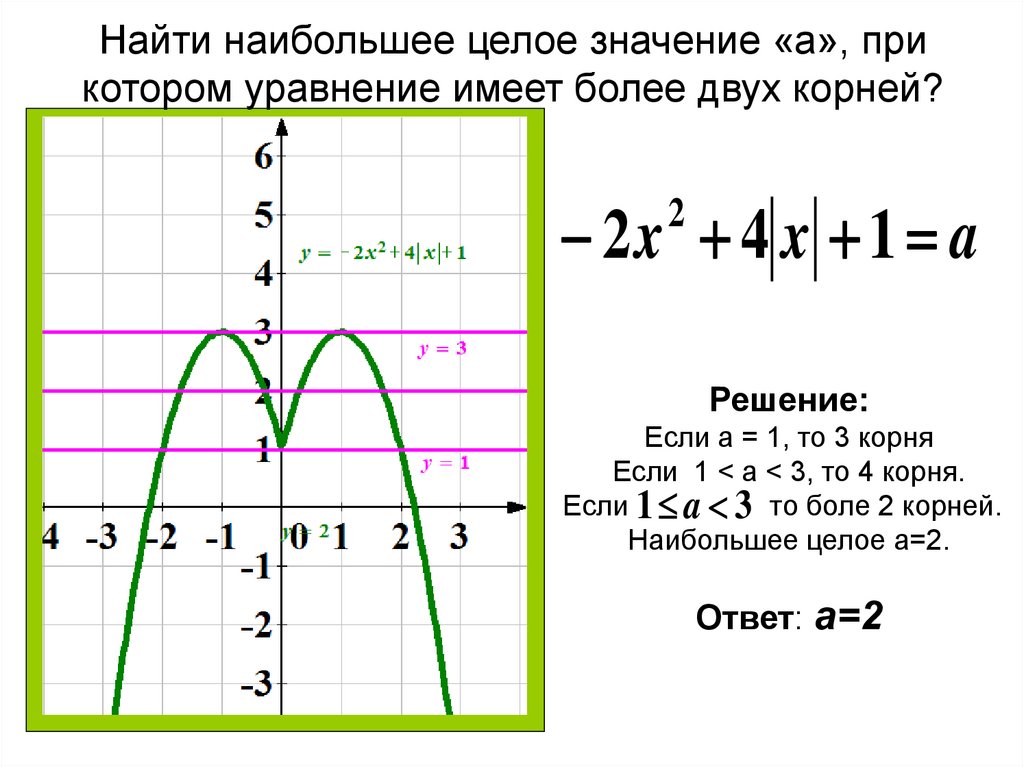
В [34]:
импортировать plotly.express как px df = px.data.gapminder() fig = px.choropleth(df, location="iso_alpha", color="lifeExp", hover_name="country", animation_frame="year", range_color=[20,80]) рис.шоу()
Полярные координаты¶
Подробнее о полярных графиках.
В [35]:
импортировать plotly.express как px
df = px.data.wind()
рис = px.scatter_polar(df, r="частота", тета="направление", цвет="сила", символ="сила",
color_discrete_sequence=px.colors.sequential.Plasma_r)
рис.шоу()
В [36]:
импортировать plotly.express как px
df = px.data.wind()
fig = px.line_polar(df, r="частота", theta="направление", color="сила", line_close=True,
color_discrete_sequence=px.colors.sequential.Plasma_r)
рис.шоу()
Узнайте больше о полярных гистограммах.
В [37]:
импортируйте plotly.express как px. df = px.data.wind() рис = px.bar_polar(df, r="частота", theta="направление", цвет="сила", template="plotly_dark", color_discrete_sequence= px.colors.sequential.Plasma_r) рис.шоу()
Трехмерные координаты¶
Узнайте больше о трехмерных точечных диаграммах.
В [38]:
импортировать plotly.express как px
df = px.data.election()
fig = px.scatter_3d(df, x="Joly", y="Coderre", z="Bergeron", color="winner", size="total", hover_name="district",
symbol="result", color_discrete_map = {"Жоли": "синий", "Бержерон": "зеленый", "Кодер":"красный"})
рис.шоу()
Троичные координаты¶
Узнайте больше о троичных диаграммах.
В [39]:
импортировать plotly.express как px
df = px.data.election()
fig = px.scatter_ternary(df, a="Joly", b="Coderre", c="Bergeron", color="winner", size="total", hover_name="district",
size_max=15, color_discrete_map = {"Жоли": "синий", "Бержерон": "зеленый", "Кодер":"красный"} )
рис. шоу()
шоу()
А как насчет Dash?¶
Dash — это платформа с открытым исходным кодом для создания аналитических приложений, не требующая Javascript и тесно интегрированная с графической библиотекой Plotly.
Узнайте, как установить Dash, по адресу https://dash.plot.ly/installation.
Везде на этой странице, где вы видите fig.show() , вы можете отобразить один и тот же рисунок в приложении Dash, передав его аргументу figure компонента Graph из встроенного dash_core_components пакет вроде этого:
import plotly.graph_objects как go # или plotly.express как px
fig = go.Figure() # или любая функция Plotly Express, например. px.bar(...)
# fig.add_trace( ... )
# fig.update_layout( ... )
импортировать тире
импортировать dash_core_components как DCC
импортировать dash_html_components как html
приложение = тире.Dash()
app.layout = html.Div([
dcc.Graph(рисунок=рис)
])
app.run_server(debug=True, use_reloader=False) # Отключить перезагрузку, если внутри Jupyter
Справка в Интернете — Быстрая справка
Все книгиКниги, не связанные с программированием Руководство пользователя Учебные пособия Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия МОКА Орглаб | ||
Последнее обновление: 04. Создать новый график функцииOrigin поддерживает отображение 4 видов функций: 2D-функции, 2D-параметрические функции, 3D-функции и 3D-параметрические функции. Чтобы построить график функции:
или
Добавление функционального графика к существующему графику
Примечание: Если вы выберете график функции 3D, когда активное окно графика является 2D, этот раскрывающийся список не будет отображаться.
| ||

 д.
д.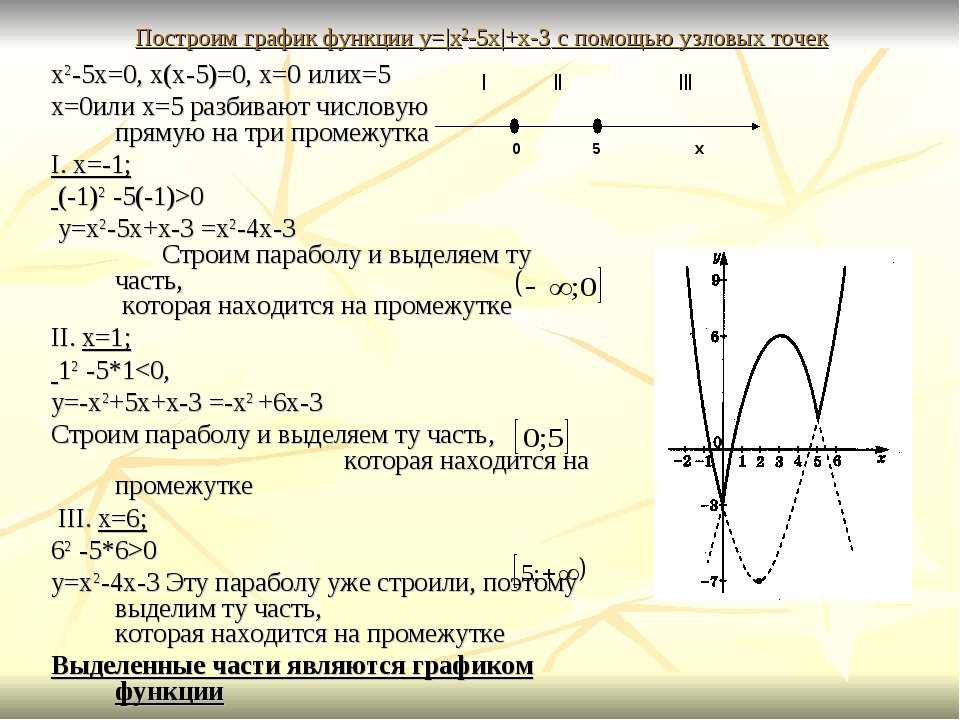 express как px
express как px  Атрибуты traces
Атрибуты traces 

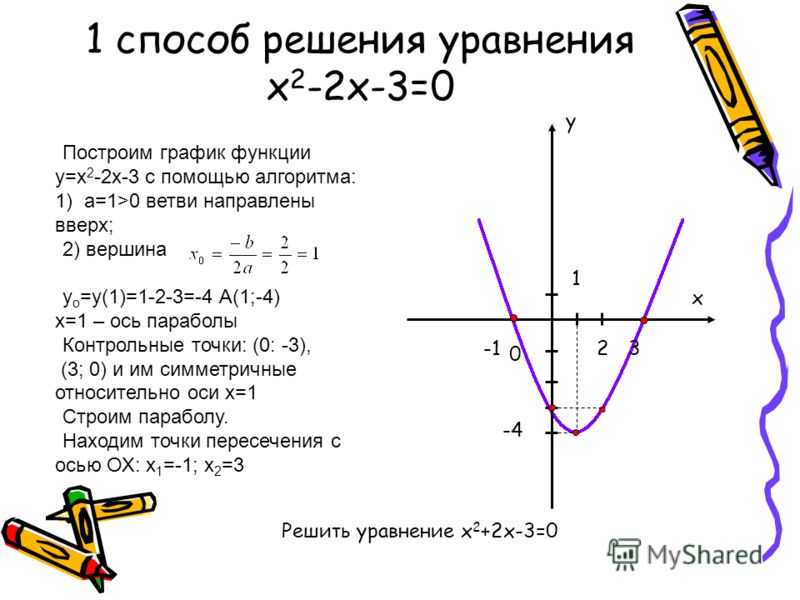 express как px
df = px.data.iris()
рис = px.scatter(df, x="sepal_width", y="sepal_length", color="species")
рис.шоу()
express как px
df = px.data.iris()
рис = px.scatter(df, x="sepal_width", y="sepal_length", color="species")
рис.шоу()
 bar(df, x="медаль", y="количество", цвет="нация",
pattern_shape="нация", pattern_shape_sequence=[".", "x", "+"])
рис.шоу()
bar(df, x="медаль", y="количество", цвет="нация",
pattern_shape="нация", pattern_shape_sequence=[".", "x", "+"])
рис.шоу()
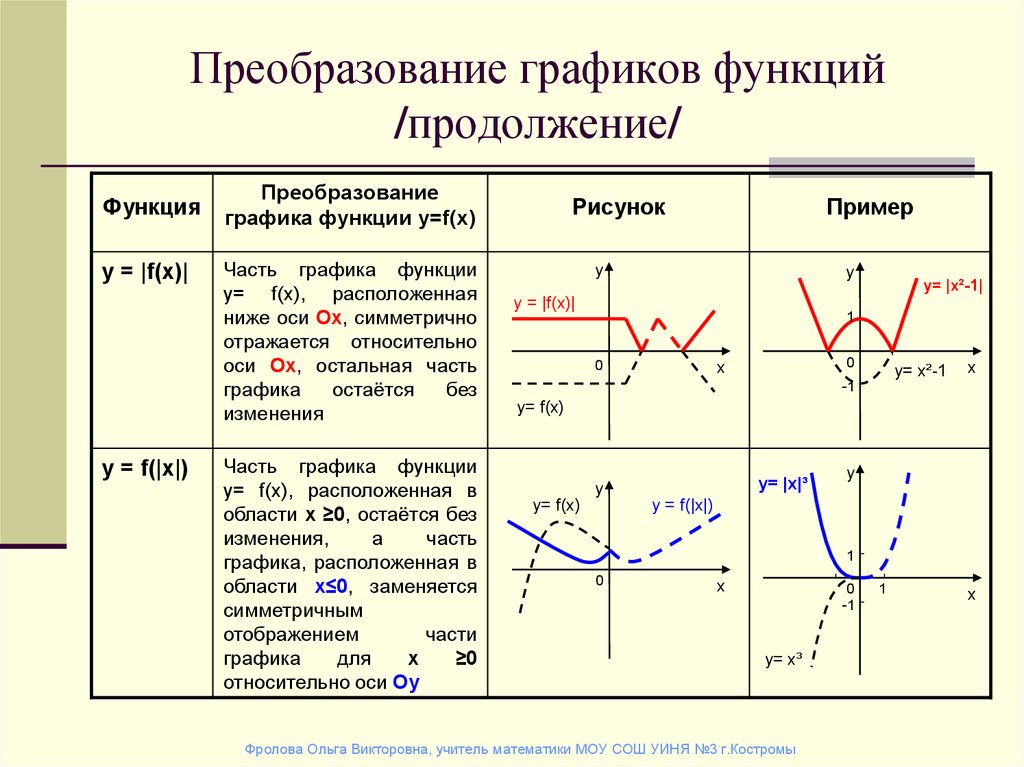 parallel_coordinates(df, color="species_id", labels={"species_id": "Виды",
"sepal_width": "Ширина чашелистика", "sepal_length": "Длина чашелистика",
"petal_width": "Ширина лепестка", "petal_length": "Длина лепестка", },
color_continuous_scale=px.colors.diverging.Tealrose, color_continuous_midpoint=2)
рис.шоу()
parallel_coordinates(df, color="species_id", labels={"species_id": "Виды",
"sepal_width": "Ширина чашелистика", "sepal_length": "Длина чашелистика",
"petal_width": "Ширина лепестка", "petal_length": "Длина лепестка", },
color_continuous_scale=px.colors.diverging.Tealrose, color_continuous_midpoint=2)
рис.шоу()
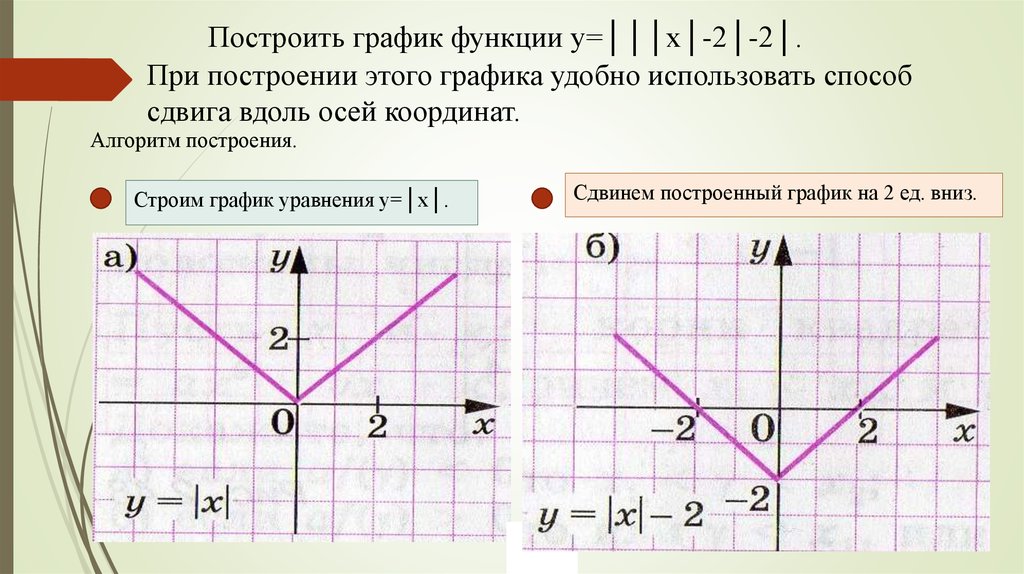 data.gapminder()
рис = px.scatter(df, x="gdpPercap", y="lifeExp", анимация_frame="год", анимация_группа="страна",
размер = "поп", цвет = "континент", hover_name = "страна", facet_col = "континент",
log_x=Истина, size_max=45, range_x=[100,100000], range_y=[25,90])
рис.шоу()
data.gapminder()
рис = px.scatter(df, x="gdpPercap", y="lifeExp", анимация_frame="год", анимация_группа="страна",
размер = "поп", цвет = "континент", hover_name = "страна", facet_col = "континент",
log_x=Истина, size_max=45, range_x=[100,100000], range_y=[25,90])
рис.шоу()
 импортировать панд как pd
df = pd.DataFrame([
dict(Task="Job A", Start='2009-01-01', Finish='2009-02-28', Resource="Alex"),
dict(Task="Job B", Start='2009-03-05', Finish='2009-04-15', Resource="Alex"),
dict(Task="Job C", Start='2009-02-20', Finish='2009-05-30', Resource="Max")
])
fig = px.timeline(df, x_start="Начало", x_end="Готово", y="Ресурс", color="Ресурс")
рис.шоу()
импортировать панд как pd
df = pd.DataFrame([
dict(Task="Job A", Start='2009-01-01', Finish='2009-02-28', Resource="Alex"),
dict(Task="Job B", Start='2009-03-05', Finish='2009-04-15', Resource="Alex"),
dict(Task="Job C", Start='2009-02-20', Finish='2009-05-30', Resource="Max")
])
fig = px.timeline(df, x_start="Начало", x_end="Готово", y="Ресурс", color="Ресурс")
рис.шоу()
 e6, 'country'] = 'Другие страны' # Представляет только большие страны
fig = px.pie(df, values='pop', names='country', title='Население европейского континента')
рис.шоу()
e6, 'country'] = 'Другие страны' # Представляет только большие страны
fig = px.pie(df, values='pop', names='country', title='Население европейского континента')
рис.шоу()
 data.gapminder().query("год == 2007")
fig = px.icicle(df, path=[px.Constant('мир'), 'континент', 'страна'], values='pop',
color='lifeExp', hover_data=['iso_alpha'])
рис.шоу()
data.gapminder().query("год == 2007")
fig = px.icicle(df, path=[px.Constant('мир'), 'континент', 'страна'], values='pop',
color='lifeExp', hover_data=['iso_alpha'])
рис.шоу()
 express как px
df = px.data.tips()
рис = px.ecdf(df, x="total_bill", color="sex")
рис.шоу()
express как px
df = px.data.tips()
рис = px.ecdf(df, x="total_bill", color="sex")
рис.шоу()
 express как px.
данные = [[1, 25, 30, 50, 1], [20, 1, 60, 80, 30], [30, 60, 1, 5, 20]]
рис = px.imshow (данные,
labels=dict(x="День недели", y="Время дня", color="Производительность"),
x=['Понедельник', 'Вторник', 'Среда', 'Четверг', 'Пятница'],
y=['Утро', 'День', 'Вечер']
)
fig.update_xaxes (сторона = "сверху")
рис.шоу()
express как px.
данные = [[1, 25, 30, 50, 1], [20, 1, 60, 80, 30], [30, 60, 1, 5, 20]]
рис = px.imshow (данные,
labels=dict(x="День недели", y="Время дня", color="Производительность"),
x=['Понедельник', 'Вторник', 'Среда', 'Четверг', 'Пятница'],
y=['Утро', 'День', 'Вечер']
)
fig.update_xaxes (сторона = "сверху")
рис.шоу()
 IceFire, size_max=15, масштаб=10,
mapbox_style="карто-позитрон")
рис.шоу()
IceFire, size_max=15, масштаб=10,
mapbox_style="карто-позитрон")
рис.шоу()
 bar_polar(df, r="частота", theta="направление", цвет="сила", template="plotly_dark",
color_discrete_sequence= px.colors.sequential.Plasma_r)
рис.шоу()
bar_polar(df, r="частота", theta="направление", цвет="сила", template="plotly_dark",
color_discrete_sequence= px.colors.sequential.Plasma_r)
рис.шоу()
 шоу()
шоу()
 09.2019
09.2019 Нажмите OK, чтобы получить график. Подробнее [примеры 3D-функций]
Нажмите OK, чтобы получить график. Подробнее [примеры 3D-функций]