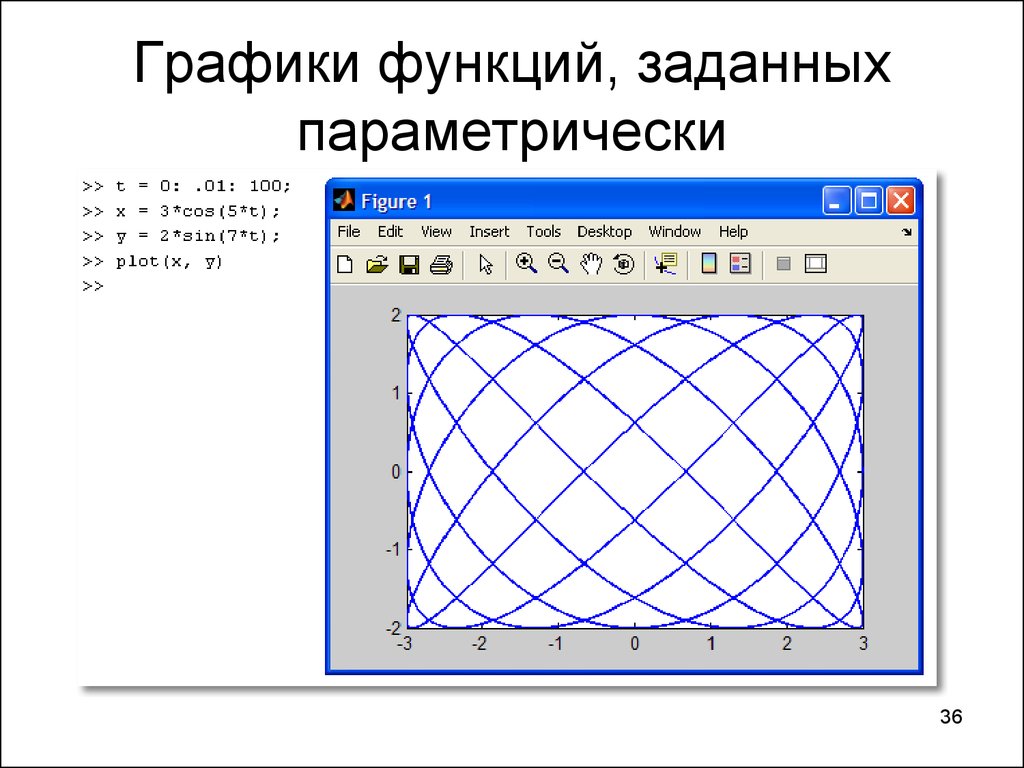
Построение параметрических кривых в inkscape
Конечно, редактор inkscape не может соперничать с математическими пакетами, однако пара инструментов (в виде расширений) у него имеется.
Мы поговорим о двух таких расширениях: «Параметрические кривые» и «Построитель графиков».
Посмотрим, что скажет википедия на запрос параметрические кривые.
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.
Ух. Давайте совсем просто. Есть некая переменная t от которой зависят две других величины х и у. Переменную t называют параметром. Этот параметр принимает значения в определенном диапазоне.
Кривую, построенную по функциям для х и у, называют параметрической кривой.
Векторный редактор inkscape имеет расширение с одноименным названием для построения параметрических кривых. Давайте посмотрим как работать с этим расширением.
Давайте посмотрим как работать с этим расширением.
Расширение «Параметрические кривые»
Запустите редактор и нарисуйте небольшой прямоугольник (или квадрат), например 50 на 50 px. Размеры прямоугольника (квадрата) будут задавать масштаб по осям Х и У.
А теперь приступаем.
Сам инструмент можно найти в Расширения- отрисовка- параметрические кривые. Ниже окно настроек документа.
Вкладок всего три. В первой вкладке Диапазон и выборка мы задаем диапазон для изменяемого параметра t, еще ниже масштабы по осям и сами функции для х и у. В большинстве случаев стоит оставить отмеченным чекбокс умножить t— диапазон на 2pi.
Чем больше диапазон, тем большее число необходимо указывать в поле выборки.
Вкладка Как использовать содержит минимальную справку по расширению, а во вкладке Функции перечислены допустимые в расширении функции.
Построение Спирали
Для построения спирали укажите значения как на рис. ниже
После применения мы получим вот такую спираль
Если квадрату задать заливку, то и спираль будет построена с заливкой.
Все возможности по заливке и обводки фигуры сохраняются.
Кардиоида
Для построения кардиоиды укажите следующие значения в настройках
Результатом будет вот такая кривая
Можно поиграться с величинами в функциях и посмотреть как будет изменяться вид кривой.
Астроида
Для этой параметрической кривой задаем вот такие значения
А вот и результат работы программы
Фигуры Лиссажу
В качестве примера построения фигур Лиссажу давайте возьмем такие параметры
Вот что получается
Поищите в сети другие уравнения параметрических кривых и попробуйте построить самостоятельно.
Самый качественный (и самый быстрый) способ получить на экране сердце не рисуя его.

Укажите такие параметры
И вот вам стилизованное сердце.
Используем панель заливка и обводка и вот у нас сердце в цвете.
Да-да, у сердца есть уравнение.
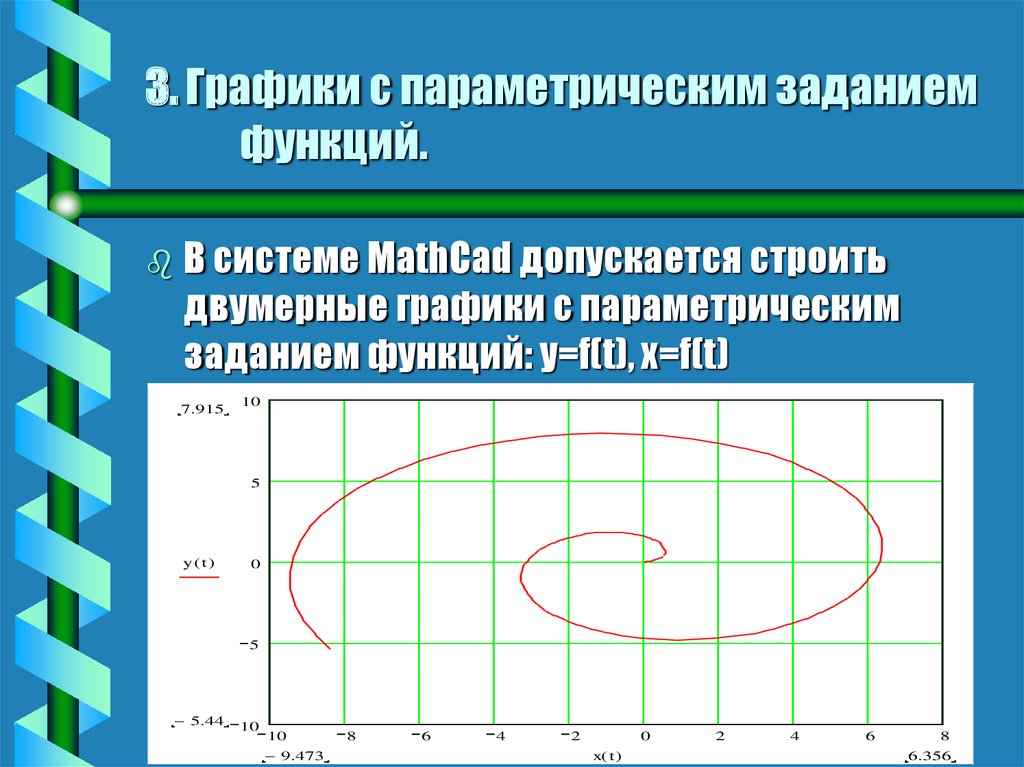
Расширение «Построитель графиков»
После того как мы разобрались с расширением Параметрические кривые данное расширение не будет сложным для понимания. Да и особой разницы между ними нет. Это видно по окну настроек.
Давайте построим график y=sin (x). Открываем Расширения- отрисовка- построитель графиков. Ниже окно настроек документа.
После применения расширения получаем график нашей функции
Ну и неплохо бы добавить оси. Оси, добавляемые самим расширением, не дают нужного результата.
На у а теперь можно тренироваться в построении любых мыслимых и немыслимых графиков. Пока все.
Строим математический график на Python
Сегодня мы поговорим про то, как построить математический график при помощи языка Python за 10 минут. Мы рассмотрим построение параметрических кривых в трехмерном и двумерном пространстве с использованием различных примеров.
Мы рассмотрим построение параметрических кривых в трехмерном и двумерном пространстве с использованием различных примеров.
У многих из нас со школьной скамьи остались не самые приятные воспоминания о математике. Кто-то воспринимал её как необходимое зло: сложное и скучное, но обязательное. Кто-то же отказывался понимать математику от слова совсем.
Так или иначе, но наше школьное образование было ориентировано скорее на запоминание и заучивание, а не на размышления. По большому счету не было никакой мотивации разбираться в основах математики или в том, как она на самом деле работает. Идея заключалась в том, чтобы просто узнать, какие задачи решает определенная формула, запомнить правильный набор шагов и воспроизвести все это на экзамене.
Однако математика намного обширнее и интереснее того, что мы учили в школе. Если взять, например, кинематику, можно увидеть настоящую магию математики. Кинематика известна как «геометрия движения» – это изучение взаимодействия между движущимися телами во времени.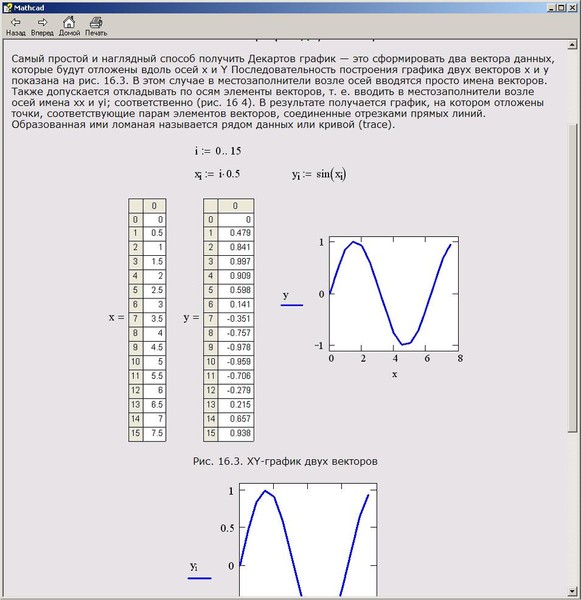 Хотя бы раз увидите такое визуальное представление математических функций — и они оживут для вас. Возможно, в тот момент вы почувствуете, что впервые понимаете их правильно.
Хотя бы раз увидите такое визуальное представление математических функций — и они оживут для вас. Возможно, в тот момент вы почувствуете, что впервые понимаете их правильно.
Итак, давайте научимся самостоятельно моделировать данные и начнем писать собственные скрипты. Сегодня мы поговорим о параметрических кривых и как их строить, используя Python и такие библиотеки, как NumPy, SymPy и Matplotlib.
Построение параметрических кривых
Параметрические кривые поистине завораживают! Если говорить простым языком, параметрическую кривую можно понимать как след, оставляемый движением частицы в пространстве. Говоря более формально, этот след моделируется функцией, определяемой от интервала I до различных точек в пространстве E.
Для трехмерного случая, если x, y и z заданы как функции переменной t в I (это параметр), мы получаем уравнения x = f(t), y = g(t) и z = h(t). Оценивая каждое значение параметра t в каждом из этих уравнений, мы получаем точку
Оценивая каждое значение параметра t в каждом из этих уравнений, мы получаем точку p(t) = (x(t),y(t),z(t)) в пространстве. Проделав эту процедуру для значений t, меняющихся в интервале I, мы получим параметрическую кривую.
Проведя небольшое исследование, попробовав несколько моделей вручную и потратив много часов на работу над сценарием, мы нашли решение. Оно выглядит следующим образом:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
t = sp.Symbol('t')
function_x = sp.sympify('sin(t)')
function_y = sp.sympify('cos(t)')
function_z = sp.sympify('t**2')
interval = np.arange(0, 100, 0.1)
x_values = [function_x.subs(t, value) for value in interval]
y_values = [function_y.subs(t, value) for value in interval]
z_values = [function_z. subs(t, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show()
subs(t, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show() Приведенный выше скрипт позволяет нам генерировать графики для параметрических кривых. К примеру, вот так выглядит график параметрической спирали p(t) = (sin(t),cos(t),sqrt(t3)), для интервала от 0 до 100.
Как работает скрипт
Скрипт, который мы привели выше, использует такие библиотеки, как SymPy, NumPy и Matplotlib. Давайте разберемся со всем по порядку.
SymPy — это библиотека Python для символьной математики. Она стремится стать полнофункциональной системой компьютерной алгебры (CAS). При этом сохраняется максимально простой код (а значит, понятный и масштабируемый). Библиотека SymPy, кстати, полностью написана на Python.
NumPy — это основной пакет для научных вычислений в Python. Эта библиотека предоставляет:
- объекты многомерного массива,
- различные производные объекты (такие как маскированные массивы и матрицы)
- набор подпрограмм для быстрых операций с массивами, включая математические и логические, манипуляции с фигурами, сортировку, выборку, ввод-вывод, дискретные преобразования Фурье, основные операции линейной алгебры, основные статистические операции и случайное моделирование.

И последняя библиотека из нашего списка — Matplotlib. Это обширная библиотека для создания статических, анимированных и интерактивных визуализаций на Python.
Подготовка
Чтобы использовать перечисленные выше библиотеки в нашем скрипте, мы должны сначала установить их на свой компьютер, выполнив следующую инструкцию в терминале:
pip install numpy sympy matplotlib
Теперь, когда библиотеки установлены, мы можем импортировать их в нашу программу:
import sympy as sp import numpy as np import matplotlib.pyplot as plt
Построение графика трехмерной параметрической кривой
Символьные вычисления в SymPy выполняются с помощью символов. Переменные SymPy являются объектами класса Поскольку мы говорим о параметрических функциях, нас интересует оценка функции на последовательности вещественных значений в пределах интервала. Для этого мы используем функцию Функция Наш код будет выглядеть так: После создания массива интервалов нам нужно перебрать значения О генераторах списков можно почитать в статье «Генераторы списков в Python для начинающих». Функция Выглядит это примерно следующим образом: Мы повторяем эту процедуру для значений Symbols. Выражение  2 = 25
2 = 25arange() в NumPy.np.arange(start, stop, step) создает массив NumPy со значениями в интервале (start,stop) с приращением шага, то есть мы идем от start до stop-1 с определенным шагом step.interval = np.arange(0, 10, 1)
print(interval)
>>> array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
t и оценить каждое значение внутри функции. Для этого мы будем использовать генератор списков в Python и функцию subs() библиотеки SimPy.
subs() получает символ t (который мы сохранили в переменной t) и значение каждого из элемента в качестве параметров.z_values = [function_z.subs(t, value) for value in interval]
print(z_values)
>>> [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
x_values и y_values
Наконец, с помощью библиотеки Matplotlib мы создаем график, соответствующий нашей параметрической кривой. В трехмерном случае, чтобы указать Matplotlib, что мы хотим сделать трехмерный график, мы используем следующий оператор:
ax = plt. axes(projection='3d')
axes(projection='3d')
Кроме того, мы можем заменить функции и интервал на новые и получить самые разные кривые. Давайте попробуем еще раз, но с другими значениями.
Например, напишем следующий код:
function_x = sp.sympify('2*t + 10')
function_y = sp.sympify('t**2')
function_z = sp.sympify('sin(t**2) + cos(t**2)')
interval = np.arange(-5, 5, 0.05) Запустим наш код и получим такой график:
Немного поэкспериментируем
Давайте немного поэкспериментируем с нашим кодом: попробуем различные значения и посмотрим, что получится. С помощью параметрических кривых можно создать множество фигур. Некоторые комбинации могут генерировать кривые с уникальной симметрией и красотой.
Если вы хотите поиграть со скриптом самостоятельно, можете открыть эту ссылку и заменить значения для function_x, function_y, function_z и interval. 2')
interval = np.arange(-10, 10, 0.1)
x_values = [function_x.subs(symbol_x, value) for value in interval]
y_values = [function_y.subs(symbol_x, value) for value in interval]
z_values = [function_z.subs(symbol_x, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show()
2')
interval = np.arange(-10, 10, 0.1)
x_values = [function_x.subs(symbol_x, value) for value in interval]
y_values = [function_y.subs(symbol_x, value) for value in interval]
z_values = [function_z.subs(symbol_x, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show()
Запустив его, мы получим такой результат:
Поиграйтесь сами и посмотрите, какие удивительные параметрические кривые можно создать!
Построение 2D параметрических кривых
С некоторыми модификациями данный скрипт также можно использовать и для построения двумерных параметрических кривых.
Например, давайте построим двумерный график, полученный путем оценки выражения x = t − 1,6 ∗ cos(24 ∗ t) и y = t − 1,6 ∗ sin(25 ∗ t) на интервале I=[1.5,20.5].
Выглядеть это будет примерно следующим образом:
Для того, чтобы смоделировать параметрическую кривую, показанную выше, можно воспользоваться следующим скриптом:
import sympy as sp import numpy as np import matplotlib.pyplot as plt t = sp.Symbol('t') function_x = sp.sympify('t - 1.6*cos(24*t)') function_y = sp.sympify('t - 1.6*sin(25*t)') interval = np.arange(1.5, 20.5, 0.01) x_values = [function_x.subs(t, value) for value in interval] y_values = [function_y.subs(t, value) for value in interval] plt.figure(figsize=(10, 10)) plt.plot(x_values, y_values) plt.show()
Давайте проверим наш код с другими функциями и новым интервалом. К примеру, возьмем следующие значения:
function_x = sp.sympify('4*sin(5*t)')
function_y = sp.sympify('5*cos(3*t)')
interval = np.arange(0, 6.5, 0.001)Запустим наш скрипт и получим следующий график:
Теперь давайте проделаем это ещё раз, но уже с новыми значениями:
function_x = sp. sympify('cos(16*t) + (cos(6*t) / 2) + (sin(10*t) / 3)') function_y = sp.sympify('sin(16*t) + (sin(6*t) / 2) + (cos(10*t) / 3)') interval = np.arange(0, 3.16, 0.01)
Тогда результат будет таким:
Удивительно! Не правда ли?
Построение математических функций
Как только мы закончили написание скрипта для моделирования параметрических кривых, приходит осознание, что с помощью всего нескольких строк кода мы можем создать плоттер для математических функций как в двух, так и в трех измерениях! Невероятно! Это же так удобно!
К примеру, давайте рассмотрим скрипт для построения графиков математических функций в двух и трех измерениях в интервале от a до b. То есть, консоль запросит у пользователя как функцию, так и значения a и b для интервала. Вот такой код у нас получится:
import sympy as sp import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D symbol_x = sp.Symbol('x') symbol_y = sp.Symbol('y') def get_vector(a, b): return np.arange(a, b + 1, 0.1) def plot_2d_function(function, a, b): # Create the sympy function f(x) f_x = sp.sympify(function) # Create domain and image domain_x = get_vector(a, b) image = [f_x.subs(symbol_x, value) for value in domain_x] # Plot the 2D function graph fig = plt.figure(figsize=(10, 10)) plt.plot(domain_x, image) plt.show() def plot_3d_function(function, a, b): # Create sympy function f(x, y) f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function)) # Create domains and image domain_x = get_vector(a, b) domain_y = get_vector(a, b) domain_x, domain_y = np.meshgrid(domain_x, domain_y) image = f_xy(domain_x, domain_y) # Plot the 3D function graph fig = plt.figure(figsize=(10, 10)) ax = plt.axes(projection='3d') ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis') plt.
show() function = input('>> Enter the function: ') a_value = float(input('>> Enter the [a, ] value: ')) b_value = float(input('>> Enter the [, b] value: ')) if "x" and not "y" in function: plot_2d_function(function, a_value, b_value) elif "x" and "y" in function: plot_3d_function(function, a_value, b_value) else: print("You must enter a function in terms of x and/or y")
Вы можете протестировать приведенный выше скрипт здесь. Запустите скрипт и введите свою конфигурацию функции и интервала.
Например, возьмем следующий код:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp. sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.show()
function = "x*cos(5*x)"
a_value = 0
b_value = 10
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.show()
function = "x*cos(5*x)"
a_value = 0
b_value = 10
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
Запустим его и получим следующий результат:
А теперь давайте поменяем значения на следующие:
import sympy as sp import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D symbol_x = sp.Symbol('x') symbol_y = sp.Symbol('y') def get_vector(a, b): return np.arange(a, b + 1, 0.1) def plot_2d_function(function, a, b): # Create the sympy function f(x) f_x = sp.sympify(function) # Create domain and image domain_x = get_vector(a, b) image = [f_x.subs(symbol_x, value) for value in domain_x] # Plot the 2D function graph fig = plt.figure(figsize=(10, 10)) plt.plot(domain_x, image) plt.show() def plot_3d_function(function, a, b): # Create sympy function f(x, y) f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function)) # Create domains and image domain_x = get_vector(a, b) domain_y = get_vector(a, b) domain_x, domain_y = np.meshgrid(domain_x, domain_y) image = f_xy(domain_x, domain_y) # Plot the 3D function graph fig = plt.figure(figsize=(10, 10)) ax = plt.axes(projection='3d') ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis') plt.
show() function = "x**2 + cos(y**2)" a_value = -3 b_value = 3 if "x" and not "y" in function: plot_2d_function(function, a_value, b_value) elif "x" and "y" in function: plot_3d_function(function, a_value, b_value) else: print("You must enter a function in terms of x and/or y")
Если мы это запустим, то получим такой график:
Заключение
Что ж, вот вы и дошли до конца этой статьи, поздравляем! Сегодня мы обсудили, как построить математический график на Python всего за 10 минут. Мы поговорили про построение различных параметрических кривых в двумерном и трёхмерном пространстве и разобрали процесс построения на примерах. Теперь вы видите, какой завораживающей на самом деле может быть математика! Кроме того, построение параметрических кривых, как вы понимаете, не такой уж и сложный процесс.
Надеемся, данная статья была вам полезна! Успехов в написании кода!
Перевод статьи «How to Plot Mathematical Functions in 10 Lines of Python».
Параметрические кривые
Параметрические кривые (c) Copyright Foundation Coalition (SA Fulling) 1997Класс 6.
 2 (и 4.М, 6.М и 7.М)
2 (и 4.М, 6.М и 7.М)Задание по чтению на среду, 8 октября
- Стюарт 9.1 и 11.7
- Ознакомьтесь с инструкцией по Лаборатория 4.М (Написание букв с использованием параметризованных кривых)
- Эта веб-страница
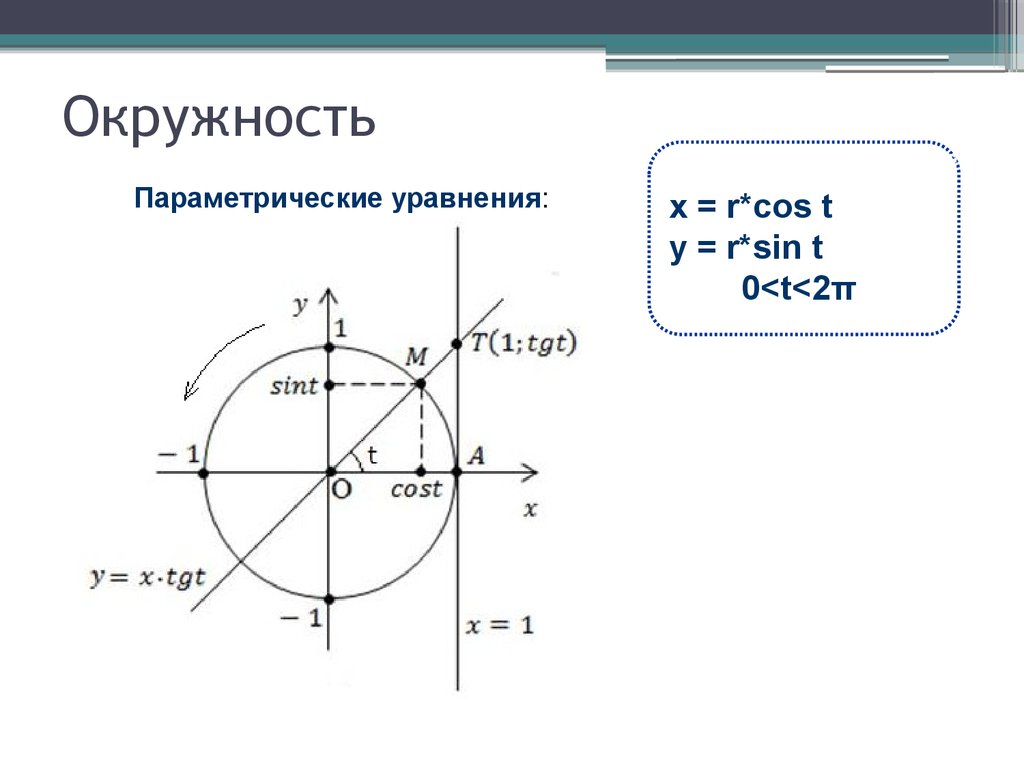
Параметрическое представление кривых
Что такое параметрические уравнения и откуда они берутся? Рассмотрим несколько сценариев.- Сорвиголова Боб мчался на своем мотоцикле по пустыне все быстрее и быстрее.
По отношению к его автофургону (и с расстояниями, измеряемыми в милях) его положение в качестве
функция времени была дана
х = 2 cos(1 + t 2 ) (восток-запад),
y = 2 sin(1 + t 2 ) (север-юг).
Он стартовал в полдень ( t = 0 ). В t = sqrt(2*Pi - 1) он очутился в исходной точке и ударил по тормозам. Мы видим, что путь Боба удовлетворяет
х 2 + у 2 = 4 ,
и что, следовательно, это круг с радиусом 2 мили (окружность 4*пи миль).

- В память о подвиге Боба служба парка построила асфальтированную дорогу вдоль его
маршрут. Когда необходимо заполнить выбоины, передовая бригада записывает свои действия.
местоположение, отметив их расстояние по дороге от начальной точки.
Точка на расстоянии s находится в
= .
Областью определения этой вектор-функции является интервал с между 0 и 4*Пи. (Те же уравнения использовались геодезистами при строительстве дороги в первое место.)
- Сестра Боба, Сара, осталась дома, изучая математический анализ.
В одной задаче она встретила круг с уравнением
х 2 + у 2 = 4 .
Она увидела, что невозможно решить y как функция от x , потому что при выборе знака квадратного корня она потеряет половину круга. По той же причине круг не может быть представлен цифрой 9.0002 x как один функция y . Сара поняла, что хороший способ представить круг — это рассматривать x .
 и y поровну, записав каждое из них как функцию угла, и , по кругу.
и y поровну, записав каждое из них как функцию угла, и , по кругу.х = 2 cos(u) , у = 2 sin(u) .
Здесь следует отметить несколько концептуальных моментов.
- В третьем сценарии мы начали с кривой (геометрического объекта) и нашел его параметрическое представление. В первой истории мы начали с параметризации, возникшей как описание движения и вывести из него кривую (или «орбиту»). (Второй сценарий можно рассматривать в любом случае, в зависимости от того, строить дорогу или ремонтировать ее.)
- Для заданной кривой параметрическое представление не является уникальным.
Мы видели три разные пары параметрических уравнений, которые все описывают
тот же круг.
Вторая и третья параметризации кажутся более простыми и естественными, но
первый подходил к конкретной физической задаче.
(Параметр расстояния s называется длина дуги и является
геометрически естественный способ параметризации произвольной кривой, для которой
"угол" не имеет значения.
 )
) - В первом сценарии параметр имел физическое значение время , такая же "реальная" переменная, как координаты x и y сами себя. В остальных случаях параметр вводился более произвольно, т.е. в основном как инструмент для описания кривой. Наша интуиция движения настолько сильна, что часто используется язык точка, «движущаяся» по кривой даже в более абстрактных ситуациях, когда кривая не имеет механической интерпретации (точно так же, как мы говорим о скалярной ценная функция «изменяется», даже если независимая переменная не является временем).
- Во втором рассказе мы записали параметризацию как векторнозначную функция параметра, а в двух других случаях мы писали два отдельных скалярные уравнения. Свобода выбора любой из этих точек зрения ценность, как мы увидим ниже при обсуждении скорости.
Легко записать простые параметрические уравнения, такие как
х = т 2 , у = т 5 ,
, которые описывают не очень знакомые кривые. И наоборот, есть знакомые кривые, такие как гиперболы, для которых
параметризация может быть не сразу очевидной.
В домашнем задании вы увидите множество примеров параметризованных кривых.
и в лаборатории 6.М (Полет бейсбольного мяча).
Однако наш главный интерес
находится в (а) параметризованных кривых абстрактно, как общие двумерные
движения в физике; и (б) самые простые случаи, прямые и
круги.
Мы, наверное, уже достаточно сказали о кругах.
И наоборот, есть знакомые кривые, такие как гиперболы, для которых
параметризация может быть не сразу очевидной.
В домашнем задании вы увидите множество примеров параметризованных кривых.
и в лаборатории 6.М (Полет бейсбольного мяча).
Однако наш главный интерес
находится в (а) параметризованных кривых абстрактно, как общие двумерные
движения в физике; и (б) самые простые случаи, прямые и
круги.
Мы, наверное, уже достаточно сказали о кругах.
Линия имеет параметрические уравнения
х = х 0 + v х т, у = у 0 + v у т,
, где x 0 , y 0 , v x , и v y — константы.
Если t меняется через все действительные числа,
кривая изображения — вся линия; меньшие интервалы для t сегменты линии доходности.
Приятной особенностью параметрического представления является то, что вертикальные линии не
следует рассматривать как отдельный случай: это как раз те, для которых v x = 0 . Два параметрических уравнения могут быть объединены в векторное параметрическое уравнение
уравнение
Два параметрических уравнения могут быть объединены в векторное параметрическое уравнение
уравнение
r = r 0 + v t .
При таком выборе обозначений должно быть ясно, что эта формула описывает движение свободной частицы с начальным положением г 0 = 0, у 0 > и скорость v = x, v y > .
Касательные векторы; векторная скорость и ускорение
В приведенном выше примере вектор скорости v , точки вдоль линии. (В лабораторный раздаточный материал он был построен путем вычитания координат одной точки на линии от чужого.) Отметим также, что его компоненты могут быть получены дифференцированием параметрические уравнения:
v x = dx/dt, v y = dy/dt.
Эти производные являются константами (одинаковы для всех т ) в этом особом случае.
Производные более общей системы параметрических уравнений имеют аналогичный
значение. Для примера
Для примера
х = т 2 , у = т 5 ,
находим
dx/dt = 2t, dy/dt = 5t 4 .
Мы можем объединить их в вектор
v (t) = d r /dt = 4> .
Построим кривую и прикрепим вектор против (0,8) в точке r (0,8).
[Вставить чертеж.] (временный скрин с обоими рисунками)
Мы видим, что вектор касается кривой (и точек на направление увеличения параметра). В целом это верно, потому что можно показать (см. стр. 554 (раздел 9.2) Стюарта) что наклон вектора v (t) совпадает с наклоном кривой в точке р (т) :
(dy/dt)/(dx/dt) = dy/dx.
(Этот факт будет легче понять после того, как мы изучим «цепное правило» на следующей неделе.)
Примечание: Если dx/dt = 0 и dy/dt не равно нулю,
тогда касательная и касательный вектор вертикальны, а наклон
кривая не определена (бесконечна) в этой точке. Если обе производные равны нулю (как при t = 0 на нашей примерной кривой),
касательный вектор не имеет четко определенного направления;
с физической точки зрения это означает, что движущаяся точка «замедлилась» до
остановка во время т . Затем следует выбрать лучшую параметризацию
(см. ниже), чтобы получить более полезный касательный вектор.
Если обе производные равны нулю (как при t = 0 на нашей примерной кривой),
касательный вектор не имеет четко определенного направления;
с физической точки зрения это означает, что движущаяся точка «замедлилась» до
остановка во время т . Затем следует выбрать лучшую параметризацию
(см. ниже), чтобы получить более полезный касательный вектор.
Касательный вектор v (t) = d r /dt также называется производная вектор-функции r (t) . Вместо того, чтобы собирать его из производных скалярнозначной координаты функции x(t) и y(t) , можно определить его непосредственно как предел разностного отношения (см. стр. 727 Стюарта).
Касательный вектор к кривой в точке не уникален; это зависит от параметризации. Касательный вектор Сары к окружности в точке под углом u , вычисляется из ее параметризации
г = ,
есть
v = .
Параметризация ее брата
г = 2), 2 sin(1 + t 2 )> .
Использование Maple или заглядывание вперед в чтение на следующей неделе, чтобы изучить цепочку правило, мы видим, что его касательный вектор равен
v = 2), 4t cos(1 + t 2 ))> .
Даже после того, как Сара подставила в нее u = 1 + t 2 формула (чтобы она и Боб одинаково помечали точки), их формулы разные. Два касательных вектора указывают в одном направлении, но имеют разные длины. Параметризация длины дуги дорожной бригады дает тангенс единицы . вектор, один с длиной 1; этот выбор является предпочтительным для некоторых целей.
[Вставить чертеж] (временный скрин с обоими рисунками)
С другой стороны, касательный вектор Боба равен скорости его
физическое движение.
(В более общем случае всякий раз, когда параметризация кривой не произвольна, а
имеет какое-то собственное значение, то то же самое относится и к соответствующему
касательный вектор. )
Поскольку вектор скорости сам является функцией t ,
можно снова дифференцировать его, чтобы получить вектор ускорения ,
компонентами которого являются (скалярные) ускорения в х и и направлений.
)
Поскольку вектор скорости сам является функцией t ,
можно снова дифференцировать его, чтобы получить вектор ускорения ,
компонентами которого являются (скалярные) ускорения в х и и направлений.
На самом деле, с точки зрения Сорвиголовы Боба, вектор ускорения самое главное, так как это то, что он контролирует с помощью педали акселератора (и руль). В механике нам обычно дают ускорение и нужно найти скорость и положение (второй закон Ньютона). В векторной ситуации это означает, что мы начинаем с векторнозначного функция a (t) и в итоге параметрическая кривая описывая движение. [пример]
Подробнее о параметрических уравнениях
Параметрические уравнения обеспечивают
полезный способ просмотра двух графиков одновременно.
Предположим, у вас есть две функции: f(t) и g(t) .
Тогда
обычный способ их графического отображения - использовать два графика, f(t) против t и г(т) против т .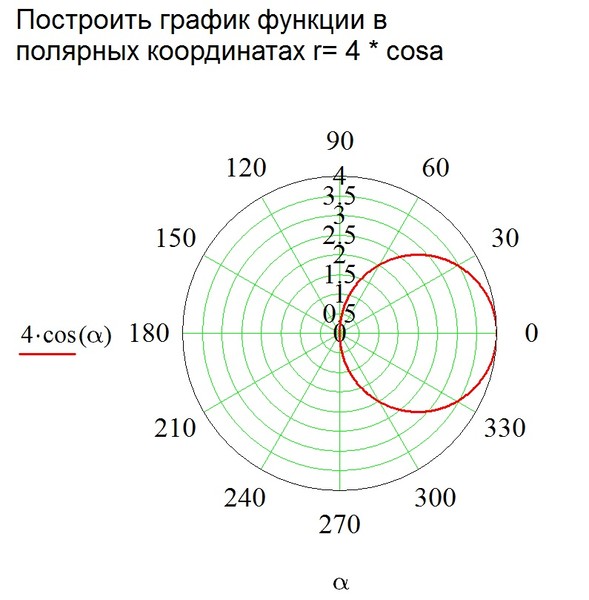 Но параметрическое построение позволяет скрыть t , чтобы показать
количества, представленные f и г построены в одной системе координат.
Но параметрическое построение позволяет скрыть t , чтобы показать
количества, представленные f и г построены в одной системе координат.
Например, популяция F лисиц в районе может меняться в зависимости от года примерно как F = 50 + 20 sin(t) , а население H зайцев в этом районе может варьироваться как H = 500 + 300 cos(t) . Затем, построение эти функции как одна параметрическая кривая в плоскости F-H (кстати, это эллипс с центром в точке (F,H) = (50500) ) дает дополнительный способ визуализации взаимодействия лисы и зайца. Это может предположить причинно-следственную связь между ними, например, больше лис привести к сокращению популяции зайцев, в то время как меньшее количество зайцев вызывает сокращение в популяции лисиц.
Пример 4 в лабораторный раздаточный материал построил прямоугольник как четыре параметризованных отрезка линии, каждый с область параметров $0 [вставить уравнения] (временный экран с обоими наборами уравнений)
Такой способ вполне адекватен и стандартен для компьютерной графики
Приложения. [вставить уравнения]
(временный экран с обоими наборами уравнений) Конечно, эти выражения можно упростить, но мы оставили их в
форма, которая делает более ясным, как они возникли из исходных параметризаций
из четырех сегментов линии. Однако иногда может быть важно учитывать
весь прямоугольник как единую параметризованную кривую.
Эта ситуация возникнет автоматически, если прямоугольник является путем
движущееся тело.
(Начинается в углу с координатами (1,1),
движется по первому отрезку к (3/2,1),
затем по четвертому отрезку до (3/2,3/2),
затем по третьему отрезку в обратном направлении до (1,1/2),
затем по второму отрезку в обратном направлении к (1,1).)
В этом случае параметрический
уравнения включают две кусочно-определенные функции вместо восьми простых
функции. Мы можем легко построить новые параметрические уравнения из старых.
помня о «смещении и изменении масштаба» первых двух недель этого
курс. Прежде всего обратите внимание, что для движения в обратном направлении вдоль сегмента
параметризовано 0 , нам просто нужно заменить т по 1 - т в формулах.
Сдвиг каждого интервала длины на 1/4, чтобы он начинался с t = 0 а затем масштабируя на 4, чтобы сделать его длиной 1, мы получаем следующие формулы:
Однако иногда может быть важно учитывать
весь прямоугольник как единую параметризованную кривую.
Эта ситуация возникнет автоматически, если прямоугольник является путем
движущееся тело.
(Начинается в углу с координатами (1,1),
движется по первому отрезку к (3/2,1),
затем по четвертому отрезку до (3/2,3/2),
затем по третьему отрезку в обратном направлении до (1,1/2),
затем по второму отрезку в обратном направлении к (1,1).)
В этом случае параметрический
уравнения включают две кусочно-определенные функции вместо восьми простых
функции. Мы можем легко построить новые параметрические уравнения из старых.
помня о «смещении и изменении масштаба» первых двух недель этого
курс. Прежде всего обратите внимание, что для движения в обратном направлении вдоль сегмента
параметризовано 0 , нам просто нужно заменить т по 1 - т в формулах.
Сдвиг каждого интервала длины на 1/4, чтобы он начинался с t = 0 а затем масштабируя на 4, чтобы сделать его длиной 1, мы получаем следующие формулы:
8.6: Параметрические уравнения — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 13880
- Дэвид Липпман и Мелони Расмуссен
- Магазин OpenTextBookStore
Многие фигуры, даже такие простые, как круги, не могут быть представлены уравнением, где \(y\) является функцией \(x\). Рассмотрим, например, путь, по которому следует луна, обращаясь вокруг планеты, которая одновременно вращается вокруг солнца. В некоторых случаях полярные уравнения позволяют представить такой путь. В других случаях нам нужен более универсальный подход, который позволяет нам представлять координаты \(x\) и \(y\) в терминах третьей переменной или параметра.
Определение: Параметрические уравнения
Система параметрических уравнений представляет собой пару функций \(x(t)\) и \(y(t)\), в которой \(x\) и \(y\) координаты являются выходными данными, представленными в терминах третьего входного параметра, \(t\).
Пример \(\PageIndex{1}\)
Двигаясь с постоянной скоростью, объект движется с постоянной скоростью по прямолинейному пути от координат (-5, 3) до координат (3, -1) за 4 секунды , где координаты измеряются в метрах. Найдите параметрические уравнения для положения объекта.
Решение
Координата \(x\) объекта начинается с -5 метров и достигает +3 метров, это означает, что направление \(x\) изменилось на 8 метров за 4 секунды, что дает нам скорость 2 метра в секунду. Теперь мы можем записать координату \(x\) как линейную функцию по времени, \(t\), \(x(t) = −5 + 2t\). Точно так же значение \(y\) начинается с 3 и достигает -1, что дает изменение значения \(y\) на 4 метра, что означает, что значения \(y\) уменьшились на 4 метра за 4 секунды, для со скоростью -1 метр на nd, что дает уравнение \(y(t)=3−t\). Вместе это параметрические уравнения для положения объекта:
Вместе это параметрические уравнения для положения объекта:
\[x(t) = -5 + 2t\нечисло\]
\[y(t) = 3 - t\нечисло\]
Используя эти уравнения, мы можем построить таблицу \(t\), значения \(x\) и \(y\). Из-за контекста мы ограничились неотрицательными значениями \(t\) для этого примера, но в целом вы можете использовать любые значения.
Из этой таблицы мы могли бы построить три возможных графика: график зависимости \(x\) от \(t\), который показывал бы горизонтальное положение во времени, график зависимости \(y\) от \( t\), который показывал бы вертикальное положение во времени, или график зависимости \(y\) от \(x\), показывающий положение объекта на плоскости.
Положение \(x\) как функция времени Положение \(y\) как функция времени Положение \(y\) относительно \(x\)
Обратите внимание, что параметр \( t\) явно не отображается на этом третьем графике. Иногда, когда параметр \(t\) действительно представляет такую величину, как время, мы можем указать направление движения на графике с помощью стрелки, как показано выше.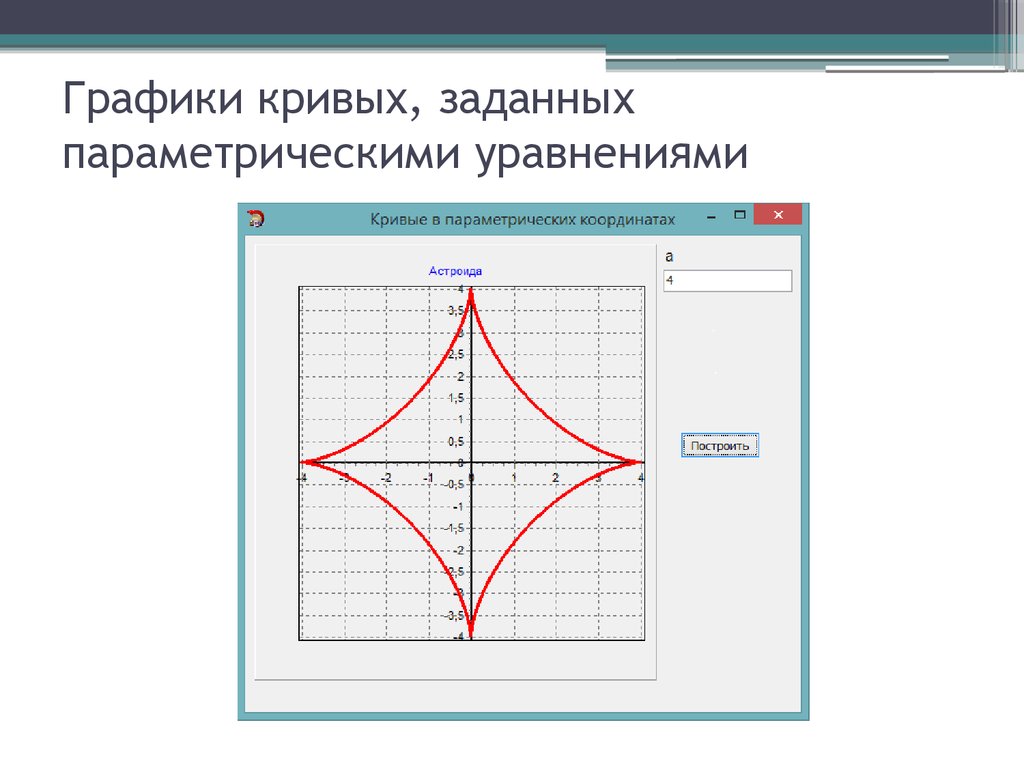
Часто для кривой не существует единого параметрического представления. В примере 1 мы предполагали, что объект движется с постоянной скоростью по прямой линии. Если бы мы сохранили предположение о пути (прямая линия), но не предполагали, что скорость постоянна, мы могли бы получить такую систему: 92 + 1\nonumber\]
\[y(t) = 2 + t\nonumber\]
Решение
Мы можем начать с создания таблицы значений. Из этой таблицы мы можем нанести на плоскость точки (\(x\), \(y\)) , начертить грубый график кривой и указать направление движения во времени с помощью стрелок.
Обратите внимание, что здесь параметрические уравнения описывают форму, для которой \(y\) не является функцией \(x\). Это пример того, почему использование параметрических уравнений может быть полезным, поскольку они могут представлять такой график как набор функций. Этот конкретный график также кажется параболой, где \(x\) является функцией \(y\), что мы скоро проверим.
Пример \(\PageIndex{3}\)
Нарисуйте график числа
\[x(t) = 3\cos(t)\nonumber\]
\[y(t) = 3\sin(t) \номер\]
Решение
Эти уравнения должны показаться вам знакомыми. Когда мы впервые узнали о синусе и косинусе, мы обнаружили, что координаты точки на окружности радиуса \(r\) под углом \(\theta\) будут \(x = r \cos(\theta) , y r \sin(\theta)\). Приведенные выше уравнения имеют ту же форму, но вместо \(\тета\) используется \(r = 3\) и \(t\).
Это предполагает, что для каждого значения \(t\) эти параметрические уравнения дают точку на окружности радиуса 3 под углом, соответствующим \(t\). При \(t = 0\) график будет в \(x = 3\cos(0), y = 3\sin(0)\), точке (3,0). Действительно, эти уравнения описывают уравнение окружности, проведенной против часовой стрелки.
Интересно, что эти аналогичные параметрические уравнения также описывают окружность радиуса 3:
\[x(t) = 3\sin(t)\nonumber\]
\[y(t) = 3\cos(t)\ не число\]
Отличие этих уравнений в том, что график начинался бы с \(x = 3\sin(0)\), \(y = 3\cos(0)\), точки (0, 3). По мере того, как \(t\) увеличивается от 0, значение \(x\) будет увеличиваться, указывая, что это уравнение будет рисовать график по часовой стрелке.
По мере того, как \(t\) увеличивается от 0, значение \(x\) будет увеличиваться, указывая, что это уравнение будет рисовать график по часовой стрелке.
При создании таблицы \(t-x-y\) нанесение точек и соединение точек плавной кривой обычно дает нам приблизительное представление о том, как выглядит график системы параметрических уравнений, обычно проще использовать технологию для создания эти таблицы и (одновременно) гораздо более красивые графики.
Пример \(\PageIndex{4}\)
Нарисуйте график \(\begin{array} {rcl} {x(t)} &= & {2\cos(t)} \\ {y(t) )} &= & {3\sin(t)} \end{array}\)
Решение
Сначала обратите внимание, что это уравнение очень похоже на уравнения из предыдущего примера, за исключением того, что коэффициенты не равны. Вы можете догадаться, что сочетание cos и sin по-прежнему будет производить вращение, но теперь \(x\) будет изменяться от -2 до 2, а \(y\) будет изменяться от -3 до 3, создавая эллипс.
Используя технологию, мы можем построить график этого уравнения, убедившись, что это действительно эллипс.
Как и при построении графика полярных уравнений, перед построением системы параметрических уравнений необходимо изменить РЕЖИМ на калькуляторе (или выбрать параметрические уравнения в графической технологии). Вы узнаете, что успешно вошли в параметрический режим, когда ввод уравнения изменился, чтобы запросить пару уравнений \(x(t)=\) и \(y(t)=\).
Упражнение \(\PageIndex{1}\)
Нарисуйте график \(\begin{array} {rcl} {x(t)} &= & {4\cos(3t)} \\ {y(t)} &= & {3\sin(2t) )} \end{массив}\). Это пример фигуры Лиссажу .
- Ответить
Пример \(\PageIndex{5}\)
Популяции кроликов и волков на острове с течением времени представлены на графиках ниже. Используйте эти графики, чтобы нарисовать график в плоскости r-w , показывающий взаимосвязь между количеством кроликов и количеством волков.
Решение
Для каждого входа \(t\) мы можем определить количество кроликов \(r\) и количество волков \(w\) из соответствующих графиков, и затем нанесите соответствующую точку на плоскость \(r-w\).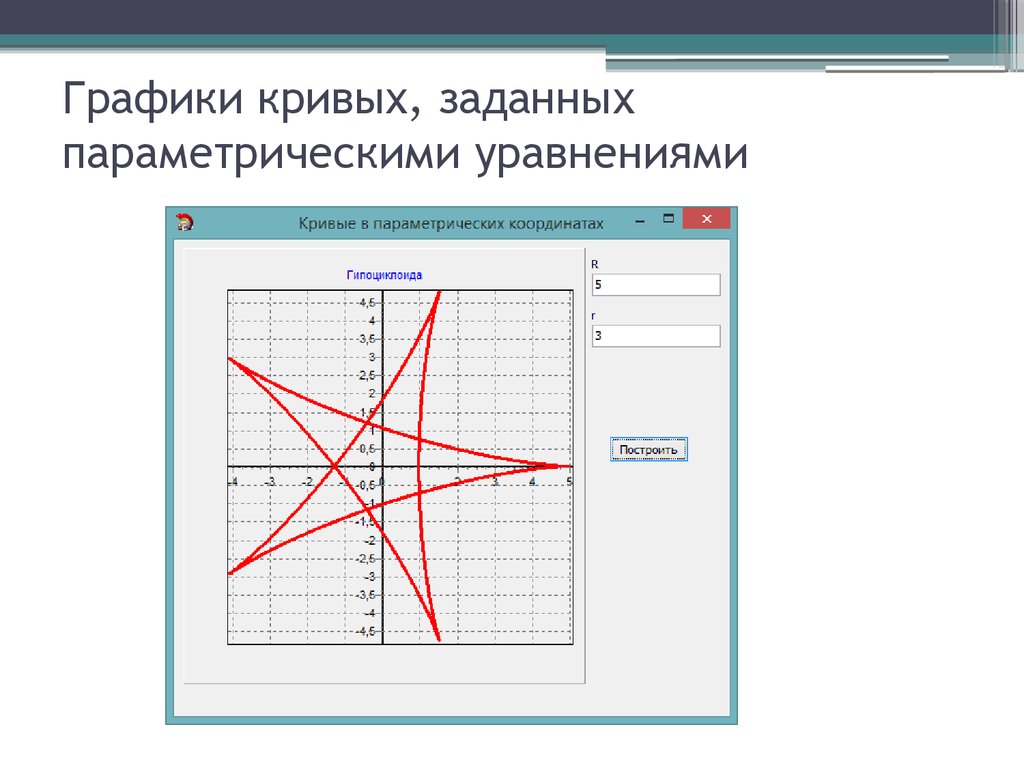
Этот график помогает выявить циклическое взаимодействие между двумя популяциями.
Преобразование из параметрического в декартово
В некоторых случаях можно исключить параметр \(t\), что позволяет записать пару параметрических уравнений в виде декартова уравнения. 92)\nonumber\]
Поскольку параметрическое уравнение определено только для \(t > 0\), это декартово уравнение эквивалентно параметрическому уравнению в соответствующей области. Параметрические уравнения показывают, что когда \(t > 0\), \(x > 2\) и \(y > 0\), область определения декартова уравнения должна быть ограничена \(x > 2\).
Чтобы гарантировать, что декартово уравнение максимально эквивалентно исходному параметрическому уравнению, мы пытаемся по возможности избегать использования ограниченных доменом обратных функций, таких как обратные триггерные функции. Для уравнений, включающих тригонометрические функции, мы часто пытаемся найти тождество, которое можно использовать, чтобы избежать обратных функций. 92}{9} = 1\nonumber\]
92}{9} = 1\nonumber\]
Это декартово уравнение для эллипса, который мы построили ранее.
Параметризация кривых
Хотя преобразование из параметрической формы в декартову может быть полезным, часто более полезно параметризовать декартово уравнение – преобразовать его в параметрическую форму.
Если декартово уравнение дает одну переменную как функцию другой, то параметризация тривиальна – независимая переменная в функции может быть просто определена как \(t\). 92 = 3\) в параметрической форме, если это возможно.
- Ответить
\[\begin{массив} {rcl} {x(t)} &= & {3\cos(t)} \\ {y(t)} &= & 3\sin(t) \end{массив} \номер\]
Помимо параметризации декартовых уравнений, мы также можем параметризовать поведение и движения.
Пример \(\PageIndex{10}\)
Робот следует по указанному пути. Создайте таблицу значений для функций \(x(t)\) и \(y(t)\), предполагая, что роботу требуется одна секунда для выполнения каждого движения.
Решение
Поскольку мы знаем направление движения, мы можем ввести последовательные значения \(t\) вдоль пути робота. Используя эти значения с координатами \(x\) и \(y\) робота, мы можем создать таблицы. Например, мы обозначаем начальную точку в (1, 1) как положение в \(t = 0\), следующую точку в (3, 1) как положение в \(t = 1\) и скоро.
Обратите внимание, что это также связано с векторами. Путешествие робота по декартовой плоскости также можно отображать в виде векторов, а общее пройденное расстояние и перемещение можно рассчитать.
Пример \(\PageIndex{11}\)
Фонарь помещается на край велосипедной шины, как показано, и велосипед начинает катиться по улице. Найдите параметрическое уравнение для положения источника света после поворота колеса на угол \(\theta\).
Решение
Относительно центра колеса положение источника света можно найти как координаты точки на окружности, но так как координата \(х\) начинается с 0 и движется в отрицательное направление, в то время как координата \(y\) начинается с наименьшего значения, координаты точки будут заданы как:
\[x = -r\sin(\theta)\nonnumber\]
\[y = -r\cos(\theta)\nonnumber\]
Тем временем центр колеса движется горизонтально. Он остается на постоянной высоте \(r\), но горизонтальное положение сдвинется на расстояние, эквивалентное длине дуги окружности, вытянутой под углом \(s = r\theta\). Положение центра круга тогда
Он остается на постоянной высоте \(r\), но горизонтальное положение сдвинется на расстояние, эквивалентное длине дуги окружности, вытянутой под углом \(s = r\theta\). Положение центра круга тогда
\[x = r\theta\nonnumber\]
\[y = r\nonnumber\]
Сочетание положения центра колеса с положением света на колесе относительно центра мы получаем следующее параметрическое уравнение w с \(\theta\) в качестве параметра:
\[x = r\theta - r\sin(\theta) = r(\theta - \sin(\theta))\nonumber\]
\[y = r - r\cos(\theta) = r (1 - \cos(\theta))\nonumber\]
Полученный граф называется циклоидой.
Пример \(\PageIndex{12}\)
Луна движется вокруг планеты, как показано, совершая один оборот за 10 дней. Планета движется вокруг солнца, как показано, совершая один оборот за 100 дней. Найдите параметрическое уравнение для положения Луны относительно центра Солнца через \(t\) дней.
Решение
В этом примере мы предположим, что орбиты круговые, хотя на самом деле они эллиптические.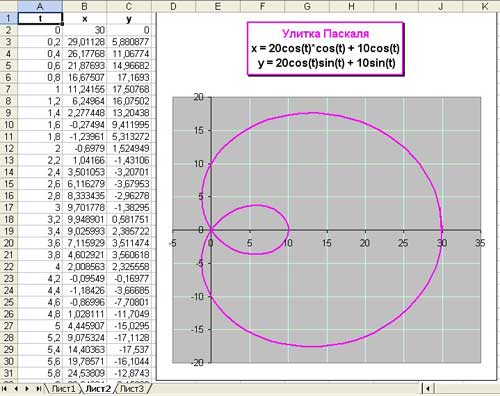
Координаты точки на окружности всегда можно записать в виде
\[x = r\cos(\theta)\nonumber\]
\[y = r\sin(\theta)\nonumber\]
Поскольку период обращения Луны вокруг планеты составляет 10 дней, уравнение положения \(луны\) \(относительно\) \(к\) \(этой\) \(планеты\) будет
\[x(t) = 6\cos(\dfrac{2\pi}{10}t) = 6\cos(\dfrac{\pi}{5}t)\nonumber\]
\[y( t) = 6\sin(\dfrac{2\pi}{10}t) = 6\sin(\dfrac{\pi}{5}t)\nonumber\]
При периоде 100 дней уравнение для положения \(планеты\) \(относительно\) \(к\) \(\) \(солнца\) будет
\[x(t) = 30\cos(\dfrac{2\ pi}{100} t) = 30 \cos (\dfrac{\pi}{50} t)\nonumber\]
\[y(t) = 30\sin(\dfrac{2\pi}{100} t ) = 30 \sin (\dfrac{\pi}{50} t)\nonumber\]
Объединив их вместе, мы можем найти положение \(луны\) \(относительно\) \(к\) \ (the\) \(солнце\) как сумма компонентов.
\[x(t) = 6\cos(\dfrac{2\pi}{5} t) = 30 \cos (\dfrac{\pi}{50} t)\nonumber\]
\[y( t) = 6\cos(\dfrac{2\pi}{5} t) = 30 \sin (\dfrac{\pi}{50} t)\nonumber\]
Полученный график показан здесь.
Упражнение \(\PageIndex{4}\)
Колесо радиуса 4 катится по внешней стороне окружности радиуса 7. Найдите параметрическое уравнение для положения точки на границе меньшего колеса. Эта форма называется эпициклоидой.
- Ответ
Центр маленького колеса вращается по окружности с радиусом 7 + 4 = 11.
Так как длина окружности маленького круга равна \(8\pi\), а длина окружности большого круга равна \(22\pi\), за время, необходимое для вращения вокруг большого круга, маленький круг повернется \(\dfrac{22\pi}{8\pi} = \dfrac{11}{4}\) оборотов. Мы используем это как фактор растяжения. Положение точки на малом круге будет комбинацией положения центра маленького колеса вокруг центра большого колеса и положения точки вокруг маленького колеса:
\[x(t) = 11 \cos(t) - 4\cos(\dfrac{11}{4} t)\nonumber\]
\[y(t) = 11\sin(t) - 4\ грех(\dfrac{11}{4}t)\номер\]
- Параметрические уравнения
- График \(x(t)\), \(y(t)\) и соответствующий график \(x-y\) Набросок графиков и построение таблицы значений
- Преобразование параметрического в декартово
- Преобразование декартовых координат в параметрические (параметризация кривых)
Эта страница под названием 8.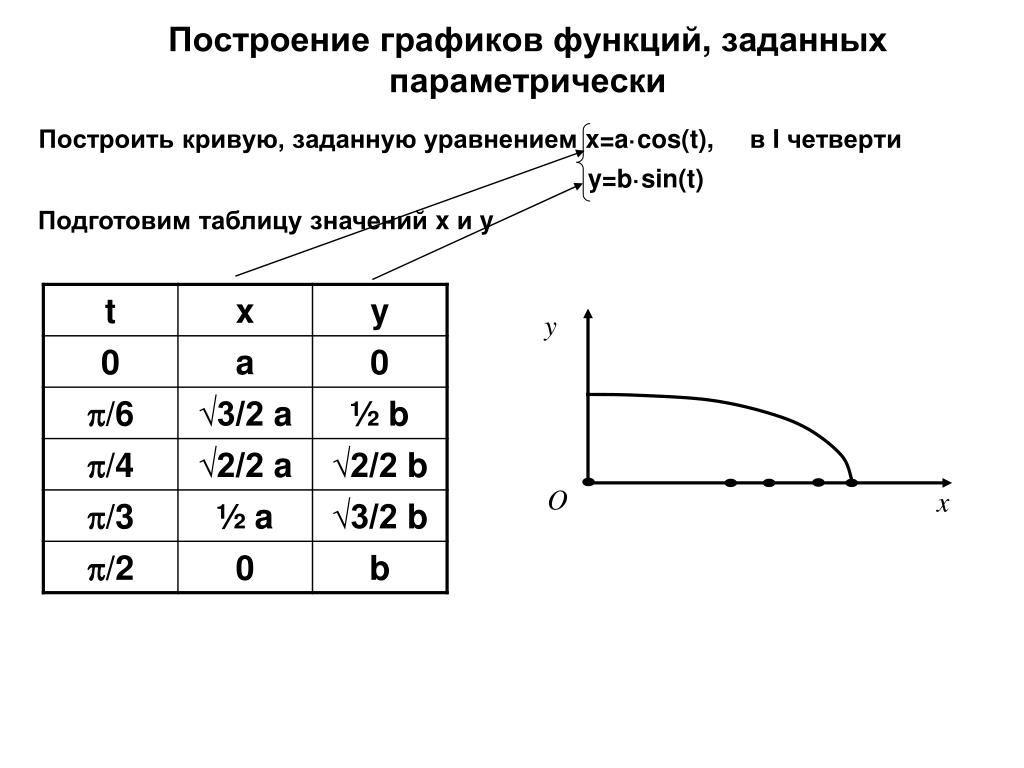

 subs(t, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show()
subs(t, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show()
 pyplot as plt
t = sp.Symbol('t')
function_x = sp.sympify('t - 1.6*cos(24*t)')
function_y = sp.sympify('t - 1.6*sin(25*t)')
interval = np.arange(1.5, 20.5, 0.01)
x_values = [function_x.subs(t, value) for value in interval]
y_values = [function_y.subs(t, value) for value in interval]
plt.figure(figsize=(10, 10))
plt.plot(x_values, y_values)
plt.show()
pyplot as plt
t = sp.Symbol('t')
function_x = sp.sympify('t - 1.6*cos(24*t)')
function_y = sp.sympify('t - 1.6*sin(25*t)')
interval = np.arange(1.5, 20.5, 0.01)
x_values = [function_x.subs(t, value) for value in interval]
y_values = [function_y.subs(t, value) for value in interval]
plt.figure(figsize=(10, 10))
plt.plot(x_values, y_values)
plt.show() sympify('cos(16*t) + (cos(6*t) / 2) + (sin(10*t) / 3)')
function_y = sp.sympify('sin(16*t) + (sin(6*t) / 2) + (cos(10*t) / 3)')
interval = np.arange(0, 3.16, 0.01)
sympify('cos(16*t) + (cos(6*t) / 2) + (sin(10*t) / 3)')
function_y = sp.sympify('sin(16*t) + (sin(6*t) / 2) + (cos(10*t) / 3)')
interval = np.arange(0, 3.16, 0.01) pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp.sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image,
rstride=1, cstride=1, cmap='viridis')
plt.
pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp.sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image,
rstride=1, cstride=1, cmap='viridis')
plt.
 sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.show()
function = "x*cos(5*x)"
a_value = 0
b_value = 10
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.show()
function = "x*cos(5*x)"
a_value = 0
b_value = 10
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
 pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp.sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.
pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp.sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.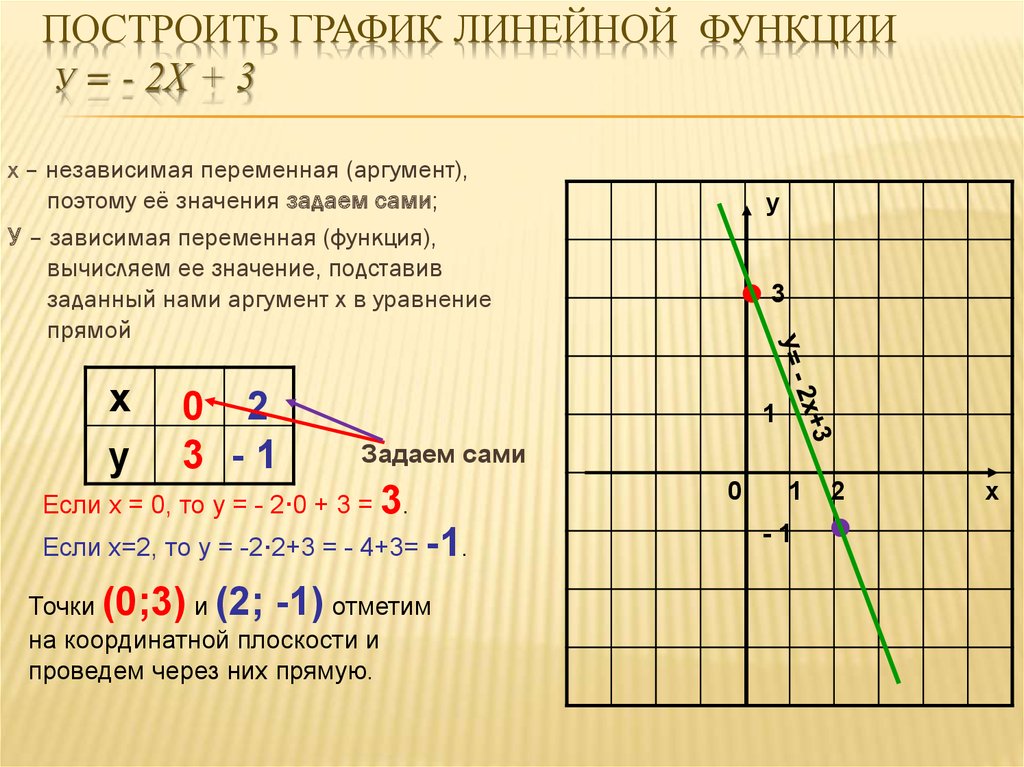 show()
function = "x**2 + cos(y**2)"
a_value = -3
b_value = 3
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
show()
function = "x**2 + cos(y**2)"
a_value = -3
b_value = 3
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
 и y поровну, записав каждое из них как функцию угла, и , по кругу.
и y поровну, записав каждое из них как функцию угла, и , по кругу. )
)