Лабораторная работа 4. Построение поверхности второго порядка
Работа по построению поверхности второго порядка (случай, когда третья координата входит в уравнение поверхности в квадрате) предполагает использование следующей методики:
1. Подготовить диапазон изменения функции по двум координатам, расположив изменения одной координаты вдоль некоторого столбца вниз, а другой – вдоль прилегающей строки вправо. Здесь требуется учесть следующую особенность – в диапазоне изменения функции необходимо дублировать значения координат.
2. Ввести на пересечение координат необходимую формулу для построения поверхности и воспользоваться маркером автозаполнения для ее копирования на всю область построения поверхности.
В формуле следует учесть поправку на положительные и отрицательные значения квадратного корня на данной области определения.
3. Выделить подготовленные данные и воспользоваться мастером построения диаграмм (тип диаграммы – Поверхность
 2)*ЕСЛИ(ОСТАТ($A3;2)=0;1;-1)
2)*ЕСЛИ(ОСТАТ($A3;2)=0;1;-1)В диапазон А3:А42 добавить повторяющиеся числа 2 и 3 (для использования в формуле).
Рис. 10. Диапазон данных и рассчитанные значения функции
П остроить поверхность, используя тип диаграммы Поверхность (рис. 11).
Рис. 11. Сфера
Самостоятельная работа
Постройте поверхность, заданную уравнением:
Таблица 4
Вариант | Задание |
1 | Эллипсоид: |
2 | Однополостный гиперболоид: |
3 | Двуполостный гиперболоид: |
4 | Эллипсоид: |
5 | Эллиптический параболоид: |
6 | Гиперболический параболоид: |
7 | Эллиптический параболоид: |
8 | Эллипсоид: |
9 | Двуполостный гиперболоид: |
10 | Эллиптический параболоид: |
Таблицу
данных и график отобразите на одном
листе в текстовом процессоре MS Word.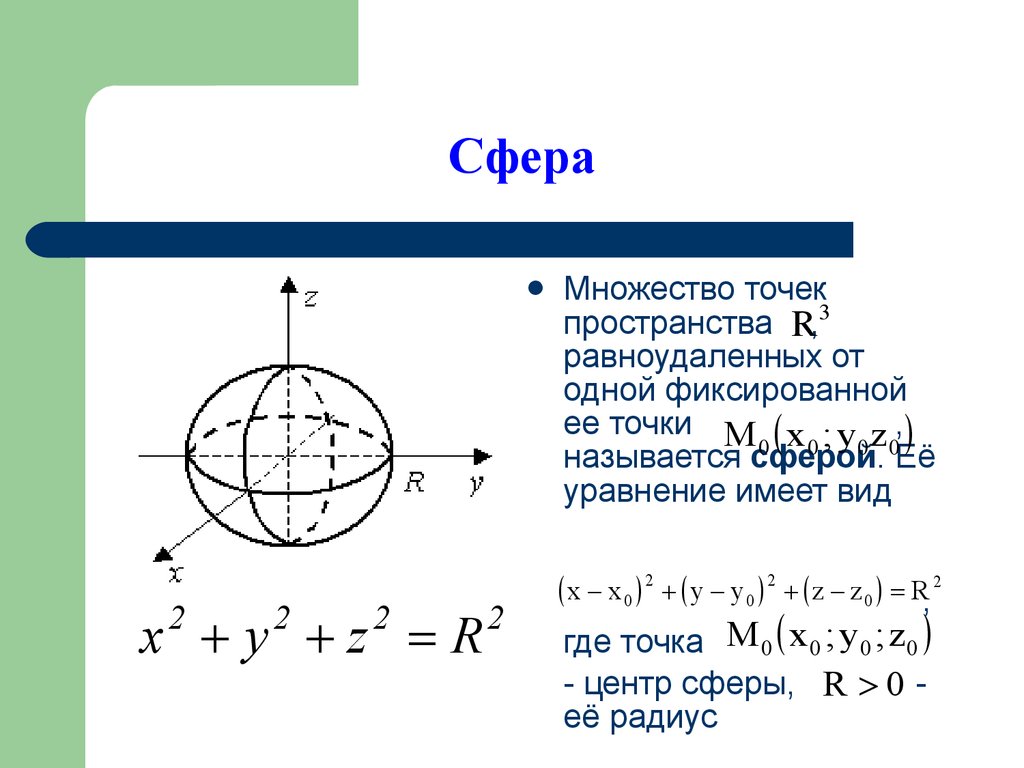
Создание сложных формул связано, как правило, с использованием встроенных логических функций Excel. Наиболее часто используется функция ЕСЛИ(), которая возвращает одно значение, если заданное условие при вычислении дает значение ИСТИНА, и другое значение, если ЛОЖЬ.
Функция ЕСЛИ используется при проверке условий для значений и формул.
ЕСЛИ(лог_выражение; значение_если_истина
; значение_если_ложь)Лог_выражение — это любое значение или выражение, принимающее значения ИСТИНА или ЛОЖЬ. Например, A10=100 — это логическое выражение; если значение в ячейке A10 равно 100, то выражение принимает значение ИСТИНА. В противном случае — ЛОЖЬ. Этот аргумент может быть использован в любом операторе сравнения.
Значение_если_истина — это значение, которое возвращается,
если лог_выражение равно ИСТИНА.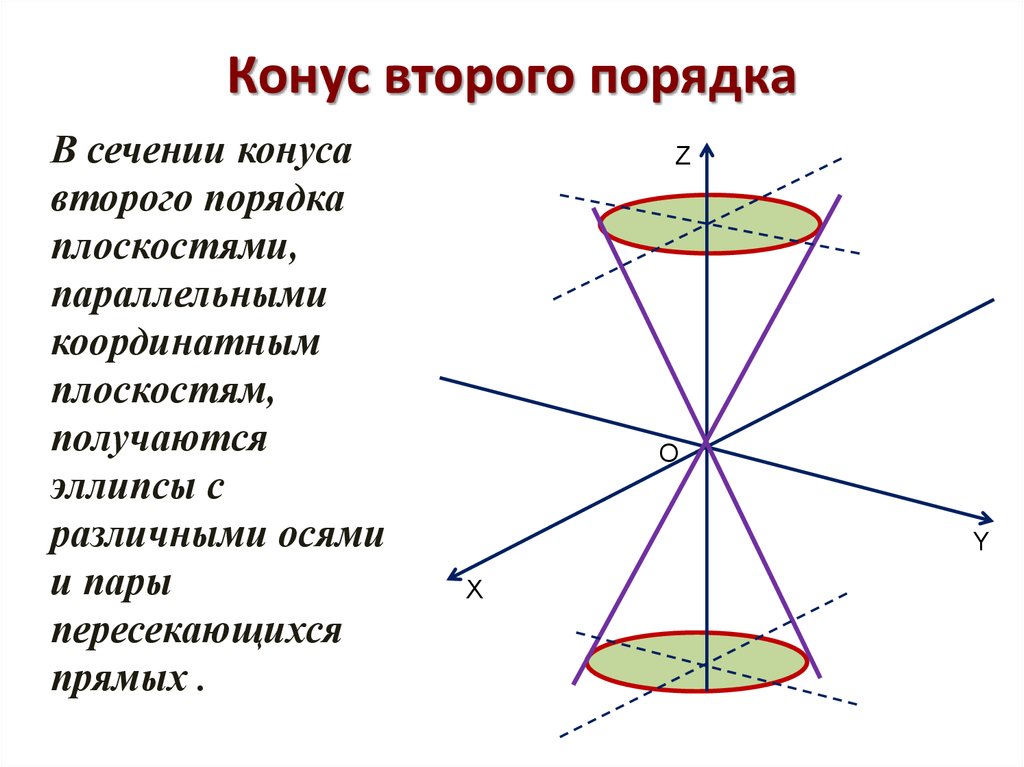 Например, если этот аргумент
— строка «В пределах бюджета» и лог_выражение равно ИСТИНА, тогда функция ЕСЛИ отобразит текст «В пределах бюджета».
Если лог_выражение равно ИСТИНА, а значение_если_истина пусто, то возвращается значение 0. Чтобы
отобразить слово ИСТИНА, необходимо
использовать логическое значение ИСТИНА
для этого аргумента.
Например, если этот аргумент
— строка «В пределах бюджета» и лог_выражение равно ИСТИНА, тогда функция ЕСЛИ отобразит текст «В пределах бюджета».
Если лог_выражение равно ИСТИНА, а значение_если_истина пусто, то возвращается значение 0. Чтобы
отобразить слово ИСТИНА, необходимо
использовать логическое значение ИСТИНА
для этого аргумента.
Значение_если_ложь — это значение, которое возвращается,
если лог_выражение равно ЛОЖЬ. Например,
если этот аргумент — строка «Превышение
бюджета» и лог_выражение равно ЛОЖЬ, то функция ЕСЛИ отобразит текст «Превышение бюджета».
Если лог_выражение равно ЛОЖЬ, а значение_если_ложь опущено
(то есть, после значение_если_истина нет точки с запятой), то возвращается
логическое значение ЛОЖЬ. Если лог_выражение равно ЛОЖЬ, а значение_если_ложь пусто (то есть после значение_если_истина стоит точка с запятой с последующей
закрывающей скобкой), то возвращается
значение 0. Значение_если_ложь может быть формулой.
Значение_если_ложь может быть формулой.
До 7 функций ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина
и значение_если_ложь для конструирования более сложных проверок.Microsoft Excel предлагает дополнительные функции, которые можно применять для анализа данных с использованием условий. Например, для вычисления числа появлений текстовой строки или числа в диапазоне ячеек используйте функцию СЧЁТЕСЛИ. Для вычисления суммы значений, попадающих в интервал, заданный текстовой строкой или числами, используйте функцию СУММАЕСЛИ
|
Заглавная страница
КАТЕГОРИИ: Археология Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 7 из 7
Построение поверхностей в Mathcad. Построение графика поверхности в системе Mathcad может осуществляться несколькими способами.
1 Построение поверхностей по матрице аппликат их точек. Поскольку элементы матрицы М – индексированные переменные с целочисленными индексами, то перед созданием матрицы требуется задать индексы в виде ранжированных переменных с целочисленными значениями, а затем из них сформировать сетку значений После указанных выше определений вводится шаблон графика (либо с помощью подменю меню Вставка, либо с помощью панели Graph). Левый верхний угол шаблона помещается в место расположения курсора. Шаблон содержит единственное место ввода – темный прямоугольник у левого нижнего угла основного шаблона. Следует заметить, так как график строится на основе матрицы, содержащей только координаты высот фигуры, то истинные масштабы по осям абсцисс и ординат неизвестны и на рисунках не проставляются. Однако можно выводить порядковые номера элементов матриц в заданном направлении. Необходимо следить за тем, как сформировать векторы Х и У, чтобы поверхность выглядела естественно и была видна нужная часть поверхности.
2 Построение трехмерных графиков без задания матрицы. В данном случае для построения достаточно задать функцию переменных х и у. В результате построение графиков поверхностей выполняется также просто, как и построение двухмерных графиков. Недостатками такого построения являются неопределенность в масштабировании и то, что не все поверхности второго порядка можно построить таким образом. Форматирование трехмерных графиков. Принцип форматирования трехмерных графиков такой же, как и форматирования двухмерных графиков. Отличие состоит лишь в большем количестве параметров форматирования. Задание 1. Построить поверхность по матрице аппликат ее точек (рисунок 30). Задание 2. Построить поверхность без задания матрицы (рисунок 31).
Рисунок 30
Рисунок 31
Уравнение поверхности не всегда задается в явном виде. Для того чтобы построить поверхность заданную неявно необходимо сначала уравнение данной поверхности разрешить относительно какой-либо переменной, а затем строить поверхности по полученным уравнениям. Задание 3.Построить поверхность, заданную уравнением (рисунок 32). Задание 4. Построить поверхность, заданную уравнением (рисунок 33). Возможности системы Mathcad позволяют строить пересекающиеся поверхности в одной системе координат. Задание 5.Построить поверхности , (рисунок 34). В пакете Mathcad также возможно построение поверхностей, заданных в параметрической форме. Примеры таких построений приведены на рисунках 36 и 37.
Рисунок 32
Рисунок 33
Рисунок 34
Рисунок 35
Рисунок 36
Рисунок 37
⇐ Предыдущая1234567 Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.
- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp.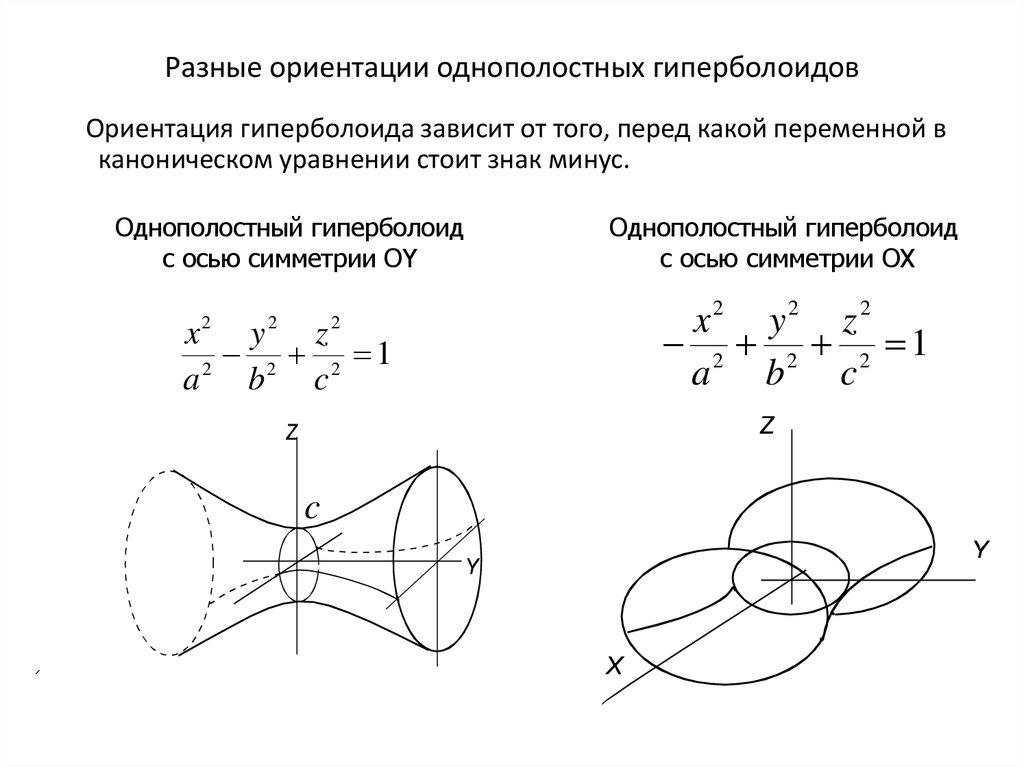 org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2022 Scientific Research Publishing Inc. Все права защищены.
верхний[PDF] Построение меры поворотных конструкций второго порядка с использованием сбалансированных неполных блочных конструкций
- ID корпуса: 17998334
title={Построение меры поворотных конструкций с уклоном второго порядка с использованием сбалансированных неполных блочных конструкций},
author={Бейджам Ре Викторбабу и Чандалури В. В.С. Сурека},
год = {2012}
}
В.С. Сурека},
год = {2012}
} - B. Victorbabu, C. Surekha
- Опубликовано в 2012 г.
- Математика
наклона и поворота для данной конструкции поверхности отклика.
gcu.edu.pk
Об измерении наклона второго порядка Вращающиеся конструкции с использованием частично уравновешенных неполных блочных конструкций
- B. Victorbabu, C. Surekha
Математика
- 2013
В данной статье предлагается новый метод построения меры поворотных конструкций второго порядка с использованием частично сбалансированных неполных блочных конструкций (PBIB) что позволяет нам оценить…
Примечание по мере поворота наклона для конструкций поверхности отклика второго порядка с использованием пары уравновешенных неполных блочных конструкций
- B. Victorbabu, C. Surekha
Математика
- 2016
Мера позволяет оценить степень поворота наклона для данной конструкции поверхности отклика. В этой статье примечание о построении меры поворота уклона для отклика второго порядка…
В этой статье примечание о построении меры поворота уклона для отклика второго порядка…
Построение меры поворота уклона второго порядка с использованием симметричных неравных блоков с двумя неравными размерами блоков
- Б. Викторбабу, К. Сурека
Математика
- 2012
Аннотация В данной статье предлагается новый метод построения меры поворотных конструкций откосов второго порядка (SOSRD) с использованием симметричных неравных блоков с двумя неравными размерами блоков…
Мера поворачиваемости откосов для второго порядка схемы поверхности отклика с использованием пары симметричных неравных блоков с двумя неравными размерами блоков
- П. Чирандживи, Б. Викторбабу
Математика
- 2020
Измерение позволяет оценить степень поворота склона для данной конструкции поверхности отклика. В этой статье мера вращаемости наклона для конструкций поверхности отклика второго порядка с использованием пары…
Мера вращаемости наклона для расчетов поверхности отклика второго порядка при внутриклассовой коррелированной структуре ошибок с использованием парно-сбалансированных планов
- Sulochana Beeraka, Victorbabu B
Математика
- 2020
В этой статье предлагается и иллюстрируется мера поворота наклона для планов поверхности отклика второго порядка с использованием попарно сбалансированных планов при внутриклассовой коррелированной структуре ошибок… — Структура ошибки диагональной корреляции с использованием симметричных неравных расположений блоков с двумя неравными размерами блоков
В этой статье измерена возможность вращения наклона для конструкций поверхности отклика второго порядка с использованием симметричных неравных расположений блоков с двумя неравными размерами блоков при трехдиагональной корреляционной ошибке…
Мера вращаемости модифицированного уклона для расчетов поверхности отклика второго порядка с использованием дополнительных наборов разностей и другие.
 (2016a, 16b), Chiranjeevi and Victorbabu (2018, 19), Nag’eno and Kipkosgei (2019), новая процедура измерения модифицированного уклона…
(2016a, 16b), Chiranjeevi and Victorbabu (2018, 19), Nag’eno and Kipkosgei (2019), новая процедура измерения модифицированного уклона…Мера для оценки степени поворота уклона в трехуровневом уклоне второго порядка Вращающиеся конструкции
Методология поверхности отклика (RSM) часто имеет дело с естественным и желательным свойством вращения, которое требует, чтобы дисперсия прогнозируемого отклика в точке оставалась постоянной во всех таких… составной план (CCD) является наиболее часто используемым дробно-факторным планом, используемым в модели поверхности отклика. Ким [1] предложил вращающиеся конструкции второго порядка (ВОРД) второго типа с использованием…
SHOWING 1-8 OF 8 REFERENCES
Construction of second order slope rotatable designs through balanced incomplete block designs
- B. R. V. Babu, V. L. Narasimhant
Mathematics
- 1991
In this paper a new method of construction of предложены наклонно-поворотные конструкции второго порядка (SOSRD) через уравновешенные неполные блочные конструкции. В этом методе необходимое количество расчетных точек…
В этом методе необходимое количество расчетных точек…
Измерение и графический метод для оценки вращаемости откосов в конструкциях поверхности отклика
- D. Jang, Sung H. Park
Математика
- 1993
Предложена мера для оценки вращаемости откосов по всем направлениям в конструкциях поверхности отклика. Эта мера используется для формирования графика дисперсии дисперсии уклона, оценивающего общий уклон… Представлено свойство вращаемости по Хантеру для конструкций поверхности отклика второго порядка в k независимых переменных. Когда такие планы используются для оценки первых производных…
Мера робастной вращаемости наклона для экспериментальных планов поверхности отклика второго порядка
- Р. Дас, Сунг Х. Парк
Математика
- 1992
В методологии наклонно-вращательности поверхности отклика и вращаемости естественные и весьма желательные свойства для регрессионных моделей второго порядка.

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 В него надо занести имя матрицы аппликат поверхности. После этого надо установить указатель мыши в стороне от графического блока и щелкнуть левой кнопкой.
В него надо занести имя матрицы аппликат поверхности. После этого надо установить указатель мыши в стороне от графического блока и щелкнуть левой кнопкой.

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.) В.С. Сурека},
год = {2012}
}
В.С. Сурека},
год = {2012}
}