описание, примеры, решение задач, уравнение прямой в отрезках
Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.
Уравнение прямой в отрезках – описание и примеры
Пусть на плоскости расположена прямоугольная система координат Oxy.
Прямая линия на плоскости в декартовой системе координат Oxy задается уравнением вида xa+yb=1, где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях Ox и Oy. Длины отрезков считаются от начала координат.
Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a, 0 и 0, b принадлежат данной прямой линии, так как aa+0b=1⇔1≡1 и 0a+bb=1⇔1≡1. Точки a, 0 и b, 0 расположены на осях координат Ox и Oy и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b. Знак «-» обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.
Точки a, 0 и 0, b принадлежат данной прямой линии, так как aa+0b=1⇔1≡1 и 0a+bb=1⇔1≡1. Точки a, 0 и b, 0 расположены на осях координат Ox и Oy и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b. Знак «-» обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.
Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат Oxy на схематическом чертеже. Уравнение прямой в отрезках xa+yb=1 применяется для построения прямой линии в декартовой системе координат Oxy. Для этого нам необходимо отметить на осях точки a, 0 и b, 0, а затем соединить эти точки линией при помощи линейки.
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.
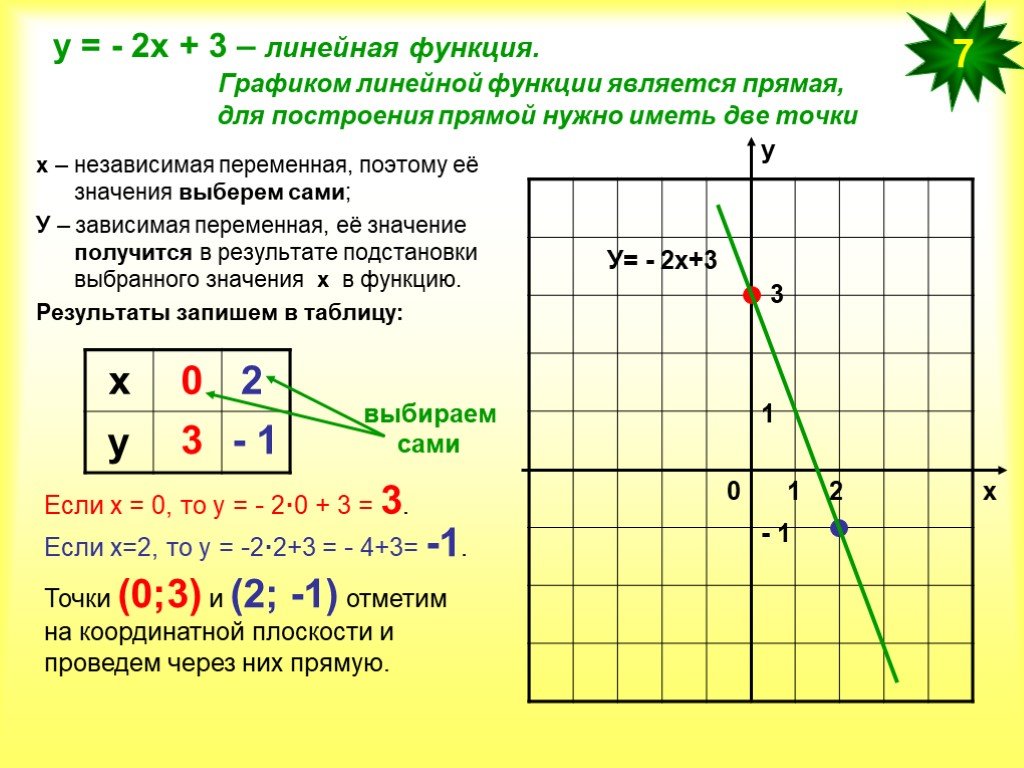
Рассмотрим пример.
Пример 1Прямая линия задана уравнением прямой в отрезках вида x3+y-52=1. Необходимо построить эту прямую на плоскости в декартовой системе координат Oxy.
Необходимо построить эту прямую на плоскости в декартовой системе координат Oxy.
Решение
Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3, 0, 0, -52. Отметим их и проведем линию.
Приведение общего уравнения прямой к уравнению прямой в отрезках
Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.
Полное общее уравнение прямой линии на плоскости имеет вид Ax+By+C=0, где А, В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на –С. При этом, коэффициенты при x и y мы отправляем в знаменатели:
Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1
Для осуществления последнего перехода мы воспользовались равенством pq=1qp, p≠0, q≠0.
В результате, мы осуществили переход от общего уравнения прямой Ax+By+C=0 к уравнению прямой в отрезках xa+yb=1, где a=-CA, b=-CB.
Разберем следующий пример.
Пример 2Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x-7y+12=0.
Решение
Переносим одну вторую в правую часть равенства x-7y+12=0⇔x-7y=-12.
Делим обе части равенства на -12: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем полученное равенство к нужному виду: 1-12x-7-12y=1⇔x-12+y114=1.
Мы получили уравнение прямой в отрезках.
Ответ: x-12+y114=1
В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.
Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида xa+yb=1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y.
xa+yb=1⇔xa+yb-1=0⇔1a·x+1b·y-1=0
Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости.
Уравнение прямой в отрезках имеет вид x23+y-12=1. Необходимо написать общее уравнение прямой на плоскости.
Решение
Действует по заранее описанному алгоритму:
x23+y-12=1⇔123·x+1-12·y-1=0⇔⇔32·x-112·y-1=0
Ответ: 32·x-112·y-1=0
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Как построить уравнение в Excel
Часто вас может заинтересовать построение уравнения или функции в Excel. К счастью, это легко сделать с помощью встроенных формул Excel.
В этом руководстве представлено несколько примеров того, как строить уравнения/функции в Excel.
Предположим, вы хотите построить следующее уравнение:
у = 2х + 5
На следующем изображении показано, как создать значения y для этого линейного уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует прямой линии, поскольку уравнение, которое мы использовали, было линейным по своей природе.
Пример 2. Построение квадратного уравненияПредположим, вы хотите построить следующее уравнение:
у = 3x 2
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11. Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует изогнутой линии, поскольку уравнение, которое мы использовали, было квадратным.
Пример 3: построение уравнения обратной связиПредположим, вы хотите построить следующее уравнение:
у = 1/х
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика под названием « Разброс ».
Автоматически появится следующий график:
Мы видим, что график следует по изогнутой линии вниз, поскольку это представляет уравнение y = 1/x.
Предположим, вы хотите построить следующее уравнение:
у = грех (х)
На следующем изображении показано, как создать значения y для этого уравнения в Excel, используя диапазон от 1 до 10 для значений x:
Затем выделите значения в диапазоне A2:B11.Затем нажмите на вкладку « Вставка ». В группе « Диаграммы » щелкните параметр графика « Разброс с плавными линиями и маркерами» .
Автоматически появится следующий график:
ВыводВы можете использовать аналогичную технику для построения графика любой функции или уравнения в Excel. Просто выберите диапазон значений x для использования в одном столбце, затем используйте уравнение в отдельном столбце, чтобы определить значения y на основе значений x.
Графики в Excel — линейная регрессия
Содержание
- Создать начальный точечный график
- Создание линии линейной регрессии (линии тренда)
- Использование уравнения регрессии для расчета наклона и перехват
- Использование расчета коэффициента R-квадрата для оценки подходит
Введение
Линии регрессии можно использовать как способ визуального изображения отношений между независимыми (x) и зависимыми (y) переменными на графике.
Прямая линия изображает линейный тренд в данных (т. е. уравнение описывающая линию имеет первый порядок. Например, y = 3x + 4. Там в этом уравнении нет переменных, возведенных в квадрат или в куб). Изогнутая линия представляет тренд, описываемый уравнением более высокого порядка (например, y = 2x 2 + 5х — 8). Важно, чтобы вы могли защитить свое использование прямая или изогнутая линия регрессии. То есть теория, лежащая в основе вашего лаборатория должна указать, связаны ли отношения независимых и зависимых переменные должны быть линейными или нелинейными.
В дополнение к визуальному изображению тенденции в данных с регрессией линии, вы также можете рассчитать уравнение линии регрессии. Этот уравнение можно увидеть в диалоговом окне и/или показать на графике. Насколько хорошо это уравнение описывает данные («подгонка»), выражается как коэффициент корреляции, R 2 (R-квадрат).
Доводчик R 2 до 1,00, тем лучше подходит. Это тоже можно рассчитать и отобразить на графике.
Приведенные ниже данные были впервые введены в базовой графический модуль и из химической лаборатории, исследующей поглощение света по решениям. Закон Бера утверждает, что существует линейная зависимость между концентрация окрашенного соединения в растворе и светопоглощение решения. Этот факт можно использовать для расчета концентрации неизвестных растворов, учитывая их показания поглощения. Это делается подгонка линии линейной регрессии к собранным данным.
Создание начальной диаграммы рассеяния
Прежде чем вы сможете создать линию регрессии, необходимо построить график из данные. Традиционно это будет точечная диаграмма. Этот модуль будет начните с точечной диаграммы, созданной в базовой графический модуль.
Рисунок 1 .
Вернуться к началу
Создание линии линейной регрессии (линии тренда)
Когда окно диаграммы выделено, вы можете добавить линию регрессии к график, выбрав Диаграмма > Добавить линию тренда…
Появится диалоговое окно (рис. 2). Выберите Linear Trend/Regression тип:
Рисунок 2 .
Выберите вкладку Параметры и выберите Показать уравнение на графике (Рисунок 3):
Рисунок 3 .
Нажмите OK , чтобы закрыть диалоговое окно. На диаграмме теперь отображается регрессия линия (рисунок 4)
Рисунок 4 .
Вернуться к началу
Использование уравнения регрессии для расчета концентраций
Линейное уравнение, показанное на графике, представляет собой взаимосвязь между Концентрация (x) и абсорбция (y) соединения в растворе.
линию регрессии можно считать приемлемой оценкой истинного зависимость между концентрацией и абсорбцией. Нам дали показания абсорбции для двух растворов неизвестной концентрации. Используя линейное уравнение (обозначенное буквой A на рис. 5), ячейка электронной таблицы может иметь уравнение, связанное с ним, чтобы сделать расчет для нас. У нас есть значение y (поглощение) и нужно решить для x (концентрация). Ниже приведены алгебраические уравнения для этого расчета:
у = 2071,9х + 0,111
г — 0,0111 = 2071,9 х
(г — 0,0111) / 2071,9 = х
Теперь мы должны преобразовать это окончательное уравнение в уравнение в электронной таблице. клетка. Уравнение, связанное с ячейкой электронной таблицы, будет выглядеть так то, что обозначено C на рисунке 8. «B12» в уравнении представляет собой y (значение поглощение неизвестного).
Тогда решение для x (концентрация) будет отображается в ячейке «C12».
- Выделите ячейку электронной таблицы для хранения «x», результата итоговое уравнение (ячейка C12, обозначенная буквой B на рис. 5).
- Нажмите в области уравнений (обозначена C, рис. 5)
- Введите знак равенства и затем скобки
- Щелкните в ячейке, представляющей ‘y’ в вашем уравнении (ячейка B12 на рисунке 5), чтобы поместить эту метку ячейки в уравнение
.- Завершите ввод уравнения
Примечание. Если ваше уравнение отличается от приведенного в этом примере, используйте уравнение
Продублируйте уравнение для другого неизвестного.
- Выделите исходную ячейку уравнения (C12 на рис. 5) и ячейка под ней (C13)
- Выберите Правка > Заливка > Вниз
Вернуться к началу
Обратите внимание: если вы выделите свое новое уравнение в C13, ссылка на ячейка B12 также увеличилась до ячейки B13.
Рисунок 5 .
Вернуться к началу
Использование расчета коэффициента R-квадрата для оценки подходит
Дважды щелкните на линии тренда, выберите вкладку Параметры в диалоговое окно Format Trendlines и установите флажок Display r-squared. значение на графике . Теперь ваш график должен выглядеть так, как показано на рис. 6. Примечание. значение R-квадрата на графике. Чем ближе к 1.0, тем лучше соответствие линии регрессии. То есть чем ближе линия проходит через все точки.
Рисунок 6 .
Теперь давайте посмотрим на другой набор данных, сделанный для этой лаборатории (рис. 7). Уведомление что уравнение для линии регрессии отличается от того, которое было в Рисунок 6. Другое уравнение рассчитывало бы другую концентрацию для двух неизвестных.
Какая линия регрессии лучше представляет «истинный» связь между поглощением и концентрацией? Посмотрите, как внимательно линия регрессии проходит через точки на рисунке 7. Кажется ли «подходить» так же хорошо, как на рисунке 6? Нет, и значение R-квадрата подтверждает этот. На рисунке 7 это 0,873 по сравнению с 0,9.95 на рисунке 6. Хотя мы потребуется принять во внимание такую информацию, как количество данных баллы, собранные для того, чтобы сделать точный статистический прогноз относительно того, как ну линия регрессии представляет истинное отношение, мы обычно можем говорят, что рисунок 6 представляет собой лучшее представление отношения поглощения и концентрации.
Рисунок 7 .
Вернуться к началу
Уравнение прямых — Высшая математика
Добро пожаловать на highmathematics. co.uk
co.uk
Хорошее понимание Уравнения прямых необходимо для успешной сдачи экзамена.
Прохождение ускоренного курса высшей математики значительно расширит ваши карьерные возможности, помогая вам поступить в колледж/университет, пройти стажировку или даже устроиться на работу. «Хороший» результат по высшей математике подготовит вас к курсу математики AH в следующем году, если вы заинтересованы. Пожалуйста, сделайте все возможное, чтобы продолжать учебу.
Для студентов, которым нужна дополнительная помощь по курсу высшей математики, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамены, доступные в онлайн-учебном пакете.
Чтобы получить доступ к множеству дополнительных бесплатных ресурсов по теме , воспользуйтесь расположенной выше панелью поиска или нажмите ЗДЕСЬ, выбрав тему, которую хотите изучить.
Мы надеемся, что вы найдете этот веб-сайт полезным, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году. Ниже вы найдете:
Ниже вы найдете:
1. Уравнения прямых линий
2. Прямые линии — рабочие листы
3. Прямые линии — видео, руководства по теории и интеллект-карты
4. Высшие математические навыки
5. Высшая математика.
6. Прошлые и практические статьи по высшей математике по темам
7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
8. Прошлые и практические статьи по высшей математике
9. 40 вопросов и ответов по высшей математике без калькулятора
10. 200 вопросов и ответов по высшей математике
11. Практические экзаменационные работы от A до H – ответы включены
12. 264 SQA экзамен с несколькими вариантами ответов. Экзаменационные вопросы по математике по темам
15. Решения для учебников по высшей математике
16. Руководства по теории высшей математики
17. Интеллект-карты по высшей математике
18. Практические оценки по высшей математике – решения включены
19. Higher Maths Past Paper Video Solutions
Higher Maths Past Paper Video Solutions
20. Рекомендуемый учебник по высшей математике
21. Онлайн-учебник, ориентированный на экзамен — для студентов, которые ищут «хороший» пропуск
Ресурсы по высшей математике969696.
1. Об уравнениях прямых линий
Чтобы узнать об уравнениях прямых линий, нажмите на ссылку Руководство по теории прямых линий (HSN) и прочитайте со страницы 12. В разделах 2 и 3 ниже вы найдете несколько видеороликов, интеллект-карты (см. раздел «Прямые линии») и рабочие листы по этой теме, которые помогут вам понять. Основные навыки 1, 2, 3, 4, 9, 19 и 29, а также рабочие листы, содержащие фактические вопросы экзамена SQA, настоятельно рекомендуются.
Если вам нужна дополнительная помощь в понимании Уравнения прямых линий в онлайн-учебном пакете есть полные, простые в использовании, пошаговые решения десятков экзаменационных вопросов Higher Maths Past & Practice по всем темам. Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на ориентированный на экзамен Online Study Pack сегодня.
Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на ориентированный на экзамен Online Study Pack сегодня.
Уравнения прямых
- Мы используем как y = mx + c , так и y – b = m(x – a)
- y = mx + c ⇒ Используйте это уравнение, если вы можете прочитать «c», точку пересечения y на графике
- y – b = m(x – a) ⇒ Используйте это уравнение, если у вас есть «m» и (a, b), но нет «c»
- м ⇒ уклон линии
- c ⇒ y точка пересечения
- (a, b) ⇒ любая точка на прямой
.
Уравнения касательной
На экзамене по высшей математике вас могут попросить определить уравнение касательной. На диаграмме ниже показана линия , касательная к окружности — знаете ли вы, как найти уравнение касательной?
.
- Касательная – это прямая линия, перпендикулярная другой линии (под прямым углом)
- Для перпендикулярных уклонов m1m2 = -1
- Мы используем уравнения y – b = m(x – a) или y = mx + c, чтобы найти уравнение прямой
- Дифференциация — это скорость изменения функции по отношению к одной из ее переменных
- Если мы продифференцируем и заменим x, то это будет градиент касательной в этой точке
- «Уравнения касательных» входят в разделы «Прямая линия» и «Дифференциация» курса высшей математики
.
.
.
2. Прямые линии — рабочие листы
Спасибо SQA и авторам за то, что они предоставили в свободный доступ приведенные ниже отличные ресурсы. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые рабочие решения для всех рабочих листов, приведенных ниже, доступны в пакете онлайн-обучения.
| Рабочие листы высшего уровня ________________________________ | Рекомендуемый ________________ | Рабочий лист _________________________________ | Без ответов ________________ | Примечания/комментарии _____________ | Предоставлено ____________________ |
| Теория прямых линий (HSN) | Рекомендуется | Теория прямых линий (HSN) | Предоставлено HSN | ||
| Heinemann Book — Straight Line | Решения для учебников | Ex 1A, 1B, 1D, 1E, 1F, 1G, 1I, 1K, 1M, 1N, 1O | Ответы по ссылкам | ||
| Практика экзамена по основным навыкам 1 | Прямая линия | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Основные навыки 1 | Медиана треугольника | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни Ренни | |
| Основные навыки 2 | Перпендикулярные биссектрисы | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Основные навыки 3 | Высота треугольника | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 4 | Уравнение касательной к кривой | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Основные навыки 9 | Пересечение линий и окружностей | Без ответов | Только ответы | Предоставлено Mr G Rennie | |
| Основные навыки 29 | Угол между линией и осью X | Без ответов | Только ответы | Предоставлено г-ном Г. Ренни | |
| Бумага Grade Booster Paper 5 | Прямые линии | Без ответов | |||
| Экзаменационный лист 1 | Рекомендуется | Прямые линии 1 (2000 — 2022) | Без ответов | 2022 Вопросы включены! | Предоставлено SQA |
| Экзаменационный лист 2 | Прямые линии 2 (2000–2019) | Без ответов | Предоставлено SQA | ||
| Экзаменационный лист 3 | Прямые линии 3 (2015–2019) | Без ответов | Предоставлено SQA | ||
| Экзаменационный лист 4 | 54 вопроса SQA | Прямые линии 4 (старое высшее) | Без ответов | Несколько вариантов ответа включены! | |
| Экзаменационный лист 5 | Прямые линии 5 (Старое высшее) | Без ответов | Предоставлено SQA | ||
| Экзаменационный лист 6 | Прямые линии 6 (2000–2013) | Схемы выставления оценок SQA | Предоставлено SQA | ||
| Экзаменационный лист 7 | Прямые линии 7 (множественный выбор) | Схемы оценки SQA | Предоставлено SQA | ||
| Рабочие листы 1 и 2 | Градиенты перпендикулярных линий 1, 2 | ||||
| Рабочий лист 3 | Формула расстояния | ||||
| Контрольный список экзаменов 11 | Прямые линии |
.
3. Прямые линии – видео, теоретические руководства и интеллект-карты
Спасибо авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
| Larbert Maths Videos ___________________________ | maths180.com Video ___________________ | HSN Theory Guide _______________________ | Интеллект-карты __________________ |
| Высоты | Прямые линии | Теория прямых линий (HSN) | Прямые линии (HSN) |
| Коллинеарность | Прямые линии 1 | ||
| Расстояние между точками | Прямые линии 2 | ||
| Уравнение прямой | |||
| Редакция градиента | |||
| Градиент от угла | |||
| Медианы | |||
| Средние точки | |||
| Биссектрисы | |||
| Перпендикулярные градиенты | |||
| Точки пересечения |
.
4. Высшие математические навыки
Спасибо г-ну Г. Ренни за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Рабочие листы основных навыков можно использовать для общего повторения, выполнения домашних заданий, закрепления темы или подготовки к оцениванию, тестам и экзаменам. Четкие, простые в использовании, пошаговые решения для всех 33 рабочих листов основных навыков, приведенных ниже, доступны в онлайн-учебном пакете.
.
5. Рабочие листы экзамена по высшей математике по темам
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Рабочие листы по темам являются фантастическим учебным ресурсом, поскольку они являются реальными вопросами прошлых бумажных экзаменов. Четкие, простые в использовании, пошаговые решения для всех новых вопросов CfE по высшей математике, приведенных ниже, доступны в онлайн-пакете для изучения.
.
6. Higher Maths Past & Practice Papers by Topic
Спасибо SQA за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Вопросы и ответы разделены по темам для удобства поиска. Четкие, простые в использовании, пошаговые решения всех приведенных ниже вопросов доступны в пакете онлайн-обучения.
| . Бумага _____________ | . Маркировка __________ | . Circles ______ | Differentiation & Optimisation ____________ | Exp’s & Logs ________ | Functions & Graphs _________ | Further Calculus ________ | . Интегрирование _________ | Полиномы и квадратичные уравнения ____________ | Повторение Отношения __________ | Прямые Линии _________ | . Векторы ________ | Волна Функция _________ | |||||||||||||||
| 2019 P1 | Marking P1 | Q3,16 | Q1 | Q14 | Q10,12 | Q6,11,17b | Q8 | Q2 | Q4 | Q5,7 | Q13, 15,17а | Q9 | |||||||||||||||
| 2019 P2 | Маркировка P2 | Q15 | Q7b,11 | Q9,12 | Q5,8 | Q2,13 | Q7,10 | Q4 | Q1 | Q6B347 | Q1 | . | |||||||||||||||
| 2018 P1 | Marking P1 | Q4 | Q6,11 | Q2,11,15 | Q3,14 | Q10 | Q7 | Q1,8 | Q13 | Q5,9 ,12 | |||||||||||||||||
| 2018 P2 | Маркировка P2 | Q5c,12 | Q3,9 | Q11 | Q6 | Q1 | Q4,7a,10 | 7b,c | Q5a,b | 77 | Q4 | ||||||||||||||||
| 2017 P1 | Marking P1 | Q2 | Q8,15c | Q12 | Q1,6,15a | Q3,13 | Q10,15b | Q4 | Q9 | Q7,11 | Q5 | Q14 | |||||||||||||||
| 2017 P2 | Маркировка P2 | Q3,10 | Q4,7 | Q9 | Q2 | Q8 | Q1 | Q6,11 | Q5 | 7 | |||||||||||||||||
| 2016 P1 | Marking P1 | Q4,8 | Q2,9 | Q14 | Q6,10,12 | Q5 | Q15 | Q3 | Q1 | Q13 | Q7,11 | ||||||||||||||||
| 2016 P2 | Маркировка P2 | Q4 | Q7 | Q6 | Q10,11b | 3b,9 | Q2,3a | Q1 | Q8b,11a | Q5 | Q87a | ||||||||||||||||
| 2015 P1 | Marking P1 | Q11,14 | Q2,7 | Q6 | Q4,5,13 | Q12,15 | Q3,8 | Q9 | Q10 | Q1 | |||||||||||||||||
| 2015 P2 | Маркировка P2 | Q5 | Q8 | Q2 | Q7a | Q4 | Q3 | Q1 | Q7b | Q6 | Q9 | ||||||||||||||||
| Specimen P1 | Marking P1 | Q11 | Q8 | Q10 | Q1 | Q4,7 | Q2,5,9 | Q6,12 | Q3 | ||||||||||||||||||
| Образец P2 | Маркировка P2 | Q5 | Q3b,8 | Q4,7 | Q9 | Q3a0347Q2 | Q1,6 | Q10 | |||||||||||||||||||
| Exemplar P1 | Marking P1 | Q1 | Q8,11 | Q10 | Q3 | Q2,5 | Q6 | Q4,7 | Q9 | ||||||||||||||||||
| Exemplar P2 | Marking P2 | Q2 | Q9,10 | Q7 | Q8 | Q4 | Q3 | Q1 | Q5,6 |
.
7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
Десятки видео по высшей математике содержат качественные уроки по темам. Также включены отличные руководства по теории, интеллект-карты и рабочие листы с актуальными экзаменационными вопросами по высшей математике. Пожалуйста, нажмите на нашу новую страницу с видео и рабочими таблицами по высшей математике по темам.
.
8. Прошлые и практические работы по высшей математике
Спасибо SQA за предоставление бесплатного доступа к превосходным ресурсам, указанным ниже. Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.
.
9. 40 Вопросы и ответы по высшей математике без калькулятора
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Начните с этих вопросов, чтобы укрепить свою уверенность. После того, как вы закончите, вы можете перейти к 200 вопросов экзамена по высшей математике в следующем разделе, проверяя свои ответы по ходу дела. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые для понимания, пошаговые решения всех 40 приведенных ниже вопросов доступны в пакете онлайн-обучения.
После того, как вы закончите, вы можете перейти к 200 вопросов экзамена по высшей математике в следующем разделе, проверяя свои ответы по ходу дела. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые для понимания, пошаговые решения всех 40 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
10. 200 вопросов и ответов по высшей математике
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, постарайтесь задать как можно больше вопросов, проверяя ответы по ходу. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
11. Практические экзаменационные работы от A до H – ответы включены
Спасибо SQA и Larkhall Academy за предоставление нижеприведенных превосходных ресурсов в свободный доступ. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для практических работ от A до E доступны в онлайн-пакете для изучения.
Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для практических работ от A до E доступны в онлайн-пакете для изучения.
.
12. Экзамен 264 SQA Вопросы и ответы с несколькими вариантами ответов
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Множественный выбор — это, прежде всего, вопросы уровня C, и это отличное место для начала проверки. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее.
.
13. Контрольные списки для экзамена по высшей математике
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Это фантастические контрольные списки для оценки ваших знаний по высшей математике. Пожалуйста, старайтесь регулярно использовать их для повторения перед тестами, предварительными экзаменами и выпускным экзаменом.
.
14. Старые экзаменационные вопросы по высшей математике по темам
Спасибо SQA за то, что они предоставили в свободный доступ превосходные ресурсы, указанные ниже. Рабочие листы по темам являются фантастическим дополнительным учебным ресурсом.
| Тема _______ | Название темы ___________________________ | Ссылка ________ | Примечания ___________________ |
| Тема 1 | Круги | ЗДЕСЬ | Ответы включены |
| Тема 2 | Дифференциация | ЗДЕСЬ | Ответы включены |
| Тема 3 | Экспоненты и логарифмы | ЗДЕСЬ | Ответы включены |
| Тема 4 | Функции | ЗДЕСЬ | Ответы включены |
| Тема 5 | Дальнейшее исчисление | ЗДЕСЬ | Ответы включены |
| Тема 6 | Графики функций | ЗДЕСЬ | Ответы включены |
| Тема 7 | Интеграция | ЗДЕСЬ | Ответы включены |
| Тема 8 | Полиномы | ЗДЕСЬ | Ответы включены |
| Тема 9 | Квадратика | ЗДЕСЬ | Ответы включены |
| Тема 10 | Рекуррентные соотношения | ЗДЕСЬ | Ответы включены |
| Тема 11 | Прямая линия | ЗДЕСЬ | Ответы включены |
| Тема 12 | Триггерные формулы сложения | ЗДЕСЬ | Ответы включены |
| Тема 13 | Триггерные графики и уравнения | ЗДЕСЬ | Ответы включены |
| Тема 14 | Векторы | ЗДЕСЬ | Ответы включены |
| Тема 15 | Волновая функция | ЗДЕСЬ | Ответы включены |
.
15. Решения для учебников по высшей математике
Спасибо AHS за предоставленные решения для учебников Heinemann по высшей математике, указанные ниже. Они окажутся чрезвычайно полезными для улучшения ваших знаний по высшей математике. Обратите внимание, что может быть нечетная арифметическая ошибка.
.
16. Пособия по высшей математике
Благодарим HSN за то, что они сделали превосходные руководства по теории высшей математики бесплатными для всех. Они окажутся фантастическим ресурсом, который поможет вам закрепить ваше понимание высшей математики.
| Теоретические руководства _________________ | Тема ____________________________________________ | Ссылка _______ |
| Руководство по теории 1 | Все темы Раздел 1 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 2 | Все темы, часть 1 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 3 | Все темы Раздел 2 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 4 | Все темы, раздел 2 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 5 | Все темы Раздел 3 Теория (HSN) | ЗДЕСЬ |
| Теоретическое руководство 6 | Все темы, раздел 3 — краткое руководство на одной странице (HSN) | ЗДЕСЬ |
| Руководство по теории 7 | Все темы Разделы 1, 2 и 3 Теория (HSN) | ЗДЕСЬ |
| Руководство по теории 8 | Теория кругов (HSN) | ЗДЕСЬ |
| Руководство по теории 9 | Теория дифференцировки (HSN) | ЗДЕСЬ |
| Руководство по теории 10 | Теория экспонент и логарифмов (HSN) | ЗДЕСЬ |
| Руководство по теории 11 | Теория функций и графиков (HSN) | ЗДЕСЬ |
| Руководство по теории 12 | Дальнейшая теория исчисления (HSN) | ЗДЕСЬ |
| Руководство по теории 13 | Теория трансформации графиков (движение и отражение) | ЗДЕСЬ |
| Теоретическое руководство 14 | Сводная таблица преобразований графиков | ЗДЕСЬ |
| Теоретическое руководство 15 | Теория интеграции (HSN) | ЗДЕСЬ |
| Руководство по теории 16 | Теория многочленов и квадратичных уравнений (HSN) | ЗДЕСЬ |
| Руководство по теории 17 | Теория последовательностей (HSN) | ЗДЕСЬ |
| Руководство по теории 18 | Теория прямых линий (HSN) | ЗДЕСЬ |
| Руководство по теории 19 | Теория тригонометрии (HSN) | ЗДЕСЬ |
| Теоретическое руководство 19 | Теория векторов (HSN) | ЗДЕСЬ |
| Руководство по теории 20 | Теория волновых функций (HSN) | ЗДЕСЬ |
.
17. Интеллект-карты высшей математики
Спасибо авторам за предоставленные ниже отличные ресурсы. Они окажутся фантастическим ресурсом, помогающим вам подготовиться к оценкам, тестам и выпускному экзамену.
.
18. Оценки по высшей математике – решения включены
Спасибо авторам за то, что они сделали приведенные ниже отличные ресурсы бесплатными для всех. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
.
19. Higher Maths Past Paper Video Solutions
Щелкните DLB Maths, чтобы просмотреть видеорешения Higher Maths Past Paper. Это отличный ресурс, который поможет вам подготовиться к оцениванию, тестам и выпускному экзамену.
.
20. Рекомендуемый учебник по высшей математике
Ниже вы найдете рекомендуемый учебник, который можно заказать, нажав на книгу/ссылку.
.
.

 Прямая линия изображает линейный тренд в данных (т. е. уравнение
описывающая линию имеет первый порядок. Например, y = 3x + 4. Там
в этом уравнении нет переменных, возведенных в квадрат или в куб). Изогнутая линия представляет
тренд, описываемый уравнением более высокого порядка (например, y = 2x 2 + 5х — 8). Важно, чтобы вы могли защитить свое использование
прямая или изогнутая линия регрессии. То есть теория, лежащая в основе вашего
лаборатория должна указать, связаны ли отношения независимых и зависимых
переменные должны быть линейными или нелинейными.
Прямая линия изображает линейный тренд в данных (т. е. уравнение
описывающая линию имеет первый порядок. Например, y = 3x + 4. Там
в этом уравнении нет переменных, возведенных в квадрат или в куб). Изогнутая линия представляет
тренд, описываемый уравнением более высокого порядка (например, y = 2x 2 + 5х — 8). Важно, чтобы вы могли защитить свое использование
прямая или изогнутая линия регрессии. То есть теория, лежащая в основе вашего
лаборатория должна указать, связаны ли отношения независимых и зависимых
переменные должны быть линейными или нелинейными. Доводчик R 2 до 1,00, тем лучше подходит. Это тоже можно рассчитать и отобразить
на графике.
Доводчик R 2 до 1,00, тем лучше подходит. Это тоже можно рассчитать и отобразить
на графике.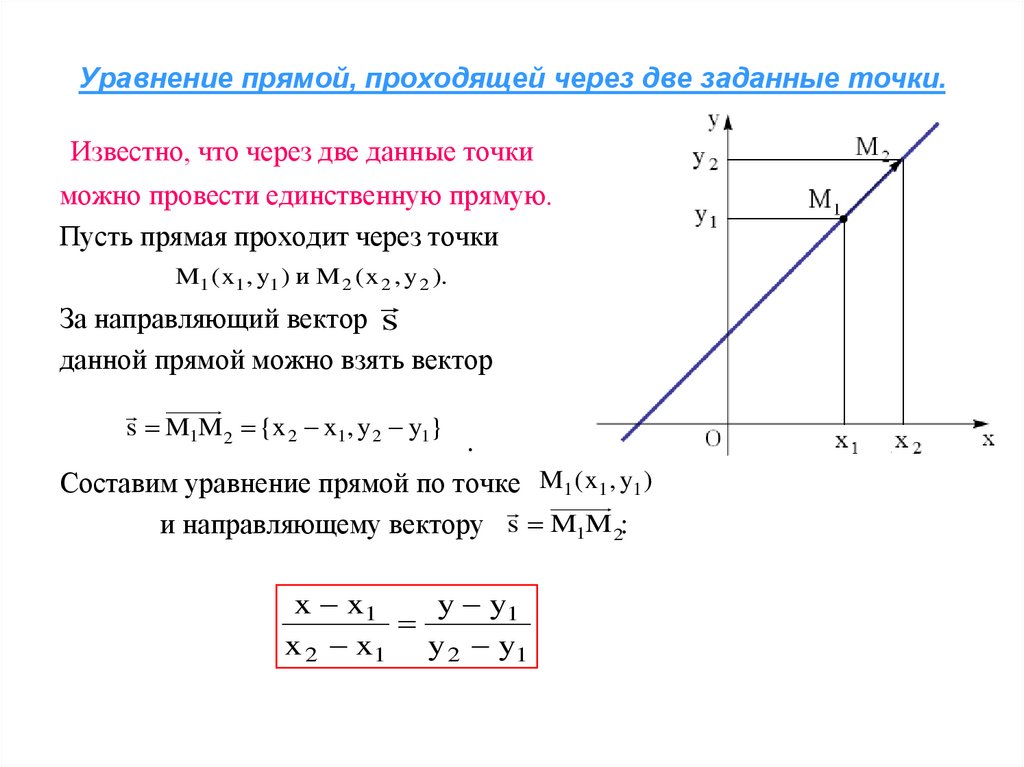


 Какая линия регрессии лучше представляет «истинный»
связь между поглощением и концентрацией? Посмотрите, как внимательно
линия регрессии проходит через точки на рисунке 7. Кажется ли
«подходить» так же хорошо, как на рисунке 6? Нет, и значение R-квадрата подтверждает
этот. На рисунке 7 это 0,873 по сравнению с 0,9.95 на рисунке 6. Хотя мы
потребуется принять во внимание такую информацию, как количество данных
баллы, собранные для того, чтобы сделать точный статистический прогноз относительно того, как
ну линия регрессии представляет истинное отношение, мы обычно можем
говорят, что рисунок 6 представляет собой лучшее представление отношения
поглощения и концентрации.
Какая линия регрессии лучше представляет «истинный»
связь между поглощением и концентрацией? Посмотрите, как внимательно
линия регрессии проходит через точки на рисунке 7. Кажется ли
«подходить» так же хорошо, как на рисунке 6? Нет, и значение R-квадрата подтверждает
этот. На рисунке 7 это 0,873 по сравнению с 0,9.95 на рисунке 6. Хотя мы
потребуется принять во внимание такую информацию, как количество данных
баллы, собранные для того, чтобы сделать точный статистический прогноз относительно того, как
ну линия регрессии представляет истинное отношение, мы обычно можем
говорят, что рисунок 6 представляет собой лучшее представление отношения
поглощения и концентрации.