Прямоугольная система координат в пространстве — Математика
Геометрия > Метод координат в пространстве > Прямоугольная система координат в пространстве
|
11 класс. Геометрия. Метод координат в пространстве. Прямоугольная система координат. — Прямоугольная система координат в пространстве. Координаты вектора.
Комментарии преподавателяЕсли через точку О в пространстве мы проведем три перпендикулярные прямые, назовем их, выберем направление, обозначим единичные отрезки, то мы получим прямоугольную систему координат в пространстве. Оси координат называются так: Ох – ось абсцисс, Оy – ось ординат и Оz – ось аппликат. Вся система координат обозначается – Oxyz. Таким образом, появляются три координатные плоскости: Оxy, Оxz, Оyz.
Приведем пример построения точки В(4;3;5) в прямоугольной системе координат (см. Рис. 1).
Рис. 1. Построение точки B в пространстве
Первая координата точки B – 4, поэтому откладываем на Ox 4, проводим прямую параллельно оси Oy до пересечения с прямой, проходящей через у=3. Таким образом, мы получаем точку K. Эта точка лежит в плоскости Oxy и имеет координаты K(4;3;0). Теперь нужно провести прямую параллельно оси Oz. И прямую, которая проходит через точку с аппликатой 5 и параллельна диагонали параллелограмма в плоскости Oxy. На их пересечении мы получим искомую точку B.
Рассмотрим расположение точек, у которых одна или две координаты равны 0 (см. Рис. 2).
Рис. 2.
Например, точка A(3;-1;0). Нужно продолжить ось Oy влево до значения -1, найти точку 3 на оси Ox, и на пересечении линий, проходящих через эти значения, получаем точку А. Эта точка имеет аппликату 0, а значит, она лежит в плоскости Oxy.
Эта точка имеет аппликату 0, а значит, она лежит в плоскости Oxy.
Точка C(0;2;0) имеет абсциссу и аппликату 0 – не отмечаем. Ордината равна 2, значит точка C лежит только на оси Oy, которая является пересечением плоскостей Oxy и Oyz.
Чтобы отложить точку D(-4;0;3) продолжаем ось Ox назад за начало координат до точки -4. Теперь восстанавливаем из этой точки перпендикуляр – прямую, параллельную оси Oz до пересечения с прямой, параллельной оси Ox и проходящей через значение 3 на оси Oz. Получаем току D(-4;0;3). Так как ордината точки равна 0, значит точка D лежит в плоскости Oxz.
Следующая точка E(0;5;-3). Ордината точки 5, аппликата -3, проводим прямые проходящие через эти значения на соответствующих осях, и на их пересечении получаем точку E(0;5;-3). Эта точка имеет первую координату 0, значит она лежит в плоскости Oyz.
Начертим прямоугольную систему координат в пространстве Oxyz. Зададим в пространстве прямоугольную систему координат Oxyz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим единичный вектор оси абсцисс, единичный вектор оси ординат , и единичный вектор оси аппликат (см. рис. 1). Эти векторы сонаправлены с направлениями осей, имеют единичную длину и ортогональны – попарно перпендикулярны. Такие вектора называют координатными векторами или базисом.
Зададим в пространстве прямоугольную систему координат Oxyz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим единичный вектор оси абсцисс, единичный вектор оси ординат , и единичный вектор оси аппликат (см. рис. 1). Эти векторы сонаправлены с направлениями осей, имеют единичную длину и ортогональны – попарно перпендикулярны. Такие вектора называют координатными векторами или базисом.
Рис. 1. Разложение вектора по трем координатным векторам
Возьмем вектор , поместим его в начало координат, и разложим этот вектор по трем некомпланарным — лежащим в разных плоскостях — векторам. Для этого опустим проекцию точки M на плоскость Oxy, и найдем координаты векторов , и . Получаем: . Рассмотрим по отдельности каждый из этих векторов. Вектор лежит на оси Ox, значит, согласно свойству умножения вектора на число, его можно представить как какое-то число x умноженное на координатный вектор . , а длина вектора ровно в x раз больше длины . Так же поступим и с векторами и , и получаем разложение вектора по трем координатным векторам:
Вектор лежит на оси Ox, значит, согласно свойству умножения вектора на число, его можно представить как какое-то число x умноженное на координатный вектор . , а длина вектора ровно в x раз больше длины . Так же поступим и с векторами и , и получаем разложение вектора по трем координатным векторам:
Коэффициенты этого разложения x, y и z называются координатами вектора в пространстве.
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.
;
1) Сложение:
2) Вычитание:
3) Умножение на число: ,
Вектор, начало которого совпадает с началом координат, называется радиус—вектором. (Рис. 2). Вектор — радиус-вектор, где x, y и z – это коэффициенты разложения этого вектора по координатным векторам , , . В данном случае x – это первая координата точки A на оси Ox, y – координата точки B на оси Oy, z – координата точки C на оси Oz. По рисунку видно, что координаты радиус-вектора одновременно являются координатами точки М.
В данном случае x – это первая координата точки A на оси Ox, y – координата точки B на оси Oy, z – координата точки C на оси Oz. По рисунку видно, что координаты радиус-вектора одновременно являются координатами точки М.
Рис. 2.
Возьмем точку A(x1;y1;z1) и точку B(x2;y2;z2) (см. рис. 3). Представим вектор как разность векторов и по свойству векторов. Причем, и — радиус-векторы, и их координаты совпадают с координатами концов этих векторов. Тогда мы можем представить координаты вектора как разность соответствующих координат векторов и : . Таким образом, координаты вектора мы можем выразить через координаты конца и начала вектора.
Рис. 3.
Рассмотрим примеры, иллюстрирующие свойства векторов и их выражение через координаты. Возьмем векторы , , . Нас спрашивают вектор . В данном случае найти это значит найти координаты вектора , которые полностью его определяют. Подставляем в выражение вместо векторов соответственно их координаты. Получаем:
Подставляем в выражение вместо векторов соответственно их координаты. Получаем:
Теперь умножаем число 3 на каждую координату в скобках, и то же самое делаем с 2:
У нас получилась сумма трех векторов, складываем их по изученному выше свойству:
Ответ:
Пример №2.
Дано: Треугольная пирамида AOBC (см. рис. 4). Плоскости AOB, AOC и OCB – попарно перпендикулярны. OA=3, OB=7, OC=4; M — сер.AC; N — сер.OC; P – сер. CB.
Найти: ,,,,,,,.
Рис. 4.
Решение: Введем прямоугольную систему координат Oxyz с началом отсчета в точке O. По условию обозначаем точки A, B и C на осях и середины ребер пирамиды – M, P и N. По рисунку находим координаты вершин пирамиды: A(3;0;0), B(0;7;0), C(0;0;4).
Так как координаты вектора — это разность координат его конца и начала, получаем:. Таким же образом находим координаты векторов и . ; .
; .
Чтобы найти координаты вектора , нужно сначала найти координаты точек M и N. По рисунку видно, что точка N имеет координаты, так как она лежит на оси аппликат. Рассмотрим . MN – средняя линия, . Значит координата точки M по оси Oz 2. Теперь проведем из точки M перпендикуляр к оси Ox, координата 1,5. Точка M лежит в плоскости Oxz, значит по оси Oy координата 0. Получаем M(1,5;0;2). Теперь зная координаты точек M и N, считаем их разность: .
Теперь найдем координаты точки P. Опустим перпендикуляр на плоскость Oxy, получаем значение 3,5 по оси ординат. И проведя перпендикуляр к оси Oz, получаем значение 2 по оси аппликат. Точка P имеет координаты (0;3,5;2). Зная координаты нужных точек, найдем координаты оставшихся векторов.
;
.
Вектора и — радиус-векторы, значит, их координаты равны координатам концов этих векторов: , .
ИСТОЧНИК
http://interneturok.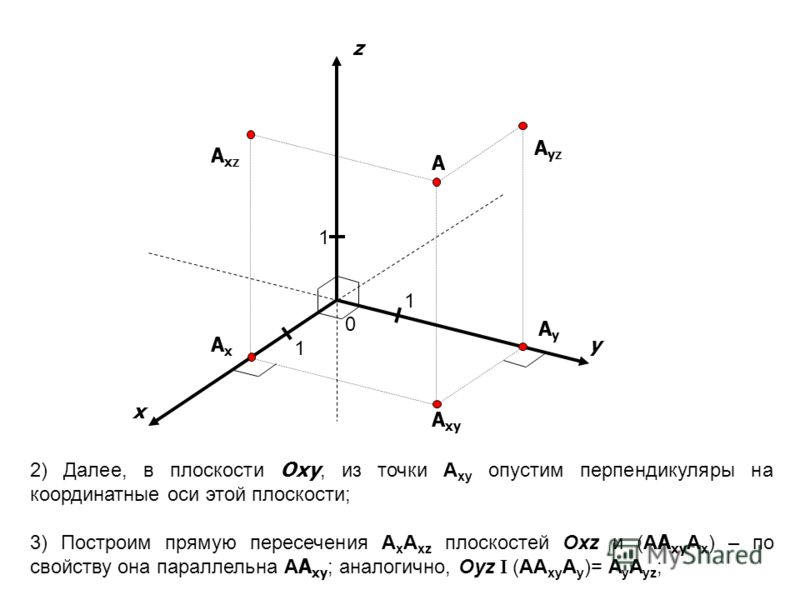 ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/pryamougolnaya-sistema-koordinat-v-prostranstve?seconds=0&chapter_id=218
ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/pryamougolnaya-sistema-koordinat-v-prostranstve?seconds=0&chapter_id=218
http://interneturok.ru/ru/school/geometry/11-klass/bmetod-koordinat-v-prostranstveb/koordinaty-vektora-2
http://www.youtube.com/watch?v=I1ls2_8OC7o
http://900igr.net/fotografii/geometrija/Prjamougolnaja-sistema-koordinat/006-Nachalo-koordinat.html
http://www.yaklass.ru/materiali?mode=lsntheme&themeid=101
http://900igr.net/fotografii/geometrija/Prjamougolnaja-sistema-koordinat-v-prostranstve/Prjamougolnaja-sistema-koordinat-v-prostranstve.html
Место в космосе — Занятие
Quick Look
Уровень: 6 (6-9)
Требуется время: 30 минут
(плюс 15-20 минут, если учащиеся строят свой собственный набор оси. )
)
Расходые затраты/группа: US $ 3,00
Размер группы: 3
Active Зависимость:
Трехмерная система координат для карт галактик: новое измерение
предметных областей: Геометрия, наука и техника
Поделиться:
TE Информационный бюллетень
Краткое содержание
Студенческие группы используют «настоящую» трехмерную систему координат для построения точек в пространстве. Изготовленная из пробкового дерева или деревянных дюбелей, система имеет три оси под прямым углом и плоскость (плоскость XY), которая может скользить вверх и вниз по оси Z. Учащимся дается несколько координат и предлагается найти эти точки в пространстве. Затем они находят координаты восьми углов коробки/куба с заданными размерами. Инженерное подключение
Инженеры используют систему координат всякий раз, когда они создают инженерные чертежи объектов и конструкций, и декартова система координат, смоделированная в этой деятельности, используется чаще всего.
Цели обучения
После этого задания учащиеся должны уметь:
- Найдите точку в пространстве, зная ее координаты и начало координат.
- Описать положение данной точки в пространстве относительно некоторого начала координат с помощью координат.
Образовательные стандарты
Каждый урок или занятие TeachEngineering
соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются Сеть стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естественные науки или математика;
внутри типа по подтипу, затем по классам, и т.д. .
, естественные науки или математика;
внутри типа по подтипу, затем по классам, и т.д. .
Общие базовые государственные стандарты — математика
- Найдите и расположите целые числа и другие рациональные числа на горизонтальной или вертикальной числовой линейной диаграмме; найти и расположить пары целых чисел и других рациональных чисел на координатной плоскости.
(Оценка
6) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Решайте реальные и математические задачи, отображая точки во всех четырех квадрантах координатной плоскости.
 Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
(Оценка
6) Подробнее
Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
(Оценка
6) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
 (Оценка
7) Подробнее
(Оценка
7) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Создавайте формальные геометрические построения с помощью различных инструментов и методов (циркуль и линейка, струна, отражающие устройства, складывание бумаги, динамическое геометрическое программное обеспечение и т.
 д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
(Оценки
9-
12) Подробнее
д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
(Оценки
9-
12) ПодробнееПосмотреть согласованную учебную программу
Международная ассоциация преподавателей технологий и инженерии — Технология
- Информационно-коммуникационные системы позволяют передавать информацию от человека к человеку, от человека к машине и от машины к человеку.
 (Оценки
6 —
8) Подробнее
(Оценки
6 —
8) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Использование символов, размеров и рисунков способствует четкому общению, предоставляя общий язык для выражения идей.
(Оценки
6 —
8) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
ГОСТ
Предложите выравнивание, не указанное вышеКакое альтернативное выравнивание вы предлагаете для этого контента?
Подписаться
Подпишитесь на нашу рассылку новостей, чтобы получить внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!
PS: Мы никому не передаем личную информацию и электронные письма.
Список материалов
- 3-футовый штифт из пробкового дерева размером ¼ дюйма x ¼ дюйма или деревянный дюбель
- быстродействующий клей, такой как пистолет для горячего клея, резиновый клей или глиняный шарик размером с мяч для гольфа
- маркер
- линейка
- Канцелярский нож или ножницы
- Квадрат 1 дюйм x 1 дюйм из гофрированного картона, пенопласта или картона для плакатов
Рабочие листы и вложения
Рабочий лист 3D-координат (pdf)
Посетите [www.teachengineering.org/activities/view/duk_dimension_tech_act], чтобы распечатать или загрузить.Больше учебных программ, подобных этому
Высший элементарный урок
Трехмерная система координат для картирования галактик: следующее измерение
Учащиеся узнают о трехмерной декартовой системе координат и получают представление о размере нашей галактики (Млечный Путь) и расстоянии до ближайшей спиральной галактики (галактики Андромеды), используя трехмерную модель. Предоставляется рабочий лист ученика.
Предоставляется рабочий лист ученика.
Трехмерная система координат для карт галактик: новое измерение
Урок средней школы
Все о линейном программировании
Учащиеся узнают о линейном программировании (также называемом линейной оптимизацией) для решения задач инженерного проектирования. Они применяют эту информацию для решения двух практических задач инженерного проектирования, связанных с оптимизацией материалов и стоимости, путем построения графиков неравенств, определения координат и уравнений из …
Все о линейном программировании
Урок средней школы
Проекции и координаты: превращение трехмерной Земли в плоскость
Учащиеся узнают о проекциях и координатах в географических науках, которые помогают нам лучше понять природу Земли и то, как описать местоположение.
Проекции и координаты: превращение трехмерной Земли в плоскость
Урок средней школы
Координаты и декартова плоскость
Краткий обзор декартовой плоскости включает в себя то, как точки записываются в формате (x, y) и ориентированы по осям, а также какие направления являются положительными и отрицательными. Затем учащиеся узнают, что означает, что отношение является функцией, и как определить домен и диапазон набора точек данных.
Координаты и декартова плоскость
Предварительные знания
Минимальный предварительный опыт построения графиков в двух измерениях полезен, но не обязателен.
Введение/Мотивация
Содержимое раздела «Введение/мотивация» урока «Трехмерная система координат для картирования галактик: следующее измерение» также служит введением в это задание.
Процедура
Перед занятием
Соберите материалы и сделайте копии рабочего листа 3D-координат.
Выполните следующие действия, чтобы построить один набор осей для каждой группы. В качестве альтернативы, пусть группы сами построят оси.
- Разрежьте пробковое дерево на три сегмента по 1 футу каждый. (Вероятно, это займет дополнительные 15-20 минут.)
- С помощью клеевого пистолета (или другого клея или глины) склейте три детали вместе так, чтобы все три были перпендикулярны друг другу и встречались в одной точке. Это формирует три оси.
- С помощью линейки и маркера сделайте отметки через каждый дюйм по каждой из трех осей, удаляясь от исходной точки. Сделайте в общей сложности 10 меток на каждой оси. При желании пронумеруйте метки так, чтобы на каждой оси «1» была ближе всего к началу координат, а «10» — дальше всего от оси.
- С помощью канцелярского ножа или ножниц вырежьте из картона, пенопласта или картона для плакатов квадрат размером 1 фут x 1 фут.
 Сделайте небольшое отверстие в одном углу квадрата, примерно на полдюйма от краев. Сделайте отверстие достаточно большим, чтобы ось из пробкового дерева прошла через него.
Сделайте небольшое отверстие в одном углу квадрата, примерно на полдюйма от краев. Сделайте отверстие достаточно большим, чтобы ось из пробкового дерева прошла через него. - Эта доска из пеноматериала служит плоскостью XY. Сдвиньте его по одной из осей (ось Z) до упора вниз, пока он не ляжет на две другие оси. Отверстие, в котором ось Z проходит через плоскость XY, теперь находится в начале координат.
- С помощью линейки начертите на плоскости сетку размером 10 x 10 дюймов. Раздвигайте сетку через каждый дюйм, чтобы они совпадали с отметками на осях X и Y. Затем пометьте оси на плоскости «X» и «Y» и пронумеруйте от 1 до 10 (снова считая по мере удаления от исходной точки. Эти цифры должны совпадать с цифрами на осях X и Y бальсовых деревянных осей.
- Вы построили трехмерную систему координат с подвижной плоскостью XY. Чтобы найти точку, сначала найдите нужные координаты X и Y на плоскости XY (традиционный двухмерный график), а затем сдвиньте всю плоскость до указанной координаты Z.

Со студентами
- Разделите класс на группы по три ученика в каждой. Дайте каждой группе набор из трех осей.
- Раздайте рабочий лист, который поможет учащимся выполнить 3D-упражнение.
Словарь/Определения
ось: В математике линия, используемая в качестве ориентира для описания местоположения точки. Например, в декартовой системе координат ось представляет собой линию, отмеченную нулем в определенной точке. Затем местоположение объекта можно описать, измерив, насколько далеко (на линии) он находится от этого начала координат и в каком направлении. Во многих отношениях ось похожа на числовую прямую, которая бесконечно продолжается в обоих направлениях (положительном и отрицательном). Ось является одномерной.
Декартова система координат: прямоугольная система координат, разработанная знаменитым математиком Декартом. Он состоит из 2 или 3 осей (X, Y и Z), расположенных под прямым углом друг к другу и пересекающихся в заданном начале координат.
размерность: Мера особой степени. То, что мы видим вокруг себя, — это трехмерный мир, потому что предметы имеют три измерения: длину, ширину и высоту. Линия находится в одном измерении, площадь (например, прямоугольник, нарисованный на листе бумаги) — в двух измерениях, а прямоугольник (куб) — в трех измерениях.
график: визуальное представление математической функции или набора чисел. В предыдущем определении упорядоченной пары, если поверхность вашего стола представляет собой график, вы нанесли на график точку (2,3), то есть представили эти числа визуально (или графически).
упорядоченная пара: два числа, используемые для описания положения точки на плоскости относительно заданной контрольной точки. Например, если вам сказали, что передний левый угол вашего стола является исходной точкой, и вы хотите найти точку, заданную упорядоченной парой (2, 3), и вы знаете, что используемая вами единица измерения — дюймы, вы начинаете с что передний левый угол вашего стола, сдвиньте на два дюйма вправо, а затем на 3 дюйма к задней части стола, и вы найдете эту точку.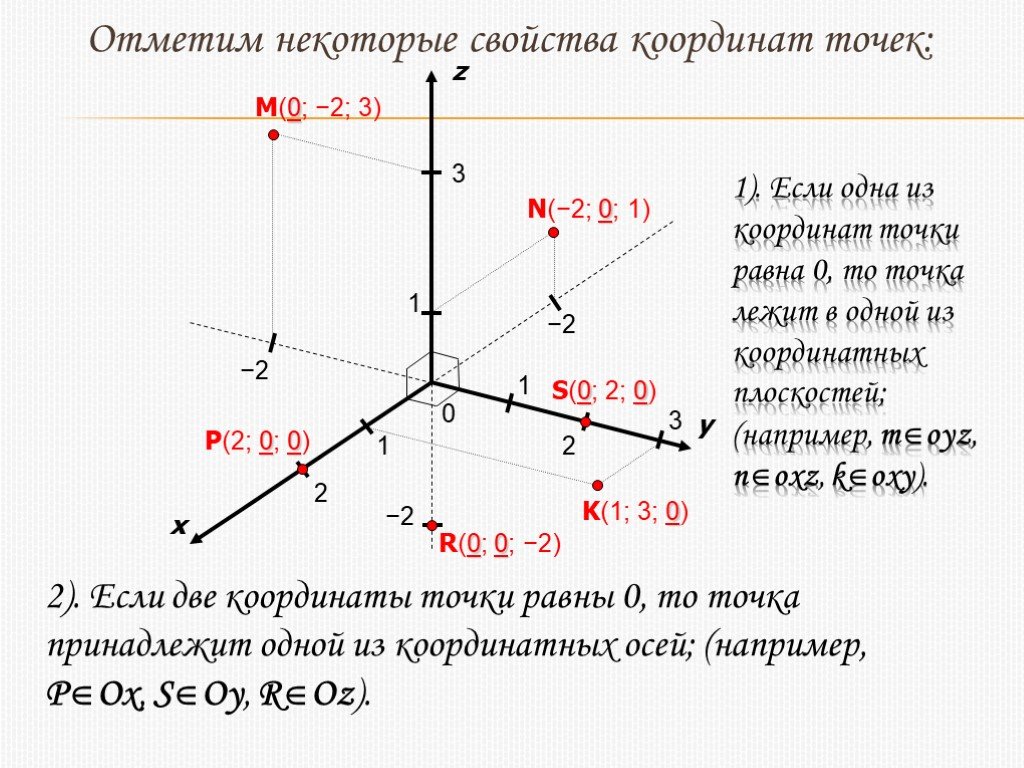
origin : указанная опорная точка [(0,0,0) в большинстве систем координат]
плоскость: множество всех точек между двумя пересекающимися прямыми. Плоскость двухмерна, поэтому это плоская поверхность. Плоскую столешницу, например, можно представить как плоскость.
Оценка
Рабочий лист : Если учащиеся могут удовлетворительно заполнить Рабочий лист 3D-координат практически без помощи учителя или сверстников, то они демонстрируют хорошее понимание основ 3D-графики.
Вопросы безопасности
- Если учащиеся используют канцелярские ножи для резки картона или пенопластовой плиты, тщательно контролируйте их и следите за опасным использованием этих острых инструментов.
- Предупредите учащихся, что клеевые пистолеты и клей сильно нагреваются. Также будьте осторожны с другими клеями и соблюдайте инструкции по безопасности .

Расширения деятельности
Предложите учащимся найти точки для описания фигур, которые сложнее коробки.
Попробуйте нарисовать 3D-оси на листе бумаги. Затем попробуйте нарисовать куб в 3D, расположив точки на осях
.Измените плоскость с плоскости XY на плоскости XZ или YZ, сдвинув ее вниз по другой оси. Точки могут быть расположены таким же образом, и учащиеся узнают, что конкретные буквы и ориентация плоскостей произвольны.
Масштабирование активности
- Предложите менее продвинутым учащимся выполнить только двухмерную часть.
- Чтобы сэкономить время и деньги, создайте только один набор трехмерных осей и представьте упражнение в виде демонстрации класса вместо того, чтобы каждая группа имела свой собственный набор осей.
Авторские права
© 2013 Регенты Университета Колорадо; оригинал © Университет Дьюка, 2004 г.
Авторы
Бен БернхэмПрограмма поддержки
Программа Techtronics, Инженерная школа Пратта, Университет ДьюкаБлагодарности
Этот контент был разработан в рамках программы MUSIC (Понимание математики через науку, интегрированную с учебной программой) Инженерной школы Пратта Университета Дьюка в рамках гранта Национального научного фонда GK-12 №. DGE 0338262. Однако это содержание не обязательно отражает политику NSF, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Последнее изменение: 15 февраля 2018 г.
Программное обеспечение для 3D-графики для инженерии, естественных наук и математики
TeraPlot имеет широкий спектр типов 3D-графиков, большинство из которых могут быть основаны либо на математических выражениях, либо на табличных данных. и все это можно объединить в один график. Например, можно добавить одну или несколько плоскостей, определенных как графики поверхности.
к точечной диаграмме, чтобы сегментировать точки в соответствии с некоторым критерием. Если бы также требовалось пометить определенные точки рассеяния,
можно добавить трехмерный текстовый график для обозначения только необходимых точек. Это всего лишь один пример того, как типы сюжетов могут быть
объединены для создания составных визуализаций. Существует также широкий спектр опций для настройки внешнего вида осей графика, стен и сетки.
В приведенном ниже списке перечислены типы графиков, доступные в графическом программном обеспечении TeraPlot 3D.
Чтобы увидеть пример графика, нажмите значок увеличительного стекла рядом с заголовком графика.
и все это можно объединить в один график. Например, можно добавить одну или несколько плоскостей, определенных как графики поверхности.
к точечной диаграмме, чтобы сегментировать точки в соответствии с некоторым критерием. Если бы также требовалось пометить определенные точки рассеяния,
можно добавить трехмерный текстовый график для обозначения только необходимых точек. Это всего лишь один пример того, как типы сюжетов могут быть
объединены для создания составных визуализаций. Существует также широкий спектр опций для настройки внешнего вида осей графика, стен и сетки.
В приведенном ниже списке перечислены типы графиков, доступные в графическом программном обеспечении TeraPlot 3D.
Чтобы увидеть пример графика, нажмите значок увеличительного стекла рядом с заголовком графика.
Дом
Оценка TeraPlot
TeraPlot — это настольное приложение Microsoft Windows (Windows XP, Vista, Windows 7, Windows 8 и 8. 1). Загрузите полнофункциональную 30-дневную ознакомительную версию..
1). Загрузите полнофункциональную 30-дневную ознакомительную версию..
Поверхностный график — регулярная сетка
Трехмерная поверхность создается путем связывания значения зависимой переменной с каждой точкой.
на сетке с постоянным интервалом в каждом независимом переменном направлении. Сетка может быть декартовой, полярной, цилиндрической или заданной.
по координатам параметрической функции (u, v). График можно определить аналитически, на основе введенных/импортированных табличных данных или на основе
на данные, прочитанные из файла. Цвет поверхности может быть одноцветным или основанным на цветовой карте. По умолчанию цвет палитры
отображаемое зависит от высоты поверхности, но существует возможность использовать произвольное табличное свойство для определения связанного с ним цвета.
с точкой поверхности. Карта текстуры (то есть изображение) может быть дополнительно наложена на поверхность. Дополнительные параметры включают: прозрачность,
отображение контуров, общее 3D-преобразование, отображение каркаса, функции, которые часто можно найти только в более дорогом программном обеспечении для 3D-графики.
Дополнительные параметры включают: прозрачность,
отображение контуров, общее 3D-преобразование, отображение каркаса, функции, которые часто можно найти только в более дорогом программном обеспечении для 3D-графики.
Поверхностный график — нерегулярные данные
Трехмерная поверхность создается путем связывания значения зависимой переменной с каждым из набора
точек, произвольно расположенных в плоскости независимой переменной. График может быть определен аналитически или на основе введенных/импортированных данных.
табличные данные. Цвет поверхности может быть одноцветным или основанным на цветовой карте. По умолчанию отображаемый цвет палитры зависит
по высоте поверхности, но существует возможность использовать произвольное табличное свойство для определения цвета, связанного с точкой поверхности.
Дополнительные параметры включают: прозрачность, общее трехмерное преобразование, отображение каркаса.
Точечная диаграмма
Рисует символ в каждой из множества точек в трехмерном пространстве. Точки могут быть определены в декартовой, полярной или цилиндрическая система координат. Программное обеспечение для построения трехмерных графиков TeraPlot также позволяет связать до двух дополнительных переменных с каждым разбросом. точка. Затем их можно визуализировать с помощью цвета и/или размера точки рассеяния.
Участок изоповерхности
Рисует поверхности постоянной w для функций вида w = f(x, y, z), т. е. трехмерный эквивалент контурных графиков.
Данные, из которых генерируются изоповерхности, могут быть определены как формула (аналитический график) или загружены из файла. Для аналитического сюжета
предполагается, что данные лежат на регулярной прямоугольной трехмерной сетке. Для данных, загруженных из файла, данные могут либо лежать на регулярной сетке, либо
могут быть указаны произвольные отдельные ячейки.
Стержни — Регулярная сетка
Рисует полосу высотой z в каждой точке графика (x,y). Точки должны лежать на прямоугольная сетка с постоянным интервалом в направлениях x и y.
Бары — нерегулярные данные
Рисует полосу высотой z в каждой из точек (x,y) заданной кривой. Точки могут быть произвольными расположен в плоскости (х, у).
СерияСюжет
Соединяет точки (x, y, z) на графике прямыми линиями, чтобы сформировать ряд (x, z) или (y, z) подкривые. Существует возможность дополнительно рисовать вертикальный лист на каждой подкривой, чтобы получить график «водопад». Точки ограничено лежать на прямоугольной сетке с постоянным интервалом в направлениях x и y.
3D линия
Соединяет набор точек в трехмерном пространстве прямыми линиями. Точки могут быть определены в декартовой, полярной
(тета, фи или широта, долгота) или цилиндрическая система координат.
Точки могут быть определены в декартовой, полярной
(тета, фи или широта, долгота) или цилиндрическая система координат.
Каркасный график
Трехмерная прозрачная каркасная поверхность создается путем связывания значения зависимой переменной с каждой точкой на сетка с постоянным интервалом в каждом независимом переменном направлении. Сетка может быть декартовой, полярной, цилиндрической или заданной неявным образом. координаты функции (u, v).
Объект Участок
Рисует набор 3D-объектов предопределенных типов. Текущие типы объектов включают сферу, куб и цилиндр. объекты описываются языком описания объектов TeraPlot (GODL). Описание можно загрузить из файла или ввести в интерактивном режиме.
Сетка
Рисует общую 3D-сетку, определяемую как набор вершин и элементов, считанных из файла с данными, отформатированными в TeraPlot.


 Аналогично с помощью точки А2определяется вторая координата (ордината) y точки А, а с помощью точки А3 третья координата (аппликата) z точки А. Координаты точки А записываются в скобках после обозначения точки: А (х; у; z), причем первой указывают абсциссу, второй ординату, третьей — аппликату.
Аналогично с помощью точки А2определяется вторая координата (ордината) y точки А, а с помощью точки А3 третья координата (аппликата) z точки А. Координаты точки А записываются в скобках после обозначения точки: А (х; у; z), причем первой указывают абсциссу, второй ординату, третьей — аппликату. Распечатай, выполни предложенные задания, отсканируй и отошли учителю
Распечатай, выполни предложенные задания, отсканируй и отошли учителю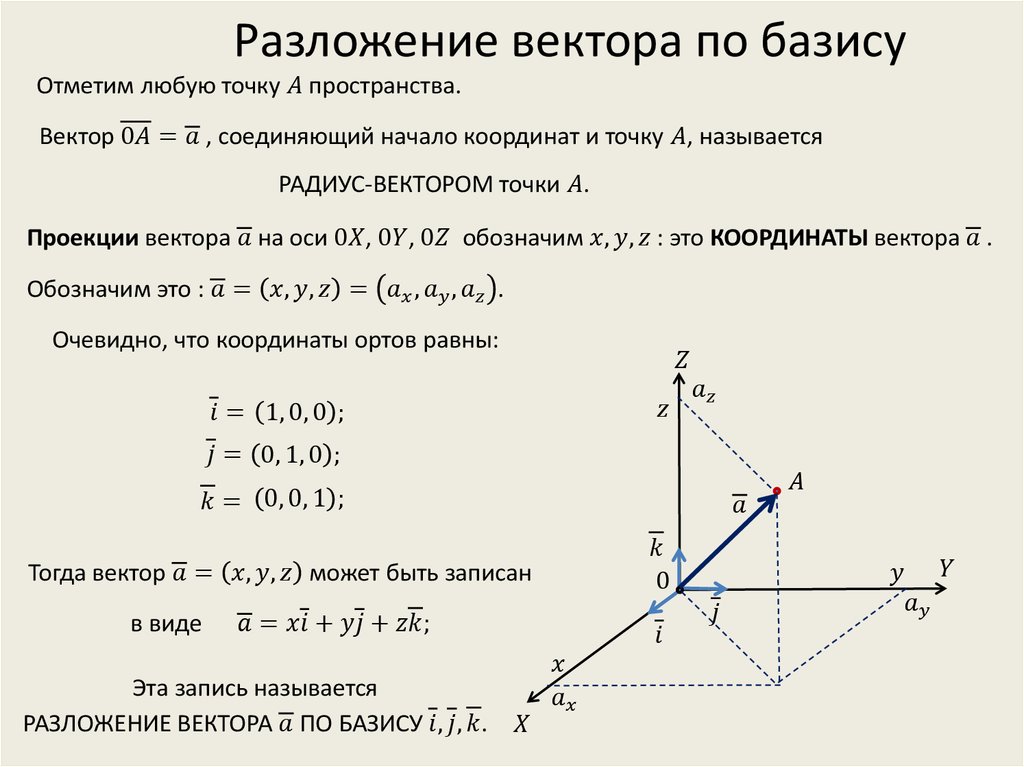 Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
(Оценка
6) Подробнее
Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.
(Оценка
6) Подробнее (Оценка
7) Подробнее
(Оценка
7) Подробнее д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
(Оценки
9-
12) Подробнее
д.). Копирование сегмента; копирование угла; разделение сегмента пополам; деление угла пополам; построение перпендикулярных линий, включая перпендикулярную биссектрису отрезка прямой; и построение прямой, параллельной заданной прямой, через точку, не лежащую на этой прямой.
(Оценки
9-
12) Подробнее (Оценки
6 —
8) Подробнее
(Оценки
6 —
8) Подробнее Сделайте небольшое отверстие в одном углу квадрата, примерно на полдюйма от краев. Сделайте отверстие достаточно большим, чтобы ось из пробкового дерева прошла через него.
Сделайте небольшое отверстие в одном углу квадрата, примерно на полдюйма от краев. Сделайте отверстие достаточно большим, чтобы ось из пробкового дерева прошла через него.