№1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; | №1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; | №1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; | №1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; |
№2. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; | №2. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; | №2. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; | №2. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; |
№3. Исследовать функцию, при помощи производной простроить график. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; | №3. Исследовать функцию, при помощи производной простроить график. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; | №3. Исследовать функцию, при помощи производной простроить график. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; | №3. Исследовать функцию, при помощи производной простроить график. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; |
№4. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 + х2 – 3х – 9; 2) у = х2 + 2х – 3; | №4. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 + х2 – 3х – 9; 2) у = х2 + 2х – 3; | №4. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 + х2 – 3х – 9; 2) у = х2 + 2х – 3; | №4. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 + х2 – 3х – 9; 2) у = х2 + 2х – 3; |
№5. Исследовать функцию, при помощи производной простроить график. 1)у = — х4 + 6х2 – 9; 2)у = — 4х3 + 12х; | №5. Исследовать функцию, при помощи производной простроить график. 1)у = — х4 + 6х2 – 9; 2)у = — 4х3 + 12х; | №5. Исследовать функцию, при помощи производной простроить график. 1)у = — х4 + 6х2 – 9; 2)у = — 4х3 + 12х; | №5. 1)у = — х4 + 6х2 – 9; 2)у = — 4х3 + 12х; |
№6. Исследовать функцию, при помощи производной простроить график. 1)у = — х4 + 4х2 – 5; 2)у = — 4х3 + 8х; | №6. Исследовать функцию, при помощи производной простроить график. 1)у = — х4 + 4х2 – 5; 2)у = — 4х3 + 8х; | №6. Исследовать функцию, при помощи производной простроить график. 1)у = — х4 + 4х2 – 5; 2)у = — 4х3 + 8х; | №6. Исследовать функцию, при помощи производной простроить график. 1)у = — х4 + 4х2 – 5; 2)у = — 4х3 + 8х; |
№1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; | №1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; | №1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; | №1. Исследовать функцию, при помощи производной простроить график. 1) у = х4 – 1; 2) у = 4х3; |
№2. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; | №2. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; | №2. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; | №2. Исследовать функцию, при помощи производной простроить график. 1)у = 1\3х3 – х2 – 3х +9; 2) у = х2 – 2х – 3; |
№3. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; | №3. Исследовать функцию, при помощи производной простроить график. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; | №3. Исследовать функцию, при помощи производной простроить график. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; | №3. Исследовать функцию, при помощи производной простроить график. 1) у = 1\4х4 – 2х2 + 7\4; 2) у = х3 – 4х; |
Главная → Видеоуроки → Алгебра. 9 класс. Функции и их свойства. Описание видеоурока: Исследовать функцию и построить график. Нахождение области определения функции. Исследование функции на четность и нечетность. Непрерывность функции и точки разрыва. Отыскание вертикальных, горизонтальных и наклонных асимптот. Валерий Волков 5 12.05.2018 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Как построить график функции (видео и практические вопросы)
Привет! Добро пожаловать в это видео о построении графиков функций! Сегодня я покажу вам, как построить график функции. В частности, мы сосредоточимся на понятии наклона , которое определяет, как функция будет принимать форму, когда мы начертим ее график.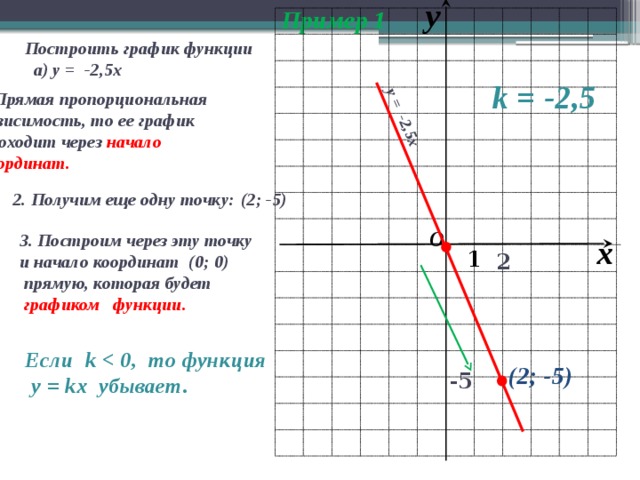 Мы также обсудим отношения между наклонами перпендикулярных и параллельных линий. Давайте начнем!
Мы также обсудим отношения между наклонами перпендикулярных и параллельных линий. Давайте начнем!
Во-первых, краткое напоминание о линейных функциях. Как вы, наверное, догадались по названию, график линейной функции представляет собой прямую линию на 9-м графике.0003 Декартова плоскость . Линия представляет каждую точку на плоскости, которая удовлетворяет линейному уравнению. Каждая точка может быть выражена в виде упорядоченной пары (x,y), которая представляет единицы по оси x и единицы по оси y. Наклон линии определяется путем измерения расстояния по вертикали между значениями y любых двух точек на линии и деления на расстояние по горизонтали, определяемое значениями x этих точек.
Давайте на минутку применим эту информацию к нескольким примерам.
Определите наклон линии, проходящей через точки (3,7) и (6,3).
Вертикальное расстояние, иногда называемое «изменением y» или «подъемом», рассчитывается путем вычитания значений y этих двух точек: 7-3=4
Горизонтальное расстояние известно как «изменение in x» или «run» и рассчитывается путем вычитания значений x: 3-6= -3
Обратите внимание, что вычитание должно быть согласованным! Мы вычли обе координаты точки G из координат точки F.
Таким образом, наклон этой линии равен \(\frac{change\; in\; y}{change \;in\; x}\) или \(\frac{-4}{3}\) . Важно отметить, что отрицательный наклон указывает, что линия наклонена вниз слева направо.
Давайте посмотрим на другой пример.
Вычислите наклон линии, проходящей через точки (1,1) и (4,3):
Шаг 1: Вычислите изменение y
3-1=2
Шаг 2: Вычислите изменение в х
4-1=3
Шаг 3: Рассчитайте наклон, разделив изменение y на изменение x.
\(Уклон=\фракция{2}{3}\). Линия с положительным наклоном будет наклонена вверх слева направо.
Умение анализировать график и знание характеристик уклона являются важными навыками.
Существуют два особых типа линий, которые не подчиняются указанным выше правилам в отношении наклона вверх или вниз в зависимости от знака их наклона.
Вот еще пример:
Вычислить наклон линии, проходящей через точки (5, 3) и (-2,3).
На этот раз, когда мы определяем вертикальное изменение или изменение y, мы получаем ответ 3-3=0
Интуитивно это имеет смысл, потому что координаты y не изменяются от одной точки к другой.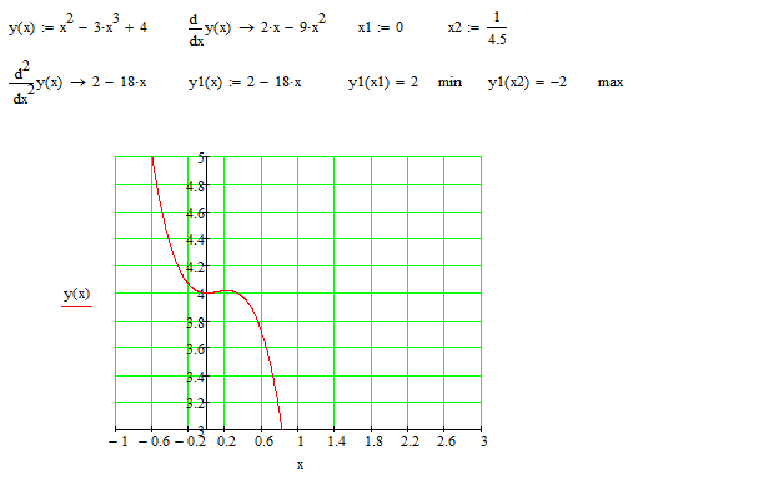 другой. Произошло изменение x; однако деление 0 на любое значение дает 0.
другой. Произошло изменение x; однако деление 0 на любое значение дает 0.
Таким образом, наклон этой линии равен \(\frac{0}{-2-5}=\frac{0}{-7}=0\)
Это верно для любых горизонтальная линия , существующая на координатной плоскости. Эти уравнения записываются в виде y=c, где c — любое значение по оси y. Соответственно, линия, показанная справа, равна y=3.
Некоторые люди считают полезным визуализировать горизонтальную линию с уклоном, который не «поднимается», а «бежит» вечно.
Рассуждая аналогичным образом, давайте исследуем характер наклона точек, лежащих на вертикальной линии.
Определите наклон линии, проходящей через точки (2,5) и (2,-1).
Просто взглянув на эти точки, мы увидим, что значения x не изменились, поэтому знаменатель при расчете наклона будет равен 0.
Наклон для этой линии рассчитывается следующим образом: \(\frac{- 1-5}{2-2}=-60\).
Возможно, вы помните, что деление на ноль «не определено». Вертикальные линии записываются в виде x=c, где c — любое значение по оси x.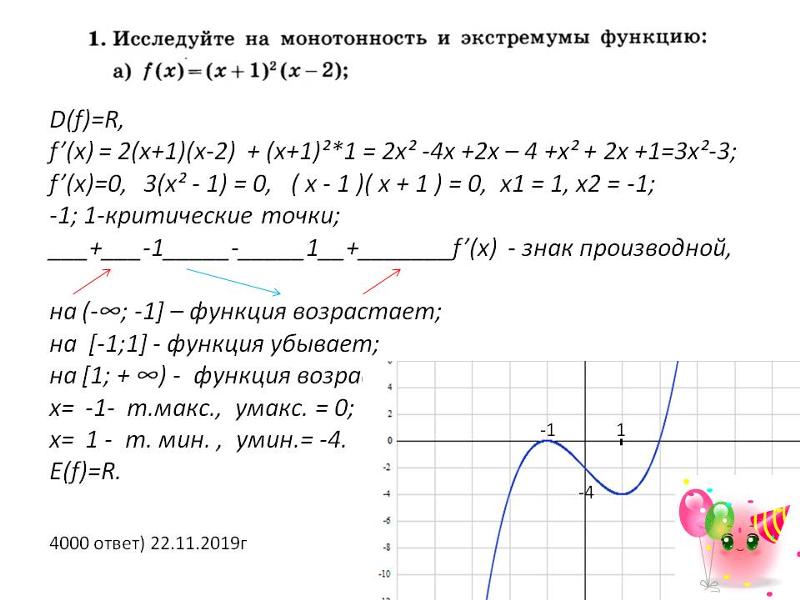 Эта строка записывается как x=2.
Эта строка записывается как x=2.
Обратите внимание, что вертикальные линии не имеют наклона, поскольку они не «наклоняются» ни в одном направлении. Эти линии «поднимаются» вечно, но не «бегут».
Для следующих графиков укажите, является ли наклон линии положительным, отрицательным, нулевым или неопределенным.
Пример 1:
Ответ: Положительный наклон
Линия имеет наклон вверх слева направо.
Пример 2:
Ответ: Наклон «не определен»
Все вертикальные линии имеют неопределенный наклон.
Пример 3:
Ответ: Наклон равен 0
Все горизонтальные линии имеют наклон=0.
Пример 4:
Ответ: Наклон отрицательный.
Линия наклонена вниз слева направо.
При построении графика линейной функции очень важен наклон. Если у нас есть одна точка и наш наклон, мы можем найти любую другую точку на линии и посмотреть, как выглядит линия. Мы только что узнали, что в нашей форме линейного уравнения с пересечением наклона, y=mx+b, буква m представляет наш наклон. Помните, что буквы x и y представляют координаты x и y любой точки, удовлетворяющей нашему уравнению. Теперь единственное, о чем нам осталось поговорить в нашем уравнении, это буква b.
Помните, что буквы x и y представляют координаты x и y любой точки, удовлетворяющей нашему уравнению. Теперь единственное, о чем нам осталось поговорить в нашем уравнении, это буква b.
B в нашей форме пересечения наклона представляет точку пересечения y уравнения. Точка пересечения с осью Y — это точка пересечения графика с осью Y, или где x=0. Таким образом, y-перехват дает нам точку, которая нам нужна, чтобы выяснить наш график. Точка будет (0,b) для любого числа в позиции b.
Давайте рассмотрим пример. Каковы наклон и y-пересечение уравнения y = ½ x + 7?
Наш наклон — это значение m, поэтому для этого уравнения наклон равен ½ .
Мы определяем точку пересечения по оси y, глядя на значение b, которое в данном случае равно 7. Помните, что это число дает нам координату по оси y для нашей точки, где x = 0. Таким образом, точка пересечения по оси y в этом уравнении равна (0 , 7).
Теперь, когда мы знаем, как определить наклон и точку пересечения по оси Y, давайте посмотрим, как мы можем использовать эти две вещи для построения графика нашего уравнения.
Наш первый шаг — определить точку пересечения по оси y. Для нашего уравнения выше мы уже сделали это. Наш y-перехват равен (0, 7).
Второй шаг — нанести эту точку на наш график. Итак, мы поместим точку в (0, 7).
Теперь мы хотим посмотреть на наш наклон, который мы нашли ранее равным ½. Помните, наклон — это отношение нашего изменения y к нашему изменению x или нашего подъема к пробегу.
В-четвертых, мы собираемся использовать наш наклон, чтобы найти другую точку на линии. Начните с точки пересечения y и двигайтесь вверх (или вверх) на одну и двигайтесь вправо (или бегите) на две, и поместите здесь еще одну точку.
Поскольку у нас есть две точки, мы можем провести прямую линию. Итак, наш последний шаг — провести прямую линию между двумя точками, обязательно поставив стрелки на обоих концах линии, чтобы указать, что она продолжается вечно в любом направлении.
И это так просто! Давайте попробуем другой пример, следуя шагам, которые мы видели выше.
Нарисуйте график уравнения y = 2x -4.
Шаг 1: Определите точку пересечения оси Y. Наше значение b в этом уравнении отрицательно, поэтому точка пересечения по оси y также будет отрицательной. (0, -4).
Шаг 2: Нанесите точку пересечения оси Y на график.
Шаг 3: Определите уклон. Помните, что наклон — это наше m-значение, поэтому в данном случае оно равно 2.
Шаг 4: Используйте наклон для построения второй точки. Когда нам дано целое число, мы можем превратить его в дробь, поместив над 1. Это не изменит значение числа, потому что любое число, деленное на 1, есть само. Итак, наш наклон теперь выглядит как 2/1. Это означает, что из нашего y-перехвата мы собираемся подняться на 2 значения и выполнить 1.
Шаг 5: Проведите линию между двумя точками.
Я хочу, чтобы вы попробовали еще один. На этот раз попробуй сделать это без моей помощи.
Нарисуйте линию y = -2/3x +1.
[пауза]
Думаешь, у тебя получилось? Давайте пройдёмся по нему вместе.
Наша точка пересечения по оси y находится в точке (0, 1), поэтому сначала мы нанесем ее на график.
Теперь смотрим на наш склон, -2/3. Это говорит нам о том, что мы собираемся пройти 3 места и опуститься на 2. Мы идем вниз, а не вверх, потому что наш наклон отрицателен.
Теперь, когда у нас есть две точки, мы проводим через них линию и добавляем стрелки.
Прежде чем мы пойдем, я хочу еще кое-что узнать о склонах, которые полезно знать.
Есть еще два очень важных типа линий, которые имеют особые соотношения наклона. Рассмотрим следующие графики:
Эти линии имеют особое отношение, будучи равноудаленными или параллельными. Это означает, что они находятся на одинаковом расстоянии друг от друга для каждого значения как с положительной, так и с отрицательной стороны оси x. Как мы уже говорили, наклон определяет «наклон» линии, и ясно, что равноудаленные линии имеют одинаковый наклон.
Другими словами, параллельные прямые имеют одинаковый наклон.
Уравнения в форме пересечения наклона для этих линий: \(y=\frac{2}{3}x-1\) и \(y=\frac{2}{3}x+2\)
Наклон 23 четко различим в обоих уравнениях. Если даны два уравнения, прямые параллельны, если наклоны одинаковы.
Если даны два уравнения, прямые параллельны, если наклоны одинаковы.
На этом графике показаны две линии, особенностью которых является то, что они пересекаются под прямым углом. В результате эти линии считаются перпендикулярными.
Уравнения для этих линий:
\(y=3x-1\) и \(y= \frac{-1}{3}x-2\)
Опять же, кажется, что существует связь между наклонами, \(m=3\ ) и \(m= \frac{-1}{3}\). Есть предположения?
На самом деле между этими значениями наклона есть два явных различия.
Знаки противоположны: наклон одной линии положительный, а наклон другой отрицательный.
Значения наклона являются обратными, что означает, что числитель и знаменатель «перевернуты».
Если эти два изменения распознаются в наклонах двух линейных уравнений, то линии, которые они представляют, перпендикулярны.
Давайте попрактикуемся в этой информации. Посмотрите, сможете ли вы самостоятельно ответить на эти вопросы:
Пример 1
Каков наклон линии, параллельной \(y=\frac{5}{7}x-2\)?
Ответ: Наклон этой параллельной линии равен \(\frac{5}{7}\). Помните, параллельные прямые имеют одинаковый наклон.
Помните, параллельные прямые имеют одинаковый наклон.
Пример 2
Каков наклон линии, перпендикулярной \(y=\frac{2}{5}x+1\)
Ответ: Наклон этой перпендикулярной линии равен \(\ дробь{-5}{2}\). Помните, что перпендикулярные линии имеют наклоны, противоположные обратным.
Пример 3
Укажите, являются ли линии параллельными, перпендикулярными или ни тем, ни другим:
\(y=3x+4\) и \(y= \frac{-1}{3}x-8\)
Ответ: Перпендикуляр. Наклоны являются противоположными обратными.
Пример 4: Попробуйте то же самое для строк здесь:
\(y= -x+5\) и \(y=\frac{1}{2}x+2\)
Ответ: Ни то, ни другое.
Наклоны не одинаковы и наклоны не являются противоположными обратными величинами.
Эти линии пересекаются, но НЕ под прямым углом.
И еще один:
\(y=x+2\) и \(y=x-5\)
Ответ: Параллельно. Оба наклона равны 1.
Надеюсь, я развеял все недоразумения, которые могли возникнуть у вас в отношении наклона и графических линейных уравнений. Как видите, наклон является движущей силой построения графиков и является ключом к определению особых отношений между линиями.
Как видите, наклон является движущей силой построения графиков и является ключом к определению особых отношений между линиями.
На этом обзоре все! Спасибо за просмотр и удачной учебы!
Вопрос №1:
Какая прямая параллельна прямой, проходящей через точки \((3,-1)\) и \((-2,4)\)?
\(y=-x-5\)
\(y=x+5\)
\(y=-5x-1\)
\(y=5x+1\)
Показать ответ
Ответ:
Так как параллельные прямые имеют одинаковый наклон, первым шагом будет найти наклон прямой, проходящей через точки \((3,-1)\) и \((-2,4) \). Формула наклона: \(\frac{\text{Изменение} y}{\text{Изменение} x}\). Изменение в y равно \(4-(-1)=5\), а изменение x равно \(-2-3=-5\). Следовательно, наклон линии, проходящей через точки, равен \(\frac{5}{-5}=-1\), а наклон линии \(y=-x–5\) также равен -1.
Скрыть ответ
Вопрос № 2:
Что верно в отношении наклона прямой, проходящей через точки \((-2,3)\) и \((4,3)\)?
Положительный наклон
Отрицательный наклон
Нулевой наклон
Неопределенный наклон
Показать Ответ
Ответ:
График горизонтальной линии имеет нулевой наклон. Есть два способа найти решение этой проблемы. Первый способ состоит в том, чтобы построить линию, которая образует горизонтальную линию, из которой можно сделать вывод, что наклон равен нулю. Второй способ — использовать формулу наклона, которая имеет вид \(\frac{\text{Изменение} y}{\text{Изменение} x}\). Изменение y равно \(3-3=0\), а изменение x равно \(4-(-2)=4+2=6\). Дробь с нулем в числителе равна нулю, наклон прямой.
Есть два способа найти решение этой проблемы. Первый способ состоит в том, чтобы построить линию, которая образует горизонтальную линию, из которой можно сделать вывод, что наклон равен нулю. Второй способ — использовать формулу наклона, которая имеет вид \(\frac{\text{Изменение} y}{\text{Изменение} x}\). Изменение y равно \(3-3=0\), а изменение x равно \(4-(-2)=4+2=6\). Дробь с нулем в числителе равна нулю, наклон прямой.
Скрыть ответ
Вопрос №3:
Каковы наклон и y -пересечение прямой, представленной уравнением \(y=3x–9\)?
Наклон -3, y -Интерцепция -9
Наклон -3, y -интерцепт -9 0005
Наклон — y -Intercept -3
наклон —9, y 11111111100005
—9, Y 111111111111111111111111111111111111111111111111111111111111111111н. -intercept is 3
Показать ответ
Ответ:
Уравнение прямой записывается в форме наклона-пересечения, то есть \(y=mx+b\), где м — уклон, б — y — точка пересечения.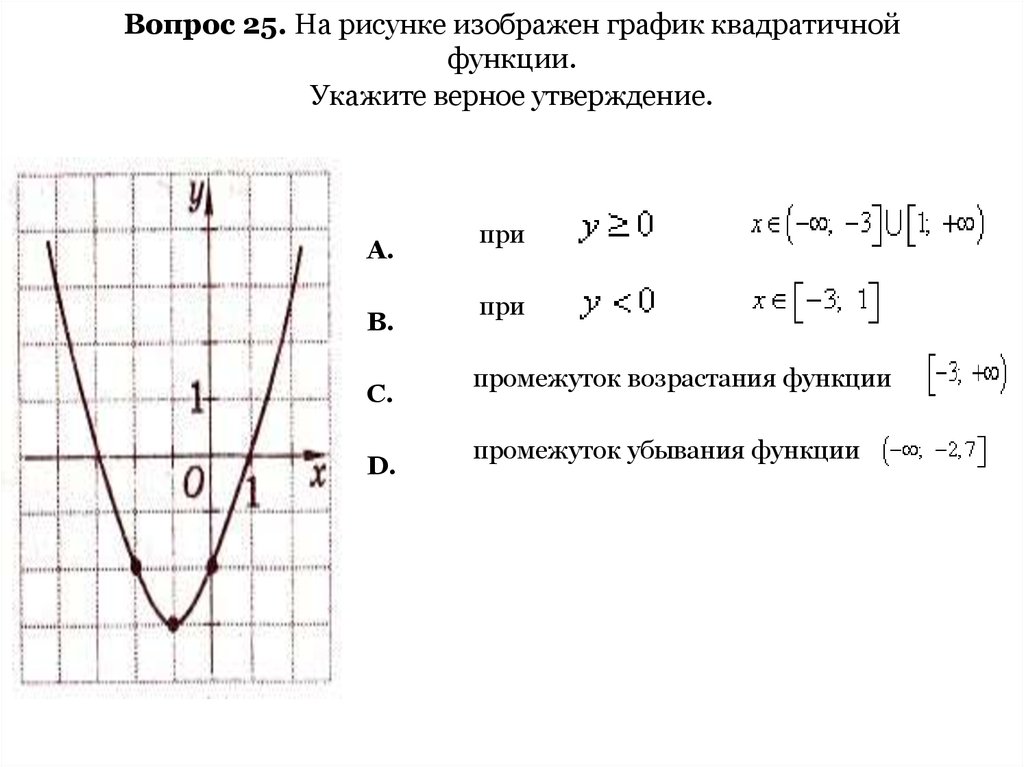 Следовательно, наклон линии равен 3, а точка пересечения и равна -9.
Следовательно, наклон линии равен 3, а точка пересечения и равна -9.
Скрыть ответ
Вопрос №4:
Показан график линии.
Какое уравнение представляет собой график прямой?
\(y=-2x-2\)
\(y=-2x+2\)
\(y=-\frac{1}{2}x-2\)
\(y= -\frac{1}{2}x+2\)
Показать ответ
Ответ:
Чтобы найти наклон линии, мы можем использовать две точки на линии и применить формулу наклона, \(\frac{\text{Изменение} y}{\text{Изменение} x }\) или посчитайте подъем и бег по графику между двумя точками, как показано ниже. Линия идет вниз на 2 и вправо на 1, что означает, что она имеет наклон -2. Чтобы найти точку пересечения линии y , мы можем либо посмотреть, где график пересекает ось y , либо подставить точку на линии в форму уравнения наклона и точки пересечения с наклоном и решить для б .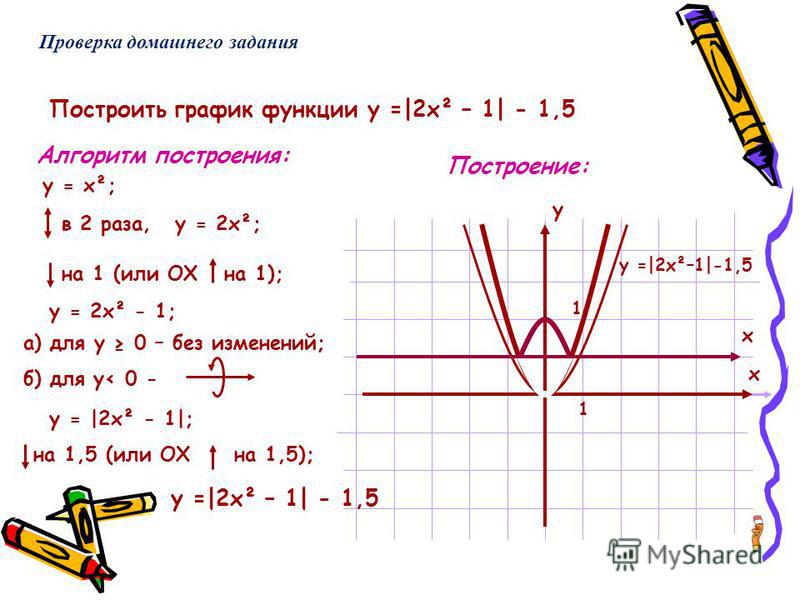 Линия достигает оси y в точке \(y=-2\), поэтому точка пересечения y равна -2.
Линия достигает оси y в точке \(y=-2\), поэтому точка пересечения y равна -2.
Скрыть ответ
Вопрос № 5:
Наклон линии равен \(\frac{3}{5}\) и проходит через точку \((0,-4)\). Что такое уравнение прямой?
\(y=-\frac{3}{5}x+4\)
\(y=-\frac{3}{5}x-4\)
\(y=\frac{3 {5}x+4\)
\(y=\frac{3}{5}x-4\)
Показать ответ
Ответ:
Уравнение прямой, записанное в виде точки пересечения, \(y=mx+b\), показывает наклон, м , а y — точку пересечения, b . В задаче говорится, что наклон равен \(\frac{3}{5}\), и, если мы помним, точка, где значение x равно 0, находится на оси y . Следовательно, если прямая проходит через точку \((0,-4)\), она должна быть точкой пересечения y линии.
Скрыть ответ
Какие существуют типы разрывов? Объяснение с помощью графиков, примеров и интерактивного руководства
$$ \definecolor{importantColor}{RGB}{255,0,0} \definecolor{secondaryColor}{RGB}{255,0,255} $$
Краткий обзор
- Разрывы можно классифицировать как прыжок , бесконечный , съемный , конечная точка или смешанный .
- Устранимые разрывы характеризуются тем, что предел существует.
- Устранимые разрывы можно «исправить», переопределив функцию.
- Остальные типы разрывов характеризуются тем, что предела не существует. Конкретно,
- Разрывы перехода: оба односторонних предела существуют, но имеют разные значения.
- Бесконечные разрывы: оба односторонних предела бесконечны.
 +} f (x) = M}.
$$
+} f (x) = M}.
$$Функция приближается к разным значениям в зависимости от направления, откуда исходит $$x$$. Когда это происходит, мы говорим, что функция имеет разрыв скачков в точке $$x=a$$.
Бесконечные разрывы
На приведенном ниже графике показана функция, разрывная в точке $$x=a$$.
Стрелки на функции указывают на то, что она будет бесконечно увеличиваться по мере того, как $$x$$ приближается к $$a$$. Поскольку функция не приближается к определенному конечному значению, предела не существует. это бесконечный разрыв .
Следующие два графика также являются примерами бесконечных разрывов в точке $$x = a$$. Обратите внимание, что во всех трех случаях оба односторонних предела бесконечны.
Съемные разрывы
На приведенных ниже графиках в функции есть дыра в точке $$x=a$$. Эти отверстия называются
съемными разрывамиОбратите внимание, что для обоих графиков, даже если в точке $$x = a$$ есть дыры, существует предельное значение в точке $$x=a$$.
 92-4}$$
92-4}$$Решение
График функции показан ниже для справки.
Чтобы исправить разрыв, нам нужно знать $$y$$-значение дыры в графе. Чтобы определить это, мы находим значение $$\lim\limits_{x\to 2} f(x)$$.
Рассматривая форму предела, мы видим 92-4} = \фракция 0 0$$
Деление на ноль в форме $$\frac 0 0$$ говорит нам о том, что в этой точке определенно имеется разрыв.
Затем, используя методы, описанные в предыдущих уроках (см. Неопределенные пределы — Факторизуемые), мы можем легко определить
$$\displaystyle\lim_{x\to 2} f(x) = \frac 1 2$$
Предельное значение также является $$y$$-значением дыры в графе.
 Теперь мы можем переопределить исходную функцию в кусочной форме:
92-4}, & \mbox{для всех } x \neq 2\\[6pt]
%
\frac 1 2, & \mbox{для } x = 2
\конец{массив}
\верно.
\\
$$
Теперь мы можем переопределить исходную функцию в кусочной форме:
92-4}, & \mbox{для всех } x \neq 2\\[6pt]
%
\frac 1 2, & \mbox{для } x = 2
\конец{массив}
\верно.
\\
$$Первая часть сохраняет общее поведение функции, а вторая часть затыкает дыру.
Разрывы конечной точки
Когда функция определена на интервале с закрытой конечной точкой, ограничение не может существовать в этой конечной точке. Это связано с тем, что предел должен проверять значения функции при приближении $$x$$ с обеих сторон.
Например, попробуйте найти $$\displaystyle\lim\limits_{x\to0} \sqrt x$$ (см. график ниже).
Обратите внимание, что $$x=0$$ — это левая конечная точка области определения функций: $$[0,\infty)$$, и функция там технически не непрерывна, поскольку предела не существует (поскольку $$x $$ не может подойти с обеих сторон).


 Исследовать функцию, при помощи производной простроить график.
Исследовать функцию, при помощи производной простроить график.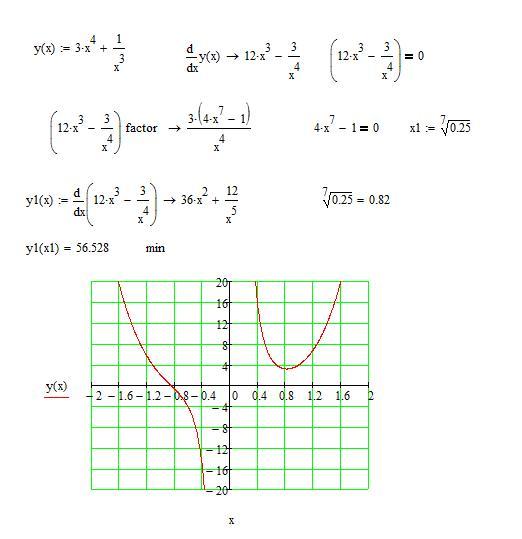
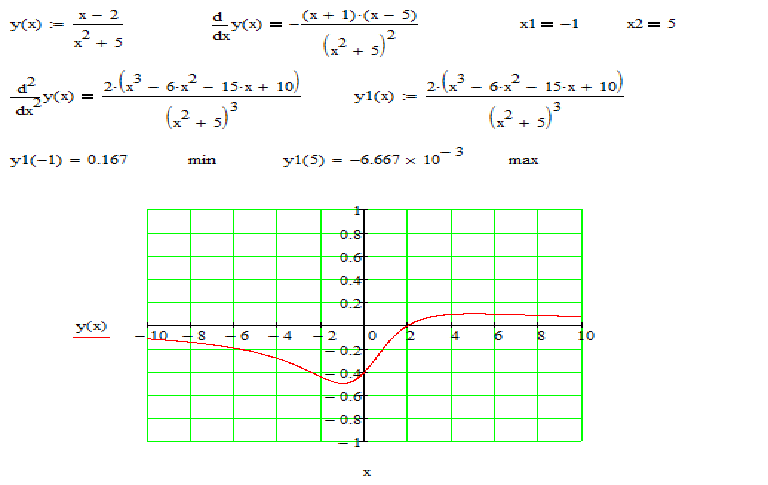 Исследовать функцию, при помощи производной простроить график.
Исследовать функцию, при помощи производной простроить график.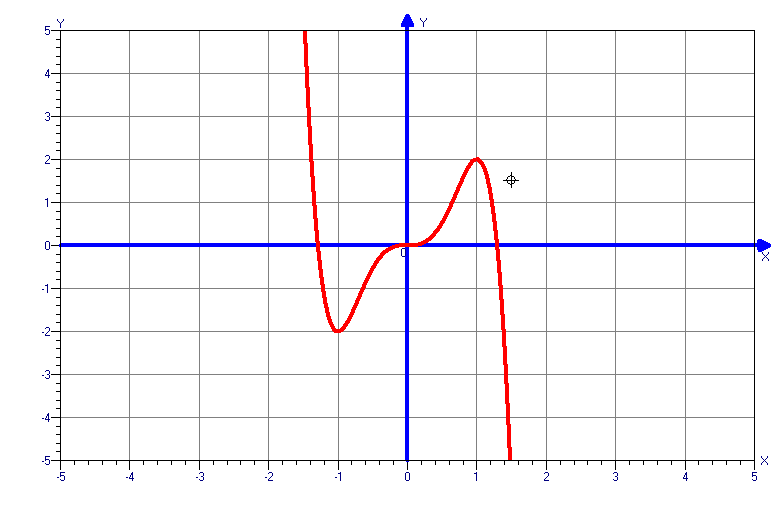
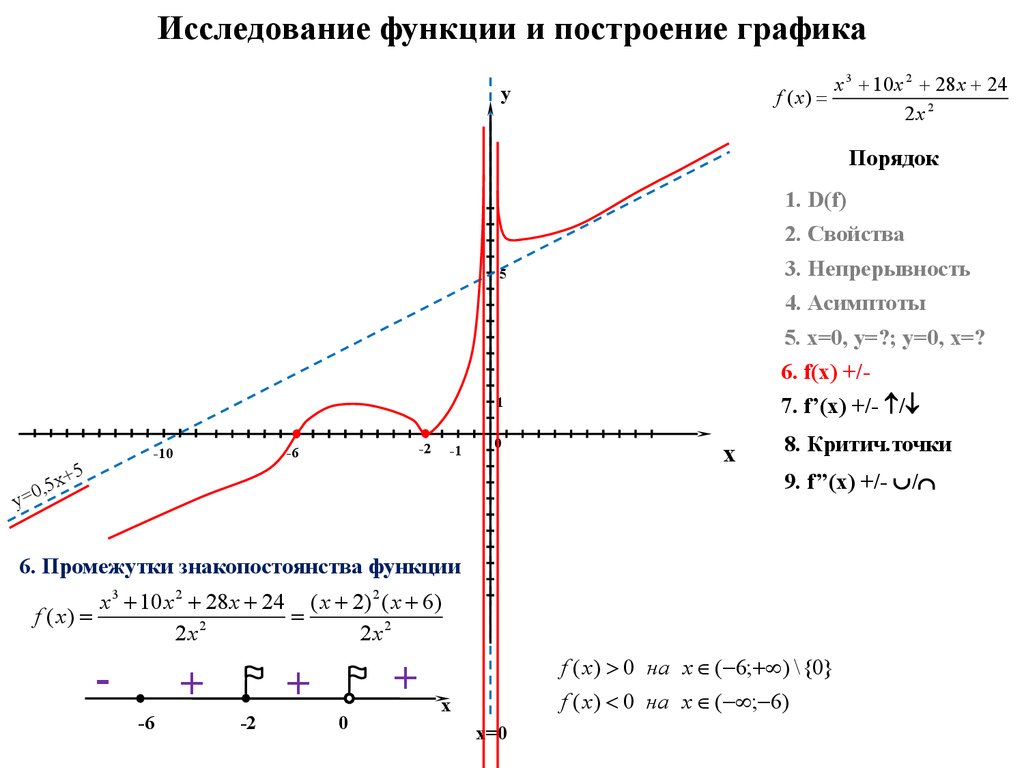 Исследовать функцию, при помощи производной простроить график.
Исследовать функцию, при помощи производной простроить график.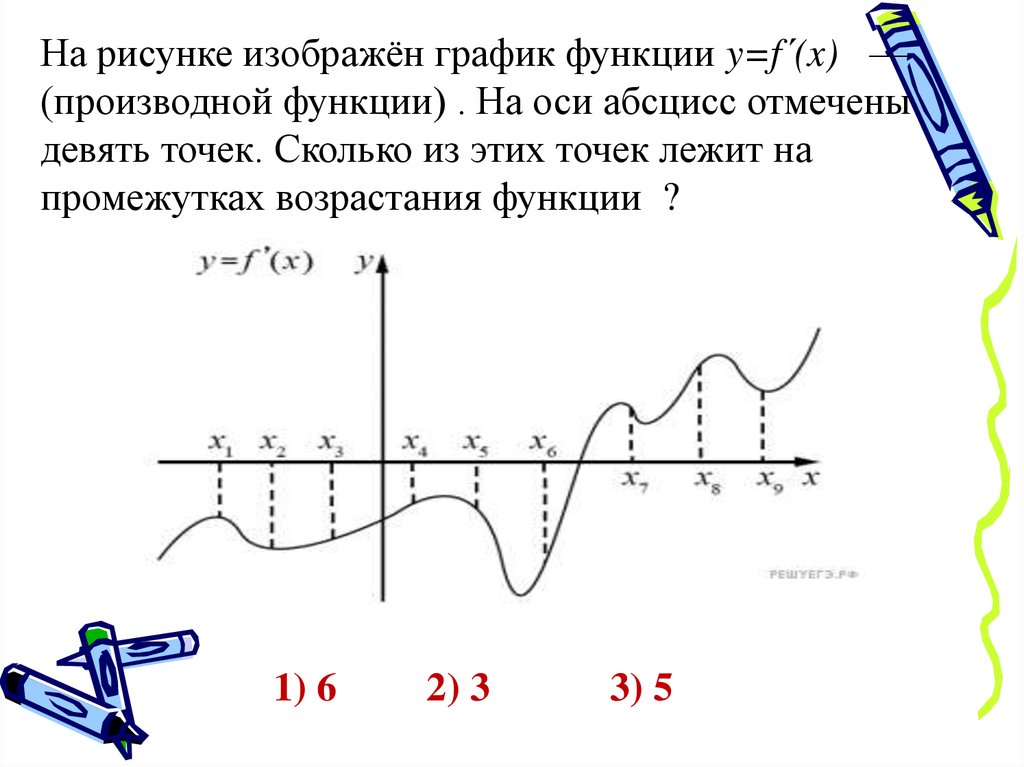 Нахождение экстремумов и интервалов монотонности функции. Нахождение интервалов выпуклости (вогнутости) вверх и вниз графика функции и точек перегиба. Нахождение точек пересечения графика функции с осями координат и интервалов знакопостоянства функции. Построение графика функции.
Нахождение экстремумов и интервалов монотонности функции. Нахождение интервалов выпуклости (вогнутости) вверх и вниз графика функции и точек перегиба. Нахождение точек пересечения графика функции с осями координат и интервалов знакопостоянства функции. Построение графика функции.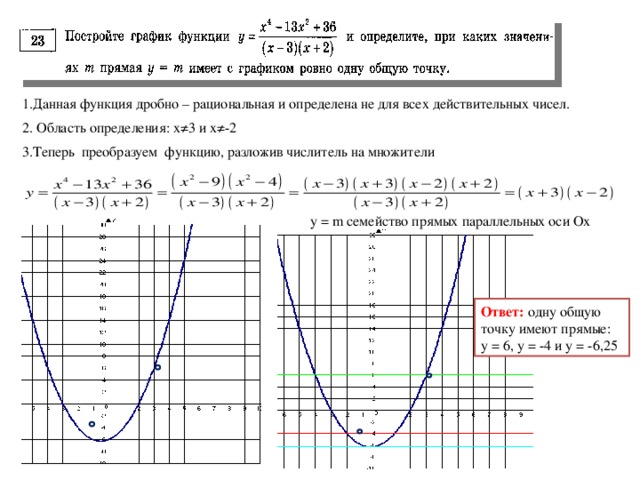
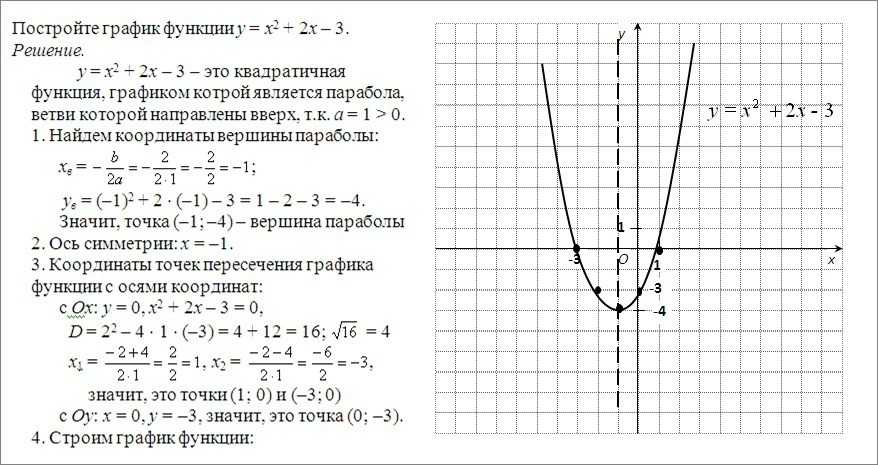 10 — 11 класс.
10 — 11 класс.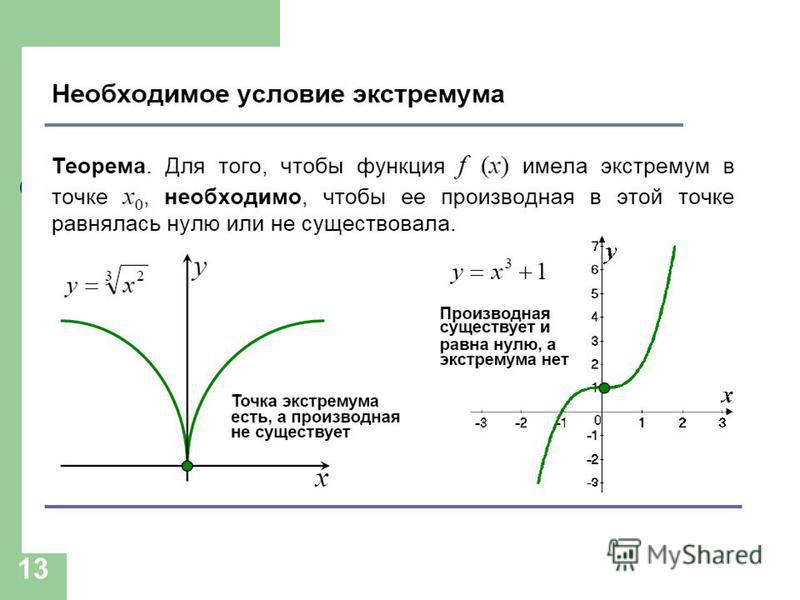
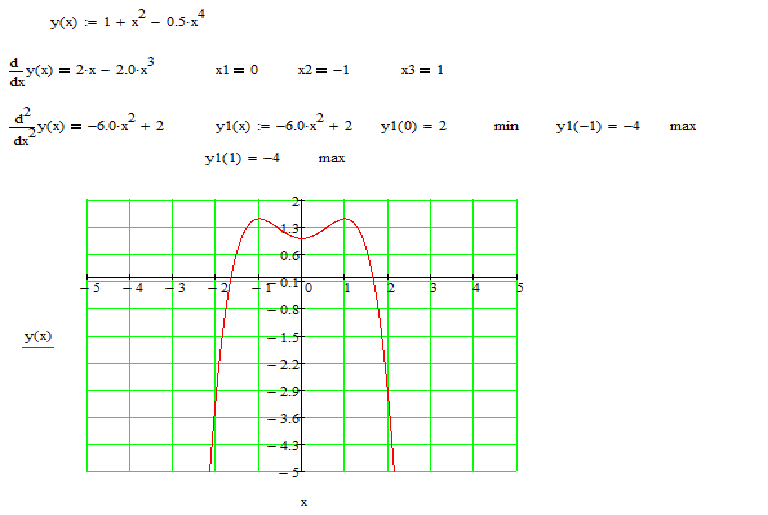 +} f (x) = M}.
$$
+} f (x) = M}.
$$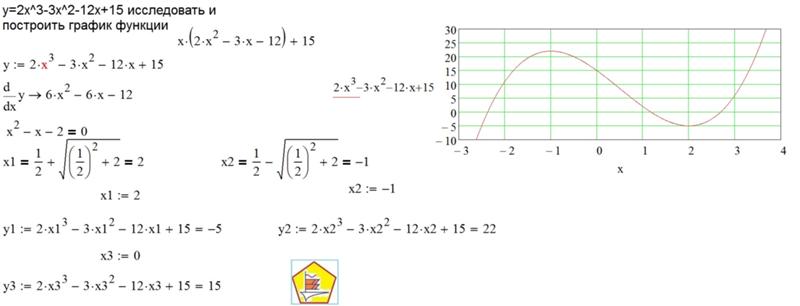 92-4}$$
92-4}$$ Теперь мы можем переопределить исходную функцию в кусочной форме:
92-4}, & \mbox{для всех } x \neq 2\\[6pt]
%
\frac 1 2, & \mbox{для } x = 2
\конец{массив}
\верно.
\\
$$
Теперь мы можем переопределить исходную функцию в кусочной форме:
92-4}, & \mbox{для всех } x \neq 2\\[6pt]
%
\frac 1 2, & \mbox{для } x = 2
\конец{массив}
\верно.
\\
$$