как построить – сложное простыми словами — ЕГЭ/ОГЭ
График модуля, как построить – очень просто. Особенно, если знать несколько закономерностей. О них расскажу в статье. С помощью них вы поймете как построить график модуля легко и играючи. Без поиска пробных точек.
На самом деле построение графиков функций с модулями – это удовольствие. Раньше они вызывали у вас в лучшем случае пренебрежение? Забудьте – после прочтения статьи вы будете первым по скорости построения графика.
Построение различных видов графиков, содержащих модуль:
- Главный миф о сложности графиков модуля
- Воландеморт среди модулей
- Как калькулятор может помочь при построении графика?
- Как построить график модуля и одновременно решить уравнение
- Война среди модулей
Господа, перед тем, как мы приступим к светской беседе с модулем. (В которой отдадим дань уважения каждому его виду). Я бы хотел обратить ваше внимание, что
Я бы хотел обратить ваше внимание, что
Подмечайте фишки каждой функции, но главное – держите в голове его «неотрицательность».
Главный миф о сложности графиков модуля – полный модуль по правой частиЗабудьте сказки про сложность модуля – ведь теперь вы скоро узнаете о методе «Зеркало».
Модуль всей правой части y = |f(x)| отражает график относительно оси X. Все, что было под осью Ox зеркально отражается наверх.
Почему так? Обратите внимание, что значение функции (то есть y) является результатом вычисления модуля. Оно не может быть отрицательным. Согласны? Значит, его заменяют на противоположное ему по знаку. А в построении функций эти зеркальные превращения и есть смена знака у функции.
Уже чувствуете себя как Алиса в Зазеркалье? Ничего страшного – объясню на примере:
Пример: y = |X – 3|
Видите, график функции y = |X – 3| состоит из двух ветвей.
Можете так себя проверять – сначала просто отзеркальте конец, который улетает в отрицательную бесконечность (под ось Ох). А потом посмотрите, действительно ли он совпадает с минусовой версией подмодульного выражения. Уверяю, если вы были аккуратны – совпадет.
*Читайте понятное определение модуля в статье «Простая инструкция: как решать любые уравнения с модулем». После ее прочтения вы научитесь расправляться со всеми видами уравнений с модулем с помощью всего 1 инструкции!
А теперь перейдем к функции, которая заставляет поежиться от недовольства слишком многих. Если б они знали, что ее настолько просто начертитить…то стали бы решать уравнения с ней только графически.
Модуль всей левой части |y| = f(x) отражает график относительно оси X.
Все, что было над осью Oх зеркально отражается вниз.
Смотрим, что является результатом вычисления подмодульного выражения? Ага, все, что стоит справа. Значит, в данном случае Рубиконом является ось Oy – отзеркаливаем относительно нее.
Пример: |y| = X – 3
Мы разобрали две базы графиков с модулями. Дальше уже идут вариации с дополнительными математическими па: поднимите график, опустите, сузьте – расширьте. Давайте и их разберем!
Как калькулятор может помочь при построении графика? — График содержащий модуль
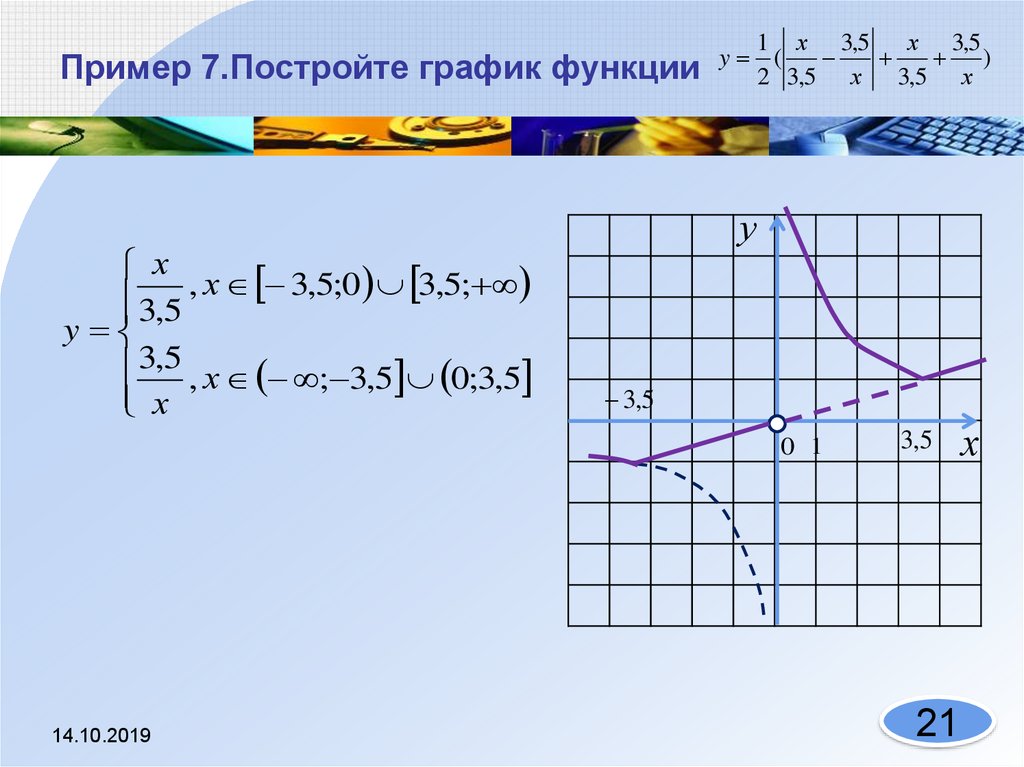
Это пример сложной функции, такие функции строятся по этапам. Сложной – не потому что она поддается только сильнейшим умам. Просто в ней собрано несколько последовательных действий: модуль и сложение с «потусторонним членом».
С такими функциями работает способ «калькулятор».
Представьте, что вам нужно вычислить выражение: (217 – 327)/72. С чего вы начнете? Вероятно, с возведения в степень, продолжите подсчетом числителя и только потом перейдете к делению. Будете идти от малого к большому.
С чего вы начнете? Вероятно, с возведения в степень, продолжите подсчетом числителя и только потом перейдете к делению. Будете идти от малого к большому.
Тот же метод работает и со сложной функцией. Начните с ядра и продолжайте справляться со всеми остальными прибамбасами вокруг него.
Пример: y = |x–3| + 5 ( ядром является график прямой y=x-3)
1. Y = X – 3 {строим график прямой}
2. Y = |X –3| {отражаем график относительно оси X}
3. Y = |X – 3| + 5 {поднимаем график 2. на +5}.
Вспомните суперспособности графиков – положительное число поднимает график, а отрицательное опускает (вверх/вниз относительно оси Ox). Причем, нет ничего страшного в том, что модульная галка окажется под прямой Ox (в отрицательной области) – это необходимые последующие действия с графиком.
Иногда в качестве «потустороннего члена» выступает переменная. Тут уж хитрить с отражениями и подниманиями – не получится. Придется раскрывать алгебраически модуль для каждого интервала – и уже по вычисленному выражению чертить ветви графика.
Тут уж хитрить с отражениями и подниманиями – не получится. Придется раскрывать алгебраически модуль для каждого интервала – и уже по вычисленному выражению чертить ветви графика.
О том, как легко раскрыть модуль – написано в статье – Решение уравнений с модулем.
А мы двигаемся навстречу забора из модуля. По правде, такой вид функций очень полезно уметь чертить. Этот скилл способен сэкономить вам время. Ведь частенько по графику намного точнее и проще найти корни уравнения такого вида.
Как построить график модуля и одновременно решить уравнение — Модуль внутри модуляПример: y = ||X–2|–3|
{Порядок действий как при работе со сложной функцией – пользуемся методом «Калькулятор»}
1. Y = X – 2
2. Y = |X – 2|
3. Y = |X – 2|–3
4. Y = ||X – 2|–3|
Согласитесь, что раскрывать уравнения такого типа довольно муторно. Да и велик риск просчитаться.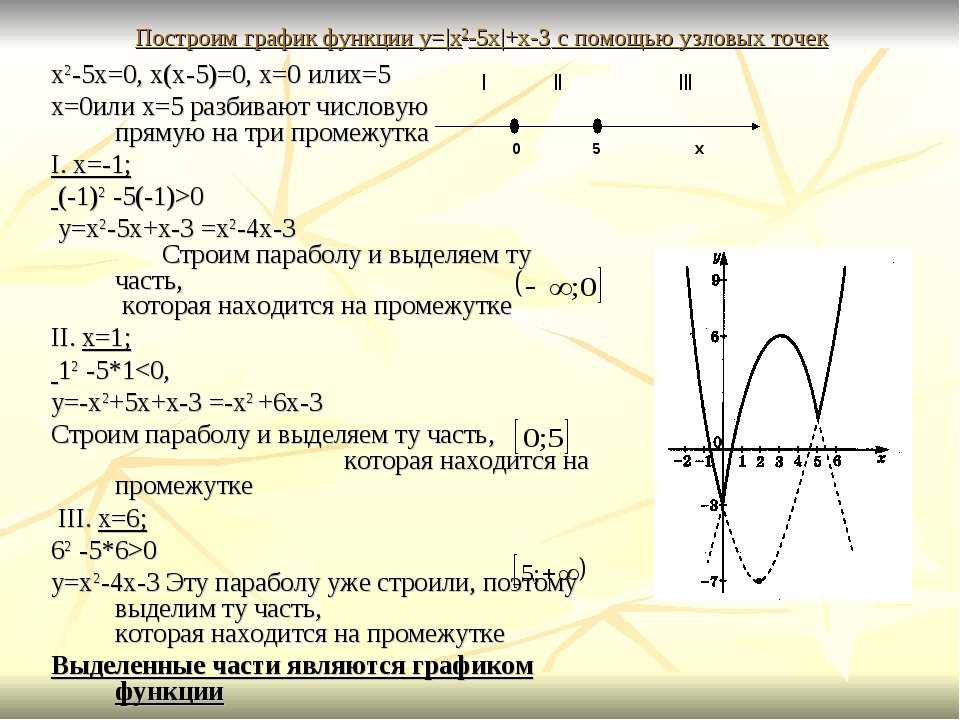 Начертить график и по нему оценить корни (иногда точно их посчитать) супер просто.
Начертить график и по нему оценить корни (иногда точно их посчитать) супер просто.
Поэтому графический метод решения уравнений нужно эксплуатировать на все 100% именно в этом случае.
Теперь нас ждет один из самых непредсказуемых графиков из всего рода модулей. Никогда не знаешь, что именно он приподнесет. Но и с этой неприятной неожиданностью научимся работать)
Война среди модулей — Несколько модулей
Что делать если в бой вступает сразу несколько модулей? – К сожалению, бороться с ними приходится с помощью арифметики и алгебры. Приходится аккуратно раскрывать на разных областях. Так же, как при решении модульных уравнений – алгебраически.
*Подробнее о том, как раскрывать модуль читайте в статье «Простая инструкция: как решать любые уравнения с модулем». В ней на пальцах объяснено, как раскрыть забор из модулей и НЕ запутаться.
Y = |X–2|+|X+2|
I ) X ∈ (–∞;–2] {1 модуль с «–» , 2 модуль с «–»}
Y1 = – (X – 2) – (X + 2)
Y1 = – X + 2 – X – 2
Y1 = –2X
II ) X ∈ (–2;2] {1 модуль с «–» , 2 модуль с «+»}
Y2 = – (X – 2) + (X + 2)
Y2 = – X + 2 + X + 2
Y2 = 4
III) X ∈ (2; +∞) {1 модуль с «+» , 2 модуль с «+»}
Y3 = (X – 2) + (X + 2)
Y3 = 2X
Вот такая галочка получилась из трех кусочков различных функций.
Вы уже заметили, что все модульные функции являются кусочно заданными? Их особенностью является то, что они существуют только на определенных интервалах.
Главное в модулях – понять закономерности. Дальше все пойдет как по маслу. Надеюсь, мне удалось хоть немного прояснить график модуля, как его построить и не надорваться в счете.
Остались вопросы? – обращайтесь! Я с удовольствием проведу первую консультацию бесплатно. Запишитесь на первое бесплатное занятие: напишите мне на почту или в сообщениях ВКонтакте)
До встречи, Ваш Михаил
График функции с модулем | Алгебра
Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.
Рассмотрим примеры таких заданий.
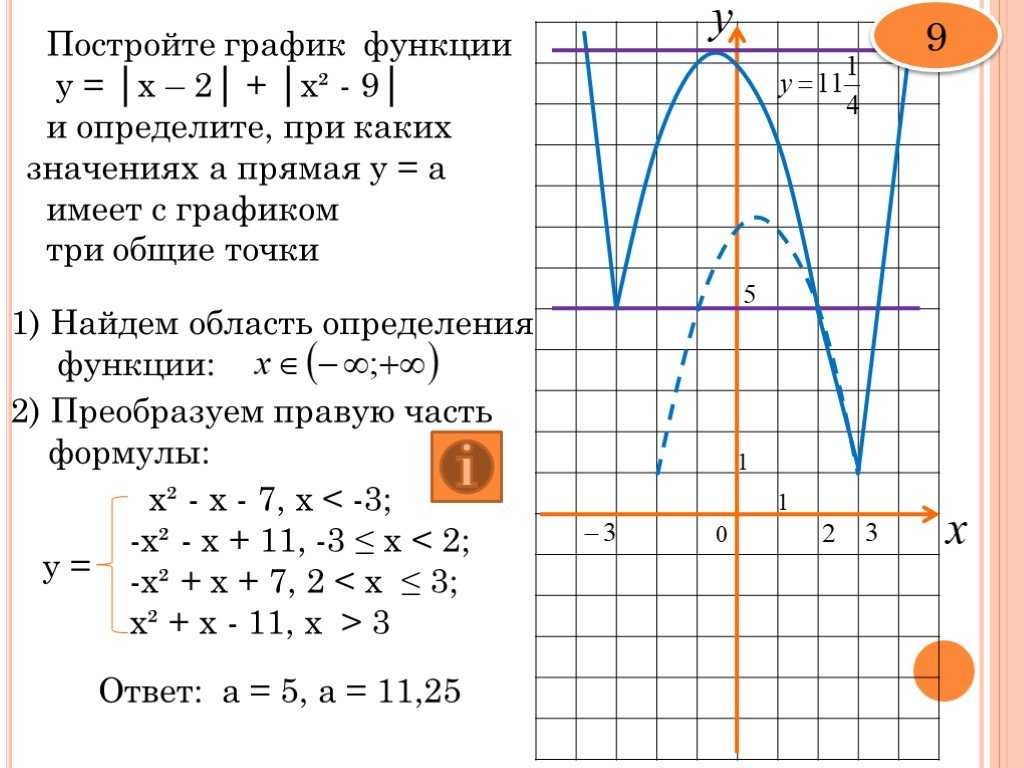
1) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
Область определения функции D(y): x∈R.
1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
x-2=0, x=2.
Найдём значение функции при x=2.
y(2)=5·0-2²+5∙2-3∙0-6=0.
Получили точку (2;0).
2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.
Если x-2>0, то есть при x>2, |х-2|=x-2,
y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.
y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
Координаты вершины параболы
то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).
3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.
Если x-2<0, то есть при x<2, |х-2|=-(x-2),
y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.
y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.
Координаты вершины параболы
то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².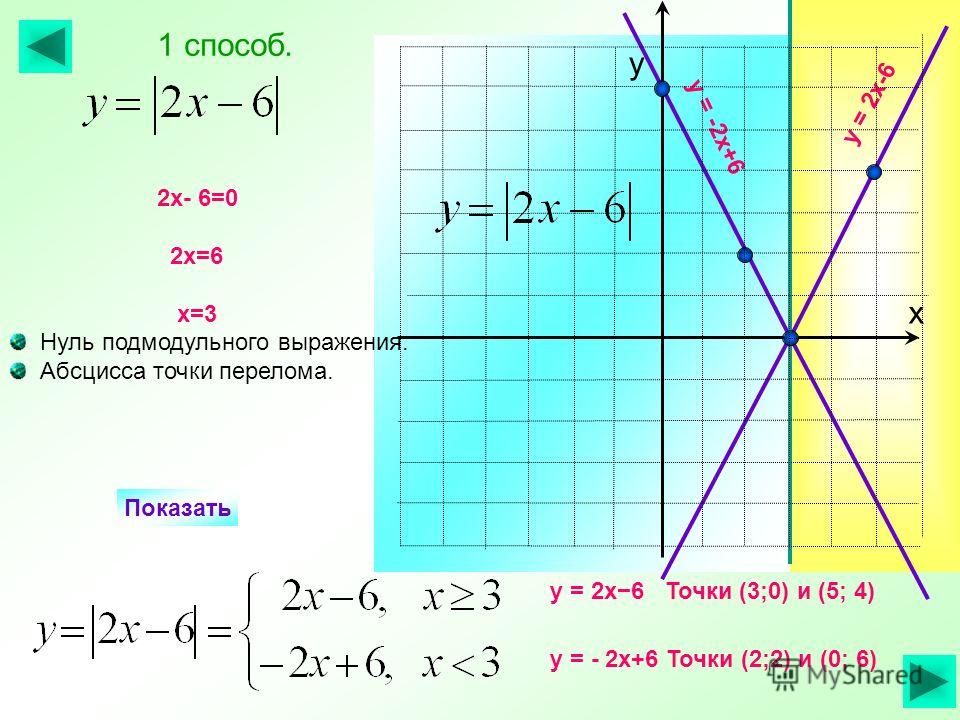
Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:
График функции с модулем можно рассматривать и как график кусочной функции:
Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:
Ответ: 0; 4.
2) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.
y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).
Координаты вершины параболы
Так как a=1, от вершины (3;-10) строим график y=x².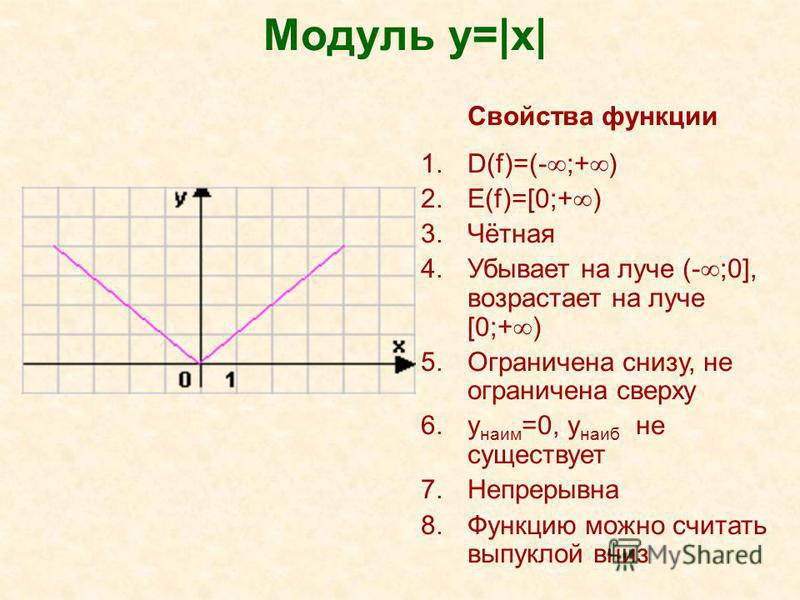
|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.
y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.
Координаты вершины параболы
от вершины (-3;-8) строим график y=x².
Или:
Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:
Ответ: -8; 1/36.
3) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x=0, y=|0|·0+3·|0|-5·0=0.
2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.
y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).
Координаты вершины параболы
От вершины (1;-1) строим параболу y=x² (так как a=1).
3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.
y=-x²-8x — квадратичная функция.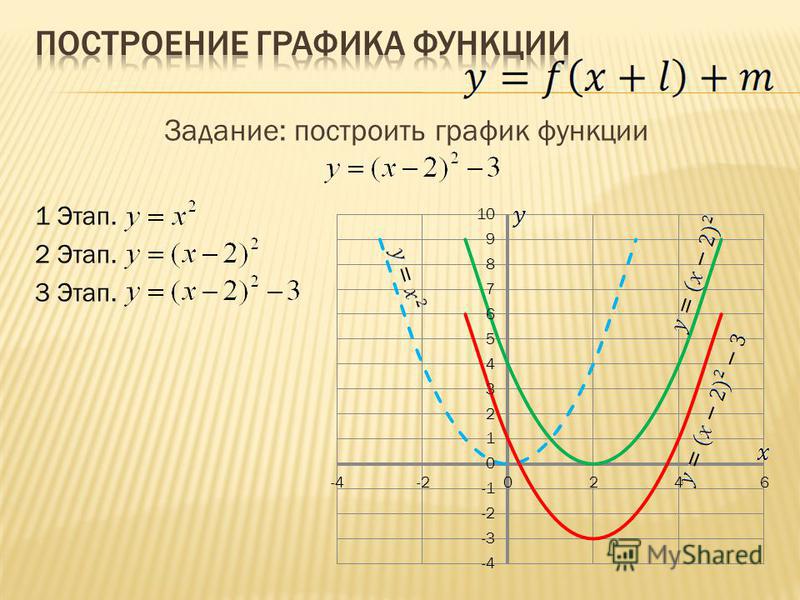 График — парабола ветвями вниз (a=-1<0).
График — парабола ветвями вниз (a=-1<0).
Координаты вершины параболы
От вершины (-4;16) строим параболу y=-x² (так как a=-1).
Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:
Альтернативный вариант:
Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:
Ответ: -1; 16.
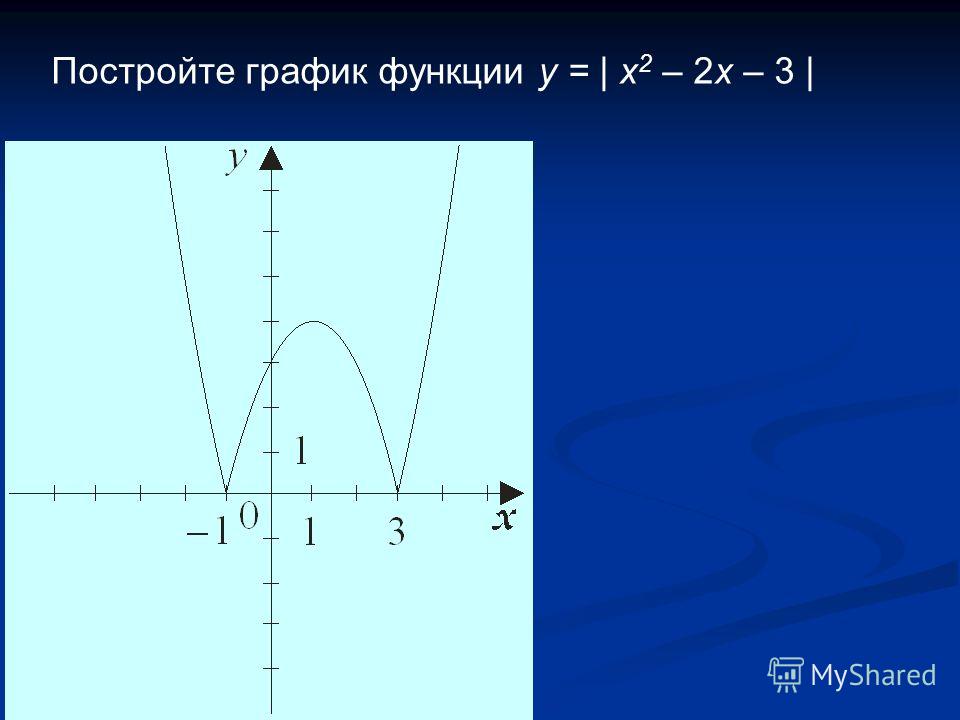
4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение:
Область определения функции D(y): x∈R.
Построим график функции y=x²+2x-3.
Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.
Координаты вершины параболы
, то есть вершина параболы — точка (-1;-4).
От вершины строим график функции y=x²:
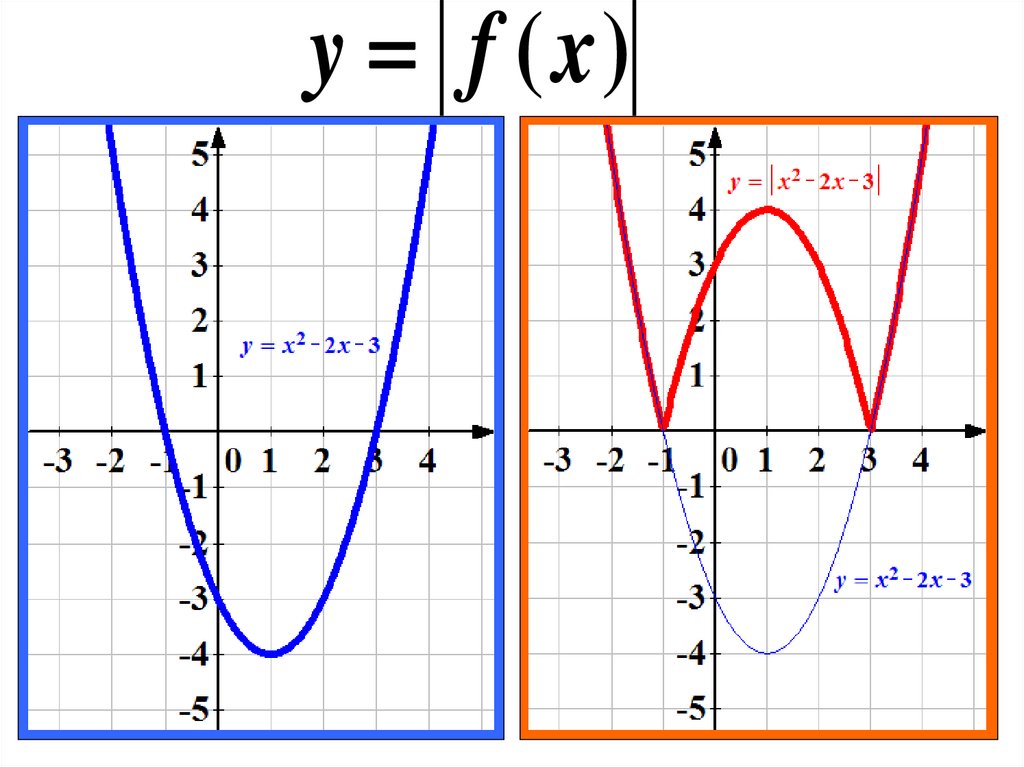
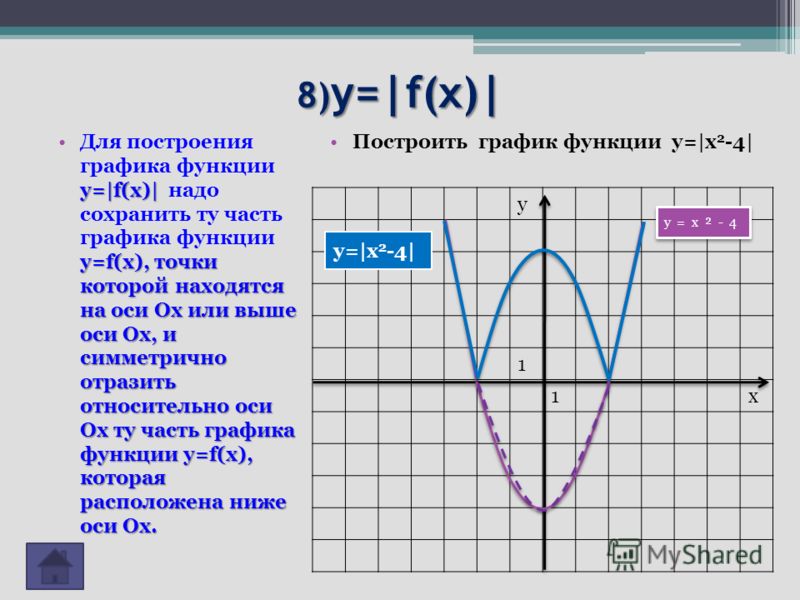
График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.
Или y=|x²+2x-3|
Вершина параболы (-1;-4) при этом переходит в точку (-1;4):
Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).
Ответ: 4.
Рубрика: ОГЭ задание 22 | КомментарииМетоды построения графиков функций содержащих модуль
- Мусина Диляра Фаиковна, учитель
Презентация к уроку
Загрузить презентацию (201 кБ)
Цель урока:
- повторить построение графиков функций содержащих знак модуля;
- познакомиться с новым методом построения графика линейно-кусочной функции;
- закрепить новый метод при решении задач.
Оборудование:
- мультимедиа проектор,
- плакаты.
Ход урока
Актуализация знаний
На экране слайд 1 из презентации.
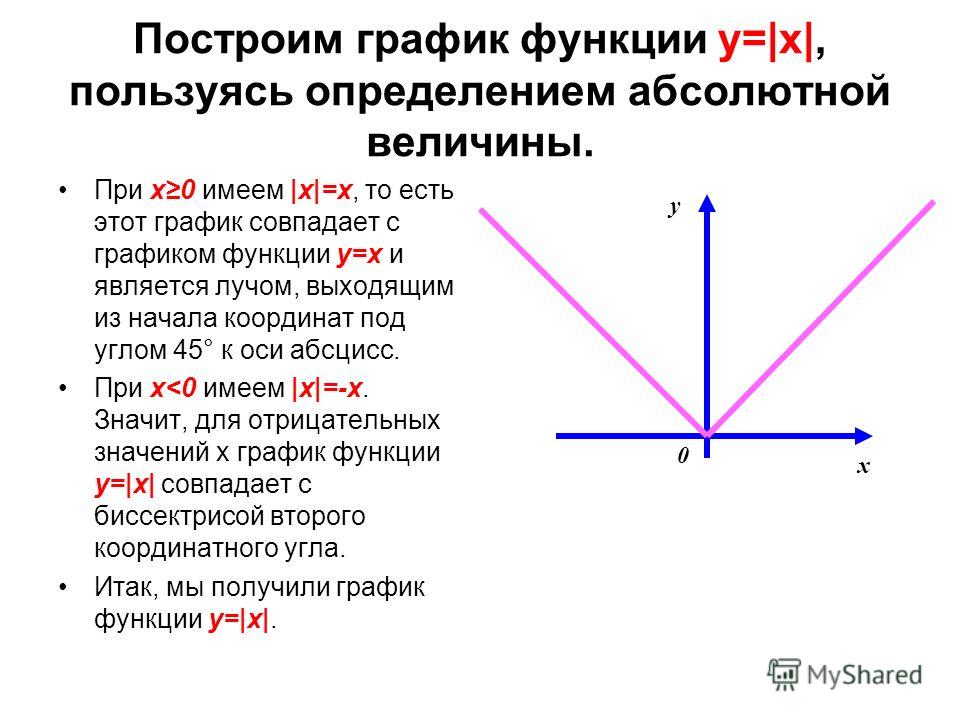
Что является графиком функции y=|x| ? (слайд 2).
(совокупность биссектрис 1 и 2 координатных углов)
Найдите соответствие между функциями и графиками, объясните ваш выбор (слайд 3).
Рисунок 1
y=| x+3|
y=| x| +3
y=-2| x| -2
y=6-| x-5|
y=1/3| x-6| -3
Расскажите алгоритм построения графиков
функций вида y=|f(x)| на примере функции y=|x
Ученик: чтобы построить график данной функции нужно
— построить параболу y=x2-2x-3
— часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ (слайд 5)
Рисунок 2
Рисунок 3
Расскажите алгоритм построения графиков
функций вида y=f(|x|) на примере функции y=x2-2|x|-3
(слайд 6).
Ученик: Чтобы построить график данной функции нужно:
— построить параболу.
— часть графика при х 0 сохраняется и отображается симметрии относительно оси ОУ (слайд 7)
Рисунок 4
Расскажите алгоритм построения графиков функций вида y=|f(|x|)| на примере функции y=|x2-2|x|-3| (слайд 8).
Ученик: Чтобы построить график данной функции нужно:
— нужно построить параболу у=x2-2x-3
— строим у= x2-2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ
— часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ (слайд 9)
Рисунок 5
Следующее задание выполняем письменно в тетрадях.
1. Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|
Ученик на доске с комментарием:
— находим нули подмодульных выражений х1=-2, х2=1, х3=3
— разбиваем ось на промежутки
— для каждого промежутка запишем функцию
при х < -2, у=-х-4
при -2 х<1, у=х
при 1 х<3, у = 3х-2
при х 3, у = х+4
— строим график линейно-кусочной функции.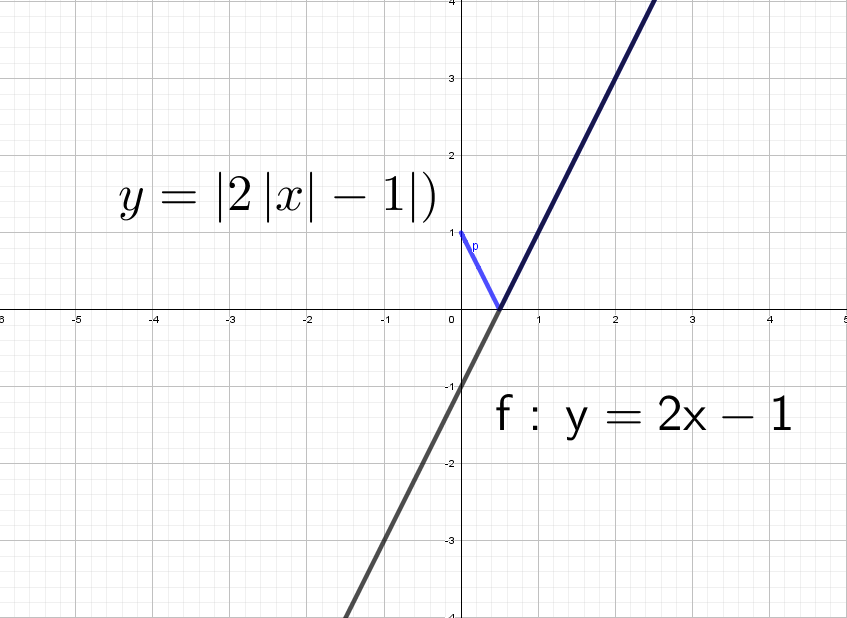
Мы с вами построили график функции используя определение модуля (слайд 10).
Рисунок 6
Предлагаю вашему вниманию “метод вершин”, который позволяет строить график линейно-кусочной функции (слайд 11). Алгоритм построения дети записывают в тетрадь.
Метод вершин
Алгоритм:
- Найдем нули каждого подмодульного выражения
- Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
- Нанесем точки на координатную плоскость и соединим последовательно
2. Разберем этот метод на той же функции у=|х+2|+|х-1|-|х-3|
Учитель на доске, дети в тетрадях.
Метод вершин:
— найдем нули каждого подмодульного выражения;
— составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
х -3 -2 1 3 4
у -1 -2 1 7 8
— нанесем точки на координатную плоскость и
соединим последовательно.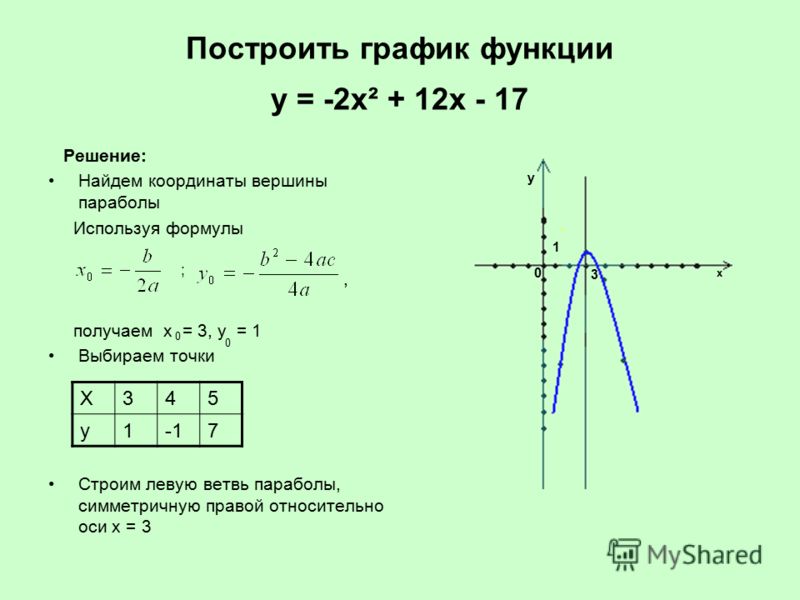
Графиком линейно-кусочной функции является ломанная с бесконечными крайними звеньями (слайд 12) .
Рисунок 7
Каким же методом график получается быстрее и легче?
3. Чтобы закрепить данный метод предлагаю выполнить следующее задание:
При каких значения х функция у=|х-2|-|х+1| принимает наибольшее значение.
Следуем алгоритму; ученик на доске.
у=|х-2|-|х+1|
х1=2, х2=-1
у(-2)=4-1=3
у(-1)=3
у(2)=-3
у(3)=1-4=3, соединяем последовательно точки.
унаиб = 3
4. Дополнительное задание
При каких значениях а уравнение ||4+x|-|x-2||=a имеет два корня.
5. Домашняя работа
а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2| принимает наименьшее значение.
б) Построить график функции y=||x-1|-2|-3| .
Графики прямой, параболы, гиперболы, с модулем
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).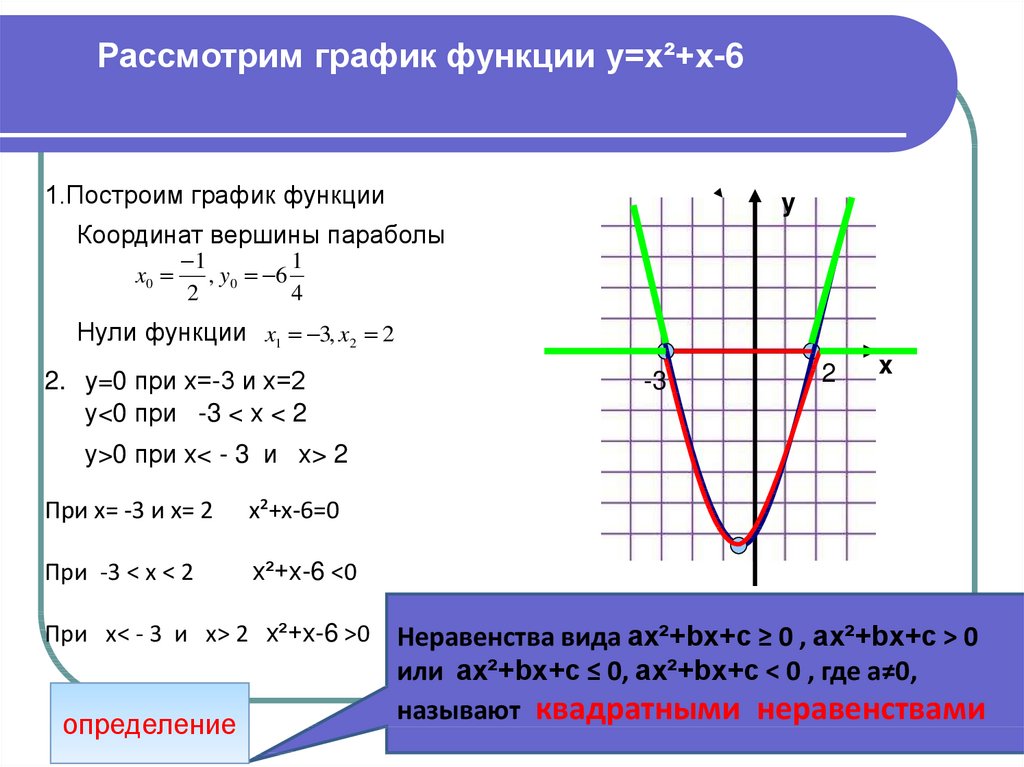
Получается такая зеленая «галочка».
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х.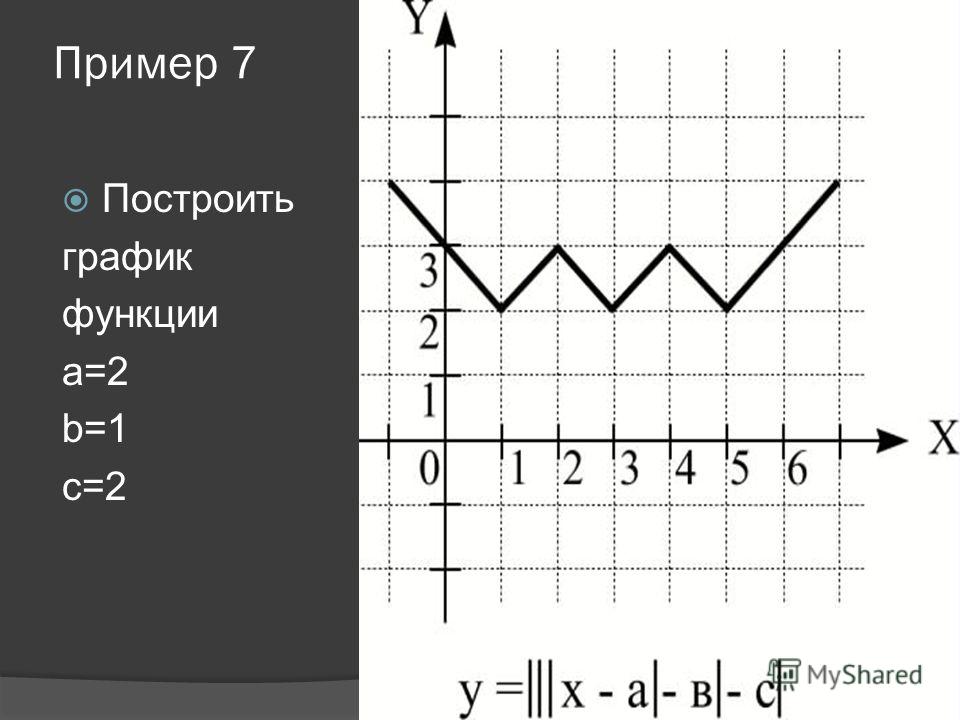 Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.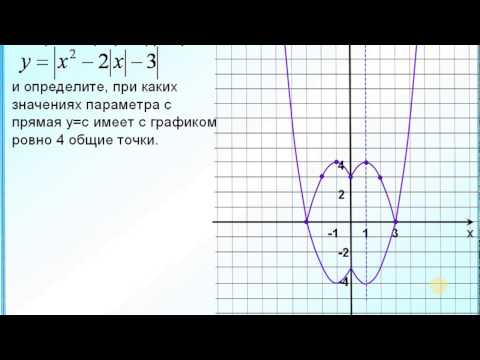
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.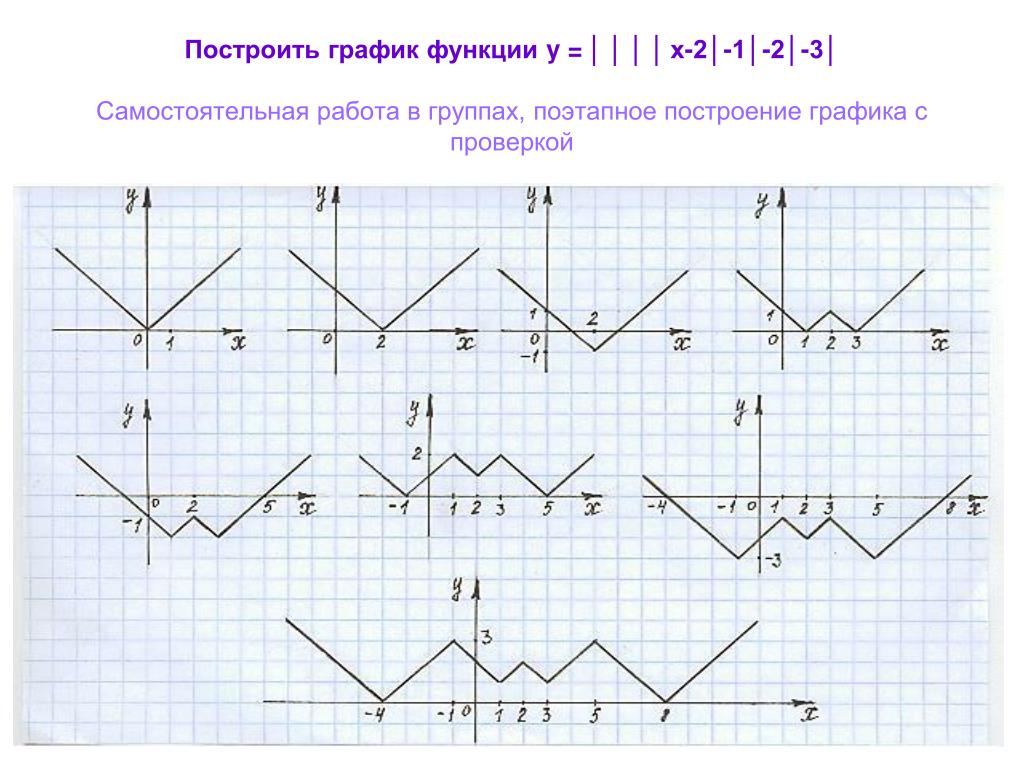
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:
Таким способом, медленно и кропотливо можно построить любой график!
Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.

- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Будь в курсе новых статеек, видео и легкого математического юмора.
Графики функций с модулем — Студопедия
Поделись
Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.
Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.
Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.
Правило: график функции получается из графика функции следующим образом: при график функции сохраняется, а при «сохранённая часть» отображается симметрично относительно оси .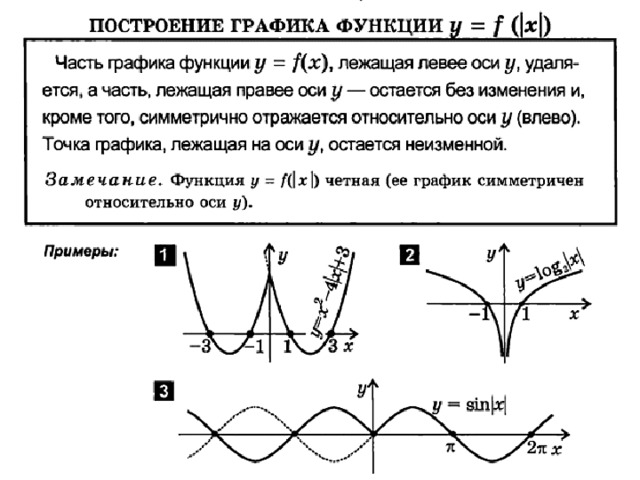
Пример 22
Построить график функции
И снова вечная картина:
Согласно правилу, при график сохраняется:
И сохранившаяся часть отображается симметрично относительно оси в левую полуплоскость:
Действительно, функция – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.
Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае:
То есть, правая волна графика задаётся функцией , а левая волна – функцией (см. Пример 13).
Пример 23
Построить график функции
Аналогично, ветвь «обычной» экспоненты правой полуплоскости отображаем симметрично относительно оси в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .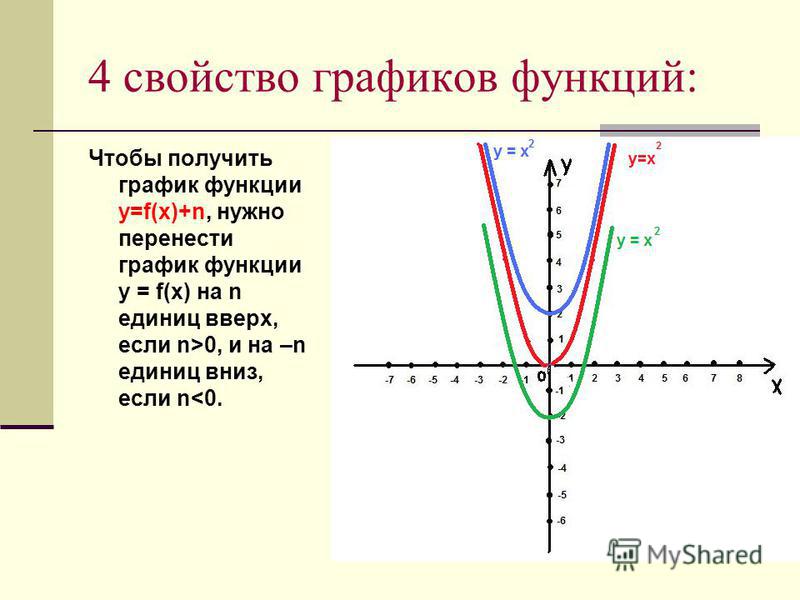
Модуль не имеет смысл «навешивать» на аргумент чётной функции: и т.п. (проанализируйте, почему).
И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.
Правило: график функции получается из графика функции следующим образом: часть графика , лежащая НАД осью сохраняется, а часть графика , лежащаяПОД осью отображается симметрично относительно данной оси.
Странно, что широко известный график модуля «икс» оказался на 24-ой позиции, но факт остаётся фактом =)
Пример 24
Построить график функции
Сначала начертим прямую, известную широкому кругу лиц:
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси – отображается симметрично в верхнюю полуплоскость:
Модуль функции также раскрывается аналитически в кусочном виде:
Внимание! Формула отличается от формулы предыдущего пункта!
В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .
Кстати, – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и к самой функции: . Изучим более «жизненную» ситуацию:
Пример 25
Построить график функции
Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси в верхнюю полуплоскость:
Согласно формуле , распишем функцию аналитически в кусочном виде: .
Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.
На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .
Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:
Пример 26
Построить график функции .
Изобразим сами знаете что =)
И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :
Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.
Распишем функцию в кусочном виде:
Решив два простейших школьных неравенства , получаем:
, где – любое целое число.
Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)
Желаю успехов!
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Непрерывность функции.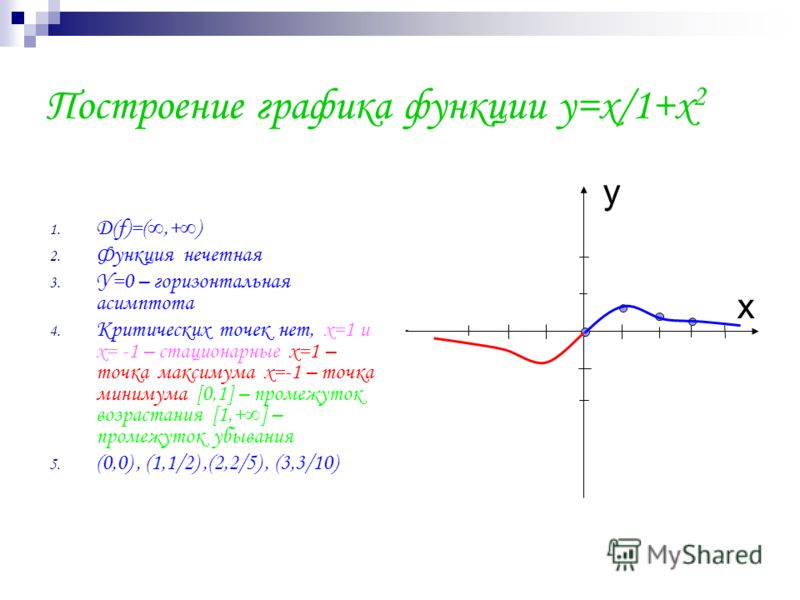 Точки разрыва.
Точки разрыва.
Как исследовать функцию на непрерывность?
Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!
На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность. Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.
Что нужно знать и уметь?Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции. Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций.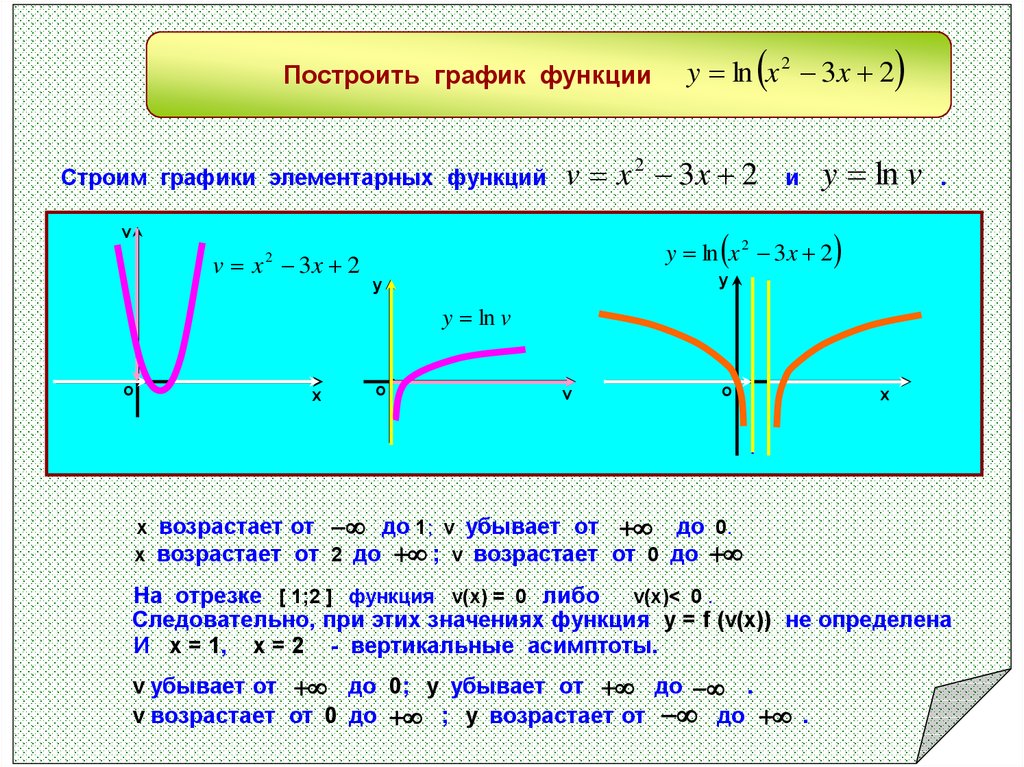 Также желательно ознакомиться с геометрическими преобразованиями графиков, поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!
Также желательно ознакомиться с геометрическими преобразованиями графиков, поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!
Простая физика — EASY-PHYSIC
Здравствуйте, уважаемые посетители! В этой статье мы попробуем подробно разобраться, как построить график функции, если эта функция содержит модуль. В статье разобраны различные примеры с пошаговым построением и подробным объяснением, как получен тот или иной график.
1. Начнем с построения графика
В «основе» его лежит график функции
и все мы знаем, как он выглядит:
Теперь построим график
Чтобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:
Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:
Теперь необходимо умножить на два все ординаты, чтобы получить график функции
Наконец, сдвигаем график вверх на две единицы:
Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):
2. Теперь построим график функции
Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:
При х>2/3 функция запишется так:
То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (левее) мы строим функцию
а в другой (правее) — график функции
Строим:
3. Следующий график — также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:
Посмотрим, в каких точках подмодульные выражения меняют знак:
Расставим знаки для подмодульных выражений на координатной прямой:
Раскрываем модули на первом интервале:
На втором интервале:
На третьем интервале:
Таким образом, на интервале (-∞; 1. 5] имеем график, записанный первым уравнением, на интервале [1.5; 2] — график, записанный вторым уравнением, и на интервале [2;∞) — график по третьему уравнению:
5] имеем график, записанный первым уравнением, на интервале [1.5; 2] — график, записанный вторым уравнением, и на интервале [2;∞) — график по третьему уравнению:
Строим:
4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:
В основе опять знакомый нам график функции
но, если в знаменателе x стоит под знаком модуля,
то график имеет вид:
Теперь произведем сдвиг на три единицы,
при этом сдвинутся обе части: правая — вправо, левая — влево (своеобразное зеркало : отходишь дальше — видно больше)
График этой функции, умноженной на два,
выглядит так:
Теперь можно поднять график по оси у:
и тогда он будет таким:
Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:
5.Очень интересно выглядит график функции
В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) — второе:
На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) — второе:
6. Две следующие функции отличаются знаком, и графики их выглядят по-разному:
7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:
Первый:
Второй:
8.Теперь построим график такой функции:
Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:
А на интервале [4; ∞) так:
Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:
9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:
Однако многочлен в числителе раскладывается на множители:
Точки перемен знака подмодульных выражений — 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:
На первом интервале (-∞; -2):
На втором интервале (-2;4):
На третьем интервале (4;∞):
Строим:
Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:
Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:
На первом интервале (-∞; -2):
На втором интервале (-2;4):
На третьем интервале (4;∞):
График изменится:
10. Наконец, последний график мы построим для функции
Наконец, последний график мы построим для функции
Начнем построение с «базовой» для этого графика функции
она выглядит так:
Далее добавим знак модуля под корень:
Теперь опустим этот график вниз на 4 единицы по оси у:
«Опрокинем» все, что ниже оси х, вверх,
и не забудем поделить все ординаты на 2:
Модульная арифметика. Почему комплексная функция по модулю $1 \bmod z$ выглядит очень похожей на дзета-функцию Римана на графике?
$\begingroup$
Недавно я посмотрел видео 3Blue1Brown о дзета-функции Римана. Примерно на отметке 11:00 есть интересная визуализация функции на комплексной плоскости. Ради любительского интереса я создал сложный графический калькулятор, используя HSL-графику в JavaScript, учитывая только оттенок для сложного аргумента. Я определил сложную операцию по модулю как $z_1 \bmod z_2 = z_1 — z_2 \left\lfloor \frac{z_1}{z_2} \right\rfloor$ и комплексную функцию пола как $\lfloor z \rfloor = \lfloor \Re (z) \rfloor + \lfloor \Im(z) \rfloor$.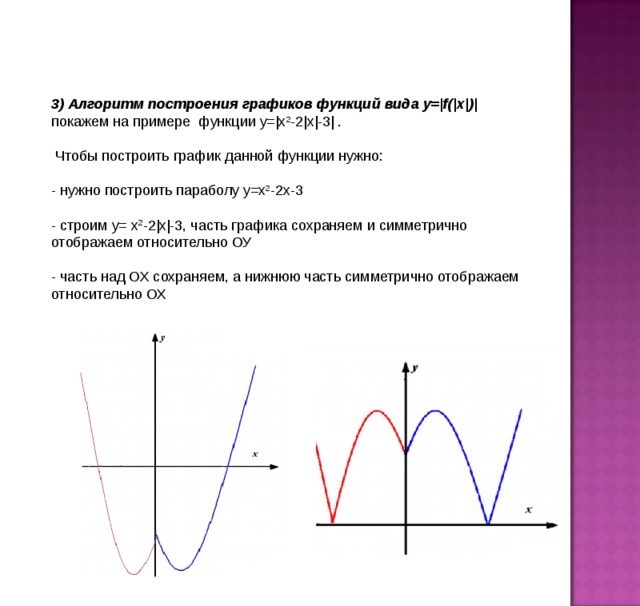 Вот график функции $1 \bmod z$ в сравнении с графиком 3Blue1Brown:
Вот график функции $1 \bmod z$ в сравнении с графиком 3Blue1Brown:
Я мало что знаю о комплексном анализе, но эти две функции имеют одинаковую базовую структуру, по крайней мере, на мой взгляд. Какая связь существует между функцией по модулю и дзета-функцией Римана? Я также не думаю, что видел эту форму раньше в математике. Есть ли другие места, где появляется эта форма? Простите мое невежество, если ответы тривиальны. Кроме того, большое спасибо за то, что вы нашли время, чтобы ответить на вопросы новичков в математике, таких как я.
- комплексный анализ
- модульная арифметика
- графические функции
- дзета Римана
$\endgroup$
8
$\begingroup$
То, что создает эти круговые арки на графике дзета-функции Римана, на самом деле является поведением вокруг полюса s=1. Посмотрите это видео: преобразование функции. По мере приближения к s=1 дзета-функция Римана ведет себя примерно так: $$f(z)=\frac{1}{z-1} + \gamma$$. Это главные члены разложения в ряд Лорана для $\дзета(ы)$. Таким образом, эти круглые арки на самом деле происходят от термина $\frac{1}{1-s}$. Если бы вы построили параметрическую функцию $f(t) = \frac{1}{(a+it) — 1}$ на комплексной плоскости, вы бы получили следующее уравнение для окружности 92}$$
Посмотрите это видео: преобразование функции. По мере приближения к s=1 дзета-функция Римана ведет себя примерно так: $$f(z)=\frac{1}{z-1} + \gamma$$. Это главные члены разложения в ряд Лорана для $\дзета(ы)$. Таким образом, эти круглые арки на самом деле происходят от термина $\frac{1}{1-s}$. Если бы вы построили параметрическую функцию $f(t) = \frac{1}{(a+it) — 1}$ на комплексной плоскости, вы бы получили следующее уравнение для окружности 92}$$
Я написал полный вывод здесь: Короче говоря, когда вы применяете функцию к линиям сетки в комплексной плоскости, создаются круги. Чем ближе линия к полюсу функции, тем больше созданный круг. Вот почему визуально все круги в преобразовании дзета-функции Римана кажутся расширяющимися от полюса в точке s=1.
Интересно, что это преобразование проявляется в виде внезапных изменений цвета на вашем графике HSL. Это означает, что отображаемый шаблон круглой арки на самом деле представляет собой границы, где ваша функция пола имеет разрывы (выход функции внезапно меняется на другую часть сложной плоскости). 2}$$
Это окружности, касающиеся воображаемой оси (или у). Обратите внимание, что этот круг представляет собой только горизонтальные линии после преобразования. Аналогичный вывод можно сделать для $t+bi$, чтобы получить окружности, касающиеся вещественной оси. В качестве проверки, подставив значения для 1,2,3, вы получите круги с радиусом 1, 1/2, 1/4 соответственно. Это те же самые круги, которые появляются на вашем графике.
2}$$
Это окружности, касающиеся воображаемой оси (или у). Обратите внимание, что этот круг представляет собой только горизонтальные линии после преобразования. Аналогичный вывод можно сделать для $t+bi$, чтобы получить окружности, касающиеся вещественной оси. В качестве проверки, подставив значения для 1,2,3, вы получите круги с радиусом 1, 1/2, 1/4 соответственно. Это те же самые круги, которые появляются на вашем графике.
$\endgroup$
3
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Функция модуля — формула, график, свойства, примеры
Функция модуля дает величину числа независимо от его знака. Ее также называют функцией абсолютного значения. В математике модуль действительного числа x задается функцией модуля , обозначаемой |x|. Это дает неотрицательное значение x. Модуль или абсолютное значение числа также рассматривается как расстояние числа от начала координат или нуля.
Ее также называют функцией абсолютного значения. В математике модуль действительного числа x задается функцией модуля , обозначаемой |x|. Это дает неотрицательное значение x. Модуль или абсолютное значение числа также рассматривается как расстояние числа от начала координат или нуля.
В этой статье мы узнаем об определении функции модуля, вычислении модуля для чисел, переменных и многочленов, а также решенных примерах и вопросах функции модуля.
| 1. | Что такое функция модуля? |
| 2. | Формула функции модуля |
| 3. | Домен и диапазон функции модуля |
| 4. | Применение модульной функции |
| 5. | График функции модуля |
| 6. | Свойства функции модуля |
| 7. | Производная и интеграл функции модуля |
8. | Часто задаваемые вопросы о модульной функции |
Что такое функция модуля?
Функция модуля , которую также называют функцией абсолютного значения, дает модуль или абсолютное значение числа независимо от того, является ли число положительным или отрицательным. Он всегда дает неотрицательное значение любого числа или переменной. Функция модуля обозначается как y = |x| или f(x) = |x|, где f: R → (0,∞) и x ∈ R.
|x| — модуль x, где x — действительное число. Если x неотрицательно, то f(x) будет иметь то же значение x. Если x отрицательно, то f(x) будет величиной x, то есть f(x) = -x, если x отрицательно. Подытожим приведенную ниже формулу функции модуля.
Формула функции модуля
Значение функции модуля всегда неотрицательно. Если f(x) является функцией модуля, то мы имеем:
- Если x положителен, то f(x) = x
- Если х = 0, то f(x) = 0
- Если х < 0, то f(x) = -x
Это означает, что если значение x больше или равно 0, то функция модуля принимает фактическое значение, но если x меньше 0, то функция принимает минус фактическое значение «x».
Домен и диапазон функции модуля
Мы можем применить функцию модуля к любому вещественному числу. Диапазон функции модуля — это набор неотрицательных действительных чисел, который обозначается как (0, ∞), а область определения функции модуля — R (где R относится к набору всех действительных чисел). Следовательно, область определения функции модуля составляет R , а диапазон равен (0,∞).
Применение модульной функции
Теперь, когда мы знаем формулу функции модуля, давайте рассмотрим несколько примеров, чтобы понять ее применение. Шаги для расчета функции модуля приведены ниже:
Пример: Рассмотрим функцию модуля f(x) = |x|.
- Если x = − 3, то y = f(x) = f(−3) = −(−3) = 3, здесь x меньше 0.
- Если x = 3, то y = f(x) = f(3) = 3, здесь x больше 0
- Если x = 0, то y = f(x) = f(0) = 0, здесь x равно 0
Обратите внимание, что здесь f(-3) = f(3). Другими словами, |3| = |-3| = 3.
Другими словами, |3| = |-3| = 3.
График функции модуля
Теперь давайте посмотрим, как построить график для функции модуля. Давайте рассмотрим x как переменную, принимающую значения от -5 до 5. Вычисляя модуль для положительных значений «x», линия на графике представляет собой «y = x», а для отрицательных значений «x» на графике изображена линия «y = -x».
| х | f(x) = |x| |
|---|---|
| -5 | 5 |
| -4 | 4 |
| -3 | 3 |
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
Свойства функции модуля
Теперь, когда у нас есть формула для функции модуля и график функции модуля, давайте теперь исследуем свойства функции модуля:
Производная и интеграл функции модуля
Поскольку мы знаем, что функция модуля f(x) = |x| равно x, если x > 0, и -x, если x < 0, поэтому производная функции модуля равна 1, если x > 0, и -1, если x < 0.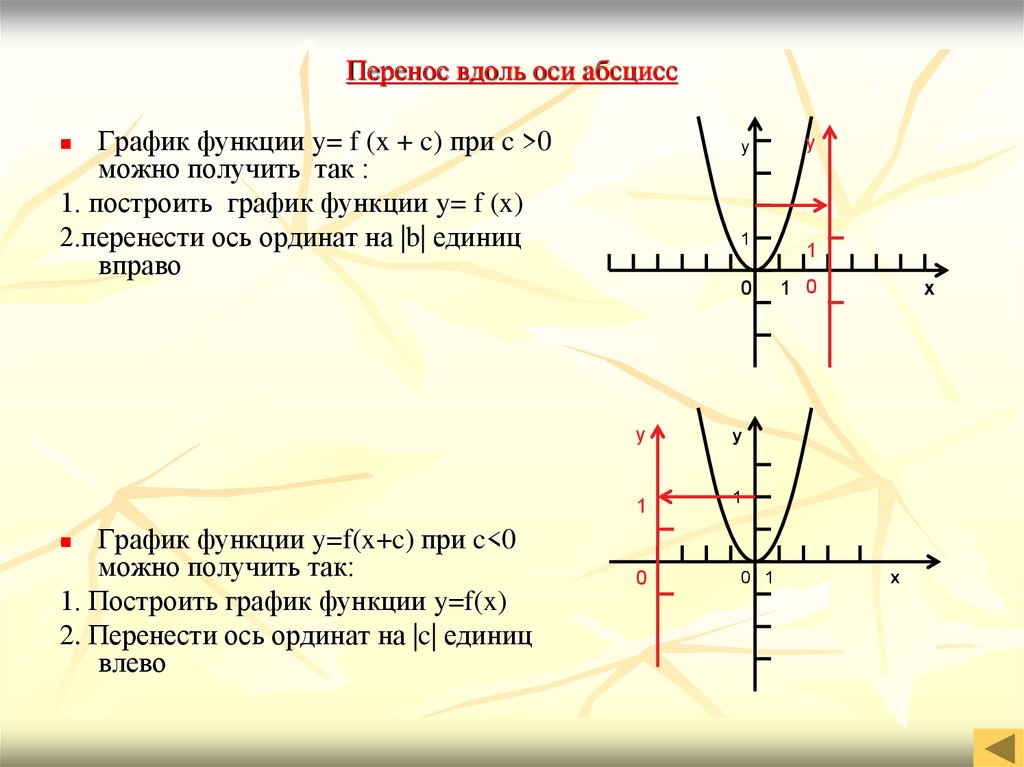 Производная функции модуля не определена для x = 0. Следовательно, производная функции модуля может быть записана как d(|x|)/dx = x/|x| , для всех значений x и x, не равных 0.
Производная функции модуля не определена для x = 0. Следовательно, производная функции модуля может быть записана как d(|x|)/dx = x/|x| , для всех значений x и x, не равных 0.
Используя формулу функции модуля и формулы интегрирования, интеграл функции модуля равен (1/2)x 2 + C, если x ≥ 0, и его интеграл равен -(1/2)x 2 + C, если x < 0. Таким образом, интегрирование функции модуля можно представить как:
- ∫|x| dx = (1/2)x 2 + C, если x ≥ 0
- ∫|х| dx = -(1/2)x 2 + C, если x < 0
Важные замечания о функции модуля
- Функция модуля также называется функцией абсолютного значения и представляет собой абсолютное значение числа. Обозначается |x|.
- Область определения модульных функций — это множество всех действительных чисел.
- Диапазон функций модуля — это набор всех действительных чисел, больших или равных 0.
- Вершина графика модулей y = |x| равно (0,0).

- Вершина функции модуля y = a |x — h| + k равно (h, k).
Тема, связанная с функцией модуля
- Модуль комплексного числа
- Калькулятор абсолютного значения
- Калькулятор модов
Часто задаваемые вопросы о модульной функции
Что такое функция модуля?
Функция модуля дает модуль или абсолютное значение числа независимо от того, является число положительным или отрицательным. Функция модуля обозначается как y = |x| или f(x) = |x|, где f: R → R и x ∈ R. Это также называется функцией абсолютного значения.
Что такое домен и диапазон функции модуля?
Областью определения функции модуля является R (где R относится к набору всех положительных действительных чисел), а диапазон функции модуля представляет собой набор неотрицательных действительных чисел, который обозначается как (0,∞).
Что такое интегрирование модульной функции?
Интегрирование функции модуля зависит от значения x. Это:
Это:
- ∫|x| dx = (1/2)x 2 + C, если x ≥ 0
- ∫|х| dx = -(1/2)x 2 + C, если x < 0
Как дифференцировать функцию модуля?
Имеем f(x) = |x| равно x, если x > 0, и -x, если x < 0, следовательно, производная модульной функции равна 1, если x > 0, и -1, если x < 0. Производная модульной функции не определена для x = 0 Подводя итог, можно сказать, что производная функции модуля |x| равно x/|x|, где x не равно 0.
Всегда ли функция модуля положительна?
Модуль положительного числа положителен. Модуль отрицательного числа получается при игнорировании знака минус. Таким образом, функция модуля всегда положительна.
Почему функция модуля не дифференцируема?
Функция модуля |x| не дифференцируема при x = 0, так как график Mod(x) имеет острую точку при x = 0. Кроме того, левый и правый предел производной не равны при x = 0.
Как вы решаете задачи на модульную функцию?
Задачи модульных функций можно решить, применяя модуль к неотрицательному числу, а отрицательное число всегда дает одно и то же число.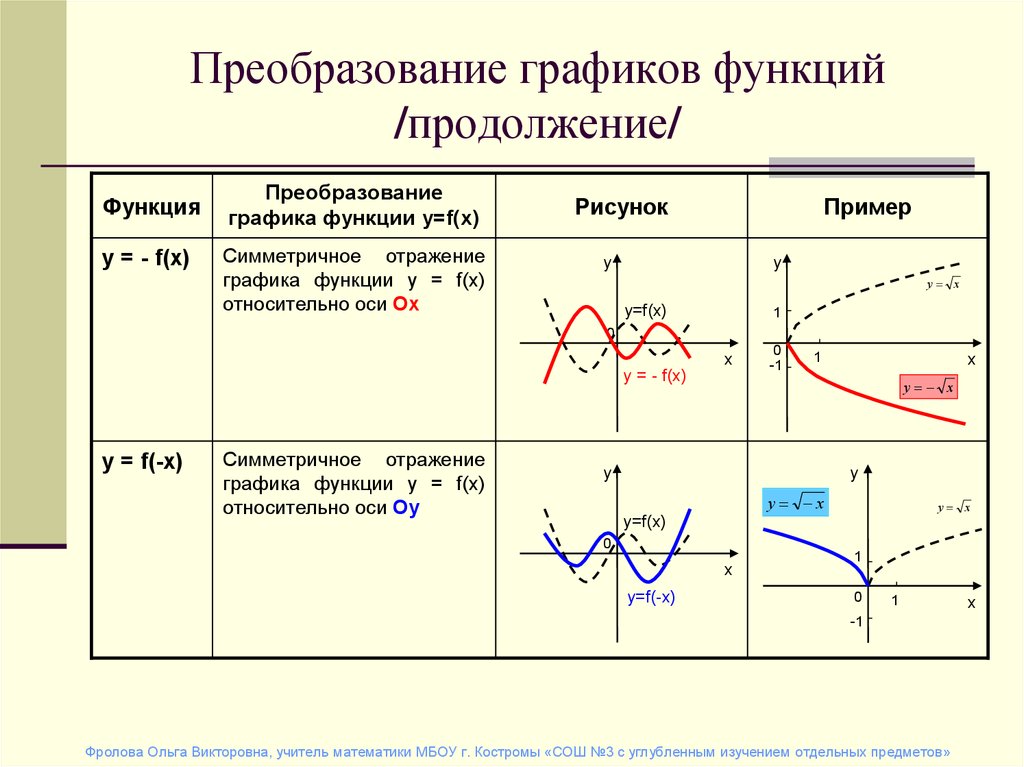
Как построить график функции модуля?
Возьмем несколько положительных и отрицательных значений x. Также возьмем x = 0. Создайте таблицу с двумя столбцами x и y со всеми случайными значениями x, которые мы выбрали. Вычислите модуль каждого числа и заполните столбец y. Затем просто начертите все упорядоченные пары (x, y) и соедините их линиями. Мы получим V-образный график, и это график функции модуля.
Модульные функции: определение, уравнения и правила
Модульные функции (также известные как функции абсолютного значения) обычно представляются как . Модуль числа x будет числом той же величины, но положительным.
Но что стоит за этим? Это происходит потому, что он представляет собой расстояние от нуля до числа x на числовой прямой.
Расстояние от нуля до 2 равно 2, а расстояние от нуля до -2 также равно 2, поэтому , и
Функция модуля на числовой прямой, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Вот почему представляет значение числа x без учета его знака.
Если у вас есть выражение внутри функции модуля, вычислите значение внутри, а затем найдите положительную версию результата.
Если у вас есть функция find
Уравнение модульных функций
Уравнение модульной функции обозначается следующим образом: , а диапазон — это набор всех действительных чисел, больших или равных нулю. Из уравнения мы можем сказать, что если число внутри функции модуля уже положительное, вы оставляете его таким, но если число отрицательное, то результатом будет положительная версия этого числа (как если бы вы умножали отрицательное число на -1).
Свойства функций модуля
. функция может быть положительной или отрицательной, вам нужно решить уравнение с учетом обоих случаев, поэтому вы получите два решения.
Для уравнения мы можем получить 2 возможных решения следующим образом:
1) Решение 1:
2) Решение 2:
Как построить график модульных функций?
Чтобы нарисовать график функции модуля, вам нужно подставить значения x в , чтобы получить соответствующие значения y, как . Вы получите таблицу значений x и y, которые вам нужно будет нанести на координатную плоскость. Подставим значения x от -2 до 2.
Вы получите таблицу значений x и y, которые вам нужно будет нанести на координатную плоскость. Подставим значения x от -2 до 2.
| x | y |
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
Modulus function graph, Marilú García De Taylor — StudySmarter Originals
Чтобы начертить график функции модуля, вам нужно начертить и отразить часть линии, которая идет ниже оси x, в ось x.
Нарисуйте график, показывающий точки пересечения осей координат.
Не обращая внимания на модуль, необходимо построить график
Когда ,
Линия пересекает ось х в точке (1, 0)
- Когда ,
- -ось в точке (0, -1)
Пример графика функции модуля, Марилу Гарсиа Де Тейлор — StudySmarter Originals
- Для отрицательных значений y отразите по оси x.
 В этом случае (0, -1) становится (0, 1)
В этом случае (0, -1) становится (0, 1)
Пример графика модульной функции, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Решение уравнений с использованием модульных функций
Если у вас есть уравнение типа , вы можете использовать его график, чтобы найти его решение, выполнив следующие шаги:
Решение уравнений с использованием модульных функций, Марилу Гарсия Де Тейлор — StudySmarter Originals
Определите точки пересечения двух графиков. В этом случае A соответствует точке пересечения между y = 5 и исходным участком графика , а B представляет собой пересечение между и отраженным участком графика .
Find both solutions:
A:
B:
Solving inequalities involving modulus functions
Based on the предыдущий пример, теперь мы собираемся решить неравенство.
 Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны и .
Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны и .После того, как у вас есть точки пересечения, вы можете посмотреть на график, чтобы определить значения x, которые удовлетворяют неравенству.
Решение неравенств с использованием модульных функций, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Неравенство верно, когда график выше графика , это происходит, когда или . В системе обозначений:
Обратная функция модуля
обратная функция модуля не является функцией , если только вы не ограничите его домен так, чтобы он мог быть функцией «один к одному». Чтобы добиться этого, нам нужно ограничить область его применения только половиной графа. Вы можете выбрать любую половину, если она не указана в вопросе.
Найти обратную функцию
Обратную функцию модуля, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Мы ограничим область определения функции только отраженным участком графика (слева от x = -1), который можно обозначить как для .
 Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.
Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.Следуя шагам, чтобы найти обратную функцию:
- Заменить F (x) на Y
- SWAP X и Y, и решайте для Y
обратная функция
Область определения обратной функции — это диапазон исходной функции, т. е. . Следовательно, область определения обратной функции равна .
Как отличить модульную функцию?
Чтобы найти производную функции модуля, нам нужно снова взглянуть на уравнение функции модуля:
Мы знаем, что , поэтому мы можем сказать следующее:
В общем, для всех значений x, кроме
Если мы подставим некоторые значения x в предыдущее уравнение, то увидим, что утверждения в приведенной выше кусочной функции верны:
Как интегрировать модульную функцию?
Чтобы найти интеграл модульной функции, мы можем действовать следующим образом:
Мы знаем, что модульная функция определяется следующим образом,
Следовательно, нам нужно вычислить интеграл для x и -x.

Помните, что x имеет показатель степени 1 ()
Используя формулу интегрирования:
Функции модуля — Основные выводы
- Модуль числа x будет тем же числом, но положительным.
- Модуль числа x представляет собой расстояние от нуля до этого числа x на числовой прямой.
- Чтобы начертить график функции модуля, вам нужно начертить и отразить часть линии, которая идет ниже оси x, в ось x.
- Наброски графиков уравнений или неравенств, включающих модульные функции, могут помочь решить их, найдя x-координаты точек пересечения двух графиков.
- Функция, обратная модульной функции, не является функцией, если только вы не ограничите ее область определения только половиной графика, чтобы она могла быть взаимно однозначной функцией.
- При нахождении производной и интеграла модульной функции будет два возможных решения, учитывая, когда (для ) и когда (для ).
Функция модуля — определение, формула, домен, диапазон, график!
Модульная функция — это тип функции, которая предоставляет нам абсолютное значение заданного числа или переменной.
Функция модуля Он дает нам величину любой переменной или числа. В этой конкретной статье о функции модуля или функции модуля мы узнаем о том, что такое модуль с определением, доменом и диапазоном функции модуля, за которым следует график функции модуля, свойства и многое другое.
Он дает нам величину любой переменной или числа. В этой конкретной статье о функции модуля или функции модуля мы узнаем о том, что такое модуль с определением, доменом и диапазоном функции модуля, за которым следует график функции модуля, свойства и многое другое.Тип функции, которая дает нам абсолютное значение данного числа или переменной, называется функцией модуля. То есть функция mod возвращает величину числа независимо от его знака. Функция Mod в математике также называется функцией абсолютного значения.
В математике модуль x представлен функцией модуля, обозначаемой |x|. Как понятно из названия и представления, он обеспечивает неотрицательное значение x. То есть результат этой конкретной функции всегда положителен, независимо от того, какие входные данные были предоставлены функции. Модуль или абсолютное значение количества также рассматривается как расстояние числа от начала координат/нуля.
Формула функции модуляФункция \(f\left(x\right)=\left|x\right|\) называется функцией модуля.

Здесь |х| обозначает модуль x, где x — действительное число. Если x неотрицательно, то f(x) будет иметь эквивалентное значение x. Однако, если x отрицательно, то f(x) будет обозначать величину x, то есть f(x) = -x, если x отрицательно. Показана итоговая формула модульной функции.
\(\begin{Bmatrix}f\left(x\right)&=x&x\ge0\\
f\left(x\right)&=-x &x<0\end{Bmatrix}\)Указывает, что если значение x больше или равно 0, то функция модуля улавливает фактическое значение, но если в случае, если x меньше 0, то функция ловит минус фактического значения или оригинала.
Также читайте о последовательностях и сериях здесь.
Домен и диапазон функции модуляМы можем использовать функцию модуля для каждого действительного числа. Диапазон функции модуля определяется как набор неотрицательных действительных величин и выражается как [0, ∞), тогда как область определения функции — R, где R относится к набору всех положительных действительных чисел.

Следовательно, домен |x| есть R, а его диапазон равен [0, ∞).
Если f: P → Q — функция, то множество P называется областью определения функции f, а множество Q — областью определения функции f.
Если f: P → Q — функция, то диапазон f состоит из тех компонент Q, которые связаны хотя бы с одним элементом P. Он выражается через f(P).
Таким образом, f(P) = {y : y = f(x) для некоторого x ∈ P}
Также проверьте эту статью о множествах.
График функции модуляТеперь давайте разберемся, как построить график mod x или график функции модуля. Рассмотрим x как переменную, принимающую значения от -6 до 6. При определении модуля для положительных значений «x» линия, очерченная на графике, представляет собой «y = x», а для отрицательных значений «x». линия, нарисованная на графике, это «y = -x».
x f(x) = |x| -6 6 -5 5 -4 4 -3 3 -2 2 -1 1 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Также читайте о матрицах здесь.

Линейный график модульной функции простирается в первом и втором квадрантах, поскольку координаты точек на графике соответствуют образцу (x, y), (-x, y). Функция f: R →R определяется как f(x) = |x| для каждого x ∈ R называется функцией модуля. Это означает, что для каждого неотрицательного значения x функция f(x) эквивалентна x. Хотя при отрицательных условиях x значение f(x) отрицательно относительно значения x. 92\leftrightarrow a<|x|
Также читайте о многострочных графиках здесь.
Если a отрицательно, то:
\(\left(a\right)\ |x|\ge a,\text{ или }|x|\ne a\ x\in R\)
\(\left(b\right)\ |x|\le a,x=ϕ\)
Для любых действительных чисел x и y:
\(\left(a\right)\ |xy|= |x||y|\)
\(\left(b\right)\ \left|\frac{x}{y}\right|=\left|\frac{x}{y}\right|\ текст{ для }y\ne0\)
\(\left(c\right)\ |x+y|\le|x|+|y|\)
\(\left(d\right)\ |x−y|\le|x|+|y|\)
\(\left(e\right)\text{ Для }x,y\ge0\ текст{ или }x,y<0,|x+y|=|x|+|y|\)
\(\left(f\right)|x+y|\ge|x|−|y| \)
\(\left(g\right)|x−y|\ge|x|−|y|\)
\(\left(h\right)\text{ Для }x,y\ge0 \text{ и }|x|\ge|y|\text{ или }x,y<0\text{ и }|x|\ge|y|,|x−y|=|x|−|y| \)
Абсолютное значение имеет следующие четыре основных свойства (a, b — действительные числа):
\(a]\ ∣a∣\ge0\text{ Неотрицательность}\)
\(b]\ ∣a∣=0⟺a=0\text{ Положительная определенность}\)
\(c]\ ∣ab∣=∣a∣∣b∣\text{ Мультипликативность}\)
\(d]\ ∣a+b∣\le∣a∣+∣b∣\text{ Субаддитивность, особенно неравенство треугольника}\)
Подробнее о пределах и непрерывности читайте здесь.
Производная модульной функции
Имея хорошее представление о различных свойствах модульных функций, мы узнаем о дифференцировании по модулю x или производной по модулю x. До сих пор мы знали, что модульная функция f(x) = |x| равно x, если x > 0, и -x, если x < 0,
\(\begin{Bmatrix}f\left(x\right)&=x&x\ge0\\
f\left(x\right)&=-x &x<0\end{Bmatrix}\)Отсюда , производная модульной функции равна 1, если x > 0, и -1, если x < 0. Следует учитывать, что производная модульной функции не определена для x = 0.
\(\begin{matrix }\frac{d\left\{f\left(x\right)\right\}}{dx}&=1&x>0\\
\frac{d\left\{f\left(x\right)\ right\}}{dx}&=-1&x<0\end{matrix}\)Таким образом, производная mod-функции может быть сформулирована как: \(\frac{d\left(\left|x\right|\ вправо)}{dx}=\frac{x}{\left|x\right|}\)
Для всех значений x и x, которые не равны 0.
Узнайте больше об интегральном исчислении здесь.
Интегрирование модульной функцииС учетом формулы модульной функции и формул интегрирования интеграл модульной функции задается следующим образом:
Если f(x) = |x| равно x, если x > 0, и -x, если x < 0, то интегрирование для функции:
\(\begin{Bmatrix}f\left(x\right)&=x&x\ge0\\
f\ влево(х\вправо)&=-x &x<0\end{Bmatrix}\) 92+C&\text{if }x<0\end{matrix}\)Также изучите различные приложения производных здесь.
Решенные примеры функций модуля
Зная знак модуля, определение и различные свойства, давайте теперь узнаем, как решать вопросы модуля с некоторыми решенными примерами:
Решенный пример 1: Получите область и диапазон для функции y = |4−x|.
Решение:
Дана функция y = |4−x|.
Ясно, что мы можем сказать, что это уравнение определено для x ∈ R. Следовательно, областью определения является R.
Теперь |4−x| ≥ 0 для всех x ∈ R
Следовательно, область значений равна [0, ∞)
Решено Пример 2: Получить область определения и определить диапазон заданной функции y = 3 − |2 − x|.
Решение:
y = 3 − |2 − x|
Ясно, что мы можем сказать, что эта функция определена для x ∈ R. Таким образом, областью определения данной функции является R.
Теперь, как мы знаем, |2−x|≥0 для всех x∈R
или может сказать:
−|2−x|≤0
3−|2−x|≤3 для всех x∈R
Следовательно, диапазон равен (−∞,3]
Ознакомьтесь с этой статьей по среднему отклонению
Решено Пример 3: Получить область определения и ранжировать заданную функцию
\(y=\frac{2}{\sqrt{x−|x|}}\)
Решение:
Здесь
\(x−\left|x\right|=\begin{matrix}x−x&=0&\text{ if }x\ge0\\
x+x&=2x&\text{ if } х\le0\конец{матрица}\)Следовательно, \(y=\frac{2}{\sqrt{x−|x|}}\) не определено для всех x ∈ R
Следовательно, область определения функции равна ϕ.
Решено Пример 4: Найти значение модульной функции |x| для x = -12 и x = 11
Решение: Если x = -12, то |x| = |-12| = 12
Если x = 11, то |x| = |11| = 11
Отсюда следует, что для |x| =12 для x = -12 и |x| = 11 для x = 11.
Это удовлетворяет свойству функции mod, которое говорит, что для отрицательного или положительного числа вывод |x| является только положительным числом.
Решено Пример 5: Решить |x + 4| = 9 с использованием определения функции mod.
Решение: Мы знаем, что выход функции модуля всегда неотрицательный. Следовательно, у нас будет два случая:
Если x + 4 > 0, то значение |x + 4| = x + 4, а если x + 4 < 0, то значение |x + 4| = -(х + 4).
Случай 1: Если x + 4 > 0, мы имеем
|x + 4| = x + 4
⇒ x + 4 = 9
⇒ x = 9- 4 = 5
Случай 2: Если x + 4 < 0, имеем
|х + 4| = -(x + 4)
⇒ -(x + 4) = 9
⇒ -x – 4 = 9
⇒ x = -4 – 9 = -13
Ответ: Следовательно, решение х = 5, -13.

Также читайте об арифметических прогрессиях в этой статье.
Мы надеемся, что приведенная выше статья о модульных функциях поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о функции модуляВ.1 Что такое функция модуля?
Ответ 1 Функция модуля — это тип функции, которая дает нам абсолютное значение заданного числа или переменной.
Q.2 Что такое модуль в математике?
Ответ 2 В математике модуль x представлен функцией модуля, обозначенной |x|.
Q.3 Какова область определения функции модуля?
Ответ 3 Домен функции mod R.
Q.
 4 Каков диапазон функции модуля?
4 Каков диапазон функции модуля? Ответ 4 Диапазон функции модуля представляет собой набор неотрицательных действительных величин, который выражается как [0,∞).
В.5 Какие существуют типы функций?
Ответ 5 Существуют следующие типы функций: функция «многие к одному», функция «один к одному», функция «на одно», функция «один и на», постоянная функция, тождественная функция, квадратичная функция, полиномиальная функция, рациональная функция, сигнум-функция, функция наибольшего целого числа и так далее.
Q.6 Каковы домены и диапазоны функции?
Ответ 6 Если f: P → Q — функция, то множество P называется областью определения функции f. Аналогично. Если f: P → Q является функцией, то диапазон f состоит из тех компонентов Q, которые связаны хотя бы с одним элементом P.
Q.7 Что вы подразумеваете под функцией?
Ответ 7 Функция относится к определенному отношению, которое описывает каждый элемент одного набора только с одним элементом, относящимся к другому набору.
Скачать публикацию в формате PDF
More from testbook.com
Domain of a Function: Meaning and Calculation with Graphs and Examples Atomic Number – Know Atomic Mass Number, Isotopes, Isobars & Understand with Examples Chemistry in Повседневная жизнь – использование химии в мыле, моющих средствах, антацидах, лекарствах и многом другом Электронная конфигурация, правила распространения, стабильность атомов с примерами Галогеналканы и галоарены: Знайте о галогенных производных углеводородов, типах и свойствах Что такое модульный оператор (%) в Python?
Когда мы видим «%», первое, что приходит нам на ум, это «знак процента», но когда мы думаем об этом с точки зрения компьютерного языка, этот знак на самом деле имеет другое имя и значение. В вычислениях операция по модулю (%) находит остаток или знаковый остаток после деления одного числа на другое (называемый модулем операции).

Для двух положительных чисел, a и n, модуль n (a % n, сокращенно mod n) представляет собой остаток от евклидова деления числа a на n, где a — делимое, а n — делитель.
В основном, операция Python по модулю используется для получения остатка от деления. Оператор по модулю ( % ) считается арифметической операцией, наряду с +, –, /, *, **, //. В большинстве языков оба операнда этого оператора по модулю должны быть целыми числами. Но Python Modulo в этом случае универсален. Операнды могут быть либо целым числом , либо числом с плавающей запятой .
Синтаксис:
а % б
Здесь a делится на b, и возвращается остаток от этого деления.
Код:
Python3
a=13b=5c=a%bprint(a,"mod", b,"=",c, sep=" ")d=15. 0
0 e=7.0f=d%eprint(d,"mod", e,"=",f, sep=" ")Выход:
13 mod 5 = 3 15,0 по модулю 7,0 = 1,0
Это был простой пример, показывающий использование синтаксиса и базовую операцию, выполняемую оператором по модулю. Предположим, мы хотим вычислить остаток от каждого числа от 1 до n при делении на фиксированное число k.
Python3
deffindRemainder(n, k):foriinrange(1, n+1):REM=I%KПечать(I,"MOD"(I,"MOD"(I,"(I,"(I,"(I,"0 , k,"=",rem, sep=" ")if__name__=="__main__":n=5k=3findRemainder(n, k)Output:
1 mod 3 = 1 2 по модулю 3 = 2 3 мод 3 = 0 4 по модулю 3 = 1 5 мод 3 = 2
Исключения
Единственное исключение, которое вы получаете с операцией по модулю python, — это ZeroDivisionError .
 Это происходит, если операнд делителя оператора по модулю становится равным 9.0067 ноль . Это означает, что правый операнд не может быть равен нулю . Давайте посмотрим на следующий код, чтобы узнать об этом исключении Python.
Это происходит, если операнд делителя оператора по модулю становится равным 9.0067 ноль . Это означает, что правый операнд не может быть равен нулю . Давайте посмотрим на следующий код, чтобы узнать об этом исключении Python.Python3
a=14b=0try:print( а,'мод', б,'=',a%b, sep=" ")exceptZeroDivisionError as err:print('Нельзя делить на ноль!'+
1 ) 9019'Изменить значение правого операнда. '
' Вывод:
Нельзя делить на ноль! Изменить значение правого операнда.
Функция модуля | Редакция
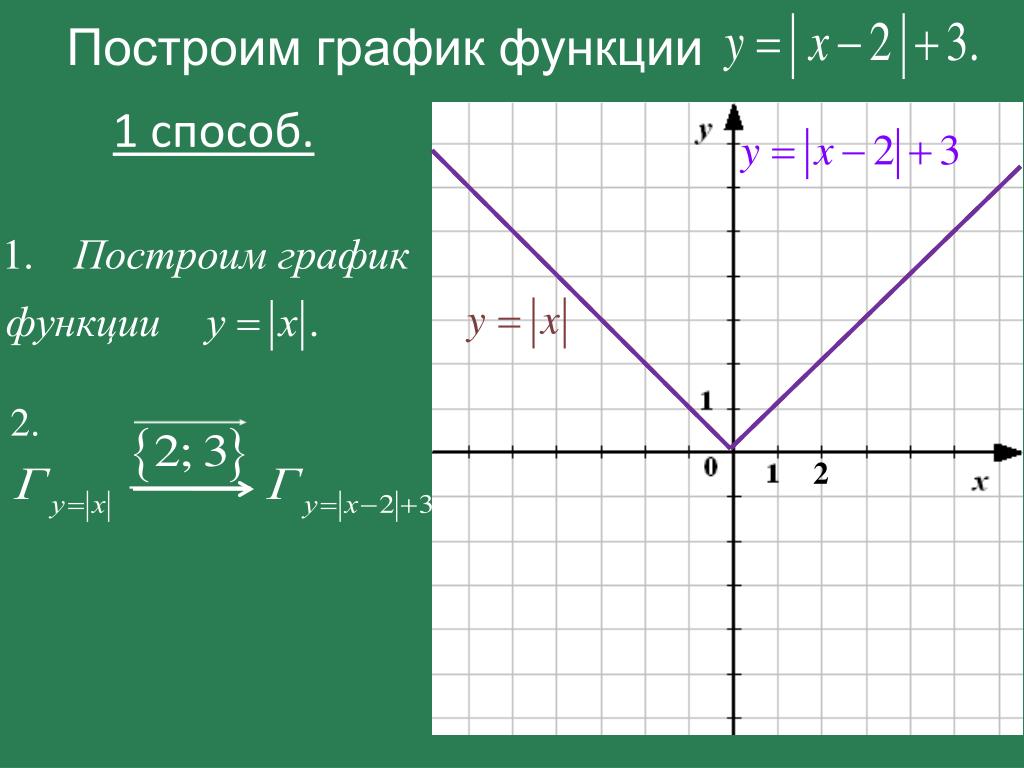
Уровень
Обозначение модуляСледующие обозначения относятся к модулю :
- Модуль числа, например. х записывается как |х|.
- Как правило, |x| = x для x \geq 0 и |x| = -x для x <0
- Функции также имеют модуль: напр. если f(x) = -2, то |f(x)| = 2
- |ф(х)| = f(x), когда f(x) \geq 0 и |f(x)| = -f(x), когда f(x)<0
- Если модуль находится внутри функции, т.е. f(|x|), то вы применяете модуль к значению x перед применением функции, то есть f(|-4|) = f(4)
Уровень
Графики модульных функций – прямые линииСуществует 3 типа графиков модуля , которые вам могут предложить нарисовать:
- y = |f(x)| — все отрицательные значения f(x) становятся положительными на , отражающий отрицательный участок графика f(x) по оси x .
 Это ограничивает диапазон до |f(x)| \geq 0 (или подмножество внутри |f(x)| \geq 0, например, |f(x)| \geq 2.
Это ограничивает диапазон до |f(x)| \geq 0 (или подмножество внутри |f(x)| \geq 0, например, |f(x)| \geq 2. - y = f(|x|) – отрицательные значения x дают тот же результат, что и соответствующие положительные значения x, поэтому график f(x) для x \geq 0 отражается на оси y , для отрицательных значений x.
- у = |f(-x)| - знак перестановки значений x (т.е. с положительного на отрицательное или с отрицательного на положительное), поэтому график f(x) отражается по оси y. Затем все отрицательные значения f(x) становятся положительными с помощью , отражающего отрицательный участок графика f(x) по оси x. Диапазон ограничен, как и в случае y = |f(x)|.
Лучший и самый простой способ построить эти графики — сначала построить график зависимости y = f(x), а затем отразить его на соответствующей оси или осях.
Пример: Для f(x) = 2x-1 нарисуйте графики
\begin{aligned} y &= |f(x)| \\ y &= f(|x|) \\ y &= f|(-x)| \end{выровнено} 92-2x, нарисуйте графики
\begin{aligned} y &= |f(x)| \\ y &= f(|x|) \\ y &= |f(-x)| \end{выровнено}
Уровень
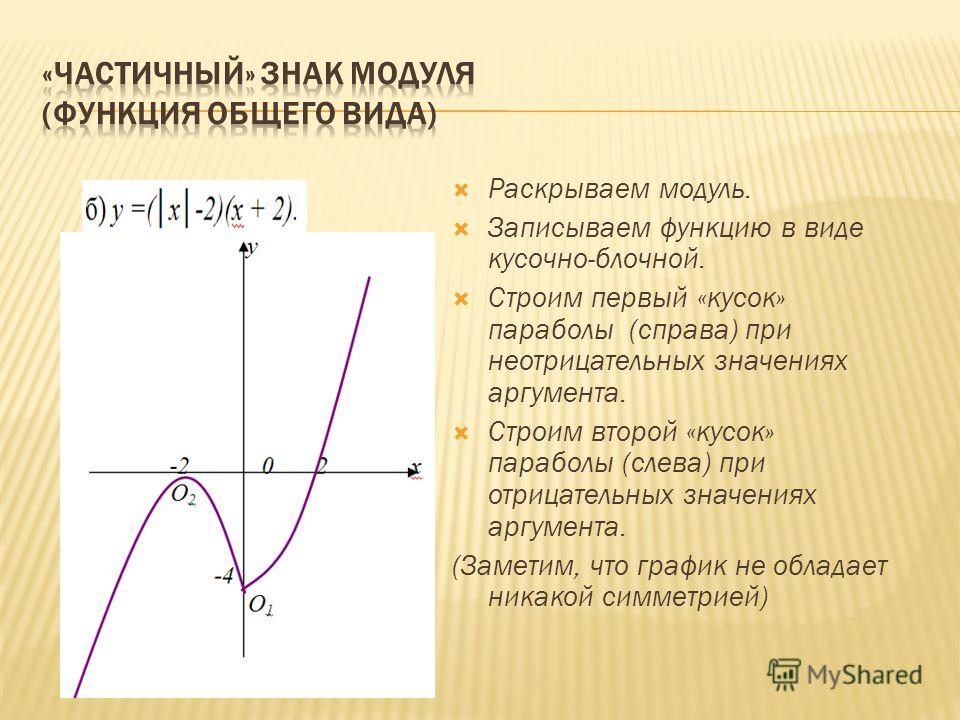
Графическое решение уравнений модуляЧтобы решить уравнений модуля формы |f(x)| = n или |f(x)| = |g(x)|, вы можете решить их графически , используя следующий метод:
Шаг 1: Нарисуйте графики y = |f(x)| и y = n на той же паре осей.

Шаг 2: Определите диапазоны значений x, для которых f(x) \geq 0 и f(x) < 0 из графика.
напр. f(x) \geq 0 для x \leq \textcolor{red}{a} или x \geq \textcolor{blue}{b} и f(x) < 0 для \textcolor{red}{a} < x < \textcolor{blue}{b}
Шаг 3: Используйте шаг 2, чтобы написать 2 новых уравнения, по одному для каждого диапазона x:
f(x) = n для x \leq \textcolor{red} {a} или x \geq \textcolor{blue}{b}
- f(x) = n для \textcolor{red}{a} < x < \textcolor{blue}{b}
Шаг 4: Решите каждое уравнение по очереди и убедитесь, что решения верны, и удалите все, которые находятся за пределами диапазона x для этого уравнения.
Шаг 5: Проверьте правильность решений, взглянув на график.
Примечание: Используйте тот же метод для |f(x)| = |g(x)|, заменив n на g(x).
Уровень
Алгебраическое решение уравнений модуляДля уравнений вида |f(x)| = n и |f(x)| = g(x) вы можете решить их алгебраически вместо графически — если вы чувствуете, что достаточно хорошо разбираетесь в теме.

Пример: Решить |2x+2| = x+4
Шаг 1: Решите для положительных значений:
\begin{aligned} 2x + 2 &= x+4 \\ \textcolor{red}{x} &= \textcolor{red}{2 } \end{align}
Шаг 2: Решение для отрицательных значений:
\begin{aligned} -(2x + 2) &= x+4 \\ 3x &= -6 \\ \textcolor{red} {x} &= \textcolor{red}{-2} \end{aligned} 92 + 14x + 8 &= 0 \\ (3x+2)(x+4) &= 0 \end{aligned}
Шаг 3: Итак, решения:
\textcolor{red}{x = - \dfrac{2}{3}} и \textcolor{red}{x = -4}
Уровень
Примечание:С помощью этих методов можно также решить модульных неравенств . Графический метод решения неравенств будет полезен, так как часто используется квадратное уравнение. Еще одно полезное правило:
|x-a| < b \, \ тогда и только тогда, когда \, a - b < x < a + b
Продукт
Переходные математические карточки
8,99 фунтов стерлингов
Переходные математические карточки — идеальный способ охватить темы более высокого уровня GCSE, а также познакомиться с новыми темами по математике уровня A, которые помогут вам подготовиться к 12 классу.
 Ваше идеальное руководство для начала работы с математикой уровня А! Прибыль от каждого пакета реинвестируется в создание бесплатного контента на MME, что приносит пользу миллионам учащихся по всей стране.
Ваше идеальное руководство для начала работы с математикой уровня А! Прибыль от каждого пакета реинвестируется в создание бесплатного контента на MME, что приносит пользу миллионам учащихся по всей стране.Посмотреть продукт
Уровень
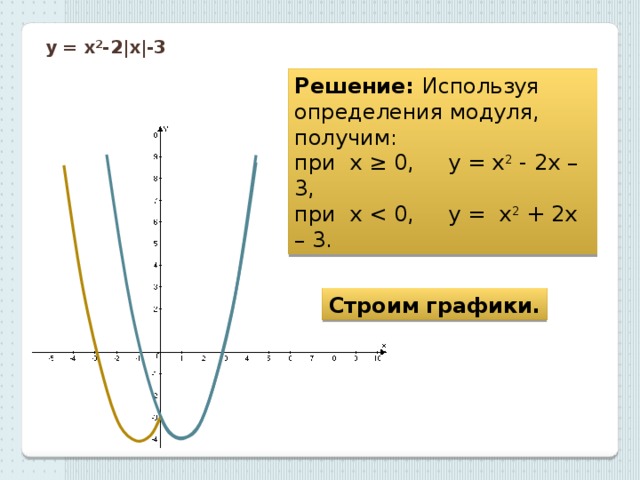
Пример 1: графическое решение уравнений модуля – прямые линииРешить |2x+3| = x+2
[3 балла]
Шаг 1: Нарисуйте графики y = |2x+3| и y = x+2 на той же паре осей.
Шаг 2: Определите диапазоны значений x, для которых f(x) \geq 0 и f(x) < 0, из графика:
2x+3 \geq 0 для x \geq - \dfrac{3 {2} и 2x+3 < 0 для x < - \dfrac{3}{2}
Шаг 3: Используйте шаг 2, чтобы написать 2 новых уравнения, по одному для каждого диапазона x:
(1) 2x+3 = x+2 для x \geq - \dfrac{3}{2}
(2) - (2x+3) = x+2 для x < - \dfrac{3}{2}
Шаг 4: Решите каждое уравнение по очереди и убедитесь, что решение верно, и удалите все которые находятся за пределами диапазона x для этого уравнения.

Решение (1): x=-1 (это верно, поскольку -1 \geq - \dfrac{3}{2})
Решение (2): 3x = -5 \Rightarrow x = - \dfrac{5 }{3} (действительно, поскольку - \dfrac{5}{3} < - \dfrac{3}{2}) 92 + 4(2) - 9 = 11
г) - |f(2)| = - |11| = - 11
a)i) Отрицательное сечение должно быть отражено по оси x:
ii) Для отрицательных значений x отразите линию по оси y:
iii ) Отразите f(x) по оси y, а затем отразите отрицательное сечение по оси x:
b)
Сначала нарисуйте графики y = |3x - 3| (используя часть a)i)) и y = \dfrac{3}{2} на той же паре осей:
3x - 3 \geq 0 при x \geq 1 и 3x - 3 < 0 при x < 1
Таким образом, мы можем составить два уравнения: \dfrac{3}{2} для x \geq 1
(2) -(3x-3) = \dfrac{3}{2} для x < 1
Тогда мы можем решить следующие задачи:
Решение (1): 3x = \dfrac{9}{2} \Rightarrow x = \dfrac{3}{2} для x \geq 1 (это справедливо, поскольку \dfrac{3}{2} \ экв 1)
Решение (2): 3x = \dfrac{3}{2} \Rightarrow x = \dfrac{1}{2} для x < 1 (это верно, поскольку \dfrac{1}{2} < 1 )
Судя по графику, оба решения кажутся правильными.

- Для отрицательных значений y отразите по оси x.

 Все, что было над осью Oх зеркально отражается вниз.
Все, что было над осью Oх зеркально отражается вниз.
 В этом случае (0, -1) становится (0, 1)
В этом случае (0, -1) становится (0, 1) Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны и .
Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны и .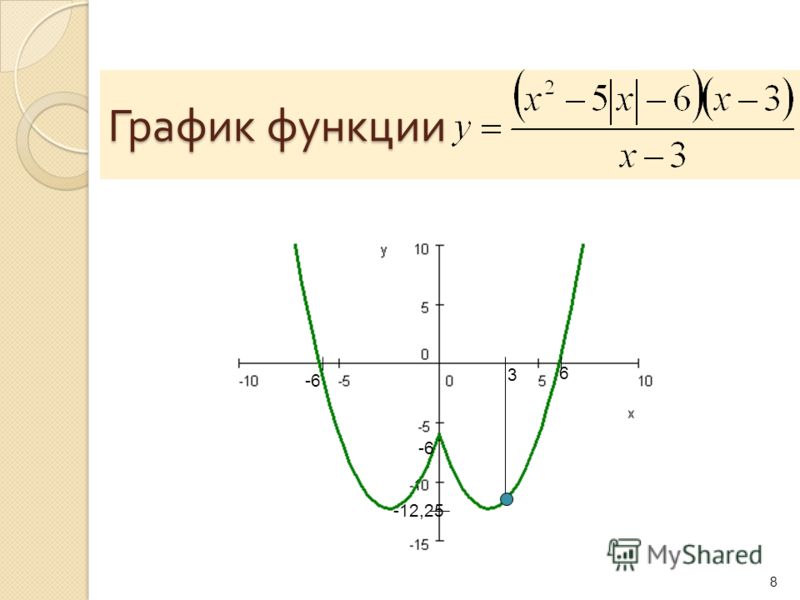 Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.
Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.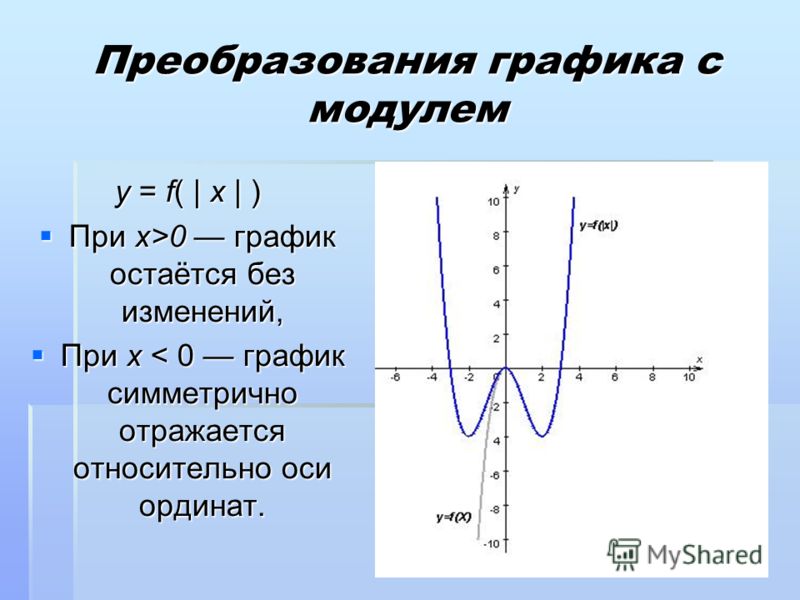
 Он дает нам величину любой переменной или числа. В этой конкретной статье о функции модуля или функции модуля мы узнаем о том, что такое модуль с определением, доменом и диапазоном функции модуля, за которым следует график функции модуля, свойства и многое другое.
Он дает нам величину любой переменной или числа. В этой конкретной статье о функции модуля или функции модуля мы узнаем о том, что такое модуль с определением, доменом и диапазоном функции модуля, за которым следует график функции модуля, свойства и многое другое.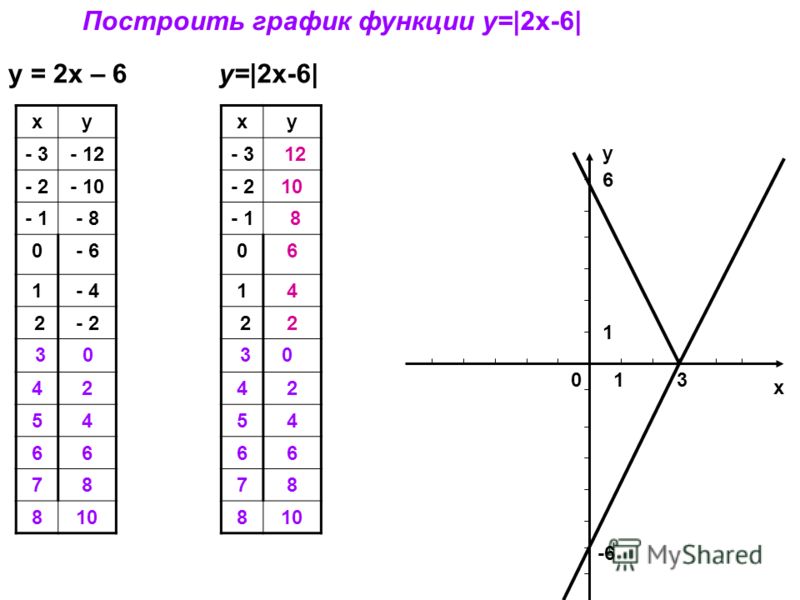



 4 Каков диапазон функции модуля?
4 Каков диапазон функции модуля? 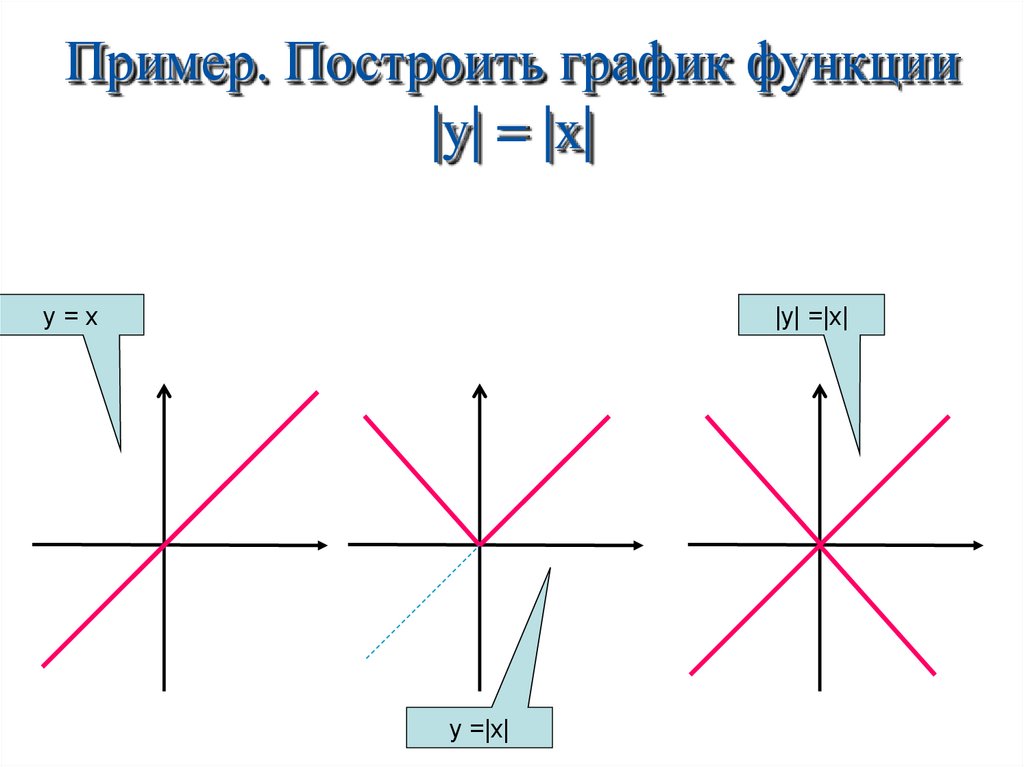
 0
0  Это происходит, если операнд делителя оператора по модулю становится равным 9.0067 ноль . Это означает, что правый операнд не может быть равен нулю . Давайте посмотрим на следующий код, чтобы узнать об этом исключении Python.
Это происходит, если операнд делителя оператора по модулю становится равным 9.0067 ноль . Это означает, что правый операнд не может быть равен нулю . Давайте посмотрим на следующий код, чтобы узнать об этом исключении Python. '
'  Это ограничивает диапазон до |f(x)| \geq 0 (или подмножество внутри |f(x)| \geq 0, например, |f(x)| \geq 2.
Это ограничивает диапазон до |f(x)| \geq 0 (или подмножество внутри |f(x)| \geq 0, например, |f(x)| \geq 2.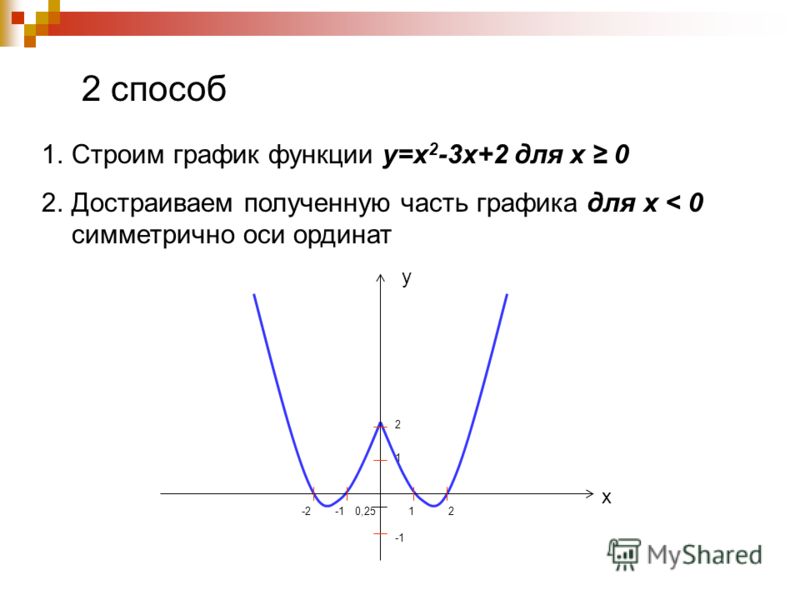
 Ваше идеальное руководство для начала работы с математикой уровня А! Прибыль от каждого пакета реинвестируется в создание бесплатного контента на MME, что приносит пользу миллионам учащихся по всей стране.
Ваше идеальное руководство для начала работы с математикой уровня А! Прибыль от каждого пакета реинвестируется в создание бесплатного контента на MME, что приносит пользу миллионам учащихся по всей стране.