|
Причем, чем больше значение k, тем круче идет прямая.
,_esli_izvesten_grafik_funkcii_y_=_f(x)_10.5.jpg)
| 1. |
Вспомогательная система координат
Сложность: лёгкое |
|
2.
|
Параллельный перенос графика функции
Сложность: лёгкое |
2 |
| 3. |
Направление сдвига графика функции
Сложность: лёгкое |
2 |
4.
|
Формула функции
|
2 |
| 5. |
Уравнение параболы
Сложность: среднее |
2 |
6.
|
Значение функции
Сложность: среднее |
2 |
| 7. |
Построение графика квадратичной функции вида y = (x + a)² + b
Сложность: среднее |
3 |
8.
|
Метод выделения полного квадрата Сложность: сложное | 3 |
| 9. |
Функции
Сложность: сложное |
3 |
10.
|
Графическое решение системы уравнений
Сложность: сложное |
3 |
Построение графика с помощью элементарных преобразований.
Построение графика функции
y=f(kx) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; b=0)Рассмотрим сначала два частных случая при b=0,т.е. функция имеет вид y=f(kx) .
1. При |k|>1 график функции y=f(x) сжимается в |k| раз вдоль оси OX относительно оси OY.
2. При |k|<1 график функции y=f(x) растягивается в раз вдоль оси OX относительно оси OY . При k<0 полученный график дополнительно отображаем симметрично относительно оси OY.
Рассмотрим примеры:
| Построить график функции | Построить график функции |
Построение графика функции
y=f(x+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; k=1)При b>0 график функции y=f(x) сдвигается влево вдоль оси OX на b единиц.
При b<0 график функции y=f(x) сдвигается вправо вдоль оси OX на |b| единиц
Рассмотрим примеры:
| Построить график функции ( b>0 ) | Построить график функции ( b<0 ) |
Построение графика функции
y=f(kx+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0)Рассмотрим общий случай : y=f(kx+b) .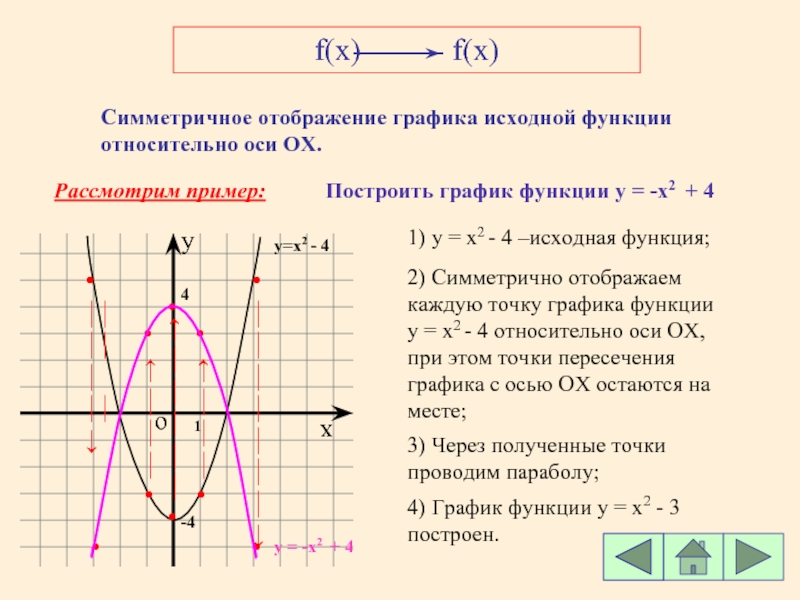
Сначала вынесем коэффициент k за скобку: .
Именно число определяет сдвиг вдоль оси OX , а не b ,
как полагают некоторые абитуриенты.
Теперь строим график функции y=f(x) . Затем строим график функции y=f(kx) , после чего сдвигаем полученный график вдоль оси OX на единиц влево или вправо в зависимости от знака этого числа.
| Рассмотрим пример: построить график функции |
Построение графика функции
y=A·f(kx+b)+B с помощью элементарных преобразоаний графика функции y=f(x)Комбинируя методы построения графиков, рассмотренные в предыдущих случаях, можно по известному графику функции y=f(x) построить график функции y=A·f(kx+b)+B с помощью растяжений, сжатий по горизонтали и вертикали,
параллельных переносов вдоль осей координат,
а также симметрий относительно координатных осей тех графиков,
которые получаются из первоначального графика последовательно применением подходящего преобразования.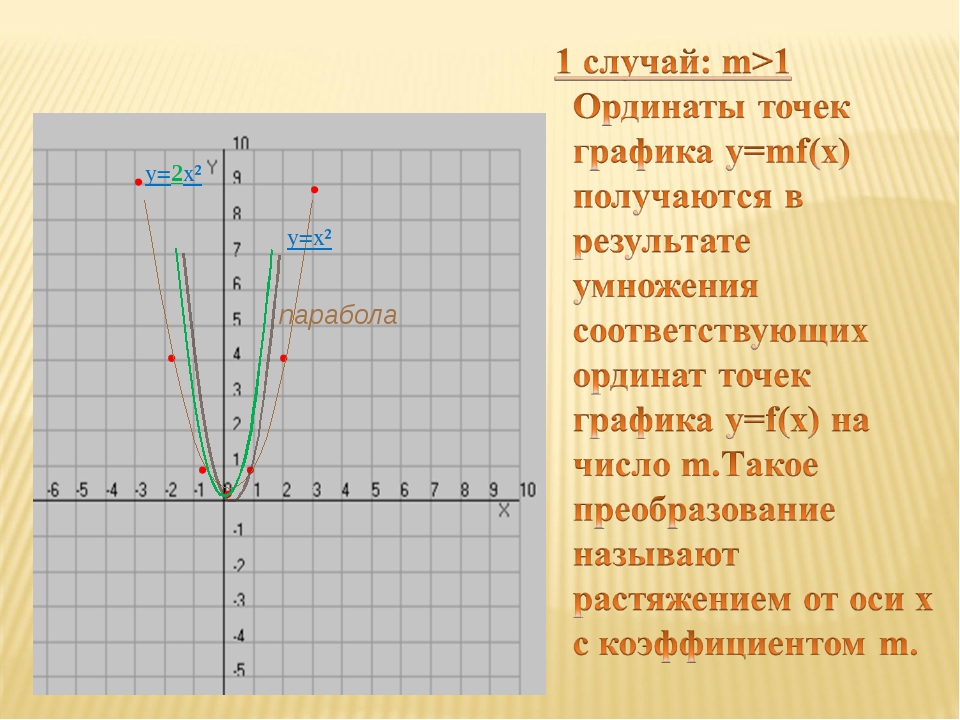
Рассмотрим примеры.
| Построить график функции | Построить график функции |
Открытая Математика. Функции и Графики. Алгебраические операции над функциями
Построение графика суммы (произведения) двух функций производится сложением (умножением) ординат точек графиков с одинаковыми абсциссами. Приведем для примера графики функций y = x + sin x и y = x sin x, являющихся соответственно суммой и произведением графиков y = x и y = sin x.
Правило построения графика функции 1f(x), если график функции f(x) уже построен.
Если x = a – вертикальная асимптота графика функции f(x), то есть limx→a+0f(x)=∞ или limx→a-0f(x)=∞, то limx→a+01f(x)=0 или соответственно limx→a-01f(x)=0.
Таким образорм, в случае, когда x = a – двусторонняя вертикальная асимптота графика функции f(x), x = a будет нулем функции 1f(x).Если у графика функции f(x) есть горизонтальная асимптота y = 0 при x→∞, то limx→∞1f(x)=∞.
Если у графика функции f(x) есть горизонтальная асимптота y = b при x→∞, то график функции 1f(x) будет иметь горизонтальную асимптоту y=1b.
Если график функции f(x) пересекает ось абсцисс в точке (x0; 0), то есть x0 – нуль функции f(x): f(x0)=0, то x=x0 – вертикальная асимптота графика функции y=1f(x).
Если точка (x0; y0) – точка максимума (минимума) функции f(x) и y0≠0, то (x0; 1y0) – точка минимума (максимума) функции 1f(x).
Промежуткам возрастания (убывания) графика функции f(x) соответствуют промежутки убывания (возрастания) графика функции 1f(x).
Пусть известен график y = f (x) и нужно построить график функции y = |f (x)|. По определению, |fx|={fxпри fx≥0,-fxпри fx<0. Значит, часть графика, лежащую в верхней координатной полуплоскости, изменять не надо, а часть графика, лежащую в нижней координатной полуплоскости, нужно отобразить симметрично оси OX.
Пусть известен график y = f (x) и нужно построить график функции y = f (|x|). Заметим, что при x ≥ 0 f (|x|) = f (x), а функция y = f (|x|) четная. Поэтому, чтобы построить график функции y = f (|x|), нужно часть графика функции y = f (x), лежащую в левой координатной полуплоскости, отбросить, а часть графика, лежащую в правой координатной полуплоскости, отобразить симметрично относительно оси OY.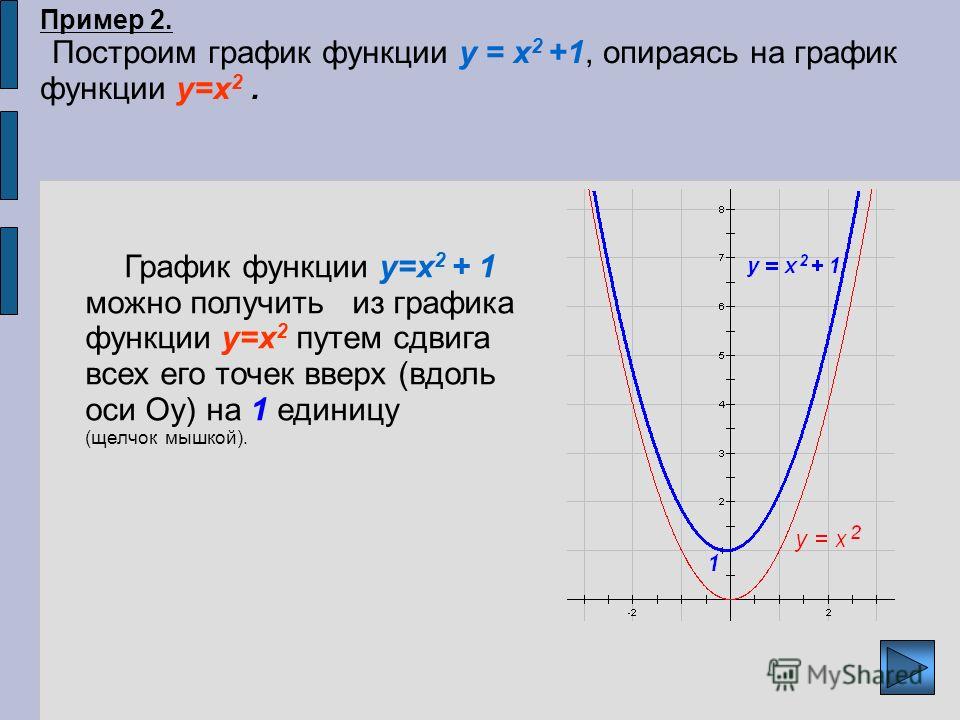
Как построить график функции y=f(x+m)+n, если известен график функции y=f(x)
График функции График функции y = f(x + m) получается параллельным переносом графика функции y=f(x) вдоль оси х на |m| единиц масштаба влево, если m > 0 и вправо, если m
Слайд 13
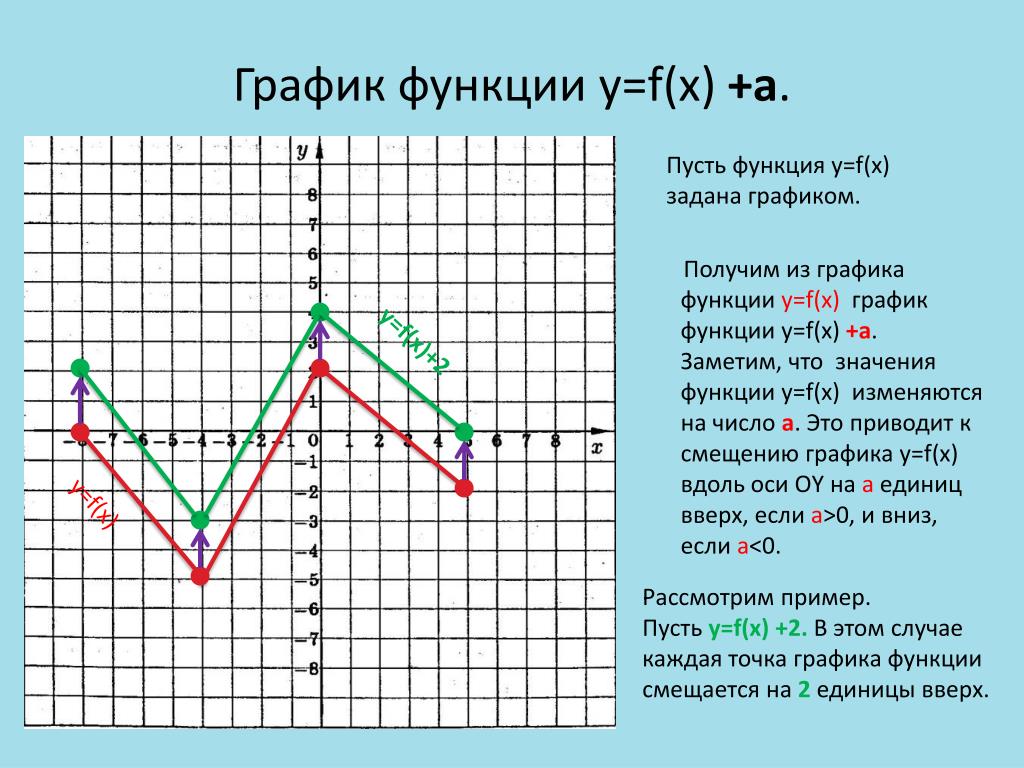
График функции График функции y = f(x)+n получается параллельным переносом графика функции y=f(x) вдоль оси y на |n| единиц масштаба вверх, если n > 0 и вниз, если n
Слайд 14
Самостоятельная работа.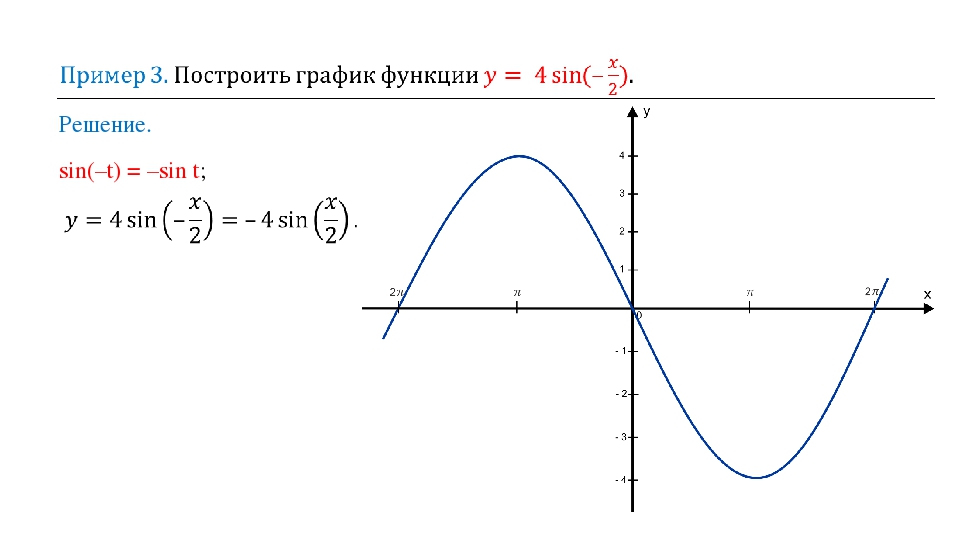
№1. Постройте графики функций. Ответьте на вопросы.
Запишите названия графиков____________________________________________
Какие изменения вы заметили у графика второй функции относительно базового графика?_________________________
Слайд 15
№2 Постройте графики функций. Ответьте на вопросы.
Запишите названия графиков_______________________
Какие изменения вы заметили у графика второй функции относительно основного графика?_____________
Слайд 16
Выводы: основные преобразования графиков элементарных функций:
Сжатие и растяжение графика вдоль
оси y у=k f(x).
Преобразование симметрии относительно оси x у = — f(x)
Сдвиг вдоль оси абсцисс y = f (x + a)
Сдвиг вдоль оси ординат y = f (x) +n
Слайд 17
вправо
вниз
вправо
вверх
Слайд 18
На одном из рисунков изображен график
функции
Укажите номер этого рисунка.
На каком рисунке изображён график
функции y= —
Слайд 19
Задайте формулой функцию
по графику,
изображенному на рисунке.,_esli_izvesten_grafik_funkcii_y_=_f(x)_10.9.jpg)
Слайд 20
Слайд 21
y
Алгоритм 1.
у=4
1. Построить график функции y=f(x)
4 ед.
2. Осуществить параллельный перенос графика y=f(x) вдоль оси х на |m| единиц масштаба влево, если m>0, и вправо, если mx
5 ед.
3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на |n| единиц масштаба вверх, если n>0, и вниз, если nХ=5
Слайд 22
y
Алгоритм 2.
у=4
1. Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые х=-m, y=n, т.е. выбрав в качестве начала новой системы координат точку (-m,n).
4 ед.
x
5 ед.
2. К новой системе координат привязать график функции y=f(x).
Х=5
Слайд 23
y
-4
x
-5
Слайд 24
y
-4
x
Слайд 25
y
x
-4
Слайд 26
Готовимся к экзамену!
Ответ: 2
Слайд 27
Готовимся к экзамену!
Ответ: 3
Слайд 28
умение получать из графика функции y=f(x) график функции y=f(x+l)+m метом движения вдоль осей координат
Технологическая карта урока
Технологическая карта урока Класс: 8 Предмет: алгебра Тема урока: Погрешность и точность измерения.
Дидактическая цель урока: создать условия для восприятия и осознания понятий абсолютная и относительная
Технологическая карта урока математики
АДМИНИСТРАЦИЯ ГОРОДСКОГО ОКРУГА ПОДОЛЬСК КОМИТЕТ ПО ОБРАЗОВАНИЮ Муниципальное общеобразовательное учреждение «Лицей 1» (МОУ «Лицей 1») Технологическая карта урока математики Урок математики в 6 классе
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Марахина Ольга Анатольевна Предмет: алгебра 7 класс УМК: А.Г. Мордкович, Алгебра 7 класс Тема урока: Взаимное расположение графиков линейных функций Тип урока: изучение
ПодробнееТехнологическая карта урока
Технологическая карта урока Предмет: математика Класс: 5 Учебник (УМК): Виленкин Н. Я., Жохов В. И., Чесноков А.
С., Шварцбурд С. И. Математика 5 класс: Учебник для общеобразовательных учреждений. — М.:
РАЗРАБОТКА УРОКА ПО ТЕМЕ «ПРОЦЕНТЫ»
РАЗРАБОТКА УРОКА ПО ТЕМЕ «ПРОЦЕНТЫ» Решение задач на основе материала о здоровом образе жизни. Ф.И.О. учителя: Силуянова Надежда Валентиновна Должность: учитель математики Предмет: математика Класс 5 Базовый
ПодробнееТехнологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
ПодробнееТехнологическая карта урока
Технологическая карта урока Предмет, класс Математика, 5А Автор (ы) УМК Н. Я. Виленкин, М.; Мнемозина, 2012 год ФИО учителя, школа Страшнова Г.
А. МОУ СОШ 2 Тема урока Умножение десятичных дробей на натуральные
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА Учитель Алтухов В. Д. Тема: Построение графика квадратичной функции. 9 класс Цель: Формирование ценностного отношения к пониманию и применению алгоритма построения квадратичной
ПодробнееТехнологическая карта урока математики
Технологическая карта урока математики Изучаемая тема: Устные и письменные приемы вычисления вида 32-5, 51-27 Место урока в изучаемой теме: 5 Дата проведения: 14.04.2017 г. Класс: 2 Программа: УМК «Перспектива»
ПодробнееТехнологическая карта открытого урока.
Технологическая карта открытого урока. Место проведения: МБОУ СОШ 22 г.о. Самара Уровень: школьный (присутствовали: методисты НМЦентра «РС Л.
В.Занков», учителя школы) Дата: 22.04.2013 года Предмет: Окружающий
Тема урока: «Десятичные дроби»
Тема урока: «Десятичные дроби» 1 ФИО ХачетловаЗалинаСаадуловна Место работы МКОУ «Гимназия 1» го Нальчик Должность Учитель математики 4 Предмет Математика 5 Класс 5 6 Тема и номер урока в теме Дествия
ПодробнееПлан-конспект. Тема: Степень числа. 5 класс
План-конспект Тема: Степень числа. 5 класс 1.Цель урока: организовать деятельность учащихся по открытию нового знания, создать условия для осознания и осмысления учебной информации по теме: «Степень числа»
ПодробнееПредмет математика класс 2 г
Предмет математика класс 2 г Тема урока Место урока по теме (в разделе/главе) Закрепление изученного по теме «Умножение и деление» «Умножение и деление» 18 из 20 Тип урока Форма урока, форма учебной деятельности,
ПодробнееУрок русского языка 2 класс
Урок русского языка 2 класс Тема: «Правописание корней в родственных словах».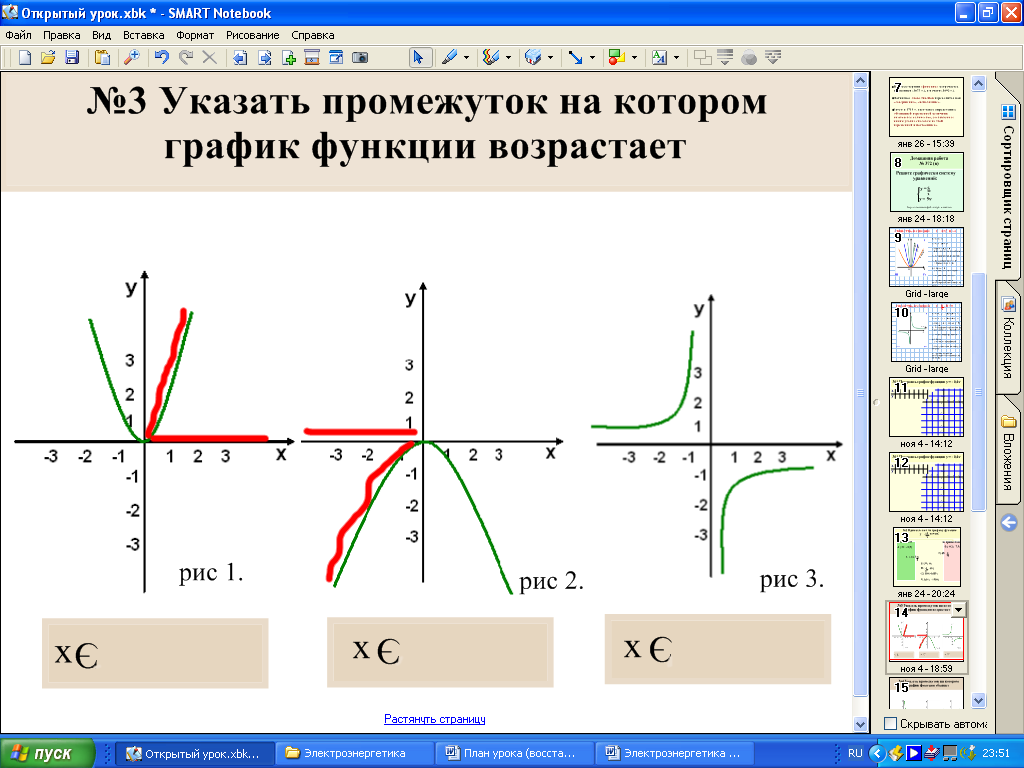
1. Краткая аннотация. Тип урока: закрепление пройденного материала, использование проблемно-диалогической технологии. 2. Учебник
ПЛАН-КОНСПЕКТ УРОКА Уравнения
1. ФИО (полностью) Савгильдина Любовь Васильевна 2. Место работы ГБОУ СОШ д.екатериновка 3. Должность Учитель математики 4. Предмет Математика 5. Класс 5 6. Тема и номер урока в теме Уравнения, 1-2 урок
ПодробнееКонспект урока по математике в 6 классе
Конспект урока по математике в 6 классе УМК: Н.Я.Виленкина, В.И.Жохова, А.С.Чеснокова, С.И.Шварцбурда «Математика 5», «Математика 6», издательства М.: «Мнемозина». Тема урока: Умножение обыкновенных дробей.
ПодробнееТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Этап урока Деятельность учителя Деятельность ученика 1 2 4 5 Организационный момент Актуализация знаний.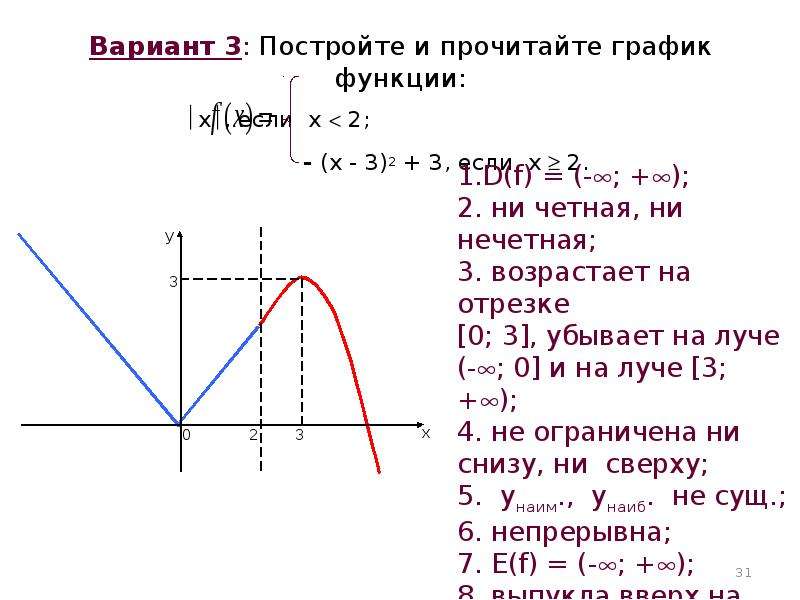
Целеполагание и мотивация Изучение нового материала. Закрепление изученного материала. Решение задач.
Технологическая карта урока
Технологическая карта урока 1. ФИО Сергеева Марианна Кононовна 2. Место работы МБОУ «Сунтарская средняя общеобразовательная школа 1 им.а. П. Павлова» 3. Должность учитель математики 4. Предмет математика
ПодробнееТехнологическая карта урока
Технологическая карта урока Тема: Площадь прямоугольного треугольника. Класс: 4 класс. Предмет: математика. УМК (авторы): УМК «Перспектива», автор Л.Г. Петерсон Тип урока: открытие нового знания. Планируемые
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Кривцовой О. И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика.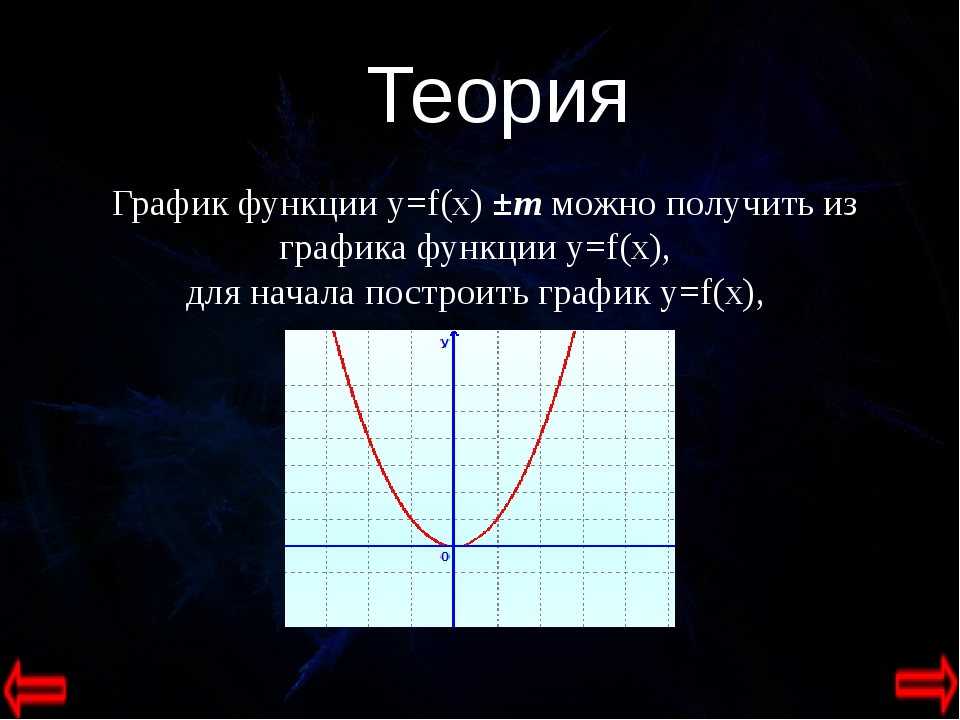
Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
Технологическая карта урока
Технологическая карта урока Тема урока: «Прямоугольник» Класс: 5 Учитель: Рыжова Лидия Петровна Тип урока: урок «открытия» нового знания Цели по содержанию: обучающие: изучить свойства прямоугольника развивающие:
ПодробнееТехнологическая карта урока
Технологическая карта урока ФИО Попенкова Татьяна Сергеевна КЛАСС 3 УМК «Начальная школа XXI век» ПРЕДМЕТ Математика ТЕМА Умножение многозначного числа на двузначное. ТИП Урок открытия нового знания. ЦЕЛЬ
ПодробнееТехнологическая карта урока
Технологическая карта урока ФИО Суркова Зинаида Ивановна Класс 5 Глава 1. Натуральные числа и шкалы (18 часов).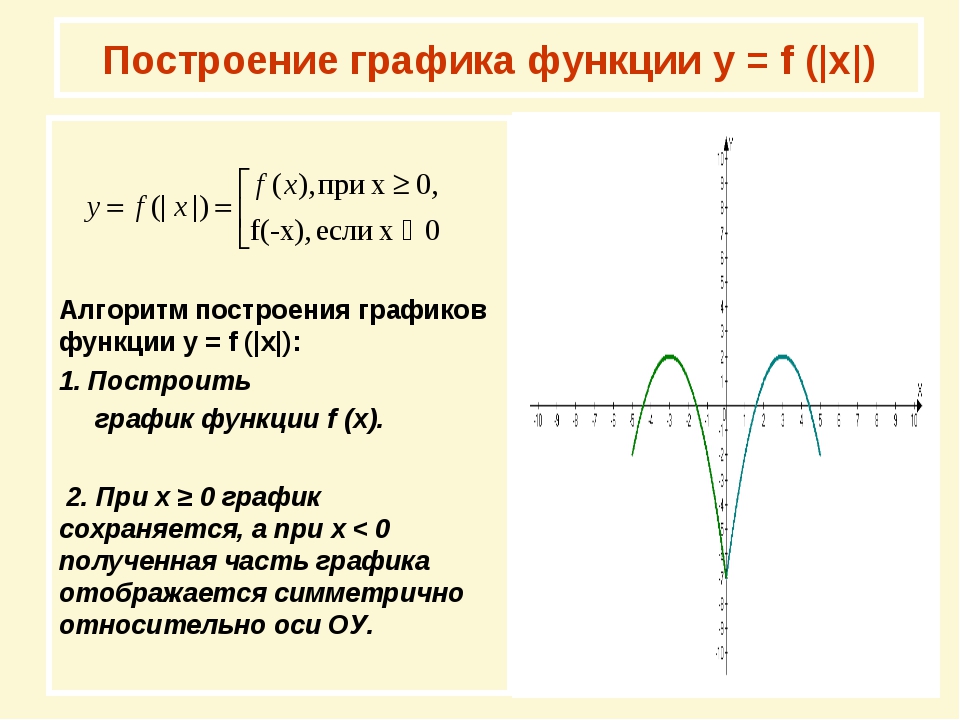
Тема «Шкалы и координаты»- 10 урок, 3 часа. Урок 1. Тема урока «Шкалы и координаты». Вид
Планируемый результат
Технологическая карта урока английского языка по ФГОС. 2016 год Учебный предмет: английский язык Класс: 4 класс УМК: «Английский с удовольствием» авт. М. З. Биболетова, О. А. Денисенко, Н.Н. Трубанева
ПодробнееПояснительная записка
Пояснительная записка Данный урок является уроком открытия нового знания по теме «Свойства степени с натуральным показателем», расширяющий кругозор учащихся. Урок может быть проведён учителем, работающим
ПодробнееКак построить график функции y = f (x+l) и y = f (x)+m, если известен график функции y = f(x). 8-й класс
Цели:
- повторить правила построения и свойства графиков функций у = x2, , , у =| x |;
- выяснить правила построения графиков функций у = f (x + l) и у = f (x) + m;
- развить умение строить графики функций;
- развивать познавательную активность учащихся.
Оборудование: интерактивная доска, проектор, презентация к уроку.
ХОД УРОКА
1. Организационный момент
2. Устная работа (Приложение. Слайды 2-8.)
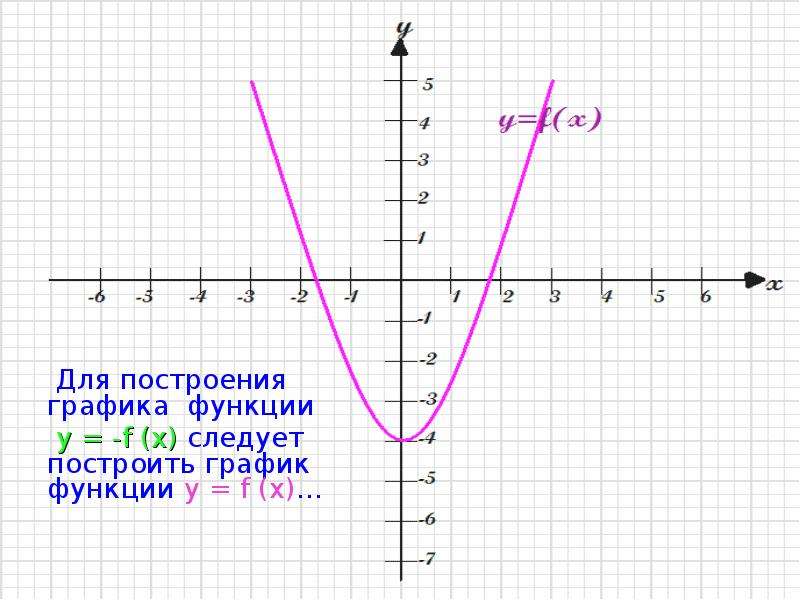
Задание: Графики каких функций
изображены на рисунках? (у = x2, у = – x2,
, , ,
, у =| x |, у =
– | x |).
Для каждой из функций сформулировать ее свойства
и правила построения графика функции.
3. Изучение нового материала (Приложение)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = x2 +1. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вверх. (Слайд 10.)
На координатной плоскости в тетрадях учащиеся
по точкам строят графики функций у = x2
и у = x2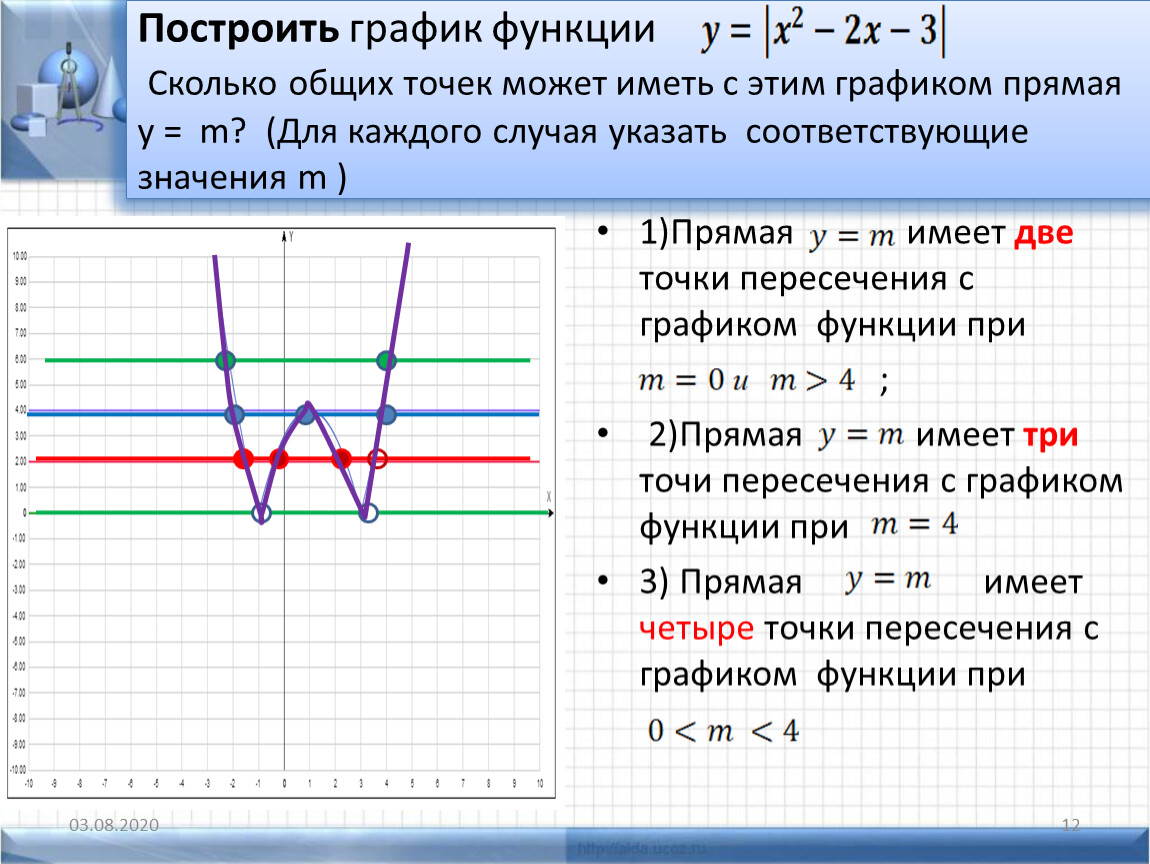– 1.
Учащиеся
самостоятельно приходят к выводу о сдвиге
параболы (параллельном переносе) на 1 единицу
вниз. (Слайд 11.)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x – 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вправо. (Слайд 12.)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x + 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу влево. (Слайд 13.)
С помощью учителя учащиеся формулируют правило
построения графика функции у = f (x + l) и
графика функции у = f (x) + m с помощью
сдвига графика функции у = f (x).
(Слайды 14-18. Анимация сдвигов графиков на
слайдах помогает лучшему восприятию правила.
)
Затем рассматривается вариант построения графика функции у = f (x + l) и графика функции у = f (x) + m с помощью сдвига графика функции у = f (x), если известен график функции у = f (x) с помощью сдвига осей координат. (Слайды 19-23. Анимация сдвигов осей координат на слайдах помогает лучшему восприятию правила построения графиков.)
Правила построения графиков функций у = f (x + l) и у = f (x) + m записываются в тетрадь.
4. Закрепление материала
№ 19.6, № 20.6, № 19.11(в), № 19.12(в), № 19.13(в), № 19.14(в), № 20.11(в), № 20.12(в), № 20.13(в), № 20.14(в).
5. Домашнее задание
Параграф 19, 20 учебника, № 19.5, № 20.5, № 19.11–19.14(а), № 20.11–20.14(а).
6. Подведение итогов урока
% PDF-1.3 % 2 0 obj > эндобдж 8 0 объект [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0750750 278 333 474 556 556 889 722 238 333 333 389 584 278 333 278 278 556 556 556 556 556 556 556 556 556 556 333 333 584 584 584 611 975 722 722 722 722 667 611 778 722 278 556 722 611 833 722 778 667778722 667 611 722 667 944 667 667 611 333 278 333 584 556 333 556 611 556 611 556 333 611 611 278 278 556 278 889 611 611 611 611 389 556 333 611 556 778 556 556 500 389 280 389 584 750 556750 278 556 500 1000 556 556 333 1000 667 333 1000 750 611 750 750 278 278 500 500 350 556 1000 333 1000 556 333 944 750 500 667 278 333 556 556 556 556 280 556 333 737 370 556 584 333 737 552 400 549 333 333 333 576 556 278 333 333 365 556 834 834 834 611 722 722 722 722 722 722 1000 722 667 667 667 667 278 278 278 278 722 722 778 778 778 778 778 584 778 722 722 722 722 667 667 611 556 556 556 556 556 556 889 556 556 556 556 556 278 278 278 278 611 611 611 611 611 611 611 549 611 611 611 611 611 556 611 556 ] эндобдж 11 0 объект [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0750750 278 278 355 556 556 889 667 191 333 333 389 584 278 333 278 278 556 556 556 556 556 556 556 556 556 556 278 278 584 584 584 556 1015 667 667 722 722 667 611 778722 278 500 667 556 833 722 778 667778722 667 611 722 667 944 667 667 611 278 278 278 469 556 333 556 556 500 556 556 278 556 556 222 222 500 222 833 556 556 556 556 333 500 278 556 500 722 500 500 500 334 260 334 584 750 556750 222 556 333 1000 556 556 333 1000 667 333 1000 750 611 750 750 222 222 333 333 350 556 1000 333 1000 500 333 944 750 500 667 278 333 556 556 556 556 260 556 333 737 370 556 584 333 737 552 400 549 333 333 333 576 537 278 333 333 365 556 834 834 834 611 667 667 667 667 667 667 1000 722 667 667 667 667 278 278 278 278 722 722 778 778 778 778 778 584 778 722 722 722 722 667 667 611 556 556 556 556 556 556 889 500 556 556 556 556 278 278 278 278 556 556 556 556 556 556 556 549 611 556 556 556 556 500 556 500 ] эндобдж 14 0 объект [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0750750 278 278 355 556 556 889 667 191 333 333 389 584 278 333 278 278 556 556 556 556 556 556 556 556 556 556 278 278 584 584 584 556 1015 667 667 722 722 667 611 778722 278 500 667 556 833 722 778 667778722 667 611 722 667 944 667 667 611 278 278 278 469 556 333 556 556 500 556 556 278 556 556 222 222 500 222 833 556 556 556 556 333 500 278 556 500 722 500 500 500 334 260 334 584 750 556750 222 556 333 1000 556 556 333 1000 667 333 1000 750 611 750 750 222 222 333 333 350 556 1000 333 1000 500 333 944 750 500 667 278 333 556 556 556 556 260 556 333 737 370 556 584 333 737 552 400 549 333 333 333 576 537 278 333 333 365 556 834 834 834 611 667 667 667 667 667 667 1000 722 667 667 667 667 278 278 278 278 722 722 778 778 778 778 778 584 778 722 722 722 722 667 667 611 556 556 556 556 556 556 889 500 556 556 556 556 278 278 278 278 556 556 556 556 556 556 556 549 611 556 556 556 556 500 556 500 ] эндобдж 16 0 объект ] / Длина 749 / Фильтр / FlateDecode >> поток x = n0p, hQ; q # ttr1PoCTDɤDVSTxz | Eȟze + gu:]%} qme | o: g mͷle / VLͳC_khl 蒌 7ac)
% PDF-1.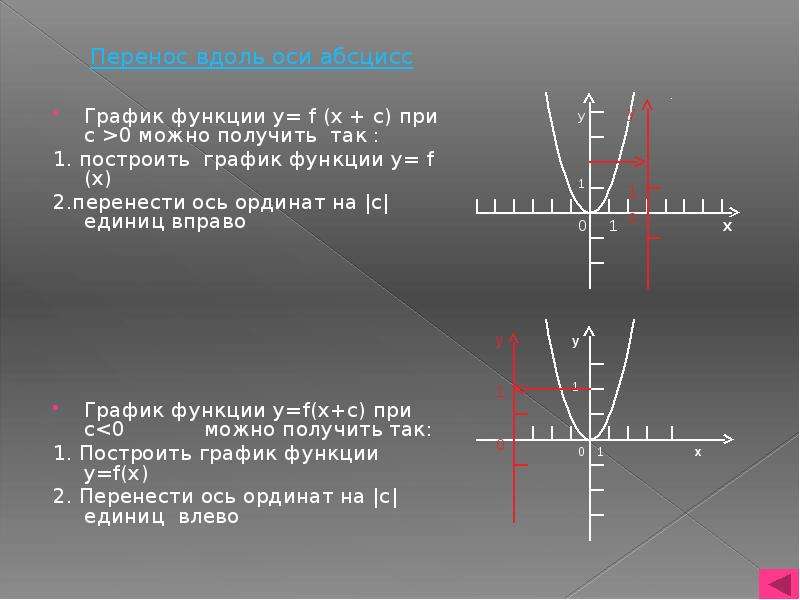
3
%
2 0 obj
>
эндобдж 8 0 объект
[
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 778 778
250 333 408 500 500 833 778 180 333 333 500 564 250 333250 278
500 500 500 500 500 500 500 500 500 500 278 278 564 564 564 444
921 722 667 667 722 611 556 722 722 333 389 722 611 889 722 722
556 722 667 556 611 722 722 944 722 722 611 333 278 333 469 500
333 444 500 444 500 444 333 500 500 278 278 500 278 778 500 500
500500 333 389 278 500 500 722 500 500 444 480 200 480 541 778
500 778 333 500 444 1000 500 500 333 1000 556 333 889 778 611 778
778 333 333 444 444 350 500 1000 333 980 389 333 722 778 444 722
250 333 500 500 500 500 200 500 33 3760 276 500 564 333 760 500
400 549 300 300 333 576 453250 333 300 310 500 750 750 750 444
722 722 722 722 722 722 889 667 611 611 611 611 333 333 333 333
722 722 722 722 722 722 722 564 722 722 722 722 722 722 556 500
444 444 444 444 444 444 667 444 444 444 444 444 278 278 278 278
500 500 500 500 500 500 500 549 500 500 500 500 500 500 500 500
]
эндобдж 11 0 объект
[
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 778 778
250 333 555 500 500 1000 833 278 333 333 500 570 250 333250 278
500 500 500 500 500 500 500 500 500 500 333 333 570 570 570 500
930 722 667 722 722 667 611 778 778 389 500 778 667 944 722 778
611 778 722 556 667 722 722 1000 722 722 667 333 278 333 581 500
333 500 556 444 556 444 333 500 556 278 333 556 278 833 556 500
556 556 444 389 333 556 500 722 500 500 444 394 220 394 520 778
500 778 333 500 500 1000 500 500 333 1000 556 333 1000 778 667 778
778 333 333 500 500 350 500 1000 333 1000 389 333 722 778 444 722
250 333 500 500 500 500 220 500 33 37 47 300 500 570 33 37 47 500
400 549 300 300 333 576 540 250 333 300 330 500 750 750 750 500
722 722 722 722 722 722 1000 722 667 667 667 667 389 389 389 389
722 722 778 778 778 778 778 570 778722 722 722 722 722 611 556
500 500 500 500 500 500 722 444 444 444 444 444 278 278 278 278
500 556 500 500 500 500 500 549 500 556 556 556 556 500 556 500
]
эндобдж 15 0 объект
[
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 778 778
250 333 420 500 500 833 778 214 333 333 500 675 250 333250 278
500 500 500 500 500 500 500 500 500 500 333 333 675 675 675 500
920 611 611 667 722 611 611 722 722 333 444 667 556 833 667 722
611 722 611 500 556 722 611 833 611 556 556 389 278 389 422 500
333 500 500 444 500 444 278 500 500 278 278 444 278 722 500 500
500 500 389 389 278 500 444 667 444 444 389 400 275 400 541 778
500 778 333 500 556 889 500 500 333 1000 500 333 944 778 556 778
778 333 333 556 556 350 500 889 333 980 389 333 667 778 389 556
250 389 500 500 500 500 275 500 333 760 276 500 675 333 760 500
400 549 300 300 333 576 523 250 333 300 310 500 750 750 750 500
611 611 611 611 611 611 889 667 611 611 611 611 333 333 333 333
722 667 722 722 722 722 722 675 722 722 722 722 722 556 611 500
500 500 500 500 500 500 667 444 444 444 444 444 278 278 278 278
500 500 500 500 500 500 500 549 500 500 500 500 500 444 500 444
]
эндобдж 19 0 объект
[
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 778 778
250 389 555 500 500 833 778 278 333 333 500 570 250 333250 278
500 500 500 500 500 500 500 500 500 500 333 333 570 570 570 500
832 667 667 667 722 667 667 722 778 389 500 667 611 889 722 722
611 722 667 556 611 722 667 889 667 611 611 333 278 333 570 500
333 500 500 444 500 444 333 500 556 278 278 500 278 778 556 500
500 500 389 389 278 556 444 667 500 444 389 348 220 348 570 778
500 778 333 500 500 1000 500 500 333 1000 556 333 944 778 611 778
778 333 333 500 500 350 500 1000 333 1000 389 333 722 778 389 611
250 389 500 500 500 500 220 500 33 37 47 266 500 606 33 37 47 500
400 549 300 300 333 576 500 250 333 300 300 500 750 750 750 500
667 667 667 667 667 667 944 667 667 667 667 667 389 389 389 389
722 722 722 722 722 722 722 570 722 722 722 722 722 611 611 500
500 500 500 500 500 500 722 444 444 444 444 444 278 278 278 278
500 556 500 500 500 500 500 549 500 556 556 556 556 444 500 444
]
эндобдж 21 0 объект
>
поток
x ڭ n_’s0; E6Ɏ} @Im;%) j ^ ͣ) Y0 ָ 꺫 K? eă {W & H6 @ xDk3e \ O ֝ zJ3ȗTY
c)} T «& lUIlKs ~ KҴ $ yA> # 7 ^ Y7 # 2» #F {P`% P [M8M i $ B (L ~ ͋o.V [e {f3h̡ ݨ ~ ܠ2 MVQNq; Tv_̢ * a34Q -!} S ܟ? \ 2 i: Dtb = n \ cй%? = T6ԍ85R1mQ
Общедоступные типы | |||
| enum | CurveType { Yfx , Xfy } | ||
| enum | CurveStyle { NoCurve , Строки , Палочки , Ступени , точек , UserCurve = 100 } | ||
| enum | CurveAttribute { Inverted = 1, Установлено = 2 } | ||
| enum | PaintAttribute { PaintFiltered = 1, ClipPolygons = 2 } | ||
Функции общедоступных членов | |||
| QwtPlotCurve () | |||
| QwtPlotCurve (const QwtText & title) | |||
| QwtPlotCurve | QwtPlotString 900 | ~ QwtPlotCurve () | |
| виртуальный int | rtti () const | ||
| void | setCurveType (CurveType) | ||
| CurveType | curveType () const | ||
| void | setPaintAttribute (PaintAttribute, bool | testPaintAttribute (PaintAttribute) const | |
| void | setRawData (const double * x, const double * y, int size) | ||
| void | setData (const double * xData, const double * yData, int size) | ||
| void | setData (const QwtArray | ||
| void | setData (const QPolygonF & data) | ||
| void | setData (const QwtData ) | ||
| int | closestPoint (const QPoint & pos, double * dist = NULL) const | ||
| QwtData & | data () | ||
| const QwtData & | data () const | ||
| int | dataSize () const | ||
| double | x (int i) const | ||
| double | y (int i) const | ||
| virtual QwtDoubleRect | boundingRect () const | ||
| double | minXValue () const | ||
| double | maxXValue () const | ||
| double | minYValue () const | ||
| double | maxYValue () const | ||
| void | setCurveAttribute (CurveAttribute, bo21ol on = | ||
| bool | testCurveAttribute (CurveAttribute) const | ||
| void | setPen (co nst QPen &) | ||
| const QPen & | pen () const | ||
| void | setBrush (const QBrush &) | ||
| const QBrush & | brush () const | ||
| void | setBaseline (double ref) | ||
| double | baseline () const | ||
| void | setStyle (CurveStyle style) | ||
| CurveStyle | style () const | ||
| void | setSymbol (constSymbol Qwt & s) | ||
| const QwtSymbol & | символ () const | ||
| void | setCurveFitter (QwtCurveFitter *) | ||
| QwtCurveFitter * | curveFitter () const | ||
| virtual void | draw (QPainter * p, const QwtScaleMap & xMap, const QwtScaleMap & yMap, const QRect &) const | ||
| virtual void | p, const QwtScaleMap & xMap, const QwtScaleMap & yMap, int from, int to) const | ||
| void | draw (int from, int to) const | ||
| virtual void | updateLegend (QwtLegend *) const | ||
Защищенные функции-члены | |||
| void | init () | ||
| virtual void | drawCurve (QPainter * p, int style, const QwtScaleMap & xMap, const QwtScaleMap & yMap, int from, int to) const | ||
| virtual void | drawSymbols (QPainter * p, const QwtSymbol &, const QwtScaleMap & xMap, const QwtScaleMap & yMap, int from, int to) const | ||
| drawLines (QPainter * p, const QwtScaleMap & xMap, const QwtScaleMap & yMap, int from, int to) const | |||
| void | drawSticks (QPainter * p, const QwtScaleMap & xMap, const QwtMap, int & xMap, const QwtMap, int & xMap to) const | ||
| void | drawDots (QPainter * p, const QwtScaleMap & xMap, const QwtScaleMap & yMap, int from, int to) const | ||
| void | drawSteps (QPainter * p, const QwtScaleMap, const QwtScaleMap, const QwtScaleMap & yMap, int from, int to) const | ||
| void | fillCurve (QPainter *, const QwtScaleMap &, const QwtScaleMap &, QwtPolygon &) const | ||
| void | closePolyline (const QwtScalewScale &, const QwtScalewScale &, const QwtPolygon &) const | ||
Microsoft Word — icat2e # 09.doc
% PDF-1.4 % 214 0 объект >>>>>>] / ON [216 0 R 217 0 R] / Order [] / RBGroups [] >> / OCGs [216 0 R 217 0 R 218 0 R] >> / Страницы 209 0 R / Тип / Каталог >> эндобдж 215 0 объект > / Шрифт >>> / Поля 201 0 R >> эндобдж 210 0 объект > поток 2016-11-30T12: 44: 06ZWord2017-01-11T11: 29: 27 + 01: 002017-01-11T11: 29: 27 + 01: 00Mac OS X 10.12 Quartz PDFContextapplication / pdf