| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
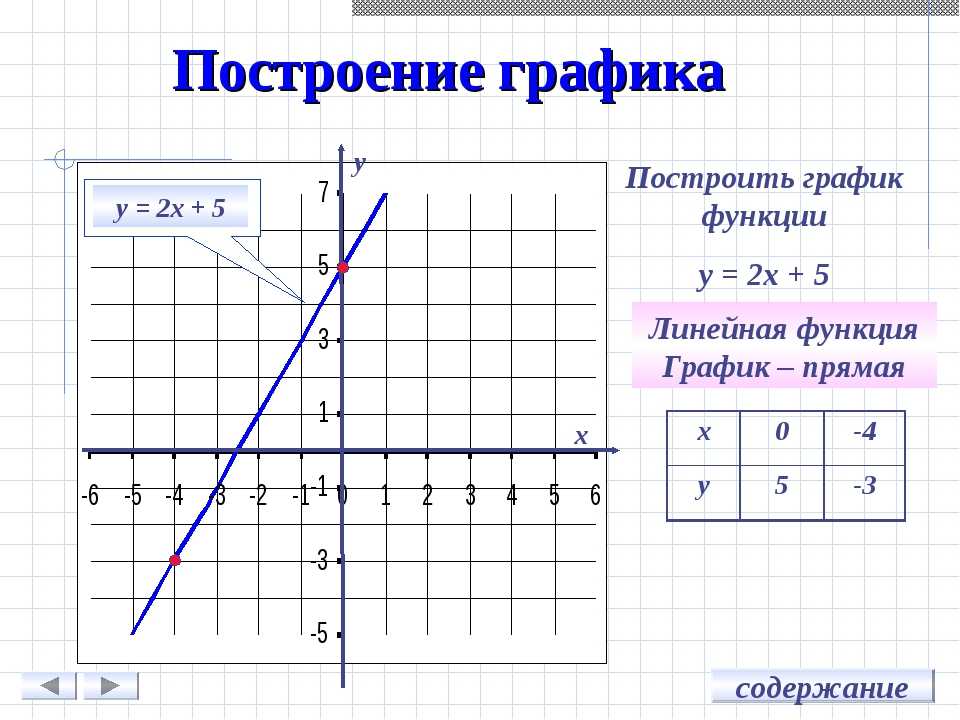
Построение графика функции y=f(x) — Построения графиков линейных функций, содержащих переменную под знаком модуля
w3.org/1999/xhtml» align=»left»>
Построение графика функции y=f(x)
|
1.3.3.26. Точечная диаграмма
1.3.3.26. Точечная диаграмма| 1.
Исследовательский анализ данных 1.3. Методы ЭДА 1.3.3. Графические приемы: Алфавитный
| |||
| Цель: Проверка на родство | Точечная диаграмма (камеры
1983) выявляет отношения или связь между двумя
переменные.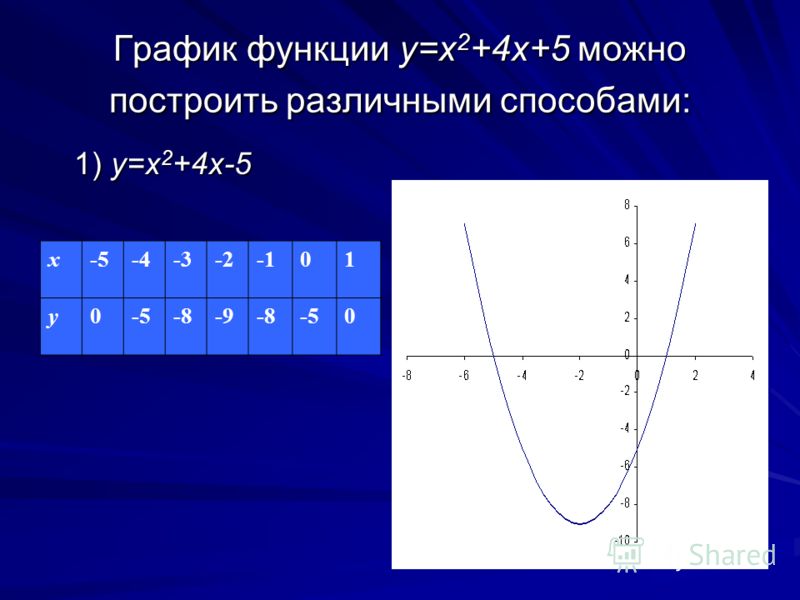 Такие отношения проявляются любым
неслучайная структура сюжета. Различные распространенные типы шаблонов
демонстрируются на примерах. Такие отношения проявляются любым
неслучайная структура сюжета. Различные распространенные типы шаблонов
демонстрируются на примерах. | ||
| Пример графика: линейных отношений Между переменными Y и X | Этот образец участка данные трубопровода Аляски показывают линейная зависимость между двумя переменными, указывающая на то, что модель линейной регрессии может быть уместно. | ||
| Определение: Y против X | Точечная диаграмма представляет собой график значений Y в зависимости от
соответствующие значения X :
| ||
| вопросов | Диаграммы рассеяния могут дать ответы на следующие вопросы:
| ||
| Примеры |
| ||
| Объединение точечных диаграмм | Точечные диаграммы также можно объединять в несколько диаграмм на странице для
помочь понять структуру более высокого уровня в наборах данных с более чем
две переменные.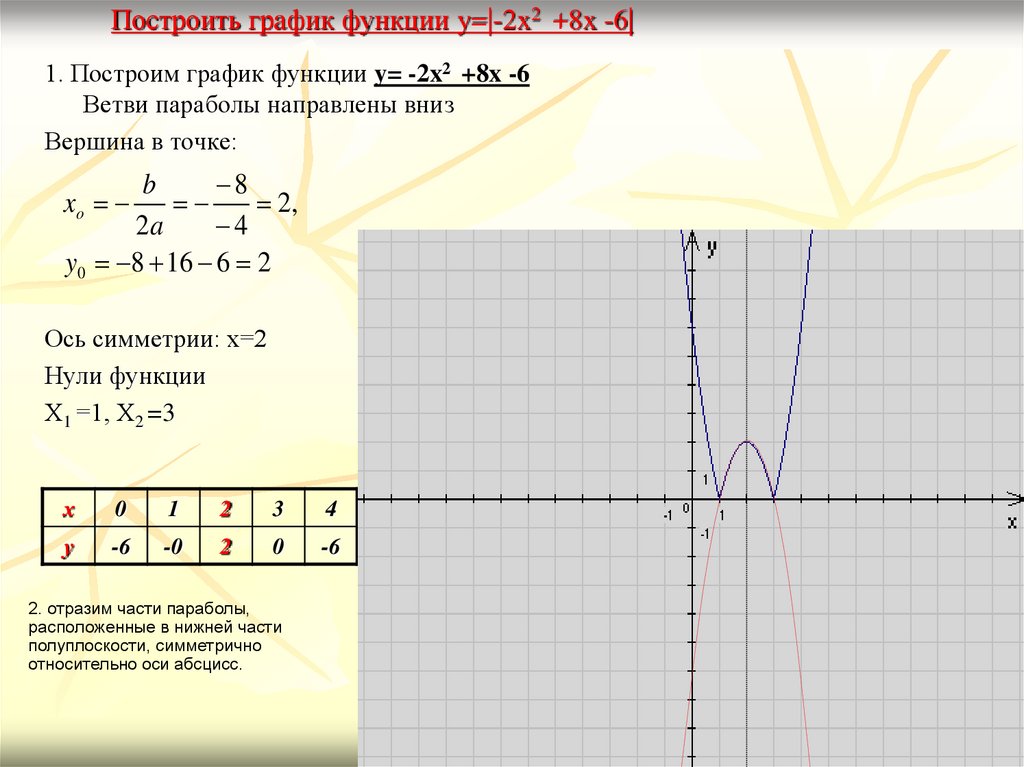 Матрица диаграммы рассеяния генерирует все попарные диаграммы рассеяния на одной странице. участок кондиционирования, также называемый совместный график или подмножество графиков, генерирует точечные графики Y по сравнению с X зависит от значения третьей переменной. | ||
| Причинность не доказана ассоциацией | Точечная диаграмма раскрывает отношения в
данные. «Отношения» означают, что существует некоторая структурированная
связь (линейная, квадратичная и т. д.) между X и Y .
Заметьте, однако, что, хотя
Диаграммы рассеяния — полезный диагностический инструмент
для определения ассоциации, но если таковая
ассоциация существует, сюжет может подсказывать, а может и не подсказывать
лежащий в основе причинно-следственный механизм.
Точечная диаграмма никогда не может «доказать» причину и
эффект — в конечном счете только исследователь
(в зависимости от лежащей в основе науки/техники)
кто может заключить, что причинность действительно существует. | ||
| вид | Самое популярное представление точечной диаграммы
Другие варианты формата точечной диаграммы включают
В обоих случаях полученный график называется разбросом. участок, хотя прежний (дискретный и несвязный) является личное предпочтение автора, так как ничего не попадает на экран, кроме данных — нет интерполяционных артефакты, искажающие интерпретацию. | ||
| Связанные методы | Выполнить график последовательности Блок-график Блочный график | ||
| Практический пример | График рассеяния показан на
данные калибровки тензодатчика
тематическое исследование.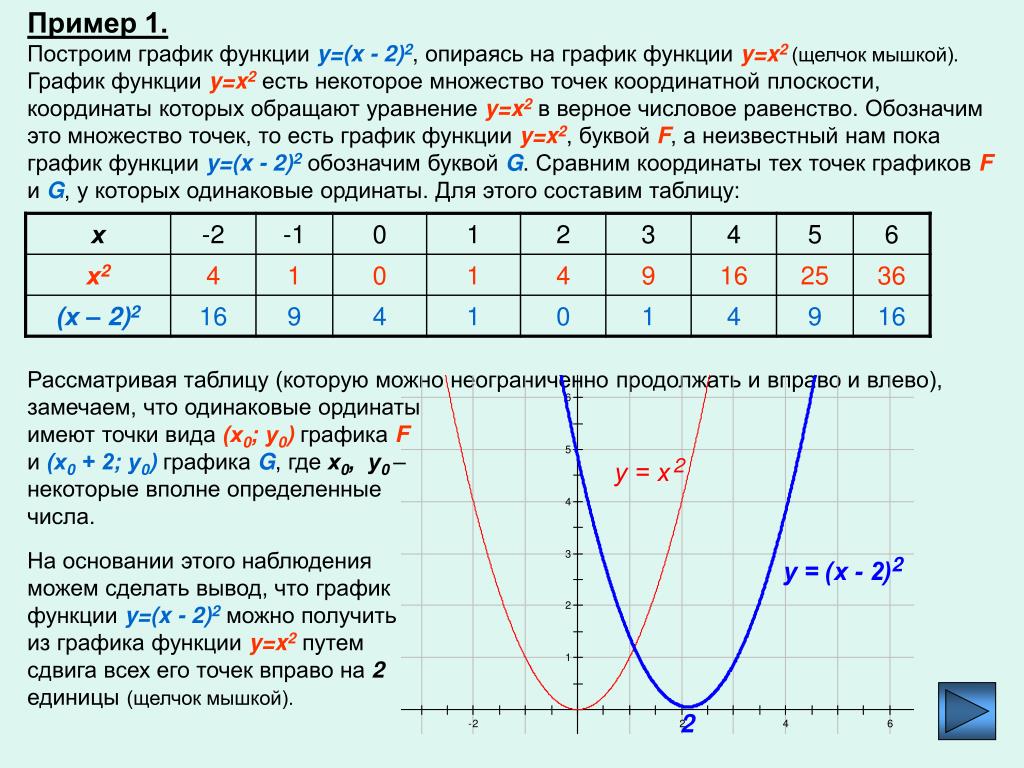 | ||
| Программное обеспечение | Диаграммы рассеяния — это фундаментальный метод, который должен быть доступен в любой статистической программе общего назначения. Графики рассеяния также доступен в большинстве программ для работы с графикой и электронными таблицами. | ||
Как отображать точки данных X и Y в Excel
Мы можем использовать Excel для построения графика XY, также известного как диаграмма рассеивания или диаграмма XY. С помощью таких диаграмм мы можем напрямую просматривать тенденции и корреляции между двумя переменными на нашей диаграмме. В этом уроке мы узнаем, как строить графики X и Y, добавлять метки осей, метки данных и много других полезных советов.
Мы создадим таблицу данных в столбцах A и B, а затем воспользуемся точечной диаграммой; мы будем отображать, изменять и форматировать наши графики X и Y.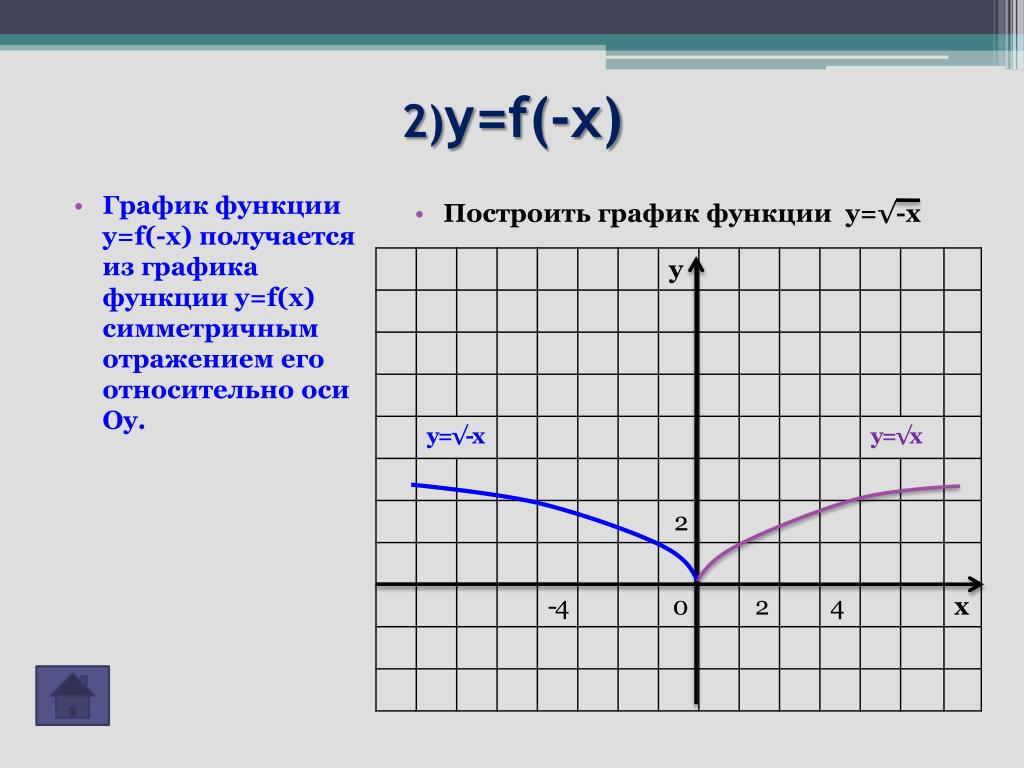
- Мы настроим нашу таблицу данных, как показано ниже.
Рисунок 2 – Построение графика в Excel
- Далее мы выделим наши данные и перейдем на вкладку «Вставка».
Рисунок 3 – График X и Y в Excel
- Если мы используем Excel 2010 или более раннюю версию, мы можем найти группу Scatter на вкладке «Вставка»
- В Excel 2013 и более поздних версиях мы перейдем на вкладку «Вставка» ; мы перейдем к группе диаграмм и выберем диаграмму X и Y Scatter. В раскрывающемся меню мы выберем второй вариант.
Рисунок 4 – Как нанести точки в Excel
- Наша Диаграмма будет выглядеть так:
Рисунок 5 – Как построить график x и y в Excel
Добавить заголовки осей к График X и Y в Excel- Если мы хотим добавить другие детали к нашему графику, такие как названия горизонтальной оси, мы можем щелкнуть график, чтобы активировать вкладку инструментов диаграммы.
 Здесь мы перейдем к элементам диаграммы и выберем заголовок оси из раскрывающихся списков, что приведет к еще одному раскрывающемуся меню, где мы можем выбрать нужную ось.
Здесь мы перейдем к элементам диаграммы и выберем заголовок оси из раскрывающихся списков, что приведет к еще одному раскрывающемуся меню, где мы можем выбрать нужную ось.
Рисунок 6 – График в Excel
- Если мы добавим названий осей к горизонтальной и вертикальной оси, мы можем получить это
Рисунок 7 – Графики в Excel
Добавление меток данных к графикам X и YМы также можем добавить меток данных к нашему графику. Эти метки данных могут дать нам четкое представление о каждой точке данных без необходимости ссылаться на нашу таблицу данных.
- Мы можем щелкнуть Plot , чтобы активировать вкладку Chart Tools. Мы перейдем к Элементы диаграммы и выберем Метки данных из раскрывающихся списков, что приведет к еще одному раскрывающемуся меню, где мы выберем Дополнительные параметры таблицы данных
Рисунок 8 – Как нанести точки в Excel
- В диалоговом окне Format Data Table, , мы убедимся, что X-значения и Y-значения отмечены.

Рисунок 9. Как построить график зависимости x от графика в Excel
- Наша диаграмма будет выглядеть так;
Рисунок 10. График зависимости x от y в Excel
- Чтобы Форматировать ось диаграммы , мы можем щелкнуть правой кнопкой мыши на графике и выбрать Формат оси
Рисунок 11 – Ось форматирования в excel на графике x и y
- В диалоговом окне «Формат оси » , мы можем изменить минимальное и максимальное значения .
Рисунок 12 – Как построить график зависимости x от y в Excel
- Наша диаграмма становится;
Рисунок 13 – Как отобразить точки данных в Excel
Мгновенная связь с экспертом через нашу службу Excelchat В большинстве случаев проблема, которую вам нужно будет решить, будет более сложной, чем простое применение формулы или функции. Если вы хотите сэкономить часы исследований и разочарований, попробуйте наш онлайн-сервис Excelchat! Наши эксперты по Excel доступны круглосуточно и без выходных, чтобы ответить на любой вопрос, который у вас может возникнуть.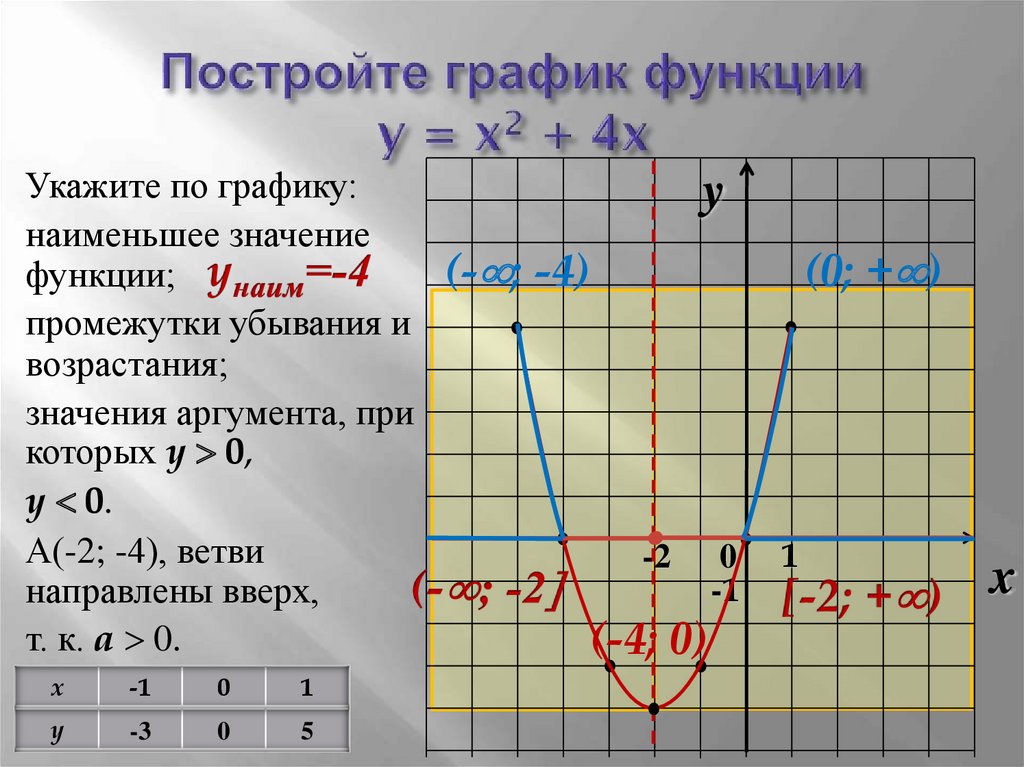

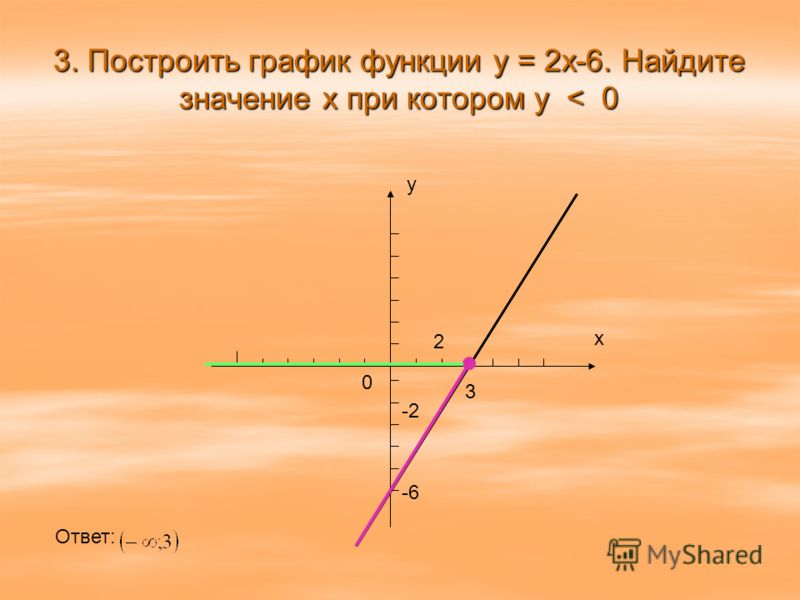 Причем, чем больше значение k, тем круче идет прямая.
Причем, чем больше значение k, тем круче идет прямая.
 Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).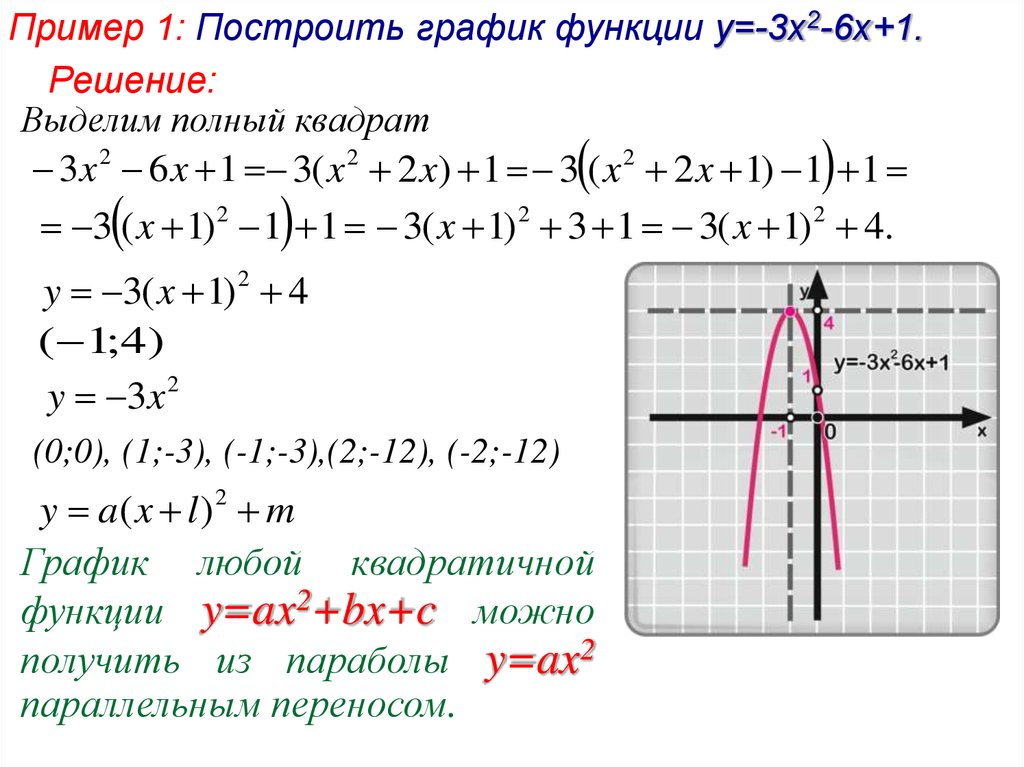 Здесь мы перейдем к элементам диаграммы и выберем заголовок оси из раскрывающихся списков, что приведет к еще одному раскрывающемуся меню, где мы можем выбрать нужную ось.
Здесь мы перейдем к элементам диаграммы и выберем заголовок оси из раскрывающихся списков, что приведет к еще одному раскрывающемуся меню, где мы можем выбрать нужную ось.