Помогите решить / разобраться (М)
1.Будьте осторожнее с такими картинками: препода кондратий может хватить…
dima_1985 в сообщении #1217911 писал(а):
Можно нарисовать направление стрелок не решая ДУ?
Можно: вводя переменную , получим систему типа 2., и стрелки рисуются автоматически. Обратите внимание на знаки компонент вектора:
в разных частях плоскости векторочки смотрят в разные квадранты, вообще говоря.
dima_1985 в сообщении #1217911 писал(а):
Я старался рисовать стрелки под 45 градусов( так как функции и одного порядка при ) это важно?
Это верно при больших (т.е., если и велики, то стрелки — почти под 45).
Переписав полученную систему в виде (или: выражая из найденных Вами решений черех , а затем — через ), получите уравнения фазовых кривых. Средствами матана, нарисуйте график одной из них (остальные получатся из нее сдвигами).
— 22.05.2017, 10:21 —
2. На картинке отсутствуют самые важные детали: сепаратрисы Вашего узла. Ну, на самом деле они есть —
это оси «другой» системы координат. Присобачьте им стрелочки…
dima_1985 в сообщении #1217911 писал(а):
как новая система координат деформируется относительно старой?
Для кратных: так же. При этом, кратному корню может соответствовать два собственных вектора (и будет дикритический узел, с фазовыми кривыми — прямыми), или один (вырожденный узел: тогда надо искать присоединенный (к собственному) вектор, в базисе из полученной пары рисовать портрет (он будет сильно кривой), и деформировать картинку соответствующим линейным преобразованием (возврат к старому базису)).
Для комплексных корней: выходить в комплексную плоскость
не надо, конечно. Но можно так: линейным преобразованием сделайте матрицу системы «красивой» (диагональные — равны, два других — различаются знаком). Система с такой матрицей в полярных координатах явно и хорошо решается (фазовые кривые — логарифмические спирали — для фокуса, или окружности — для центра).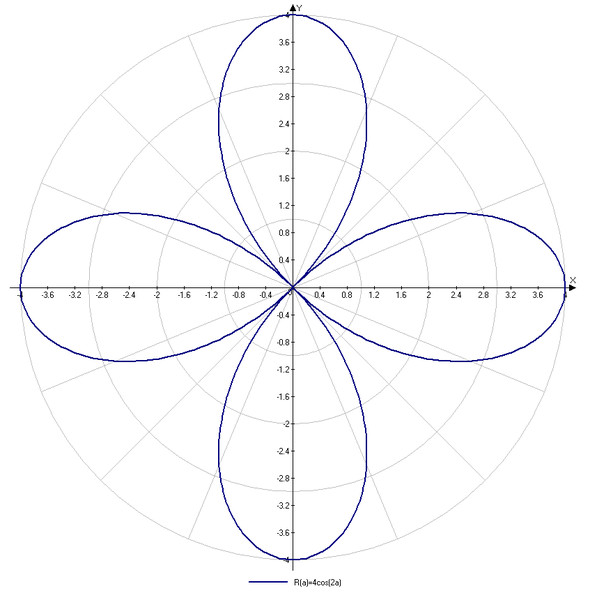 Обратное преобразование их маленько сплющит, ну и ладно: портрет готов!
Обратное преобразование их маленько сплющит, ну и ладно: портрет готов!
dima_1985 в сообщении #1217911 писал(а):
Если система имеет несколько особых точек то графики рисуются отдельно для каждой точки ?
Да — в малой окрестности каждой (если «графики» — это их фазовые портреты). Но после этого, надо еще дорисовать портрет в оставшейся части плоскости. А это еще та проблема! И не всегда это удается сделать точно и полно. Например, в системе могут быть предельные циклы (замкнутые фазовые кривые), далеко отстоящие от особых точек. Даже для квадратичных систем (справа в системе — многочлены второй степени) вопрос об описании ф.портрета еще не полностью исследован. Даже нет ответа на вопрос, сколько циклов может быть в такой системе.
(Оффтоп)
Есть, правда, «программа Дюмортье»: надо исследовать порядка сотни квадратичных систем (каждая — материал для кандитатской диссертации!), и ответ — будет. Программа пока реализована примерно на две трети…
Программа пока реализована примерно на две трети…
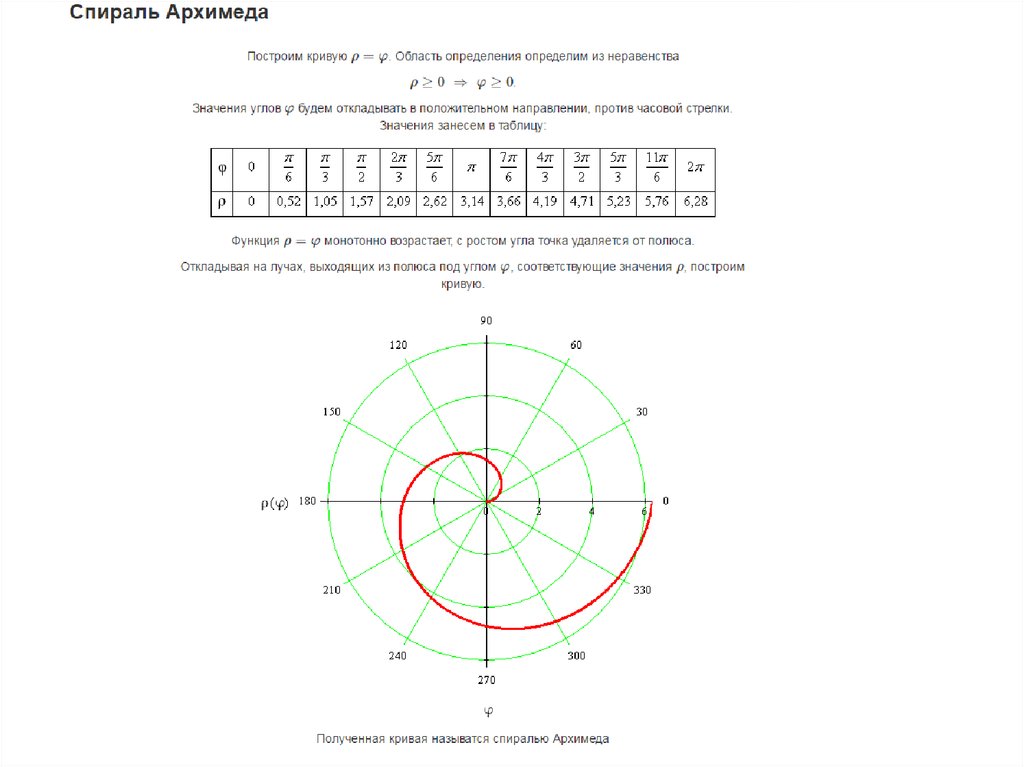
Как построить параметризированную геометрию спирали Архимеда
Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).
Что такое спираль Архимеда?
Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.
Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.
В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.
Уравнение спирали Архимеда в полярной системе координат записывается, как:
r=a+b\theta
где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 \pi b. Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью. Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.
Задание параметризированной геометрии спирали Архимеда
Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.
Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.
Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:
\begin{align*} x_{component}=rcos(\theta) \\ y_{component}=rsin(\theta) \end{align*}
После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:
\begin{align*} x_{component}=(a+b\theta)cos(\theta) \\ y_{component}=(a+b\theta)sin(\theta) \end{align*}
В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_{initial} и a_{final}, соответственно, и количество витков n. Показатель роста спирали b находится, как:
b=\frac{a_{final}-a_{initial}}{2 \pi n}
Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f, соответственно.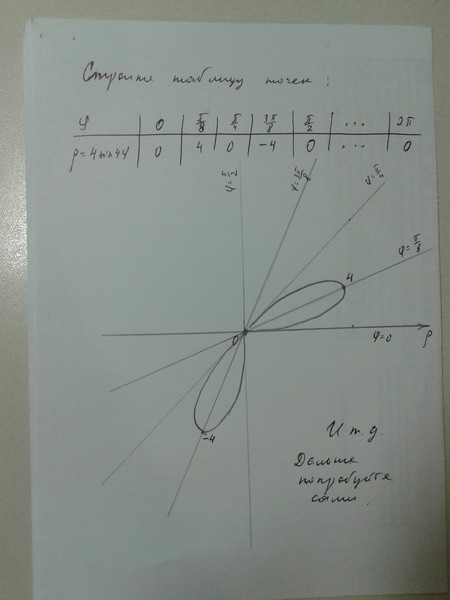 Давайте с них и начнём — theta_0=0 и theta_f=2 \pi n. Исходя из заданной информации, определяем параметры для построения геометрии спирали.
Давайте с них и начнём — theta_0=0 и theta_f=2 \pi n. Исходя из заданной информации, определяем параметры для построения геометрии спирали.
Параметры, которые используются для построения геометрии спирали.
Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):
\begin{align*} X_{fun}=(a+bs)cos(s) \\ Y_{fun}=(a+bs)sin(s) \\ \end{align*}
Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.
Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve.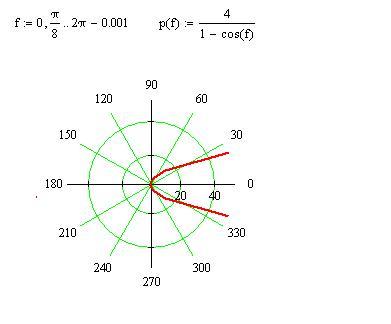 Во вкладке Parameter задаём параметр s от начального угла, theta_0, до его конечного значения, theta_f=2 \pi n.
Во вкладке Parameter задаём параметр s от начального угла, theta_0, до его конечного значения, theta_f=2 \pi n.
Настройки для Parametric Curve (Параметрической кривой).
Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.
До этого момента параметрами нашей кривой были начальный (a_{initial}) и конечный (a_{final}) радиусы и количество витков n. Теперь мы хотим добавить ещё один – толщину спирали.
Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 \pi b. Что эквивалентно \frac{a_{final}-a_{initial}}{n}. Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap.
Расстояние между витками определяется толщиной спирали и величиной зазора.
Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:
\begin{align*} distance=\frac{a_{initial}-a_{final}}{n} \\ gap=distance-thick \end{align*}
После этого выражаем показатель роста спирали через толщину:
\begin{align*} distance=2\pi b \\ b=\frac{gap+thick}{2\pi} \end{align*}
Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:
\begin{align*} \theta_{final}=2 \pi n \\ a_{final}=\text{total distance}+a_{initial} \\ a_{final}=2 \pi bn+a_{initial} \\ n=\frac{a_{final}-a_{initial}}{2 \pi b} \\ \theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\ \theta_{final}=\frac{a_{final}-a_{initial}}{b} \end{align*}
Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0.
2 }} \end{align*}
где N_x и N_y определяются аналитическими функциями в COMSOL Multiphysics, аналогично X_{fun} и Y_{fun} в первом примере. Внутри функции используется оператор производной,
d(f(x),x), как показано на скриншоте ниже.
Примеры оператора производной, который используется в аналитической функцииФункции X_{fun}, Y_{fun}, N_x, и N_y могут быть использованы в выражениях для задания параметрической кривой, как с одной стороны:
\begin{align*} x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\ y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2} \end{align*}
Так и с другой:
\begin{align*} x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\ y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2} \end{align*}
Выражения для второй смещённой параметрической кривой.Чтобы соединить концы, добавим ещё две параметрические кривые, используя незначительные изменения уравнений выше. Для кривой, которая будет соединять спираль в центре, необходимо задать X_{fun}, Y_{fun}, N_x, и N_y для начального значения угла, theta.
Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:
\begin{align*} X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\ Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2} \end{align*}
Уравнения кривой на конце:
\begin{align*} X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\ Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2} \end{align*}
В этих уравнениях параметр s изменяется от -1 до 1, как показано на скриншоте ниже.
Уравнения кривой, соединяющей спираль в центре.В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.
Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics
В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.
Дополнительные ресурсы по проектированию и расчёту спиралей
- Для улучшения навыков моделирования спиралей, ознакомьтесь со следующими учебными моделями:
- Спирально-щелевая антенна
- Познакомьтесь с опытом одного из наших пользователей: Анализ спиральных резонаторных фильтров
бесплатных онлайновых материалов курса MIT для старших классов | Анализ плоских кривых
- Отправить эту страницу по электронной почте
Выберите тему —выберите тему—Анализ графиковПределы функцийАсимптотическое и неограниченное поведениеНепрерывность: свойство функцийПараметрические, полярные и векторные функцииПонятие о производнойПроизводная в точкеПроизводная как функцияВторые производныеПрименения производныхВычисление производныхИнтерпретации и свойства определенных интеграловПрименения интеграловФундаментальная теорема исчисленияАнтидифференциация АнтидифференцированиеЧисленные приближения к определенным интеграламПонятие о рядахРяды константРяд Тейлора
Выберите подтему —выберите подтему—Анализ плоских кривых
Этот раздел содержит документы, созданные из отсканированных оригинальных файлов и других
документы, которые нельзя было сделать доступными для программы чтения с экрана.«#»
символ используется для обозначения таких документов.
- Конспект лекций
- Онлайн-учебник Глава
- Экзаменационные вопросы
- Java-апплеты
Конспект лекций
Параметрические уравнения
Раздел 1, стр. 1 — стр. 2
Представление декартовых координатных кривых с использованием явных и неявных форм. Представление кривых с использованием параметрических уравнений, которые определяют x и y с точки зрения третьей переменной. Включает примеры параметрических уравнений для круга, эллипса и снаряда, выпущенного под углом.
Курс: 18.01 Расчет с одной переменной, осень 2005 г.
Преподаватель: проф. Джейсон Старр
Предыдущие знания: нет
Наверх
Имплицитизация
Раздел 2, стр. 2 — стр. 3
Нахождение неявных форм для параметризованных кривых.
Использует примеры из предыдущего раздела примечаний.
Курс: 18.01 Расчет с одной переменной, осень 2005 г.
Преподаватель: проф. Джейсон Старр
Предварительные знания: Параметрические уравнения (раздел 1 этой лекции)
Наверх
Кривые в полярных координатах
Раздел 3, стр. 5 — стр. 6
Определение с примерами окружностей и горизонтальной линии, заданной в полярных координатах.
Курс: 18.01 Исчисление с одной переменной, осень 2005 г.
Преподаватель: профессор Джейсон Старр
Предварительные знания: Параметрические уравнения (раздел 1 лекции 21)
Параметрическое представление кривой
Документ
Использование параметрических уравнений для определения кривой в двух или трех измерениях и свойства параметрических уравнений.
Курс: 18.013A Исчисление с приложениями, весна 2005 г.
Параметрические уравнения
PDF — 2,2 МБ #
От задачи 4E-1 (стр. 31) до задачи 4E-9 (стр. 31)
Девять вопросов, которые включают поиск уравнений в прямоугольных координатах для тех, которые заданы в параметрической форме, или составление прямоугольного уравнения в параметрической форме.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нетРешение (PDF — 4,0 МБ) # Страницы с 58 по 59
Вернуться к началу
Графики полярных координат
PDF- 2.2 MB #
От задачи 4H-1 (стр. 32) к задаче 4H-3 (стр. 33)
Три вопроса, состоящие из нескольких частей, которые включают преобразование прямоугольных координат в полярные координаты, преобразование полярных уравнений в прямоугольные уравнения , а графические кривые даны в полярных координатах.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF — 4,0 МБ) # Страницы с 62 по 63
Вернуться к началу Полярные кривые
Задача 4 (стр. 5)
Рисование кривой в полярных координатах и маркировка квадрантов, конечных точек, наклонов касательной и углов кривой.
Курс: 18.01 Исчисление одной переменной, осень 2005 г.
Преподаватель: проф. Джейсон Старр
Предыдущие знания: нет
Решение (PDF) Страницы с 3 по 4
Наверх
Область внутри полярной кривой
Задача 5 (стр. 1)
Начертить кривую, заданную в полярных координатах, и найти площадь внутри нее.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) # Страница 1
Наверх
Полярные координаты
Задача 9 (стр. 1)
Начертить кривую, заданную в полярных координатах, и найти точки пересечения этой и других кривых.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) # Страница 1
Наверх
Полярные координаты
Задача 5 (стр. 1)
Представление окружности в прямоугольных и полярных координатах.
Курс: 18.
01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) # Страница 1
Наверх
Интегралы в полярных координатах: лунное затмение
Проблема 6 (стр. 1)
Настройка и оценка интеграла для представления непокрытой площади двух лун, участвующих в лунном затмении на другой планете.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) # Страница 1
Наверх
Полярные координаты: спираль
Задача 5 (стр. 1)
Зарисовка спирали, заданной в полярных координатах, подсчет количества пересечений ею оси X и определение площади определенных участков спирали.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) # Страница 1
Наверх
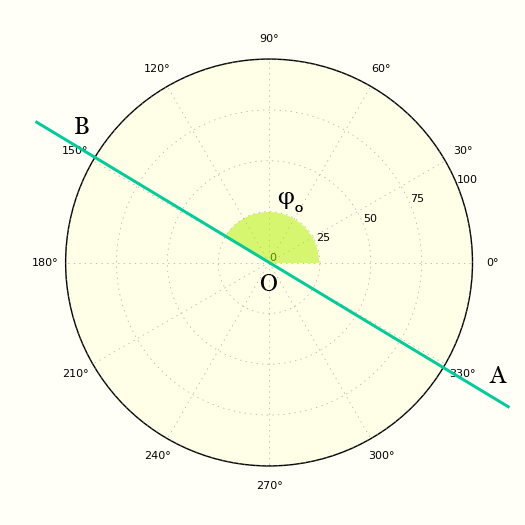
линий в полярных координатах
Проблема 6 (стр. 1)
Нахождение уравнения в полярных координатах и соответствующего диапазона тета для линии, заданной в прямоугольных координатах.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) # Страница 1
Наверх
Полярные кривые
Задача 14 (стр. 2)
Начертить кривую, заданную в полярных координатах, и найти площадь, заметаемую отрезком прямой при движении одной из конечных точек по этой кривой.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) # Стр. 1
Наверх
Апплеты Java
Полярный плоттер
Java-апплет
Требуется виртуальная машина Java
Апплет для отображения графика функции, заданной в полярных координатах.
Курс: 18.013A Исчисление с приложениями, весна 2005 г.
Преподаватель: проф. Дэниел Дж. Клейтман
Вернуться к началу
Кривые в двух измерениях
Апплет Java
Требуется виртуальная машина Java
Апплет для построения кривых, определенных в прямоугольной или параметрической форме.
Курс: 18.013A Исчисление с приложениями, весна 2005 г.
0007
suchoptionen
Исследование полярного графика • Конструктор действий от Desmos
учитель.десмос.com › activitybuilder › custom
Учащиеся исследуют круги, розы и лимаконы и пытаются определить, как каждая часть уравнения влияет на график . Нет предварительных знаний о полярных …
Полярные графики • Конструктор занятий от Desmos — Teacher Desmos
student.desmos.com › activitybuilder › custom
Сегодня мы собираемся изучить полярные графики. Вы захотите сделать несколько заметок по ходу дела. Мы официально оформим наши выводы позже на этой неделе.
Полярные графики • Конструктор занятий от Desmos — Teacher Desmos
student.desmos.com › activitybuilder › custom
Цель: • Это задание дает вам возможность использовать знания о полярных координатах и полярных графиках для моделирования нескольких полярных функций.
Исследование полярных графиков 2020 • Activity Builder от Desmos
student.
desmos.com › activitybuilder › custom
Давайте воспользуемся технологиями для поиска закономерностей с некоторыми другими полярными графиками. Запишите краткое изложение своих выводов в свой лист записи. 1 …
Polar Graphing — Справочный центр Desmos
help.desmos.com › 4406895312781-Polar-Graphing
27.08.2021 · Графический калькулятор Desmos считает любое уравнение или неравенство, записанное в терминах r r и θ, полярным форме и построит ее как …
Es fehlt: activity | Muss Folgendes enthalten:activity
Polar Graphing — An Introduction • Activity Builder от Desmos
student.desmos.com › activitybuilder › custom
На этом уроке вы узнаете, как наносить точки с использованием полярных координат и как выполнять преобразование между системами координат.
8.4 Введение в построение полярных графиков • Конструктор действий от Desmos
student.desmos.com › activitybuilder › custom
2Измените радиус под каждым углом, чтобы создать потрясающий полярный график.
В этом упражнении мы рассмотрим, как форма уже известных нам общих функций будет …
Изучение полярных графиков • Конструктор действий от Desmos
student.desmos.com › activitybuilder › custom
Создайте учетную запись или войдите, чтобы назначить это занятие своим классам. … Сделайте замечание о графиках полярных уравнений с косинусом и синусом.
Введение в полярные графики • Конструктор действий от Desmos
учитель.десмос.com › activitybuilder › custom
Моим отличникам Precalculus потребовалось 20-30 минут, чтобы выполнить это задание. У них не было опыта работы с полярными графами. Я создал это задание из бумаги- …
Ähnliche Fragen
Как строить полярные графики в Desmos?
Исследование полярных графиков • Конструктор действий от … — Учитель Демос
Teacher.desmos.com › activitybuilder › custom
Предварительное знание полярных графиков не предполагается. Предупреждение! В этом действии используется функция «Копировать предыдущую», которая больше не поддерживается.

 2 }} \end{align*}
2 }} \end{align*}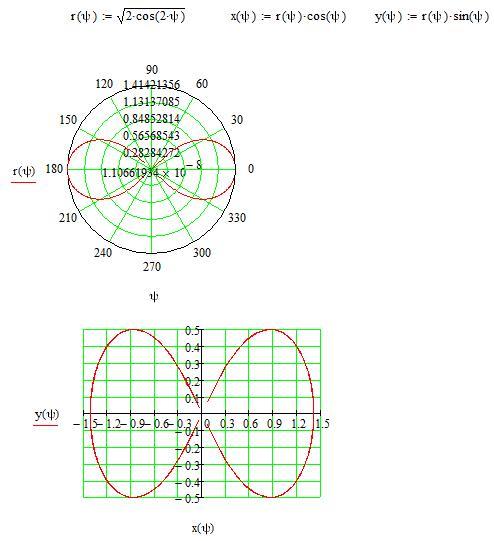 Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:
Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:
 «#»
«#»  Использует примеры из предыдущего раздела примечаний.
Использует примеры из предыдущего раздела примечаний.

 01 Исчисление одной переменной, осень 2006 г.
01 Исчисление одной переменной, осень 2006 г.
 0007
0007 desmos.com › activitybuilder › custom
desmos.com › activitybuilder › custom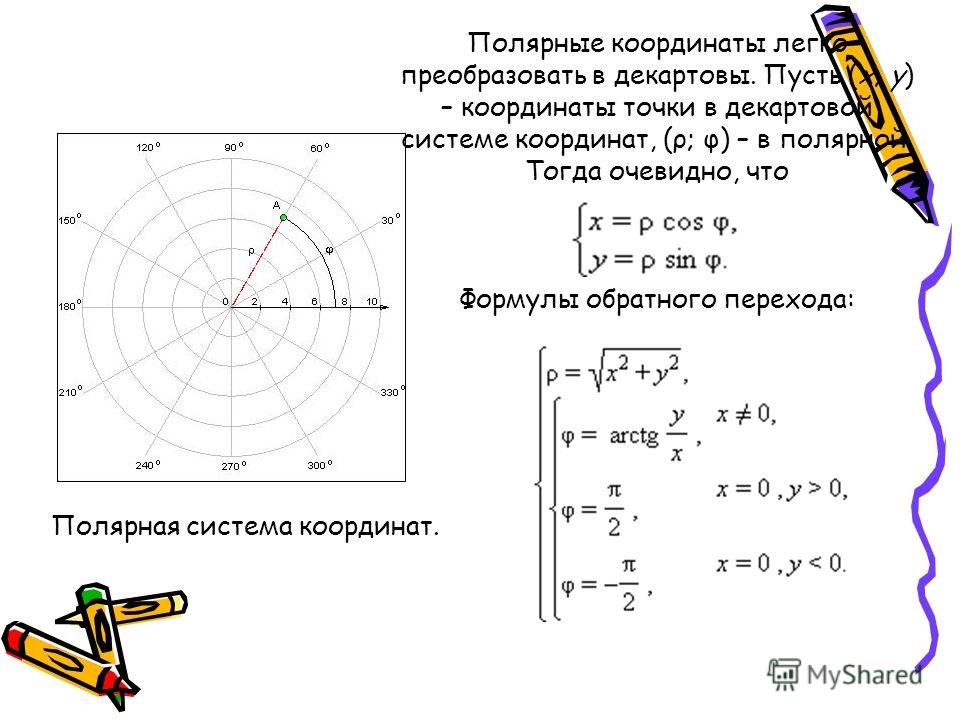 В этом упражнении мы рассмотрим, как форма уже известных нам общих функций будет …
В этом упражнении мы рассмотрим, как форма уже известных нам общих функций будет …