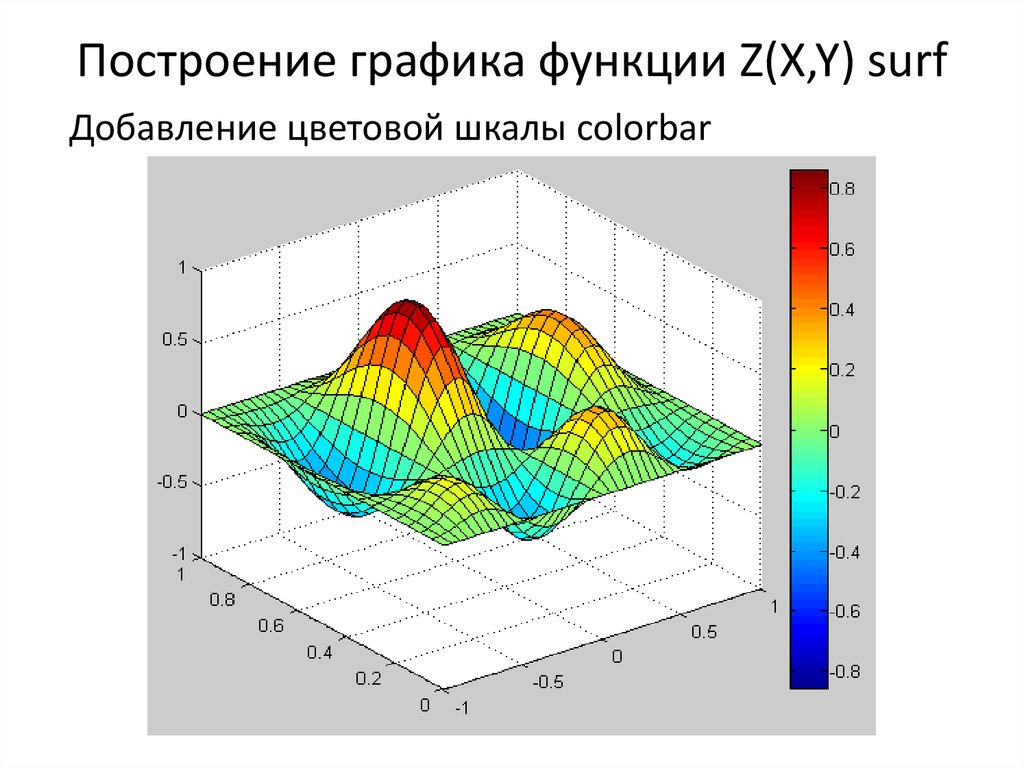
§9.2. Линии уровня функции двух переменных
Линии на плоскости xOy, заданные уравнениями , где С – произвольная константа, называются линиями уровня функции .
Линии уровня являются линиями пересечения поверхности, заданной функцией и плоскости z = C, параллельной плоскости xOy. С помощью линий уровня можно изучать форму поверхности, заданной функцией .
Пример 9.2. Найти линии уровня и определить форму поверхности, заданной уравнением .
Решение. Уравнения линий уровня в
данном случае имеют вид
.
При C < 0 уравнение дает пустое множество решений
(следовательно, вся поверхность
расположена выше плоскости xOy).
При C = 0 уравнению
линии уровня удовлетворяет только одна
точка x = 0, y = 0 (с плоскостью xOy поверхность пересекается только вначале
координат). При C >
0 линии уровня являются эллипсами
,
с полуосями и
.
Рис.9.3 Рис. 9.4
§9.3. Частные производные первого порядка
Пусть в некоторой области D плоскости xOy задана функция , и пусть – некоторая точка области D.
Частной производной функции в точке по переменной x (обозначается или ) называется
, (9.1)
если данный предел существует и конечен.
Частной производной функции в точке по переменной y (обозначается или ) называется
, (9.2)
если данный предел существует и конечен.
Частной производной функции n переменных в точке по переменной xi называется
,
(9.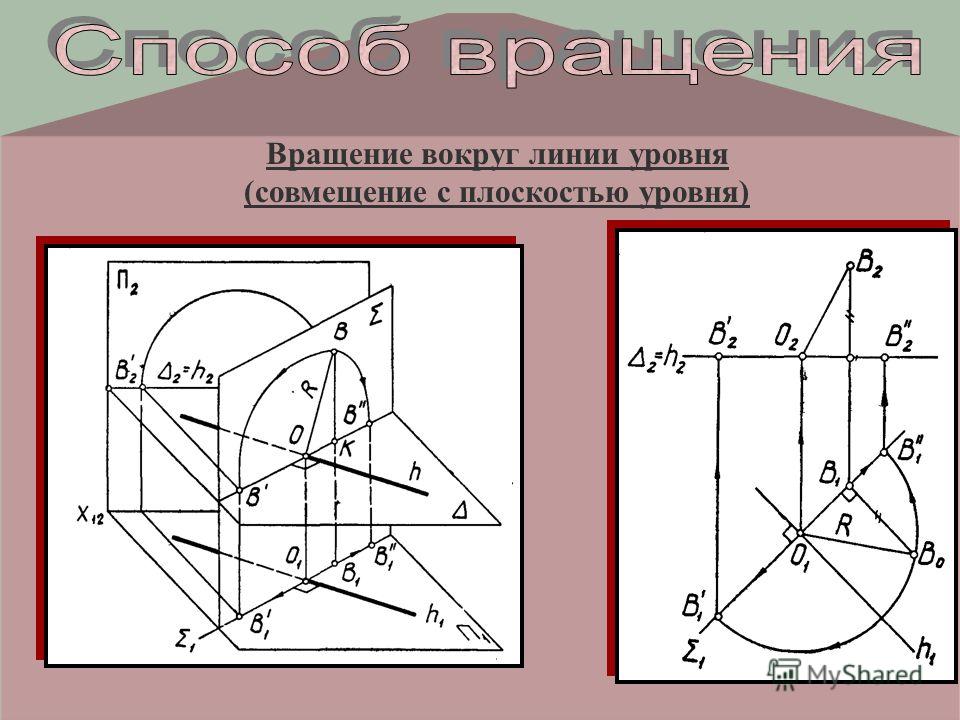 3)
3)
если данный предел существует и конечен.
Как видно из формул (9.1) – (9.3), частные производные определяются аналогично тому, как определялась производная функции одной переменной. При вычислении предела приращение получает только одна из переменных, остальные переменные приращения не получают и остаются постоянными. Следовательно, частные производные можно вычислять по тем же правилам, что и обычные производные, обращаясь со всеми свободными переменными (кроме той, по которой производится дифференцирование) как с константами.
Пример 9.3. Найти частные производные функции
.
Решение. .
.
Решение. При дифференцировании данной функции по переменной x мы пользуемся правилом дифференцирования степенной функции, а при нахождении частной производной по переменной y – правилом дифференцирования показательной функции:
,
.
Пример 9.5. Вычислить частные производные функции в точке .
Решение. Применяя правило дифференцирования сложной функции, найдем частные производные
,
,
.
Подставляя в частные производные координаты точки М, получим
,
,
.
§9.4. Градиент функции нескольких переменных. Производная по направлению
Градиентом функции в точке называется вектор, составленный из частных производных данной функции, вычисленных в данной точке:. (9.4)
Если в точке градиент функции отличен от нулевого вектора, то он
направлен в сторону наибольшего
возрастания данной функции в точке М0.
Это означает, что существует такое
достаточно малое число > 0, что в точке
,
находящейся от точки на расстоянии r < (),
приращение функции будет максимальным, если направление
вектора совпадает с направлением вектора
.
Производной функции в точке по направлению вектора называется проекция вектора градиента данной функции, вычисленного в точке М0, на данное направление
Из формулы (9.5) следует, что по знаку производной по направлению в точке М0 можно определить поведение функции (возрастание или убывание) в данной точке и в данном направлении. Угол между векторами и острый (функция в данном направлении возрастает), тогда и только тогда, когда производная по направлению вектора в точке М0 больше нуля. Угол между векторами и тупой (функция в данном направлении убывает), тогда и только тогда, когда производная по направлению вектора в точке М0 меньше нуля.
Вычисляя проекцию вектора на вектор в соответствие с формулой (2.6) первой части пособия, получим
. (9.6)
(9.6)
Замечая, что , где – угол, который вектор образует с осью OX, получим еще одну формулу для вычисления производной по направлению вектора
. (9.7)
Пример 9.6. Найти градиент функции в точке М0(4; 2) и производную по направлению вектора
Решение. Найдем частные производные
Вычислим значения частных производных в точке М0:
Градиент функции в точке М0 найдем по формуле (9.4):
Производную функции в точке М0 по направлению вектора найдем по формуле (9.6):
Пример 9.7. В точке М0(0; 1)
вычислить производную функции по направлению биссектрисы второго
координатного угла и сделать вывод о
поведении функции в данном направлении.
Решение. Найдем частные производные функции :
,
.
Вычислим значения частных производных и градиент функции в точке М0:
,
,
.
Производную функции в точке М0 по направлению биссектрисы второго координатного угла (данное направление составляет с осью OX угол = 135) найдем по формуле (9.7):
.
Так как прозиводная по данному направлению отрицательна, то, следовательно, в точке М0 по выбранному направлению функция убывает.
Скалярное поле. Векторное поле. Основные понятия и задачи
- Понятие поля в математике
- Скалярное поле: определение, поверхности уровня и линии уровня
- Векторное поле: определение, векторные линии
Теория поля является разделом математики, однако понятие поля лежит в основе многих
представлений современной физики. В общем случае говорят, что в пространстве задано поле некоторой
величины u, если в каждой точке пространства (или некоторой его
части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать
несколько полей: температурное поле (в каждой точке температура имеет определённое значение), поле
давлений, поле скоростей и другие поля.
В общем случае говорят, что в пространстве задано поле некоторой
величины u, если в каждой точке пространства (или некоторой его
части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать
несколько полей: температурное поле (в каждой точке температура имеет определённое значение), поле
давлений, поле скоростей и другие поля.
Поле величины u называется стационарным, (или установившимся), если u не зависит от времени t. В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки M и времени t.
В задачах физики чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные.
Пусть D — некоторая область на плоскости или в пространстве.
Определение скалярного поля. Если в области D каждой точке M(x,y,z) пространства или точке M(x,y) плоскости в каждый момент времени t по определённому закону ставится в соответствие значение
скалярной величины u, то функция u(x,y,z,t)
в случае пространства или u(x,y,t) в случае плоскости
называется скалярным полем.
Если в области D каждой точке M(x,y,z) пространства или точке M(x,y) плоскости в каждый момент времени t по определённому закону ставится в соответствие значение
скалярной величины u, то функция u(x,y,z,t)
в случае пространства или u(x,y,t) в случае плоскости
называется скалярным полем.
Понятия скалярного поля и функции, определённой в области D, совпадают.
Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, расположенных дальше от источника тепла. Можно привести и такие примеры, как поле освещённости, поле плотности массы и тому подобные.
Для получения более полного представления о скалярном поле используется его
графическое изображение — поверхности уровня в пространстве и линии уровня на плоскости.
Линии уровня широко используются при составлении топографических и метеорологических карт. На топографических картах линия уровня — линия, в точках которой отмечена одна и та же высота над уровнем моря. На метеорологических картах строят два вида линий уровня — изотермы (линии одинаковой температуры) и изобары (линии одинакового давления).
Определение. Поверхностью уровня скалярного поля
Уравнение поверхности уровня скалярного поля u(x,y,z):
u(x,y,z) = C.
При постоянном изменении значения C поверхности уровня заполняют всю
область пространства. Если поверхности уровня размещены плотно, скалярное поле изменяется быстро.
Если же поверхности уровня расположены редко, скалярное поле изменяется медленно.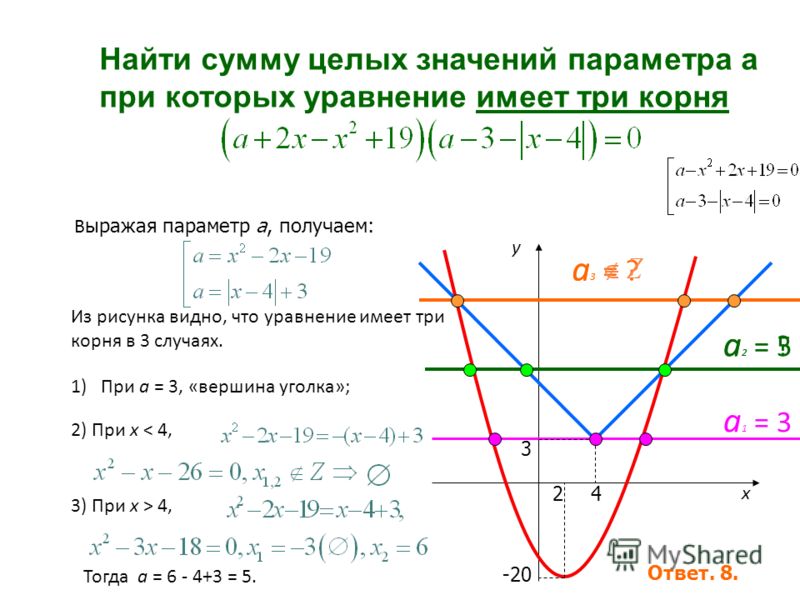
Определение. Линией уровня скалярного поля называется множество всех тех точек на плоскости, в которых скалярное поле постоянно.
Уравнение линии уровня скалярного поля u(x,y):
u(x,y) = C.
Пример 1. Определить поверхности уровня скалярного поля и их вид.
Решение. Уравнением поверхностей уровня данного скалярного поля является
или
.
Поверхностями уровня являются конусы с вершиной в начале координат и осью вращения Oy. Так как по области определения , то одновременно не может быть x = 0 и z = 0. Поэтому следует исключить вершину конусов.
Пример 2. Определить линии уровня скалярного поля и их вид.
Решение. Уравнением линий уровня данного скалярного поля является
Уравнением линий уровня данного скалярного поля является
.
Из этого уравнения выразим «игрек»:
.
Так как arcsinC — также константа, обозначим её C1. Тогда
Графиками этих линий являются параболы с вершиной в точках и ветвями вниз. На рисунке изображены линии уровня в трёх случаях: C1 = 1 — красная линия, C1 = 2 — зелёная линия, C1 = 3 — синяя линия.
Понятие векторного поля во многом аналогично понятию скалярного поля.
Определение векторного поля. Если в некоторой области пространства каждой точке M по определённому закону ставится в соответствие вектор , то векторная функция называется полем вектора или векторным полем.
Таким образом, векторным полем является векторная функция точки пространства
Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или
газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером
векторного поля может служить поле сил любой природы.
Вообще, примером
векторного поля может служить поле сил любой природы.
Мы будем рассматривать только стационарные векторные поля, то есть поля, не зависящие от времени.
Проекции вектора , соответствующего точке M, на координатные оси обозначим P = P(x,y,z), Q = Q(x,y,z), R = R(x,y,z). Тогда векторное поле сможем задать через компоненты:
.
Таким образом, векторное поле можно определить тремя скалярными функциями P, Q, R. Пусть эти функции и их частные производные по переменным x,y,z являются непрерывными функциями.
Определение. Векторной линией называется линия, направление которой в каждой точке касательной совпадает с направлением вектора поля в этой точке (рисунок ниже).
Векторные линии поля силы обычно называют линиями силы, векторные линии поля скоростей
потока жидкости или газа — векторами потока. У стационарного потока жидкости линии потока совпадают с
траекториями частиц жидкости.
У стационарного потока жидкости линии потока совпадают с
траекториями частиц жидкости.
Уравнения векторных линий можно найти, решив систему дифференциальных уравнений
.
Пример 3. Найти линии вектора поля .
Решение. Так как , , , получаем систему дифференциальных уравнений
.
Из первого равенства получаем
где . Из последнего равенства следует . Таким образом, получаем
И получаем уравнения векторных линий данного векторного поля:
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Поделиться с друзьями
Контурный плоттер | Academo.org — бесплатный, интерактивный, образовательный.
Вы можете использовать этот инструмент для создания контурных линий для любой функции, которую вы вводите.
Математика Геометрия Контур
Код контурных линий:
Если вы когда-либо смотрели на карту, особенно холмистой или гористой местности, вы, возможно, заметили такие группы линий:
Они известны как контурные линии, и каждая точка на линии находится на одной высоте. Однако контурные линии не ограничиваются тем, что дают нам информацию о горах, они могут помочь нам визуализировать поверхность, описываемую математической функцией. 92. Итак, если x = 2 и y = 2, z будет равно 4 — 4 = 0. Попробуйте навести курсор на точку (2,2) выше. На боковой панели вы должны увидеть, что индикатор (x,y,z) отображает (2,2,0).
Итак, это объясняет, почему мы видим контурную линию вдоль линии x = y. Потому что вдоль этой линии z всегда равно нулю. Попробуйте выбрать другую контурную линию и следуйте за ней с помощью мыши. Посмотрите, как значение z всегда остается неизменным.
Вы также можете заметить, что если у вас есть много контурных линий, расположенных близко друг к другу, если вы немного отклонитесь от линии, значение z быстро отклонится от значения z линии. Это связано с тем, что вы смотрите на очень крутую часть графика, и небольшое изменение x или y будет иметь большое влияние на значение z.
Это связано с тем, что вы смотрите на очень крутую часть графика, и небольшое изменение x или y будет иметь большое влияние на значение z.
Нет ничего особенного в том, какие контурные линии отображаются, это просто вопрос выбора. Вы можете изменить значения, которые должны отображаться на контурных линиях, с помощью ползунков «Диапазон уровней контура» и «Количество уровней контура». По умолчанию они установлены на (-100,100) и 21 соответственно, так что это означает, что отображаемые уровни контура будут начинаться с -100 и увеличиваться до +100 включительно с интервалами в 20. Вы можете видеть, как линии контура соответствуют цвета в ключе чуть ниже графика.
Чтобы обновить функцию, отображаемую на графике, введите новую функцию в поле ввода и нажмите «Обновить».
В таблице ниже перечислены функции, которые можно ввести в поле выражения.
| Выражение | Описание |
|---|---|
| грех(х) | Синус x в радианах |
| кос(х) | Косинус x в радианах |
| желтовато-коричневый(х) | Тангенс x в радианах |
| асин(х), акос(х), атан(х) | Обратное значение трех тригонометрических функций, перечисленных выше |
кв. (х) (х) | Квадратный корень из х (только для положительного х) |
| журнал(х) | Натуральный логарифм x |
| пау(х, у) | Сила х в у |
Контурные линии могут быть немного сложными для понимания, поэтому, если у вас возникли проблемы, вам может пригодиться плоттер 3D-поверхности, который помогает визуализировать фактическую форму 3D-поверхности.
Включите JavaScript для просмотра комментариев с помощью Disqus.
Help Online — Tutorials — Contour Plots and Color Mapping
Все книгиКниги, не связанные с программированием Руководство пользователя Учебники Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия OrgMOCA0004 | |||||||||
Содержание
Резюме Origin предлагает прямоугольные, полярные и троичные контурные графики. Доступно множество опций для настройки контурных диаграмм, таких как установка различных основных и второстепенных уровней изолиний, отображение контурных линий только на основных уровнях, применение цветовых палитр, а также контроль пользовательской границы в случае контурных диаграмм, созданных непосредственно из рабочий лист. Чему вы научитесьЭтот туториал покажет вам, как:
Создать контурный график из матрицы
Настройка уровней, линий и цветовой картыOrigin позволяет легко настроить каждый аспект контурного графика, включая цветовую шкалу и добавление меток:
Создание контурного графика из данных XYZ Origin может создавать контурные графики непосредственно из данных XYZ на рабочем листе без необходимости использования промежуточной матрицы.
Показать сетку триангуляции
Применить пользовательскую границу Пользовательская граница может быть применена к контурным графикам, созданным непосредственно из данных XYZ, где пользователь предоставляет точки данных для границы в дополнительных столбцах того же рабочего листа.
| |||||||||

 Для прямоугольные контурные графики , данные могут быть либо в матрице, либо на рабочем листе в формате XYZ. Полярные контурные графики могут быть созданы из трех столбцов данных на рабочем листе, организованных либо как R Z, либо как R Z. Тройные контурные графики могут быть созданы из данных рабочего листа, организованных в формате X Y Z Z, где 2-й Z-столбец содержит 4-й параметр которое является значением высоты в данной точке XYZ в троичном пространстве.
Для прямоугольные контурные графики , данные могут быть либо в матрице, либо на рабочем листе в формате XYZ. Полярные контурные графики могут быть созданы из трех столбцов данных на рабочем листе, организованных либо как R Z, либо как R Z. Тройные контурные графики могут быть созданы из данных рабочего листа, организованных в формате X Y Z Z, где 2-й Z-столбец содержит 4-й параметр которое является значением высоты в данной точке XYZ в троичном пространстве.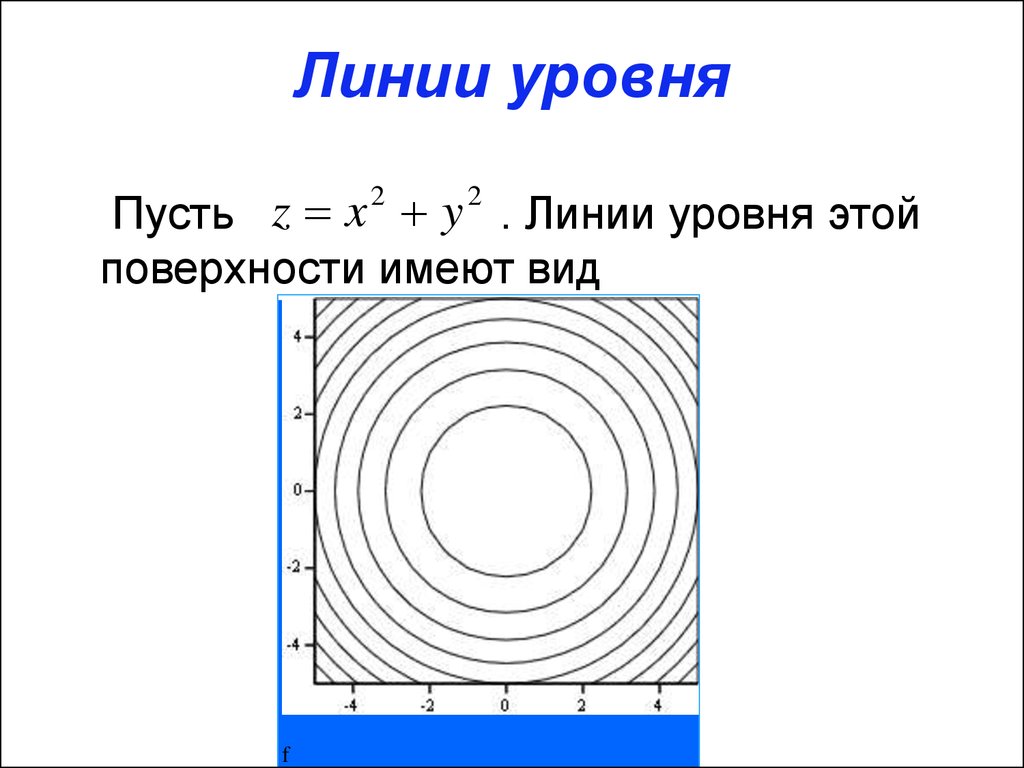 Переместите курсор в левый верхний угол матрицы, пока форма указателя не изменится, как на следующем изображении, и щелкните, чтобы выбрать всю матрицу.
Переместите курсор в левый верхний угол матрицы, пока форма указателя не изменится, как на следующем изображении, и щелкните, чтобы выбрать всю матрицу. Создайте контурный график, активировав матрицу и выбрав Plot > Contour: Contour — Color Fill . График должен выглядеть так, как показано ниже:
Создайте контурный график, активировав матрицу и выбрав Plot > Contour: Contour — Color Fill . График должен выглядеть так, как показано ниже: Затем выберите палитру Rainbow из раскрывающегося списка.
Затем выберите палитру Rainbow из раскрывающегося списка. Триангуляция Делоне используется для вычисления и рисования горизонталей.
Триангуляция Делоне используется для вычисления и рисования горизонталей. dat . Перетащите этот файл на пустой рабочий лист, чтобы импортировать его.
dat . Перетащите этот файл на пустой рабочий лист, чтобы импортировать его.  Эта функция полезна при наличии определенных граничных данных, определяющих контур объекта, например профиль двигателя, где контур показывает температуру двигателя.
Эта функция полезна при наличии определенных граничных данных, определяющих контур объекта, например профиль двигателя, где контур показывает температуру двигателя.