Построить прямую онлайн по уравнению: Построение графика функции онлайн

Уравнения прямой в пространстве

• Канонические уравнения прямой в пространстве
• Уравнения прямой, проходящей через две данные точки
• Прямая как линия пересечения плоскостей
• Параметрические уравнения прямой в пространстве

Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.

Пусть дана точка и направляющий вектор . Произвольная точка лежит на прямой l только в том случае, если векторы и коллинеарны, т. е. для них выполняется условие:

.

Приведённые выше уравнения и есть канонические уравнения прямой.

Числа m, n и p являются проекциями направляющего вектора на координатные оси. Так как вектор ненулевой, то все числа m, n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю.

В аналитической геометрии допускается, например, такая запись:

,

которая означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz, т. е. плоскости yOz.

Пример 1. Составить уравнения прямой в пространстве, перпендикулярной плоскости и проходящей через точку пересечения этой плоскости с осью Oz.

Решение. Найдём точку пересечения данной плоскости с осью Oz. Так как любая точка, лежащая на оси Oz, имеет координаты , то, полагая в заданном уравнении плоскости x = y = 0, получим 4z — 8 = 0 или z = 2. Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2). Поскольку искомая прямая перпендикулярна плоскости, она параллельна вектору её нормали . Поэтому направляющим вектором прямой может служить вектор нормали заданной плоскости.

Теперь запишем искомые уравнения прямой, проходящей через точку A = (0; 0; 2) в направлении вектора :

или

.

Прямая может быть задана двумя лежащими на ней точками и В этом случае направляющим вектором прямой может служить вектор . Тогда канонические уравнения прямой примут вид

.

Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.

Пример 2. Составить уравнение прямой в пространстве, проходящей через точки и .

Решение. Запишем искомые уравнения прямой в виде, приведённом выше в теоретической справке:

или

.

Так как , то искомая прямая перпендикулярна оси Oy.

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и , т. е. как множество точек, удовлетворяющих системе двух линейных уравнений

Уравнения системы называются также общими уравнениями прямой в пространстве.

Пример 3. Составить канонические уравнения прямой в пространстве, заданной общими уравнениями

Решение. Чтобы написать канонические уравнения прямой или, что то же самое, уравнения прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например

yOz и xOz.

Точка пересечения прямой с плоскостью yOz имеет абсциссу x = 0. Поэтому, полагая в данной системе уравнений x = 0, получим систему с двумя переменными:

Её решение y = 2, z = 6 вместе с x = 0 определяет точку A (0; 2; 6) искомой прямой. Полагая затем в заданной системе уравнений y = 0, получим систему

Её решение x = -2, z = 0 вместе с y = 0 определяет точку B (-2; 0; 0) пересечения прямой с плоскостью xOz.

Теперь запишем уравнения прямой, проходящей через точки A (0; 2; 6) и B (-2; 0; 0):

,

или после деления знаменателей на -2:

,

где .

Если даны некоторая точка и направляющий вектор, то можно составить не только канонические, но и параметрические уравнения прямой в пространстве. Пусть даны и направляющий вектор .

Тогда

где t — параметр .

Пример 4. Даны точка и направляющий вектор . Составить параметрические уравнения прямой.

Решение:

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Прямая и плоскость

Всё по теме «Прямая и плоскость»

• Плоскость
• Уравнения плоскости, взаимное расположение плоскостей
• Прямая в пространстве
• Уравнения прямой в пространстве
• Задачи на плоскость и прямую в пространстве
• Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке
• Прямая на плоскости
• Уравнение прямой с угловым коэффициентом
• Общее уравнение прямой на плоскости
• Уравнение прямой в отрезках
• Каноническое уравнение прямой на плоскости
• Параметрические уравнения прямой на плоскости
• Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
• Угол между двумя прямыми

Уравнение прямой — виды уравнения прямой: проходящее через точку, общее, каноническое, параметрическое и т.

д.

О чем статья

Уравнение прямой проходящей через точку и нормальный вектор

Рассмотрим уравнение прямой проходящей через точку и нормальный вектор. Пусть в системе координат задана точка и ненулевой вектор (рис. 1).

Как видим, существует единственная прямая , что проходит через точку перпендикулярно направлению вектора (в этом случае называют нормальным вектором прямой ).

Рис. 1

Докажем, что линейное уравнение

+

(1)

это уравнение прямой , то есть координаты каждой точки прямой удовлетворяют уравнение (1), но координаты точки, что не лежит на , уравнения (1) не удовлетворяют.

Для доказательства, обратим внимание, что скалярное произведение векторов и = в координатной форме совпадает с левой частью уравнения (1).

x = .

(2)

Дальше используем очевидное свойство прямой : векторы и перпендикулярны тогда, и только тогда, когда точка лежит на . А при условии перпендикулярности обоих векторов их скалярное произведение (2) превращается в для всех точек , что лежат на , и только для них. Значит, (1) – уравнение прямой .

Уравнение (1) называется уравнением прямой, что проходит через данную точку   с нормальным вектором = . 

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Общее уравнение прямой

Превратим уравнение (1)

+ + – = .

Обозначив = , получим

.

(3)

– общее уравнение прямой.

Таким образом, прямой линии отвечает линейное уравнение вида (3). Наоборот, за данным уравнением вида (3), где хотя бы один из коэффициентов и не равен нулю, можно построить прямую.

Действительно, пусть пара чисел удовлетворяют уравнение (3), то есть

.

Отнимая последнее от (3), получим соотношение , которое определяет прямую за вектором и точкой .

Исследование общего уравнения прямой

Полезно знать особенности размещения прямой в отдельных случаях, когда одно либо два из чисел равны нулю.

1. Общее уравнение выглядит так: . Ему удовлетворяет точка , значит, прямая проходит через начало координат. Его можно записать: = – x (см. рис. 2).

Рис. 2

Считаем, что:

–>.

Если положить , тогда , получается ещё одна точка (см. рис. 2).

2. , тогда уравнение выглядит так , где = –. Нормальный вектор лежит на оси , прямая . Таким образом, прямая перпендикулярна в точке , либо же параллельна оси (см. рис. 3). В частности, если и , тогда и уравнение – это уравнение оси ординат.

Рис. 3

3. Аналогично, при уравнение записывается , где . Вектор принадлежит оси . Прямая в точке (рис. 4) .

Рис. 4

Если же , тогда уравнение оси .

Исследование можно сформулировать в такой форме: прямая параллельна той координатной оси, смена которой в общем уравнении прямой отсутствует.

Например:

1. прямая , слагаемое с отсутствует, поэтому .

2. прямая .

Уравнение прямой в отрезках

Построим прямую по общему уравнению при условии, что – не равны нулю. Для этого достаточно найти две точки, что лежат на этой прямой. Такие точки иногда удобнее находить на координатных осях.

Положим , тогда = –.

При , тогда = –.

Обозначим – = , – = . Найдены точки и . Отложим на осях и и через них проведём прямую (см. рис. 5).

Рис. 5

От общего можно перейти к уравнению, в которое будут входить числа и :

И тогда получается:

Либо, согласно обозначению, получим уравнение,

+ =

(4)

Которое называется уравнением прямой в отрезках. Числа и с точностью к знаку равняются отрезкам, которые отсекаются прямой на координатных осях.

Уравнение прямой с угловым коэффициентом

Чтобы узнать, что такое уравнение прямой с угловым коэффициентом, рассмотрим уравнение (1):

+ = – x

Обозначив – = , получим

=

(5)

уравнение прямой, которая проходит через точку в заданном направлении.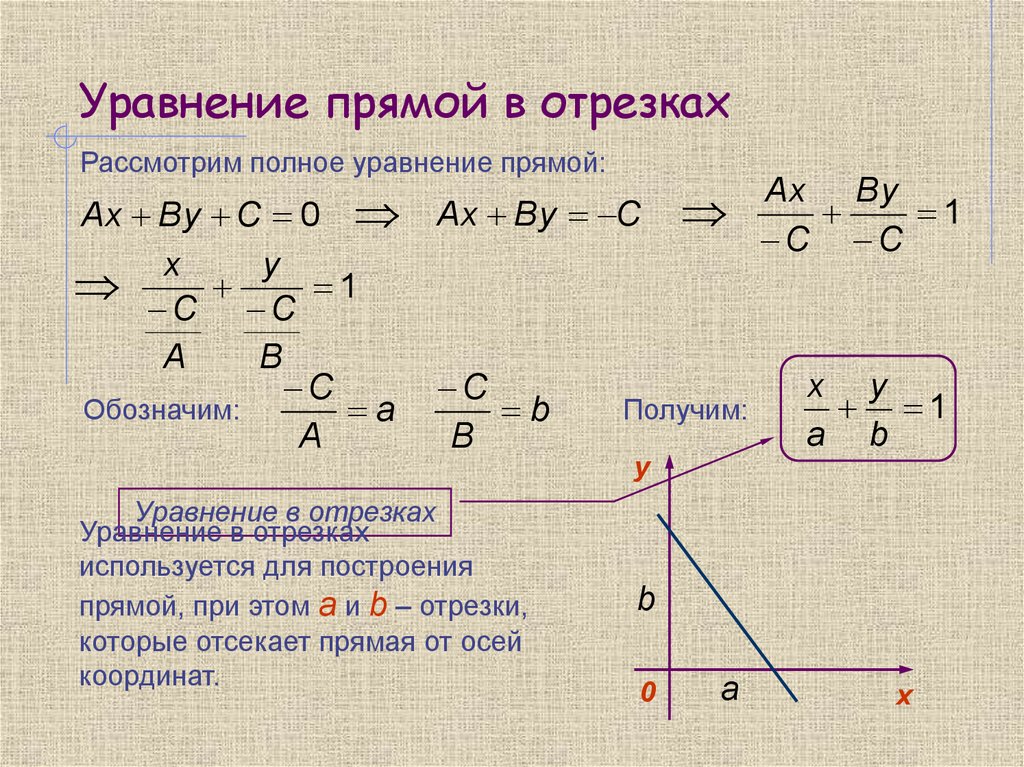 Геометрическое содержание коэффициента понятно из рис. 6.

В       = = , где – наименьший угол, на который нужно повернуть положительное направление оси вокруг общей точки до совмещения её с прямой . Очевидно, что если угол – острый, тогда ; если же – тупой угол, тогда .

Раскроем скобки в (5) и упростим его:

=

(6)

где . Соотношение (6) – уравнение прямой с угловым коэффициентом. При , – отрезок, который отсекает прямую на оси (см. рис. 6).

 

Обратите внимание!

 Для перехода от общего уравнения прямой к уравнению с угловым коэффициентом необходимо сначала решить относительно .

Рис. 6

= – x + – =

где обозначено = –, = –. Если же , тогда из исследования общего уравнения уже известно, что такая прямая перпендикулярна оси .

Каноническое уравнение прямой

Рассмотрим каноническое уравнение прямой при помощи примера.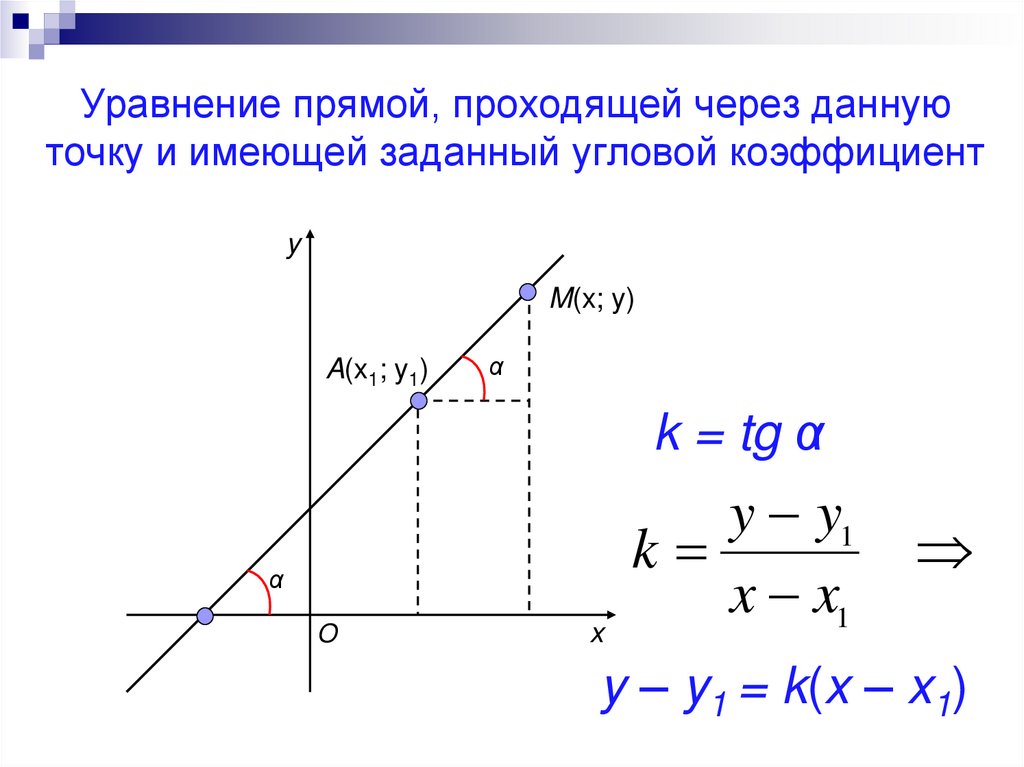

Пусть в системе координат задана точка и ненулевой вектор (рис. 7).

Рис. 7

Необходимо составить уравнение прямой, что проходит через точку параллельно вектору , который называется направляющим вектором. Произвольная точка принадлежит этой прямой тогда и только тогда, когда . Так как вектор – задан, а вектор  , тогда согласно условию параллельности, координаты этих векторов пропорциональны, то есть:

= .

(7)

 

Соотношение (7) называется уравнением прямой, которая проходит через заданную точку в заданном направлении или каноническом уравнением прямой.

Обратим внимание, что к уравнению вида (7) можно перейти, например, от уравнения пучка прямых (4)

= ,

или от уравнения прямой через точку и нормальный вектор (1):

=

Выше предполагалось, что направляющий вектор – ненулевой, но может так случиться, что одна из его координат, например, . Тогда выражение (7) формально запишется:

= ,

который, вообще не имеет смысла. Однако, принимают и получают уравнение прямой перпендикулярной оси . Действительно, из уравнения видно, что прямая определена точкой и направляющим вектором , перпендикулярным оси . Если в этом уравнении освободиться от знаменателя, тогда получим:

. , либо – уравнение прямой, перпендикулярной оси . Аналогично было бы получено  для вектора .

Параметрическое уравнение прямой

Чтобы понять, что такое параметрическое уравнение прямой, необходимо вернуться к уравнению (7) и приравнять каждую дробь (7) до параметра . Так как хотя бы один из знаменателей в (7) не равен нулю, а соответствующий числитель может приобретать произвольные значения, тогда область смены параметра – вся числовая ось.

Получим:

= ,   =

или

(8)

 

Уравнение (8) называется параметрическим уравнением прямой.

Примеры задач на прямую линию

Конечно же, сложно что-либо решить исключительно по определениям, ведь нужно решить самостоятельно хотя бы несколько примеров или задач, которые помогут закрепить пройденный материал.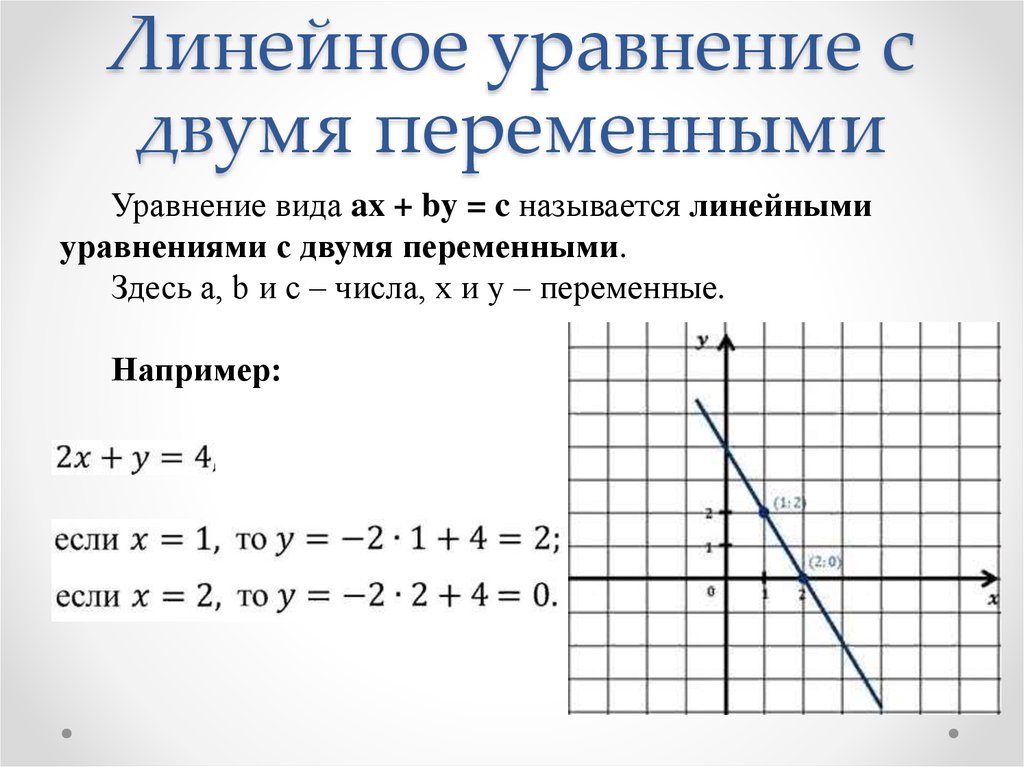 Поэтому, давайте разберём основные задачи на прямую линию, так как похожие задачи часто попадаются на экзаменах и зачётах.

Каноническое и параметрическое уравнение

Пример 1

На прямой линии заданной уравнением , найти точку , которые находятся от точки этой прямой на расстоянии 10 единиц.

Решение:

Пусть искомая точка прямой, тогда для расстояния запишем . При условии . Так как точка принадлежит прямой , у которой есть нормальный вектор , тогда уравнение прямой можно записать: = = и далее получается:

Тогда расстояние . При условии , или . Из параметрического уравнения:

Ответ: .

Пример 2

Задача

Точка движется равномерно со скоростью по направлению вектора от начальной точки . Найти координаты точки через от начала движения.

Решение

Сначала нужно найти единичный вектор . Его координаты – это направляющие косинусы:

= = ; = =

Тогда вектор скорости:

= x = x = .

Каноническое уравнение прямой теперь запишется:

= = , = – параметрическое уравнение. После этого нужно воспользоваться параметрическим уравнением прямой при .

Ответ

.

Угол между двумя прямыми

Пример

В равнобедренном прямоугольном треугольнике известна вершина прямого угла и уравнение гипотенузы .  Составить уравнение катетов.

Решение:

Уравнение прямой, которая проходит через точку находим по формуле пучка прямых , где угловой коэффициент для прямой и = для прямой .

При условии , , поэтому и находим по формуле :

=

(9)

Учитывая рисунок, где видно, что между прямыми и – два угла: один острый , а второй – тупой . Согласно формуле (9) – это тот угол между прямыми и , на который нужно повернуть прямую против часовой стрелки относительно их точки пересечения до  совмещения её с прямой .

Итак, формулу вспомнили, с углами разобрались и теперь можно вернуться к нашему примеру. Значит, учитывая формулу (9) находим сначала и уравнения катета .

Так как поворот прямой на угол против часовой стрелки относительно точки  приводит к совмещению с прямой , тогда в формуле (9) , а . Из уравнения :

, поэтому

= Далее следует:

=  = = = .

По формуле пучка уравнения прямой запишется:

= .

Аналогично находим , а ,

= Далее:

= = .

Уравнение прямой :

= .

Ответ: , .

Уравнение прямой линии – формула, формы, примеры

Общее уравнение прямой линии имеет вид y = mx + c, где m – наклон прямой, а c – точка пересечения с осью y. Это наиболее распространенная форма уравнения прямой, которая используется в геометрии. Уравнение прямой линии может быть записано в различных формах, таких как форма точки-наклона, форма наклона-пересечения, форма пересечения, стандартная форма и т. д.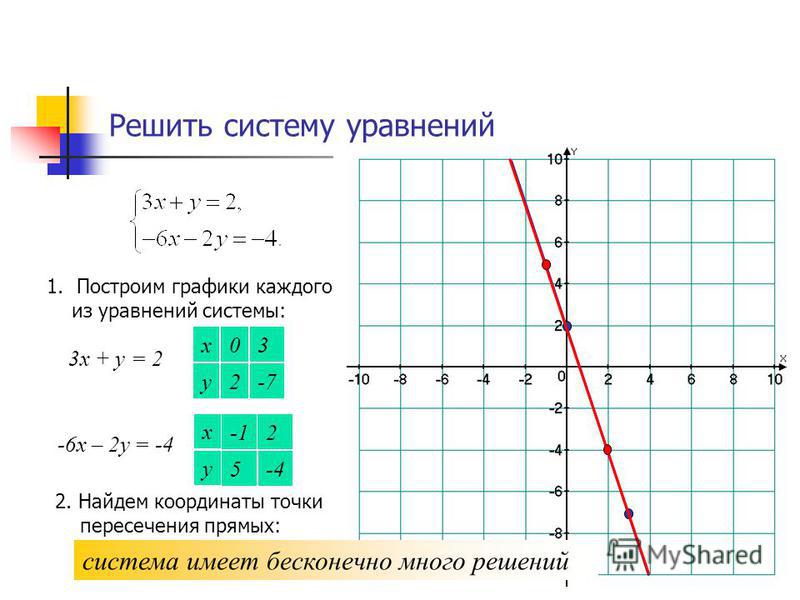 Прямая линия представляет собой двумерный геометрический объект, который простирается с обоих концов до бесконечности.

В этой статье мы рассмотрим концепцию уравнения прямой линии в различных формах. Попробуйте решить несколько интересных примеров и вопросов, чтобы лучше понять концепцию.

1.	Что такое уравнение прямой линии?
2.	Уравнение формул прямой линии
3.	Формы уравнения прямой линии
4.	Уравнение прямой на графике
5.	Часто задаваемые вопросы по уравнению прямой

Что такое уравнение прямой линии?

Уравнение прямой линии является линейным уравнением с двумя переменными (обычно x и y) и удовлетворяется каждой точкой на прямой. то есть это математическое уравнение, которое дает отношение между координатными точками, лежащими на этой прямой. Он может быть записан в разных формах и сообщает наклон, пересечение по оси x и пересечение по оси y линии. Его также можно использовать для поиска точек на линии. В основном уравнение прямой линии находится с использованием формы точка-наклон, форма наклона-пересечения, форма с двумя точками, стандартная форма и т. Д. Давайте рассмотрим формулу уравнения прямой линии.

Наиболее распространенные формулы для нахождения уравнения прямой приведены ниже.

Уравнение формул прямой линии

Формула уравнения прямой линии зависит от того, какая информация доступна о линии, например, наклон, точки пересечения и т. д. Обратите внимание, что наклон линии с двумя точками (x ₁ , y ₁ ) и (x ₂ , y ₂ ) вычисляется по формуле m = (y ₂ — y ₁ )/(х ₂ — х ₁ ). Вот различные формулы прямой линии.

Различные формы прямых линий	Уравнение прямой
Двухконечная форма (Для двух точек (x 1 , y 1 ) и (x 2 , y 2 ) на линии)	у — у 1 = (у 2 — у 1 )/(х 2 — х 1 ) (х — х 1 )
Форма точки-наклона (Данный уклон m и точка (x 1 , y 1 ))	у — у 1 = м (х — х 1 )
Уклон — Форма пересечения (Данный наклон m и точка пересечения y (0, c))	у = мх + с
Форма перехвата (Учитывая точки пересечения a и b)	х/а + у/б = 1
Обычная форма (Данный θ = угол, образованный нормалью с положительным направлением оси x и p = расстояние линии от начала координат)	x cos θ + y sin θ = p
Общая/стандартная форма линии	топор + по = с
Уравнение вертикальной линии с некоторой точкой (a, b) на ней	х =
Уравнение горизонтальной линии с некоторой точкой (a, b) на ней	у = б

Мы подробно изучим каждый из них в следующем разделе.

Формы уравнения прямой линии

Уравнение прямой обычно включает наклон. Предположим, что линия l образует угол θ с положительным направлением оси x, угол θ называется наклоном линии, а tan θ называется наклоном линии. Обратите внимание, что ось x имеет наклон 0. На самом деле все линии, параллельные оси x, имеют наклон 0. Кроме того, наклон всех линий, параллельных оси y, включая ось y, не определен.

Теперь давайте рассмотрим различные формы уравнений прямой.

Форма «точка-наклон»

Уравнение прямой линии с наклоном m и проходящей через точку (x ₁ , y ₁ ) находится с использованием формы «точка-наклон». Уравнение формы точка-наклон:

y — y ₁ = m (x — x ₁ ), где (x, y) — произвольная точка на прямой.

Давайте посмотрим, как найти форму точка-наклон. Мы выведем эту формулу, используя уравнение для наклона линии. Рассмотрим прямую, наклон которой равен m. Предположим, что (x ₁ , y ₁ ) — известная точка на прямой. Пусть (x, y) — любая другая случайная точка на прямой, координаты которой неизвестны. Мы знаем, что уравнение для наклона линии:

Наклон = разница в координатах y / разница в координатах x

⇒ m = (y — y ₁ )/(x — x ₁ )

Умножая обе части на (x — x ₁ ),

m (x — x ₁ ) = (y — y ₁ )

Это можно записать как

(y — y ₁ ) = m (x — x ₁ )

Таким образом, точечно-наклонная форма уравнения прямой доказана.

Форма с двумя точками

Рассмотрим прямую с двумя точками (x ₁ , y ₁ ) и (x ₂ , y ₂ ). Тогда его наклон можно рассчитать по формуле m = (y ₂ — y ₁ )/(x ₂ — x ₁ ). Подставляя это в приведенную выше форму точка-наклон, мы получаем двухточечную форму как y — y ₁ = (у ₂ — у ₁ )/(х ₂ — х ₁ ) (х — х ₁ ).

Форма Slope-Intercept

Теперь предположим, что вам дана линия с ее наклоном m и точкой пересечения с осью y. Скажем, прямая пересекает ось у в точке (0, с). Используя форму точка-наклон, мы имеем y — c = m (x — 0) ⇒ y = mx + c, где c — точка пересечения с осью y. Это называется формой линии с пересечением наклона.

Примечание: Если d является точкой пересечения с осью x, то форма уравнения прямой с пересечением наклона имеет вид y = m(x — d).

Форма перехвата

Если (a, 0) и (0, b) точки пересечения линии по осям x и y соответственно. Тогда его наклон равен m = (b — 0)/(0 — a) = -b /a. Тогда его уравнение с использованием формы точка-наклон:

y — 0 = -b/a (x — a)

Умножение обеих сторон на a

ay = -bx + ab

bx + ay = ab

Разделив обе стороны на ab,

x/a + y/b = 1

Стандартная форма

Стандартная форма прямой линии задается ax + by = c, где a, b, c — действительные числа. Мы можем рассматривать любую форму линии в стандартной форме. Рассмотрим пример преобразования уравнения y = 2x — 1 к стандартной форме. Отнимите 2x от обеих частей уравнения, у нас есть

y — 2x = 2x — 1 — 2x

⇒ y — 2x = -1

⇒ 2x — y = 1

Итак, мы получаем стандартную форму уравнения прямой как 2x — y = 1.

Уравнение прямой на графике

График линейного уравнения с одной переменной x образует вертикальную линию, параллельную оси y, а график уравнения прямой линии с одной переменной y представляет собой горизонтальную линию, параллельную оси x График линейное уравнение с двумя переменными x и y образует прямую линию с некоторым наклоном.

Если прямая линия увеличивается слева направо, ее наклон положительный. Если он уменьшается, его наклон отрицательный.

Важные замечания по уравнению прямой линии:

• Уравнение прямой называется также линейным уравнением с двумя переменными.

• Если произведение наклонов двух прямых равно -1, то прямые перпендикулярны друг другу.

• Если две прямые параллельны друг другу, то они имеют одинаковый наклон.

• Форма уклона точки: (y — y ₁ ) = m (x — x ₁ )

• Форма пересечения наклона: y = mx + c

• Стандартная форма = ax + by = c

☛ Связанные темы:

• Формула линейного уравнения
• Калькулятор уравнения звездной линии

Cuemath — одна из ведущих в мире платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Часто задаваемые вопросы об уравнении прямой

Что такое уравнение прямой линии в координатной геометрии?

Уравнение прямой линии — это линейное уравнение относительно x и y, которое дает отношение между точками координат, лежащими на этой линии. Уравнение прямой линии обычно имеет вид y = mx + c, где m — наклон прямой, а c — ее точка пересечения с осью y.

Какая формула уравнения прямой линии?

Уравнение прямой можно найти по разным формулам:

• Форма точки-наклона: y — y ₁ = m (x — x ₁ )
• Двухточечная форма: у — у ₁ = [(у ₂ -у ₁ ) / (х ₂ -х ₁ )] (х — х ₁ )
• Форма пересечения наклона: y = mx + c
• Форма перехвата: x/a + y/b = 1
• Общая форма: ax + by = c
• Нормальная форма: x cos θ + y sin θ = p

Как найти уравнение прямой?

Уравнение любой прямой линии можно найти, используя форму точка-наклон y — y ₁ = m (x — x ₁ ), где

• м = наклон линии, и его можно рассчитать по формуле tan θ (или) (y ₂ — y ₁ ) / (x ₂ — x ₁ ).
• (x ₁ , y ₁ ) — точка на прямой.

Как преобразовать уравнение прямой линии из формы «точка-наклон» в форму «наклон-пересечение»?

Уравнение прямой линии можно преобразовать из формы «точка-наклон» в форму «наклон-отрезок», просто упростив его таким образом, чтобы в левой части уравнения был только y, а все остальные члены были перемещены в правую часть. Например, y — 2 = 3 (x — 1) находится в форме точка-наклон. Если мы упростим это, y — 2 = 3x — 3, добавив 2 с обеих сторон, y = 3x — 1, что находится в форме пересечения наклона.

Как найти наклон и точку пересечения Y уравнения прямой линии?

Преобразовав уравнение прямой линии в форму y = mx + c, мы можем найти ее наклон m и точку пересечения с y. Например, если уравнение 2x — 3y = 1, чтобы найти его наклон и точку пересечения с y, нам сначала нужно решить его для y. Тогда получаем у = (2/3)х — 1/3. Сравнивая это с y = mx + c, мы получаем наклон, m = 2/3 и точку пересечения y = (0, c) = (0, -1/3).

Как написать уравнение для вертикальной и горизонтальной линий?

• Уравнение горизонтальной прямой, проходящей через точку (a, b), имеет вид y = b.
• Уравнение вертикальной линии, проходящей через точку (a, b), имеет вид x = a.

Как найти уравнение прямой, если даны две точки?

Уравнение прямой линии, соединяющей две точки (x ₁ , y ₁ ) и (x ₂ , y ₂ ), задается двухточечной формой y — y ₁ = (x — х ₁ )[(у ₂ — у ₁ )/(х ₂ — х ₁ )]. В качестве альтернативы мы можем сначала найти его наклон, используя m = (y ₂ — y ₁ )/(x ₂ — x ₁ ), а затем используйте форму точка-наклон y — y ₁ = m (x — x ₁ ).

Как построить прямую линию, используя ее уравнение?

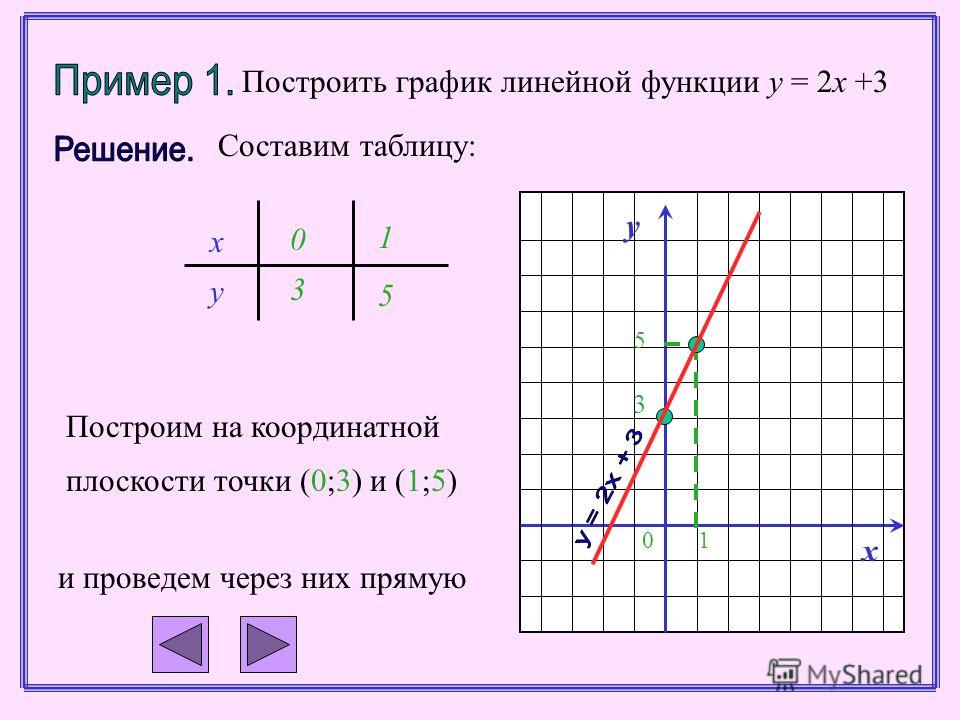
Чтобы построить прямую линию, найдите на ней любые две точки, используя ее уравнение. Например: рассмотрим уравнение y = 3x + 2. Здесь мы предполагаем любые два случайных числа для x и находим соответствующие значения y, используя уравнение.

х	г
0	у = 3(0) + 2 = 2
1	у = 3(1) + 2 = 5

Следовательно, (0, 2) и (1, 5) — две точки на данной прямой. Простое их построение и соединение их линией дает график.

Когда мы используем нормальную форму, чтобы найти уравнение прямой линии?

Когда а нормаль от начала координат к линии образует угол θ с положительным направлением оси х, а ее перпендикулярное расстояние от начала координат равно p, то ее уравнение можно найти, только используя нормальную форму, которая устанавливает x cos θ + y sin θ = p.

Графики линейных уравнений — Krista King Math

Фрагменты формы уравнения прямой

Линейное уравнение – это уравнение прямой. Когда вы рисуете линейное уравнение, лучше всего записывать уравнение в форме пересечения наклона: ???y=mx+b???.

Помнишь ???м??? наклон линии и ???b??? является ???y???-перехватом (???y???-координата точки, в которой линия пересекает ???y???-ось).

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Если мы запишем уравнение в форме ???y=mx+b???, мы можем сначала построить точку пересечения ???y???, а затем использовать наклон, чтобы найти другую точку на линии.

Технически, для создания прямой линии нужно всего две точки, но построение трех или четырех точек позволит создать более точный график, если вы строите график вручную.

Как построить график уравнения прямой

Пройти курс

Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого. 🙂

Узнать больше

Нахождение точки пересечения оси Y из формы точки пересечения наклона

Пример

Что такое ???y???-пересечение линии?

???y=-\frac{2}{3}x???

Это уравнение представлено в виде точки пересечения наклона, но точка пересечения ???y??? отсутствует. Однако на самом деле мы могли бы переписать уравнение прямой как

???y=-\frac{2}{3}x+0???

Записав таким образом, мы вообще не изменили значение ни одной из частей уравнения, но мы можем видеть, что ???y???-перехват равен ???0???.

Давайте посмотрим на пример графического отображения линейных уравнений.

Технически, для построения прямой линии нужно всего две точки, но построение графика по трем или четырем точкам даст более точный график, если вы строите график вручную.

Пример

Нарисуйте линию.

???y=3x-2???

Это уравнение находится в форме пересечения наклона, поэтому его можно изобразить в виде графика. Начните с рисования декартовой системы координат. Не забудьте пометить оси ???x???- и ???y???- и деления. Засечки — это очень-очень короткие линии, расположенные на равном расстоянии друг от друга по осям. Мы помечаем деления цифрами, чтобы указать значения ???x??? и ???й??? в местах расположения делений на осях ???x???- и ???y???- соответственно.

Затем постройте точку пересечения ???y??? (???b??? в уравнении). ???y???-перехват в этом случае равен ???-2???, что означает, что точка будет в ???-2??? по оси ???y??? (вниз на ???2??? от начала координат).

Затем используйте наклон (???m??? в уравнении), чтобы найти дополнительные точки на графике. Хорошей практикой является идти вверх (если наклон положительный) или вниз (если наклон отрицательный) для подъема, а затем идти вправо для разбега. Как только вы научитесь это делать, вы можете «вернуться назад», двигаясь вверх (если наклон отрицательный) или вниз (если наклон положительный) для подъема, а затем двигаясь влево для бега.

Поскольку наш наклон положителен ???3??? (что может быть записано как ???3/1???), мы начнем с ???y???-перехвата и поднимемся ???3??? единиц и вправо ???1??? единица. Мы будем:

1. Нанесем три-четыре точки для точности

2. Соединим точки прямой линией и продолжим линию за точки

3. Завершим линию стрелками в обоих направлениях, начиная с уравнения прямой простирается до бесконечности (продолжается вечно в обоих направлениях)

Давайте попробуем еще один пример графического отображения линейных уравнений.