Множества.Математические модели.ГДЗ.Математика 5 класс.Дорофеев Г.В.Часть.1.Глава 1.Параграф 2.Задание 201 – Рамблер/класс
Множества.Математические модели.ГДЗ.Математика 5 класс.Дорофеев Г.В.Часть.1.Глава 1.Параграф 2.Задание 201 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Не помню как это делается, кто сможет ?
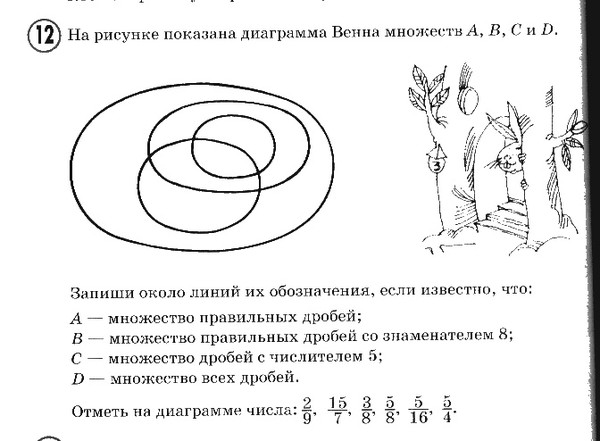
А — множество делителей числа 16, а В — множество делителей числа 28.
а) Запиши множества А и В с помощью фигурных скобок.
б) Построй диаграмму Эйлера-Венна множеств А и В, найди их объединение
и пересечение. Сделай записи, используя знаки множества
в) D = {2, 4, 8}. Какие из высказываний верны:
ответы
Это множества, все просто :
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
Репетитор
Химия
Алгебра
похожие вопросы 5
Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191
Укажите начало отсчёта и координаты точек А, В, С, (Подробнее…)
ГДЗЗубарева И.И.Математика5 класс
Помогите установить соответствие между неравенствами.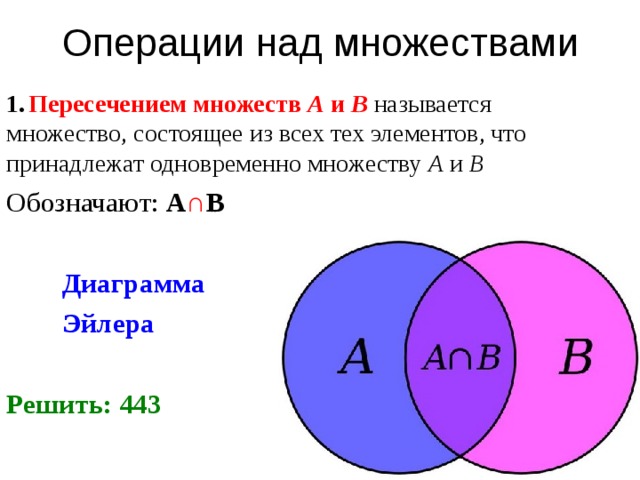 Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.
Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?
ГДЗМатематика6 классДорофеев Г. В.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Множества. Диаграмма Венна. Задачи по математике 3 класс
Задание 1
Назови каждый элемент множества В = {2; m;}. Принадлежит ли этому множеству число 2, буква а? Запиши соответствующие предложения:
- Решение
- Число 2 и буква a принадлежит множеству B.
Задание 2
На рисунке изображена диаграмма множества А. Зашипи, какие элементы принадлежат множеству Л, а какие ему не принадлежат. Прочитай полученные записи.
- b принадлежит множеству A
- 8 принадлежит множеству A
- e не принадлежит множеству A
- 4 не принадлежит множеству A
- не принадлежит множеству A
- принадлежит множеству A
Задание 3
Отметь элементы , , d, 10, , 5 на диаграмме множества С, если известно, что:
Задание 4
Имеется множество М = {а; Ь; ; С; }.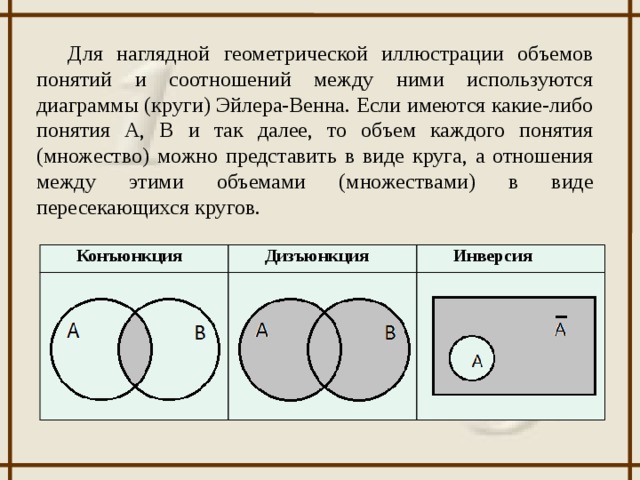 Поставь знак ∈ или ∉ .
Поставь знак ∈ или ∉ .
Решение
- a ∈ M
- ∉ M
- ∉ M
- ∈ M
- c ∈ M
- 8 ∉ M
Задание 5
- D — множество двузначных чисел.
- а) Запиши, используя знаки ∈ или ∉, являются ли числа 26, 307, 8, 940, 15, 60 элементами множества D?
- б) Запиши самое маленькое и самое большое число, принадлежащее множеству D.
- в) Сколько элементов содержит множество D?
Решение
- а)
- 26 ∈ D,
- 307 ∉ D,
- 8 ∉ D,
- 940 ∉ D,
- 15 ∈ D,
- 60 ∈ D.
- б) Самое маленькое число множества D — 8, самое большое число множества D — 60.
- г) Множетво D содержит 3 элемента.
Задание 6
Запиши множество трёхзначных чисел, у которых все три цифры одинаковые. Сколько существует таких чисел?
Решение
- а)
- 111
- 222
- 333
- 444
- 555
- 666
- 777
- 888
- 999
- б) Трехзначных чисел, у которых все три цифры одинаковые всего 9.
Задание 7
А — множество девочек с мячом, а В — м ножество девочек с цветком. Построй диаграммы множеств A и В.
Сколько девочек принадлежит множеству А, но не принадлежит множеству В? Сколько девочек принадлежит множеству B, но не принадлежит А? Сколько общих элементов у множеств А и В?
- Множеству A принадлежит 3 девочки.
- Множеству B принадлежит 5 девочек.
- У множеств A и B нет общих элементов.
Задание 8
Бабушка Гамми сварила 45 л яблочного сока и 85 л вишнёвого. Из них на завтрак медведи израсходовали 18л сока, а на обед — в 2 раза больше, чем на завтрак. Сколько сока у медведей ещё осталось?
Решение
- Вычисляем сколько всего сока у медведей 45 + 85 = 130.
- Вычисляем сколько медведи израсходовали на обед 18 * 2 = 36.
- Вычисляем сколько всего израсходовали медведи 36 + 18 = 54.
- Вычисляем сколько осталось сока у медведей 130 — 54 = 76.
- У медведей осталось 76 литров сока.
Задание 9
Вычисли устно:
Задание 10
- а) У Вадима a открыток.
 Их в 2 раза меньше, чем у Алёши. Сколько открыток у Алёши?
Их в 2 раза меньше, чем у Алёши. Сколько открыток у Алёши? - б) У Лены Ь марок. Их на С марок меньше, чем у её сестры. Сколько марок у них вместе?
- в) Артем нашёл n ягод земляники. Из них сестре он подарил k ягод, а бабушке — в 3 раза больше. Сколько ягод у него осталось?
- г) Из X белых и Y красных гвоздик сделали букеты по 5 гвоздик в каждом. Сколько получилось букетов?
Решение
- а) 2 * a
- б) (b + c) + b
- в) n — (k * 3 + k)
- г) (X + Y) : 5
Задание 11
- Найди значения выражений:
- б) 4 • (30 • 8) — 9 • 8 : 12 — (100 — 8 • 8) =
Решение
- а) 360 : 6 • 5 — 450 : (25 • 2) — 70 • 6 : 3 = 300 — 90 = 210 — 140 = 70
- б) 4 • (30 • 8) — 9 • 8 : 12 — (100 — 8 • 8) = 960 — 6 = 964 — 36 = 918
Задание 12
Заполни таблицу, а затем запиши найденные значения X в порядке убывания:
Решение
Далее
На странице использованы задачи и задания из книги Л. Г. Петерсон «Математика. 3 класс. Часть1.» 2008г.
Г. Петерсон «Математика. 3 класс. Часть1.» 2008г.
Ссылка на сайт автора: www.sch3000.ru
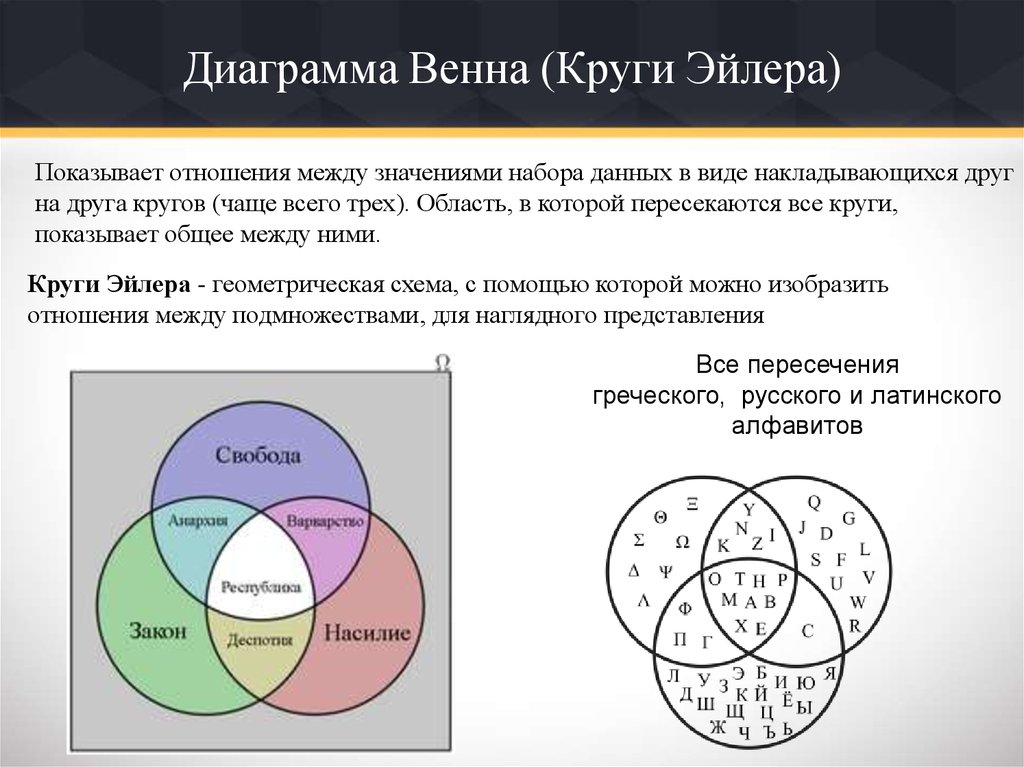
Диаграммы Венна и диаграммы Эйлера с объяснением на примерах
Дата обновления:
Диаграммы Венна и диаграммы Эйлера выглядят очень похоже, поэтому понятно, что многие люди не могут определить разницу. Хотя оба типа диаграмм основаны на теории множеств, существуют некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья рассеет ваши сомнения по поводу диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы было понятнее.
Венн против Эйлера: определение
Что такое диаграмма Венна?
Проще говоря, диаграмма Венна иллюстрирует логическую связь между двумя или более наборами элементов. Он визуально представляет различия и сходства между двумя концепциями.
Что такое диаграмма Эйлера?
Диаграмма Эйлера — это еще одна диаграмма, которая представляет наборы и их отношения. Это похоже на диаграмму Венна, поскольку обе используют круги для создания диаграммы. Однако в то время как диаграмма Венна представляет все множество, диаграмма Эйлера представляет часть множества. Диаграмма Венна показывает пустое множество, затеняя его, тогда как на диаграмме Эйлера эта область может просто отсутствовать.
В чем разница между диаграммой Венна и диаграммой Эйлера?
Оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между наборами множеств. Но диаграмма Эйлера показывает только те отношения, которые существуют в реальном мире.
Хотя диаграммы Венна и диаграммы Эйлера являются инструментами, используемыми для представления множеств и их отношений, между ними есть некоторые важные различия.
| Элемент | Диаграмма Венна | Диаграмма Эйлера |
| Перекрытие | Перекрытие между двумя или более наборами представлено на диаграмме общей областью.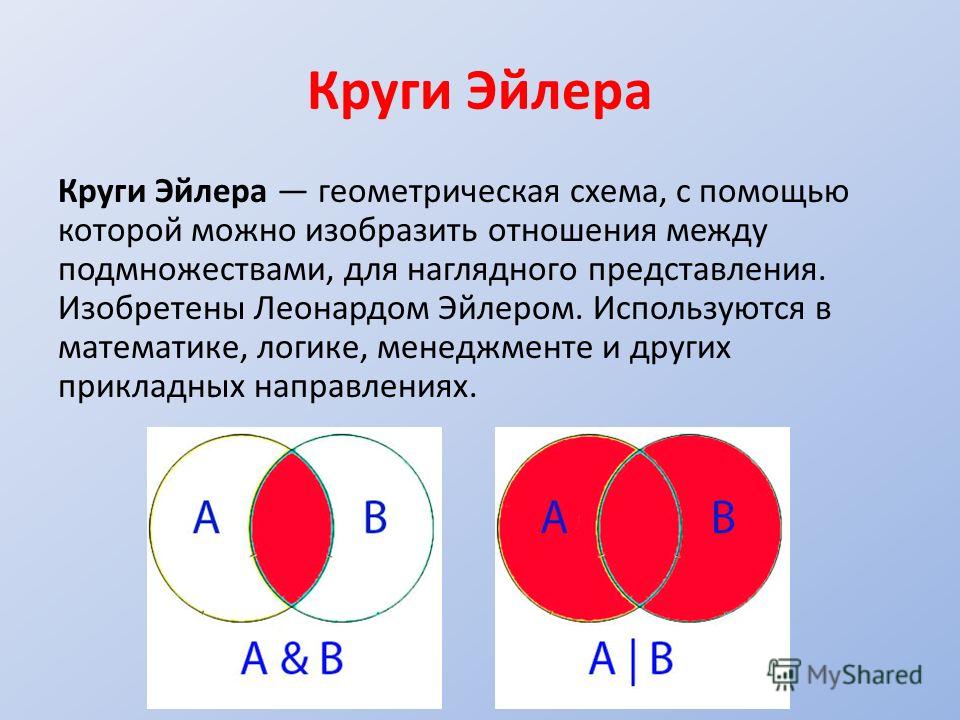 | Может использовать перекрывающиеся или вложенные фигуры для представления взаимосвязей между наборами и может вообще не иметь общих областей. |
| Полнота | Разработаны, чтобы быть полными, что означает, что они показывают все возможные отношения между наборами. | Могут быть частичными или неполными, что означает, что они могут не отображать все возможные отношения между наборами. |
| Выразительность | Ограниченная в своей выразительности, так как они могут представлять установленные отношения только в терминах объединения, пересечения и различия. | Можно использовать перекрывающиеся и вложенные фигуры для представления более широкого диапазона отношений и зависимостей между наборами. |
| Сложность | Может стать сложным и трудным для чтения при представлении отношений между более чем тремя наборами. | Может быть разработан для обработки более сложных взаимосвязей, и в таких случаях его легче интерпретировать.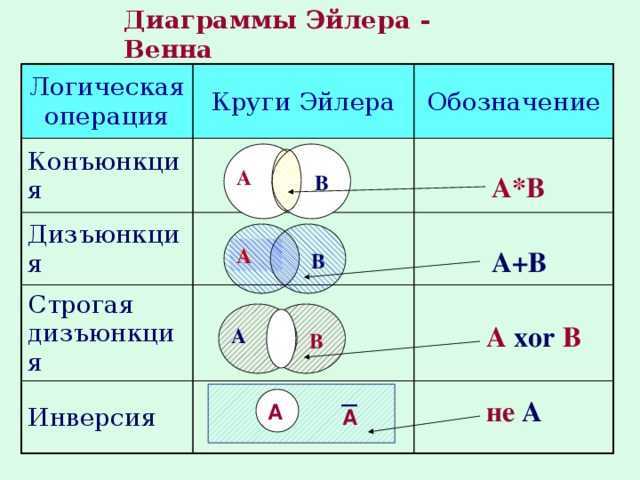 |
В общем, диаграммы Венна идеально подходят для визуализации простых отношений множеств и могут быть полезны для обучения основным понятиям теории множеств. Однако диаграммы Эйлера более гибки и универсальны, поэтому их можно использовать для визуализации более широкого диапазона отношений между множествами. Это делает их полезными для более сложных ситуаций и приложений.
Диаграммы Венна против
Диаграммы Эйлера ПримерыНачнем с очень простого примера. Давайте рассмотрим надмножество Animals с млекопитающими и птицами в качестве подмножеств. Диаграмма Венна показывает пересечение двух множеств, хотя в реальном мире такой возможности не существует. Диаграмма Эйлера, с другой стороны, не показывает пересечения.
Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии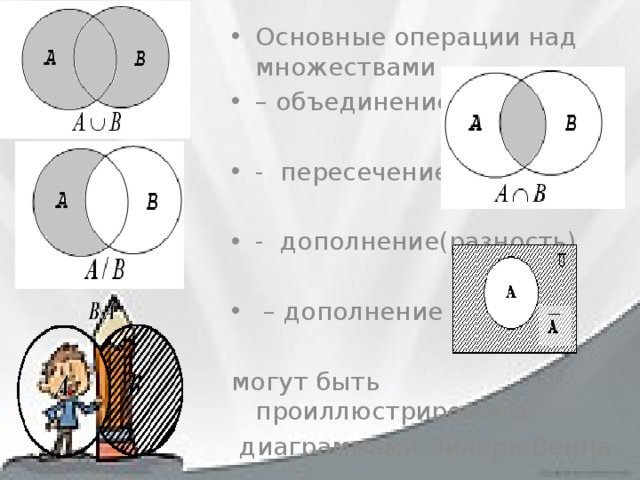 Возьмем карты как надмножество, а черные карты, красные карты и бубны — как подмножества. Как одни и те же данные представляются по-разному с использованием диаграмм Венна и диаграмм Эйлера
Возьмем карты как надмножество, а черные карты, красные карты и бубны — как подмножества. Как одни и те же данные представляются по-разному с использованием диаграмм Венна и диаграмм ЭйлераКак видно из приведенного выше примера, диаграммы Венна показывают четыре пересечения, которые не содержат никаких данных, поскольку должны показывать все возможные комбинации.
Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера и наоборот. Посмотрите эту замечательную вики-статью о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера. Я надеюсь, что приведенные выше примеры помогли вам развеять ваши сомнения относительно диаграмм Венна и диаграмм Эйлера. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.
Рисуете ли вы диаграммы Венна или диаграммы Эйлера, Creately предоставляет вам все необходимые инструменты. Вы можете быстро приступить к работе, используя шаблоны диаграмм Венна, доступные нашим пользователям, или начать с нуля в области рисования. Если вы хотите добавить значки и изображения на диаграмму Венна, это можно легко сделать с помощью встроенного поиска изображений Google, доступного на левой боковой панели. С таким количеством супер крутых функций вы не ошибетесь с Creately.
Вы можете быстро приступить к работе, используя шаблоны диаграмм Венна, доступные нашим пользователям, или начать с нуля в области рисования. Если вы хотите добавить значки и изображения на диаграмму Венна, это можно легко сделать с помощью встроенного поиска изображений Google, доступного на левой боковой панели. С таким количеством супер крутых функций вы не ошибетесь с Creately.
диаграммы эйлера теория множеств диаграммы венна диаграммы венна против диаграммы эйлера венн против эйлера
Автор
Вернуться к началу
Диаграммы Эйлера и Венна: они не только для развлечения
(источник)
К тому времени, когда вы закончите читать этот пост в блоге, вы должны быть в третьей группе. Диаграммы Венна и Эйлера (произносится как «майлер») невероятно популярны в Интернете как забавные диаграммы. Они предлагают простой способ изображения понятий теории множеств.
Итак, в чем разница между ними? Почему они смешные? Полезны ли они для реальных данных?
Оба типа диаграмм используются для отображения понятий из теории множеств:
Объединение – Комбинация двух множеств.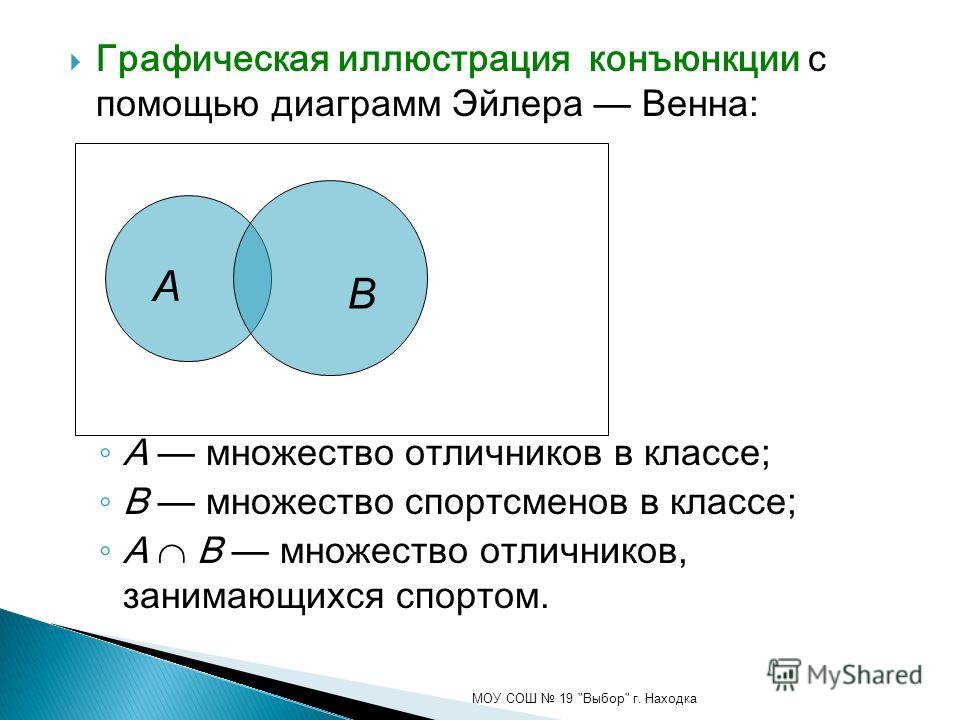 На диаграммах Венна и Эйлера.
На диаграммах Венна и Эйлера.
Пересечение – Входит в оба набора. На диаграммах Венна и Эйлера.
Разность – Все, кроме пересечения двух множеств. На диаграммах Венна и Эйлера.
Относительное дополнение – В одном наборе, а не в другом. На диаграммах Венна и Эйлера.
Абсолютное дополнение – Все, чего нет в другом наборе. Только на диаграммах Эйлера.
Подмножество — Набор, полностью содержащийся в другом наборе. Только на диаграммах Эйлера.
Непересекающиеся – Два множества, не имеющие общих элементов. Только на диаграммах Эйлера.
Все диаграммы Венна являются диаграммами Эйлера, но не все диаграммы Эйлера являются диаграммами Венна. Диаграммы Эйлера имеют только те комбинации пересечений, которые действительно существуют в реальном мире. Диаграммы Венна представляют все гипотетически возможные логические отношения между категориями.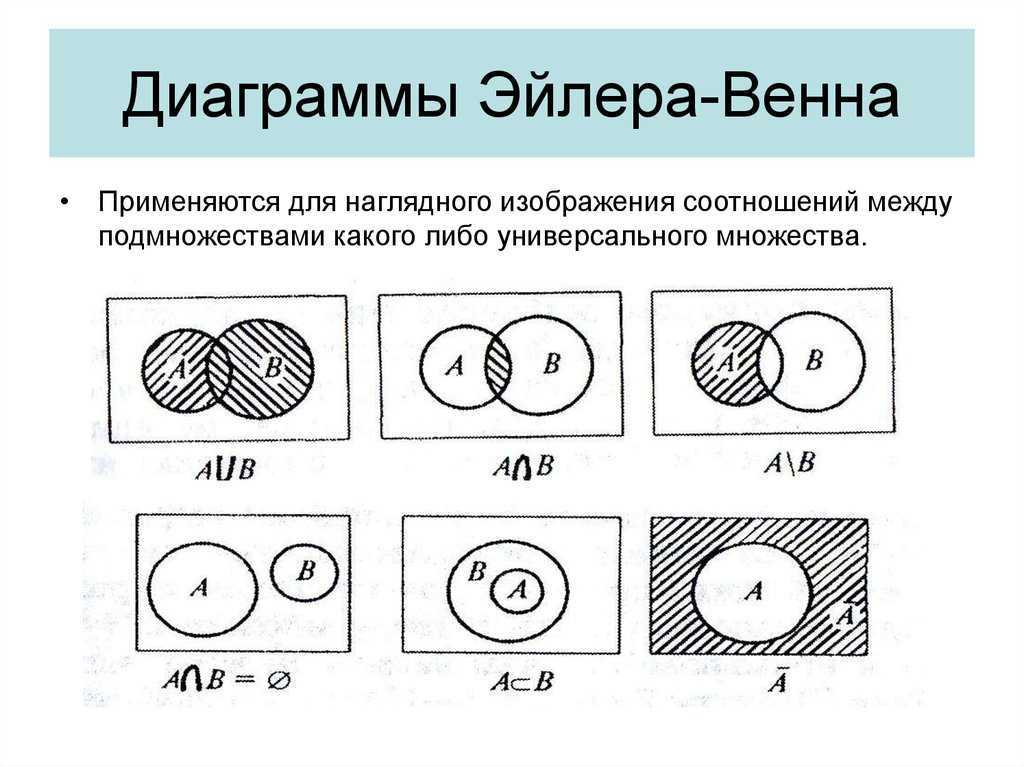
Диаграммы Венна по определению должны отображать все возможные комбинации пересечений, что создает некоторые интересные проблемы с компоновкой.
Когда есть три круга, показывается каждое пересечение, но как только вы доберетесь до четырех категорий, круги не работают.
Эллипсы могут работать до пяти категорий, но помимо пяти странные формы должны использоваться для вплетения и выхода из всех комбинаций пересечений.
Пять уже довольно сложно читать, но как только эти странные формы вступают в игру, чтение диаграмм становится почти невозможным, а текстовые описания взаимосвязей часто легче понять.
Это подводит нас к тому, почему так много забавных диаграмм.
Диаграмма Венна для позвоночных и беспозвоночных, которую мы показали вам ранее, предполагает, что некоторые животные могут одновременно иметь позвоночник и не иметь позвоночника.
Хотя это может и не смешно, любой, кто посещал уроки естествознания в шестом классе, скажет вам, что это довольно глупо.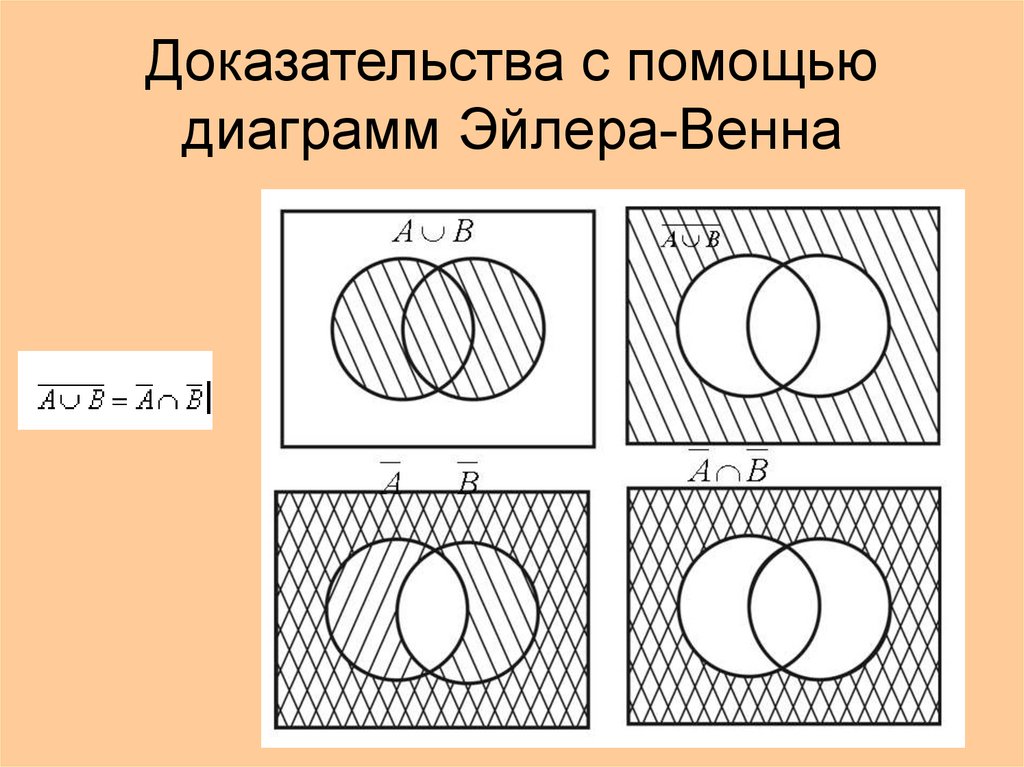 С лучшей темой указание на отношения, которые не существуют, может быть довольно забавным.
С лучшей темой указание на отношения, которые не существуют, может быть довольно забавным.
На некоторых диаграммах можно добиться юмора, поместив что-либо в категорию, которой оно не принадлежит, или в категорию, в которую вы обычно не ожидаете его попадания. Некоторая творческая маркировка (как на диаграмме Эйлера ниже) тоже всегда помогает.
Мы знаем, что диаграммы Эйлера могут быть забавными, но могут ли они быть полезными?
Некоторые диаграммы содержат количественную информацию, используя площадь каждой части диаграммы.
Одним из хороших примеров этого является Глобальная карта социальных сетей 2011 от Global Web Index. Сами по себе диаграммы Эйлера, подобные этой, дают вам довольно хорошее общее представление о задействованных значениях.
Считать из них точное количество было бы немного сложно, но для общего обзора они хороши. На этом конкретном графике эти диаграммы Эйлера используются как небольшие множители, что позволяет сравнивать регионы.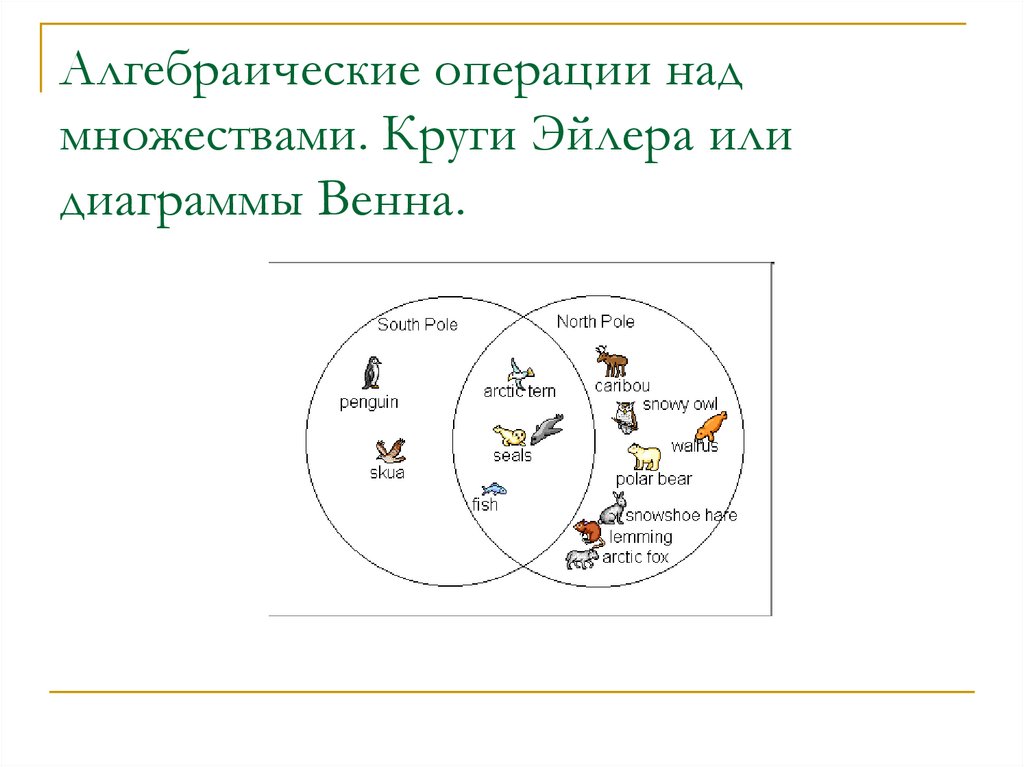


 Их в 2 раза меньше, чем у Алёши. Сколько открыток у Алёши?
Их в 2 раза меньше, чем у Алёши. Сколько открыток у Алёши?