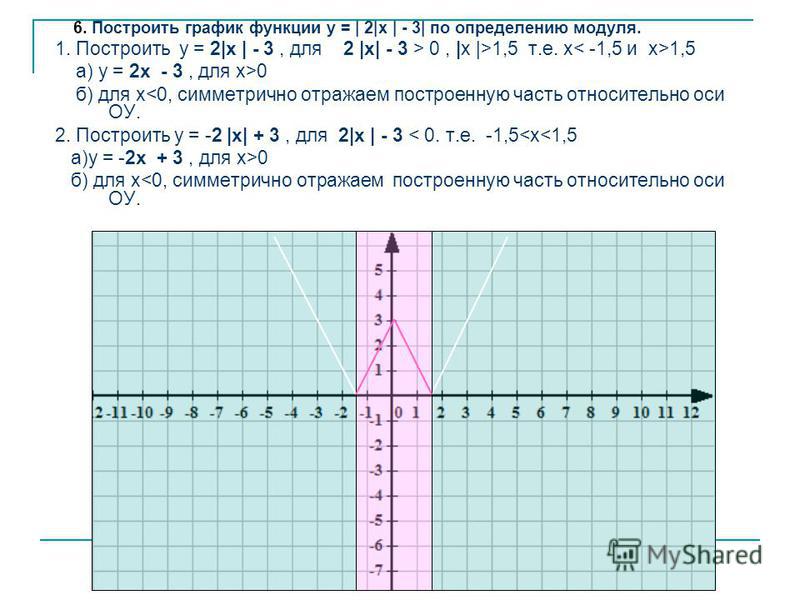
Постройте график функции x 3 x 2: Постройте график функции y = x^3 – x^2

Содержание

Y x2 3x график. Постройте график функции y=

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3.

Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. 2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.

Квадратичная функция

Рис 1. Общий вид параболы

Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.

Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).

Основные свойства квадратичной функции

1. При х =0, у=0, и у>0 при х0

2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.

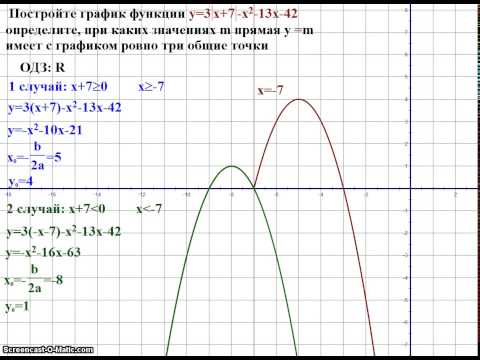
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке , потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.

Ответ: при k принадлежащей интервалу (-∞;-2)U}

2.8 Лабораторная работа «Решение дифференциальных уравнений второго порядка»

cos v

Цель работы

Обретение навыков решения неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Теоретические основы

Рекомендуется изучить раздел «Уравнения высших порядков» в пособии Интегральное исчисление и дифференциальные уравнения:

Учебное пособие / Ельцов А. А., Ельцова Т. А. — 2003. 235 с.

Порядок выполнения работы

Порядок выполнения работы рассмотрим на примере решения заданий.

Задание 1. Найти частное решение дифференциального уравнения второго порядка

d 2 y	dy	16.25y sin 2t ,	удовлетворяющее начальным условиям y(0) = 0.1, y (0) 0 .
dt2	dt

Дифференциальное уравнение решить с помощью функции Odesolve на промежутке [0; 20].

Построить график решения.

Задание 2. Тело массы m = 1 кг находилось в покое в момент времени t0 = 0 в точ-

ке x = 2 на оси X . Затем под действием переменной силы F = sin( x) t2 1 sin t те-

ло стало двигаться вдоль оси X . Найти положение тела x и его скорость v в момент времени t1 = 20 с.

Решить полученное дифференциальное уравнение методом Рунге-Кутта на промежутке [0; t1].

Применить функцию Rkadapt.

Полученные в виде таблицы решение x(t) и его производную x (t) интерполировать кубическим сплайном при помощи функций interp и cspline. Построить график решения на промежутке [0; t1].

Найти значения x(t1), x (t1), x (t1) , подставить в разность между левой и правой частями уравнения и найти невязку Err(t1).

					45
Решение.
1. При помощи блока команд Given…Odesolve решаем дифференциальное уравнение:
Given
d2 y(x) d		y(x) 16.25 y(x) sin (2 x)			0
dx2	dx
y(0)	0. 1	y'(0)	0
y	Odesolve (x 20)
Результатом решения является функция y(x), график которой представлен на рисунке.
	0.15
	0.1
	0.05
y(x)	0
	0.05
	0. 1
	0.15 0		5	10	15
				x
2. Дифференциальное уравнение имеет вид:

d 2 x	sin x	cos(v)	sin t
dt2		t2 1

Решим данное уравнение. Устанавливаем начало индексации и точность:

ORIGIN 1

TOL 10 5

Вводим правую часть уравнения:

f (x x’ t)	sin (x)	cos(x’)	sin (t)
		t2 1

Указываем начальные условия:

t0 0	x0		x’0 0

		2

Указываем правый конец промежутка и число итераций:

t1 20

N 2000

Решаем дифференциальное уравнение посредством функции Rkadapt:

x	x0	D(t x)		x2
x		D(t x)
	x’0		f x1 x2		t
R	Rkadapt(x t0 t1 N D)

Результат решения – матрица R, состоящая из трёх столбцов. Извлекаем из полученной матрицы столбец аргументов T, столбец соответствующих значений искомой функции X (положений тела на оси х в данные моменты времени) и столбец скоростей тела в данные моменты времени X’:

T R 1

X R 2

X’ R 3

Для получения непрерывной функции у(х) применяем кубическую интерполяцию. Решение получаем при помощи блока функций cspline, interp:

V1	cspline (T X)	x(t) interp (V1 T X t)
V2	cspline (T X’)	x'(t) interp (V2 T X’ t)

Находим положение тела и его скорость в момент времени t1:

x(t1) 6.675

x'(t1) 2.072

Находим вторую производную от решения, функцию невязки и подставляем значения аргумента на конце интервала:

x» (t) ddt x'(t)

Err (t) x» (t) f (x(t) x'(t) t)

Err (t1) 1. 875 10 6

Строим график зависимости координаты тела и его скорости от времени:

2
0
2
x(t)
x'(t)
4
6
80	5	10	15	20
		t

Задание

1. Найти частное решение дифференциального уравнения второго порядка

d 2 y	6	dy	9 y 10sin x , удовлетворяющее начальным условиям	y (0) y(0) 0 .
dt2		dt

Дифференциальное уравнение решить с помощью функции Odesolve на промежутке [0; 20].

Построить график решения.

2. Тело массы m = 1 кг находилось в покое в момент времени t0 = 0 в точке x = 0

на оси X . Затем под действием переменной силы F = cos( xt) тело стало двигаться вдоль v 2

оси X . Найти положение тела x и его скорость v в момент времени t1 = 12 с.

Решить полученное дифференциальное уравнение методом Рунге-Кутта на промежутке [0; t1]. Применить функцию Rkadapt.

Контрольные вопросы

1.Что называют дифференциальным уравнением второго порядка?

2.Приведите примеры задач, сводящиеся к решению дифференциальных уравнений второго порядка.

3.Дайте определение общего и частного решений для уравнений второго порядка.

4.Интегрирование однородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Приведите примеры.

5.Метод вариации интегрирования линейных неоднородных уравнений второго порядка. Приведите примеры.

6.Метод подбора частных решений по виду правой части линейных неоднородных уравнений второго порядка. Приведите примеры.

Нарисуйте график кусочной функции 𝑓(x) = { 4 if x

Предварительный расчет Предварительный расчет Предварительный расчет

Джейн П.

спросил 09.03.22

Постройте график кусочной функции 𝑓(x) = { 4, если x<1

{ |x-2| если -1≤x<3

{ 2x-5, если x≥3

ниже. Не забудьте пометить оси и показать масштаб. Укажите интервалы, в которых график является возрастающим, убывающим и постоянным.

помогите решить!

Подписаться І 1

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Марк С. ответил 13.05.22

Репетитор

5 (4)

Инженер-программист | Бывший учитель математики средней школы

Смотрите таких репетиторов

Я создал решение, предполагающее, что первая функция должна иметь значение x < -1, что имеет больше смысла в контексте других функций.

Кусочная функция означает, что функция состоит из «кусков» или сегментов, которые рисуются в основном независимо друг от друга.

Первая функция указывает, что y = 4 идет от отрицательной бесконечности до -1 и, следовательно, является прямой горизонтальной линией. Однако, поскольку x < -1, -1 не может быть включено в наш ответ и должно быть оставлено с «дырой» на этом конце нашей строки. Значение x = -1 будет вычислено как часть следующей функции.
Вторая функция указывает, что y = | х — 2 | от -1 до 3, не включая 3. Тем не менее, мы все равно должны найти, каким значение «было бы», если бы 3 было включено для создания полного графика. Просто вычислите значения y для каждого из целых чисел от -1 до 3. (Есть лучшие способы решения задач с абсолютными значениями, но в этом случае подстановка только 5 чисел быстрее.) Нанесите эти точки на график, затем соедините точки. Убедитесь, что это не включает конечное значение для x = 3 как часть этого графика.
Третья функция указывает, что y = 2x — 5, начиная с x = 3 и уходя в положительную бесконечность. Эта функция задается в форме пересечения наклона, что упрощает построение графика. Для дальнейшего упрощения я подставил x = 3 и использовал это значение y в качестве отправной точки. Затем я просто использовал наклон 2/1 (помните, что наклон — это подъем/спуск), обозначенный цифрой 2 в уравнении, чтобы нанести дополнительные точки на линию.

Выполнив эти три шага, вы решите граф. Вот как в итоге выглядел мой: https://1drv.ms/u/s!ApWIaKiDDnULrfZvrpoEo0e15Qlgmg?e=0zVS7D

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Алгебра — графические многочлены

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.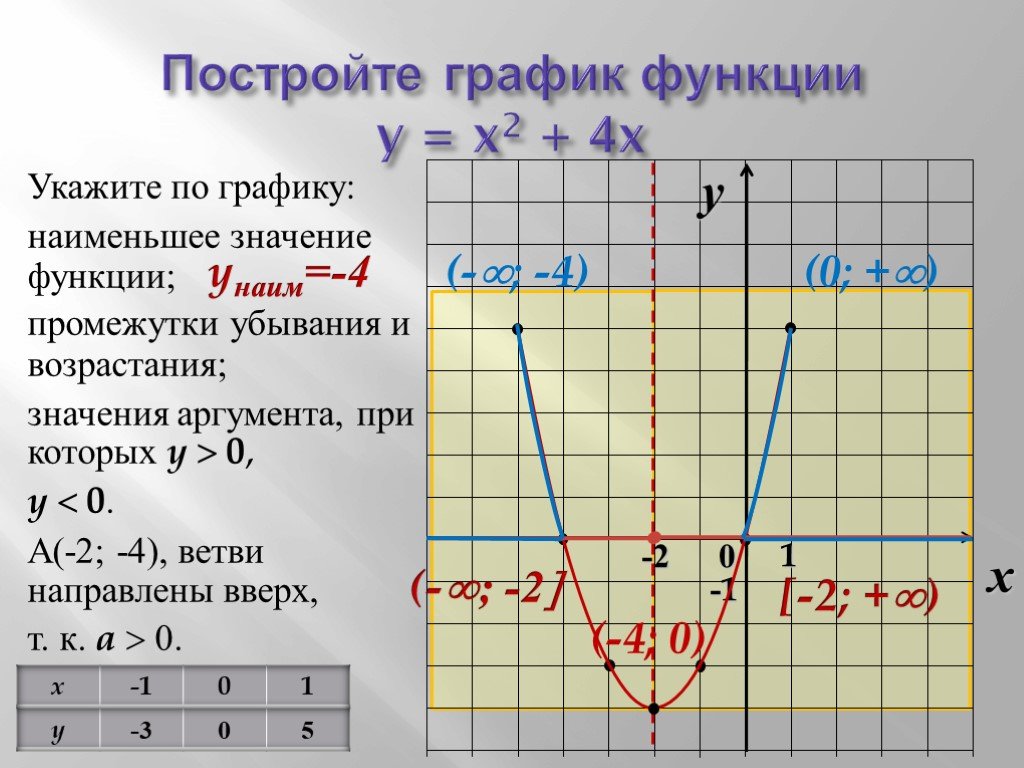 Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5.3: Графические полиномы

В этом разделе мы рассмотрим метод получения грубого наброска общего многочлена. Единственная реальная информация, которая нам понадобится, — это полный список всех нулей (включая кратность) многочлена.

В этом разделе нам либо дадут список нулей, либо их будет легко найти. В следующем разделе мы рассмотрим метод определения большей части списка для большинства многочленов. Сначала мы строим график, так как метод нахождения всех нулей многочлена может быть немного длинным, и мы не хотим загромождать детали этого раздела беспорядком поиска нулей многочлена.

Начнем с графика пары многочленов.

Не беспокойтесь об уравнениях для этих многочленов. Мы приводим их только для того, чтобы использовать их для иллюстрации некоторых идей о многочленах.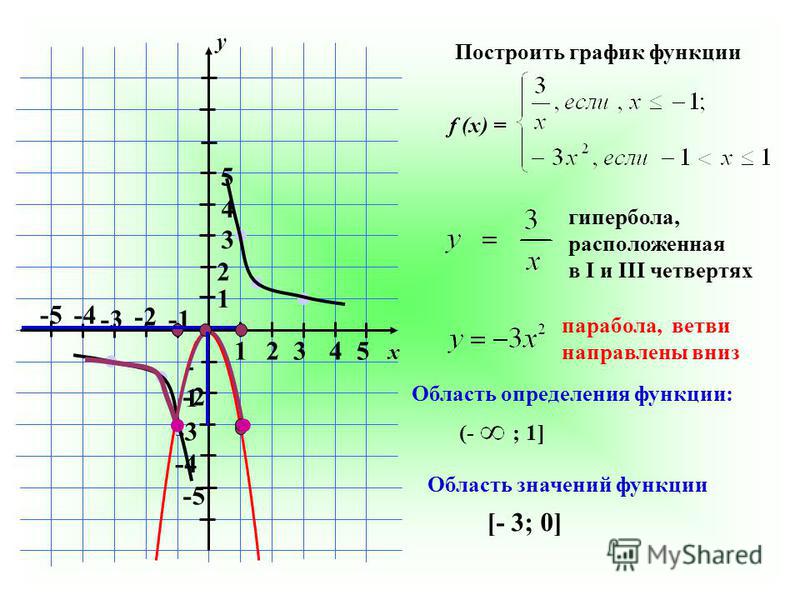

Во-первых, обратите внимание, что графики красивые и плавные. На графике нет дыр или разрывов, а также нет острых углов на графике. Графики многочленов всегда будут красивыми гладкими кривыми.

Во-вторых, «горбы», где график меняет направление с возрастания на убывание или с убывания на возрастание, часто называют поворотных моментов . Если мы знаем, что полином имеет степень \(n\), то мы будем знать, что в графе будет не более \(n — 1\) поворотных точек.

Хотя это не сильно поможет в реальном графическом процессе, это будет хорошей проверкой. Если у нас есть полином четвертой степени с 5 точками поворота, то мы будем знать, что сделали что-то не так, поскольку полином четвертой степени будет иметь не более 3 точек поворота.

Далее нам нужно исследовать связь между \(x\)-отрезками графика многочлена и нулями многочлена. Напомним, что для нахождения \(x\)-отрезков функции нам нужно решить уравнение

\[P\влево( х \вправо) = 0\]

Также напомним, что \(x = r\) является нулем полинома \(P\left( x \right)\), если \(P\left( r \right) = 0\). Но это означает, что \(x = r\) также является решением \(P\left( x \right) = 0\).

Другими словами, нули полинома также являются точками пересечения x графа. Кроме того, напомним, что \(x\)-отрезки могут либо пересекать ось \(x\), либо просто касаться оси \(x\), фактически не пересекая ось.

Также обратите внимание на приведенные выше графики, что точки пересечения \(x\) могут либо сглаживаться при пересечении оси \(x\), либо проходить через ось \(x\) под углом.

Следующий факт свяжет все эти идеи с множественностью нуля.

Факт

Если \(x = r\) является нулем многочлена \(P\left( x \right)\) с кратностью \(k\), то

Если \(k\) равно нечетно, то точка пересечения \(x\), соответствующая \(x = r\), пересечет ось \(x\).
Если \(k\) четно, то точка пересечения \(x\), соответствующая \(x = r\), будет только касаться оси \(x\), а не пересекать ее.

Более того, если \(k > 1\), то график выровняется в точке \(x = r\).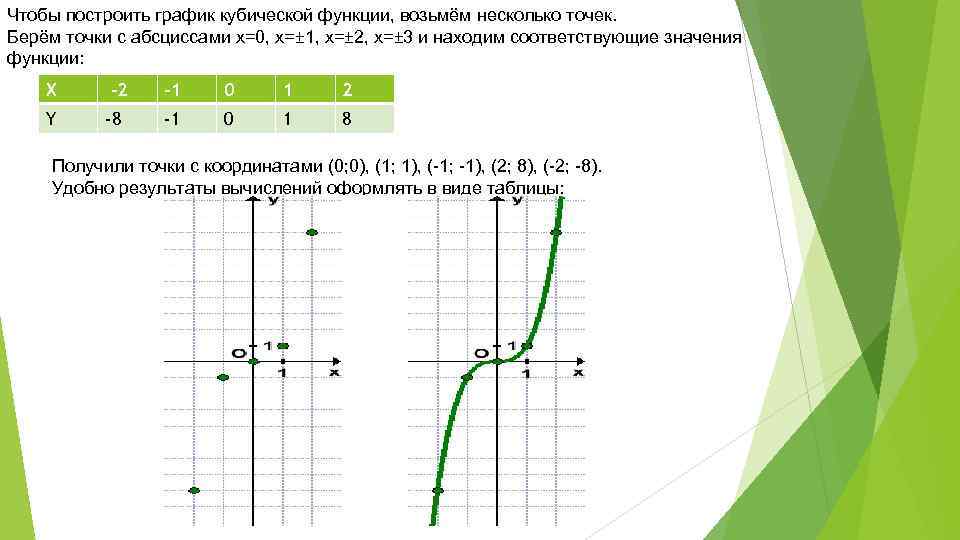

Наконец, обратите внимание, что если мы позволим \(x\) стать большим как в положительном, так и в отрицательном смысле (, т. е. на обоих концах графика), тогда график будет либо неограниченно увеличиваться, либо неограниченно уменьшаться. Это всегда будет происходить с каждым многочленом, и мы можем использовать следующий тест, чтобы определить, что произойдет в конечных точках графика. 9п} + \cdots\]

Мы не знаем, есть ли в многочлене какие-либо другие члены, но мы знаем, что первым членом должен быть указанный член, поскольку он имеет степень \(n\). Теперь у нас есть следующие факты о графе \(P\left( x \right)\) на концах графа.

Если \(a > 0\) и \(n\) четно, то график \(P\left( x \right)\) будет неограниченно возрастать в обеих конечных точках. Хорошим примером этого является график x ² .
Если \(a > 0\) и \(n\) нечетно, то график \(P\left( x \right)\) будет неограниченно возрастать на правом конце и неограниченно убывать на левом конце. Хорошим примером этого является график x ³ .
Если \(a < 0\) и \(n\) четно, то график \(P\left( x \right)\) будет неограниченно уменьшаться в обоих концах. Хорошим примером этого является график - х ² .
Если \(a < 0\) и \(n\) нечетно, то график \(P\left( x \right)\) будет неограниченно убывать на правом конце и неограниченно возрастать на левом конце. Хорошим примером этого является график - x ³ .

Хорошо, теперь, когда мы разобрались со всем этим, мы можем, наконец, описать процесс получения грубого наброска графика многочлена.

Процесс построения полинома

Определите все нули полинома и их кратность. Используйте приведенный выше факт, чтобы определить пересечение \(x\), которое соответствует каждому нулю, пересечет ось \(x\) или просто коснется ее, и будет ли пересечение \(x\) плоским или нет.
Определить точку пересечения \(y\), \(\left( {0,P\left( 0 \right)} \right)\).
Используйте тест старшего коэффициента, чтобы определить поведение многочлена в конце графика.
Нарисуйте еще несколько точек. Это оставлено намеренно расплывчатым. Чем больше точек вы нанесете, тем лучше будет эскиз. По крайней мере, вы должны нанести по крайней мере одну на каждом конце графика и по крайней мере одну точку между каждой парой нулей.

Мы должны быстро предупредить об этом процессе, прежде чем пытаться его использовать. Этот процесс предполагает, что все нули являются действительными числами. Если есть сложные нули, то этот процесс может упустить некоторые довольно важные особенности графика. 92} — 20х — 40\).

Показать решение

Мы нашли нули и кратности этого полинома в предыдущем разделе, поэтому мы просто запишем их здесь для справочных целей.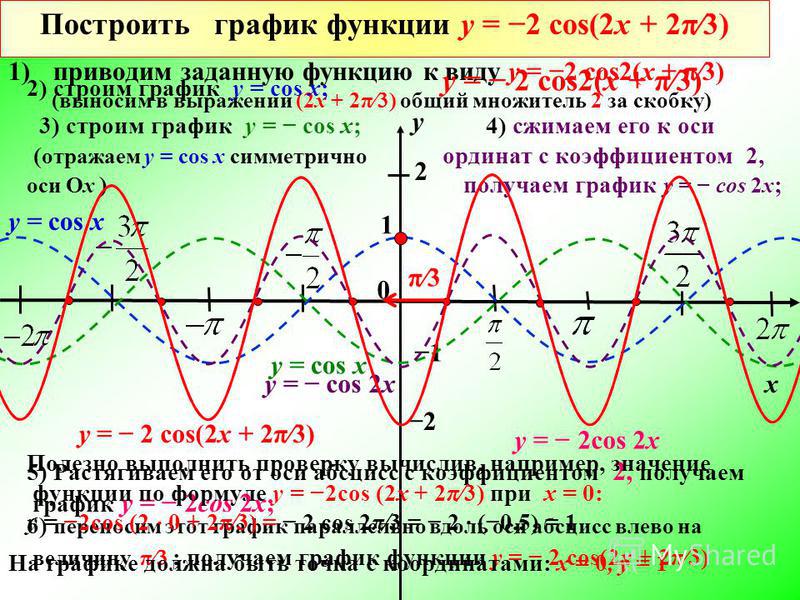

\[\begin{align*}x & = — 1 & \hspace{0,25in} & \left( {{\mbox{кратность 2}}} \right)\\ x & = 2 & \hspace{0,25in} &\left( {{\mbox{кратность 3}}} \right)\end{align*}\]

Итак, из того факта, что мы знаем, что \(x = — 1\) просто коснется оси \(x\), а не пересечет ее, и что \(x = 2\) пересечет \(x\ ) и будут плоскими при этом, так как кратность больше 1. Кроме того, оба будут плоскими при пересечении оси \(x\), поскольку кратность для обоих больше 1.

Далее, \(y\)-перехват равен \(\left( {0, — 40} \right)\).

Коэффициент при члене степени 5 ^th положителен, и, поскольку степень нечетна, мы знаем, что этот многочлен будет неограниченно возрастать на правом конце и неограниченно уменьшаться на левом конце.

Наконец, нам просто нужно вычислить многочлен в паре точек. Точки, которые мы выбираем, на самом деле не так уж важны. Мы просто хотим выбрать точки в соответствии с рекомендациями в процессе, описанном выше, и точки, которые будет довольно легко оценить.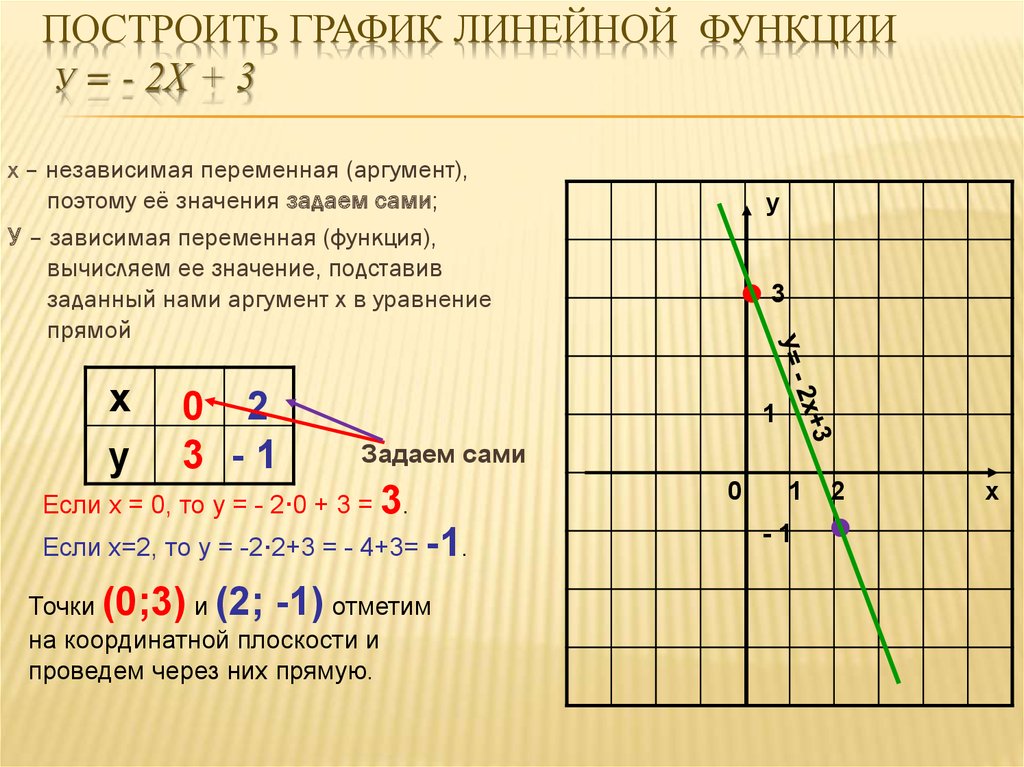 Вот некоторые моменты. Мы оставим вам возможность проверить оценки.

\[P\left( { — 2} \right) = — 320\hspace{0.25in}\hspace{0.25in}P\left( 1 \right) = — 20\hspace{0.25in}\hspace{0.25in }P\влево( 3\вправо) = 80\]

Теперь, чтобы набросать график, мы начнем с левого конца и будем продвигаться к правому концу. Во-первых, мы знаем, что на левом конце график неограниченно убывает по мере того, как мы делаем \(x\) все более и более отрицательными , и это согласуется с точкой, которую мы оценили в \(x = — 2\).

Таким образом, по мере того, как мы движемся вправо, функция на самом деле будет возрастать в точке \(x = — 2\), и мы будем продолжать увеличиваться до тех пор, пока не столкнемся с первой точкой пересечения x- в точке \(x = — 1\). . На данный момент мы знаем, что график просто касается оси \(x\), фактически не пересекая ее, и при этом будет плоским.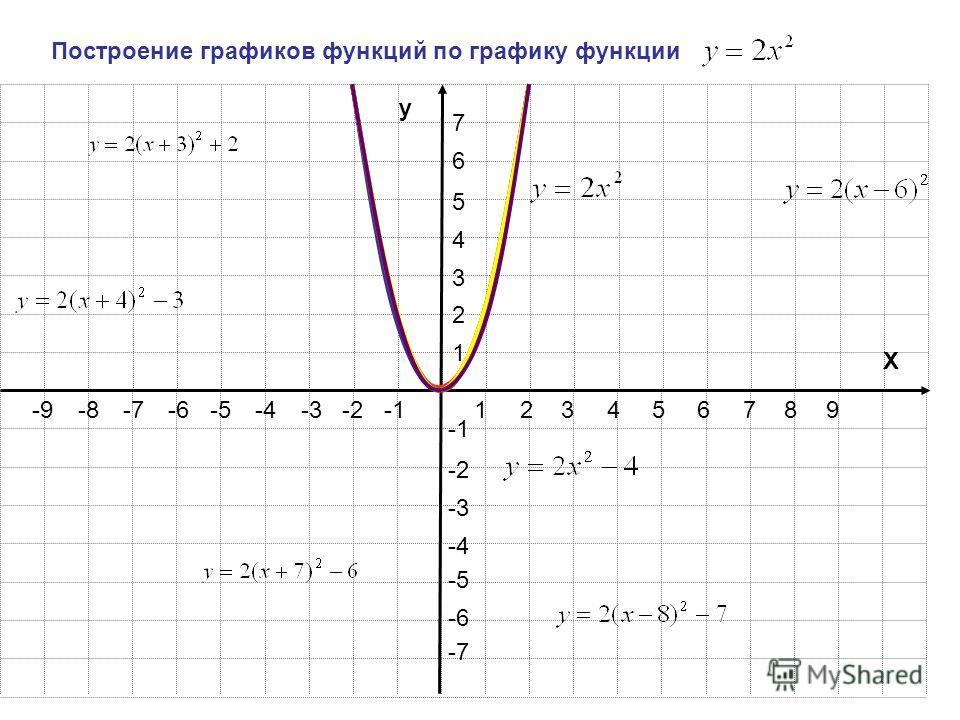 Это означает, что при \(x = -1\) на графике должна быть точка поворота.

Теперь график уменьшается по мере продвижения вправо. Опять же, это согласуется со следующей точкой, с которой мы столкнемся, — \(y\)-перехватом.

Теперь, согласно следующей точке, которую мы получили, \(x = 1\), граф должен иметь другую поворотную точку где-то между \(x = 0\) и \(x = 1\), так как график выше при \(x = 1\), чем при \(x = 0\). На этом уровне очень трудно определить, где именно произойдет этот поворотный момент, поэтому мы не будем беспокоиться о попытках его найти. На самом деле определение этой точки обычно требует некоторого исчисления.

Итак, мы движемся вправо и функция увеличивается. Следующая точка, в которую мы попали, это \(x\)-пересечение в \(x = 2\), и эта точка пересекает \(x\)-ось, поэтому мы знаем, что здесь не будет точки поворота, так как там был на первом \(x\)-перехвате. Кроме того, график будет плоским, поскольку он касается оси \(x\), потому что кратность больше единицы. Таким образом, график будет продолжать увеличиваться через эту точку, ненадолго сглаживаясь, когда он касается оси \(x\), пока мы не достигнем последней точки, в которой мы оценили функцию в \(x = 3\).

К этому моменту мы достигли всех точек пересечения \(x\) и знаем, что график будет неограниченно увеличиваться на правом конце, поэтому все, что нам нужно сделать, это нарисовать возрастающую кривую.

Вот набросок многочлена.

Обратите внимание, что одна из причин нанесения точек на концах состоит в том, чтобы увидеть, насколько быстро график увеличивается или уменьшается. Из оценок видно, что график убывает на левом конце гораздо быстрее, чем растет на правом конце. 92}\влево( {х — 3} \вправо)\влево( {х + 2} \вправо)\]

Вот список нулей и их кратности.

\[\begin{align*}x & = — 2 & \hspace{0.25in} & \left( {{\mbox{кратность 1}}} \right)\\ x & = 0 & \hspace{0.25in} & \left( {{\mbox{кратность 2}}} \right)\\ x & = 3 & \hspace{0,25in} & \left( {{\mbox{кратность 1}}} \right)\end{ выровнять*}\]

Таким образом, нули при \(x = — 2\) и \(x = 3\) будут соответствовать \(x\)-пересечениям, пересекающим ось \(x\), так как их кратность нечетна и будет делайте это под углом, поскольку их кратность НЕ меньше 2.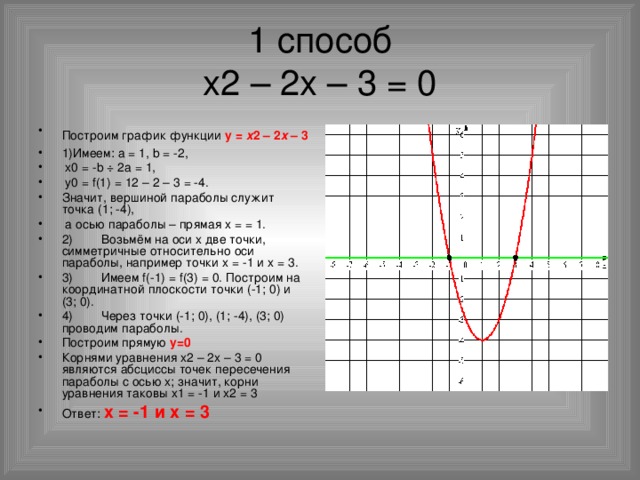 Нуль в точке \(x = 0\) не будет пересекать ось \(x\), поскольку его кратность четна, но будет плоским, когда он касается \( x\)-оси, так как кратность больше единицы.

Перехват \(y\) равен \(\left( {0,0} \right)\) и обратите внимание, что это также перехват \(x\).

Коэффициент при члене степени 4 ^th положителен, и, поскольку степень четная, мы знаем, что полином неограниченно возрастает на обоих концах графика.

Наконец, вот некоторые оценки функций.

\[P\left( { — 3} \right) = 54\hspace{0.25in}P\left({- 1} \right) = — 4\hspace{0.25in}P\left( 1 \right) = — 6\hпробел{0,25 дюйма}P\влево( 4\вправо) = 96\]

Теперь, начиная с левого конца, мы знаем, что по мере того, как мы делаем \(x\) все более и более отрицательным, функция должна неограниченно возрастать. Это означает, что по мере нашего движения вправо график будет уменьшаться.

При \(x = — 3\) график будет уменьшаться и продолжит уменьшаться, когда мы попадем в первый \(x\)-перехват в точке \(x = — 2\), так как мы знаем, что это \(x \)-отрезок пересечет ось \(x\).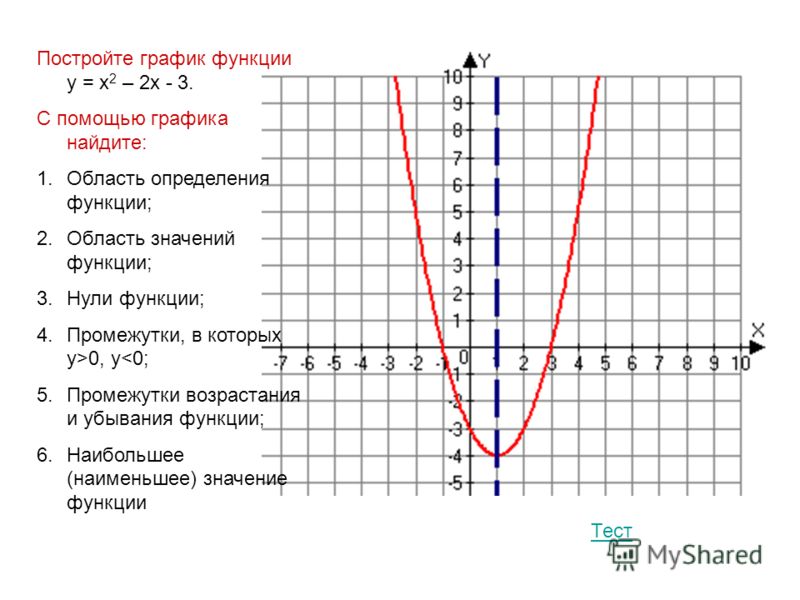

Далее, поскольку следующий \(x\)-отрезок находится в точке \(x = 0\), нам нужно будет где-то иметь поворотную точку, чтобы график мог увеличиваться обратно до этого \(x\)-перехвата. Опять же, мы не будем беспокоиться о том, где на самом деле находится этот поворотный момент.

Как только мы попали в точку пересечения \(x\) в точке \(x = 0\), мы знаем, что у нас должна быть точка поворота, так как эта точка пересечения \(x\) не пересекает точку \(x \)-ось. Следовательно, справа от \(x = 0\) график теперь будет убывающим. Напомним, однако, что, поскольку кратность больше единицы, она будет плоской, поскольку касается оси \(x\).

Он будет продолжать уменьшаться, пока не достигнет другой поворотной точки (в какой-то неизвестной точке), чтобы график мог вернуться к оси \(x\) для следующего \(x\)-пересечения в \(x = 3\). Это последний \(x\)-перехват, и, поскольку в этой точке график увеличивается и должен неограниченно увеличиваться в этом конце, мы закончили. 93}\влево( {х — 2} \вправо)\влево( {х + 2} \вправо)\]

Обратите внимание, что мы сначала вынесли на множитель знак минус, чтобы сделать остальную часть разложения немного проще. Вот список всех нулей и их кратности.

\[\begin{align*}x & = — 2 & \hspace{0.25in} & \left( {{\mbox{кратность 1}}} \right)\\ x & = 0 & \hspace{0.25in} & \left( {{\mbox{кратность 3}}} \right)\\ x & = 2 & \hspace{0.25in} & \left( {{\mbox{кратность 1}}} \right)\end{ выровнять*}\]

Итак, все три нуля соответствуют \(x\)-пересечениям, которые действительно пересекают ось \(x\), так как все их кратности нечетны, однако только \(x\)-пересечение в точке \(x = 0\) будет пересекать ось \(x\) в сплющенном виде.

Перехват \(y\) равен \(\left( {0,0} \right)\) и, как и в предыдущем примере, это также перехват \(x\).

В этом случае коэффициент при 5 ^-м-м члене степени отрицателен, и, поскольку степень нечетна, график будет неограниченно возрастать с левой стороны и неограниченно уменьшаться с правой стороны.

Вот некоторые оценки функций.

\[P\left( { — 3} \right) = 135\hspace{0.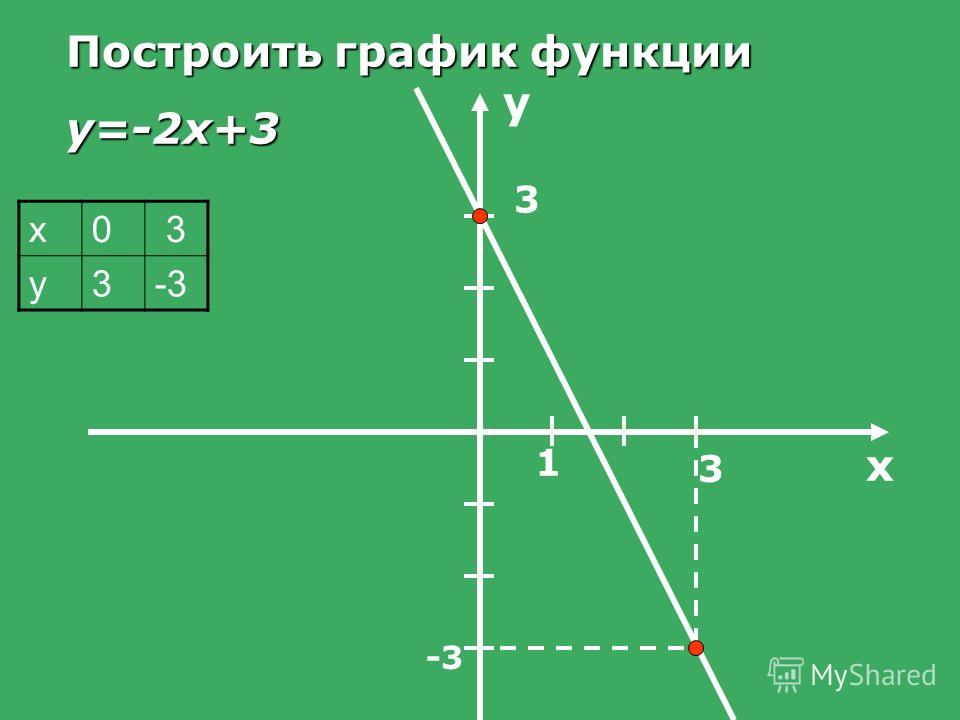 25in}\,\,\,P\left( {- 1} \right) = — 3\hspace{0.25in}\,\ ,\,\,\,P\влево( 1 \вправо) = 3\hspace{0,25 дюйма}P\влево( 3 \вправо) = — 135\]

Хорошо, этот график будет начинаться так же, как и предыдущий график. На левом конце график будет уменьшаться по мере нашего движения вправо и будет уменьшаться через первый \(x\)-отрезок в точке \(x = — 2\), поскольку известно, что этот \(x\)-перехват пересекает \(x\)-ось.

Теперь в какой-то момент мы получим поворотную точку, чтобы график мог вернуться к следующему \(x\)-отрезку в точке \(x = 0\), и график продолжит увеличиваться через эту точку, так как он также пересекает ось \(х\). Обратите также внимание, что в этой точке график также должен быть плоским, поскольку кратность больше единицы.

Наконец, график достигнет еще одной поворотной точки и начнет уменьшаться, чтобы вернуться к последнему пересечению \(x\) в точке \(x = 2\). Поскольку мы знаем, что график будет неограниченно уменьшаться на этом конце, мы закончили.