Постройте график функции y 2x в квадрате: постройте график данной функции используя алгогитм y = 2x в квадрате -3x-2

а) значения функции при значении аргумента, равном -3; -2; -1; б) значения аргумента, если значение функции равно 0; -1; -4; в) наименьшее и наибольшее значения функции на отрезке -1; 3; г) координаты точек пересечения параболы y=-x в квадрате и прямой y=2x. — Школьные Знания.net

• Все предметы

• Математика

• Литература

• Алгебра

• Русский язык

• Геометрия

• Английский язык

• Физика

• Биология

• Другие предметы

• История

• Обществознание

• Окружающий мир

• География

• Українська мова

• Информатика

• Українська література

• Қазақ тiлi

• Экономика

• Музыка

• Беларуская мова

• Французский язык

• Немецкий язык

• Психология

• Оʻzbek tili

• Кыргыз тили

• Астрономия

• Физкультура и спорт

Ответ дан

Vitalik1Kilber2

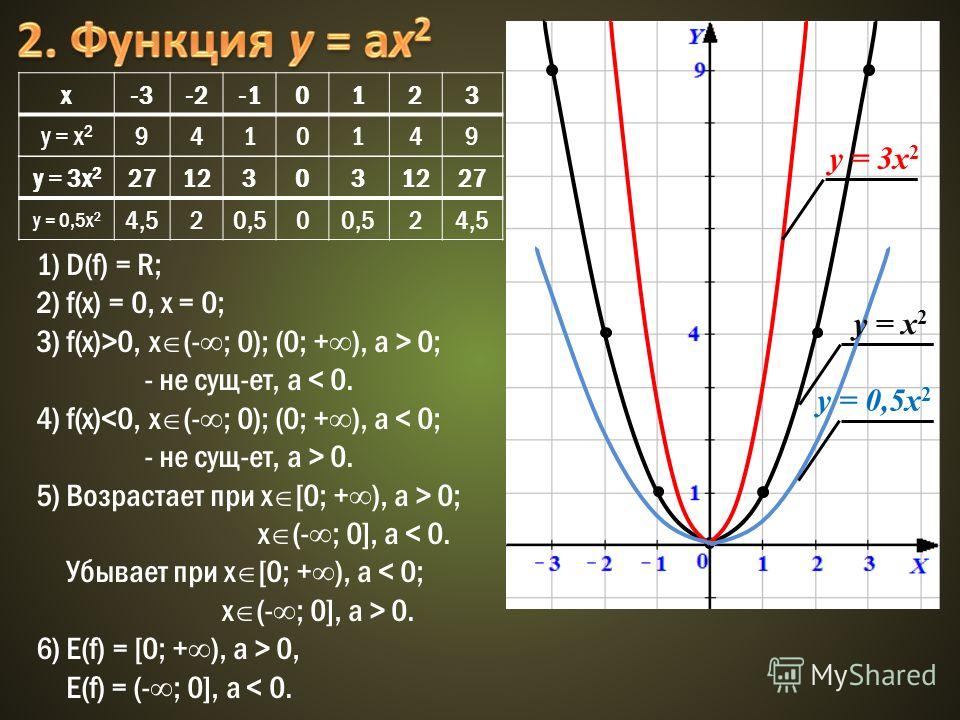
Постройте график функции y=x2. С помощью графика найдите: а) значения функции при значении аргумента, равном -4;0;2; б) значения аргумента, если значение функции равно 1;0;9; в)наибольшее и наименьшее значения функции на отрезке [-1;2]; г) значения аргумента, при которых 1<y<9если у = 9, то х =3, х=-3если у = 1, то х =1, х=-1если у = 0, то х =0Значения функции определяются по графикуу=х2 = 2 в квадрате = 4у=х2=(-4)2 = 16у=х2 = 0 в квадрате = 0Находим значния функцииНаибольшее значение функции равно 4, при х =2Находим значение аргументаНаименьшее значении функции равно 0, при х=0график этой функции является парабола с центром  точке (0;0)

Дискриминант онлайн

Примеры решенийРанг матрицы Умножение матриц Метод Гаусса Найти производную Найти интегралРешение СЛАУ методом Крамера Диф уравнения онлайнОпределитель матрицы Точки разрыва функции

Квадратичная функция имеет вид: ax2+bx+c=0
Формула дискриминанта: D=b2-4ac

Онлайн-калькулятор предназначен для нахождения дискриминанта и корней функции для уравнений вида: ax2+bx+c=0.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Инструкция. Введите соответствующие коэффициенты:

a = b = c =

Вид: x²+x+1 Например для уравнения x2-8x+7=0 коэффициенты равны: a=1, b=-8, c=7

Как построить параболу ax2+bx+c=0.

Виды дискриминантов

Формула дискриминанта зависит от степени многочлена anxn + an-1xn-1 + ... + a1x + a0 = 0.

Свойства дискриминанта

• Дискриминант равен 0, когда многочлен имеет кратные корни (равные корни).
• Дискриминант является симметрическим многочленом относительно корней многочлена и поэтому является многочленом от его коэффициентов; более того, коэффициенты этого многочлена целые независимо от расширения, в котором берутся корни.

Классификация дискриминантов

D>0	D=0	D
При D > 0 корней — два. Формула для вычислений:	при D = 0 корень один кратности 2 (корни равны). Формула для вычислений:	при D < 0 вещественных корней нет. Существуют два комплексных корня. Формула для вычислений:
При a > 0, x12. При a < 0, x1 > x2 Что означает, если дискриминант больше нуля: значит существуют вещественные корни, график квадратичной функции пересекает ось Х в двух местах.	x1 = x2 = -b/2a Что означает, если дискриминант равен нулю: значит существует один вещественный корень, график функции пересекает ось Х в одном месте.	Что означает, если дискриминант меньше нуля: значит не существует вещественных корней, а только комплексные корни. График функции не пересекает ось Х.

Пример расчета для дискриминанта больше нуля
2x²+3x+1=0
Находим дискриминант: D=3²-4·2·1=1
Корни уравнения: ;

Пример расчета для дискриминанта равного нулю
⁹/₄x²+3x+1=0
Находим дискриминант: D=3²

-4·⁹/₄·1=0
Корни уравнения:

Пример расчета для дискриминанта меньше нуля
2x²+3x-4=0
Находим дискриминант: D=3²-4·2·(-4)=41
Корни уравнения: ;

Результат:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

{2}-4ac}}{2a}.

x=\frac{-3±\sqrt{9-4\times 2\left(-y-9\right)}}{2\times 2}

Square 3.

x=\frac{- 3±\sqrt{9-8\left(-y-9\right)}}{2\times 2}

Умножить -4 раза 2.

x=\frac{-3±\sqrt{9+8y +72}}{2\times 2}

Умножьте -8 на -9-у.

x=\frac{-3±\sqrt{8y+81}}{2\times 2}

Прибавьте 9 к 72+8y.

x=\frac{-3±\sqrt{8y+81}}{4}

Умножить 2 раза на 2.

x=\frac{\sqrt{8y+81}-3}{4}

Теперь решите уравнение x=\frac{-3±\sqrt{8y+81}}{4}, когда ± равно плюсу. Добавьте -3 к \sqrt{81+8y}. 9{ 2 } — 4 x — 5 = 0

Тригонометрия

4 \sin \theta \cos \theta = 2 \sin \theta

Линейное уравнение

y = 3x + 4

Арифметика 3 0 3 0 9

90

Матрица

\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]

Одновременное уравнение

\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right. 92 + с

Давайте начнемАнализ эффекта при > 1Анализ эффекта при 0 Анализ эффекта, когда Практика Словарь ActivityJournal Activity

Имея словесные, графические или символические описания графика y = a x ² + c, учащийся будет исследовать, описывать и предсказывать влияние на график, когда «a» измененный.

Стандарты TEKS и ожидания учащихся

A(7)  Квадратичные функции и уравнения. Учащийся применяет стандарты математического процесса при использовании графиков квадратичных функций и связанных с ними преобразований для представления различными способами и определения с помощью технологий и без них решений уравнений. Ожидается, что учащийся:

A(7)(C) определит влияние на график родительской функции f( x) = x ² , когда f( x ) заменяется на аф( x ), f( x ) + d, f( x – c), f(b x ) для конкретных значений a, b, c и d 

Цели ресурсов

Определите эффект изменения значения «а» на графике

y = a x ² + c

Основные вопросы больше 1 в уравнении y = a x ² ?

Как повлияет на параболу, если в уравнении y = a x ² + c значение «a» находится в диапазоне от 0 до 1?

Как изменится парабола, если в уравнении y = a x ² + c значение «а» меньше 1?

Словарь

• Квадратное уравнение
• Парабола

 

Давайте посмотрим, как изменение значения «а» на число больше 1 повлияет на график числа 9.