Поток вектора: Поток вектора | это… Что такое Поток вектора?

Поток вектора магнитной индукции

Определение 1

Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:

Φ=BScos α=BnS=B→S→ с углом между n→ и B→, обозначаемым α, n→ является нормалью к площадке S.

Формула магнитного потока

Φ равняется количеству линий магнитной индукции, пересекающих площадку S, как показано на рисунке 1. Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S. Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.

Рисунок 1

В чем измеряется магнитный поток

В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки dS, рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока dΦ производится через эту поверхность. Запись примет вид:

dΦ=BdScos α=B→dS→.

Нахождение полного потока через поверхность S:

Φ=∫SBdScos α=∫SB→dS→.

Основной единицей измерения магнитного потока в системе СИ считаются веберы (Вб). 1 Вб=1 Тл1 м2.

Связь магнитного потока и работы сил магнитного поля

Элементарная работа δA, совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции dΦ:

δA=IdΦ.

Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:

A=IΦ2-Φ1 с Φ1, обозначаемым потоком через контур в начале перемещения, Φ2 является  потоком через контур в конце перемещения.

Теорема Гаусса для магнитного поля

Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:

∮B→dS→=0.

Выражение ∮B→dS→=0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:

∮E→dS→=qε0.

Запись ∮B→dS→=0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.

Пример 1

Дан бесконечно длинный прямой проводник с током I, недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I’. Сторона рамки равна a. Она располагается в одной плоскости с проводом, как показано на рисунке 2. Значение расстояния от ближайшей стороны рамки до проводника равняется b. Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Рисунок 2

Решение

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.

Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.

За основу возьмем формулу магнитного потока и работы, которая их связывает:

A=I’Φ2-Φ1 (1.1), где I’ принимают за силу тока в рамке, Φ1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b. Φ2=0. Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы (1.1) изменится:

A=-I’Φ1 (1.2).

Перейдем к нормали n→ и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n→ и вектором B→ равняется π. Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:

dΦ=-BdS=-B·a·dx=-μ02πIldxx (1.3), значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:

B=μ02πxIl (1.4).

Отсюда следует, что для нахождения всего потока из (1.3) потребуется:

Φ1=∫S-μ02πIldxx=-μ02πIl∫bb+adxx=-μ02πIl·lnb+ab (1.5).

Произведем подстановку формулы (1.5) в (1.2). Искомая работа равняется:

A=I’μ02πIl·lnb+ab.

Ответ: A=μ02πII’l·lnb+ab.

Пример 2

Найти силу, действующую на рамку, из предыдущего примера.

Решение

Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние dx. Это говорит о совершении силой работы, равной:

δA=Fdx (2.1).

Элементарная работа δA может быть выражена как:

δA=I’dΦ (2.2).

Произведем то же с силой, применяя формулы (2.1), (2.2). Получаем:

Fdx=I’dΦ→F=I’dΦdx (2.3).

Используем выражение, которое было получено в примере 1:

dΦ=-μ02πIldxx→dΦdx=-μ02πIlx (2.4).

Произведем подстановку dΦdx в (2.3). Имеем:

F=I’μ02πIlx (2.5).

Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны AB и DC равные по модулю и противоположные по направлению. Выражение принимает вид:

FAB→+FDC→=0 (2.6), то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:

F→=FAD→+FBC→ (2.

6).

Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:

F=FAD-FBC (2.7).

Произведем поиск силы FAD, действующей на сторону AD, применив формулу (2.5), где x=b:

FAD=I’м02πIlb (2.8).

Значение FBC будет:

FBC=I’μ02πIlb+a (2.9).

Для нахождения искомой силы:

F=I’μ02πIlb-I’μ02πIlb+a=II’μ0l2π1b-1b+a.

Ответ: F=II’μ0l2π1b-1b+a. Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.

Автор: Роман Адамчук

Преподаватель физики

Навигация по статьям

Предыдущая статья

Основные интерференционные схемы

Следующая статья

Вихревой характер магнитного поля

• Вихревой характер магнитного поля
• Закон Био-Савара. Теорема о циркуляции
• Закон электромагнитной индукции Фарадея
• Классификация магнетиков
• Классическое описание диамагнетизма
• Все темы по физике

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Современные подходы к лечению тревожных расстройств у взрослых

• Вид работы:

  Курсовая работа

• Выполнена:

  21 ноября 2022 г.

• Стоимость:

  3 100 руб

Заказать такую же работу

Надо сделать вариант

• Вид работы:

  Контрольная работа

• Выполнена:

  27 октября 2022 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

Гестозы во время беременности

• Вид работы:

  Курсовая работа

• Выполнена:

  16 июня 2022 г.

• Стоимость:

  3 200 руб

Заказать такую же работу

Ошибки и осложнения при лапароскопической холецистэктомии

• Вид работы:

  Реферат

• Выполнена:

  3 марта 2022 г.

• Стоимость:

  1 400 руб

Заказать такую же работу

Дистанционный экзамен

• Вид работы:

  Онлайн-помощь

• Выполнена:

  5 января 2022 г.

• Стоимость:

  2 400 руб

Заказать такую же работу

Физиологическая характеристика избранного вида спорта ИВС

• Вид работы:

  Контрольная работа

• Выполнена:

  13 октября 2021 г.

• Стоимость:

  1 100 руб

Заказать такую же работу

Смотреть все работы по фармацевтической химии

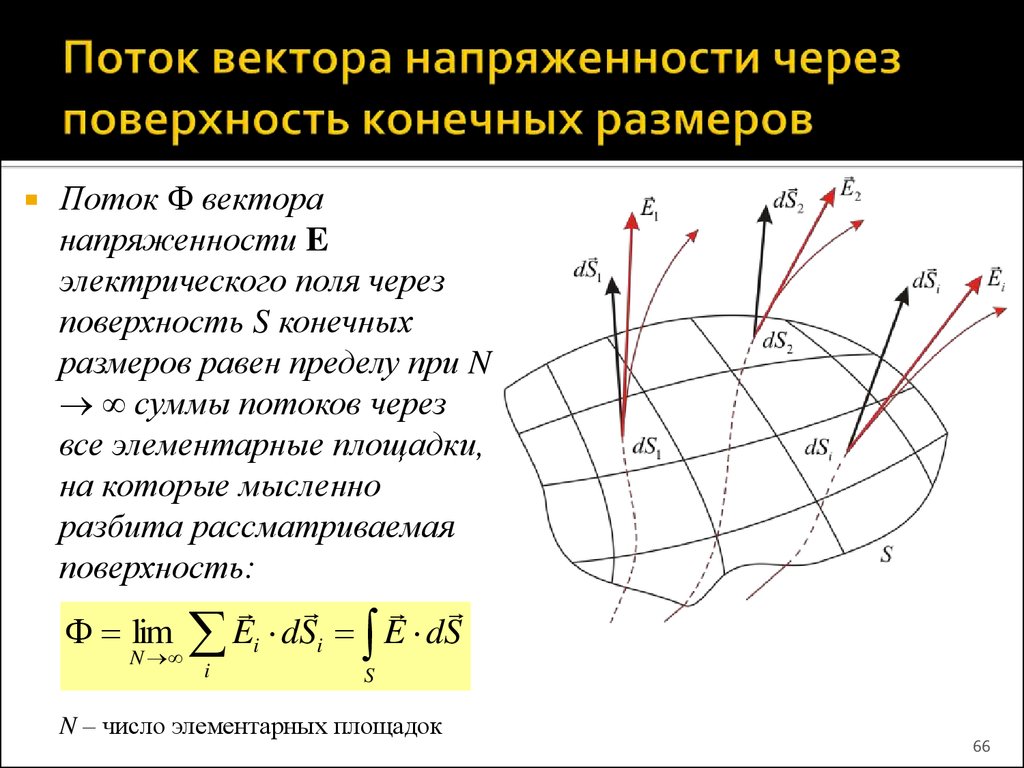
2.2. Поток вектора напряженности

Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью пронизывают некоторую площадкуS, топоток вектора напряженности(число силовых линий через площадку) будет определяться формулой

где E_n– произведение векторана нормальк данной площадке (рисунок 2. 5).

Рисунок 2.5

Полное число силовых линий, проходящих через поверхность S, называется потоком вектора напряженности Ф_Е через эту поверхность.

Элементарный поток вектора напряженности через площадку dS(рис. 5) определится соотношением:

,

где – проекцияна направление нормали.

В векторной форме можно записать – скалярное произведение двух векторов, где вектор.

Таким образом, поток вектора есть скаляр, который в зависимости от величины углаα может быть как положительным, так и отрицательным.

Полный поток вектора напряженности через любую площадку Sможно определить тогда, а поток через замкнутую поверхность, окружающую заряд или заряженное тело равен.

Так как напряженность поля, созданного в любой точке пространства зависит от величины заряда, создающего это поле, то поток вектора напряженности электростатического поля через любую площадку, находящуюся в этом поле также зависит от величины заряда.

Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.

Рисунок 2.6 Рисунок 2.7

Для рисунка 2.6 – поверхность А₁ окружает положительный заряд и поток здесь направлен наружу, т.е.ПоверхностьА₂– окружает отрицательный заряд, здесьи направлен внутрь. Общий поток через поверхностьАравен нулю.

Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность Аотрицательный.

Таким образом, поток вектора напряженности зависит от заряда.

К.Ф. Гаусс (1777–1855) выдающийся немецкий математик, астроном и физик в 1839г. предложил теорему, которая устанавливает связь потока вектора напряженности электрического поля череззамкнутую поверхность со значением зарядаq, находящегося внутри этой поверхности.Эта теорема выведена математически для векторного поля любой природы русским математиком М. В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.

Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :

.

Докажем эту теорему. Пусть поле создается точечным зарядом q. Окружим заряд замкнутой поверхностьюSпроизвольной формы. Разобьем замкнутую поверхность на элементарные площадкиdS, к каждой из которых проведем вектор нормали.

Элементарный поток вектора напряженности через площадкуdS(рис. 2.8) определится соотношением:

,

где –проекцияна направление нормали. Тогда, где- элементарный телесный угол, под которым элементвиден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхностьSот точечного зарядаq, находящегося внутри этой поверхности.

,

так как , то

.

Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS₁иdS₂, находящиеся внутри телесного углаdΩ(рис. 2.9) равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Тогда , следовательно, поток напряженности электрического поля через любую поверхностьS, не охватывающую заряды равен нулю, т.е.Ф_Е=0.

Пусть внутри замкнутой поверхности имеется зарядов, тогда алгебраическим суммированием (согласно принципу суперпозиции) находим, что общий поток вектора напряженности через замкнутую поверхность равен .

Теорема доказана.

Таким образом теорему Гаусса можно сформулировать следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :

(1),

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то теорема Гаусса имеет вид:

(2)

где интеграл справа берется по объему V, охватываемому поверхностьюS.

Необходимо обратить внимание на следующее обстоятельство: в то время как само поле зависит от конфигурации всех зарядов, потоксквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхностиS. Это значит, чтоесли передвинуть заряды внутри замкнутой поверхности, тоизменится всюду, и на поверхностиS, апоток вектора через эту поверхность останется прежним.

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на , то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.

Рассмотрим примеры применения теоремы Гаусса.

поток векторного поля в nLab

Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

Содержание

Контекст

Дифференциальная геометрия

Синтетическая дифференциальная геометрия

Введение

0003

Дифференциалы

• дифференциация, цепное правило

• дифференцируемая функция

• бесконечно малое пространство, бесконечно малая утолщенная точка, удивительное правое сопряжение

V-образные коллекторы

• дифференцируемый коллектор, координатная карта, атлас

• гладкий коллектор, гладкая структура, экзотическая гладкая структура

• аналитический коллектор, комплексный коллектор

• формальное гладкое многообразие, производное гладкое многообразие

гладкое пространство

• диффеологическое пространство, пространство Фрелихера

• многообразная структура пространств отображения

Касание

• касательный пучок, рамочный пучок

  • векторное поле, многовекторное поле, касательный алгеброид Ли;

  • дифференциальные формы, комплекс де Рама, комплекс Дольбо

    • обратный образ дифференциальных форм, инвариантная дифференциальная форма, форма Маурера-Картана, горизонтальная дифференциальная форма,

    • совместный дифференциал форма

    • интеграция дифференциальных форм

• локальный диффеоморфизм, формально этальный морфизм

• субмерсия, формально гладкий морфизм,

• погружение, формально неразветвленный морфизм,

• пространство де Рама, кристалл

• бесконечно малый пучок дисков

Волшебные алгебраические факты

• вложение гладких многообразий в формальные двойственные R-алгебры

• гладкая теорема Серра-Свана

• производных гладких функций являются векторными полями

Теоремы

• Лемма Адамара

• Теорема Бореля

• Теорема Бомана

• Теорема Уитни о продолжении

• Аппроксимационная теорема Стинрода-Воккеля

• Теорема вложения Уитни

• Лемма Пуанкаре

• Теорема Стокса

• Теорема де Рама

• Теорема Хохшильда-Костанта-Розенберга

• дифференциальные когомологии шестиугольника

Аксиоматика

• Аксиома Кока-Ловера

  • гладкие топосы, супергладкие топосы

  • микролинейное пространство

  • аксиома интеграции

сплоченность

• (модальность фигуры ⊣\dashvflat модальность ⊣\dashvsharp модальность)

  (ʃ⊣♭⊣♯)(\эш \тире \бемоль \тире \диез )

  • дискретный объект, содискретный объект, конкретный объект

  • Преобразование

    точек в части

  • структуры в связке

• dR-образная модальность⊣\dashvdR-плоская модальность

  ʃdR⊣♭dR\esh_{dR} \dashv \flat_{dR}

касательное сцепление

• диаграмма дифференциальных когомологий

дифференциальное сцепление

• (модальность сокращения ⊣\dashvinfinitesimal модальность формы ⊣\dashvinfinitesimal плоская модальность)

  (ℜ⊣ℑ⊣&)(\Re \dashv\Im\dashv\&)

  • редуцированный объект, корредуцированный объект, формально гладкий объект

  • формально этальная карта

  • конструкции в дифференциальном сцеплении

градуированное дифференциальное сцепление

единичное сцепление

id⊣id∨∨fermionic⇉⊣⇝bosonic⊥⊥bosonic⇝⊣rhrheonomic∨∨rededℜ⊣ℑinfinitesimal⊥⊥infinitesimalℑ⊣ & étale∨∨cohesiveʃ⊣ ♭ Discrete⊥⊥discrete ♭ ⊣♯ Соответствующий** \множество{ && идентификатор &\dashv& идентификатор \\ && \ви && \ви \\ &\stackrel{fermionic}{}& \rightrightarrows &\dashv& \rightsquigarrow & \stackrel{bosonic}{} \\ && \бот && \бот \\ &\stackrel{bosonic}{} & \rightsquigarrow &\dashv& \mathrm{R}\!\!\mathrm{h} & ​​\stackrel{rheonomic}{} \\ && \ви && \ви \\ &\stackrel{уменьшенный}{} & \Re &\dashv& \Im & \stackrel{бесконечно малый}{} \\ && \бот && \бот \\ &\stackrel{бесконечно малый}{}& \Im &\dashv& \& & \stackrel{\text{éсказка}}{} \\ && \ви && \ви \\ &\stackrel{связный}{}& \esh &\dashv& \flat & \stackrel{дискретный}{} \\ && \бот && \бот \\ &\stackrel{discrete}{}& \flat &\dashv& \sharp & \stackrel{continuous}{} \\ && \ви && \ви \\ && \emptyset &\dashv& \ast }

Модели

• Модели для гладкого инфинитезимального анализа

• Cahiers topos

• гладкий ∞-группоид

• формальный гладкий ∞-группоид

• суперформальный гладкий ∞-группоид

Теория лжи, ∞-теория лжи

• Алгебра Ли, n-алгебра Ли, L-∞ алгебра

• Группа Ли, 2-группа Ли, гладкая ∞-группа

дифференциальные уравнения, вариационное исчисление

• D-геометрия, D-модуль

• реактивный пучок

• вариационный бикомплекс, комплекс Эйлера-Лагранжа

• Уравнение Эйлера-Лагранжа, формализм де Дондера-Вейля,

• фазовое пространство

Теория Черна-Вейля, ∞-теория Черна-Вейля

• соединение на жгуте, соединение на ∞-пучке

• дифференциальные когомологии

  • обыкновенные дифференциальные когомологии, комплекс Делиня

  • дифференциальная К-теория

  • дифференциальные кобордизмы когомологии

• параллельный транспорт, высший параллельный транспорт, интегрирование волокон в дифференциальных когомологиях

• голономия, высшая голономия

• Калибровочная теория

  , высшая калибровочная теория

• Линия Уилсона, поверхность Уилсона

Геометрия Картана (супер, выше)

• Геометрия Клейна, (высшая)

• G-образная конструкция, кручение G-образной конструкции

• Евклидова геометрия, гиперболическая геометрия, эллиптическая геометрия

• (псевдо)риманова геометрия

  • ортогональная структура

  • изометрия, Векторное поле Киллинга, Спинор Киллинга

  • пространство-время, супер-пространство-время

• сложная геометрия

• симплектическая геометрия

• конформная геометрия

• Идея
• Определение
• Традиционное определение
• Синтетическое определение
• Свойства
• Каталожные номера

Идея

Дана касательное векторное поле на дифференцируемом многообразии XX, тогда его 91).

Определение

(интегральные кривые/потоковые линии)

Интегральная кривая или поточная линия векторного поля vv является дифференцируемой функцией вида

γ:U⟶X \гамма \;\двоеточие\; U \longrightarrow Икс

для U⊂ℝU \subset \mathbb{R} открытый интервал со свойством, что его касательный вектор в любой t∈Ut \in U равен значению векторного поля vv в точке γ(t)\gamma(t ):

∀t∈U(dγt=vγ(t)). \underset{t \in U}{\forall} \левый( д \ gamma_t = v _ {\ gamma (t)} \правильно) \,.

Определение

(поток векторного поля)

Глобальный поток vv является функцией вида

Φ:X×ℝ⟶X \Фи\;\двоеточие\; X \times \mathbb{R} \longrightarrow X

такое, что для каждого x ∈ Xx \in X функция ϕ(x,−):ℝ→X\phi(x,-) \colon \mathbb{R} \to X является интегральной кривой vv (по опр. ).

Область потока — это открытое подмножество O⊂X×ℝO \subset X \times \mathbb{R} такое, что для всех x∈Xx \in X пересечение O∩{x}×ℝO \cap \{x \} \times \mathbb{R} — открытый интервал, содержащий 00,

поток vv в области течения O⊂X×ℝO \subset X \times \mathbb{R} является дифференцируемой функцией

X×ℝ⊃O⟶ϕX X \times \mathbb{R} \supset O \overset{\phi}{\longrightarrow} X

такое, что для всех x∈Xx \in X функция ϕ(x,−)\phi(x,-) является интегральной кривой vv (по опр. ).

Определение

(полное векторное поле)

Векторное поле vv называется полным векторным полем , если оно допускает глобальный поток (по опр. ). 9Икс }

это поток для вв.

Свойства

Предложение

Пусть ϕ\phi — глобальный поток векторного поля vv (по опр. ). Это дает действие аддитивной группы (ℝ,+)(\mathbb{R},+) действительных чисел на дифференцируемом многообразии XX диффеоморфизмами, в этом

• ϕv(-,0)=idX\phi_v(-,0) = id_X;

• ϕn(-,t2)∘ϕv(-,t1)=ϕv(-,t1+t2)\phi_n(-,t_2) \circ \phi_v(-,t_1) = \phi_v(-, t_1 + t_2);

9{-1}.

Предложение

(основная теорема о потоках)

Пусть XX — гладкое многообразие и v∈Γ(TX)v \in \Gamma(TX) — гладкое векторное поле. Тогда vv имеет единственный максимальный поток (по опр. ).

Этот уникальный поток часто обозначается ϕv\phi_v или exp(v)\exp(v) (см. также на экспоненциальную карту ).

напр. Ли, теорема 12.9

Предложение

Пусть XX — компактное гладкое многообразие. Тогда каждое гладкое векторное поле v∈Γ(TX)v \in \Gamma(TX) является полным векторным полем (по опр. ), следовательно, имеет глобальный поток (по опр. ).

напр. Ли, теорема 12.12

Литература

• Джон Ли, глава 12 «Интегральные кривые и потоки» из Введение в гладкие многообразия (pdf)

Последняя редакция: 1 августа 2018 г., 12:11:38. См. историю этой страницы для получения списка всех вкладов в нее.

Платформа автоматизации физической безопасности на основе данных

Перейти к содержимому

Платформа автоматизации физической безопасности на основе данныхadmin2023-01-24T12:24:59-05:00

ВЕБИНАР ПО ЗАПРОСУ: Цифровая трансформация и автоматизация в современном мире физической безопасности

Узнать больше

15625px,218px;h:auto,auto,auto,39px;» data-frame_1=»e:power4.inOut;» data-frame_999=»o:0;e:power4.inOut;st:w;sR:5700;»> Идентификация и автоматизация на основе ИИ

Идентификация сотрудников

и безопасность доступа Узнать больше

Уменьшить физическую безопасность Риски и затраты

inOut;st:w;sR:5700;»> AI-Driven
SOC Automation

Узнать больше

Рассчитайте экономию на операциях безопасности

SOC Automation

Калькулятор рентабельности инвестиций Узнать больше

Подключенный технологический интерфейс

См. пресс-релизы

Управление данными

Физическая безопасность
Достижение совершеннолетия Прочитать историю

Платформа для анализа безопасности на основе данных

  Физическая безопасность ● Отслеживание в режиме реального времени ● Данные в действие

Платформа физической безопасности на основе данных

Получите 360-градусный обзор в режиме реального времени по различным аспектам операций физической безопасности и инфраструктуры. Автоматизируйте монотонные задачи безопасности, применяйте передовые алгоритмы искусственного интеллекта (ИИ), управляйте рисками безопасности, угрозами или исключениями, связанными с идентификацией, а также функциями доступа или оптимизации операций в вашем центре управления безопасностью (SOC). Защитите людей, здания и вещи по всему миру.

Подробнее

Управление доступом к физической идентификации сотрудников

Оптимизирует идентификацию на плате и вне ее ● Предоставление физического доступа ● Анализ рисков

Интеллектуальное предоставление прав на физический доступ Подробнее

Always ON Security

& Аудит

Алгоритмы на основе ИИ контролируют, кто имеет какой доступ и почему

Подробнее

Предоставить сотрудникам возможность мгновенного самообслуживания

Запросить мгновенный доступ во время поездок с помощью мобильного телефона

Узнать больше

Просмотреть внутренние угрозы и принять соответствующие меры

Необходимо отслеживать и заранее выявлять угрозы?

Подробнее

Управление доступом в чрезвычайных ситуациях/пандемиях

Мгновенное ограничение присутствия в чрезвычайной ситуации

Подробнее

Автоматизация SOC

Глубокая автоматизация для SOC ● Уменьшение количества тревог ● Оптимизация операций

SOC Alarm Reduction Manager

Уменьшение числа аварийных сигналов и экономия средств за считанные минуты

Подробнее

SOC Governance Manager

Повышение эффективности операций SOC

Подробнее

SOC Predictive Maintenance Manager и устранение рисков для бизнеса

2 неисправные устройства

Узнать больше

Конфигурация SOC

Автоматизация

Обеспечьте унифицированное представление мультивендорных и многоплатформенных технологий

Узнать больше

Отраслевые цитаты

«Построение устойчивой стратегии безопасности, способной противостоять невзгодам, никогда не было более важным, чем сейчас, после пандемии COVID. Физическая безопасность нуждается в гибких и инновационных инструментах. Размещение данных в нужном месте для автоматизации , Vector Flow создала множитель силы с доступностью информации и автоматическими действиями.Ключевым примером является работа по снижению ложных срабатываний, позволяющая операторам мониторинга быть более эффективными.Теперь любая группа физической безопасности может использовать платформу Vector Flow для снижения затрат, обеспечивая при этом более высокую безопасность в режиме реального времени».

Эд Чандлер, Председатель Security By Design, Inc.

«Vector Flow обладает уникальными возможностями для реализации возможностей больших данных, искусственного интеллекта и машинного обучения в мире физической безопасности. Принятие решений на основе данных лежит в основе успешных программ безопасности. Возможность анализировать и визуализировать тысячи и даже сотни тысяч точек данных, собранных системами безопасности, являются критически важным компонентом такого принятия решений.