Сравнение обыкновенных дробей – правила (5 класс, математика)
4.4
Средняя оценка: 4.4
Всего получено оценок: 191.
4.4
Средняя оценка: 4.4
Всего получено оценок: 191.
Сравнение обыкновенных дробей – это сложная задача для изучающих курс математики 5 класса. Дроби ведут себя не так, как простые числа, поэтому иногда приходится их преобразовывать перед сравнением. Все хитрости сравнения дробей рассмотрим вместе.
Что такое дробь?
Дробью зовут число, которое обозначает часть целого. Дробное число записывается с помощью дробной черты. Под чертой пишут знаменатель, который обозначает, на сколько частей разделили целое. Над чертой пишут числитель, который говорит о том, сколько частей было взято для расчета.
Обыкновенную дробь придумали еще в Древней Греции. Ни на одну минуту в мире не прекращалось использование обыкновенной дроби. Когда-то с ее помощью даже отмечали процент кредита, но со временем перешли на десятичные дроби.
Какие дроби зовутся обыкновенными ?
Выделяют следующие виды дробей:
- Правильные. То есть дроби, числитель которых меньше знаменателя.
- Неправильные. Это дроби, которые больше 1, то есть целого. У таких дробей числитель больше знаменателя.
- Смешанная дробь. Это число из двух частей: целой и дробной. Образуется такое число в результате выделения целой части неправильной дроби.
- Десятичная дробь. Дробь, которая записывается с помощью разделительной запятой.
Обыкновенная и правильная дробь – это одно и то же. Иногда обыкновенными дробями называют сразу блок дробей: правильные, неправильные и смешанные. Это не совсем верно.
Алгоритм сравнения дробей
Сначала скажем о случаях, когда преобразовывать дробь не требуется. Это три правила сравнения дробей:
- Если у двух дробей одинаковые числители, но разные знаменатели, то больше дробь, знаменатель которой меньше.
- Если у дробей одинаковые знаменатели, но разные числители, то больше та дробь, числитель которой больше.
- Если числители и знаменатели двух дробей одинаковы, то такие дроби равны.
Если у дробей разный числитель и знаменатель, то их приводят к одному знаменателю, после чего все сводится ко 2 правилу сравнения.
Алгоритм сравнения дробей выглядит так:
- Дробь проверяется на соответствие приведенным правилам. Если число не попадает под одно из утверждений, требуется привести дробь к общему знаменателю.
- Находится общий знаменатель. Это НОК двух знаменателей дробей
- Два числа приводятся к одному знаменателю
- После преобразований большей дробью становится число с наибольшим числителем.
Что мы узнали?
Мы поговорили о сравнении обыкновенных дробей. Вспомнили, что такое дробь и поговорили о видах дробей. Сказали, что обыкновенная и правильна дробь это одно и то же. Привели три правила сравнения обыкновенных дробей.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Марина Туровец
5/5
Анжелика Афраилова
5/5
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 191.
А какая ваша оценка?
Правила умножения дробей
- Арифметика
- Геометрия
- Таблицы
- Арифметика
- Правила умножения дробей
Для того чтобы произвести арифметические действия умножения над дробями, следует перемножить их числители и знаменатели, а результат записать в соответствующей форме.
Умножение простой дроби на число
При умножении простой дроби на натуральное число, ее числитель следует умножить на этот множитель, а знаменатель оставить без изменения.
3 8 |
× | 4 | = | 3 × 4 8 |
= | 12 8 |
= | 1 | 4 8 |
= | 1 | 1 2 |
Умножение смешанной дроби на число
При необходимости умножения смешанной дроби на натуральное число следует произвести данное арифметическое действие с целым числом этой дроби и её числителем.
| 1 | 2 5 |
× | 3 | = | 1 × 3 | + | 2 × 3 5 |
= | 3 | 6 5 |
= | 4 | 1 5 |
Умножение дроби на дробь
Когда нужно умножить простую дробь на простую дробь, следует перемножить числители, а затем знаменатели.
3 6 |
× | 4 8 |
= | 3 × 4 6 × 8 |
= | 12 48 |
= | 1 4 |
Умножение смешанной дроби на смешанную дробь
При выполнении операции умножения смешанных чисел, их следует записать в виде неправильных дробей, после чего перемножить их по соответствующим правилам.
| 2 | 1 3 |
× | 4 | 3 5 |
= | 7 3 |
× | 23 5 |
= | 7 × 23 3 × 5 |
= | 161 15 |
= | 10 | 11 15 |
© 2012 – 2022
Правило ключевой дроби – Математика для учителей начальных классов
Дроби
Мы знаем, что это ответ на задачу на деление:
представляет собой сумму пирога, которую получает отдельный ребенок, когда пироги делятся поровну между детьми.
Что произойдет, если мы удвоим количество пирогов и удвоим количество детей? Ничего такого! Количество пирога на ребенка осталось прежним:
Например, как показано на рисунке, и оба дают по два пирога каждому ребенку.
И утроение числа пирогов и числа детей также не меняет итоговое количество пирогов на одного ребенка, как и учетверение каждого числа или умножение чисел на триллион миллиардов!
Это заставляет нас хотеть верить:
Правило ключевой дроби
(по крайней мере, для целых положительных чисел ).
Мы говорим, что дроби и эквивалентны .
Пример: Дроби, эквивалентные 3/5
Например,
дает тот же результат, что и
и
Подумай / Соедини / Поделись
Запишите множество эквивалентных дробей для , для и для 1.
Пример: Возвращение назад0075 отменили
или взяли общий делитель 4 из числителя и знаменателя.Математики называют этот процесс сокращением дроби до наименьших членов. (Мы уменьшили числитель и знаменатель, насколько это возможно!)
Учителя обычно говорят, что мы упрощаем дробь. (Вы должны признать, что это выглядит проще, чем .)
Пример: Как низко вы можете опуститься?
В качестве другого примера можно, безусловно, упростить, заметив, что в числителе и знаменателе есть общий делитель 10:
Мы можем пойти дальше, так как 28 и 35 кратны 7:
Таким образом, разделение 280 пирогов среди 350 детей дает тот же результат, что и разделение 4 пирогов среди 5 детей!
Поскольку 4 и 5 не имеют общих делителей, это все, что мы можем сделать в этом примере (оставаясь целыми числами).
Самостоятельно
Смешай и подбери: вверху находятся некоторые дроби, которые не были упрощены.
Подумай / Соедини / Поделись
Используйте «Модель пирогов на ребенка», чтобы объяснить , почему действует правило ключевой доли. То есть объясните, почему каждый отдельный ребенок получает одинаковое количество пирога в этих двух ситуациях:
- , если у вас есть пироги и дети, или .
- , если у вас есть пироги и дети.
Упрощение сложных дробей — ChiliMath
ПоискЕсли «нормальная» дробь содержит дроби либо в числителе, либо в знаменателе, либо в обоих, то мы считаем ее сложной дробью. Этот тип фракции также известен как составная фракция.
Существует два метода , используемых для упрощения такой дроби.
Метод 1
Основные шаги :
- Создайте одну дробь в числителе и знаменателе.
- Примените правило деления дробей, умножив числитель на обратную или обратную величину знаменателя.
- При необходимости упростите.
Метод 2
Основные этапы :
- Найдите наименьший общий знаменатель (НОД) всех знаменателей сложных дробей.
- Умножьте этот LCD на числитель и знаменатель сложной дроби.
- При необходимости упростите.
После рассмотрения нескольких примеров вы должны понять, что Метод 2 намного лучше, чем Метод 1 , потому что почти всегда для получения окончательного ответа требуется меньше шагов.
Примеры упрощения сложных дробей
- Использование метода 1
И числитель, и знаменатель сложной дроби уже выражены в виде отдельных дробей. Это замечательно!
Следующим шагом является применение правила деления путем умножения числителя на обратную величину знаменателя.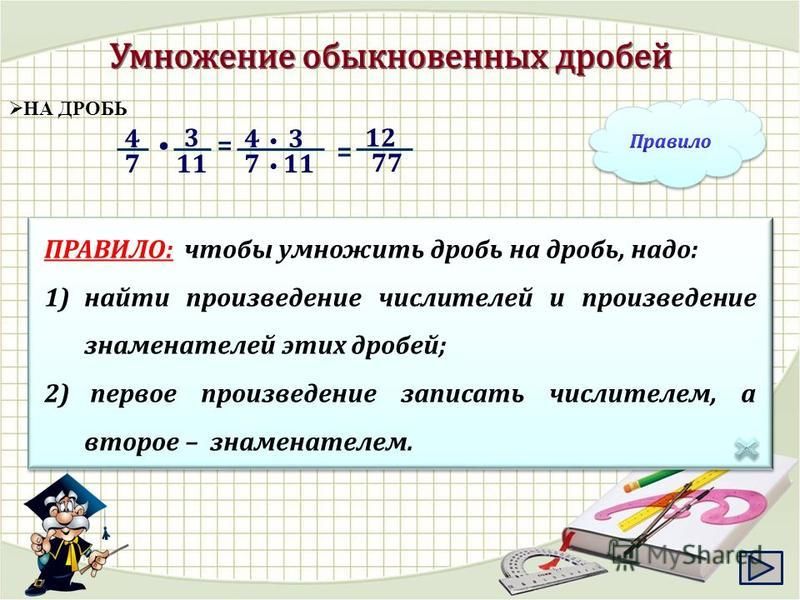
Завершите, отменив общие факторы, чтобы получить окончательный ответ.
- Используя метод 2
Найдите ДК всей задачи, то есть ДК верхнего и нижнего знаменателей.
Так как LCD 3y и 6y это просто \textbf{6y}, теперь мы умножим комплексный числитель и знаменатель на этот LCD. После этого мы можем ожидать, что задача будет сведена к одной дроби, которую можно упростить, как обычно.
Пример 2: Упростите приведенную ниже сложную дробь.
- Используя метод 1
В этом методе мы хотим создать одну дробь как в числителе, так и в знаменателе. Очевидно, что эта задача потребует, чтобы мы сделали это, прежде чем выполнять деление. 92} Умножьте верх и низ на этот ЖК-дисплей.
Пример 3: Упростите приведенную ниже сложную дробь.
- Используя метод 1
Создайте отдельные дроби как в числителе, так и в знаменателе, затем разделите дроби.