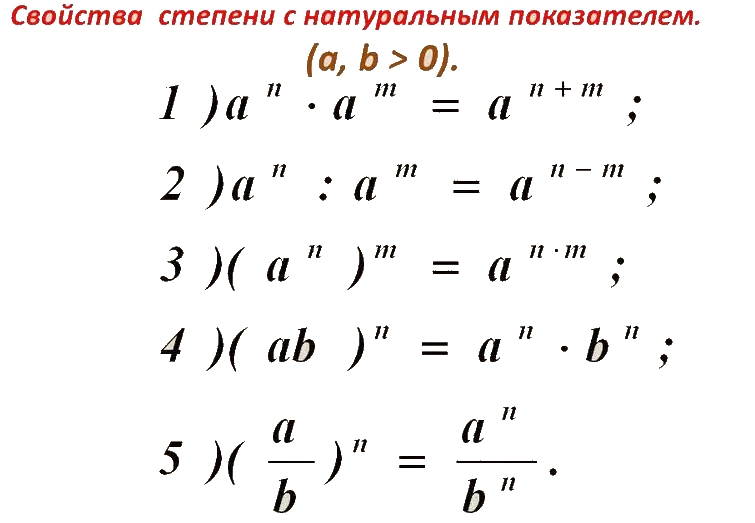Правила сложения степеней с одинаковыми основаниями: Свойства степеней, действия со степенями

Содержание

Деление степеней с одинаковыми основаниями

Похожие презентации:

Умножение и деление степеней с одинаковым основанием

Умножение и деление степеней с одинаковыми показателями

Степень числа. Тайны степени

Сложение и вычитание дробей с одинаковыми знаменателями

Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями

Умножение и деление степеней. Основное свойство степени

Сложение и вычитание дробей с одинаковыми знаменателями

Сложение и вычитание дробей с одинаковыми знаменателями. 8 класс

Больше, меньше, одинаковые

1. деление степеней

Проверка дополнительного
задания
Работа в парах
Вычислите:
10 6
( 3)
4
1
555
23
1000000
2 2 256
5
— 81
2
5
3
-1
25 : 23
32
3 3
5
4
4 :4
?
а а
?
35
15
8
32
5
4
19683
Тема урока:
Деление степеней с одинаковыми
основаниями.

Цели урока:
вывести правила деления степеней с
одинаковыми основаниями;
научиться применять правила деления степеней
с одинаковыми основаниями;
научиться возводить число в степень с нулевым
показателем.

5. Основное свойство степени

Для любого числа a и
произвольных натуральных
чисел m и n
m
a
n
a
=
m+n
a

6. Выбираем правильный ответ

33 · 3 6
0,057 · 0,0512
65 ·
64
52 ·54
(-3,1)5 · (-3,1)10
4,37
4,34 ·
4,33
19
9
0,05
6
56
(-3,1)15
413
26 ·
27
9
9
36
242(-3,1)5
3
7
18
43
3
13
15
2
(3,1)
10
6
0,112 4,39 0,0512 256
Молодцы!

7. Найдем частное двух степеней a7 и a3

a≠0
a7 = a3 ∙ a4
a7 : a3
a4 = a7 : a3
= a 7- 3
a7 : a3 = a 7-3 = a4

8. свойство степени

am : an = am-n
Для любого числа a ≠ 0
и произвольных
натуральных чисел m и
n, таких, что m > n,
m
a
:
n
a
=
m-n
a

9.

Правило деления степенейПри делении степеней с одинаковыми
основаниями основание оставляют прежним, а
из показателя степени делимого вычитают
показатель степени делителя.
Примеры:

10. Выбираем правильный ответ

331 : 36
a5 :a
h22 : h6
0.29 :
0.25
x16 :x4
(-3)15 : (3)6
3523 :
3510
Молодцы!
7
4
37
18 9
x
3h
a
33
(-3)
7
35
0,2
3h
20
25
621
a
x
3
(-3)
13
14
35
0,2
12
331
a
h
x
23
35
0,2
394

11. Проверочная работа

Представить в виде степени:
Вариант I
Вариант II

12. Подведем итог:

Какую
цель мы с вами ставили сегодня на
уроке?
Смогли мы его достичь?
Что мы умеем?
Что было трудно?
Кому что не понятно?

13. Рефлексия:

Выскажите
свое мнение одним
предложением , взяв за начало следующие
фразы.
1 Сегодня я узнал…
2 Было трудно…
3 Я понял , что…
4 У меня получилось…
5 Мне захотелось…

14.

Домашнее задание:

English Русский Правила

Умножение и деление степеней с одинаковыми основаниями

Урок алгебры в 7 классе

Гришко Е.М., учитель математики МБОУ «СОШ №4», г.Красноперекопск, Республика Крым

Цели урока:
— вывести правила умножения и деления степеней с одинаковыми основаниями;

— дать определение нулевой степени числа, не равного нулю;
— формировать умение выполнять указанные действия со степенями.

Задачи урока:
Образовательные (формирование познавательных УУД):
— познакомить учащихся со степенью с натуральным показателем;
— тренировать способность к использованию выведенного алгоритма;
— организовать деятельность учащихся по приобретению необходимых умений и навыков;
— повторить и закрепить;
Воспитательные (формирование коммуникативных и личностных УУД):
— содействовать развитию познавательного интереса учащихся к предмету;
— прививать учащимся навыки организации самостоятельной работы;
— умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

Развивающие (формирование регулятивных УУД): развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей.

Тип урока: изучение и первичное закрепление новых знаний.
Оборудование: презентация, раздаточный материал; лист целеполагания (Приложение 1) и лист самоконтроля (Приложение 2).

Ход урока:

Презентация

I. Организационный (мотивационный) момент

Здравствуйте, ребята! Садитесь! Прежде чем начать урок, мне бы хотелось рассказать одну притчу.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому вопрос. У первого спросил: «Что ты делал целый день»? И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?».

И тот ответил: «А я добросовестно выполнял свою работу». Третьему человеку задал свой вопрос мудрец и в ответ услышал: «А я принимал участие в строительстве храма!»
Желаю и вам, ребята, сегодня принять участие в строительстве храма ваших знаний.

II. Актуализация знаний и фиксация затруднения в деятельности (актуализировать учебный материал необходимый для изучения нового, зафиксировать затруднения в деятельности)

1. Проверка домашнего задания (Слайд 2)

Откройте тетради, запишите число и классная работа. Что было задано на дом? (№377, 386 (а,в), 388 (а-г), 400)
Проверка домашнего задания № 388.

Решение:
а) –1³ + (–2)³ = –1 + (–8) = –9;
б) –6² – (–1)⁴ = –36 – 1 = –37;
в) –8³ + (–3)³ = –512 + (–27) = –539;
г) 10 – 5 · 2⁴ = 10 – 5 · 16 = 10 – 80 = –70;

Поменяйтесь тетрадями с партнёром по плечу, оцените работу партнёра с решением, которое представлено на доске.

2. Устная работа (Слайды 3-5)

Для дальнейшей работы по этой теме нам нужно будет вспомнить элементарные правила степеней. Ответьте на вопросы:
а) Что такое степень?
б) Чему равна степень отрицательного числа с четным показателем?
в) Чему равна степень отрицательного числа с нечетным показателем?
г) Что получится при возведении в степень с натуральным показателем числа нуль?

3. Вычислите: Слайд 6
4. Проверочная работа. Найдите значение выражения: Слайд 7
5. Работа в парах. Вычислите: Слайд 8

(Возникает затруднение при выполнении последних двух заданий)

Выход на проблему и постановка учебной задачи на урок (задачу на урок ставят сами дети)

III. Постановка цели и задач урока. Мотивация учебной деятельности

Слайд 9

Построение проекта выхода из затруднения и открытие нового знания.
Записывают тему урока и разрабатывают план действий:
— представить степени в виде произведения,
— вычислить значение степени,
— провести анализ полученного затруднения,
— записать формулу в общем виде,
— сформулировать соответствующее правило

Работа с учебником (стр.99-101)

Слайды 10-11

Вернемся к тем заданиям, где возникли затруднения в ходе устной работы

IV. Усвоение новых знаний и способов действий
Первичное закрепление (учебник «Алгебра 7 класс», автор Макарычев Ю.Н.)

№ 403 (а, е, ж,з), № 405 (а-г), № 407, 409 (а, в, д, е), 410 (а, в, д), 411 (а-г), 414 (а, в, з), 416 (а, б, в), 417 (а, б)

№ 403

Решение:
а) x⁵x⁸ = x^{5 + 8} = x¹³;
е) yy¹² = y^{1 + 12} = y¹³;
ж) 2⁶2⁴ = 2^{6 + 4} + 2¹⁰; з) 7⁵7 = 7^{5 + 1} = 7⁶.

№ 405

Решение:
а) a¹⁵ = a^{6 + 9} = a⁶ ∙ a⁹; б) a¹⁵ = a^{9 + 6} = a⁹ ∙ a⁶;
в) a¹⁵ = a^{2 + 13} = a² ∙ a¹³; г) a¹⁵ = a^{14 + 1} = a¹⁴ ∙ a = a ∙ a¹⁴.

№ 407

Решение:
Представим число 6 в виде суммы двух натуральных чисел всеми возможными способами:
6 = 1 + 5; 6 = 2 + 4; 6 = 3 + 3.
Значит, a⁶ = a ∙ a⁵; a⁶ = a² ∙ a⁴; a⁶ = a

³ ∙ a³.

№ 409

Решение:
а) m³m²m⁸ = m^{3 + 2 + 8} = m¹³; в) xx⁴x⁴x = x^{1 + 4 + 4 + 1} = x¹⁰;
д) 7⁸ ∙ 7 ∙ 7⁴ = 7^{8 + 1 + 4} = 7¹³; е) 5 ∙ 5² ∙ 5³ ∙ 5⁵ = 5^{1 + 2 + 3 + 4} = 5¹¹.

№ 410

(При выполнении этого упражнения ученики сами определяют основание степени, которое будет являться общим для двух степеней)

Решение:
а) 5⁸ ∙ 25 = 5

8 ∙ 5² = 5^{8 + 2} = 5¹⁰;
в) 6¹⁵ ∙ 36 = 6¹⁵ ∙ 6² = 6^{15 + 2} = 6¹⁷;
д) 0,4⁵ ∙ 0,16 = 0,4⁵ ∙ 0,4² = 0,4^{5 + 2} = 0,4⁷;
е) 0,001 ∙ 0,1⁴ = 0,1³ ∙ 0,1⁴ = 0,1^{3 + 4} = 0,1⁷.

№ 411

Решение:
а) 2⁴ ∙ 2 = 2^{4 + 1} = 2⁵ = 32;
б) 2⁶ ∙ 4 = 2⁶ ∙ 2² = 2^{6 + 2} = 2⁸ = 256;
в) 8 ∙ 2⁷ = 2³ ∙ 2⁷ = 2^{3 + 7} = 2¹⁰ = 1024;
г) 16 ∙ 32 = 2⁴ ∙ 2⁵ = 2^{4 + 5} = 2⁹ = 512.

№ 414

Решение:
а) x⁵ : x³ = x^{5 – 3} = x²;
в) a²¹ : a = a^{21 – 1} = a²⁰;
з) 0,7⁹ : 0,7⁴ = 0,7^{9 – 4} = 0,7⁵.

№ 416

Решение:
а) 5⁶ : 5⁴ = 5^{6 – 4} = 5² = 25;
б) 10¹⁵ : 10¹² = 10^{15 – 12} = 10³ = 1000;
в) 0,5¹⁰ : 0,5⁷ = 0,5^{10 – 7} = 0,5³ = 0,125;
г) ;
д) 2,73¹³ : 2,73¹² = 2,73^{13 – 12} = 2,73;
е) .

Используя правила умножения и деления степеней, упростите выражение.

а) x⁸ ∙ x

³ : x⁵; б) x²⁰ : x¹⁰ ∙ x;
в) x⁷ : x³ : x³; г) x¹⁴ : x⁹ ∙ x⁵.

Решение:
а) x⁸ ∙ x³ : x⁵ = x^{8 + 3} : x⁵ = x¹¹ : x⁵ = x^{11 – 5} = x⁶;
б) x²⁰ : x¹⁰ ∙ x = x^{20 – 10} ∙ x = x¹⁰ ∙ x = x^{10 + 1} = x¹¹;
в) x⁷ : x³ : x³ = x^{7 – 3} : x³ = x⁴ : x³ = x^{4 – 3} = x;
г) x¹⁴ : x⁹ ∙ x⁵ = x^{14 – 9} ∙ x⁵ = x⁵ ∙ x⁵ = x^{5 + 5} = x¹⁰.

№ 417

Решение:
а) = 8⁶ : 8⁴ = 8^{6 – 4} = 8² = 64;
б) = 0,8⁷ : 0,8⁴ = 0,8^{7 – 4} = 0,8³ = 0,512;
в) = (–0,3)⁵ : (–0,3)³ = (–0,3)^{5 – 3} = (–0,3)² = 0,09.

V. Физкультминутка

VI. Контроль и самоконтроль знаний и способов действий

Самостоятельная работа (по вариантам)
Раздается каждому учащемуся, решение можно выполнять прямо на листочках. После выполнения работы проверяются в классе, и каждый ученик оценивает себя сам.

VII. Включение в систему знаний и повторение.

Слайды 12-13

Задача «Определить во сколько раз масса земного шара больше массы всего окружающего его воздуха».
Решение. Чтобы убедиться, насколько облегчаются практические вычисления при пользовании степенным изображением больших чисел, выполним такой расчет: определим, во сколько раз масса земного шара больше массы всего окружающего его воздуха.
На каждый кв. сантиметр земной поверхности воздух давит, мы знаем, с силой около килограмма. Это означает, что вес того столба атмосферы, который опирается на 1 кв.см, равен 1 кг. Атмосферная оболочка Земли как бы составлена вся из таких воздушных столбов. Их столько, сколько кв. сантиметров содержит поверхность нашей планеты; столько же килограммов весит вся атмосфера. Заглянув в справочник, узнаем, что величина поверхности земного шара равна 510 млн. кв. км, т.е. 51 × 10⁷ кв. км.
Рассчитаем, сколько квадратных сантиметров в квадратном километре. Линейный километр содержит 1000 м, по 100 см в каждом, т.е. равен 10⁵ см, а кв. километр содержит (10⁵)² = 10¹⁰ кв. сантиметров. Во всей поверхности земного шара заключается поэтому

51 × 10⁷× 10¹⁰ = 51 × 10¹⁷кв. сантиметров.

Столько же килограммов весит и атмосфера Земли. Переведя в тонны, получим:
51 × 10¹⁷ : 1000 = 51 × 10¹⁷ : 10³=51 × 10^17-3 = 51 × 10¹⁴.

Масса же земного шара выражается числом
6 × 10²¹ тонн.

Чтобы определить, во сколько раз наша планета тяжелее ее воздушной оболочки, производим деление:
6 × 10²¹ : 51 × 10¹⁴ ≈ 10⁶,
т. е. масса атмосферы составляет примерно миллионную долю массы земного шара

VIII. Рефлексия учебной деятельности на уроке, подведение итогов

Дайте определение степени с натуральным показателем.
Сформулируйте правило возведения отрицательного числа в четную степень, в нечетную степень.
Какой знак имеет результат возведения любого числа в квадрат?
Сформулируйте правила сложения и умножения степеней с одинаковыми основаниями.
Чему равно значение выражения 2⁰; (–1)¹?

Заполнить пункты «знаю» и «умею» таблицы целеполагания.
Заполнение листов самоконтроля.

Пожалуйста, поделитесь своими мыслями о сегодняшнем занятии (хотите одним предложением). Вам для этого помогут слова:
* Сегодня на уроке я закрепил…
* На что мне нужно обратить внимание…

IX. Информация о домашнем задании(Слайд 14)

П.16 выучить правила. Решить задания:
I уровень: №404, 408, 415, 418;
II уровень: №406, 412, 419 (б,г,е), 533.
Выразить массу Земли и Луны в различных единицах массы (в граммах, килограммах, в центнерах и тоннах)

Приложение 1
Лист целеполагания
Ф.И.___________________________________________

Вопросы	Знаю	Не знаю	Хочу знать
Что такое степень с натуральным показателем?
Как возвести отрицательное число в степень?
Как умножать степени с одинаковыми основаниями?
Как делить степени с одинаковыми основаниями?
Как возвести число в степень с нулевым показателем?

Приложение 2
Лист самоконтроля
Ф. И.________________________________________________

№	Виды работ	Оценка
1	Проверка домашнего задания
2	Устная работа
3	Работа в парах
4	Самостоятельная работа по вариантам
5	Решение задачи

	Средняя оценка:

Используемые учебники и учебные пособия:
Учебник для общеобразовательных учреждений /Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под редакцией С.А. Теляковского

Источник: uchportal.ru

Дробные степени (как складывать, вычитать, умножать, делить)

Определение дробных показателей

Дробные показатели представляют собой способ одновременного представления степеней и корней. Когда показатель степени дробный, числитель равен степени, а знаменатель — корню.

Например, х ^{³ ⁄ ₂} = ² √(х ³ ). Мы видим, что числитель дробного показателя степени равен 9.0019 3 , что возводит x в третью степень. Знаменатель дробного показателя степени равен 2 , который берет квадратный корень (также называемый вторым корнем) из x .

Порядок применения степени и корня к нашему числу или переменной значения не имеет. В примере мы написали x ^{³ ⁄ ₂} = ² √(x ³ ). Это заставило нас вычислить x ³, а затем извлечь из этого квадратный корень.

Мы получим такое же решение, если запишем его в виде x ^{³ ⁄ ₂} = (² √x) ³ . В этом случае мы будем вычислять квадратный корень из x, а затем возводить этот результат в третью степень.

Хотите неограниченный доступ к калькуляторам и урокам Voovers?

Присоединяйтесь сейчас

100% без риска. Отменить в любое время.

Как выполнять операции с дробными показателями

В этом разделе мы рассмотрим, как складывать, вычитать, умножать и делить дробные степени. Имейте в виду, что выполнение этих операций с дробными показателями — это тот же процесс, что и с обычными показателями, с дополнительными соображениями, которые мы должны учитывать при работе с дробями.

Добавление дробных степеней

Если термины имеют одинаковое основание a и одинаковую дробную степень ⁿ ⁄ _m , мы можем их сложить. Правило задается как:

Ca ^{ⁿ ⁄ _м} + Da ^{ⁿ ⁄ _м} = (C + D)a ^{90 009 n} ⁄ _m

Вот пример сложения дробных степеней :

2x ^{² ⁄ ₅} + 7x ^{² ⁄ ₅} = 9x ^{90 009 2} ⁄ ₅

Вычитание дробных степеней

Вычитание членов с дробными степенями следует тем же правилам, что и сложение членов с дробными степенями. Термины должны иметь одинаковую базу a и тот же дробный показатель степени ⁿ ⁄ _m . Правило задается как:

Ca ^{ⁿ ⁄ _м} — Da ^{ⁿ ⁄ _м} = (C — D)a 9 0009 ^п ⁄ _м

Вот пример вычитания дробных показателей:

2x ^{² ⁄ ₅} — x ^{² ⁄ ₅} = x 90 009 ² ⁄ ₅

Умножение дробных степеней

Если термины с дробными степенями имеют одинаковое основание и , то мы можем умножить их путем сложения дробных степеней. Правило задается следующим образом:

(a ^{ⁿ ⁄ _m} )(a ^{^p ⁄ _r} ) = a 9 0009 ( ^п ⁄ _м + ^р ⁄ _r )

Вот пример умножения дробных степеней:

(у ^{⁴ ⁄ ₅} )(у ^{⁶ ⁄ ₅} ) = у ^{2 900 11}

Деление дробных степеней

Если члены с дробными степенями имеют одинаковое основание и , то мы можем разделить их, вычитая дробные степени. Правило задается как:

^{(a ^{ⁿ ⁄ _m} )} ⁄ _{(a ^{^p ⁄ 900 12 р}} ) = а ^{( ⁿ ⁄ _m — ^p ⁄ _r )}

Вот пример деления дробных степеней:

^{(г ^{³ ⁄ ₄} )} ⁄ _{(г ^{² ⁄ ₄} )} = у ^{¹ ⁄ ₄}

Изучение математики никогда не было проще.

Получите неограниченный доступ к более чем 165 персонализированным урокам и 69интерактивные калькуляторы.

Присоединяйтесь к Voovers+ сегодня