Вычитание дробей с разными примеры. Вычитание дробей с разными знаменателями. Сложение и вычитание обыкновенных дробей
Дробные выражения сложны для понимания ребёнком. У большинства возникают сложности, связанные с . При изучении темы «сложение дробей с целыми числами», ребёнок впадает в ступор, затрудняясь решить задание. Во многих примерах перед тем как выполнить действие нужно произвести ряд вычислений. Например, преобразовать дроби или перевести неправильную дробь в правильную.
Объясним ребёнку наглядно. Возьмём три яблока, два из которых будут целыми, а третье разрежем на 4 части. От разрезанного яблока отделим одну дольку, а остальные три положим рядом с двумя целыми фруктами. Получим ¼ яблока в одной стороне и 2 ¾ — в другой. Если мы их соединим, то получим целых три яблока. Попробуем уменьшить 2 ¾ яблока на ¼, то есть уберём ещё одну дольку, получим 2 2/4 яблока.
Рассмотрим подробнее действия с дробями, в составе которых присутствуют целые числа:
Для начала вспомним правило вычисления для дробных выражений с общим знаменателем:
На первый взгляд всё легко и просто. Но это касается только выражений, не требующих преобразования.
Но это касается только выражений, не требующих преобразования.
Как найти значение выражения где знаменатели разные
В некоторых заданиях необходимо найти значение выражения, где знаменатели разные. Рассмотрим конкретный случай:
3 2/7+6 1/3
Найдём значение данного выражения, для этого найдём для двух дробей общий знаменатель.
Для чисел 7 и 3 – это 21. Целые части оставляем прежними, а дробные – приводим к 21, для этого первую дробь умножаем на 3, вторую – на 7, получаем:
6/21+7/21, не забываем, что целые части не подлежат преобразованию. В итоге получаем две дроби с одним знаменателям и вычисляем их сумму:
3 6/21+6 7/21=9 15/21
Что если в результате сложения получается неправильная дробь, которая уже имеет целую часть:
2 1/3+3 2/3
В данном случае складываем целые части и дробные, получаем:
5 3/3, как известно, 3/3 – это единица, значит 2 1/3+3 2/3=5 3/3=5+1=6
С нахождением суммы всё понятно, разберём вычитание:
Из всего сказанного вытекает правило действий над смешанными числами, которое звучит так:
- Если же от дробного выражения необходимо вычесть целое число, не нужно представлять второе число в виде дроби, достаточно произвести действие только над целыми частями.

Попробуем самостоятельно вычислить значение выражений:
Разберём подробнее пример под буквой «м»:
4 5/11-2 8/11, числитель первой дроби меньше, чем второй. Для этого занимаем одно целое число у первой дроби, получаем,
3 5/11+11/11=3 целых 16/11, отнимаем от первой дроби вторую:
3 16/11-2 8/11=1 целая 8/11
- Будьте внимательны при выполнении задания, не забывайте преобразовывать неправильные дроби в смешанные, выделяя целую часть. Для этого необходимо значение числителя разделить на значение знаменателя, то что получилось, встаёт на место целой части, остаток – будет числителем, например:
19/4=4 ¾, проверим: 4*4+3=19, в знаменателе 4 остаётся без изменений.
Подведём итог:
Перед тем как приступить к выполнению задания, связанного с дробями, необходимо проанализировать, что это за выражение, какие преобразования нужно совершить над дробью, чтобы решение было правильным. Ищите более рациональные способ решения. Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Чтобы не произошло путаницы при решении дробных выражений, необходимо руководствоваться правилом последовательности. Решайте всё внимательно, не торопясь.
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:
Короче, в общем виде:
А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:
Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:
Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…
Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…
Итак, нам надо сложить два дробных выражения:
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит.
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)
Порешаем немного?)
Вычислить:
Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Ваш ребенок принес домашнее задание из школы, и вы не знаете как его решить? Тогда этот мини урок для вас!
Как складывать десятичные дроби
Десятичные дроби удобнее складывать в столбик. Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:
- Разряд должен находиться под разрядом, запятая под запятой.
Как вы видите на примере, целые единицы находятся друг под другом, разряд десятых и сотых находится друг под другом. Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.
Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.
Сложение дробей с равными знаменателями
Чтобы выполнить сложение с общим знаменателем, надо сохранить знаменатель без изменения, найти сумму числителей и получим дробь, которая будет являться общей суммой.
Сложение дробей с разными знаменателями методом нахождения общего кратного
Первое, на что надо обратить внимание – это на знаменатели. Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:
- 1/3 + 3/4 = 13/12, для решения этого примера нам надо найти наименьшее общее кратное число (НОК), которое будет делиться на 2 знаменателя. Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
- Перемножаем множители и выполняем сложение полученных чисел, получаем 13/12 – неправильную дробь.

- Для того чтобы перевести неправильную дробь в правильную, разделим числитель на знаменатель, получим целое число 1, остаток 1 – числитель и 12 – знаменатель.
Сложение дробей методом умножения крест на крест
Для складывания дробей с разными знаменателями существует еще один способ по формуле “крест на крест”. Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.

- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Алгебра. Урок 1. Числа и вычисления
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
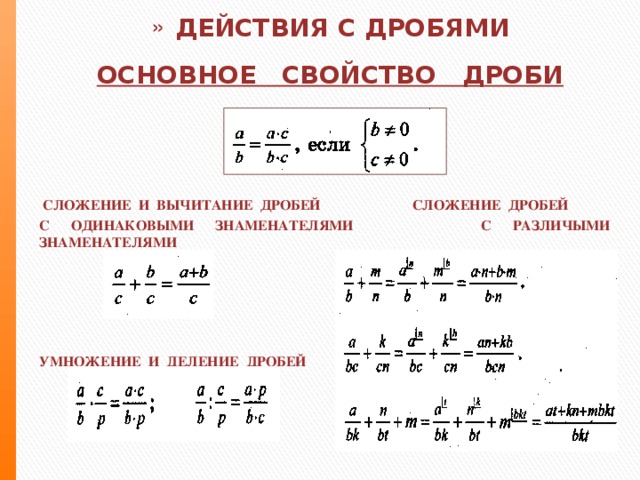
Действия с дробями
- Обыкновенная дробь
Основное свойство дроби
Правильная/неправильная дробь
Сократимая/несократимая дробь
- Смешанная дробь
- Десятичная дробь
- Сложение и вычитание дробей
- Умножение и деление дробей
- Сравнение дробей
Действия со степенями
- Степень числа
- Свойства степеней
- Возведение отрицательных чисел в степень
Примеры решений заданий из ОГЭ
Понятие обыкновенной, десятичной, смешанной дроби.
Обыкновенная дробь – дробь вида
ab
где число a – числитель дроби, число b – знаменатель.
Примеры:
12;65;31;715.
Обыкновенная дробь может быть правильной или неправильной, сократимой или несократимой:
Дробь называется правильной, если числитель (a) меньше знаменателя (b).
Примеры:
56;34.
Дробь называется неправильной, если числитель (a) больше знаменателя (b).
Примеры:
65;31.
Основное свойство обыкновенной дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число (натуральные числа – числа, которые используются при счете: 1, 2, 3, …), то получится дробь, равная данной.
Дробь называется сократимой, если числитель и знаменатель имеют общие множители (числитель и знаменатель можно поделить на одно и то же число).
Примеры сократимых дробей:
1216=3?44?4=34
2114=3?72?7=32
Дробь называется несократимой, если числитель и знаменатель дроби не имеют общих множителей.
Примеры несократимых дробей:
25;911;125126.
Дробь называется смешанной, если у нее есть целая часть. То есть саму дробь можно представить в виде суммы целого числа и обыкновенной дроби.
Примеры смешанных дробей:
312;278;901277.
Смешанную дробь всегда можно перевести в неправильную обыкновенную дробь.
312=3⋅2+12=72
278=2⋅8+78=238
901277=90⋅77+1277=694277
Дробь называется десятичной, если она представлена в десятичной записи.
Примеры десятичных дробей:
56,002; 4,125; 12,3; 0,01.
Десятичную дробь всегда можно перевести в смешанную дробь или в обыкновенную дробь с числителем и знаменателем. Так поступают, когда необходимо совершить действие между обыкновенной дробью и десятичной.
Перевод в смешанные дроби:
56,002=5621000=561500
56,002=5621000=561500
Перевод в обыкновенные дроби:
12,3=12310=12⋅10+310=123100,01=1100
Сложение и вычитание дробей.
Для того, чтобы складывать и вычитать смешанные дроби между собой, необходимо действовать следующим образом:
- превратить дроби из смешанных в неправильные, если такие дроби есть,
например: \[2\frac{7}{8} = \frac{{2 \cdot 8 + 7}}{8} = \frac{{23}}{8}\] - найти наименьший общий знаменатель у полученных дробей и домножить числители на недостающие множители;
- произвести сложение или вычитание числителей дробей, подписав под суммой или разностью общий знаменатель.
Примеры:
(1)216+178=2⋅6+16+1⋅8+78=136+158=13⋅46⋅4+15⋅38⋅3=52+4524=9724=4124
(2)3712−2316=3⋅12+712−2⋅16+316=4312−3516=43⋅412⋅4−35⋅316⋅3=172−10548=6748=11948
(3)2314−0,6=2⋅14+314−610=3114−35=31⋅514⋅5−3⋅145⋅14=155−4270=11370=14370
Умножение и деление дробей.
При умножении двух дробей числитель первой дроби умножается на числитель второй дроби, знаменатель первой дроби умножается на знаменатель второй:
\[\frac{a}{b} \cdot \frac{c}{d} = \frac{{a \cdot c}}{{b \cdot d}}\]
Чтобы умножить дробь на число, необходимо представить это число в виде дроби со знаменателем-единицей:
\[\frac{a}{b} \cdot c = \frac{a}{b} \cdot \frac{c}{1} = \frac{{a \cdot c}}{{b \cdot 1}} = \frac{{a \cdot c}}{b}\]
При делении двух дробей необходимо первую дробь умножить на «перевёрнутую» предыдущую, то есть у дроби-делителя поменять местами числитель и знаменатель и поставить операцию умножения вместо операции деления между этими дробями:
\[\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{{a \cdot d}}{{b \cdot c}}\]
Чтобы разделить дробь на число, необходимо представить это число в виде дроби со знаменателем-единицей:
\[\frac{a}{b} \div c = \frac{a}{b} \div \frac{c}{1} = \frac{a}{b} \cdot \frac{1}{c} = \frac{{a \cdot 1}}{{b \cdot c}} = \frac{a}{{b \cdot c}}\]
Примеры:
(1)234⋅811÷0,5=11141⋅82111÷51102=2÷12=2⋅21=4
(2)6÷2,25⋅1,5=61÷214⋅151102=61÷94⋅32=631⋅493⋅3121=4
Сравнение дробей.
Для того, чтобы сравнивать две дроби между собой, нужно уметь выполнять действия с дробями (сложение, вычитание, умножение, деление). При сравнении дробей, особенно в заданиях, где требуется расположить дроби в порядке возрастания или убывания, удобно приводить обыкновенную дробь к виду десятичной.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Примеры:
\[\frac{4}{7} < \frac{5}{7};\;\;\;\; \frac{3}{{14}} > \frac{1}{{14}};\;\;\;\; \frac{2}{3} < \frac{{55}}{3}.\]
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Примеры:
\[\frac{2}{7} < \frac{2}{5};\;\;\;\; \frac{7}{6} > \frac{7}{{11}};\;\;\;\; \frac{5}{4} > \frac{5}{5}. 6} = 1000000.\]
6} = 1000000.\]
Скачать домашнее задание к уроку 1.
Как считать с дробями
| Как считать с дробями |
При подсчете событий или людей мы имеем дело с целыми числами… 0,1,2,3,…также называемыми целыми числами.
Однако в случае измерения галлонов, температуры или длины объекта
может получиться любое значение между целыми числами.
Такие числа мы называем дроби или реалы.
В этой статье объясняются правила расчетов с дробями.
Обозначение
На картинке ниже плитка шоколада разрезана на пять равных частей. На этом рисунке точка «.» означает умножение.
Каждая часть составляет одну пятую часть.
Верхнее число (1) называется числителем.
Меньшее число (5) называется знаменателем.
Числитель — исходный объект.
Знаменатель — это количество равных частей, которые вместе составляют объект.
На следующем рисунке делим 2 плитки шоколада на 5 равных частей
Дополнение
Как сложить дроби?Это правило прямо следует из дистрибутивного закона:
Прописью: при равенстве знаменателей сложить (вычесть) числители.
Умножение
Для этого правила мы используем плитку шоколада с общей поверхностью 1,На приведенном выше рисунке показано, что:
Общее правило:
Словами: числитель * числитель, знаменатель * знаменатель.
Нет необходимости в равенстве знаменателей.
для доказательства нам понадобится переместительный закон умножения: ab = ba
Равные дроби
Дробь не изменится, если числитель и знаменатель умножить (поделить) на одно и то же число.Это правило прямо следует из правила умножения:
пруф:
Сокращение
По приведенному выше правилу дроби можно уменьшить, разделив. числитель и знаменатель на общий (простой) множитель.

См. пример ниже:
Добавление любых дробей
Это можно сделать, сначала перемножив дроби, чтобы получить равные знаменатели. Примечание:
Умножение знаменателей может привести к большим числам, чем это необходимо.
Подойдет наименьшее общее кратное знаменателей.
Скажем, L = LCM(b,d) и G = GCD(b,d) и зная, что L . G = bd, тогда:
Это приводит к наименьшему возможному знаменателю, и результирующая дробь не нуждается в сокращении.
Пример:
Сочетание целых чисел и дробей
| запись целого числа в виде дроби | запись | сочетание целого числа и дроби |
Использование карманного калькулятора для извлечения целой части из дроби:
Обратная дробь
Если числитель и знаменатель дроби поменять местами, получится обратная дробь .Дробь, умноженная на обратную, дает «1».

Деление на дробь
Деление на дробь осуществляется путем умножения на обратное значение.
Пример:
Примечание:
У суперкомпьютера Cray-1 не было инструкций для деления.
Вместо этого он вычислял обратные значения и использовал умножение.
Проценты
Процент — это числитель дроби, в знаменателе которой 100.Пример записи дроби в процентах:
С помощью карманного калькулятора просто введите: 100 x 22 : 27 = 81,84
Приложение
Дробь типа 3/5 можно рассматривать как- 1. три предмета, которые все разделены на 5 частей, по 1 части от каждого
2. один предмет, разделенный на 5 частей, состоящий из 3 частей
1. Распределение
Сумма в 12000 долларов должна быть распределена между тремя людьми A, B, C так, чтобы A:B:C = 2:3:5.
Сколько человек получает?
2+3+5 = 10.
А получает: (2/10)*12000 = 2400
B получает: (3/10)*12000 = 3600
C получает: (5/10)*12000 = 6000
2. Вероятность
Вероятность
При бросании игральной кости возможны 6 исходов: 1..6.
Шанс на 6 равен 1/6.
При бросании двух игральных костей возможно 6*6=36 исходов: (1,1)..(6,6).
Вероятность (6,6) равна 1/36.
Когда мы бросаем 2 кости сто раз, мы ожидаем (1/36)*100 = 2….3 раза (6,6) результата.
3. Расход воды
На рисунке ниже показана система трубопроводов для воды.
В точке A поток делится: 1/4 потока поступает в B, поэтому 1-(1/4)=3/4 потока в C.
Поток A-B-D: 1/4. 2/5 = 1/10
Поток A-C-F: 3/4. 7/10 = 21/40
Поток A-B-E: 1/4. 3/5 = 3/20
Поток A-C-E: 3/4. 3/10 = 9/40
Расход из E: 3/20 + 9/40 = 15/40 = 3/8
проверка: добавление расхода из D, E, F: 1/10 + 3/8 + 21/40 = 1
На каждую тысячу галлонов воды, поступающей в точку A,
(3/8) * 1000 = 375 галлонов вытекает в точке E.
Примечание:
последовательный поток: умножение дробей.
параллельно: добавить дроби.
Дроби, Определение и правила дробей, Проверка дробей
Оператор: + — * /
Решение:
Определение дроби
Число, записанное в виде $\frac{a}{b}$ или a/b, где $a$ — целое число, а $b$ — целое число, отличное от нуля, называется дробью .
Число $a$ равно числитель , а $b$ — знаменатель .
Дробь представляет собой либо часть целого, либо любое количество равных частей.
Знаменатель показывает, сколько равных частей составляет целое, а числитель показывает, сколько этих частей мы имеем в виду.
Примеры дробей
Пример 1: Бекки, Мерри и Джон хотят поровну разделить плитку шоколада.
Какую часть бруска займет каждый из них?
В какой части бара Бекки и Мерри будут вместе?
Детям нужно разделить брусок на три части. Таким образом, каждый возьмет $\frac{1}{3}$ плитки шоколада.
Две девушки вместе будут иметь
две части, следовательно, математически говоря, они будут иметь $\frac{2}{3}$ бруска.
Пример 2: Какая часть солдат желтая?
Пример 3: Какой части яблок не хватает?
Правила дроби
Сложение: (те же знаменатели)
$\frac{A}{B} +\frac{C}{B} = \frac{A + C}{B}$
Вычитание: (те же знаменатели)
$\frac{A}{B} -\frac{C}{B} = \frac{A — C}{B}$
Сложение: (разные знаменатели)
$\frac{A}{B} +\frac{C}{D} = \frac{A\cdot D}{B\cdot D} +\frac{B\cdot C}{B\cdot D} = \frac{A\cdot D + B\cdot C}{B\cdot D}$
Вычитание: (разные знаменатели)
$\frac{A}{B} -\frac{C}{D} = \frac{A\cdot D}{B\cdot D} -\frac{B\cdot C}{B\cdot D} = \frac{A\cdot D — B\cdot C}{B\cdot D}$
Умножение:
$\frac{A}{B}\times\frac{C}{D} = \frac{A\cdot C}{B\cdot D}$
Деление:
$\frac{A}{B}\div\frac{C}{D} = \frac{A}{B}\times\frac{D}{C}= \frac{A\ cdot D}{B\cdot C}$
Свойства фракций
Свойство I: Все заштрихованные части окружностей представляют собой половину $\frac{1}{2}, \frac{2}{4}$ и $\frac{3}{6}$, следовательно, $\frac{1}{2} = \frac{2}{4} = \frac{3}{6}$
Мы получим $\frac{2}{4}$, если умножим числитель и знаменатель дроби $\frac{1}{2}$ на $2$.
Получим $\frac{3}{6}$, умножив числитель и знаменатель $\frac{1}{2}$ на $3$.
Пусть $a$ — целое число, а $b$ и $c$ — ненулевые целые числа.
Тогда:
$\frac{a}{b}=\frac{a\cdot c}{b\cdot c}$ и $\frac{a}{b}=\frac{a:c}{b:c}$
Свойство II: Если две дроби имеют одинаковые знаменатели, то дробь с большим числителем больше.
Если $a$, $b$ и $c$ являются целыми числами и $c \ne 0$, то:
$\frac{a}{c}>\frac{b}{c}$, если $a>b$
Пример: $\frac{4}{5} > \frac{3}{5} > \frac{2}{5}$
Свойство III: Если у двух дробей числители равны, то больше та дробь, у которой знаменатель меньше.
Если $a$, $b$ и $c$ являются целыми числами, а $b$ и $c$ не равны нулю, то:
$\frac{a}{b}>\frac{a}{c}$, если $b
Пример: $\frac{3}{4} > \frac{3}{5} > \frac{3}{20}$
Тест фракций
1. Теннисист выиграл 6$ из первых 12$ сетов. Затем он выиграл все оставшиеся сеты по $6$. Какую часть сетов выиграл игрок?
Какую часть сетов выиграл игрок?
$\frac{1}{3}$
$\фракция{2}{3}$
$\фракция{1}{2}$
2. У мальчика было $\$36$. После пары часов покупок у него осталось $\$8$.
Какую часть своих денег он потратил?
$\фрак{2}{9}$
$\фракция{2}{7}$
$\фракция{7}{9}$
3. В классе с 30$ учениками было 12$ девочек. Затем к классу присоединились $6$ мальчиков.
Какую часть класса составляют девочки?
$\фракция{1}{2}$
$\фракция{3}{5}$
$\фракция{1}{3}$
4. Если дробь $\frac{n}{40}$ находится между $\frac{1}{5}$ и $\frac{1}{4}$, то
н это
$8$
$9$
$10$
5. $\frac{6}{24}$ равно:
$\frac{1}{4}$
$\фракция{3}{4}$
$\фракция{6}{12}$
6. Какая из дробей вдвое больше $\frac{3}{8}$?
$\фрак{6}{16}$
$\фракция{3}{16}$
$\frac{3}{4}$
7. * Какая из следующих дробей наибольшая: $\frac{12}{13}, \frac{13}{14}, \frac{14} {15}$ или $\frac{15}{16}$?
$\фрак{15}{16}$
$\фракция{12}{13}$
$\frac{14}{15}$
8. В какой из следующих последовательностей дроби расположены в порядке убывания?
1: $\frac{7}{11}, \frac{5}{8}, \frac{3}{5}, \frac{2}{3}$;
2: $\frac{4}{3}, \frac{7}{11}, \frac{5}{8}, \frac{3}{5}$;
3: $\frac{21}{11}, \frac{2}{3}, \frac{3}{5}, \frac{5}{8}$
$2$ $3$ $1$
9.