Положительные и отрицательные числа
Определение положительных и отрицательных чисел
Для определения положительных и отрицательных чисел воспользуемся координатной прямой, которая располагается горизонтально и направлена слева направо.
Замечание 1
Началу отсчета на координатной прямой соответствует число нуль, которое не относится ни к положительным, ни к отрицательным числам.
Определение 1
Числа, соответствующие точкам координатной прямой, которые лежат правее от начала отсчета, называются положительными.
Определение 2
Числа, соответствующие точкам координатной прямой, которые лежат левее от начала отсчета, называются отрицательными.
Из данных определений вытекает, что множество всех отрицательных чисел противоположно множеству всех положительных чисел.
Отрицательные числа всегда записывают со знаком «–» (минус).
Пример 1
Примеры положительных чисел:
- Натуральные числа $3$, $13$, $333$, $578$, $10456$ и т.
д. - Иррациональные числа $π$, $е$, $\sqrt[3]{2}$, бесконечная непериодическая десятичная дробь $103,1012341981…$
д.Замечание 2
Все натуральные числа являются положительными.
Пример 2
Примеры отрицательных чисел:
- Рациональные числа $-\frac{9}{17}$, $-4 \frac{11}{23}$, $–5,25$, $–4,(79)$.
- Иррациональные числа$ -\sqrt[3]{2}$, бесконечная непериодическая десятичная дробь $–103,1012341981…$
Для упрощения записи перед положительными числами часто не записывают знак «+» (плюс), а перед отрицательными знак «–» записывают всегда. В подобных случаях необходимо помнить, что запись «$17,4$» равносильна записи «$+17,4$», запись «$\sqrt{5}$» равносильна записи «$+\sqrt{5}$» и т.д.
Таким образом, можно использовать следующее определение положительных и отрицательных чисел:
Определение 3
Числа, записанные со знаком «+», называются положительными
, а со знаком «–» – отрицательными.
Используется определение положительных и отрицательных чисел, которое основано на сравнении чисел:
Определение 4
Положительными числами являются числа больше нуля, а отрицательными числами – числа меньше нуля.
Замечание 3
Таким образом, число нуль разделяет положительные и отрицательные числа.
Правила чтения положительных и отрицательных чисел
Замечание 4
При чтении числа со знаком впереди него сначала читается его знак, а затем само число.
Пример 3
Например, «$+17$» читают «плюс семнадцать»,
«$-3 \frac{4}{11}$» читают «минус три целых четыре одиннадцатых».
Замечание 5
Стоит отметить, что названия знаков «плюс» и «минус» не склоняются, в то время как числа могут склоняться.
Пример 4
Например, «$x=-18$» можно читать как «икс равен минус восемнадцать», так и «икс равен минус восемнадцати».
Интерпретация положительных и отрицательных чисел
Положительные числа используются для обозначения увеличения какой-нибудь величины, прихода, прибавки, возрастание значения и т.
д.
Отрицательные числа применяют для противоположных понятий – для обозначения уменьшения какой-нибудь величины, расхода, недостатка, долга, снижения значения и т.д.
Рассмотрим примеры.
Читатель взял в библиотеке $4$ книги. Положительное значение числа $4$ показывает число книг, которые есть у читателя. Если ему нужно сдать $2$ книги в библиотеку, можно использовать отрицательное значение $–2$, которое будет указывать на уменьшение числа книг у читателя.
Положительные и отрицательные числа часто используют для описания значений различных величин в измерительных приборах. Например, термометр для измерения температуры имеет шкалу, на которой отмечены положительные и отрицательные значения.
Похолодание на улице на $3$ градуса, т.е. снижение температуры, можно обозначить значением $–3$, а повышение температуры на $5$ градусов – значением $+5$.
Принято отрицательные числа изображать синим цветом, что символизирует холод, низкую температуру, а положительные числа – красным цветом, что символизирует тепло, высокую температуру.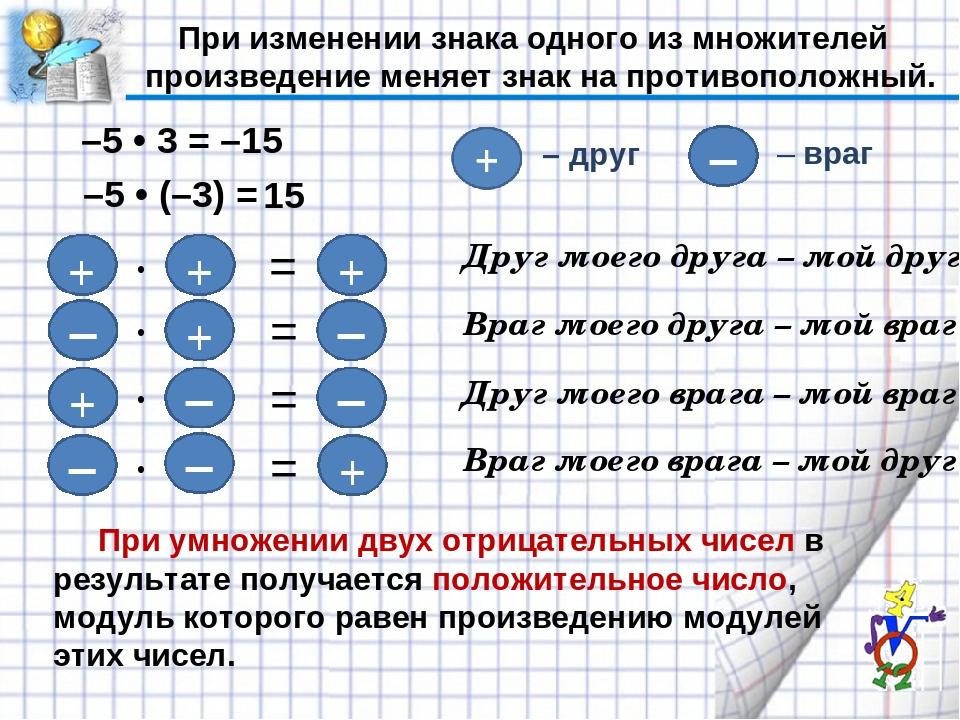
Положительные и отрицательные числа
Натуральные числа, противоположные им числа и число 0 называются целыми числами. Положительные числа (целые и дробные), отрицательные числа (целые и дробные) и число 0 составляют группу рациональных чисел.
Рациональные числа обозначаются большой латинской буквой R. Число 0 относится к целым рациональным числам. С натуральными и дробными положительными числами мы ознакомились ранее. Рассмотрим подробнее отрицательные числа в составе рациональных чисел.
Отрицательное число с древних времен ассоциируется со словом «долг», тогда как положительное число можно ассоциировать со словами «наличие» или «доход». Значит, положительные целые и дробные числа при вычислениях — это то, что мы имеем, а отрицательные целые и дробные числа — это то, что составляет долг.
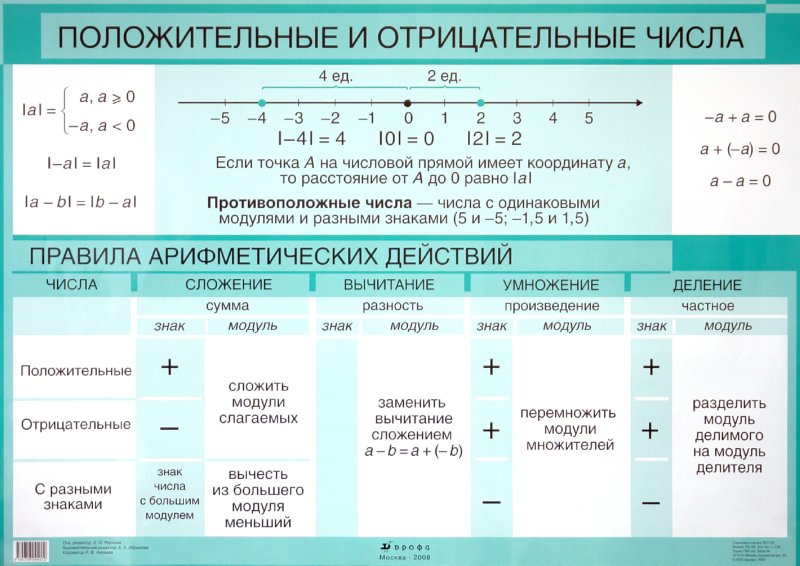
Отрицательные целые и дробные числа записываются со знаком «минус» («-») перед числом. Численная величина отрицательного числа — это его модуль. Соответственно, модуль числа — это значение числа (и положительного, и отрицательного) со знаком плюс. Модуль числа записывается так: |2|; |-2|.
Каждому рациональному числу на числовой оси соответствует единственная точка. Рассмотрим числовую ось (рисунок внизу), обозначим на ней точку О.
Точке О поставим в соответствие число 0. Число 0 служит границей между положительными и отрицательными числами: справа от 0 — положительные числа, величина которых изменяется от 0 до плюс бесконечности, а слева от 0 — отрицательные числа, величина которых тоже изменяется от 0 до минус бесконечности.
Правило. Всякое число, стоящее на числовой оси правее, больше числа, стоящего левее.
Исходя из этого правила, положительные числа растут слева направо, а отрицательные убывают справа налево (при этом модуль отрицательного числа увеличивается).
-
Всякое положительное число и 0 больше любого отрицательного числа.
-
Всякое положительное число больше 0. Всякое отрицательное число меньше 0.
-
Всякое отрицательное число меньше положительного числа. Положительное или отрицательное число, стоящее правее, больше положительного или отрицательного числа, стоящего левее на числовой оси.
Определение. Числа, которые отличаются друг от друга только знаком, называются
Например, числа 2 и -2, 6 и -6. -10 и 10. Противоположные числа расположены на числовой оси в противоположных направлениях от точки О, но на одинаковом расстоянии от нее.
Дробные числа, представляющие собой в записи обыкновенную или десятичную дробь, подчиняются тем же правилам на числовой оси, что и целые числа.
Из двух дробей больше та, которая стоит на числовой оси правее; отрицательные дроби меньше положительных дробей; всякая положительная дробь больше 0; всякая отрицательная дробь меньше 0.
Например: Противоположные дроби: 0,5 и -0,5;
Запись опубликована в рубрике Математика с метками числа. Добавьте в закладки постоянную ссылку.
Вычитание положительных и отрицательных чисел
Вычитание
положительных и отрицательных чисел также может быть сложным, потому что есть несколько правил
, которые нужно запомнить и соблюдать.
.
Пример 1: Не позволяйте всем этим разговорам о положительных и отрицательных числах сбить вас с пути
— если вы видите положительное число минус положительное число, вычтите
вроде нормально! Например, если вы видите 5-3, вычтите как обычно! 5 – 3 = 2.
Правило 2: Вычитание положительного числа из отрицательного — начните с отрицательного числа
и считайте в обратном порядке дополнительную сумму, которую вы вычитаете.
Пример 2: Допустим, у нас есть задача -5 – 3. Это будет читаться как «минус
пять минус три». Это можно представить на числовой прямой, что означает, что мы идем
, чтобы начать с отрицательного числа (-5) и продолжаем отсчитывать -3, достигая
Большая красная точка над -5 показывает, что именно с этого мы начинаем нашу проблему.
Красная стрелка показывает, что мы считали в обратном порядке (вычитали) 3. Красный кружок вокруг
-8 показывает, что это наш ответ.
Таким образом, -5 – 3 = -8.
Вы также можете думать об этих задачах как о задачах на сложение — вы складываете числа
вместе (5 + 3 = 8), а затем, поскольку оба числа имеют знак минус перед
их, вы бы добавили знак минус перед своим ответом, например: -8.
Если этот
имеет больше смысла, вы можете решить эти задачи так, но только задачи, которые
записываются так: -5 – 3. Если есть какие-либо другие знаки (сложение, вычитание,
и т. д.), вам нужно следовать правилу для такого типа проблемы.
Правило 3: Вычитание отрицательного числа из отрицательного числа — когда вы видите
знак вычитания (минус), за которым следует знак минуса, превратите два знака в
плюс. Таким образом, вместо вычитания минуса вы добавляете плюс.
Итак, – -5 становится +5, и продолжайте сложение обычным образом.
Пример 3: Допустим, у нас была проблема -6 – -3. Это будет читаться как «минус
шесть минус минус три». Это можно представить на числовой прямой, что означает
, с которого мы собираемся начать, изменив -3 на +3, например:
.
Теперь наша задача имеет вид -6 + 3, и мы можем решить ее как обычную задачу на сложение 9.0003 числовая строка, например:
Большая красная точка над -6 показывает, что именно здесь мы начинаем нашу проблему.
Синяя стрелка показывает, что мы посчитали вперед (добавлено) 3. Синий кружок вокруг
Правило 4: Вычитание отрицательного числа из положительного — когда вы видите
знак вычитания (минус), за которым следует отрицательный знак, превратите два знака в
знак плюса. Таким образом, вместо вычитания минуса вы добавляете плюс,
, поэтому у вас есть простая проблема сложения.
Пример 4: Допустим, у нас была задача 5 – (-3). Это будет читаться как «пять
минус минус три». Это будет работать так же, как и в предыдущем примере, поэтому
— (-3) изменится на +3; следовательно, ваша новая задача будет выглядеть как 5 + 3, что
является простой задачей на сложение, в результате чего получится 8.
Проблемы
| 1. 4 – 2 | 2. -8 – 5 | 3. -4 – (-7) | 4. 6 – (-3) | 5. -9 – 1 |
| 6. -10 – (-8) | 7. 9 – 4 | 8. 2 – (-7) | 9. -7 – 8 | 10. -5 – (-6) |
Решения
| 1. 2 | 2. -13 | 3. 3 | 4. 9 | 5. -10 |
| 6. -2 | 7. 5 | 8. 9 | 9. -15 | 10. 1 |
S ау каждое целое число вслух или про себя. «Посмотрите, у меня есть четыре номера, я нужно сказать каждый из них про себя. первое число минус три и шесть десятых, следующий две и восемь десятых, третий отрицательный одна и две десятых, а последний — одна и пять десятых. P мазь каждому целому числу и найдите отрицательный знаки.
I идентифицировать является ли каждое целое число положительным или отрицательным.
E оценка значение каждого целого числа с использованием правил значения. «Посмотрим. Я нарисую числовую линию, чтобы помочь мне оценить. Я поставлю ноль в посередине, и, как и в моей таблице t, поставьте + справа и — справа слева от нуля.» «Правило №1 гласит, что положительные целые числа всегда больше. У меня есть два положительных целых числа, 2,8 и 1,5, поэтому я поместите их в числовую строку первыми. Я знаю, что эти двое будут больше чем два отрицательных числа, -3,6 и -1,2». Правило №2 гласит, что при положительном числа, целое число дальше от нуля имеет большую ценность. Для двух положительных целых чисел если я проведу линию от нуля до каждого из них, 2,8 будет дальше всего от нуль. С выбрать целое число наибольшего значения. «Я знаю, что положительные числа больше, и что 2,8 — самое большое из положительных чисел. я собираюсь поставить #1 под 2.8 и #2 менее 1,5. Затем я посмотрю на свои отрицательные числа. Использование правила # 3, я знаю, что -1,2 больше, чем -3,6, потому что -1,2 ближе к ноль на числовой прямой. |
Остальные два числа я напишу
в столбце +.»
Используя это правило, 2,8 является наибольшим из двух положительных чисел.
Для отрицательных чисел это противоположно положительным числам. Правило
# 3 говорит, что с отрицательными числами целое число ближайший до нуля имеет большее значение. Для двух отрицательных целых чисел, если
Я провожу линию от нуля к каждому из них, -1,2 ближе всего к нулю. С использованием
по этому правилу -1,2 больше из двух отрицательных чисел.»