Законы сложения векторов. Правило параллелограмма / Векторы / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Законы сложения векторов. Правило параллелограмма
Теорема
Для любых векторов , и справедливы равенства: 10. + = + (переместительный закон). 20. ( + ) + = + ( + ) (сочетательный закон). |
Доказательство
Дано: , и .
Доказать: 10. + = + ; 20. ( + ) + = + ( + ).
Доказательство:
10. Пусть векторы и коллинеарны.
От произвольной точки А отложим векторы = и = , т.е. векторы и будут лежать на одной прямой и на той же прямой от точки А отложим векторы = и = .
+ = , + = , тогда , , при этом , так как модуль вектора — это длина отрезка, следовательно, . Поэтому точки С и С1 совпадают, значит, = (по определению равных векторов), значит, + = + .
Пусть теперь векторы и не коллинеарны.
От произвольной точки А отложим векторы = и = и на этих векторах построим параллелограмм АВСD.
Противоположные стороны ВС и АD параллелограмма равны, при этом векторы и сонаправлены, следовательно, = = (по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы и сонаправлены, следовательно, = = .
По правилу треугольника = + = + . Аналогично = + = + , поэтому + = + .
20. От произвольной точки А отложим вектор = , от точки В — вектор = , а от точки С — вектор = .
Применяя правило треугольника, получим:
( + ) + = ( + ) + = + = ,
+ ( + ) = + ( + ) = + = .
Следовательно, ( + ) + = + ( + ).
Теорема доказана.
Правило параллелограмма
| Чтобы сложить неколлинеарные векторы и , нужно отложить от какой-нибудь точки А векторы = и = и построить параллелограмм АВСD |
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 764, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 770, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 784, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 785, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 906, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 908, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 909, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1067, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
как производится в пространстве, законы, формулы с примерами
- Основные законы сложения векторов в геометрии
- Как происходит сложение по правилу треугольника
- Сложение по правилу параллелограмма
- Как и когда применяется правило многоугольника
- Задачи с примерами решения
Содержание
- Основные законы сложения векторов в геометрии
- Как происходит сложение по правилу треугольника
- Сложение по правилу параллелограмма
- Как и когда применяется правило многоугольника
- Задачи с примерами решения
Основные законы сложения векторов в геометрии
Суммой двух векторов \(\vec a+\vec b\) называют третий вектор \(\vec c\), который проведен из начала \(\vec a\) и упирается в конец \(\vec b\) при условии, что конец \(\vec a\) совпадает с началом \(\vec b\).
На плоскости найти сумму векторов можно, воспользовавшись формулой:
\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y\right\}\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если ситуация переходит в пространственное измерение, то достаточно всего лишь а тот же пример добавить новую координату:
\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y;a_z+b_z\right\}\)
Основные законы:
-
Переместительный закон (или коммутативный). Суть его свойства заключается в формуле: \(\vec a+\vec b=\vec b+\vec a\).
-
Сочетательный закон. Выглядит, как \(\left(\vec a+\vec b\right)+\vec c=\vec a+\left(\vec b+\vec c\right)\).
Примечание
Помимо покоординатного сложения направленных отрезков, существуют геометрические нормы, которые позволяют узнать их сумму.
Как происходит сложение по правилу треугольника
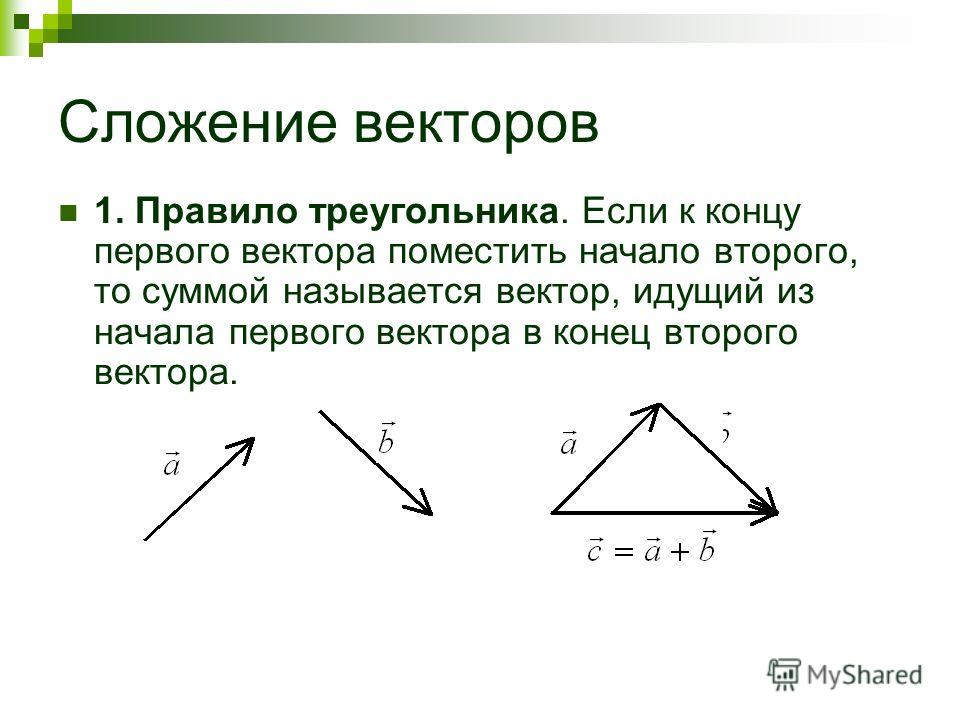
Чтобы узнать сумму векторов x и y, необходимо из произвольной точки отложить первый из них, а затем из его конца уже отложить второй. Следующий шаг — построить направленный отрезок, который соединит начало \vec x с концом \vec y. Образовавшаяся сторона треугольника и будет результатом сложения двух векторов. Теорема считается доказанной.
Сложение по правилу параллелограмма
Найти сумму векторов можно без построения треугольника. Для этого от начала первого вектора нужно отложить второй вектор. Дополним получившийся чертеж до параллелограмма. Две его стороны у нас уже имеются. Выстроить оставшиеся поможет способ параллельного переноса. Диагональ готовой фигуры, которая исходит из начальной точки векторов, считается их суммой. Теорема доказана.
Как и когда применяется правило многоугольника
Данный способ потребуется для того, чтобы сложить более двух векторов.
Принцип действий в данном случае похож на последовательность шагов, как в случае с треугольником. Из произвольной точки провести первый вектор. Из его конца — второй, из второго — третий и так далее. Затем окончание последнего вектора соединить с началом первого — это будет результат сложения всех векторов. Доказательство теоремы выполнено.
Задачи с примерами решения
Задача 1
Дано
\(\vec a=\left\{2; 3\right\}, \vec b=\left\{5; 7\right\}\).
Найти \(\vec a+\vec b\).
Решение
\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y\right\}=\left\{2+5; 3+7\right\}=\left\{7; 10\right\}\)
Задача 2
С помощью правила треугольника постройте сумму заданных векторов a и b.
Решение 1
Параллельным переносом совмещаем конец вектора a с началом b. Далее соединяем исходную точку вектора a с конечной вектора b. Выходит \(\vec c\). Длина отрезка, изображающего этот направленный отрезок, и будет общим значением \(\vec a\) и \(\vec b\).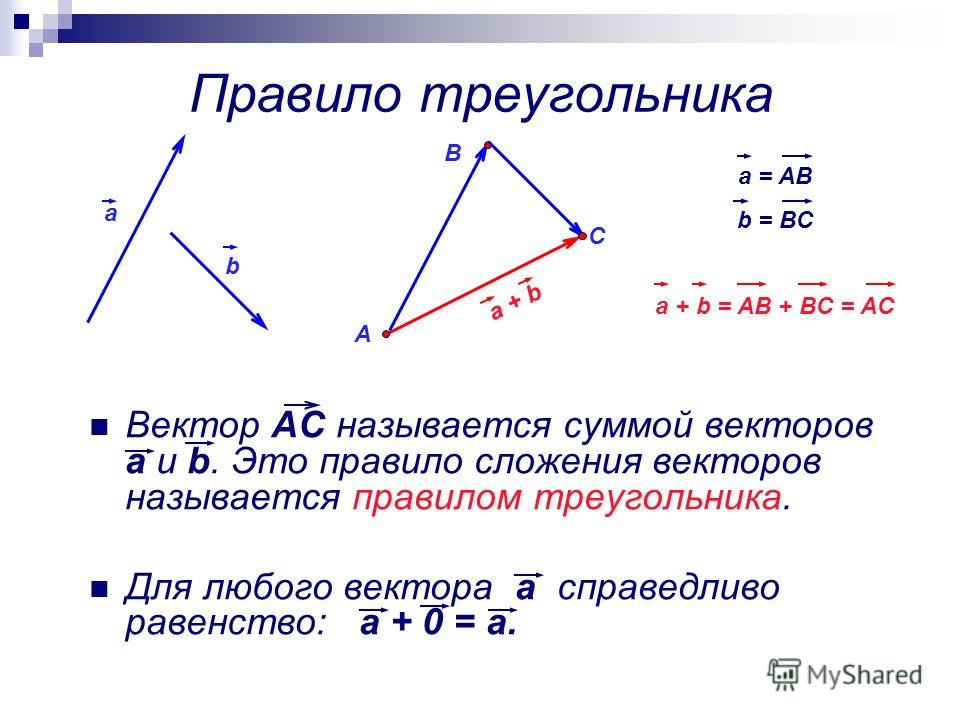
Решение 2
С помощью параллельного переноса устанавливаем конец \(\vec b\) таким образом, чтобы он совпадал с началом \(\vec a\). Затем конечную точку первого совмещаем с началом второго. Получилось \(\vec c=\vec b+\vec a\).
Одна цель достигнута разными способами, что наглядно демонстрирует действие переместительного закона.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши
Поиск по содержимому
СУММА ДВУХ ВЕКТОРОВ. ЗАКОН СЛОЖЕНИЯ ВЕКТОРОВ. ПРАВИЛО ПАРАЛЛЕЛОГРАММА презентация, доклад
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему СУММА ДВУХ ВЕКТОРОВ.
ЗАКОН СЛОЖЕНИЯ ВЕКТОРОВ. ПРАВИЛО ПАРАЛЛЕЛОГРАММА, предмет презентации: Разное. Этот материал содержит 9 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
СЛОЖЕНИЕ ДВУХ ВЕКТОРОВ
повторим
A
B
C
D
O
СЛОЖЕНИЕ ДВУХ ВЕКТОРОВ
повторим
A
B
C
D
O
Равны ли векторы?
СЛОЖЕНИЕ ДВУХ ВЕКТОРОВ
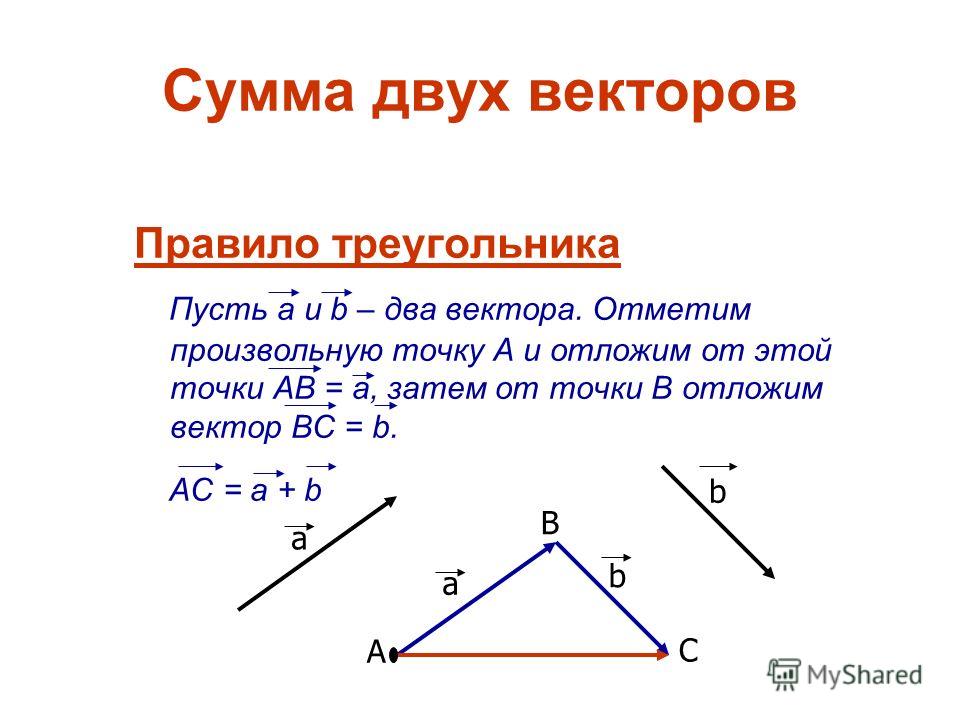
Правило треугольника
Чтобы найти сумму двух ве́кторов нужно:
А
1) Отметить произвольную точку А;
В
C
Нажать для просмотра материала
СЛОЖЕНИЕ ДВУХ ВЕКТОРОВ
Что произойдет если найти сумму векторов от другой точки?
А
В
C
А1
В1
C1
Нажать для просмотра материала
СЛОЖЕНИЕ ДВУХ ВЕКТОРОВ
Что произойдет если сложить нулевой вектор с ненулевым?
N
Нажать для просмотра материала
Законы сложения векторов
Нажать
для
просмотра
материала
Проверим:
А
В
C
F
Р
W
Законы сложения векторов
Нажать
для
просмотра
материала
Проверим:
А
В
C
F
R
Q
Законы сложения векторов
Правило параллелограмма
Нажать
для
просмотра
материала
Проверим:
А
В
C
F
Р
W
Законы сложения векторов
Правило параллелограмма
Нажать
для
просмотра
материала
Проверим:
А
В
C
D
F
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте.
Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
классическая механика — как пришли к правилу сложения векторов?
Спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 111 раз
$\begingroup$
Я учусь по математике на уровне A2 igsce и впервые сдаю механику по математике на этом занятии.
Хотел спросить о том, как они пришли к правилу сложения векторов.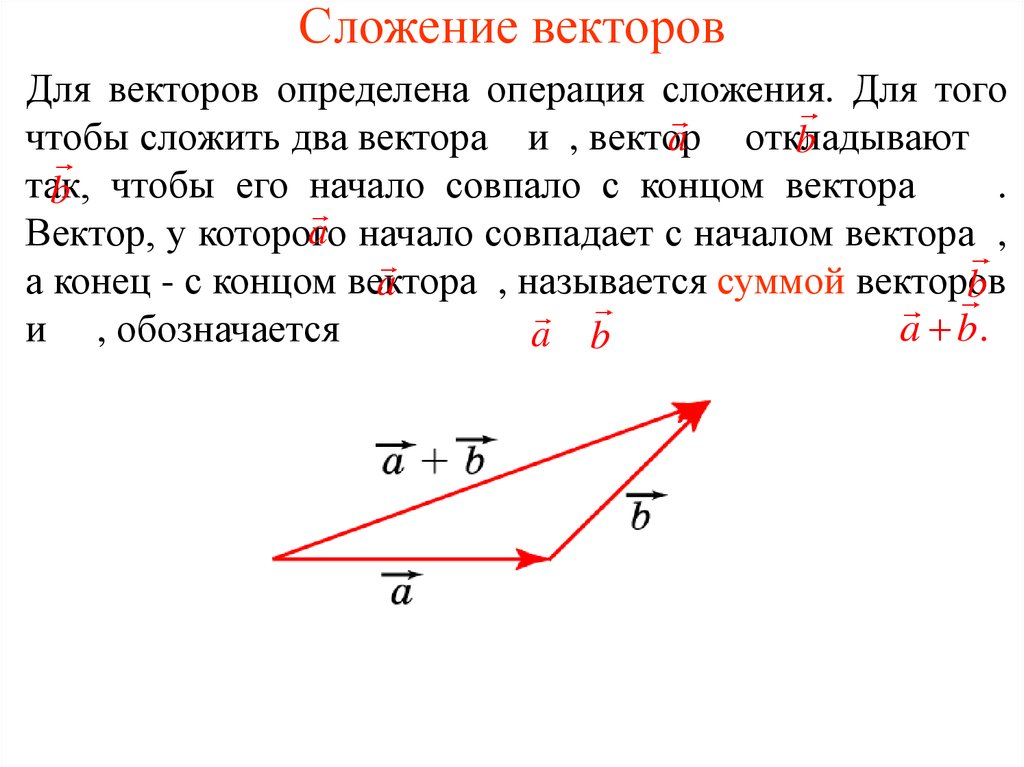
Откуда они знали, что если мы сложим X и Y двух векторов, они получат третий вектор, который имеет точно такое же направление и величину силы, которая могла бы заменить эти два вектора или силы.
Я убежден, что это правильно, и могу почувствовать или увидеть направление, в котором точка ускорится, если к ней приложить две определенные силы. И может чувствовать, как равнодействующая сила стремится приблизиться к большей силе и как, если две равные силы приложены под одним и тем же углом, результирующая сила окажется точно между ними.
Так что я уверен, что тот, кто изобрел векторы, тоже имел те же чувства и видения, но как он пришел к этому простому методу, чтобы получить такие увлекательные и точные результаты, ему удалось не только получить направление, но и величину результирующей слишком!
- векторы
- классическая механика
$\endgroup$
5
$\begingroup$
Векторов в реальности не существует, это всего лишь математическая модель, описывающая некоторые аспекты реальности.
Физика — это не математика, и не все утверждения можно вывести просто логически (даже если этот факт кажется верным и в математике в определенном смысле). Поэтому я думаю, что было проведено много экспериментов, чтобы понять природу сил и то, как они «суммируются» друг с другом.
Вы, кажется, привязаны к чрезвычайно линейной модели истории математики и физики: нет «кто изобрел векторы». Человеческий разум не является формальной системой, и мысль о том, что математическая и физическая история следуют прямолинейному пути современной книги, является чистой иллюзией.
$\endgroup$
$\begingroup$
Я думаю, важно понимать, что реальность особенная . В нем есть какая-то структура , можем ли мы понять, что это такое или нет. И даже есть кардинально разные хорошие приближения в разных масштабах. В человеческом масштабе космические объекты подчиняются евклидовой геометрии.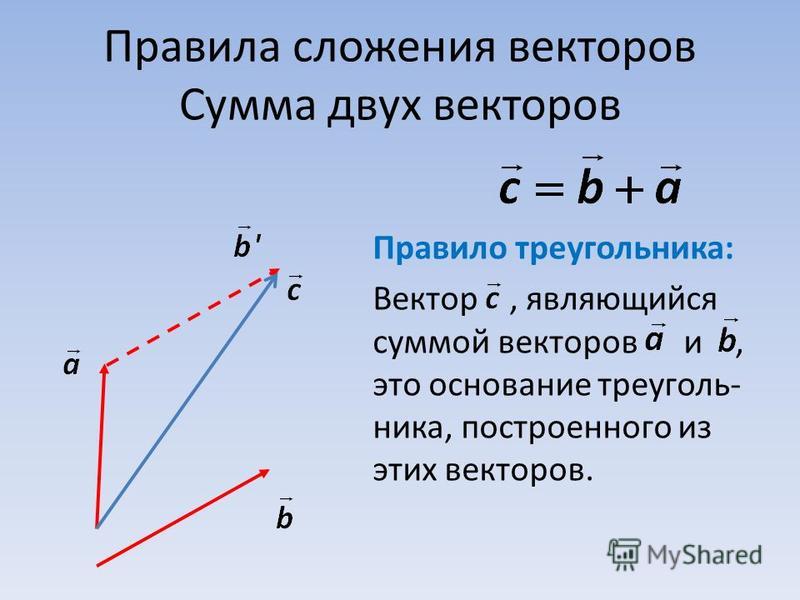
3$, и наблюдается, что сложение двух сил индуцирует сумму соответствующих ускорений, и, следовательно, две силы, приложенные к одной и той же массе, вызывают точно такое же ускорение, как векторная сумма этих сил, приложенных к этой массе. Потратьте некоторое время, чтобы подумать об этом; это действительно не просто вопрос открытия, но есть некоторое основное математическое ограничение, учитывая наблюдаемую связь между силами и положениями через ускорение.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Добавление векторов | Суперпроф
В этой статье мы обсудим, как складывать и вычитать векторы. Но прежде чем перейти к обсуждению сложения и вычитания векторов, сначала давайте определим векторы.
Вектор относится к величине, которая описывается величиной, а также направлением. Он изображен алфавитом со стрелкой вправо вверху. Например, и т. д. используются для представления векторов.
Другими словами, мы можем сказать, что векторы относятся к геометрическим представлениям величины и направления. Величина и направление изображаются прямыми стрелками, которые начинаются с одной точки на оси координат и заканчиваются в другой точке. Величина векторов на самом деле является их длиной. Эта длина представляет некоторое значение, так что вектор сопоставим с другим вектором. Стрелки векторов показывают, что они имеют направление. Это основное различие между скаляром и вектором, поскольку скаляры — это величины без направления.
Ключевые моменты, которые следует помнить для векторов
Некоторые из ключевых моментов, которые вы должны помнить для векторов:
- Двумя компонентами векторов являются величина и направление.
- Примеры векторов в реальной жизни включают ускорение, расстояние, силу и скорость, потому что эти термины описываются как величиной, так и направлением.
- Мы определяем векторы не только по их величине, но и по их ориентации, соответствующей набору координат.
- Когда мы пытаемся анализировать векторы, мы часто разбиваем их на разные части или компоненты. Для двумерных векторов эти части являются горизонтальными и вертикальными. С другой стороны, для трехмерных векторов часть величины одинакова, однако мы изображаем часть направления в терминах x, y и z.
Лучшие репетиторы по математике
Поехали
Сложение двух векторов
Для сложения двух векторов и , вы должны соединить хвост одного вектора с головой другого вектора, как показано на рисунке ниже .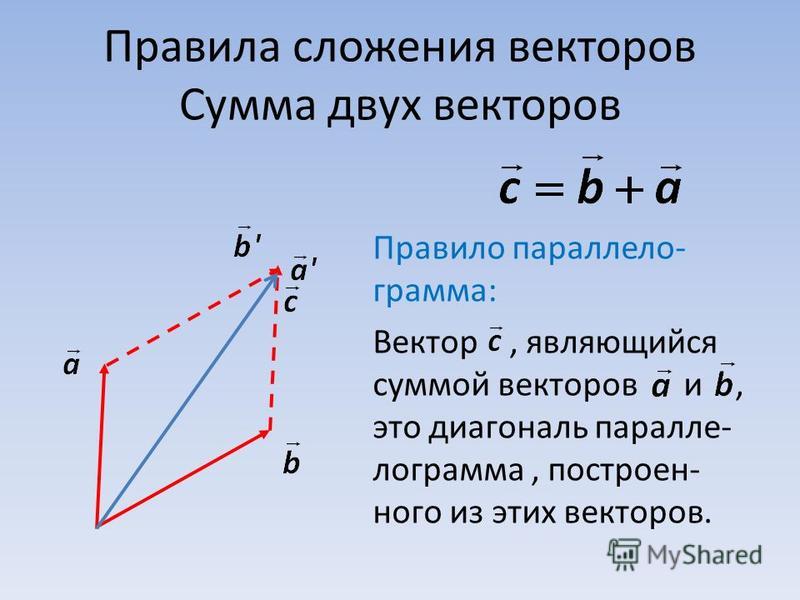
Правило параллелограмма
Вы также можете использовать правило параллелограмма для сложения векторов. Для этого нарисуйте векторы так, чтобы их хвосты (начальные точки) совпадали друг с другом. После этого следует начертить линии, чтобы получился параллелограмм. Диагональ, идущая от начальной точки к противоположной вершине параллелограмма, является результатом этого сложения.
Это правило показано на рисунке ниже.
Видно, что хвосты векторов и совпадают друг с другом. Затем из головок обоих векторов мы нарисовали линии, чтобы получить параллелограмм. В конце мы нарисовали диагональ от начальной точки до противоположной вершины, которая изображена зеленой линией. Эта диагональ является результатом сложения и математически представляется как .
Если вам даны два вектора и , то как вы будете складывать эти векторы?
Ну, дополнение простое.
Все, что вам нужно сделать, это сложить компоненты векторов следующим образом:
Свойства сложения векторов
Некоторые свойства сложения векторов приведены ниже:
Ассоциативное свойство
Ассоциативное свойство сложения векторов: математически обозначается как:
Коммутативность
Коммутативность сложения векторов математически представляется как:
Аддитивное свойство
Согласно аддитивному свойству сложения векторов, если к вектору добавить нулевой вектор, то результатом будет сам вектор:
Аддитивное обратное или противоположное свойство векторы говорят, что:
Вычитание векторов
Теперь, когда вы знаете, как складывать два вектора, вам может быть интересно, как вычесть два вектора, потому что сложение и вычитание векторов тесно связаны. Меняется только знак между компонентами. Изображение вычитания через треугольник показано на рисунке ниже:
Чтобы вычесть два вектора и , нужно сложить вектор с противоположностью вектора
Математически это представляется как:
В следующем разделе мы решим некоторые примеры, связанные со сложением векторов.
Найдите репетитора по математике рядом со мной на Superprof.
Пример 1
Если и то найти и .
Решение
=
Теперь узнаем . Для этого перепишем как
Если , то
Пример 2
Если и то найти и .
Решение
=
Теперь узнаем . Для этого перепишем как
Если , то
Пример 3
Если и то найдем и .
Решение
=
Теперь узнаем . Для этого перепишем как
Если , то
Пример 4
Если и то найдем и .
Решение
=
Сейчас узнаем .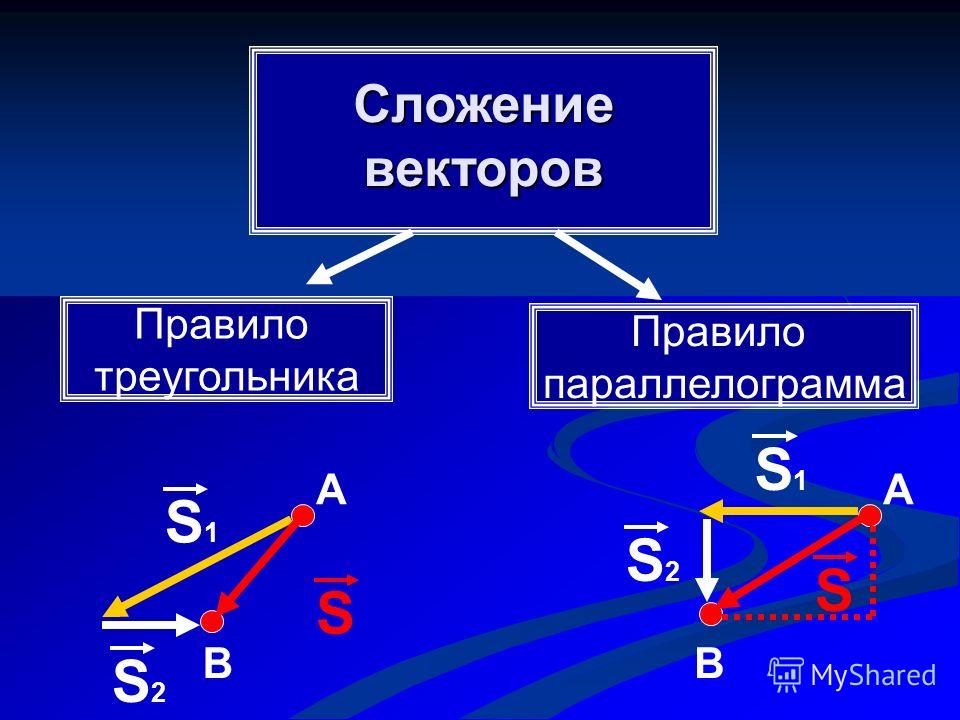
Для этого перепишем как
Если , то
Пример 5
Если и то найдем и .
Решение
=
Теперь узнаем . Для этого мы перепишем как
Если , то
Сложение, вычитание и векторы – Блог учителя математики
В начале начального курса алгебры студентов учат складывать и вычитать числа со знаком. Сложению чисел со знаком обучают, давая учащимся набор правил, которым они могут следовать, чтобы получить правильный ответ. Некоторые диаграммы с числовыми линиями добавлены для иллюстрации сложения чисел со знаком. Вычитанию чисел со знаком обычно обучают по правилу «сложить противоположное». Это правило звучит правдоподобно, однако оно не дает учащимся никакого представления о том, что представляет собой вычитание с геометрической точки зрения. Вы можете спросить: «Разве недостаточно научиться применять набор правил, чтобы получить ответ?» На мой взгляд, это не так.
Как я уже неоднократно говорил в предыдущих постах, по возможности учащиеся должны понимать математическую концепцию как с алгебраической, так и с геометрической точек зрения. Основная цель этого поста — показать, как я использовал векторные диаграммы для иллюстрации сложения и вычитания действительных чисел и двумерных векторов. Я также буду обсуждать геометрические интерпретации выражений и отношений, таких как (a + b)/2, |x – 4| < 5 и |x – 5| > 7.
Исходя из моего собственного опыта, большинство детей быстро учатся применять правила сложения и вычитания положительных и отрицательных чисел. При упрощении полиномиальных выражений, рациональных полиномиальных выражений и полиномиальном длинном делении большинство ошибок возникает на этапе вычитания отрицательного числа. Студенты, как правило, довольно хорошо умеют складывать числа со знаком, но немного слабы, когда дело доходит до вычитания чисел со знаком. Вот почему моя любимая школьная учительница математики Вивиан Джонс говорила: «При вычитании числа просто измените знак числа и прибавьте».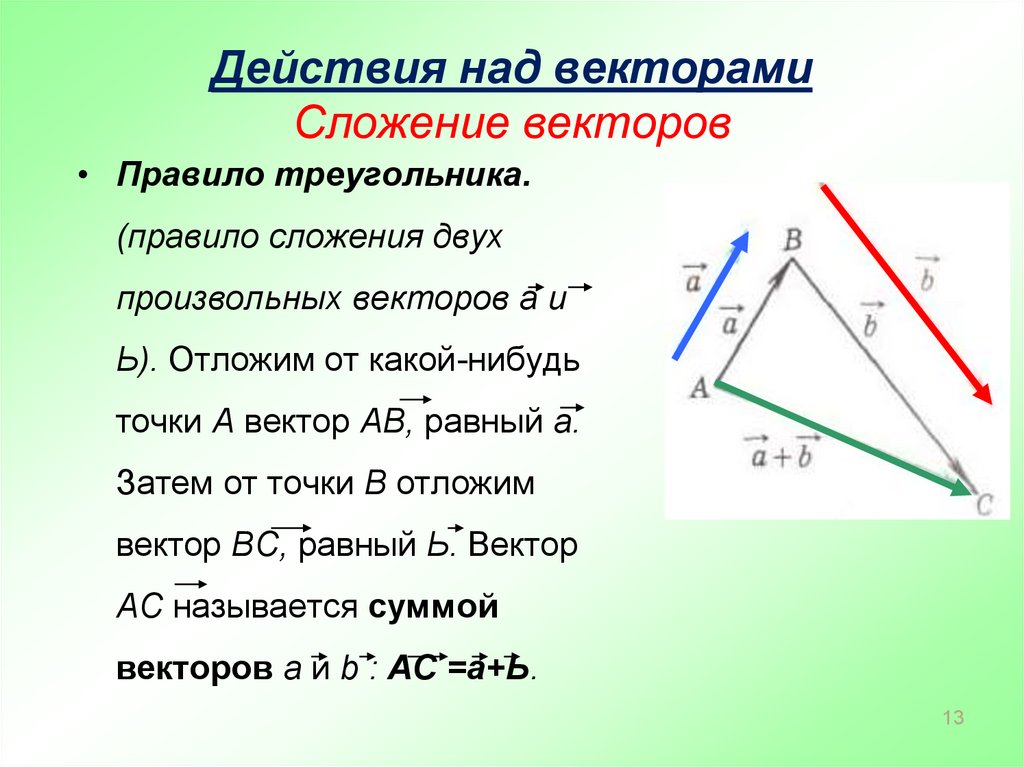
Это то, что я говорю своим студентам, изучающим алгебру в колледже, когда они выполняют полиномиальное деление в длину. Согласно учебнику по развивающей алгебре, правила сложения и вычитания чисел со знаком следующие:
Сложение двух действительных чисел a и b
- Если a и b имеют одинаковый знак, сложите их абсолютные значения. Используйте общий знак a и b в качестве знака ответа.
- Если a и b имеют разные знаки, вычтите их абсолютные значения. Знак ответа — это знак числа, имеющего наибольшее абсолютное значение.
Вычитание двух действительных чисел a и b
- a – b = a + (- b )
- Другими словами, a – b равно a плюс противоположное b
Векторные диаграммы, подобные приведенным ниже диаграммам A, B и C, используются для иллюстрации того, как работают правила сложения и вычитания для чисел со знаком.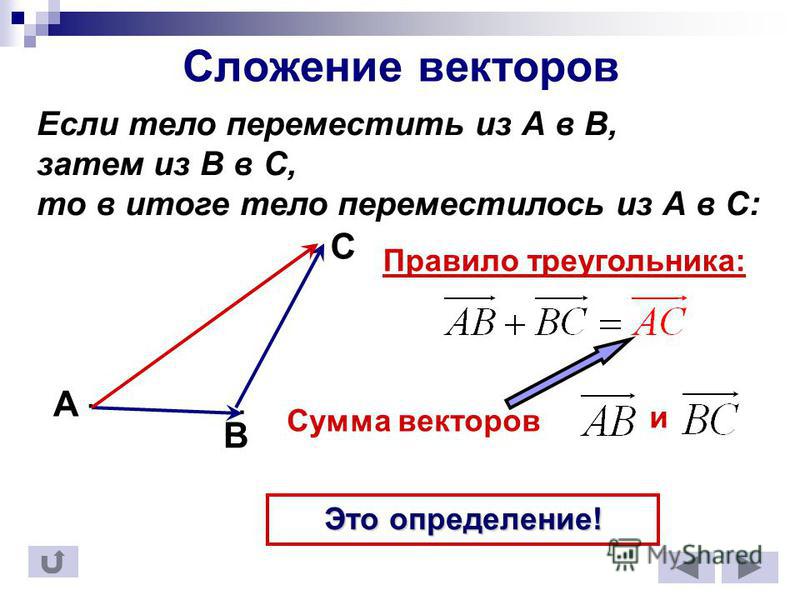
Нижняя половина диаграммы А показывает, что два минуса не обязательно дают плюс.
Диаграммы B и C иллюстрируют правило вычитания для чисел со знаком. Проблема с правилом вычитания и соответствующей векторной диаграммой заключается в том, что они не дают нам никакого представления о том, что такое вычитание с геометрической точки зрения.
Диаграммы D и E ниже иллюстрируют идею о том, что вычитание двух действительных чисел дает нам направленное расстояние между двумя действительными числами. Концепция направленного расстояния является фундаментальной для понимания вычитания с геометрической точки зрения. Для действительных чисел a и b , направленное расстояние от b до a = a – b , и направленное расстояние от a до b = b a 90. Положительное расстояние или просто расстояние от a до b = |a – b| = |б – а| . Теперь мы рассмотрим двумерные векторы, которые необходимы для понимания различных концепций математики и физики. Мы можем рассматривать двумерные векторы как отрезки, обладающие свойствами длины и направления. Любые два вектора эквивалентны тогда и только тогда, когда они имеют одинаковую длину и направление. В этом посте 2D-векторы будут обозначаться жирным шрифтом заглавными буквами, а пара вертикальных полос абсолютного значения будет обозначать длину или звездную величину вектора. На приведенном ниже графике показано, как добавляются два 2D-вектора. Все векторы, нарисованные одним цветом, равны друг другу, потому что имеют одинаковую длину и направление. Все двумерные векторы могут быть представлены парой действительных чисел вида < x, y > , где x и y равны компонентам x и y вектора. Зная компоненты вектора x-y, легко, по крайней мере для студентов, изучающих триггеры, вычислить величину и направление вектора. На приведенном ниже графике показано, как вычитаются два двумерных вектора. Как только учащийся поймет сложение и вычитание с геометрической точки зрения, решение многих математических задач станет намного проще. Задача 1: Предположим, что показатель IQ равен 9.0039 I 
Концепция расстояния связана со многими понятиями в математике, такими как величина изменения переменной, насколько значение данных отклоняется от некоторой фиксированной константы, предел погрешности и т. д. Обратите внимание, что задачи на вычитание на диаграммах D и E одинаковы. задачи на диаграммах B и C. После сравнения диаграмм B и C с диаграммами D и E становится ясно, что диаграммы D и E дают нам гораздо лучший способ понять вычитание с геометрической точки зрения.
Стрелка на одном конце сегмента указывает направление вектора. Геометрические лучи имеют бесконечную длину, поэтому двумерные векторы представляют собой , а не геометрических лучей. Попутно упомяну, что двумерные векторы — это всего лишь частный случай абстрактного математического объекта, называемого вектором. Если вы хотите расширить свой ум, пройдите курс бесконечномерных векторных пространств. Версии моего бесплатного раздаточного материала Introduction to Vectors для студентов и преподавателей можно загрузить, перейдя в раздел тригонометрии на нашей странице учебных материалов.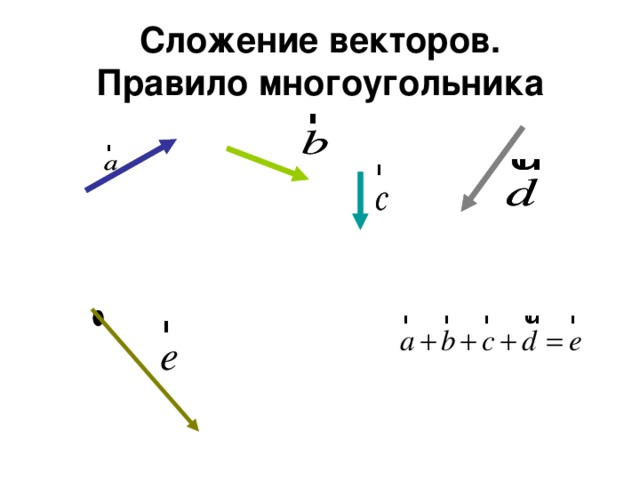
Изучая график, обратите внимание на следующее:
Вычитание вектора дает нам вектор, представляющий разность вектора между вершинами двух векторов. Вектор A – B имеет хвост на конце B и голову на конце A . Vector B – A имеет хвост на кончике A и его головка на конце B . Все векторы, нарисованные одним цветом, равны друг другу, потому что имеют одинаковую длину и направление. Изучая график, обратите внимание на следующее: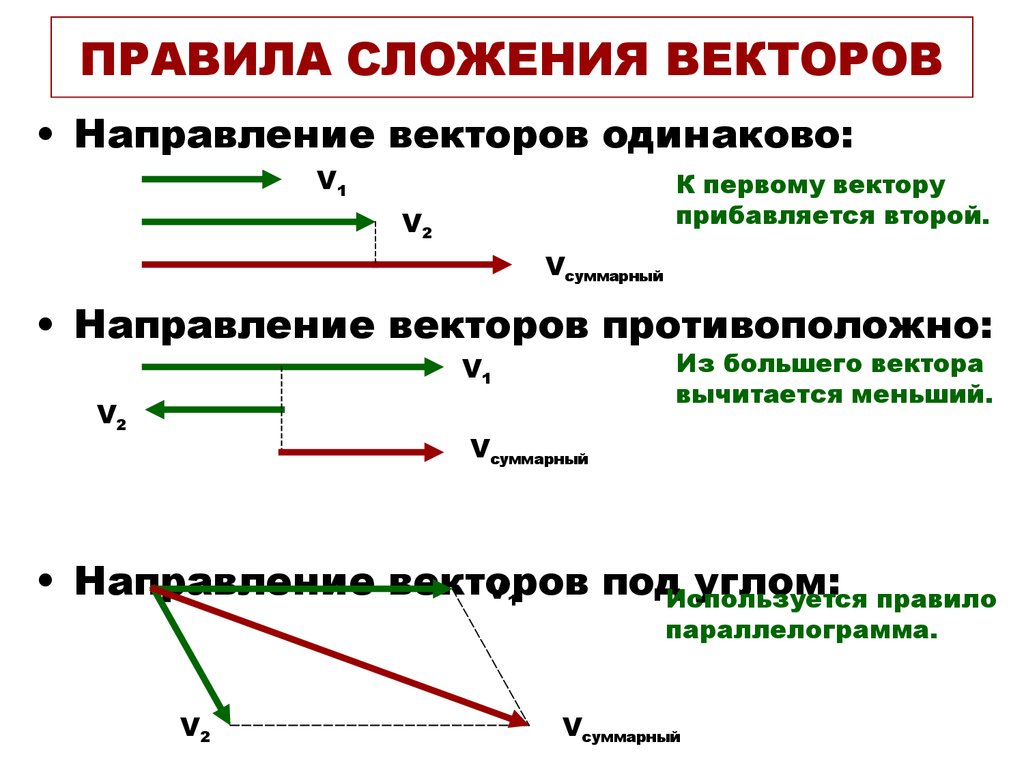
Рассмотрим три стандартные математические задачи, показанные ниже.
Решение: Выражение | I – 100| дает нам положительное расстояние переменной I от 100. Следовательно, диапазон нормальных показателей IQ описывается неравенством | I – 100| ≤10.
Проблема 2: Деталь не пройдет проверку, если ее диаметр d отклоняется от 2,5 см более чем на 0,001 см. Какой интервал на числовой прямой и неравенстве описывает область отбраковки?
Решение: Деталь не пройдет проверку, если положительное расстояние от 2,5 до d больше 0,001 см. Поэтому область отторжения можно описать неравенством | д – 2,5| > 0,001.
Конечно, мы молчаливо предполагаем, что существуют практические ограничения на значения d.
Проблема 3 : График закрытого интервала [0,84, 2,68] показан ниже. Найдите следующее:
- Длина интервала
- Координата средней точки M
- Радиус интервала
- Запишите неравенство, описывающее интервал.
Решение: (Многие из моих студентов, изучающих элементарную статистику, поначалу борются с подобными задачами обзора.)
- Длина интервала = 2,68 – 0,84 = 1,84
- Координата средней точки M = (0,84 + 2,68)/2 = 1,76
- Радиус интервала = 1,84/2 = 2,68 – 1,76 = 1,76 – 0,84 = 0,92
- Неравенство: | х – 1,76 | ≤ 0,92
Разные факты, которые я рассказываю своим ученикам:
- Если из большего числа вычесть меньшее, ответ положительный.
- Если из меньшего вычесть большее число, ответ будет отрицательным.
- Если из 9 вычесть положительное число0039 n , ответ меньше, чем n .
- Если из вашей личной жизни удаляется положительное влияние, качество вашей личной жизни падает.
- Если из n вычесть отрицательное число, ответ будет больше, чем n .
- Если вы устраните негативное влияние из своей личной жизни, ваша личная жизнь улучшится.
- Если к n добавить отрицательное число, ответ будет меньше, чем n .
- Если в вашу личную жизнь привносится негативное влияние, ваша личная жизнь ухудшается.
- Чтобы узнать, на каком расстоянии друг от друга находятся два числа, вычтите числа.
- Чтобы найти число, находящееся на полпути между двумя числами, найдите среднее число чисел.
Я закончу этот пост реальной историей о прозрении, которое я испытал в начале своей преподавательской карьеры. Это был обычный школьный урок геометрии.