08.2. Первый замечательный предел
Первый замечательный предел
В математике получено не так уж много результатов, название которых сопровождается такой восторженной оценкой. Однако строгое построение математической теории иногда все-таки допускает эмоциональный всплеск по поводу достигнутого результата. Чем же замечателен предел
,
Который нам предстоит изучить?
Поведение функции
(9. 25)
Легко угадывается для достаточно больших по модулю значений x. Однако при малых по абсолютной величине значениях аргумента предвидеть поведение этой функции трудно: и числитель , и знаменатель x стремятся к 0 при . Даже самые современные ЭВМ, достигнув своего порога возможностей, уже не смогут осуществить вычисление функции (9.25). Мы можем лишь предположить, что близок к 1 или, может, даже равен 1. Не исключено, однако, что этим пределом могло бы быть, к примеру, число 0,9999999993 или же 1,000000002. Непосредственные расчеты просто не позволяют в точности это установить, какими бы мощными вычислительными средствами мы ни располагали.
.
Существуют еще и другие неопределенности, которые мы изучим в дальнейшем.
Докажем, что
,
Раскрыв при этом указанную неопределенность.
|
Рис. 9.10. График функции . |
Функция (рис. 9.10) четна, поэтому доказательство существования предела достаточно провести только для положительных значений x. Рассмотрим дугу BmC единичной окружности (рис. 9.11), соответствующую углу x радиан. Построим и хорду BC. Площадь сектора OBmC больше площади треугольника OBC, но меньше площади треугольника OBA. Используя этот факт, получим:
(9. 26)
|
Рис. |
Функции и , входящие в последнее двойное неравенство, являются четными, поэтому оно справедливо для любого . Следовательно, при предел отношения заключен между 1 и .
Докажем, что
(9. 27)
Рассмотрим неравенство
И найдем соответствующую проколотую D–Окрестность нуля:
(9. 28)
Согласно неравенствам (9.26),
Поэтому
Это означает, что значения x, при которых справедливо неравенство
, (9. 29)
Удовлетворяют и неравенствам (9.28).
Еще раз отметим, что нас интересует не точная оценка всех значений x, обеспечивающих выполнение неравенства , а всего лишь факт существования проколотой D–Окрестности, охватывающей, возможно, и не все значения x, при которых это неравенство справедливо. Поэтому, решая более простое неравенство (9.29), получаем
Поэтому, решая более простое неравенство (9.29), получаем
Значит, по любому положительному числу можно выбрать D–Окрестность, полагая, что
|
Доказан для , измеряемых в радианах. Где этот факт использован при выводе? Каким будет этот предел, если угол измеряется в градусах? |
Итак, предел (9.27) существует. Таким образом, по теореме о пределе промежуточной функции, тоже равен 1, что и требовалось доказать.
| < Предыдущая | Следующая > |
|---|
Доказательство второго замечательного предела и следствий
Приводится доказательство второго замечательного предела и его следствий.
Второй замечательный предел и его следствия
Второй замечательный предел – это предел, на основе которого вычисляются производные показательной функции и логарифма.
Лемма. Второй замечательный предел
.
Здесь x – действительное число.
Доказательство ⇓
Следствия второго замечательного предела
1) ;
2) ; ;
3) ; ;
4) ; ; ; .
Доказательство ⇓
Доказательство второго замечательного предела
Формулировка ⇑
При доказательстве мы будем использовать тот факт, что последовательность строго возрастает и имеет конечный предел, равный числу e: .
Доказательство приведено на странице «Число e – его смысл и доказательство сходимости последовательности».
Сначала рассмотрим правый предел
.
Для его существования должна существовать такая окрестность точки , на которой функция определена. В нашем случае, определена при . Но мы можем выбрать любую окрестность. Для удобства считаем, что .
Пусть – функция, которая означает, целую часть числа x. Например: . Она не убывает. Рассмотрим сложную функцию
.
Докажем, что она имеет предел при , равный числу e: .
Поскольку последовательность строго возрастает, а функция не убывает, то сложная функция не убывает. Тогда по теореме о пределе монотонной функции, имеет конечный или бесконечный предел при :
.
Покажем, что . Для этого используем определение предела функции по Гейне, согласно которому, если функция имеет предел при : , то для любой последовательности , сходящейся к , последовательность сходится к A: . Возьмем последовательность . Она сходится к . Тогда . Но последовательность совпадает с :
.
Поэтому ее предел равен . Таким образом A = e:
(1) .
Сделаем подстановку . Заметим, что . Заменив переменную t на x получим:
(2) .
Теперь воспользуемся тем, что . Тогда
;
(3) .
Далее замечаем, что
, .
Применяем арифметические свойства предела функции и пределы (1) и (2):
;
.
Применяя к (3) теорему о промежуточной функции, получаем, что
.
Теперь рассмотрим левый предел
.
Считаем, что . Сделаем подстановку . Тогда . При .
.
Применяем арифметические свойства предела функции.
.
Поскольку существуют равные пределы справа и слева, то существует и двусторонний предел
.
Второй замечательный предел доказан.
Доказательство следствий второго замечательного предела
Формулировка ⇑
1) Докажем, что .
Делаем замену переменной . Тогда . При . Поэтому
.
Заметим, что фактически мы представили как сложную функцию , где . Далее мы применили теорему о пределе сложной функции.
Следствие 1) доказано.
2) Докажем, что .
Выполняем преобразования, учитывая что показательная функция является обратной к логарифмической:
.
Делаем замену переменной . В силу непрерывности показательной функции,
. Поскольку при , то
.
В предпоследнем равенстве мы воспользовались непрерывностью логарифмической функции и теоремой о пределе непрерывной функции от функции. В последнем равенстве мы применили следствие второго замечательного предела.
В последнем равенстве мы применили следствие второго замечательного предела.
Также заметим, что применяя подстановку, мы представили функцию как сложную:
, где , и применили теорему о пределе сложной функции.
Применяем арифметические свойства предела функции:
.
Также здесь мы воспользовались свойством логарифма: .
Полагая a = e, имеем:
.
Следствие 2) доказано.
3) Докажем, что .
Выполняем преобразования.
.
Функция определена при . Логарифм непрерывен на своей области определения. Применяем доказанное выше следствие 1 и теорему о пределе непрерывной функции от функции:
.
Также здесь мы воспользовались свойством логарифма: .
Подставляя a = e, получаем:
.
4) Докажем, что .
Для этого воспользуемся определением гиперболического синуса и следствием 2) ⇑. Выполняем преобразования.
.
Докажем, что .
Для этого используем определения гиперболических функций и предыдущий предел.
;
.
Докажем, что .
Для этого сделаем замену переменной .
Тогда при ; при ;
(см. «Обратные гиперболические функции, их графики и формулы»).
.
Докажем, что .
Сделаем замену переменной .
Тогда при ; при ;
при (см. «Обратные гиперболические функции, их графики и формулы»).
.
Следствия доказаны.
Автор: Олег Одинцов. Опубликовано: Изменено:
Исчисление— Ограничение функции -1/0 в порядке?
спросил
Изменено 6 лет, 10 месяцев назад
Просмотрено 10 тысяч раз
$\begingroup$
Быстрый вопрос, я определяю предел этой функции:
$$\lim_{x→1}\frac{x^2 — 2x}{x^2 -2x +1}$$ 9+\;$ (значение: приближается к нулю с положительной стороны), поэтому ваш предел — отрицательная бесконечность.
Некоторые могут определить это как «предел не существует», но я думаю, что правильнее будет сказать «предел не существует конечно» и/или «предел существует в широком смысле этого слова», «функция расходится к $\;-\infty\;$» или что-то подобное.
$\endgroup$
4
$\begingroup$ 92-2x+1}_{\to 0+}}=\color{red}{-\infty}$$
$\endgroup$
1.4: Односторонние пределы — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4153
- Грегори Хартман и др.

- Военный институт Вирджинии
Мы мягко ввели понятие предела, аппроксимировав их значения графически и численно. Далее последовало строгое определение предела вместе с, по общему признанию, утомительным методом их оценки. В предыдущем разделе мы дали нам инструменты (которые мы называем теоремами), которые позволяют нам с большей легкостью вычислять пределы. Главными среди результатов были факты, что полиномы и рациональные, тригонометрические, экспоненциальные и логарифмические функции (и их суммы, произведения и т. д.) ведут себя «хорошо». В этом разделе мы строго определяем, что мы подразумеваем под «хорошо».
В разделе 1.1 мы исследовали три причины, по которым пределы функций не существовали:
- Функция подходила к разным значениям слева и справа,
- Функция неограниченно растет, и
- Функция колеблется.
В этом разделе мы подробно исследуем концепции, лежащие в основе #1, путем введения одностороннего предела . Мы начнем с формальных определений, которые очень похожи на определение предела, данное в разделе 1.2, но обозначения немного отличаются, и «\(x\neq c\)» заменяется либо «\(x
Мы начнем с формальных определений, которые очень похожи на определение предела, данное в разделе 1.2, но обозначения немного отличаются, и «\(x\neq c\)» заменяется либо «\(x
означает, что для любого \(\epsilon > 0\) существует \(\delta > 0\) такое, что для всех \(x Правый предел Пусть \(I\) — открытый интервал, содержащий \(c\), и пусть \(f\) — функция, определенная на \(I\), за исключением, возможно, точки \(c\ ). Предел \(f(x)\), как \(x\) приближается к \(c\) из справа, равен 9-\) означает, что мы смотрим на значения \(x\) слева от \(c\). Обозначение не имеет ничего общего с положительными или отрицательными значениями \(x\) или \(c\). Аналогичное утверждение верно для оценки правых пределов; там мы рассматриваем только значения \(x\) справа от \(c\), т. Фраза «если и только если» означает, что два утверждения эквивалентны : они либо оба истинны, либо оба ложны. Если предел равен \(L\), то левый и правый пределы оба равны \( L\). Если предел не равен \(L\), то хотя бы один из левого и правого пределов не равен \(L\) (может даже не существовать). В примерах 17–20 следует учитывать один момент: значение функции может быть или не быть равным значению (значениям) ее левого/правого пределов, даже если эти пределы совпадают. 9-} f(x)=1.\) Пример 20: вычисление пределов кусочно-определенной функции 9+} f(x) =\lim\limits_{x\to 1} f(x) =f(1) = 1.\] В примерах 17-20 нас попросили найти как \(\lim\limits_{x\to 1}f(x)\), так и \(f(1)\). Рассмотрим следующую таблицу: \[\begin{array}{ccc} & \lim\limits_{x\to 1}f(x) & f(1) \\ \hline \text{Пример 17} & \text{не существует} & 1 \\ \text{Пример 18} & 1 & \text{не определено} \\ \text{Пример 19} & 0 & 1 \\ \text{Пример 20} & 1 & 1 \\ \end{массив}\ ] Только в примере 20 и функция, и предел существуют и согласуются. Это кажется «хорошим», на самом деле это кажется «нормальным». Это на самом деле важная ситуация, которую мы исследуем в следующем разделе, озаглавленном «Непрерывность». Эта страница под названием 1.4: One Sided Limits распространяется под лицензией CC BY-NC 3.0, ее автором, ремиксом и/или куратором выступили Gregory Hartman et al. через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. +}f(x) = L.\]
+}f(x) = L.\] 9+} f(x)\)
9+} f(x)\)
\(\text{РИСУНОК 1.23}\): График \(f\) в примере 19 когда \(х\) приближается к 1, равно 0. Таким образом, также ясно, что 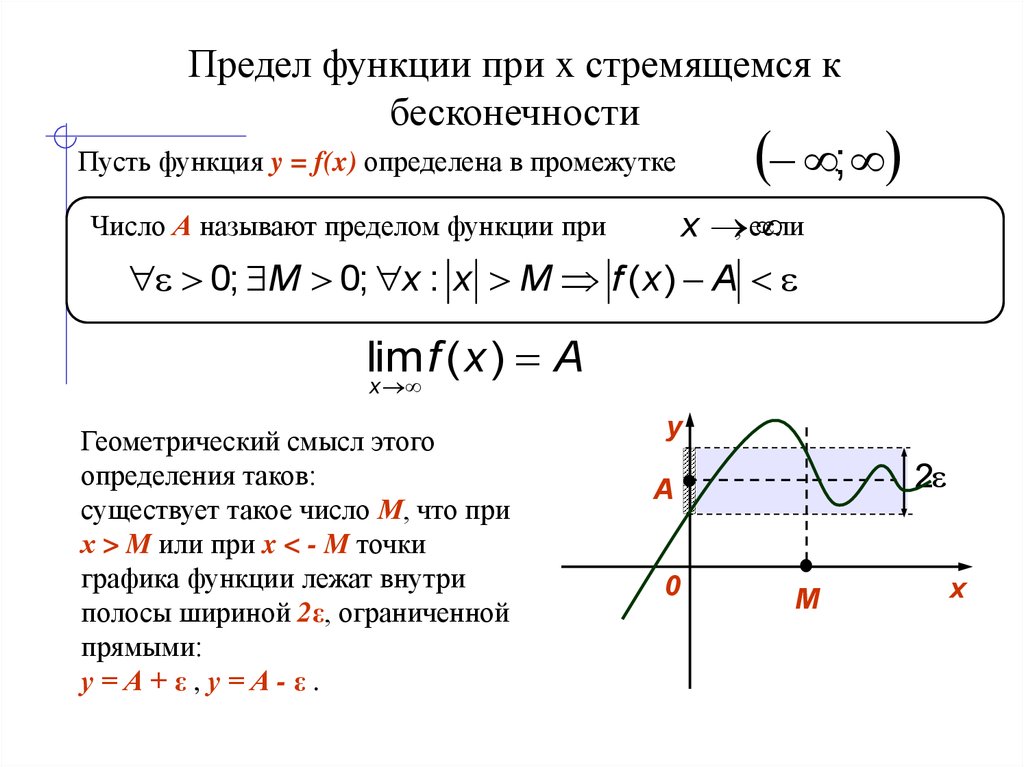 Короче говоря, непрерывная функция — это функция, в которой, когда функция приближается к значению как \(x\rightarrow c\) (т. е. когда \(\lim\limits_{x\to c} f(x) = L\)), она на самом деле достигает этого значения в \(c\). Такие функции ведут себя хорошо, поскольку они очень предсказуемы.
Короче говоря, непрерывная функция — это функция, в которой, когда функция приближается к значению как \(x\rightarrow c\) (т. е. когда \(\lim\limits_{x\to c} f(x) = L\)), она на самом деле достигает этого значения в \(c\). Такие функции ведут себя хорошо, поскольку они очень предсказуемы.

 9.11. Сравнение площадей вспомогательных фигур, используемое для доказательства первого
9.11. Сравнение площадей вспомогательных фигур, используемое для доказательства первого 