Синус ⚠️ бесконечности: чему равен предел, доказательство
Содержание:
- Что такое Синус (sin) бесконечности
- Предел тригонометрической функции
- Требование к выполнению тригонометрического тождества
- Результат решения уравнения
Содержание
- Что такое Синус (sin) бесконечности
- Предел тригонометрической функции
- Требование к выполнению тригонометрического тождества
- Результат решения уравнения
Что такое Синус (sin) бесконечности
Примечание
Предел синуса на бесконечность не поддается определению.
Известно, что sin(x) имеет любое значение в пределах [-1, 1]. Когда указывается, что x стремится к бесконечности, это означает, что x увеличивается. Изобразив это графически, мы увидим колеблющийся ряд, где \(-1\leqslant x\leqslant1\).
\(x \mapsto ∞ \\\) не приближается к какому-либо фиксированному значению y.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Колеблющиеся значения синуса означают, что для каждого действительного числа R существуют числа x, y⩾R, такие что sin (x) = 1 и что sin (y) = -1.
Предел тригонометрической функции
Неопределенность предела синуса на бесконечности доказывается через тригонометрическую функцию. Допустим, что существует некий предел выражения:
\(\lim_{n\rightarrow\infty}\sin\left(n\right)\)
Этот предел предполагает, что выражение стремится к какой-то конечной величине на бесконечности.
2n=1
\)
Результат решения уравнения
Исходя из вышеописанного, если \(\lim_{n\rightarrow\infty}\sin\left(n\right)\) существует, то будет применимо условие \(\lim\;\sin\left(n\right)=0\)
Но тогда cos(n) должен стремиться к нулю, а sin(n) к единице. Подобное заключение не соответствует здравому смыслу. Следовательно, доказано, что для синуса предел на бесконечности не определяется.
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
§ 2. Односторонние пределы функции
Пусть а и А — конечные числа.
Определение. Число А называют правым
пределом функции при и пишут: или
,
если для любого, сколь угодно малого,
числа можно указать число такое, что как только и
,
так сейчас же (т.
е. для всех оказывается
;
здесь — правая полуокрестность точки а).
Определение. Число А называют левым пределом функции при и пишут: или , если для любого, сколь угодно малого, числа можно указать число такое, что как только и , так сейчас же (т. е. для всех оказывается ; здесь — левая полуокрестность точки а).
Замечание 1. Справедливы утверждения:
1) если у функции при существует предел А в обычном смысле, т. е. двусторонний, то существуют оба односторонних предела: и , причем оба они равны А;
2) если у функции при существуют оба односторонних предела: и и оба они равны числу А, то у при существует двусторонний предел, равный указанным односторонним пределам, т. е. числу А.
В качестве упражнения утверждения 1) и 2) предлагается доказать самостоятельно.
Замечание 2.
В определении односторонних пределов
функции при число А предполагалось конечным. Отметим, что
§ 3. Предел отношения синуса к своей дуге
Установим, что
. (1)
► Так как , то , если эти пределы существуют.Поэтому, чтобы установить (1), достаточно доказать, что существует и равен 1 хотя бы один односторонний предел функции при , например, правый, т. е. достаточно доказать, что
. (2)
Так как мы станем устанавливать справедливость соотношения (2), то можно рассматривать лишь значения , удовлетворяющие неравенству: . В круге радиуса рассмотрим угол , радианная мера которого ; хорду и касательную к окружности в точке А (см. рис. 3.1). Имеем очевидные неравенства: площадь < площади сектора < площади (при этом мы пользуемся теми сведениями о площадях элементарных фигур, которые известны из школьного курса), или
,
откуда
.
(3)
Рис. 3.1. К выводу формулы (1) |
Разделим каждый из членов неравенства (3) на (). Получим
.
Вычитая из 1 каждый из членов последнего неравенства, будем иметь
. (4)
Но (в силу(3)). Следовательно, вместо неравенства (4) будем иметь
. (5)
Возьмем — любое, сколь угодно малое (можно считать, что ). Ясно, что если положить (), то для всех , удовлетворяющих неравенству , будет
,
ибо если
,
то
.
Значит,
,
если
.
Последнее означает, что
.
Видим, что соотношение (2)
установлено, а значит, доказано и
соотношение (1).
◄
§ 4. Число e
Определение. Числом е называется предел переменной
при натуральном, стремящемся к бесконечности.
Чтобы оправдать это определение, надо установить, что у переменной существует конечный предел при . Мы установим, что существует, конечный, если покажем, что переменная — возрастающая и ограниченная сверху.
► 1. Покажем, что переменная — возрастающая.
Применяя формулу бинома Ньютона, -й член последовательности можно написать в виде
,
или
. (2)
Аналогично, для -го члена последовательности находим
. (3)
Заметим, что правая
часть соотношения (2) имеет слагаемых, а правая часть (3) имеет слагаемых.
Сравнивая и , видим, что первые слагаемые в правых частях (2) и (30 одинаковы, второе, третье и т д. -е слагаемое у больше, чем у , ибо
.
Кроме того, в составе имеется еще -е слагаемое, которого в составе нет и которое является числом положительным. Значит , для любого , и, следовательно, переменная — возрастающая.
2. Покажем теперь, что переменная ограничена сверху. Для этого снова воспользуемся формулой (2). Заменим все разности, стоящие в скобках в правой части этой формулы, на единицы, отчего правая часть увеличится (ведь каждая такая разность меньше единицы). Получим
.
Но
.
Поэтому и подавно
.
Так как
,
то получаем
,
для любого
,
т. е. переменная ограничена сверху.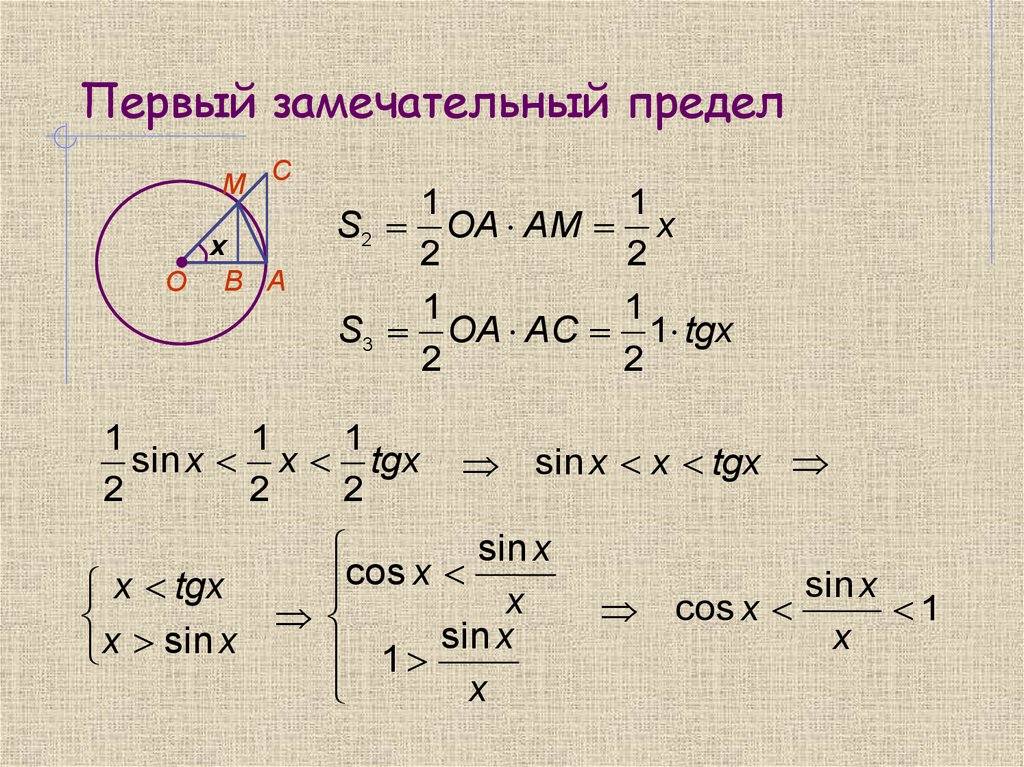
(Из формулы (2) видно,
что и, следовательно, при всех
.)
Итак, показано, что переменная монотонно возрастает и ограничена сверху. Поэтому существует конечный , величина которого заключена между числами 2 и 3. Этот предел обозначается буквой e. ◄
Число е играет большую роль в математическом анализе и его приложениях. Доказано, что е — число иррациональное. Имеются приемы, позволяющие вычислить любое число знаков в его представлении бесконечной десятичной дробью. При этом установлено, что
е = 2,718281828459045… .
Рассмотрим теперь переменную , где — положительные числа, большие 2 ( — не обязательно целые).
Справедливо утверждение: если , то
.
► 1. Рассмотрим сначала случай, когда все
значения переменной являются целыми положительными числами.
Возьмем — любое, сколь угодно малое.
Мы знаем, что . Значит, взятому отвечает номер такой, что для всех будет
По условию . Поэтому можно утверждать, что, начиная с некоторого места, т. е. при () будет: . У нас, по предположению, все значения переменной — целые положительные числа. Поэтому при всех будет иметь место неравенство
.
А это означает, что .
Отметим, что даже в рассмотренном случае переменная не обязательно монотонно возрастающая.
2. Пусть теперь значения переменной — положительные числа, большие 2, не обязательно целые.
Пусть ( — наибольшее натуральное число, удовлетворяющее неравенству: ). Ясно, что ; , если . Имеем
.
А тогда
(4)
Имеем
;
.
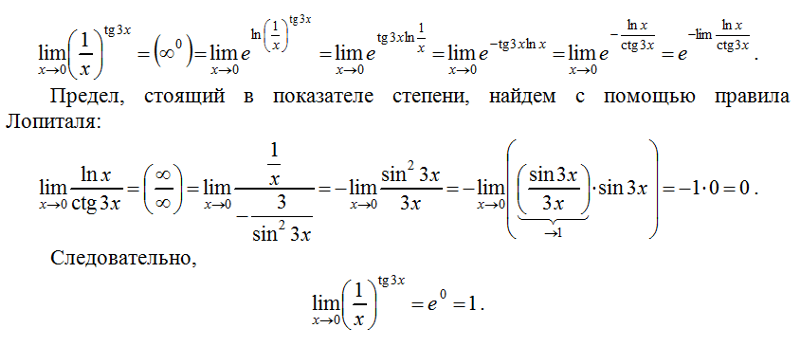
А тогда из (4), по теореме о сжатой переменной, находим
.
Подчеркнем еще раз, что здесь переменная — любая стремящаяся к . ( может и не быть монотонной). ◄
исчисление — пределы функций синуса и косинуса
$\begingroup$
Недавно я прошел тест, в котором мне дали эти два предела для оценки:
$\lim_\limits{h \to 0}\frac{\sin(x+h)-\sin{(x)}}{h}$ и $\lim_\limits{h \to 0}\frac{\ cos(x+h)-\cos{(x)}}{h}.$ Я использовал формулы сложения синуса и косинуса и нашел значение каждого предела по отдельности, в конечном итоге сократив $\sin x\cdot \frac1h$ и $ \cos x\cdot \frac1h$, потому что я узнал, что мы можем оценивать пределы по частям. В результате я получил два ответа $\cos x $ и $-\sin x$. Однако мой учитель пометил это неправильно, сказав, что мы не можем отменить $\sin{x}\cdot\frac1h$ или $\cos{x}\cdot\frac1h$, потому что этих ограничений не существует. Может кто-нибудь объяснить, почему это не работает? Я подумал, что мы можем отменить эти ограничения, поскольку мы никогда не смотрим на $0,$ только около $0,$ при оценке этих двух лимитов.
Синус: $$\frac{\sin(x+h)-\sin(x)}h=\frac{\sin(x)\cos(h)+\sin(h)\cos(x)} h-\frac{\sin(x)}h$$
$$=\sin(x)\frac1h+\cos(x)-\sin(x)\frac1h=\cos(x)$$
Косинус : $ $ \ frac {\ cos (x + h) — \ cos (x)} h = \ frac {\ cos (x) \ cos (h) — \ sin (x) \ sin (h)} h- \ cos(x)\frac1h$$
$$=\cos(x)\frac1h-\sin(x)\cdot1-\cos(x)\frac1h=-\sin(x)$$
Примечание: I мне разрешено принять $\lim_\limits{x\to 0} \frac{\sin(h)}h=1,\lim_\limits{x\to 0} \frac{\cos(h)-1}h =0.$
- исчисление
- пределы
- тригонометрия
$\endgroup$
6
$\begingroup$
Это стандартный способ нахождения производных для $\sin x$ и $\cos x$ по определению.
Ваш путь был неверным, так как при $h\to 0$ у нас есть $\sin x/h \not \to 0$, чтобы правильно действовать для первого, у нас есть
$$\sin(x+h) -\sin{(x)}=\sin x\cos h+\sin h\cos x-\sin x$$ 92}=\frac12 \ подразумевает \lim_{h \to 0}\frac{1-\cos h}{h}=0$
Для другого мы можем действовать аналогичным образом.
$\endgroup$
$\begingroup$
Вы неправильно разбили пределы. Это можно сделать только тогда, когда существуют индивидуальные ограничения. $\color{red}{\lim_\limits{h \to 0} \frac{\sin x}{h}}$ и $\color{red}{\lim_\limits{h \to 0}\frac{ \cos x}{h}}$ НЕ существует.
Вот как правильно решить первое ограничение.
$$\lim_{h \to 0}\frac{\sin(x+h)-\sin x}{h}$$
$$= \lim_{h \to 0}\frac{\color {синий}{\sin x\cos h}+\cos x\sin h\color{blue}{-\sin x}}{h}$$
$$= \lim_{h \to 0}\frac {\ color {синий} {\ sin x (\ cos h-1)} + \ cos x \ sin h} {h} $ $
$ $ = \ lim_ {h \ to 0} \ frac {\ sin x (\ cos h-1)} {h} + \ lim_ {h \ to 0} \ frac {\ cos x \ sin h} {h} $ $
$ $ = \ sin x \ cdot \ lim_ {h \ до 0}\frac{\cos h-1}{h}+\cos x\cdot\lim_{h \to 0}\frac{\sin h}{h}$$
Используя $\lim_\limits{h \to 0} \frac{\sin h}{h} = 1$ и $\lim_\limits{h \to 0}\frac{\cos h-1}{h } = 0$, вы получите
$$= \sin x\cdot 0 + \cos x\cdot 1 = \cos x$$
Обратите внимание, как существуют отдельные пределы.
Следовательно, процедура правильная. Можете ли вы использовать тот же способ для решения второго предела?
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Вопрос Видео: Нахождение пределов, связанных с тригонометрическими функциями
Стенограмма видео
Найдите предел, когда 𝑥 приближается к нулю четырех 𝑥 в квадрате, деленного на квадрат греха пяти 𝑥.
Мы видим, что вопрос заключается в том, чтобы оценить предел, когда 𝑥 приближается к нулю частного двух функций. В данном случае это частное полиномиальной функции и квадрат тригонометрической функции. Первое, о чем мы должны подумать, когда нас просят оценить такое ограничение, как это, разрешено ли нам использовать прямую замену?
И в этом случае мы можем попытаться вычислить это с помощью прямой подстановки, так как мы можем вычислять многочлены и квадраты тригонометрических функций с помощью прямой подстановки. Подставляя 𝑥 равно нулю, мы получаем четыре раза ноль в квадрате, деленный на квадрат греха пяти раз ноль. И если мы вычислим это выражение, то получим неопределенную форму деления ноль на ноль.
И это не значит, что мы не можем оценить этот предел.
Это говорит нам о том, что мы не можем определить значение этого предела, используя этот метод. Поэтому нам нужно придумать другой способ попытаться оценить этот предел. Например, мы могли бы попробовать переписать этот предел в терминах пределов, которые мы знаем, как оценивать. Например, мы знаем стандартный результат тригонометрического предела, что предел, когда 𝑥 приближается к нулю, для греха 𝑥, деленного на 𝑥, равен единице. И это похоже на ограничение, данное нам в вопросе.
Однако в этом случае у нас есть 𝑥 в числителе и функция синуса в знаменателе. К счастью, мы знаем результат о пределах, который позволит нам взять обратную функцию внутри нашего предела. Мы знаем, что если предел при приближении 𝑥 к 𝑎 некоторой функции 𝑓 от 𝑥 равен 𝐿, то предел при приближении 𝑥 к 𝑎 обратной величины 𝑓 от 𝑥 равен единице, деленной на 𝐿. И, конечно же, при условии, что значение 𝐿 не равно нулю.
Мы хотим применить это к нашему стандартному результату тригонометрического предела: предел, когда 𝑥 приближается к нулю, деления 𝑥 на 𝑥 равен единице.
Итак, мы установим 𝑓 из 𝑥 как грех 𝑥, деленный на 𝑥, а 𝐿 равным единице. Поскольку значение 𝐿 не равно нулю, мы можем использовать тот факт, что предел обратной величины равен обратной величине предела. Это говорит нам, что предел, когда 𝑥 приближается к нулю обратной величины греха 𝑥, деленной на 𝑥, равен обратной единице.
Конечно, величина, обратная единице, равна единице. И мы можем взять обратную величину греха 𝑥, деленную на 𝑥, чтобы получить 𝑥, деленную на грех 𝑥. Итак, мы показали, что предел, когда 𝑥 приближается к нулю 𝑥, деленному на грех 𝑥, равен единице.
Давайте посмотрим, как мы можем использовать это, чтобы оценить предел, заданный нам в вопросе. Во-первых, мы возьмем постоянную четверку за пределы нашего предела. Далее мы замечаем, что берем частное двух квадратов. Таким образом, используя наши законы показателей, мы можем вместо этого возвести в квадрат все частное. Теперь мы можем переписать это, используя правило мощности для пределов. Это говорит нам о том, что для положительного целого числа 𝑛 предел, когда 𝑥 приближается к 𝑎 из 𝑔 из 𝑥 в 𝑛-й степени, равен пределу, когда 𝑥 приближается к 𝑎 из 𝑔 из 𝑥, возведенному в 𝑛-ю степень.
Другими словами, предел мощности равен мощности предела. Это дает нам четыре, умноженные на квадрат предела, поскольку 𝑥 приближается к нулю 𝑥, деленного на грех пяти 𝑥.
Теперь мы хотим оценить этот предел, используя предел, который мы придумали ранее. Однако мы видим, что берем в знаменателе грех в пять 𝑥. Предел, к которому мы пришли, имеет только грех 𝑥 в знаменателе. Мы обойдем это, заменив все значения 𝑥 в этом правиле ограничения на пять 𝑥. Таким образом, это дает нам предел, когда пять 𝑥 приближаются к нулю из пяти 𝑥, разделенных на грех пяти 𝑥, равно единице.
В этот момент мы должны быть осторожны, так как теперь у нас есть предел, когда пять 𝑥 приближаются к нулю, а 𝑥 приближаются к нулю. Однако если пять 𝑥 все ближе и ближе к нулю, то 𝑥 становится все меньше и меньше. На самом деле 𝑥 все ближе и ближе к нулю. Таким образом, мы можем просто переписать этот предел, поскольку 𝑥 приближается к нулю.
Далее мы можем взять постоянную пятерку за пределы нашего предела.