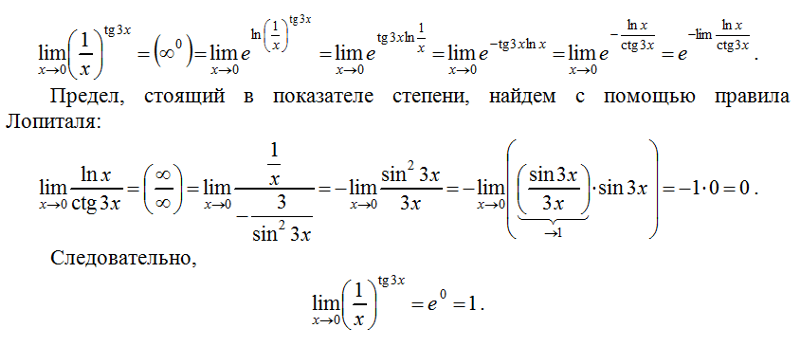примеры пределов х стремится к 0
Пределы/ Предел функции
| → | ↑ Функция f(x) ? |
|---|
Примеры
Для конечных точек:
———Слева (x0-)Справа (x0+)
График:
от до
Ввести:
{ кусочно-заданную функцию можно здесь.
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
3- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
14159..Предел 1/x при x стремящ. к 0 равен бесконеч. или не опред? : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| Andrei94 |
| ||
22/11/11 |
| ||
| |||
01.2012, 17:51 | Whitaker |
| ||
12/01/11 |
| ||
| |||
01.2012, 18:02 | Andrei94 |
| ||
22/11/11 |
| ||
| |||
| Whitaker |
| ||
12/01/11 |
| ||
| |||
| Andrei94 |
| ||
22/11/11 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 5 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Формальное определение лимита
Формальное определение лимита К концу этой лекции вы должны быть в состоянии формально определить, что такое предел, используя точный математический язык, и использовать этот язык для объяснения предельных расчетов и графиков, которые мы выполнили в предыдущих разделах.
До сих пор мы работали с неформальным определением предела:
Предел (неофициальное определение)
Если f(x) в конце концов становится все ближе и ближе к определенному значению L по мере того, как x приближается к выбранному значению c из правого , тогда мы говорим, что предел f(x) когда x приближается к c справа, L .
Если f(x) в конце концов становится все ближе и ближе к определенному значению L по мере того, как x приближается к выбранному значению c из оставшегося , тогда мы говорим, что предел от f(x), когда x приближается к c слева, равно L .
Если предел f(x) при приближении x к c одинаков справа и слева, то мы говорим, что предел f(x) при приближении x к c равен L .
Если f(x) никогда не приближается к определенному конечному значению, как x приближается к c , то мы говорим, что предел не существует .
Если f(x) имеет разные правый и левый пределы, то двусторонний предел ( lim x → c f(x) ) не существует .
Обозначение:
В частности, мы пишем:
lim x → c- f(x) = L для обозначения « предела слева от f (9x)08, поскольку
лим x → c+ f(x) = L для обозначения « предела функции f(x) при приближении x к c слева равен L »
lim x → c f(x) = L для обозначения предела как »
Однако это определение неофициальный , потому что мы формально не определили, что мы подразумеваем под «подходами» или «в конечном итоге все ближе и ближе».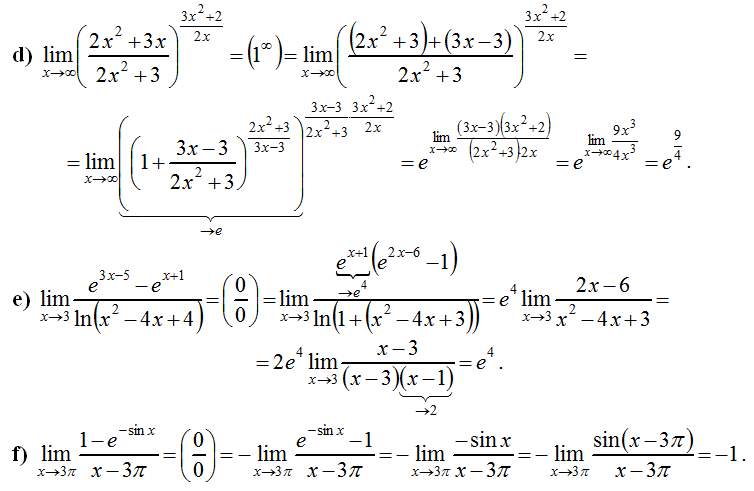
Чтобы дать формальное определение, нам нужно уточнить, когда именно мы можем сказать, что x или f(x) приближаются к определенному значению. Мы делаем это сейчас, давая формальное математическое определение:
Предел (формальное определение)
Конечные пределы:
90lim x → c f(x) = L
means that:
Для любого числа ε>0, которое мы выберем, можно найти другое число δ>0, так что:
для всех x между c-δ и c+δ (за исключением, возможно, c точно), f(x) будет находиться между L-ε и L+ε.
Другими словами, если мы выберем интервал на y -ось вокруг L, мы всегда можем найти интервал на оси x- вокруг c , который заставит f(x) оставаться в выбранном диапазоне значений y (за исключением, возможно, в f(c) ).
Вероятно, это лучше всего понять, взглянув на график:
Если нам нужно формальное определение того, что означает неограниченное увеличение или уменьшение предела, мы также можем адаптировать этот подход к этому случаю:
Бесконечные пределы :
If f(x) is a function that is defined on an open interval around x=c , then
lim x → c f(x) = +∞
означает, что:
Для любого числа M>0, которое мы выберем, можно найти другое число δ>0 так, что:
для всех x между c-δ и c+δ (за исключением, возможно, c точно), f(x) будет больше, чем M.
Другими словами, если мы выберем значение по оси y вокруг, мы всегда сможем найти интервал по оси x- вокруг c , который заставит f( x) , чтобы оставаться выше этого значения (за исключением, возможно, f(c) ).
Вероятно, лучше всего это можно понять, взглянув на график:
Мы также можем использовать эту же идею для определения пределов на бесконечности:
Пределы на бесконечности:
IF F (x) является функцией, а L — реальное число, затем
LIM x → ∞ ° С ° С ° . означает, что: Для любого числа ε>0, которое мы выбираем, можно найти другое число M>0, так что: -ε и L+ε. Другими словами, если мы выберем интервал на y -ось вокруг L, мы всегда можем найти значение отсечки на оси x-, которое заставит f(x) оставаться в выбранном диапазоне значений y , как только оно пройдет это место отсечки . Это также, вероятно, лучше всего понять, взглянув на график: Таким образом, если ограничение существует, должна быть возможность ограничить область вокруг c , что заставит f(x) оставаться в пределах любого выбранного определенного расстояния L . Для каждого из следующих примеров мы рассмотрим, как формальное определение предела позволяет нам доказать, что предел существует или что он не существует. Мы делаем это как с помощью графиков, чтобы увидеть, можем ли мы аппроксимировать соответствующие значения для δ или M, так и с помощью алгебраического подхода к уравнению. Для этой функции нас интересует предел, поскольку x приближается к 1: Мы уже вычислили этот предел как графически, так и алгебраически и определили, что он равен 2. Чтобы сделать это графически, мы можем переместить ползунок ε на интерактивной анимации ниже, пока он не достигнет 0,05. Затем мы можем переместить ползунок δ до пунктирных зеленых линий, которые представляют часть графика, где все точки находятся в пределах δ-расстояния или меньше от x = 1. Как только эти зеленые пунктирные вертикальные линии будут достаточно близко друг к другу, чтобы все f(x) между ними оставались внутри заштрихованной красным части графика, мы нашли δ, при котором f(x) на расстоянии ε от предела 2. Примерно при каком значении δ вертикальные зеленые пунктирные линии удерживают график f(x) в красной части графика? ε дельта Работая с анимацией, вы должны были обнаружить, что δ = 0,0248 или что-то близкое к этому кажется достаточно малым, чтобы гарантировать, что f(x) остается в пределах 0,05 расстояния от предела 2. Теперь, чтобы сделать это алгебраически, мы начнем с ограничения f(x) через L-ε слева и L+ε справа, а затем решим это неравенство для x . Это позволяет нам определить, какие значения x позволят нам сохранить f(x) на расстоянии ε от предела 2: Таким образом, если x остается в пределах 0,025 расстояния от c = 1, f(x) останется в пределах 0,05 расстояния от L = 2. (Конечно, любой δ меньше 0,025 также будет работать!) Нас снова интересует предел, поскольку x приближается к -2, и мы помним из нескольких последних лекций, что предел в этом случае равен -4. В этой задаче давайте искать δ, который будет работать для ε = 0,02. Для начала мы попытаемся найти δ графически, взаимодействуя с анимацией ниже, которая даст нам приблизительное значение: ε дельта Взаимодействуя с анимацией, я получил значение около 0,0206 для δ. Теперь, вычислив δ алгебраически, мы получим точное значение: Нас снова интересует предел, поскольку x приближается к -2, и мы помним из нескольких последних лекций, что предел в этом случае равен -4. Для этого примера мы снова ищем δ, который работает для ε = 0,02. Сначала мы стремимся оценить δ графически, используя анимацию ниже: ε дельта Заметим, что эта задача на самом деле ничем не отличается от предыдущей: единственное отличие здесь состоит в том, что если в предыдущем графе была дыра в x = 2, то в этом графе, помимо этой дыры, есть изолированная точка в (-2,1). Но это не влияет на лимит, потому что лимит не связан с тем, что происходит в x = c , но только то, что происходит вокруг x=c . В следующем примере мы будем использовать формальное определение предела для оценки односторонних пределов, и прежде чем мы это сделаем, мы хотим кратко ввести часть обозначений, которые мы будем использовать: Обозначение: L L и L R Мы будем использовать обозначение L R для обозначения предела, рассчитанного как x приближается к c справа, и мы будем использовать обозначение L 
Давайте посмотрим, как это определение можно применить к примерным вычислениям пределов, которые мы сделали в предыдущих лекциях. В случаях, когда предела не существует, мы должны быть в состоянии понять, почему δ не будет существовать для каждого возможного ε: другими словами, мы должны быть в состоянии найти ε в тех случаях, для которых не может быть найдено ни одного возможного δ. что заставит f(x) оставаться на расстоянии ε от L. Простой пример, где
lim x → c f(x) = f(c) :
Но теперь мы хотели бы использовать формальное определение предела, чтобы лучше понять, почему предел существует. Для этого мы собираемся найти значение (значения) δ, которое будет удовлетворять требованиям определения предела для ε = 0,05.
Пример с отверстием в точке
x=c: 
Что ты получил? Пример с функцией, имеющей разрыв скачка в точке
x=c , состоящей из одной точки : 
Так что в этом случае наше предыдущее δ=0,02 все еще будет работать, даже если точка (-2,1) не находится в пределах 0,02 от -4. Мы должны точно исключить эту точку при рассмотрении предела по определению.
Пример с функцией, которая имеет разрыв скачка в точке
x=c и разные пределы справа и слева: Здесь нас интересует предел x → 1, и мы постараемся найти δ, удовлетворяющее формальному определению предела для ε=0,1.
Так как это кусочная функция с разрывом скачком на х = 1, то сначала посмотрим на предел отдельно справа и слева:
Сначала рассмотрим предел справа, который мы уже вычислили в предыдущей лекции как 2. Сначала оценим его графически, используя интерактивную анимацию ниже, а затем посчитаем алгебраически.
ε
дельта
С помощью ползунков установите ε на 0,1, а затем переместите ползунок для δ до тех пор, пока зеленая пунктирная линия справа не удержит график f(x) слева от x =1 в пределах красной заштрихованной области. , я получил приблизительное значение δ из графика, равное 0,0777. Что ты получил?
Теперь, вычисляя δ алгебраически для правого предела:
Теперь рассмотрим предел слева, который мы уже вычислили в предыдущей лекции как -2. Опять же, мы начнем с графической оценки, используя анимацию ниже, а затем рассчитаем ее алгебраически.
ε
дельта
С помощью ползунков установите ε на 0,1, а затем переместите ползунок для δ до тех пор, пока зеленая пунктирная линия слева не удержит график f(x) слева от x =1 в пределах красной заштрихованной области. , я получил приблизительное значение δ из графика, равное 0,037. Что ты получил?
Теперь приступим к алгебраическому вычислению значения δ для левого предела:
Теперь рассмотрим двусторонний предел. Если мы попытаемся использовать формальное определение предела со значением ε = 0,1, мы столкнемся с проблемой: мы не можем выбрать такое δ, которое всегда будет удерживать f(x) на расстоянии ε от левостороннего предела -2 слева, потому что независимо от того, насколько маленьким мы делаем наше δ, всегда будет часть графика справа от x = 1, где f(x) выходит далеко за пределы области, которая на расстоянии ε или меньше от левостороннего предела.
Точно так же мы не можем выбрать любое δ, которое всегда будет сохранять f(x) в пределах расстояния ε от правого предела 2, потому что независимо от того, насколько малым мы делаем наше δ, всегда будет часть графика слева от x = 1, где f (x) находится далеко за пределами области, которая находится на расстоянии ε или меньше от правого предела.
На самом деле, нам нужно было бы иметь ε 4 или больше, чтобы все значений f(x) в окрестности x =1 находились в пределах расстояния ε как слева, так и справа. правые предельные значения. Но формальное определение говорит, что мы должны быть в состоянии найти δ для ВСЕ возможных ненулевых варианта ε. Таким образом, если мы сможем найти хотя бы одно ненулевое значение для ε, для которого невозможно никакое δ, мы показали, что предела не существует.
Пример с функцией, имеющей бесконечный разрыв (или вертикальную асимптоту) в точке
x=c : Для этой функции нас интересует предел, когда x приближается к 0.
Здесь мы видим, что мы не сможем найти δ для любого ε в этом случае, который будет работать для конечного предела, потому что f(x) здесь неограниченно увеличивается, поскольку x приближается к 0 с обеих сторон. Таким образом, в этом случае мы будем использовать формальное определение бесконечных пределов, чтобы найти значение для δ при M = 100.
Начнем с аппроксимации δ графически: с помощью ползунков на интерактивной анимации ниже.
М
дельта
Я получил приблизительное значение 0,095. Что ты получил?
Теперь найдем δ алгебраически:
Пример с функцией, которая имеет бесконечный разрыв (или вертикальную асимптоту) при
x=c, с разным предельным поведением слева и справа: Для этой функции нас интересует предел, когда x приближается к 1. Теперь посмотрим, сможем ли мы найти подходящее значение δ для M=40 справа и подходящее значение δ для M=-40 слева.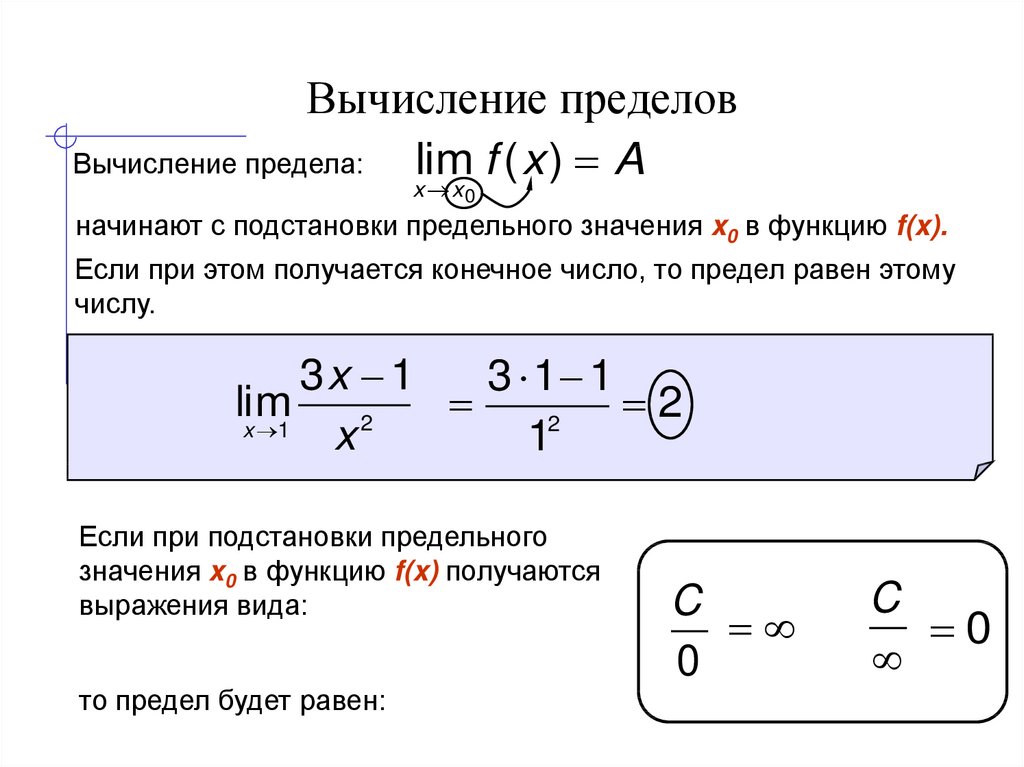
, сначала используя график для аппроксимации значения:
М
дельта
М
дельта
Как для левого, так и для правого я получил значение δ=0,026, используя ползунки на интерактивных анимациях выше. Что ты получил?
Теперь вычислим δ точно алгебраически. Сначала мы начнем с определения того, какое значение δ будет удерживать f(x) выше M (в правой части).
Теперь мы вычисляем, какое значение δ будет удерживать f(x) ниже -40 (в левой части).
Мы снова видим, почему двусторонний предел не существует в этом случае, потому что нет возможного δ, которое мы могли бы выбрать, чтобы сохранить все значения f(x) выше 40 (потому что всегда будет некоторое значения слева от x =1 включены, и все они отрицательны), независимо от того, насколько мала величина δ.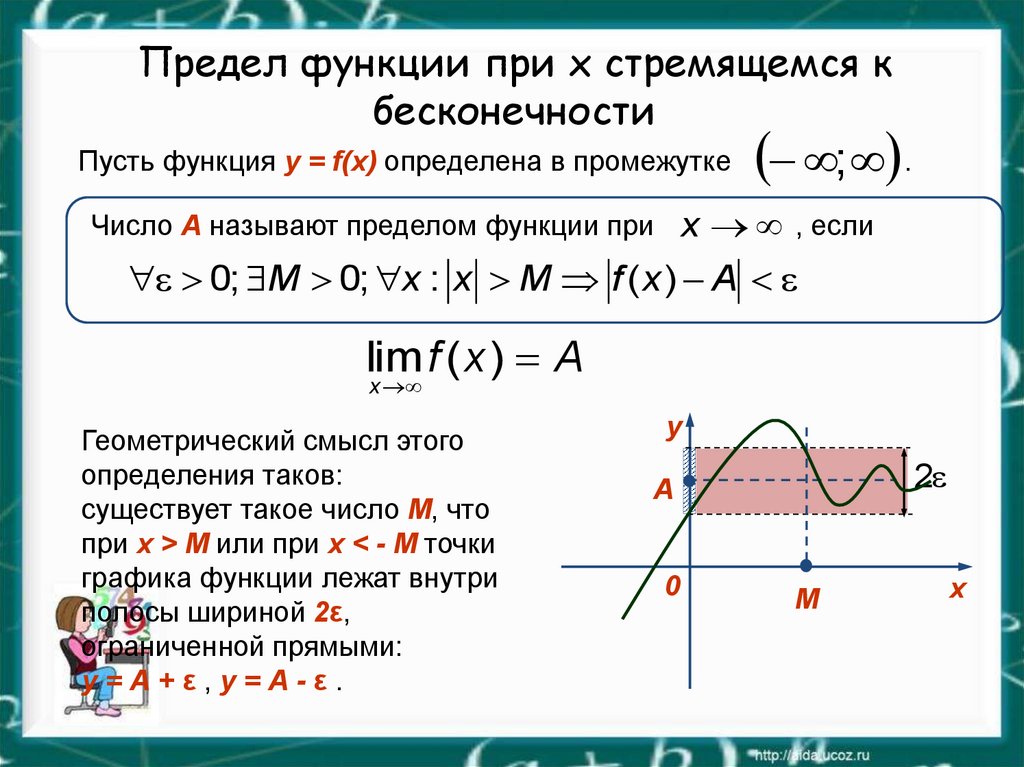
Мы столкнулись бы с аналогичной проблемой с положительными значениями f(x) справа от 1, если мы попытаемся найти δ, который работает для двустороннего предела, когда M=40 (поскольку всегда будут включены некоторые значения справа от x =1, и все они положительные).
Пример с функцией, предел которой равен нулю на бесконечности:
Для этой функции нас интересует предел, когда x приближается к -∞, и предел, когда x приближается к +∞. Мы будем искать значения M, которые будут удовлетворять формальному определению предела, когда ε равно 0,45. Из-за относительной сложности этого конкретного уравнения мы будем оценивать значения M только графически, а не проверять их алгебраически в этом случае. Используйте ползунки в интерактивной анимации ниже, чтобы найти M для ε = 0,45 для обоих пределов:
ε
М
Глядя на предел, когда x приближается к -∞, мы получаем значение M, которое приблизительно равно 4,4, и глядя на предел, когда x приближается к +∞, мы получаем значение M, которое составляет приблизительно 4,35.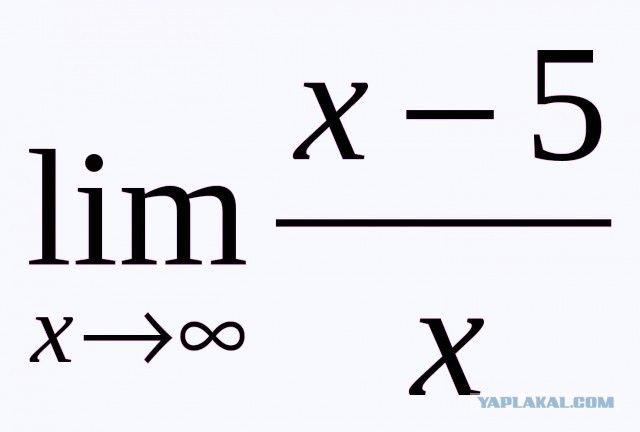
Пример с функцией, предел которой не существует на бесконечности:
Мы рассматриваем предел этой функции, когда x приближается к +∞, и мы рассматриваем, можем ли мы найти M для ε = 0,5. Опять же, для этой задачи, поскольку уравнение относительно сложное, мы используем анимацию для аппроксимации значений M, а не пытаемся найти M алгебраически. Попробуйте поэкспериментировать с ползунками ниже, чтобы увидеть, сможете ли вы найти значение для M, которое сохранит значения 9.0907 f(x) в области, заштрихованной красным, для всех x >M.
ε
М
Мы видим, что в этом примере никогда не удастся найти такое M, потому что, поскольку x неограниченно возрастает, f(x) также неограниченно увеличивается. Независимо от того, какое значение мы выберем для M, мы никогда не сможем удержать график f(x) в области, заштрихованной красным.
Пример с функцией, имеющей осциллирующий разрыв:
Мы рассматриваем предел этой функции, поскольку x приближается к 1, и мы стремимся найти δ, которое будет удовлетворять формальному определению предела для ε=0,5. Это еще одна проблема, когда нужно просто посмотреть на график, чтобы попытаться найти δ, а не пытаться найти δ алгебраически. Глядя на анимацию ниже, найдите время, чтобы поэкспериментировать с ползунками, чтобы увидеть, сможете ли вы найти δ для ε = 0,5 для одностороннего или двустороннего предела при разрешении x = 1.
ε
дельта
ε
М
Вы, наверное, заметили, что найти такое δ невозможно, потому что какое бы маленькое δ вы ни выбрали, внутри пунктирных зеленых линий всегда будет какая-то часть графика, которая колеблется до 1 и вниз до -1 .
Таким образом, не существует такого значения, которое будет удерживать график f(x) внутри заштрихованной красным области, и мы можем видеть, как формальное определение предела показывает нам, что этого предела не существует.
