Представить двойной интеграл в виде повторного интеграла: Решение двойных определенных интегралов онлайн

Содержание

Файл: Лекция 1.doc — Страницы №№1-4

Двойные интегралы. Определение двойного интеграла и его свойства. Повторные интегралы. Сведение двойных интегралов к повторным. Расстановка пределов интегрирования. Вычисление двойных интегралов в декартовой системе координат.

Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функции двух переменных. В этом случае вместо отрезка интегрирования будет присутствовать какая-то плоская фигура.

Пусть D – некоторая замкнутая ограниченная область, а f(x,y) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y=f(x) или x=g(y), где f(x) и g(y) – непрерывные функции.

Рис. 1.1

азобьем область D произвольным образом на n частей. Площадь i-го участка обозначим символом s_i. На каждом участке произвольно выберем какую-либо точку P_i, и пусть она в какой-либо фиксированной декартовой системе имеет координаты (x_i,y_i). Составим интегральную сумму для функции f(x,y) по области D, для этого найдем значения функции во всех точках P_i, умножим их на площади соответствующих участков s_i и просуммируем все полученные результаты:

. (1.1)

Назовем диаметром diam(G) области G наибольшее расстояние между граничными точками этой области.

Двойным интегралом функции f(x,y) по области D называется предел, к которому стремится последовательность интегральных сумм (1. 1) при неограниченном увеличении числа разбиений n (при этом ). Это записывают следующим образом

. (1.2)

Заметим, что, вообще говоря, интегральная сумма для заданной функции и заданной области интегрирования зависит от способа разбиения области D и выбора точек P_i. Однако если двойной интеграл существует, то это означает, что предел соответствующих интегральных сумм уже не зависит от указанных факторов. Для того чтобы двойной интеграл существовал (или, как говорят, чтобы функция

f(x,y) была интегрируемой в области D), достаточно чтобы подынтегральная функция была непрерывной в заданной области интегрирования.

Рис. 1.2

усть функция f(x,y) интегрируема в области D.

Поскольку предел соответствующих интегральных сумм для таких функций не зависит от способа разбиения области интегрирования, то разбиение можно производить при помощи вертикальных и горизонтальных линий. Тогда большинство участков области D будет иметь прямоугольный вид, площадь которых равна s_i=x_iy_i. Поэтому дифференциал площади можно записать в виде
ds=dxdy. Следовательно, в декартовой системе координат двойные интегралы можно записывать в виде

. (1.3)

Замечание. Если подынтегральная функция f(x,y)1, то двойной интеграл будет равен площади области интегрирования:

. (1.4)

Отметим, что двойные интегралы обладают такими же свойствами, что и определенные интегралы. Отметим некоторые из них.

Свойства двойных интегралов.

1⁰. Линейное свойство. Интеграл от суммы функций равен сумме интегралов:

;

и постоянный множитель можно выносить за знак интеграла:

2⁰. Аддитивное свойство. Если область интегрирования D разбить на две части, то двойной интеграл будет равен сумме интегралов по каждой этой части:

3⁰. Теорема о среднем. Если функция f(x,y) непрерывна в области D, то в этой области найдется такая точка (), что:

Далее возникает вопрос: как вычисляются двойные интегралы? Его можно вычислить приближенно, с этой целью это разработаны эффективные методы составления соответствующих интегральных сумм, которые затем вычисляются численно при помощи ЭВМ. При аналитическом вычислении двойных интегралов их сводят к двум определенным интегралам.

Повторными интегралами называются интегралы вида

. (1.5)

В этом выражении сначала вычисляется внутренний интеграл, т.е. производится сначала интегрирование по переменной y (при этом переменная x считается постоянной величиной). В результате интегрирования по y получится некоторая функция по x:

Затем полученную функцию интегрируют по x:

Пример 1.1. Вычислить интегралы:

а) , б) .

Решение. а) Произведем интегрирование по y, считая, что переменная x=const. После этого вычисляем интеграл по x:

б) Так как во внутреннем интеграле интегрирование производится по переменной x, то y³ можно вынести во внешний интеграл как постоянный множитель. Поскольку y² во внутреннем интеграле считается постоянной величиной, то этот интеграл будет табличным. Производя последовательно интегрирование по y и x, получаем

В декартовой системе координат обычно рассматривают направления вдоль осей Ox и Oy. Если область является простой в обоих направлениях, то говорят коротко – простая область, без выделения направления. Если область не является простой, то говорят, что она сложная.

а б

Рис. 1.4

юбую сложную область можно представить в виде суммы простых областей. Соответственно, любой двойной интеграл можно представить в виде суммы двойных интегралов по простым областям. Поэтому в дальнейшем мы будем рассматривать, в основном, только интегралы по простым областям.

Теорема. Если область интегрирования D – простая в направлении оси Oy (см. рис.1.4а), то двойной интеграл можно записать в виде повторного следующим образом:

; (1. 6)

если область интегрирования D – простая в направлении оси Ox (см. рис.1.4б), то двойной интеграл можно записать в виде повторного следующим образом:

. (1.7)

простая область

простая область в направлении Oy

простая область в направлении Ox

сложная область

Рис. 1.3

сли область интегрирования является правильной в обоих направлениях, то можно произвольно выбирать вид повторного интеграла, в зависимости от простоты интегрирования.

Рис. 1.5

ри сведении двойных интегралов к повторным, основная трудность возникает при расстановке пределов во внутренних интегралах. Наиболее просто это сделать для прямоугольных областей (см. рис. 1.5).

Пример 1.2. Вычислить двойной интеграл

Решение. Запишем двойной интеграл в виде повторного:

Для того, чтобы перейти от двойного интеграла к повторному следует:

построить область интегрирования;
расставить пределы в интегралах, при этом следует помнить, что пределы внешнего интеграла должны быть постоянными величинами (т.е. числами) независимо от того, по какой переменной вычисляется внешний интеграл.

Пример 1.3. Расставить пределы интегрирования в соответствующих повторных интегралах для двойного интеграла

, если а) б)

Рис. 1.6

ешение. а) Изобразим область интегрирования D (см. рис.1.6). Пусть интегрирование во внешнем интеграле производится по переменной x, а во внутреннем – по y. Расстановку пределов всегда нужно начинать с внешнего интеграла, в данном случае с переменной x. Из рисунка видно, что x изменяется от 0 до 1, при этом значения переменной y будут изменяться от значений на прямой y=x до значений на прямой y=2x. Таким образом, получаем

Пусть теперь интегрирование во внешнем интеграле производится по y, а во внутреннем – по x. В этом случае значения y будут изменяться от 0 до 2. Однако тогда верхняя граница изменений значений переменной x будет состоять из двух участков x=y/2 и x=1. Это означает, что область интегрирования нужно разбить на две части прямой y=1. Тогда в первой области y изменяется от 0 до 1, а x от прямой x=y/2 до прямой x=y. Во второй области y изменяется от 1 до 2, а x – от прямой x=y/2 до прямой x=1. В результате получим

Рис. 1.7

) Построим область интегрирования D (см. рис.1.7). Пусть во внешнем интеграле интегрирование производится по x, а во внутреннем – по y. В этом случае при изменении x от –1 до 1 изменения переменной y сверху будут ограничены двумя линиями: окружностью и прямой.

На отрезке [–1;0] y изменяется от y=0 до ; на отрезке [0;1] переменная y изменяется от y=0 до y=1–x. Таким образом,

Пусть теперь во внешнем интеграле интегрирование производится по y, а во внутреннем – по x. В этом случае y будет изменяться от 0 до 1, а переменная x – от дуги окружности до прямой x=1–y. В результате получим

Данные примеры показывают, как важно правильно выбирать порядок интегрирования.

Пример 1.4. Изменить порядок интегрирования

а) ; б) .

Рис. 1.8

ешение. а) Построим область интегрирования. На отрезке [0;1] для x переменная y изменяется от прямой y=0 до прямой y=x. В результате получается следующая область интегрирования (см. рис.1.8). На основании построенного рисунка, расставляем пределы интегрирования

б) Построим область интегрирования. На отрезке [0;9/16] для y переменная x изменяется от прямой x=y до параболы ; на отрезке [9/16;3/4] – от прямой x=y до прямой x=3/4. В результате получается следующая область интегрирования (см. рис.1.9). На основании построенного рисунка, расставляем пределы интегрирования,

Двойные интегралы. Определение двойных интегралов. Повторные интегралы. Тройные интегралы

1. ДВОЙНЫЕ ИНТЕГРАЛЫ

1.1. Определение двойных интегралов

Пусть функция f(x) определена в ограниченной замкнутой области D плоскости xOy. Разобьем эту область произвольным образом на n частей. Площадь i-го участка обозначим символом Ds_i. На каждом участке произвольно выберем какую-либо точку P_i, и пусть она в какой-либо фиксированной декартовой системе имеет координаты (x_i,y_i). Составим интегральную сумму для функции f(x,y) по области D, для этого найдем значения функции во всех точках P_i, умножим их на площади соответствующих участков Ds_i и просуммируем все полученные результаты:

. (1.1)

Двойным интегралом функции f(x,y) по области D называется предел, к которому стремится последовательность интегральных сумм (1.1) при неограниченном увеличении числа разбиений n (при этом ). Это записывают следующим образом

. (1.2)

Заметим, что если двойной интеграл существует, то он не зависит от способа разбиения области D и от способа выбора точек (x_i,y_i). Следовательно, область интегрирования можно разбивать при помощи вертикальных и горизонтальных линий. Тогда большинство участков области D будет иметь прямоугольный вид. Поэтому дифференциал площади можно записать в виде ds=dxdy. Следовательно, в декартовой системе координат двойные интегралы можно записывать в виде

. (1.3)

Если подынтегральная функция f(x,y)º1, то двойной интеграл равен площади области интегрирования:

. (1.4)

Свойства двойных интегралов.

1⁰. Интеграл от суммы функций равен сумме интегралов:

2⁰. Постоянный множитель можно выносить за знак интеграла:

3⁰. Если область интегрирования D разбить на две части, то двойной интеграл будет равен сумме интегралов по каждой этой части:

1.2. Повторные интегралы

Повторными интегралами называются интегралы вида

. (1.5)

Затем полученную функцию интегрируют по x:

Пример 1.1. Вычислить интегралы:

а) , б) .

Решение. а) Произведем интегрирование по y, считая, что переменная x=const. После этого производим интегрирование по x:

б) Так как во внутреннем интеграле интегрирование производится по переменной x, то y³ можно вынести во внешний интеграл как постоянный множитель. Поскольку y² во внутреннем интеграле считается постоянной величиной, то этот будет табличным. В результате, получаем

1.3. Расстановка пределов интегрирования

Область интегрирования называется простой в каком-либо направлении, если любая прямая, проведенная в этом направлении, пересекает границу области не более чем в двух точках. Например,

Любую сложную область можно представить в виде суммы простых областей.

Между двойными и повторными интегралами существует взаимосвязь.

Теорема. Если область интегрирования D – простая в направлении оси Oy (см. рис.1.1а), то двойной интеграл можно записать в виде повторного следующим образом:

; (1.6)

если область интегрирования D – простая в направлении оси Ox (см. рис.1.1б), то двойной интеграл можно записать в виде повторного следующим образом:

. (1.7)

Для того, чтобы перейти от двойного интеграла к повторному следует:

1) построить область интегрирования;

2) расставить пределы в интегралах, при этом следует помнить, что пределы внешнего интеграла должны быть постоянными величинами (т.е. числами) независимо от того, по какой переменной вычисляется внешний интеграл.

Пример 1.2. Расставить пределы интегрирования в соответствующих повторных интегралах для двойного интеграла

если

а) б)

Решение. а) Изобразим область интегрирования D (см. рис.1.2). Пусть интегрирование во внешнем интеграле производится по переменной x, а во внутреннем – по y. Расстановку пределов всегда нужно начинать с внешнего интеграла, в данном случае с переменной x. Из рисунка видно, что x изменяется от 0 до 1, при этом значения переменной y будут изменяться от значений на прямой y=x до значений на прямой y=2x. Таким образом, получаем

Пусть теперь интегрирование во внешнем интеграле производится по y, а во внутреннем – по x. В этом случае значения y будут изменяться от 0 до 2. Однако тогда верхняя граница изменений значений переменной x будет состоять из двух участков x=y/2 и x=1. Это означает, что область интегрирования нужно разбить на две части прямой y=1. Тогда в первой области y изменяется от 0 до 1, а x от прямой x=y/2 до прямой x=y. Во второй области y изменяется от 1 до 2, а x – от прямой x=y/2 до прямой x=1. В результате получим

Основные свойства двойного интеграла. Определение двойного интеграла Теорема о вычислении двойного интеграла

1.1. Определение двойного интеграла

Пусть D – некоторая замкнутая ограниченная область, а f (x , y ) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y =f (x ) или x =g(y ), где f (x ) и g (y ) – непрерывные функции.

Рис. 1.1

азобьем область D произвольным образом на n частей. Площадь i -го участка обозначим символом s i . На каждом участке произвольно выберем какую-либо точку P i , и пусть она в какой-либо фиксированной декартовой системе имеет координаты (x i , y i ). Составим интегральную сумму для функции f (x , y ) по области D , для этого найдем значения функции во всех точках P i , умножим их на площади соответствующих участков s i и просуммируем все полученные результаты:

. (1.1)

Назовем диаметром diam (G ) области G наибольшее расстояние между граничными точками этой области.

Двойным интегралом функции f (x , y ) по области D называется предел, к которому стремится последовательность интегральных сумм (1.1) при неограниченном увеличении числа разбиений n (при этом
). Это записывают следующим образом

. (1.2)

Заметим, что, вообще говоря, интегральная сумма для заданной функции и заданной области интегрирования зависит от способа разбиения области D и выбора точек P i . Однако если двойной интеграл существует, то это означает, что предел соответствующих интегральных сумм уже не зависит от указанных факторов. Для того чтобы двойной интеграл существовал (или, как говорят, чтобы функция f (x , y ) была интегрируемой в области D ), достаточно чтобы подынтегральная функция была непрерывной в заданной области интегрирования .

Рис. 1.2

усть функция f (x , y ) интегрируема в области D . Поскольку предел соответствующих интегральных сумм для таких функций не зависит от способа разбиения области интегрирования, то разбиение можно производить при помощи вертикальных и горизонтальных линий. Тогда большинство участков области D будет иметь прямоугольный вид, площадь которых равна s i =x i y i . Поэтому дифференциал площади можно записать в виде ds = dxdy . Следовательно, в декартовой системе координат двойные интегралы можно записывать в виде

. (1.3)

Замечание . Если подынтегральная функция f (x , y )1, то двойной интеграл будет равен площади области интегрирования:

. (1.4)

Свойства двойных интегралов.

1 0 . Линейное свойство. Интеграл от суммы функций равен сумме интегралов :

и постоянный множитель можно выносить за знак интеграла :

2 0 . Аддитивное свойство. Если область интегрирования D разбить на две части, то двойной интеграл будет равен сумме интегралов по каждой этой части :

3 0 . Теорема о среднем. Если функция f(x , y ) непрерывна в области D , то в этой области найдется такая точка (), что :

1.2. Повторные интегралы

Повторными интегралами называются интегралы вида

. (1.5)

Затем полученную функцию интегрируют по x :

Пример 1.1. Вычислить интегралы:

а)
, б)
.

Решение . а) Произведем интегрирование по y , считая, что переменная x = const . После этого вычисляем интеграл по x :

б) Так как во внутреннем интеграле интегрирование производится по переменной x , то y 3 можно вынести во внешний интеграл как постоянный множитель. Поскольку y 2 во внутреннем интеграле считается постоянной величиной, то этот интеграл будет табличным. Производя последовательно интегрирование по y и x , получаем

Между двойными и повторными интегралами существует взаимосвязь, но сначала рассмотрим простые и сложные области. Область называется простой в каком-либо направлении, если любая прямая, проведенная в этом направлении, пересекает границу области не более чем в двух точках. В декартовой системе координат обычно рассматривают направления вдоль осей Ox и Oy . Если область является простой в обоих направлениях, то говорят коротко – простая область, без выделения направления. Если область не является простой, то говорят, что она сложная .

а б

Рис. 1.4

Теорема . Если область интегрирования D – простая в направлении оси Oy (см. рис.1.4а), то двойной интеграл можно записать в виде повторного следующим образом:

; (1.6)

если область интегрирования D – простая в направлении оси Ox (см. рис.1.4б), то двойной интеграл можно записать в виде повторного следующим образом:

. (1.7)

Рис. 1.3

1.3. РАССТАНОВКА ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ

1.3.1. Прямоугольная область интегрирования

Рис. 1.5

Пример 1.2. Вычислить двойной интеграл

Решение . Запишем двойной интеграл в виде повторного:

1.3.2. Произвольная область интегрирования

Для того, чтобы перейти от двойного интеграла к повторному следует:

построить область интегрирования ;

расставить пределы в интегралах, при этом следует помнить, что пределы внешнего интеграла должны быть постоянными величинами (т. е. числами) независимо от того, по какой переменной вычисляется внешний интеграл .

, если а)
б)

Рис. 1.6

ешение . а) Изобразим область интегрирования D (см. рис.1.6). Пусть интегрирование во внешнем интеграле производится по переменной x , а во внутреннем – по y . Расстановку пределов всегда нужно начинать с внешнего интеграла , в данном случае с переменной x . Из рисунка видно, что x изменяется от 0 до 1, при этом значения переменной y будут изменяться от значений на прямой y = x до значений на прямой y =2x . Таким образом, получаем

Пусть теперь интегрирование во внешнем интеграле производится по y , а во внутреннем – по x . В этом случае значения y будут изменяться от 0 до 2. Однако тогда верхняя граница изменений значений переменной x будет состоять из двух участков x = y /2 и x =1. Это означает, что область интегрирования нужно разбить на две части прямой y =1. Тогда в первой области y изменяется от 0 до 1, а x от прямой x = y /2 до прямой x = y . Во второй области y изменяется от 1 до 2, а x – от прямой x = y /2 до прямой x =1. В результате получим

Рис. 1.7

) Построим область интегрирования D (см. рис.1.7). Пусть во внешнем интеграле интегрирование производится по x , а во внутреннем – по y . В этом случае при изменении x от –1 до 1 изменения переменной y сверху будут ограничены двумя линиями: окружностью и прямой. На отрезке [–1;0] y изменяется от y =0 до
; на отрезке переменная y изменяется от y =0 до y =1–x . Таким образом,

Пусть теперь во внешнем интеграле интегрирование производится по y , а во внутреннем – по x . В этом случае y будет изменяться от 0 до 1, а переменная x – от дуги окружности
до прямой x =1–y . В результате получим

Данные примеры показывают, как важно правильно выбирать порядок интегрирования.

Пример 1.4. Изменить порядок интегрирования

а)
; б)
.

Рис. 1.8

ешение . а) Построим область интегрирования. На отрезке для x переменная y изменяется от прямой y =0 до прямой y = x . В результате получается следующая область интегрирования (см. рис.1.8). На основании построенного рисунка, расставляем пределы интегрирования

б) Построим область интегрирования. На отрезке для y переменная x изменяется от прямой x =y до параболы
; на отрезке – от прямой x =y до прямой x = 3/4. В результате получается следующая область интегрирования (см. рис.1.9). На основании построенного рисунка, расставляем пределы интегрирования,

Свойства двойного интеграла (и их вывод) аналогичны соответствующим свойствам однократного определенного интеграла.

1° . Аддитивность . Если функция f (x , y ) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D 1 и D 2 , то функция f (x , y ) интегрируема в каждой из областей D 1 и D 2 , причем

2° . Линейное свойство . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , а α и β — любые вещественные числа, то функция [α · f (x , y ) + β · g (x , y )] также интегрируема в области D , причем

3° . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , то и произведение этих функций интегрируемо в D .

4° . Если функции f (x , y ) и g (x , y ) обе интегрируемы в области D и всюду в этой области f (x , y ) ≤ g (x , y ), то

5° . Если функция f (x , y ) интегрируема в области D , то и функция |f (x , y )| интегрируема в области D , причем

(Конечно, из интегрируемости |f (x , y )| в D не вытекает интегрируемость f (x , y ) в D .)

6° . Теорема о среднем значении . Если обе функции f (x , y ) и g (x , y ) интегрируемы в области D , функция g (x , y ) неотрицательна (неположительна) всюду в этой области, M и m — точная верхняя и точная нижняя грани функции f (x , y ) в области D , то найдется число μ , удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

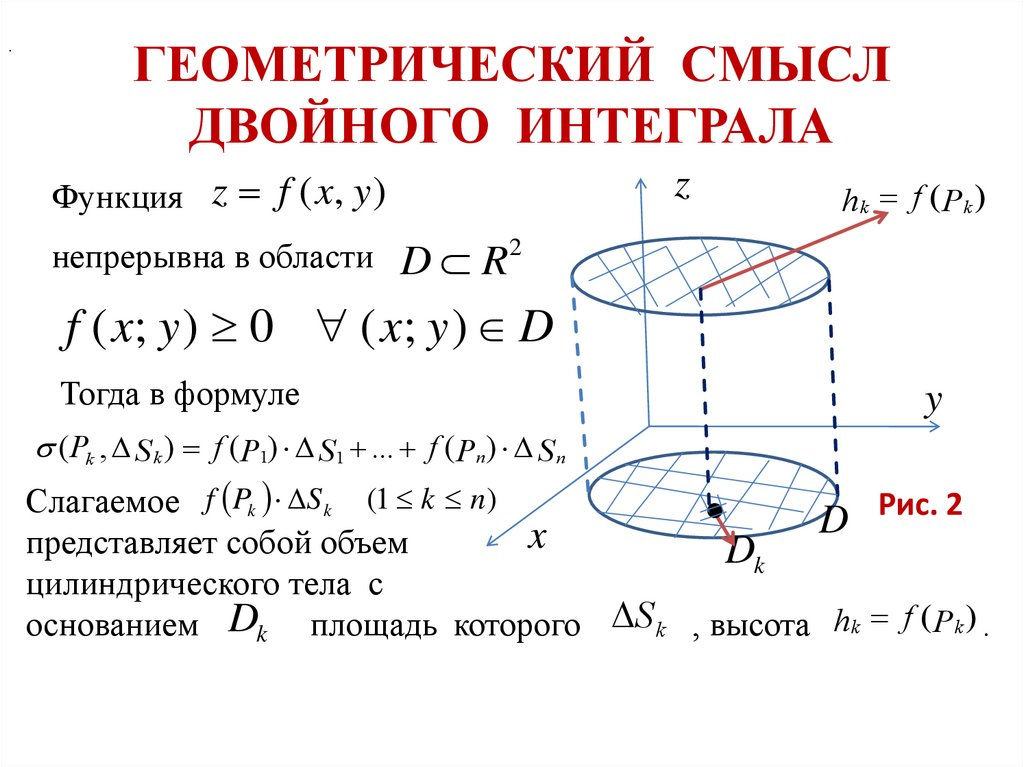
Задача, приводящая к понятию двойного интеграла.

Предположим, что на определена функция частей и запишем сумму

которая именуется интегральной.

О: Под определенным интегралом (о.и.) от функции и от выбора

Обозначение:

Числа именуют интегрируемой (по Риману) на .

Т. существования: При условии, что .

В соответствии с определением о.и. отметим, что интеграл имеет зависимость от вида , пределов и , однако не зависит от символа обозначения переменной , иначе выражаясь

В соответствии с п.17.1.1 и 17.1.2 и определением о.и. запишем формулы площади криволинейной трапеции: , работы силы

на :

Понятие двойного интеграла, интегральных сумм.

Существование двойного интеграла, т. е. предела интегральной суммы для кажется очевидным, так как этот предел дает объем цилиндрического тела. Однако это рассуждение не является строгим. В более полных курсах это утверждение строго доказывается и носит название теоремы существования двойного интеграла.

Теорема существования. Для всякой функции, непрерывной в ограниченной замкнутой области, имеющей площадь а, существует двойной интеграл, т. е. существует предел интегральных сумм при неограниченном увеличении числа малых площадок при условии, что каждая из них стягивается в точку. Этот предел не зависит ни от способа разбиения области а на части ни от выбора точек

В дальнейшем мы будем рассматривать только функции, непрерывные в области интегрирования.

Из теоремы существования следует, что мы можем, например, разбить область а на малые прямоугольники со сторонами прямыми, параллельными осям координат (рис. 230). При этом. Выбирая затем в каждом малом прямоугольнике по точке мы можем написать, согласно определению двойного интеграла

Для того чтобы подчеркнуть, что двойной интеграл можно получить как предел суммы вида вместо обозначения употребляют также обозначение

Выражение называется элементом площади в декартовых координатах и равно площади прямоугольника со сторонами параллельными координатным осям.

Заметим, что при составлении интегральной суммы площадки прилегающие к границе области а, не имеют формы прямоугольников. Однако можно доказать, что ошибка от замены таких площадок прямоугольниками с площадями в пределе сведется к нулю.

Свойства двойных интегралов

3° . Если функции f (x , y ) и g (x , y ) интегрируемы в области D , то и произведение этих функций интегрируемо в D .

4° . Если функции f (x , y ) и g (x , y ) обе интегрируемы в области D и всюду в этой области f (x , y ) ≤ g (x , y ), то

5° . Если функция f (x , y ) интегрируема в области D , то и функция |f (x , y )| интегрируема в области D , причем

(Конечно, из интегрируемости |f (x , y )| в D не вытекает интегрируемость f (x , y ) в D .)

В частности, если функция f (x , y ) непрерывна в D , а область D связна , то в этой области найдется такая точка (ξ , η ), что μ = f (ξ , η ), и формула (11) принимает вид

ДВОЙНЫЕ ИНТЕГРАЛЫ

ЛЕКЦИЯ 1

Пусть D – некоторая замкнутая ограниченная область, а f (x,y ) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y =f (x ) или x =g(y ), где f (x ) и g (y ) – непрерывные функции.

Разобьем область D произвольным образом на n частей. Площадь i -го участка обозначим символом Ds i . На каждом участке произвольно выберем какую-либо точку P i , и пусть она в какой-либо фиксированной декартовой системе имеет координаты (x i ,y i ). Составим интегральную сумму для функции f (x,y ) по области D, для этого найдем значения функции во всех точках P i , умножим их на площади соответствующих участков Ds i и просуммируем все полученные результаты:

Назовем диаметром diam (G ) области G наибольшее расстояние между граничными точками этой области.

Двойным интегралом функции f (x,y ) по области D называется предел, к которому стремится последовательность интегральных сумм (1.1) при неограниченном увеличении числа разбиений n (при этом ). Это записывают следующим образом

Заметим, что, вообще говоря, интегральная сумма для заданной функции и заданной области интегрирования зависит от способа разбиения области D и выбора точек P i . Однако если двойной интеграл существует, то это означает, что предел соответствующих интегральных сумм уже не зависит от указанных факторов. Для того чтобы двойной интеграл существовал (или, как говорят, чтобы функция f (x,y ) была интегрируемой в области D), достаточно чтобы подынтегральная функция была непрерывной в заданной области интегрирования .

Пусть функция f (x,y ) интегрируема в области D . Поскольку предел соответствующих интегральных сумм для таких функций не зависит от способа разбиения области интегрирования, то разбиение можно производить при помощи вертикальных и горизонтальных линий. Тогда большинство участков области D будет иметь прямоугольный вид, площадь которых равна Ds i =Dx i Dy i . Поэтому дифференциал площади можно записать в виде ds=dxdy . Следовательно, в декартовой системе координат двойные интегралы можно записывать в виде

Замечание . Если подынтегральная функция f (x,y )º1, то двойной интеграл будет равен площади области интегрирования:

Свойства двойных интегралов.

1 0 . Линейное свойство. Интеграл от суммы функций равен сумме интегралов :

и постоянный множитель можно выносить за знак интеграла :

2 0 . Аддитивное свойство. Если область интегрирования D разбить на две части, то двойной интеграл будет равен сумме интегралов по каждой этой части :

3 0 . Теорема о среднем. Если функция f(x,y ) непрерывна в области D, то в этой области найдется такая точка (x,h), что :

Двойной интеграл обладает свойствами, аналогичными свойствам определенного интеграла. Отметим лишь основные из них:

1. Если функции и
интегрируемы в области
, то интегрируемы в ней их сумма и разность, причем

2. Постоянный множитель можно выносить за знак двойного интеграла:

3. Если
интегрируема в области
, а эта область разбита на две непересекающиеся областии
, то

4. Если
и
интегрируемы в области
, в которой

, то

5. Если в области
функция
удовлетворяет неравенствам

,где
и
некоторые действительные числа, то

где – площадь области
.

Доказательства этих свойств аналогичны доказательству соответствующих теорем для определенного интеграла.

Вычисление двойного интеграла в прямоугольных декартовых координатах

Пусть требуется вычислить двойной интеграл
, где область- прямоугольник, определяемый неравенствами,.

Предположим, что
непрерывна в этом прямоугольнике и принимает в нем неотрицательные значения, тогда данный двойной интеграл равен объему тела с основанием, ограниченного сверху поверхностью
, с боков — плоскостями
,
,
,
:

С другой стороны, объем такой фигуры можно вычислить с помощью определенного интеграла:

где
— площадь сечения данного тела плоскостью, проходящей через точкуи перпендикулярной к оси
. А так как рассматриваемое сечение является криволинейной трапецией
, ограниченной сверху графиком функции
, гдефиксировано, а, то

Из этих трех равенств следует, что

Итак, вычисление данного двойного интеграла свелось к вычислению двух определенных интегралов; при вычислении «внутреннего интеграла» (записанного в скобках) считается постоянным.

Замечание. Можно доказать, что последняя формула верна и при
, а также в случае, когда функция
меняет знак в указанном прямоугольнике.

Правая часть формулы называется повторным интегралом и обозначается так:

Аналогично можно показать, что

Из выше сказанного следует, что

Последнее равенство означает, что результат интегрирования не зависит от порядка интегрирования.

Чтобы рассмотреть более общий случай, введем понятие стандартной области. Стандартной (или правильной) областью в направлении данной оси называется такая область, для которой любая прямая, параллельная этой оси пересекает границу области не более, чем в двух точках. Другими словами, пересекает саму область и ее границу только по одному отрезку прямой.

Предположим, что ограниченная область

и ограничена сверху графиком функции
, снизу — графиком функции
. ПустьR{,} — минимальный прямоугольник, в котором заключена данная область
.

Пусть в области
определена и непрерывна функция
. Введем новую функцию:

тогда в соответствии со свойствами двойного интеграла

И, следовательно,

Поскольку отрезок
целиком принадлежит области
то, следовательно,
при

, а еслилежит вне этого отрезка, то
.

При фиксированном можем записать:

Так как первый и третий интегралы в правой части равны нулю, то

Следовательно,

Из чего получаем формулу для вычисления двойного интеграла по области, стандартной относительно оси
путем сведения к повторному интегралу:

Если область
является стандартной в направлении оси
и определяется неравенствами,

, аналогично можно доказать, что

Замечание. Для области
, стандартной в направлении осей
и
, будут выполнены оба последних равенства, поэтому

По этой формуле осуществляется изменение порядка интегрирования при вычислении соответствующего двойного интеграла.

Замечание. Если область интегрирования не является стандартной (правильной) в направлении обеих осей координат, то ее разбивают на сумму стандартных областей и представляют интеграл в виде суммы интегралов по этим областям.

Пример . Вычислить двойной интеграл
по области
, ограниченной линиями:
,
,
.

Решение.

Данная область является стандартной как относительно оси
, так и относительно оси
.

Вычислим интеграл, считая область стандартной относительно оси
.

Замечание. Если вычислить интеграл, считая область стандартной относительно оси
, мы получим тот же результат:

Пример . Вычислить двойной интеграл
по области
, ограниченной линиями:
,
,
.

Решение. Изобразим на рисунке заданную область интегрирования.

Данная область является стандартной относительно оси
.

Пример . Изменить порядок интегрирования в повторном интеграле:

Решение. Изобразим на рисунке область интегрирования.

Из пределов интегрирования находим линии, ограничивающие область интегрирования: ,
,
,
. Для изменения порядка интегрирования выразимкак функции оти найдем точки пересечения:

,
,
.

Так как на одном из интервалов функция выражена двумя аналитическими выражениями, то область интегрирования необходимо разбить на две области, а повторный интеграл представить как сумму двух интегралов.

Исчисление III. Повторные интегралы

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4-2: Повторные интегралы

В предыдущем разделе мы дали определение двойного интеграла. Однако, как и в случае с определением одиночного интеграла, это определение очень сложно использовать на практике, поэтому нам нужно начать изучать, как мы на самом деле вычисляем двойные интегралы. Будем и дальше считать, что интегрируем по прямоугольнику

\[R = \left[ {a,b} \right] \times \left[ {c,d} \right]\]

В следующем разделе мы рассмотрим более общие регионы.

Следующая теорема говорит нам, как вычислить двойной интеграл по прямоугольнику. {{\,b}}{{f\left( {x,y} \right)\,dx}}\,dy}} \]

Эти интегралы называются повторными интегралами .

Обратите внимание, что на самом деле существует два способа вычисления двойного интеграла по прямоугольнику, а также обратите внимание, что внутренний дифференциал совпадает с пределами внутреннего интеграла, и аналогично для внешнего дифференциала и пределов. Другими словами, если внутренний дифференциал равен $dy$, то пределы внутреннего интеграла должны быть $y$ пределами интегрирования, а если внешний дифференциал равен $dy$, то пределы внешнего интеграла должны быть — $у$ пределы интегрирования. 9{{\,d}}{{f\left( {x,y} \right)\,dy}}\]

, и мы вычисляем это, удерживая $x$ постоянным и интегрируя по $y$, как если бы это был один интеграл. Это даст функцию, включающую только $x$, которую мы, в свою очередь, можем проинтегрировать.

Мы проделали аналогичный процесс с частными производными. Чтобы взять производную функции по $у$, мы рассматривали $х$ как константы и дифференцируем по $у$, как если бы это была функция одной переменной. 92}\,dA}}\), $R = \left[ {2,4} \right] \times \left[ {1,2} \right]$ Показать решение

Неважно, по какой переменной мы интегрируем первую, мы получим один и тот же ответ независимо от порядка интегрирования. Чтобы доказать это, давайте поработаем с каждым заказом, чтобы убедиться, что мы получаем один и тот же ответ.

Решение 1
В этом случае мы сначала будем интегрировать по $y$. Таким образом, повторный интеграл, который нам нужно вычислить, равен 9.2}\,dy}}\,dx}}\]

При их настройке убедитесь, что пределы соответствуют дифференциалам. Поскольку $dy$ является внутренним дифференциалом (, т.е. , мы сначала интегрируем по $y$), внутренний интеграл должен иметь пределы $y$.

Чтобы вычислить это, мы сначала выполним внутренний интеграл, и мы обычно сохраняем внешний интеграл следующим образом:

\[\begin{align*}\iint\limits_{R}{{6x{y^2}\,dA}} & = \int_{{\,2}}^{{\,4}}{{\ оставил. {{\,4}}{{14x\,dx}}\end{align*}\] 9{ — y}}} \right)\,dy}}\end{align*}\]

Мы даже не будем продолжать здесь, так как это очень трудные, если не невозможные, интегралы.

Как мы видели в предыдущем наборе примеров, мы можем выполнять интеграл в любом направлении. Однако иногда одно направление интегрирования значительно проще, чем другое, поэтому убедитесь, что вы подумали о том, какое из них вы должны сделать в первую очередь, прежде чем на самом деле выполнять интегрирование.

Следующей темой этого раздела является краткий факт, который может быть использован для упрощения вычисления некоторых повторяющихся интегралов. 9{b}{{g\влево(x\вправо)h\влево(y\вправо)\,dx}}\,dy}}\]

Обратите внимание, что в этом случае не имеет значения, какую переменную мы интегрируем первой, поскольку любой порядок приведет к одному и тому же результату с одинаковой работой.

Далее обратите внимание, что, поскольку внутренний интеграл относится к $x$ и $h\left( y \right)$ является функцией только $y$, его можно считать «константой».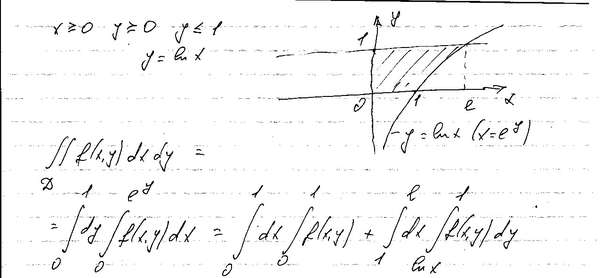 что касается интегрирования $x$ (изменение $x$ не повлияет на значение $y$!) и потому что это также раз $g\left( x \right)$ мы можем факторизовать $h\left( y \right)$ из внутреннего интеграла. Это дает 9{d}{{h\влево(y\вправо)\,dy}}\]

Другими словами, если мы можем разбить функцию на функцию только от $x$, умноженную на функцию только от $y$, то мы можем вычислить два интеграла по отдельности и перемножить их вместе.

Вот краткое изложение этой идеи.

Факт

Если $f\left( {x,y} \right) = g\left( x \right)h\left( y \right)$ и мы интегрируем по прямоугольнику $R = \left[ {a,b} \right] \times \left[ {c,d} \right]$ тогда, 9{\ frac {\ pi} {2}}} \right)\\ & = \ frac {{5 \ pi}} {8} \ end {align *} \]

У нас есть еще одна тема для обсуждения в этом разделе. Эта тема на самом деле не имеет ничего общего с повторными интегралами, но это такое же хорошее место, как и любое другое, и здесь также могут возникнуть некоторые вопросы по этому поводу, так что это такое же хорошее место, как и любое другое. .

Мы хотим обсудить одиночные неопределенные интегралы функции двух переменных. Другими словами, мы хотим посмотреть на интегралы, как показано ниже. 9{ — \frac{x}{y}}}\,dx}}\end{align*}\]

Из Исчисления I мы знаем, что эти интегралы задают вопрос, какую функцию мы продифференцировали, чтобы получить подынтегральное выражение. Однако в этом случае нам нужно обратить внимание на дифференциал ($dy$ или $dx$) в интеграле, потому что это немного изменит дело.

В случае первого интеграла мы спрашиваем, какую функцию мы продифференцировали по $y$, чтобы получить подынтегральную функцию, а во втором интеграле мы спрашиваем, какую функцию мы продифференцировали по $x$, чтобы получить подынтегральная функция. В большинстве случаев ответить на эти вопросы не так уж и сложно. Важным вопросом является то, как мы поступаем с константой интегрирования. 9{ — \frac{x}{y}}} + h\left( y \right)\end{align*}\]

Обратите внимание, что «константы» интегрирования теперь являются функциями противоположной переменной. В первом интеграле мы дифференцируем по $y$, и мы знаем, что любая функция, включающая только $x$, будет дифференцируется до нуля, поэтому при интегрировании по $y$ нам нужно признать что в функции могла быть функция только от $x$, и поэтому «константа» интегрирования есть функция от $x$.

Аналогично, во втором интеграле «константа» интегрирования должна быть функцией $y$, так как мы интегрируем по $x$. Опять же, помните, если мы продифференцируем ответ по $x$, то любая функция только $y$ будет дифференцироваться до нуля.

Повторный интеграл – определение, формула и примеры

С помощью повторного интеграла , мы теперь можем расширить основную теорему исчисления для определенных интегралов с двумя или более переменными. Знание того, как вычислять повторные интегралы, важно, если мы хотим усовершенствовать наше понимание двойных и тройных интегралов.

Повторный интеграл позволяет интегрировать функции многих переменных. Подобно частным производным, мы берем последующие частные интегралы по одной переменной за раз.

Наше обсуждение сосредоточится на определении повторных интегралов и их компонентов. Здесь мы также покажем вам процесс вычисления повторных интегралов, поэтому в этой статье предполагается знание интегральных свойств и формул. Вкратце освежите в памяти методы интеграции, которые мы изучили в прошлом, на случай, если они вам понадобятся. 9{b} f(x, y, z) &\phantom{x}dxdydz \end{aligned}

Эти два интеграла являются двумя наиболее известными примерами повторных интегралов – двойным интегралом и тройным интегралом. Благодаря повторному интегрированию мы можем легко вычислить эти типы интегралов. На протяжении всего нашего обсуждения мы будем использовать двойные интегралы в качестве примеров, начиная с определения двойных интегралов как повторных интегралов.

Определение повторного интеграла

Предположим, что $f(x, y)$ — непрерывная функция в своей прямоугольной области определения, $R = [a, b] \times [c, d]$. По теореме Фубини мы можем определить двойной интеграл от $f(x, y)$ по $dx$ и $dy$ как повторный интеграл, показанный ниже. 9

Эти две формы подчеркивают важность повторных интегралов: мы оцениваем их по отношению к сначала одну переменную, рассматривая другие переменные как константы. Мы повторяем процесс до тех пор, пока полностью не оценим полученный повторный интеграл.

Бывают случаи, когда проще начать с функции в терминах $x$ или функций, определенных $y$. Изображение выше представляет эти два случая для двойных интегралов, когда области, над которыми мы работаем, не определяются прямоугольной областью. Вот два способа записи двойного интеграла в виде повторного интеграла. 9{h_2(y)} f(x, y) dx\phantom{x} dy\end{aligned}

Теперь, когда мы рассмотрели все основные принципы, необходимые для построения повторных интегралов, давайте сразу перейдем к пониманию того, как мы можем оценивайте интегралы так. Большинство наших примеров будут охватывать двойные интегралы, поэтому, если вы хотите изучить повторные интегралы с тремя переменными, сразу после этого перейдите к нашей статье о тройных интегралах.

Как вычислить повторный интеграл?

Повторные интегралы можно вычислить, сначала интегрируя по одной переменной. Как и в случае с частными производными, мы начинаем с самого внутреннего слоя и «частично интегрируем» функцию по самой внутренней переменной. 9{d} f(x, y) \phantom{x}dy dx}\end{aligned}

· Интегрируем функцию по $x$, сначала рассматривая $y$ как константу.

· Оцените полученное выражение от $x =a$ до $x = b$.

· Проинтегрируйте функцию по $y$, считая остальное константой.

· Оцените выражение в пределах: от $y = c$ до $y = d$.

· Проинтегрируйте функцию по $y$, сначала рассматривая $x$ как константу. 9{729} – 1) $

Изображения/математические чертежи созданы с помощью GeoGebra.

Повторные интегралы — Photomath

Исследовать интегралы

С определенными интегралами мы могли бы вычислить площадь области между графиком функции, осью $$x$$ и пределами интегрирования — но что, если мы хотим вычислить площадь, ограниченную двумя кривые? Вот тут-то и появляются повторные интегралы!

Давайте подробнее рассмотрим, что это такое и чем они полезны. 9{b}{f(x,y)~dx~dy}$$

Интегралы такого типа называются повторными интегралами.

Иногда порядок интегралов меняется. Когда , спросите вы?

Порядок интегрирования часто меняется, когда самый внутренний интеграл в повторном интеграле слишком сложен для вычисления — например, если функция в самом внутреннем интеграле не имеет элементарной первообразной.

Итак, как же изменить порядок интегрирования?

Изменение порядка интегрирования означает изменение порядка переменных, которые появляются в повторном интеграле.

Например, если двойной интеграл записан так, что внутренняя переменная равна $$x$$, а внешняя переменная равна $$y$$, то изменение порядка интегрирования поменяет эти позиции так, что внутренняя переменная станет $ $y$$, а внешней переменной будет $$x$$.

При изменении порядка переменных пределы интегрирования также необходимо переписать соответствующим образом.

Однако при изменении порядка интегрирования нам все равно нужно использовать интегральные правила для ее решения. Помните этих старых друзей?

9{\ простое число} (т) dt = \ int {f (x)} dx $ $

Постоянная кратность интегралов	$$\int{(c\times f(x))}dx=c\times \int{f(x)}dx$$
Правило сумм для интегралов	$$\int{(f(x) + g(x))}dx=\int{f(x)}dx + \int{g(x)}dx$$
Правило разности интегралов
Интеграция по частям	$$\int{u}dv=uv-\int{v}du$$

Почему повторные интегралы так полезны?

Иногда нам нужно найти площадь области, ограниченной кривыми функций. В других случаях мы хотим использовать повторный интеграл, чтобы найти объем твердого тела, ограниченного положительной функцией в данной области, и среднее значение функции от двух переменных в данной области.

Например, если непрерывная функция $$f(x,y)$$ определена над прямоугольником $$R=[a,b]\times[c,d]$$, то среднее значение функции $ $f(x,y)$$ можно рассчитать по формуле $$f_{avg}=\frac{1}{(b-a)(d-c)}\int\int_R f(x,y)dA$$.

Круто, да?

Давайте научимся это делать!

Как решать повторные интегралы

Теперь, когда мы сориентировались, давайте посмотрим на некоторые повторные интегралы в действии! Мы вместе рассмотрим несколько примеров.

92)}dxdy$$

Обратите внимание, что сначала нужно вычислить интеграл как $$x$$, но это не интеграл из таблицы интегралов и не может быть решен нашими обычными методами. Итак, попробуем изменить порядок интегрирования. Сначала запишем пределы внутреннего и внешнего интегралов в виде неравенств:

$$y\leq x\leq1$$

$$0\leq y\leq 1$$

Обратите внимание, что $$y$$ больше или равно $$0$$ и меньше или равно $$x$$. Сохраняя связь между переменными, перепишем неравенства в виде составного неравенства: 92$$ и $$dx=\frac{dt}{2x}$$:

$$\int\sin{(t)}\times x\times\frac{dt}{2x}$$

Отмена из общего множителя $$x$$:

$$\int\sin{(t)}\times 1\times\frac{dt}{2}$$

Упростим выражение:

$$\int \frac{\sin{(t)}}{2}dt$$

Теперь воспользуемся свойством интеграла $$\int a\times f(x)dx=a\times\int f(x)dx, a\in \mathbb{R}$$:

$$\frac{1}{2}\int\sin{(t)}dt$$

Обратите внимание, что это интеграл из таблицы интегралов, поэтому мы можем использовать $$\int\sin{(x)}dx=-\cos{x}$$ для его оценки: 92)}}{2}\right)$$

Оцените степени:

$$-\frac{\cos{(1)}}{2}-\left(-\frac{\cos{(0 )}}{2}\right)$$

Если перед выражением в скобках стоит $$-$$, мы меняем знак каждого члена выражения и удаляем скобки:

$$- \frac{\cos{(1)}}{2}+\frac{\cos{(0)}}{2}$$

Помните, что значение $$\cos{(0)}$$ равно $$1$$, поэтому подставьте это значение в выражение:

$$-\frac{\cos{(1)}}{2}+\frac{1}{2}$$

92}dydx$$

Обратите внимание, что интеграл должен сначала вычисляться как $$y$$, но это не интеграл из таблицы интегралов и не может быть решен ни одним из наших стандартных методов.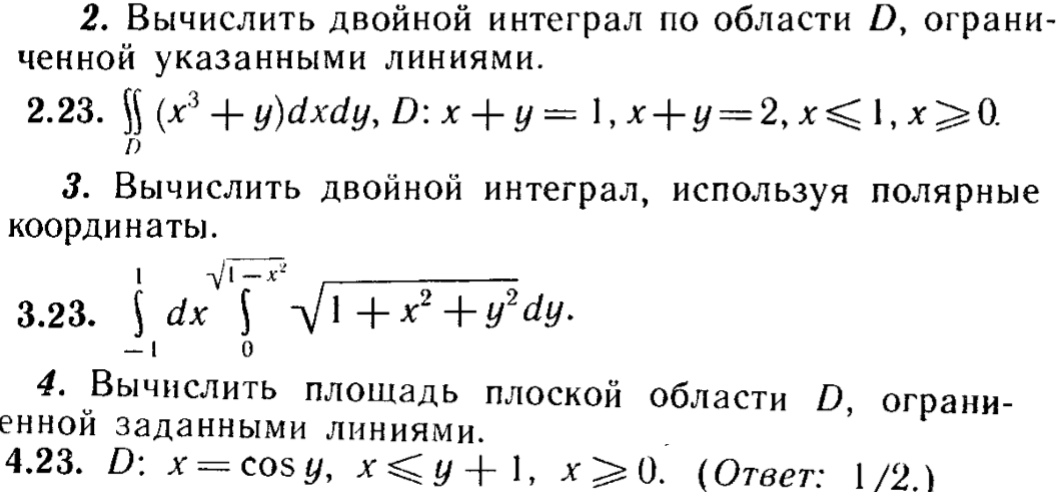 Итак, давайте попробуем изменить порядок интегрирования! Прежде всего, запишем пределы как внутреннего, так и внешнего интегралов в виде неравенств:

$$x\leq y\leq2$$

$$0\leq x\leq 2$$

Обратите внимание, что $$x$$ больше или равно $$0$$ и меньше или равно $$y$$. Сохраняя связь между нашими переменными, перепишем неравенства в виде составного неравенства: 94}+\frac{1}{2}$$

Не так уж и плохо, правда? Вы можете сделать это самостоятельно, если помните эти шаги:

Резюме исследования

При необходимости измените порядок интегрирования, чтобы упростить вычисление интегралов.
Вычислите внутренний интеграл.
Вычислите определенный интеграл. 9{16}-1}4$$
$$-\cos{(1)}+\sin{(1)}$$
$$-27\cos{(27)}+\sin{(27)}$$

Если вы запутались или боретесь, сделайте глубокий вдох и возьмите свой телефон (правда). Откройте приложение Photomath, отсканируйте задачу и вздохните с облегчением, когда мы шаг за шагом проведем вас через эту сложную задачу.

Файл: Лекция 1.doc — Страницы №№1-4

Рис. 1.4

Двойные интегралы. Определение двойных интегралов. Повторные интегралы. Тройные интегралы

1. ДВОЙНЫЕ ИНТЕГРАЛЫ

1.1. Определение двойных интегралов

1.2. Повторные интегралы

1.3. Расстановка пределов интегрирования

Основные свойства двойного интеграла. Определение двойного интеграла Теорема о вычислении двойного интеграла

1.1. Определение двойного интеграла

1.2. Повторные интегралы

Рис. 1.4

1.3. РАССТАНОВКА ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ

Вычисление двойного интеграла в прямоугольных декартовых координатах

Исчисление III. Повторные интегралы

Раздел 4-2: Повторные интегралы

Факт

Повторный интеграл – определение, формула и примеры

Определение повторного интеграла

Повторные интегралы — Photomath

Почему повторные интегралы так полезны?

Как решать повторные интегралы

Резюме исследования

Добавить комментарий Отменить ответ