Преобразование координат при повороте осей: 2.5. Изменение координат При повороте координатных осей

Содержание

2. Поворот осей координат

Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остается неизменным.

, или .

Получаем координаты точки в системе :

Тогда

Полученные формулы называются формулами поворота осей. Они позволяют определить старые координаты произвольной точки через новые координаты этой же точки , и наоборот.

На плоскости возможны одновременно два вида преобразований: параллельный перенос и поворот осей координат.

1.3. Полярная система координат

Декартовая система координат дает удобный, но не единственный способ определения положения точек плоскости при помощи чисел.

Другой практически важной системой координат является полярная система координат

Полярная система координат задается точкой , которая называется полюсом, лучом , называемым полярной осью, и единичным вектором того же направления, что и луч .

Числа  и  называются полярными координатами точки , пишут , при этом  называют полярным радиусом,   полярным углом.

Для получения всех точек плоскости достаточно полярный угол  ограничить промежутком (или ), а полярный радиус  . В этом случае каждой точке плоскости (кроме ) соответствует единственная пара чисел  и , и обратно.

Установим связь между прямоугольными и полярными координатами.

, где .

Если эти формулы разрешить относительно  и , то получим следующие формулы:

Чтобы определить величину угла , лучше использовать формулу , при этом устанавливается (по знакам и ) четверть, в которой лежит искомый угол, и учитывается, что (или ).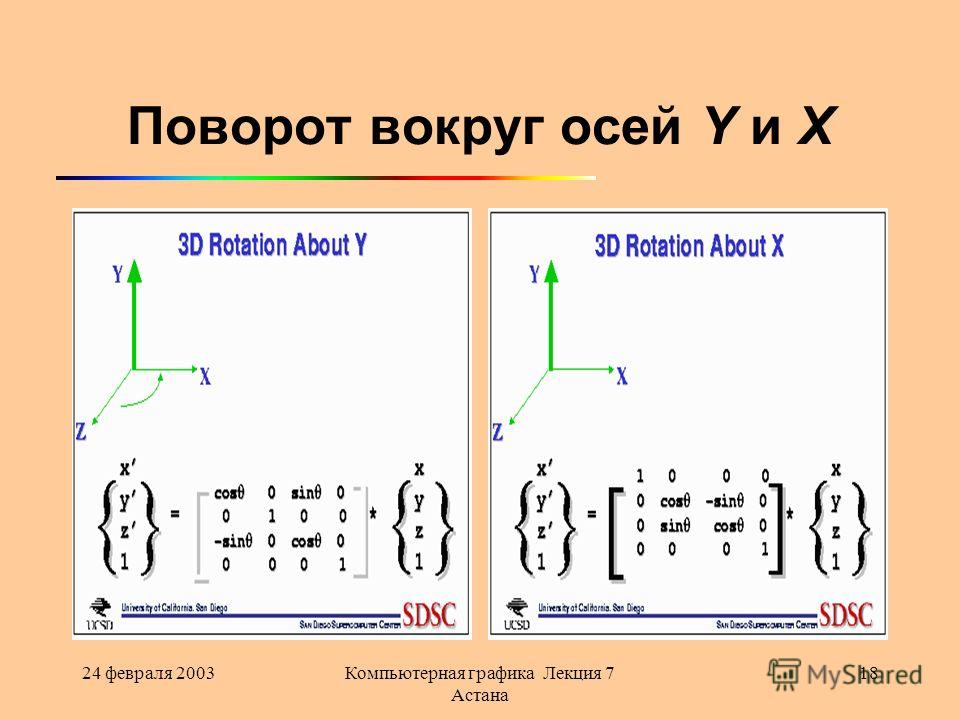

Пример 1.1. Построить точки, заданные полярными координатами:

Найти координаты точек в декартовой системе координат.

Решение.



Пример 1.2. Найти полярные координаты точки .

Решение. , следовательно, точка лежит в третьей четверти. Находим  и :

 .

Учитывая, что , получаем . Таким образом, получаем точку .



1.4. Линии на плоскости

Выше были введены координаты точек (декартовы или полярные) на плоскости, т.е. указан способ задания точек с помощью пары чисел. Метод координат в геометрии в том и состоит, что посредством координат точек геометрические объекты задают аналитически с помощью чисел, уравнений, неравенств или их систем. А это дает возможность при решении задач, доказательстве теорем использовать аналитические методы.

Метод координат на плоскости используется в геометрии для изучения линий. Линия (или кривая) плоскости задается как множество точек, обладающих некоторым только им присущим геометрическим свойством. Например, прямая, окружность, парабола, синусоида и т.д.

Линию (кривую) на плоскости можно задать:

1) уравнением в декартовой системе ;

2) уравнением в полярной системе координат;

3) параметрически;

4) векторным уравнением.

Уравнением линии (или кривой) на плоскости называется такое уравнение с двумя переменными, которому удовлетворяют координаты и каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Так, для того чтобы установить, лежит ли точка на данной линии, достаточно проверить (не прибегая к геометрическим построениям), удовлетворяют ли координаты точки уравнению этой линии в выбранной системе координат.

Задача о нахождении точек пересечения двух линий, заданных уравнениями и , сводится к отысканию точек, координаты которых удовлетворяют уравнениям обеих линий, т.е. сводится к решению системы двух уравнений с двумя неизвестными:

Если эта система не имеет действительных решений, то линии не пересекаются.

Уравнение называется уравнением данной линии в полярной системе координат, если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению.

Линию на плоскости можно задать параметрически при помощи двух уравнений:

где и  координаты произвольной точки , лежащей на данной линии, а  переменная, называемая параметром; параметр определяет положение точки на плоскости. Если параметр изменяется, то точка на плоскости перемещается, описывая данную линию. Система из двух уравнений называется параметрическими уравнениями линии.

Чтобы перейти от параметрических уравнений линии к уравнению вида , надо каким-либо способом из двух уравнений исключить параметр . Однако, заметим, такой переход не всегда целесообразен и не всегда возможен.

Пример 1.3. Построить линию, которая задана параметрически:

Составить уравнение линии в декартовой и полярной системе координат

Решение.

В первом уравнение выразим через , и подставим во второе уравнение:

 или

В полученное уравнение в декартовой системе координат подставляем , , и выражаем :

;

 уравнение данной прямой в полярной системе координат.



Пример 1.4. Составить уравнение окружности с центром в начале координат и радиусом : в декартовой, в полярной системе координат и параметрически.

Решение. Напомним, что окружность радиуса есть множество всех точек плоскости, удаленных на расстоянии от некоторой фиксированной точки (центра окружности).

В уравнение окружности в декартовой системе координат вместо и подставляем , , и выражаем :

;

 уравнение окружности в полярной системе координат.

В качестве параметра можно взять угол поворота точки при движении по окружности. Тогда

 параметрические уравнения окружности. 

Линию на плоскости можно задать векторным уравнением , где  скалярный переменный параметр.

Каждому значению соответствует определенный вектор плоскости. При изменении параметра конец вектора описывает

Векторное уравнение и параметрические уравнения линии имеют механический смысл. Если точка перемещается на плоскости, то указанные уравнения называются уравнениями движения, а линии – траекторией точки, параметр при этом есть время.

В аналитической геометрии на плоскости возникают две основные задачи:

1) зная геометрические свойства кривой, найти ее уравнение;

2) зная уравнение кривой, изучить ее форму и свойства.

Приведем примеры некоторых кривых, и укажем их уравнения:

Преобразование координат в двумерной системе

Преобразования координат в двумерной системе.

В двумерной системе координат можно выделить следующие простейшие (базовые) преобразования координат:

— перенос точки на заданный вектор;

— поворот точки на заданный угол относительно начала координат;

— перенос системы координат на заданный вектор;

— поворот системы координат на заданный угол;

— зеркальное отображение точки относительно координатной оси X;

— зеркальное отображение точки относительно оси Y;

— смена направление координатной оси;

— изменение масштаба координат по оси X;

— изменение масштаба координат по оси Y.

Рассмотрим эти базовые преобразования.

Перенос точки на заданный вектор.

Перенос точки А на заданный вектор U иллюстрируется ниже приведенным рисунком (Рис. 5.1‑2). Решение задачи рассматриваемого преобразования сводится к определению на основании старых координат новых координат заданной точки после ее перенесения на заданный вектор

Рис. 5.1‑2

Из приведенного рисунка видно, что новые координаты точки после рассматриваемого преобразования рассчитываются следующим образом:

x_a_’= x_a + u_x;

y_a_’= y_a + u_y. (5.1-1)

Перенос системы координат на заданный вектор

Перенос системы координат на заданный вектор U иллюстрируется следующим рисунком (Рис. 1.1‑3).

Рис. 5.1‑3

Координатные оси после перенесения системы обозначены как X’,Y’.

Из рисунка видно, что координаты точки А в новой системе координат X’0’Y’ будут определяться как:

x_a’ = x_a — u_x;

y_a’ = y_a – u_y. (5.1-2)

Сравнив выражение (5.1-1) и (5.1-2), можно сделать вывод, что преобразование типа «перенос системы координат на вектор U » эквивалентно обратному преобразованию типа «перенос точки на вектор U » (т. е. переносу точки на вектор –U).

Зеркальное отображение положения точки относительно координатной оси.

Зеркальное отображение точки А относительно координатных осей X и Y приведено на Рис. 1.1‑4.

Новые координаты при этих преобразовании определяются следующим образом.

Рис. 5.1‑4

При зеркальном отображении относительно оси Y (Рис. 1.1‑4a) имеем:

x_a_’=- x_a_.

При зеркальном отображении относительно оси X (Рис. 1.1‑4 b) имеем:

y_a_’=- y_a.

Смена направление осей координат иллюстртруется ниже приведенным рисунком (Рис. 5.1‑5).

Рис. 5.1‑5

Новое положение координатных осей X, Y на рисунке обозначено как X’, Y’.

Смена направленности оси X иллюстрируется на Рис. 5.1‑5a).

Как видно из рисунка, данное преобразование предполагает нахождение новых координат точки следующим образом.

x_a_’=- x_a_.

При смене направленности оси Y (Рис. 5.1‑5b) имеем:

y_a_’=- y_a.

Изменение масштабов по координатным осям предполагает следующие преобразования координат точки A:

x_a’= n x_a;

y_a’= m y_a,

где n и m — вводимые масштабные коэффициенты, соответственно, по координатным осям X и Y.

Поворот точки относительно начала координат.

Данное преобразование, предполагающее поворот точки на заданный угол относительно начала координат, иллюстрируется ниже приведенным рисунком (Рис. 1.1‑6).

Рис. 5.1‑6

На приведенном рисунке приняты следующие обозначения:

— B,B’ – соответственно, старое и новое положение точки при повороте относительно начала координат;

— a- угол поворота.

Очевидно, что новые координаты в общем случае ищутся согласно соотношениям:

x_b_’= c x_b_{+ d y_b; (5. 1-3)}

y_b_’= e x_b_{+ f y_b. (5.1-4)}

Для нахождения коэффициентов c,d,e,f этих выражений рассмотрим два частных случая.

Рассмотрим сначала поворот на заданный угол a единичного вектора по координатной оси X (Рис. 1.1‑7).

Рис. 5.1‑7

Новые координаты единичного вектора U после поворота на угол a определяются следующим образом:

x_v’_{= 1*cos a= c x_b+ d y_b= c*1 + d*0,}

откуда с = cos a;

y_v’_{= 1*sin a = e x_b+ d y_b= e*1+f*0,}

откуда e = sin a.

Рассмотрим теперь поворот на заданный угол единичного вектора U по оси Y (Рис. 1.1‑8).

Новые координаты вектора U после поворота на угол a определяются следующим образом:

x_U_’= -1*sin a= c x_U_{+ d y_U_{= c*0 + d*1,}}

откуда d = -sin a;

y_U_’= 1*sin a = e x_U_{+ d y_U_{= e*1+f*0,}}

откуда e = sin a.

координатной оси y ().

Рис. 5.1‑8

Подставив полученные значения для коэффициентов в выражение (5.1-3) и (5.1-4), будем иметь аналитические выражения для расчета новых значений

координат для преобразования типа поворота относительно начала координат:

x_b_’= x_b cos a — y_b sin a; (5.1-5)

y_b’= x_b sin a + y_b cos a. (5.1-6)

Легко показать, что преобразование типа поворота системы координат относительно ее начала соответствует обратному преобразованию типа «поворот точки относительно начала координат » .

Сложные преобразования координат

Сложные преобразования координат реализуются через соответствующую последовательность базовых преобразований.

Для примера рассмотрим преобразования, имеющие место при повороте точки относительно произвольного вектора U.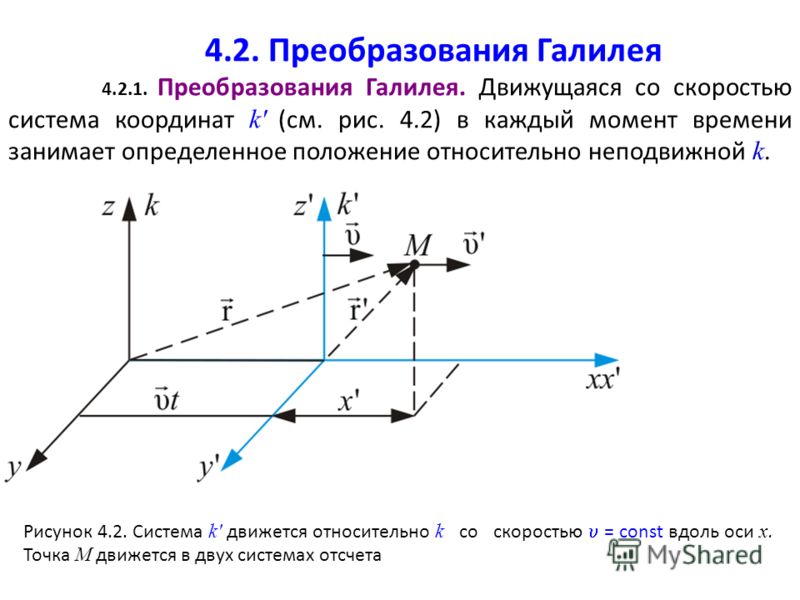

Заданное преобразование иллюстрируется ниже приведенным рисунком (Рис. 5.1‑9).

Рис. 5.1‑9

Заданное преобразование можно выполнить, реализовав три следующие базовые преобразования.

1. Перенос начало исходной системы координат в точку, принадлежащую заданному вектор (например, начальную точку вектора).

2. Поворот в новой системе координат точки на заданный угол.

3. Возврат в исходную систему координат.

На Рис. 1.1‑10 приведена последовательность описанных базовых преобразований.

Рис. 5.1‑10

Исходная система координат перемещается на вектор V и образуется новая система координат X’0’Y’, в которой заданный поворот является базовым поворотом относительно начала новой системы координат X’0’Y’.

Координаты заданной точки A в новой системе координат рассчитываются как:

x_a’= x_a — v_x= x_a — x_c;

y_a’= y_a — v_y= y_a — y_c.

Заданный поворот является базовым поворотом в новой системы координат X’0’Y’, поэтому для координат точки после поворота на угол a относительно точки 0’, используя уравнения (5.1-4) и (5.1-5), будем иметь:

x_a_’’= x_a_’ cosa — y_a_’sina= (x_a -x_c)cosa-(y_a -y_c) sina;

y_a_’’= x_a_’ sina — y_a_’cosa= (x_a -x_c) sina + (y_a -y_c) cosa.

После выполнения поворота относительно заданного вектора, система координат перемещается на вектор –V, т.е. осуществляется возврат в заданную систему координат X0Y. Координаты точки ищутся как:

x_a_’’’= x_a_’’ + x_c_{= (x_a — x_c) cosa — (y_a — y_c) sina + x_c;}

y_a’”= y_a’’ + y_c = (x_a — x_c) sina + (y_a — y_c) cosa. + y_c .

Базовые преобразования удобно представлять в виде матриц. В этом случае последовательности базовых преобразований, реализующих сложное преобразование, представляется в виде произведения соответствующих матриц базовых преобразований.

Соотношения новых и старых координат при повороте на угол a относительно начала координат, в матричной форме могут быть представлены в виде:

где:

Обратное преобразование рассматриваемого поворота будет задаваться с помощью матрицы:

Преобразования типа «перенос точки на вектор » нельзя отобразить с помощью матриц, размерностью «два на два » . Но для этого преобразования также можно использовать матричную форму, если представить координаты точки в однородной системе координат:

где:

a,b- параметры вектора переноса.

Обратное преобразование типа переноса задается в виде матрицы:

Матрица смены направленности оси X имеет вид:

Матрица зеркального отображения точки относительно координаты Y имеет точно такой вид.

Матрица смены направленности оси Y имеет вид:

Матрица зеркального отображения точки относительно координаты X имеет точно такой вид.

Матрица изменения масштабов по координатным осям имеет вид:

Люди также интересуются этой лекцией: 3.3 Построение модели изучаемой системы.

— где n и m — вводимые масштабные коэффициенты, соответственно, по координатным осям X и Y.

Преобразование типа «поворот относительно произвольного вектора » , начало которого находится в точке (a,b,c), можно реализовать в матричной форме следующим образом:

Обозначение матрицы знаком «* » означает использование расширенной матрицы. В выше приведенном выражении матрица R(a), соответствующая повороту относительно начала координат, берется в расширенной форме (добавлены одна колонка и одна строка, имеющие все нулевые элементы, кроме элемента на их пересечении, который равен «1 » ).

Основы координатной геометрии — Вращение осей

В этом уроке мы обсудим вращение координатных осей вокруг начала координат.

То есть, как изменятся координаты точки P(x, y) , если оси повернуты вокруг начала координат на угол θ ?

Вращение осей

Предположим, есть точка P(x, y) на плоскости XY .

И, предположим, мы повернули начало координат на угол θ против часовой стрелки.

Какими будут координаты P относительно новых осей?

Чтобы найти новые координаты, то есть x’ и y’ , нам нужно расстояние P от повернутых осей, выраженное в x , y и 0 .

Давайте посчитаем. Вот рисунок в помощь.

Давайте немного увеличим масштаб и пометим несколько точек.

Перпендикуляры от 9 тоже сбросил0003 D по OX и PB . Хорошо, останься со мной.

Теперь PA = x и PB = y (старые координаты). Кроме того, PC = x’ и PD = y’ (новые координаты).

В ΔPFD мы имеем ∠DPF = θ (выясните, почему). Это означает, что

PF = y’cosθ …I

Кроме того,

FD = y’sinθ

⇒ BE = y’sinθ (0, поскольку0004)… II

в Δdoe ,

OE = ODCOSθ

⇒ OE = CPCOSθ (с OD = CP )

⇒ OE = X’COSθ

⇒ x’cosθ

⇒ x’cosθ )

DE = ODSINθ

⇒ DE = X’Sinθ (с OD = CP = X ‘)

⇒ FB = X’Sinθ (с FB = DE )… IV

Мы почти закончили. Вернем фигуру.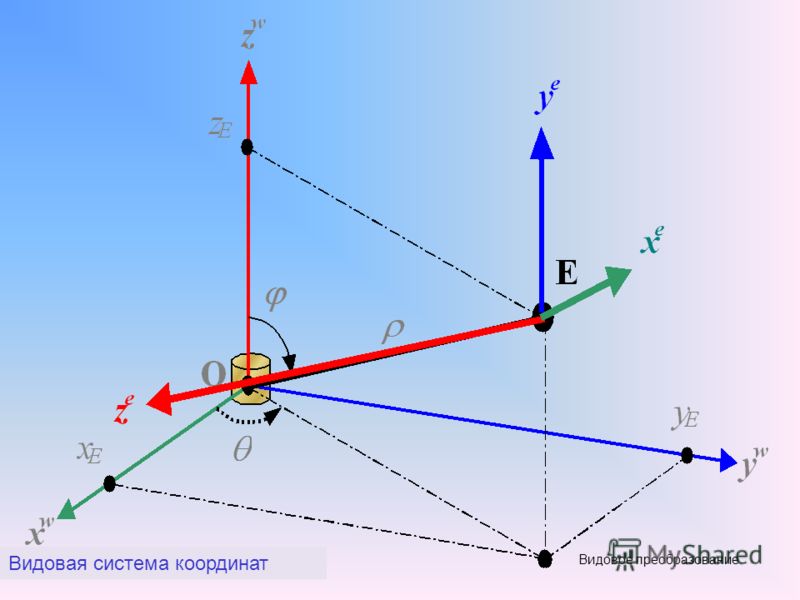

Сейчас,

PA = OB

⇒ x = OB (с PA = x )

⇒ x = OE — BE

⇒ x = x’cosθ — y»sinθ (с использованием II и III)

Аналогично,

Y = PB

⇒ Y = FB + PF

⇒ y = x’Sinθ + y’cosθ (с использованием IV и I)

Вот и все! Мы получили соотношение между старыми координатами ( x и y ) и новые ( x ‘ и y’ ):

x = x’cosθ — y’sinθ

y = x’sinθ + y’cosθ

Возможно, вы захотите вернуться к расчетам. Я предлагаю вам попробовать вывести это снова самостоятельно.

Мы также можем явно выразить x’ и y’ через x и y . Я пропущу расчеты здесь. Получим:

x’ = xcosθ + ysinθ

y’ = ycosθ – xsinθ

Вот симуляция, показывающая, как изменяются координаты точки при повороте осей вокруг начала координат.

Вы можете перетащить синюю точку, чтобы изменить угол поворота. Точку P также можно перетаскивать. Удовлетворяют ли старая и новая координаты полученному соотношению?

Резюме урока

Пусть P(x, y) будет точкой на плоскости XY . Пусть оси повернуты вокруг начала координат на угол θ против часовой стрелки. Тогда относительно повернутых осей координаты P , т. е. (x’, y’) , будут равны: ‘sinθ + y’cosθ

На следующем уроке мы обсудим несколько примеров, связанных с перемещением и вращением осей. Увидимся там!

линейная алгебра — Преобразование координат (вращение)

Вопрос задан 5 лет, 6 месяцев назад

Модифицированный 5 лет, 6 месяцев назад

Просмотрено 289 раз

$\begingroup$

Матрица вращения точки $(x,y)$ в декартовых координатах против часовой стрелки равна $$\begin{pmatrix}cosθ & -sinθ \\ sinθ & cosθ\end{pmatrix}$$

Когда вращая систему координат против часовой стрелки, вместо одной точки, используем ли мы ту же матрицу?

(Причина, по которой я спрашиваю об этом, заключается в том, что я видел в некоторых книгах, что матрица для преобразования системы координат является транспонированием этого. И это вызвало много путаницы.)
линейная алгебра
евклидова геометрия
линейные преобразования
системы координат
$\endgroup$
8
$\begingroup$
Когда вы вращаете систему координат, на самом деле вы вращаете базисные векторы системы координат. Это просто отдельные векторы, как и любой другой вектор, который вы хотите повернуть, поэтому матрицы преобразования не изменяются.
9Т$.
Если вы хотите повернуть $T$ на $\theta$ против часовой стрелки, вы можете

напрямую повернуть $T$, используя вашу матрицу, или
повернуть базисные векторы в в противоположном направлении , то есть повернуть их на угол $-\theta$.
Во втором случае, поскольку $\cos (-\theta) = \cos \theta$ и $\sin(-\theta) = -\sin\theta$, вы получите транспонирование матрицы из первого кейс.
No related posts.