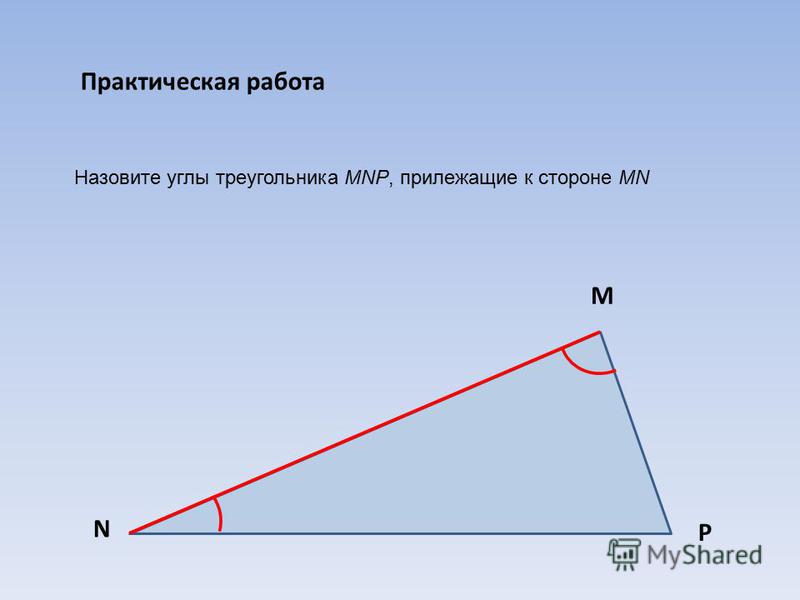
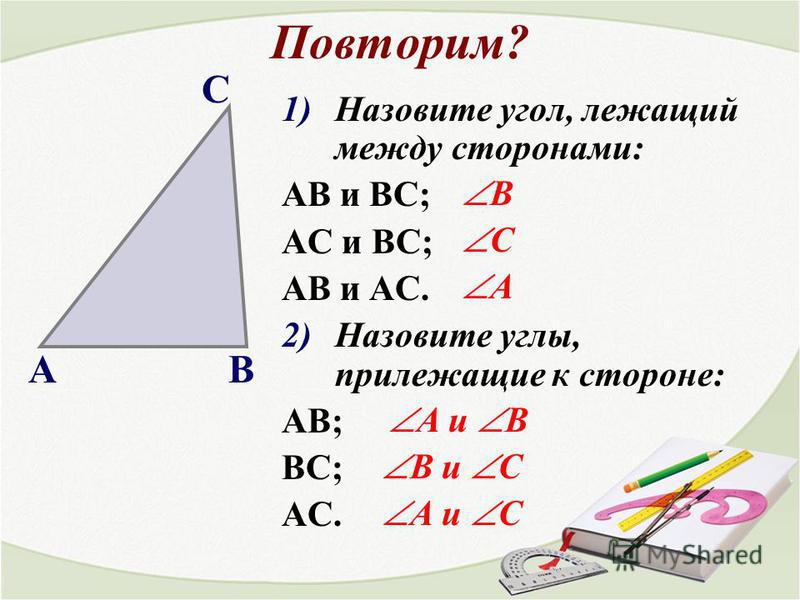
Обозначения: А, В, С — вершины, а также углы при этих вершинах; а, b, с — стороны, противолежащие углам ha , hb , hc — высоты, опущенные на стороны а, b, с соответственно; ma , mb , mc — медианы; la , lb , lc — биссектрисы; R — радиус описанной окружности; r — радиус вписанной окружности.
|
| ||||||||||||
|
| ||||||||||||
Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника: |
| ||||||||||||
Высоты треугольника пересекаются в одной точке О, называемой ортоцентром В тупоугольном треугольнике ортоцентр лежит вне треугольника. |
| ||||||||||||
Медианы треугольника пересекаются в одной точке О, являющейся центром тяжести треугольника. Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины).
| |||||||||||||
Биссектрисой угла называется луч, делящий угол пополам. Биссектрисы треугольника пересекаются в одной точке, являющейся центром впмсанной окружности. | |||||||||||||
| Два треугольника называются равными, если при наложении друг на друга они совместятся.
и соответственные углы равны
| ||||||||||||
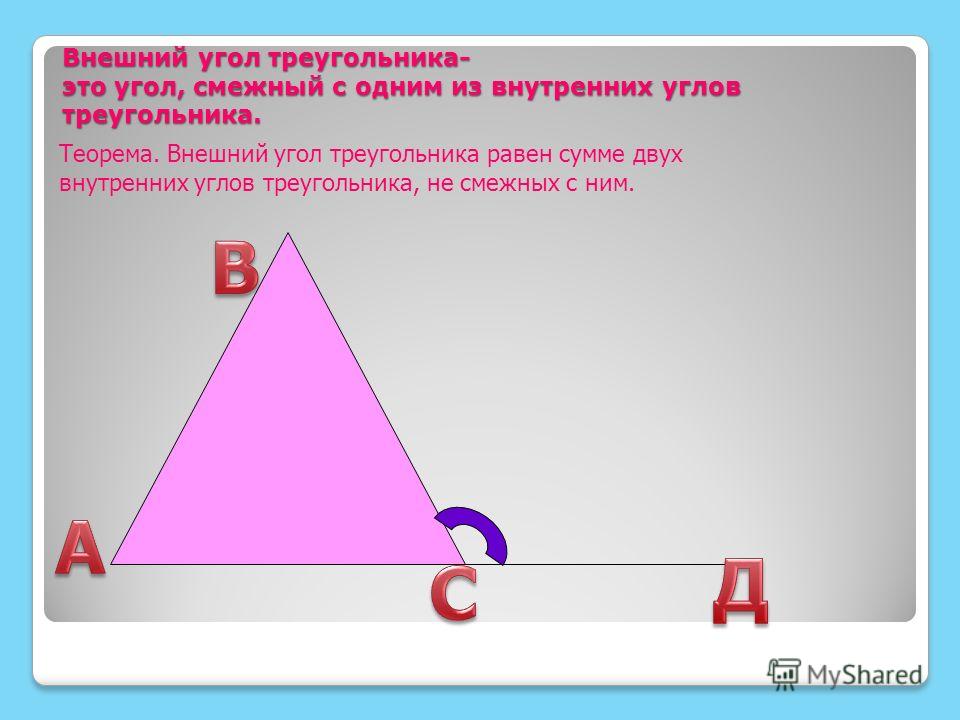
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
|
| ||||||||||||
|
| ||||||||||||
Медиана, биссектриса, высота |
| ||||||||||||
Высоты и стороны треугольника | |||||||||||||
Теорема косинусов |
| ||||||||||||
Теорема синусов | |||||||||||||
Теорема тангенсов |
| ||||||||||||
Теорема Пифагора |
| ||||||||||||
|
| ||||||||||||
Свойства равнобедренного треугольника
Главная » геометрия
Обновлено
Свойства равнобедренного треугольника 7 класс.
Свойства медианы, высоты, биссектрисы в равнобедренном
треугольнике. Равнобедренный треугольник свойства,
признаки, определения.
Равнобедренный треугольник — это треугольник,
у которого длины двух сторон равны.
Также, любой треугольник, у которого длины всех сторон
равны, является равнобедренным, исходя из определения.
В равнобедренном треугольнике,принято называть стороны
иначе. Две равные стороны называют боковыми, третью
же сторону называют основанием. Кроме того, углы,
прилежащие к основанию, называют углами при основании.
Стоит заметить, что равносторонний, как и равноугольный
треугольник, являются частными случаями равнобедренного треугольника.
Треугольник, может быть, одновременно равнобедренным и
прямоугольным треугольником, то есть сочетать свойства
одного и другого треугольника.
Такие треугольники называют
прямоугольными равнобедренными треугольниками.
Если в треугольнике градусные меры двух углов равны, а
также длины двух сторон равны, то, можно с уверенностью
сказать, что треугольник является не только равнобедренными,
но и обладает характерными только для него признаками и свойствами.
Благодаря знанию признаков и свойств равнобедренного
треугольника, в задаче, мы можем: понять чем отличается
равнобедренный треугольник от данного в задаче треугольника,
воспользоваться формулой равнобедренного треугольника, и главное
решить задачу, где требуется знание свойств и признаков.
Главное свойство равнобедренного треугольника:
две стороны имеют одинаковую длину, и не равны третьей.
Свойства равнобедренного треугольника
- Равнобедренный треугольник имеют ось симметрии,
эта ось проходит через середину основания и угол, который
образован двумя боковыми сторонами.
- Длины двух сторон равнобедренного треугольника
равны между собой, но не равны третьей стороне. - Ось симметрии равнобедренного треугольника имеет
некоторые отличия, она совпадает: с медианой, которая
проведена к основанию; высотой, проведённой из
вершинного угла; с серединным перпендикуляром. - Медианы, биссектрисы, высоты равнобедренного треугольника,
которые проведены из углов при основании, имеют равную длину. - Центр описанной и вписанной окружности равнобедренного
треугольника, лежит на отрезке, который соединяет середину
основания и вершину треугольника, от которой можно
провести высоту к основанию. - Углы, которые лежат при основании, имеют одинаковую градусную меру, равны.
- Существуют названия сторон и углов, характерный только для равнобедренного
треугольника — боковые стороны, углы при основании, вершинный угол. - Биссектриса равнобедренного треугольника, которая
проведена к основанию, является медианой и высотой. - Высота равнобедренного треугольника, которая
проведена к основанию, является медианой и биссектрисой. - Медиана равнобедренного треугольника, которая
проведена к основанию, является высотой и биссектрисой. - Сумма внутренних углов равнобедренного треугольника 180 градусов.
- При основании равнобедренного треугольника углы всегда острые.
Определения равнобедренного треугольника
- Высота равнобедренного треугольника — это отрезок перпендикуляра,
опущенного из вершины равнобедренного треугольника на его основание. - Медиана равнобедренного треугольника — это отрезок, который соединяет
вершину с серединой противоположной стороны равнобедренного треугольника. - Биссектриса равнобедренного треугольника — это луч, который исходит из
вершины угла равнобедренного треугольника и делящий этот угол на два равных угла. - Боковая сторона равнобедренного треугольника — это сторона, которая
имеет равную длину с противоположной ей стороне равнобедренного треугольника. - Основание равнобедренного треугольника — это сторона,
которая не равна никакой другой стороне. - Угол при основании равнобедренного треугольника — это угол
равнобедренного треугольника, лежащий при основании.
Что такое Теорема о внешнем угле?
Полное руководство по теореме о чередующихся внешних углах с примерами треугольников
Что такое Теорема о внешнем угле?
Содержание
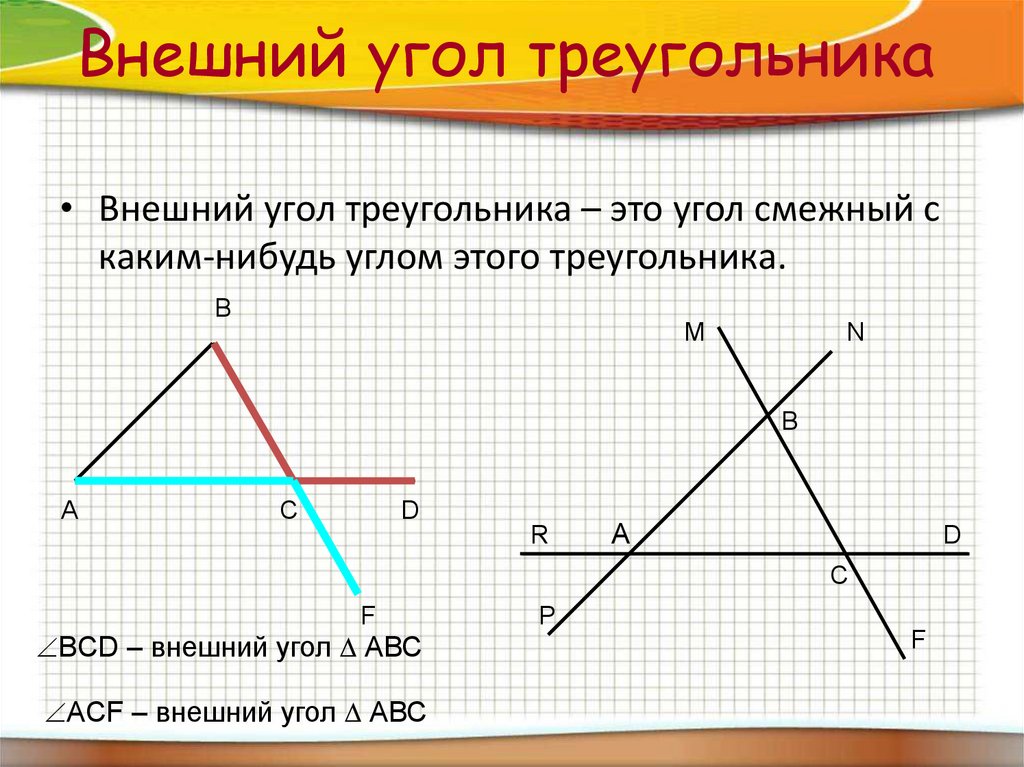
Внешний угол треугольника образован продолжением любой стороны треугольника. Внешний угол лежит не только вне треугольника, но и примыкает к внутреннему углу.
Теорема о внешнем угле также утверждает, что мера внешнего угла треугольника больше любого из двух противоположных внутренних углов (дальних внутренних углов).
Альтернативные внешние углы Теорема
Характеристики
- Внешний угол всегда равен сумме противоположных внутренних углов.
- Внешний угол всегда больше любого из двух удаленных внутренних углов.
- Внешний угол всегда дополняет смежный с ним внутренний угол.
Использование
Теорему о внешнем угле можно использовать для нахождения величин неизвестных внутренних и внешних углов треугольника.
Важность
Теорема о внешнем угле — одна из важных теорем треугольника. С помощью теоремы о внешнем угле можно легко найти неизвестные внутренние и внешние углы треугольника.
Теорема о внешнем угле треугольника
ФормулаКак показано на рисунке выше, внутренними углами треугольника являются угол 1, угол 2 и угол 3.
Угол 4 — это внешний угол, смежный с углом 3.
Угол 1 и угол 2 являются внутренними углами, противоположными внешнему углу 4. Внешняя теорема гласит, что мера внешнего угла треугольника равна сумме двух удаленных внутренних углов (противолежащих внутренних углов). ).
m∠1 + m∠2 = m∠4
Теорема о внешнем угле гласит, что мера внешнего угла треугольника больше любого из двух противоположных внутренних углов.
м∠4 > м∠1
м∠4 > м∠2
Wh at являются внешними углами треугольника?
Внешние углы треугольника — это углы, образующие смежную пару с внутренними углами за счет продолжения сторон треугольника.
Пример
В приведенном ниже треугольнике показаны внешние и внутренние углы.
Примеры теоремы о внешнем угле
Как найти внешний уголПример 1
Треугольник ABC, m∠B = 45°, m∠C = 75°.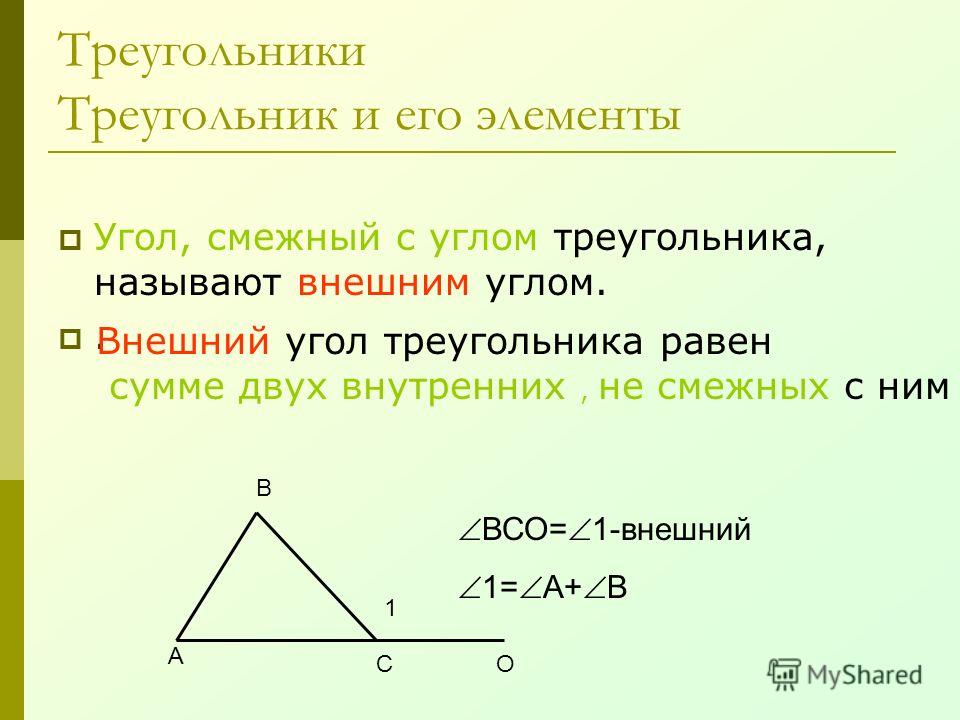
Найдите внешние углы.
Решение:
Мера внешнего угла, смежного с углом A = m∠B + m∠C = 45° + 75° = 120°.
Чтобы найти величину других внешних углов
Сначала найдите неизвестный внутренний угол.
Мы знаем, что сумма внутренних углов треугольника = 180°.
м∠А + м∠В + м∠С = 180°
м∠А + 45° + 75° = 180°
м∠А = 60°
Измерение внешнего угла, прилегающего к углу В = м ∠А + м∠С = 60° + 75° = 135°.
Мера внешнего угла, смежного с углом C = m∠A + m∠B = 60° + 45° = 105°.
Пример 2
В треугольнике ABC внешний угол в точке D представлен числом 5x + 11. Если два несмежных внутренних угла представлены числами 2x + 8 и 4x – 17, найдите значение x.
Решение:
Теорема о внешнем угле утверждает, что мера внешнего угла треугольника равна сумме двух несмежных внутренних углов.
Следовательно,
5x + 11 = (2x + 8) + (4x – 17)
5x + 11 = 6x – 9
x = 20
Пример 3
Найдите меру внешнего угла основание равнобедренного треугольника, угол при вершине которого равен 35°.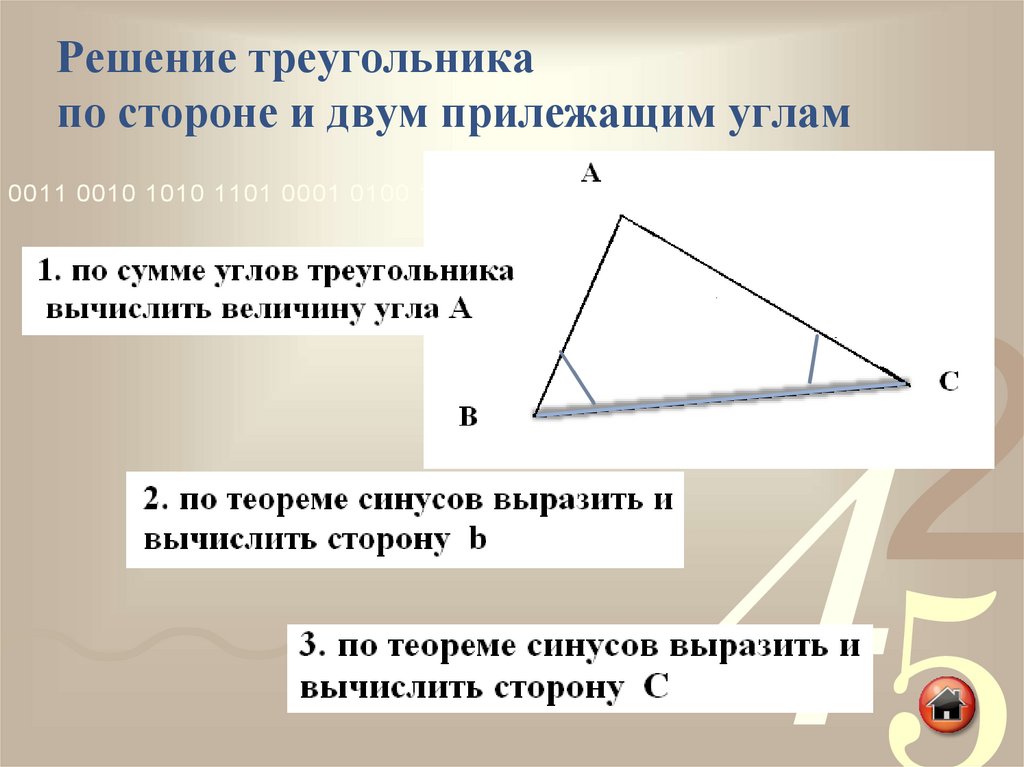
Решение:
Как мы знаем, что две стороны равнобедренного треугольника равны. Углы, противоположные равным углам, также равны. Два угла при основании равнобедренного треугольника равны, поэтому мы можем принять каждый за x.
х + х + 35 = 180 (Сумма внутренних углов треугольника равна 180°).
2x + 35 = 180
2x = 180 – 35
2x = 145
x = 72,5
Итак, внешний угол равен сумме двух несмежных внутренних углов.
Следовательно,
? = 72,5° + 35°
? = 107,5°
Пример 4
Найдите x в приведенном ниже треугольнике и, следовательно, найдите m∠ABD.
Решение:
∠C и ∠D — несмежные внутренние углы внешнего угла ABD. Теорема о внешнем угле гласит, что внешний угол равен сумме двух несмежных внутренних углов.
∠ABD = ∠C + ∠D
20x = 7x + 5 + 60
20x – 7x = 65
13x = 65
x = 5
м∠ABD = 20x
м∠ABD = 20(5)
м∠ABD = 100°
Смежная сторона в треугольнике: определения и примеры
Смежная сторона в треугольнике — это сторона, которая находится рядом или имеет общую вершину с другой стороной.
Смежные стороны в треугольнике важны для понимания отношений между сторонами и углами треугольника.
Определения:
- Треугольник: Многоугольник с тремя сторонами и тремя углами.
- Сторона: сегмент линии, являющийся частью границы многоугольника.
- Вершина: Точка, в которой пересекаются две или более линий или сегментов линий.
В треугольнике три стороны и три угла. Стороны треугольника обычно обозначаются как сторона A, сторона B и сторона C. Углы треугольника обычно обозначаются как угол A, угол B и угол C.
В треугольнике есть три пары смежных сторон. Сторона A примыкает к стороне B и стороне C. Сторона B примыкает к стороне A и стороне C. Сторона C примыкает к стороне A и стороне B.
Смежные стороны треугольника важны для понимания отношений между сторонами и углами треугольника. Например, смежные стороны прямоугольного треугольника (треугольник с одним прямым углом) — это стороны, образующие прямой угол.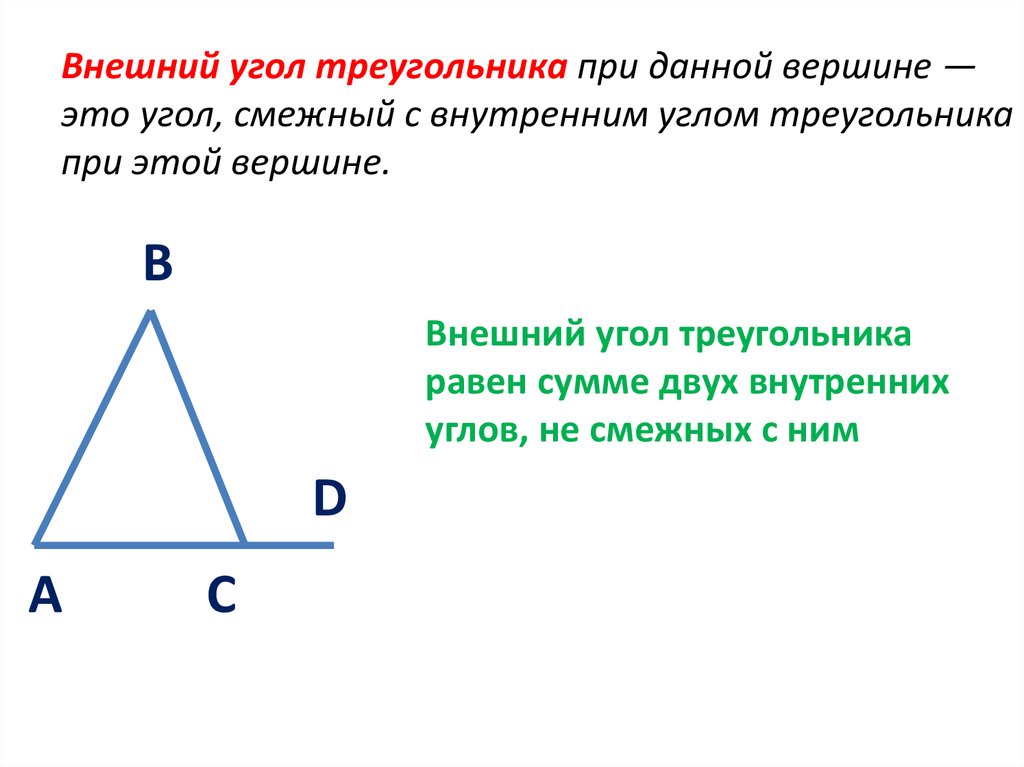
Смежными сторонами равнобедренного треугольника (треугольника с двумя равными сторонами) являются две равные стороны.
Примеры:
Пример 1:
Рассмотрим треугольник со сторонами длины 5, 12 и 13. Сторона A прилегает к стороне B и стороне C. Сторона B примыкает к стороне A и стороне C. Сторона C рядом со стороной A и стороной B.
Пример 2:
Рассмотрим прямоугольный треугольник со сторонами длины 3, 4 и 5. Сторона A является гипотенузой (сторона, противоположная прямому углу) и примыкает к стороне B и стороне C. Сторона B примыкает к сторона А и является одним из катетов прямоугольного треугольника. Сторона С примыкает к стороне А и является другим катетом прямоугольного треугольника.
Пример 3:
Рассмотрим равнобедренный треугольник со сторонами 6, 6 и 8. Сторона A прилегает к стороне B и стороне C. Сторона B примыкает к стороне A и является одной из равных сторон. Сторона C примыкает к стороне A и является другой равной стороной.
Пример 4:
Рассмотрим равносторонний треугольник со сторонами длины 6.