Error
Skip to main content
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Новостной форумКомплексные числа. Основы линейной алгебры. Системы линейных уравнений.Векторная алгебра и аналитическая геометрия.Введение в анализДифференциальное исчисление функции одной переменнойДифференциальное исчисление функции нескольких переменныхИнтегральное исчисление функции одной переменнойКратные, криволинейные и поверхностные интегралы. Элементы теории поляОбыкновенные дифференциальные уравненияТеория функций комплексного переменного. Операционное исчислениеУравнения математической физики. Основы вариационного исчисленияЛинейное программирование. Динамическое программированиеТеория вероятностейМатематическая статистикаРядыДискретная математикаМарковские процессы и системы массового обслуживанияЭлементы теории игрЭкономико-математические моделиЛинейная алгебра для экономистовДискретная математика (2017 г.
 Модульно-рейтинговая система обучения : метод. указания для студентов. I семестр Основы математической статистикиМатематическое моделирование систем и процессов. Часть 1Математическое моделирование систем и процессов. Часть 2Вероятность, случайные процессы, математическая статистикаТеория вероятностейРяды: методическое пособие для самостоятельной работы (с элементами квантования текста)Эконометрика. Дополнительные материалыМетоды оптимальных решений: лабораторный компьютерный практикумВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Приложения дифференциального исчисления функции одной переменнойТеоря вероятностей (случайные события)Математическое моделирование систем и процессов Ч. 3 Теория функций комплексного переменного. Операционное исчисление (Таирова Е.В. Ширяева Н.К.)Эконометрика (продвинутый уровень): учебное пособиеЭконометрика (продвинутый уровень): лабораторный практикумДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковОбыкновенные дифференциальные уравнения и их приложенияМатематическое моделирование (методы оптимизации)Специальные разделы высшей математикиСпециальные разделы высшей математики: практикум Алгебра и геометрия.
Модульно-рейтинговая система обучения : метод. указания для студентов. I семестр Основы математической статистикиМатематическое моделирование систем и процессов. Часть 1Математическое моделирование систем и процессов. Часть 2Вероятность, случайные процессы, математическая статистикаТеория вероятностейРяды: методическое пособие для самостоятельной работы (с элементами квантования текста)Эконометрика. Дополнительные материалыМетоды оптимальных решений: лабораторный компьютерный практикумВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Приложения дифференциального исчисления функции одной переменнойТеоря вероятностей (случайные события)Математическое моделирование систем и процессов Ч. 3 Теория функций комплексного переменного. Операционное исчисление (Таирова Е.В. Ширяева Н.К.)Эконометрика (продвинутый уровень): учебное пособиеЭконометрика (продвинутый уровень): лабораторный практикумДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковОбыкновенные дифференциальные уравнения и их приложенияМатематическое моделирование (методы оптимизации)Специальные разделы высшей математикиСпециальные разделы высшей математики: практикум Алгебра и геометрия.
Приложения двойного интеграла.
Площадь плоской фигуры
(6)
Объем цилиндрического тела, снизу ограниченного частью S плоскости (ху), сверху – поверхностью z=f(x;y), а с боков цилиндрической поверхностью, образующие которой параллельны оси Oz:
(7)
Масса плоской пластинки, занимающей область S и плотность которой задается функцией
(8)
Координаты центра тяжести плоской пластины С(хс;ус)
; (9)
Момент инерции плоской пластины относительно координатных осей
; (10)
Пример. Вычислить площадь плоской фигуры,
ограниченной линиями: х=0, у=5, у=х2+1.
Вычислить площадь плоской фигуры,
ограниченной линиями: х=0, у=5, у=х2+1.
;
Пример. Вычислить массу плоской пластины ограниченной линиями x=0, y=0, y=1-x2, если ее плотность в каждой точке равна абсциссе этой точки, =х;
;
Пример. Вычислить координаты центра тяжести однородной пластинки, ограниченной линиями x=0, y=0, y=1-x2,=const.
;
;
;
; ;
C.
ТРОЙНОЙ ИНТЕРГРАЛ
Пусть
в ограниченной замкнутой пространственной
области V задана непрерывная функция f(x;y;z). Тогда тройной интеграл от этой функции
определяется как
Тогда тройной интеграл от этой функции
определяется как
(11)
Пусть
область V снизу ограниченна поверхностью z1(x;y),
а сверху – поверхностью z2(x;y),
причем 1(x;y)2(x;y).
Проекция Vxy области V на плоскость хОу ограничена линиями: x=a, x=b, y=1(x), y=2(x),
где аb 1х2х хa, b.
Тогда тройной интеграл вычисляется по формуле
(12)
Элемент объема dV в декартовой системе координат равен произведению дифференциалов декартовых координат dV=dxdydz. Формула (12) обычно записывается в виде
(13)
При вычислении интеграла по одной из переменных все другие считаются постоянными
Пример. Вычислить , гдеV ограничена поверхностями: x=0, y=0, y=3x, z=0, z=xy.
Первые четыре уравнения в пространстве задают плоскости, пятое – гиперболический параболоид.
По формуле (13) расставляем пределы интегрирования:
Последовательно вычисляем три определенных интеграла:
;
;
; Таким образом:
.
Часто бывает удобным при вычислении тройного интеграла применять другой порядок интегрирования. Так, если V ограничена поверхностями x1(y;z) и x2(y;z), а ее проекция Vyz на координатную плоскость yOz ограничена линиями: y=a, y=b, z=1(y ), z=2(y), то вычисление тройного интеграла удобнее проводить по формуле:
(14)
Объем тела, занимающего пространственную область V:
(15)
Масса тела плотностью (x;y;z):
(16)
Статические моменты тела с плотностью (x;y;z) относительно координатных плоскостей:
; ;(17)
Координаты центра тяжести объемного тела C(xc; y
; ;(18)
Часто для вычисления
тройного интеграла удобнее перейти к
другой системе координат.
приложений двойных интегралов
приложений двойных интеграловОглавление
Приведены примеры применения двойных интегралов для вычисления объемов и площадей, а также их подробные решения. \(\)\(\)\(\)Вычислить объем с использованием двойного числа
Объем \( V \) тела, находящегося над областью \( R \) в плоскости \(xy\) и ниже поверхности \( z = f(x,y) \), при условии, что \( f (x,y) \ge 0 \), задается двойным интегралом [6] \[ \displaystyle V = \iint_R f(x,y) \;dy \;dx \] 92 \), который представляет собой окружность на плоскости \(xy\) (или \(z = 0\)) с центром в точке \((0,0)\) и радиусом, равным \(2\) Рис.2 — Область \(R\) интегрирования, представляющая собой окружность с центром в точке \((0,0)\) и радиусом, равным \(2\) Поскольку область интегрирования представляет собой окружность, эффективнее использовать двойные интегралы в полярных координатах.
Объем \( V \) вычисляется с помощью двойного интеграла
\( V = \displaystyle \iint_R f(x,y) \;dy \;dx \) , где \( R \) — область интегрирования, определяемая формулой 92}}} \примерно 0,174\)
Пример 3
Найти \( a \) так, чтобы объем тетраэдра, ограниченного плоскостями \( 2x + 2 y + z = a , a \gt 0\), \( y = 2 x \) , \( y = 0 \) и \( z = 0 \) равно \( 10 \) кубических единиц.
Решение примера 3
Ниже показаны плоскости, определяющие тело, объем которого необходимо рассчитать.
Рис.5 – Плоскости, определяющие твердое тело
Сначала найдите область интегрирования, которая представляет собой треугольник, определяемый тремя вершинами: \(O, B\) и \(C\)
\(O\) — начало системы координат.
\( B \) является точкой пересечения и \(x\)-оси и находится путем установки \(z = 0\) и \( y = 0 \) в уравнении данной плоскости \( 2x + 2 у + z = а \).
\( 2x = а \)
Найдите \( x \)
\( х = \dfrac{a}{2} \)
\(C\) является точкой пересечения плоскостей \(2x+2y+z=a\) и \(y=2x\) и находится на плоскости \(xy\). Точка на плоскости \( x y \) имеет \( z = 0 \).
Точка \(C\) получается установкой \(z=0\) в уравнении \(2x+2y+z=a\) решения полученного уравнения
\( 2x + 2 y = a \) и \( y = 2 x \)
Решите приведенное выше путем замены, чтобы получить
\(у = а/3\) и \(х = а/6\)
Следовательно, область \( R \) интегрирования на плоскости \( x y \) представляет собой треугольник с вершинами
\(O(0,0)\) , \( B(a/2,0) \) и \(C(a/6,a/3)\)
Рис. 6 — Область интегрирования
6 — Область интегрирования
Объем \(V\) тетраэдра определяется выражением
\( V = \displaystyle \iint_R f(x,y) \;dy \;dx \) , где \( R \) — область интегрирования, определяемая формулой
\( R: \dfrac{y}{2} \le x \le \\dfrac{a}{2} — y , 0 \le y \le \dfrac{a}{3} \)
92 = 4 \) и прямой \( y = — 1 \).
Ответы на вышеуказанные вопросы
Часть 1:- \( \dfrac{118}{3} \)
- \( 72 \)
- \( 45 \пи \)
- \( \dfrac{8\pi }{3}+\sqrt{3} \)
Дополнительные ссылки
- Вычисления двойных интегралов
- Двойные интегралы по общим областям
- Двойные интегралы в полярных координатах
- Ховард Антон, Irl C. Бивенс, Стивен Дэвис; Исчисление: ранние трансцендентальные; Уилли, 2012 год.
- Гилберт Странг; Массачусетский технологический институт, Исчисление, Wellesley-Cambridge Press, 1 991
- Джоэл Хасс, Калифорнийский университет, Дэвис; Военно-морская аспирантура Мориса Д.
 Вейра; Джордж Б. Томас, младший Массачусетский технологический институт; Университетское исчисление, ранние трансцендентальные, третье издание
, Бостон Колумбус, 2016, Пирсон.
Вейра; Джордж Б. Томас, младший Массачусетский технологический институт; Университетское исчисление, ранние трансцендентальные, третье издание
, Бостон Колумбус, 2016, Пирсон.
Применение двойных интегралов
Этот раздел охватывает…
В главе о линейном интеграле мы ввели понятия среднего значения, центроида и центра масс. Теперь мы распространяем эти идеи на области на плоскости точно таким же образом. Например, формула среднего значения в разделе линейного интеграла была следующей: \(\bar f = \dfrac{\int_C fdx}{\int_C ds}\text{.}\) Для двойных интегралов мы просто меняем \(ds\) в \(dA\text{,}\) и добавить интеграл. Это дает формулу \(\bar f = \dfrac{\iint_R fdA}{\iint_R dA}.\) Та же замена работает для всех интегралов, приведенных выше. Теперь у нас есть \(dm = \delta dA\) вместо \(dm=\delta ds\text{,}\), поскольку теперь плотность представляет собой массу на площадь, а не массу на длину. Мы получили длину дуги кривой \(C\), вычислив \(s=\int_C ds\text{,}\), просто сложив небольшие биты длины дуги. Мы можем получить площадь области \(R\), вычислив \(A=\iint_R dA\text{,}\), поскольку мы просто суммируем небольшие биты площади.
Мы можем получить площадь области \(R\), вычислив \(A=\iint_R dA\text{,}\), поскольку мы просто суммируем небольшие биты площади.
Формула среднего значения
Центр тяжести области \(R\) на плоскости:
\begin{уравнение*} \left(\ bar x = \frac{\iint_R x dA}{\iint_R dA}, \bar y = \frac{\iint_R y dA}{\iint_R dA}\right) \end{уравнение*}Centroid Formula
и центр масс
\begin{уравнение*} \left(\ bar x = \frac{\iint_R x dm}{\iint_R dm}, \bar y = \frac{\iint_R y dm}{\iint_R dm}\right), \text{ где \(dm=\delta dA\) } . \end{уравнение*}Центр масс Формулы 92. \end{уравнение*}
Если объект имеет большую массу, требуется много работы (передача энергии), чтобы заставить объект двигаться. Масса — это сопротивление объекта прямолинейному движению.
Когда что-то вращается, нам нужен удобный способ вычислить его кинетическую энергию. Мы покажем, что кинетическая энергия объекта, который вращается вокруг линии \(L\text{,}\) и имеет угловую скорость \(\omega\) радиан в секунду вокруг линии, точно равна
\begin{уравнение*} KE = \frac{1}{2}I \omega^2, \end{уравнение*} 92) дм . \end{уравнение*}
\end{уравнение*}Если вы никогда раньше не работали с кинетической энергией, вы можете пропустить следующее упражнение и просто попрактиковаться в использовании этих формул.
Упражнение 11.2.1
Предположим, что объект, масса которого равна \(m\text{,}\), прикреплен к струне (масса которой настолько мала, что мы ее проигнорируем). Мы вращаем объект вокруг точки, где угловая скорость равна \(\omega\) радианам в секунду. Длина строки (расстояние от точки до центра вращения) равна \(d\text{.}\) 92)\delta dA\text{.}\)
Мы можем думать о области \(R\) на плоскости как о тысячах точек \(P(x,y)\text{,}\), каждая из которых имеет массу \(dm=\delta dA\text{.}\) Поскольку мы вращаем весь объект вокруг оси \(x\) с угловой скоростью \(\omega\text{,}\), каждый маленький кусочек вносит небольшой вклад кинетической энергии. Объясните, почему полная кинетическая энергия области \(R\text{,}\) при вращении вокруг оси \(x\) с угловой скоростью \(\omega\text{,}\) равна
\begin{уравнение*} KE= \frac{1}{2}\left(\iint_R (y^2)dm\right)\omega^2 \end{уравнение*} .
(е)
Не стесняйтесь спрашивать в классе, как это связано с фигурным катанием.
Как изменится приведенная выше формула, если мы вместо этого будем вращаться вокруг оси \(y\)? Что, если мы повернемся вокруг начала координат?
Упражнение 11.2.2 Центроид и инерция треугольной области
Рассмотрим треугольную область \(R\) в первом квадранте, ограниченную линией \(\ds \frac{x}{5}+\frac{y}{7}=1\text{.}\) Предположим, что плотность объекта является константой \(\delta = c\text{.}\)
(а)
Нарисуйте область \(R\text{,}\) и дайте оценки для выполнения двойных интегралов по этой области. Проверьте свой ответ с помощью Sage (используйте любое \(f\) для подынтегральной функции, это не имеет значения, поскольку вы просто хотите убедиться, что вы правильно получили оценки).
(б)
Помните, что вы можете проверить свою работу с Sage.
Установите интегральную формулу для вычисления центра масс \(\bar x\) области \(R\text{. }\) Вычислите любые интегралы вручную, чтобы показать, что \(\bar x = \frac{ 5}{3}\text{.}\) Затем сформулируйте предположение для \(\bar y\text{.}\)
}\) Вычислите любые интегралы вручную, чтобы показать, что \(\bar x = \frac{ 5}{3}\text{.}\) Затем сформулируйте предположение для \(\bar y\text{.}\)
(с)
Настройте интегральную формулу для вычисления моментов инерции \(I_x\text{,}\) \(I_y\text{,}\) и \(I_z\text{.}\) Используйте технологию для вычисления \(I_x \text{.}\)
(г)
Вы можете сравнить свои ответы с известными списками, такими как этот список в Википедии.
Если треугольная область имеет углы в точках \((0,0)\text{,}\) \((b,0)\text{,}\) и \((0,h)\text{, }\) укажите центр масс \(\bar x\) и момент инерции \(I_x\text{.}\) Вы сможете завершить эту часть, заменив 5 и 7 в вашей формуле на \( b\) и \(h\), при условии, что вы сначала разложите действительно большие числа, например \(1715 = 5\cdot 343=5\cdot 7\cdot ?…\) (я позволю Вы заканчиваете факторинг).
Когда мы нашли среднее значение, мы хотели, чтобы высота \(\bar f\) была такой, чтобы площадь под \(f\) и площадь под \(\bar f\) были одинаковыми. В виде уравнения мы записали
В виде уравнения мы записали
, а затем, поскольку \(\bar f\) постоянна, мы вытащили его из интеграла, а затем решили для \(\bar f\), чтобы получить
\begin{уравнение*} \bar f \iint_R dA = \iint_R f dA \текст{ или } \ bar f = \ frac{\ iint_R f dA }{\ iint_R dA} . \end{уравнение*}Этот же процесс дает центр масс. Мы могли бы заменить переменное расстояние \(x\) в \(\int_C x dm\) постоянным расстоянием \(\bar x\text{,}\) и затем найти \(\bar x\) в уравнении \(\int_C \bar xdm = \int_C x dm\text{.}\) Если бы вся масса находилась в одном месте, каким должно быть это место, чтобы первые моменты массы были одинаковыми. Радиусы вращения получаются точно таким же образом. Мы будем думать о радиусе вращения как о центре масс вращения.
92)дм}{\iint_R дм}}. \end{уравнение*}, где \(dm=\delta(x,y) dA\text{.}\) Обратите внимание, что в двух измерениях мы имеем \(z=0\text{,}\), поэтому формулы для \(R_x\) и \(R_y\) проще.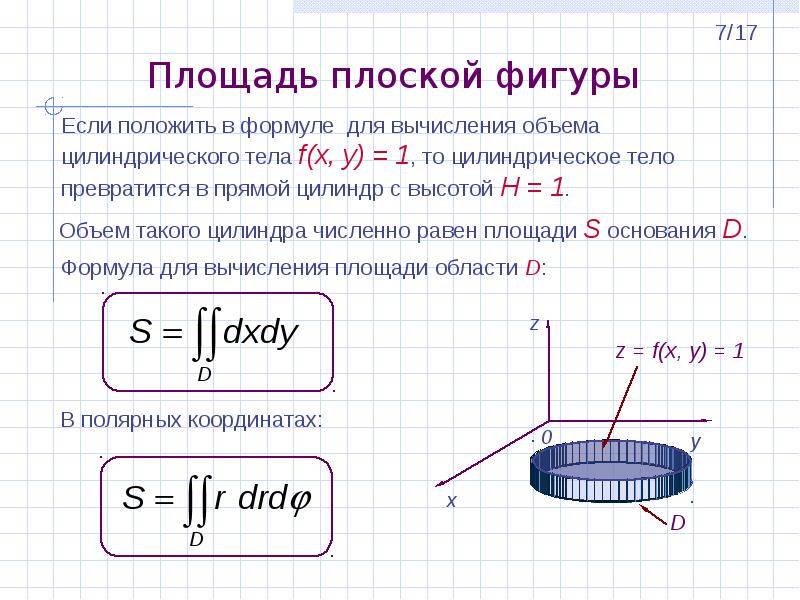
Упражнение 11.2.4
Рассмотрим прямоугольную область \(R\) в \(xy\)-плоскости, описанную \(\{(x,y)\ |\ 2\leq x\leq 11, 3\leq y\leq 7\} \text{.}\)
(а)
Установите интегральную формулу, которая дала бы \(\bar y\) для центроида \(R\text{.}\). Затем вычислите интеграл. 92=9\pi\text{.}\) Мы можем использовать этот факт для упрощения многих интегралов, требующих интегрирования по области \(R\text{.}\)
(a)
Вычислить \(\iint_R 3dA = 3\iint_RdA\text{.}\) [Чем площадь может вам помочь?]
(b)
Объясните, почему \(\iint_R x dA = \bar x A\) для любой области \(R\text{,}\), а затем вычислите \(\iint_R x dA\) для круглого диска. [Вам вообще не нужно настраивать какие-либо интегралы.]
(c)
Вычислите интеграл \(\iint_R 5x+2y dA\), используя данные о центроиде и площади.
Упражнение 11.2.7
Рассмотрим область \(R\) в плоскости \(xy\), состоящую из двух прямоугольных областей. Первая область \(R_1\) удовлетворяет \(x\in[-2,2]\) и \(y\in[0,7]\text{. }\) Вторая область \(R_2\) удовлетворяет \ (x\in[-5,5]\) и \(y\in[7,10]\text{.}\) Найдите центроиды \(R_1\text{,}\) \(R_2\) и затем, наконец, \(R\text{.}\)
}\) Вторая область \(R_2\) удовлетворяет \ (x\in[-5,5]\) и \(y\in[7,10]\text{.}\) Найдите центроиды \(R_1\text{,}\) \(R_2\) и затем, наконец, \(R\text{.}\)
Упражнение 11.2.8
Пусть \(R\) будет областью на плоскости с \(a\leq x\leq b\) и \(g(x)\leq y\leq f(x)\text{.}\) Пусть \ (A\) — площадь \(R\text{.}\)
Когда вы используете двойные интегралы для нахождения центроидов, формулы для центроида одинаковы как для \(\bar x\), так и для \(\bar y\text{.}\) В других курсах вы можете увидеть формулы на слева, потому что идеи будут представлены без знания двойных интегралов. Интегрирование внутреннего интеграла из формулы двойного интеграла дает формулы с одной переменной.
(а)
Установите повторный интеграл для вычисления площади \(R\text{.}\) Затем вычислите внутренний интеграл. Вы должны получить знакомую формулу из исчисления первого семестра. 92)\дельта(х)дх. \end{уравнение*}
Одна из основных причин, по которой мы изучаем массу, центр масс, центроиды и т.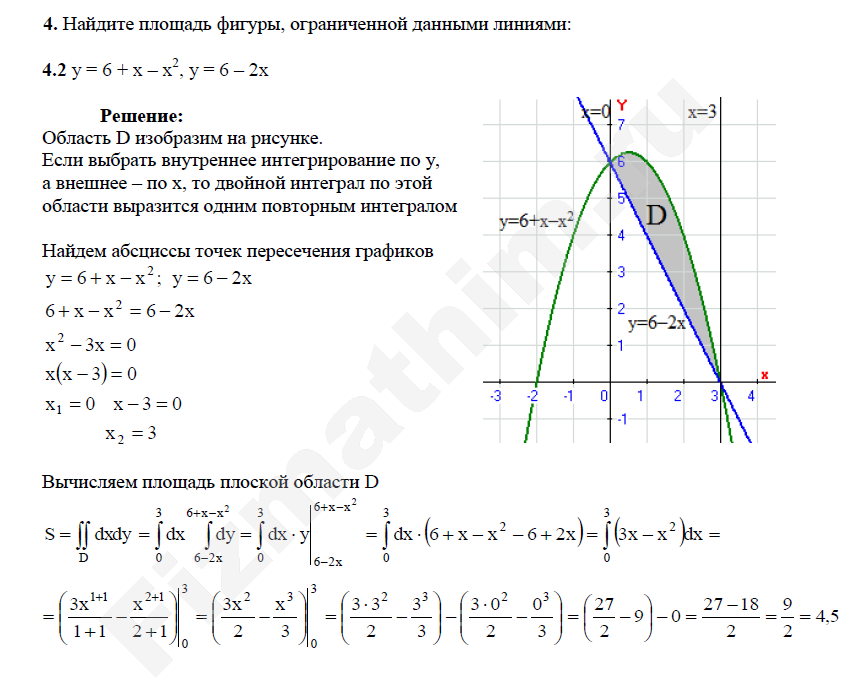

 Вейра; Джордж Б. Томас, младший Массачусетский технологический институт; Университетское исчисление, ранние трансцендентальные, третье издание
, Бостон Колумбус, 2016, Пирсон.
Вейра; Джордж Б. Томас, младший Массачусетский технологический институт; Университетское исчисление, ранние трансцендентальные, третье издание
, Бостон Колумбус, 2016, Пирсон.