Примеры 9 класс с дробями: Алгебраические дроби 9 класс онлайн-подготовка на Ростелеком Лицей

alexxlab / / Разное

Тест для подготовке к огэ 9 класс, первое задание: «Обыкновенные дроби»

Тест для подготовке к огэ 9 класс, первое задание: «Обыкновенные дроби»

12+  Свидетельство СМИ ЭЛ № ФС 77 — 70917
Лицензия на образовательную деятельность №0001058		Пользовательское соглашение     Контактная и правовая информация

 

Педагогическое сообщество
УРОК.РФ

 

Бесплатные всероссийские конкурсы

Бесплатные сертификаты
за публикации 

Нужна помощь? Инструкции для новых участников

Бесплатная   онлайн-школа для 1-4 классов

Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости

Библиотека

▪Учебно-дидактические материалы

▪КИМ

Материал опубликовал

2

#6 класс #7 класс #8 класс #9 класс #Математика #ФГОС #Учебно-дидактические материалы #КИМ #Учитель-предметник #Школьное образование

Задания для подготовке к ГИА 9 класс. Первое задание.

Обыкновенные дроби

Ответом к каждому заданию является конечная десятичная дробь или целое число.

Вариант 1

Вариант 2

Найдите значение выражения:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

Найдите значение выражения:

1)

2) 2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

Вариант 3

Вариант 4

Найдите значение выражения:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

Найдите значение выражения:

1)

2)

3) 3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

Ответы:

Вариант 1

Вариант 2

Вариант 3

Вариант 4

1) -2

2) 5,9

3) -0,3

4) 126

5) 58,4

6) 3,25

7) 0,6

8) 0,9

9) 0,24

10) 0,9

11) 4,5

12) 1,35

1) -2

2) 0,33

3) -0,375

4) 17,5

5) -8,75

6) 3,9

7) 1,25

8) 2,1

9) -0,6

10) 0,6

11) 3,3

12) 0,3

1) -3

2) 2,7

3) -0,55

4) 16,8

5) 11,75

6) 1,1

7) 0,9

8) 1,9

9) -0,1

10) 0,45

11) 0,32

12) 0,7

1)-1

2) 3,85

3) -0,35

4) 264

5) 79,2

6) 5,75

7) 0,75

8) 1,6

9) -0,62

10) 10,5

11) 8,75

12) 1,25


 

Опубликовано


Чтобы написать комментарий необходимо авторизоваться.

Закрыть

Действия с дробями. Задания 6 ОГЭ по математике

1\frac{7}{2} \cdot \frac{5}{4} — \frac{3}{8}Смотреть видеоразбор >>
2 \frac{22}{3}:\frac{2}{15} \cdot \frac{6}{5}Смотреть видеоразбор >>
3(\frac{9}{14}-\frac{10}{21}) \cdot 42Смотреть видеоразбор >>
4(\frac{11}{10}+\frac{11}{13}):\frac{22}{39}Смотреть видеоразбор >>
5(\frac{11}{10}-\frac{13}{15}):\frac{7}{60}Смотреть видеоразбор >>
6\frac{19}{6}:(\frac{5}{6}+\frac{3}{4})Смотреть видеоразбор >>
7\frac{0,9+0,7}{3,2}Смотреть видеоразбор >>
8\frac{3,2-5,7}{2,5}Смотреть видеоразбор >>
9\frac{4,7-1,4}{7,5}Смотреть видеоразбор >>
10\frac{2,4}{1,2-0,4}Смотреть видеоразбор >>
11\frac{5,6}{1,9-7,5}Смотреть видеоразбор >>
12(1,7+2,8) \cdot 4,8Смотреть видеоразбор >>
134,1 \cdot 7,7 + 0,86Смотреть видеоразбор >>
141,2 : 0,6 \cdot 1,5Смотреть видеоразбор >>
151 + \frac{1}{7} \cdot 0,77Смотреть видеоразбор >>
16\frac{5}{3}:\frac{2}{7}-\frac{11}{6}Смотреть видеоразбор >>
17\frac{5}{6}+\frac{5}{2} \cdot \frac{2}{3}Смотреть видеоразбор >>
18(\frac{5}{12}-\frac{3}{20}) \cdot \frac{45}{2}Смотреть видеоразбор >>
19(\frac{17}{35}+\frac{3}{8}):\frac{5}{28}Смотреть видеоразбор >>
20(\frac{11}{5}-\frac{13}{6}):\frac{1}{90}Смотреть видеоразбор >>
21\frac{12}{7}:(\frac{6}{7}-\frac{3}{4})Смотреть видеоразбор >>
22\frac{7,9+3,4}{0,2}Смотреть видеоразбор >>
23\frac{2,6-8,4}{2,5}Смотреть видеоразбор >>
24\frac{2,6-2,6}{7,8}Смотреть видеоразбор >>
25\frac{5,6}{1,7-1,6}Смотреть видеоразбор >>
26\frac{9,2}{0,5-2,8}Смотреть видеоразбор >>
27(1,7+2,8) \cdot 24Смотреть видеоразбор >>
285,6 \cdot 5,5 — 4,1Смотреть видеоразбор >>
29\frac{1}{4} \cdot 0,48 + 1Смотреть видеоразбор >>
30\frac{1}{\frac{1}{5}-\frac{1}{30}}Смотреть видеоразбор >>
31\frac{14}{9} \cdot \frac{3}{2}:\frac{7}{6}Смотреть видеоразбор >>
32\frac{5}{4}+\frac{7}{6}:\frac{2}{3}Смотреть видеоразбор >>
33(\frac{11}{9}+\frac{4}{9}):\frac{5}{36}Смотреть видеоразбор >>
34(\frac{5}{7}-\frac{3}{7}):\frac{2}{21}Смотреть видеоразбор >>
35(\frac{8}{25}-\frac{13}{38}):\frac{6}{19}Смотреть видеоразбор >>
363:(\frac{6}{7}-\frac{3}{4})Смотреть видеоразбор >>
37\frac{6,9+4,1}{0,2}Смотреть видеоразбор >>
38\frac{0,5-1,5}{0,8}Смотреть видеоразбор >>
39\frac{3,8}{2,6+1,2}Смотреть видеоразбор >>
40\frac{2,6}{3,1-0,6}Смотреть видеоразбор >>
41\frac{6,9}{3,2-5,7}Смотреть видеоразбор >>
42(6,9-3,4) \cdot 8,4Смотреть видеоразбор >>
435,4 \cdot 1,9 — 2,15Смотреть видеоразбор >>
44\frac{1}{6} \cdot 9,6 — 1Смотреть видеоразбор >>
45\frac{1}{\frac{1}{2}+\frac{1}{3}}Смотреть видеоразбор >>
46\frac{18}{7} \cdot \frac{14}{3} : \frac{4}{5}Смотреть видеоразбор >>
47(\frac{5}{6}+\frac{7}{15}) \cdot \frac{30}{13}Смотреть видеоразбор >>
48(\frac{3}{22}+\frac{2}{11}):\frac{5}{33}Смотреть видеоразбор >>
49(\frac{13}{6}-\frac{11}{6}):\frac{1}{90}Смотреть видеоразбор >>
50\frac{13}{7}:(\frac{1}{3}+\frac{2}{7})Смотреть видеоразбор >>
51\frac{1,8+1,9}{3,7}Смотреть видеоразбор >>
52\frac{7,5+3,5}{2,5}Смотреть видеоразбор >>
53\frac{7,3-2,5}{1,2}Смотреть видеоразбор >>
54\frac{9,4}{2,1+2,6}Смотреть видеоразбор >>
55\frac{4,4}{5,8-5,3}Смотреть видеоразбор >>
56\frac{0,6}{1,7-2,9}Смотреть видеоразбор >>
57(5,3-2,8)\cdot38Смотреть видеоразбор >>
581,32:1,2-0,8Смотреть видеоразбор >>
593-\frac{1}{4}\cdot5,6Смотреть видеоразбор >>
60\frac{1}{\frac{1}{4}-\frac{1}{5}}Смотреть видеоразбор >>
61\frac{15}{2}:\frac{5}{21}\cdot\frac{4}{3}Смотреть видеоразбор >>
62(\frac{4}{15}+\frac{1}{20})\cdot60Смотреть видеоразбор >>
63(\frac{13}{21}+\frac{3}{14}):\frac{10}{27}Смотреть видеоразбор >>
64(\frac{17}{8}-\frac{1}{16}):\frac{11}{48}Смотреть видеоразбор >>
6513:(\frac{1}{3}+\frac{2}{7})Смотреть видеоразбор >>
66\frac{4,2+3,3}{0,3}Смотреть видеоразбор >>
67\frac{2,7+5,8}{6,8}Смотреть видеоразбор >>
68(\frac{6,8-4,7}{1,4})Смотреть видеоразбор >>
69\frac{5,6}{8,5-2,9}Смотреть видеоразбор >>
70\frac{2,1}{6,6-2,4}Смотреть видеоразбор >>
71\frac{7,7}{3,7-8,7}Смотреть видеоразбор >>
723,5\cdot6,6+1,6Смотреть видеоразбор >>
732,7+1,32:1,2Смотреть видеоразбор >>
740,15:\frac{3}{7}+1Смотреть видеоразбор >>
75\frac{1}{\frac{1}{10}-\frac{1}{15}}Смотреть видеоразбор >>

Математика 9 класс Содержание

ГлавнаяПрактика

Для учащихся и родителейДля учителей и школ

Учебники

Полный каталог

Списки лидеров

Таблица лидеров учащихсяСборка лидеров классов/классовСписок лидеров школ

ЦеныПоддержка

Справочный центрСвяжитесь с нами

Авторизоваться
  • Глава 1: Целые числа
    • Свойства чисел
    • Вычисления с целыми числами
    • Множители и факторы
    • Решение задач на соотношение, норму и пропорцию
    • Решение проблем в финансовом контексте
    • Практикуйте эту главу
  • Глава 2: Целые числа
    • Целые числа
    • Практикуйте эту главу
  • Глава 3: Дроби
    • Эквивалентные дроби
    • Сложение и вычитание дробей
    • Умножение и деление дробей
    • Эквивалентные формы
    • Практикуйте эту главу
  • Глава 4: Десятичная запись дробей
    • Эквивалентные формы
    • Расчеты с десятичными дробями
    • Решать проблемы
    • Больше проблем
    • Десятичные числа в алгебраических выражениях и уравнениях
    • Рабочий лист
    • Практикуйте эту главу
  • Глава 5: Показатели
    • Редакция
    • Целочисленные показатели
    • Решение простых показательных уравнений
    • Научная нотация
    • Практикуйте эту главу
  • Глава 6: Шаблоны
    • Узоры
    • Практикуйте эту главу
  • Глава 7: Функции и отношения
    • Функции и отношения
    • Практикуйте эту главу
  • Глава 8: Алгебраические выражения
    • Алгебраический язык
    • Свойства операций
    • Объединение одинаковых терминов в алгебраические выражения
    • Умножение алгебраических выражений
    • Деление многочленов на целые числа и одночлены
    • Произведения и квадраты биномов
    • Подстановка в алгебраические выражения
    • Практикуйте эту главу
  • Глава 9: Уравнения
    • Решение уравнений путем проверки
    • Решение уравнений с использованием аддитивных и мультипликативных инверсий
    • Настройка уравнений
    • Уравнение и ситуации
    • Решение уравнений с использованием законов показателей
    • Рабочий лист
    • Практикуйте эту главу
  • Глава 10: Пересмотр и оценка
    • Редакция
    • Оценка
  • Глава 11: Построение геометрических фигур
    • Построение геометрических фигур
    • Практикуйте эту главу
  • Глава 12: Геометрия двумерных фигур
    • Геометрия 2d фигур
    • Практикуйте эту главу
  • Глава 13: Геометрия прямых линий
    • Угловые отношения
    • Найдите и назовите углы.
    • Решать проблемы
    • Практикуйте эту главу
  • Глава 14: Теорема Пифагора
    • Теорема Пифагора
  • Глава 15: Площадь и периметр двумерных фигур
    • Площадь и периметр двумерных фигур
    • Практикуйте эту главу
  • Глава 16: Пересмотр и оценка семестра 2
    • Пересмотр и оценка семестра 2

Книга для учащихся и руководство для учителя (PDF 9A, PDF 9B)

  • Математические формулы

Уравнения с дробями — Полный курс алгебры

Навыки
в
A L G E B R A

Содержание | Дом

24

Очистка фракций

2-й уровень

ЧТОБЫ РЕШИТЬ УРАВНЕНИЕ С Дробями, мы преобразуем его в уравнение без дробей, которое мы знаем, как решать. Техника называется очисткой фракций.

Пример 1.   Решите для x :

x
3		   +   x − 2
   5		  = 6,

Решение . Очистить дроби следующим образом:

Умножьте обе части уравнения — каждый член — на НОК знаменателей. Тогда каждый знаменатель будет равен разделить на его кратное. Тогда у нас получится уравнение без дробей.

НОК 3 и 5 равно 15.  Поэтому умножьте обе части уравнения на 15.

15 ·   х
3		   +   15 ·   x − 2
   5		  = 15 ·  6

Слева умножьте каждое слагаемое на 15. Теперь каждый знаменатель будет делиться на 15 — это и есть точка — и у нас получится следующее простое уравнение, «очищенное» от дробей:

5 х + 3( х — 2)  =  90.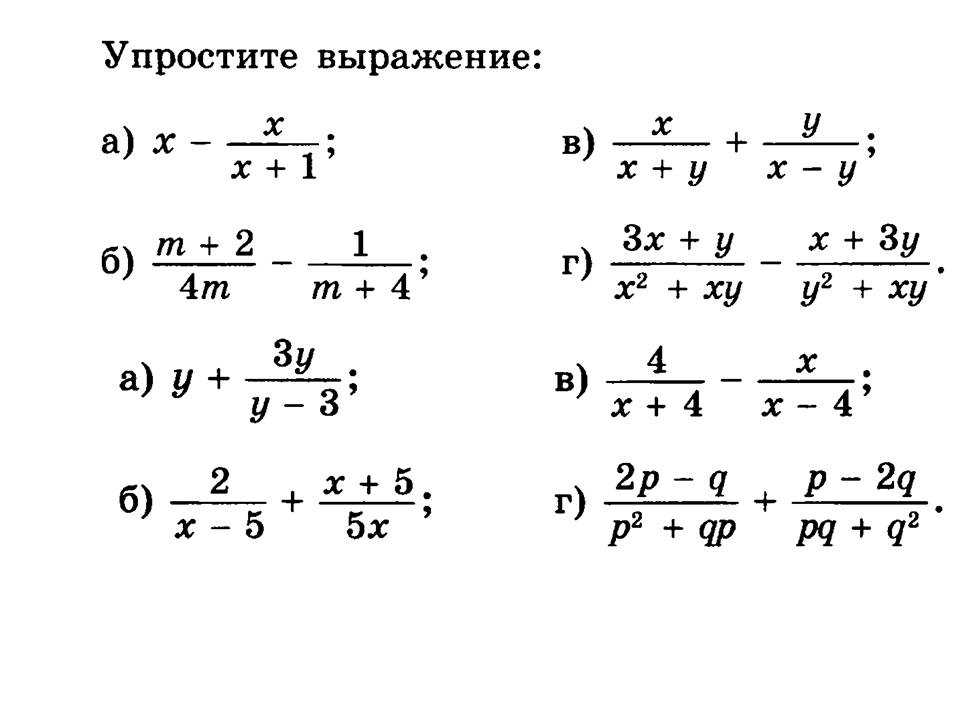
 
      Легко решается следующим образом:
 
5 x + 3 x − 6  =  90
 
8 x  =  90 + 6
 
x  =  96
8
 
   =  12.

Мы говорим «умножить» обе части уравнения, тем не менее мы пользуемся тем фактом, что порядок, в котором мы умножаем или делим, не имеет значения. (Урок 1.) Поэтому мы делим НОК сначала на каждый знаменатель и таким образом очищаем дроби.

Мы выбираем число , кратное каждого знаменателя, потому что тогда каждый знаменатель будет его делителем.

Пример 2.    Очистить дроби и решить для x :

x
2		  −   5 x
 6		  =   1
9

Решение . НОК 2, 6 и 9 равно 18. (Урок 23 арифметики.) Умножьте обе части на 18 — и сократите.

9 x − 15 x = 2,

На самом деле не обязательно писать 18.  Ученик должен просто посмотреть на и увидеть, что 2 будет входить в 18 девять (9) раз. Таким образом, этот термин становится равным 9 x .

Далее, посмотрите на и убедитесь, что 6 превратится в 18 три (3) раза. Таким образом, этот член становится равным 3 ·  -5 x = -15 x .

Наконец, посмотрите на , и увидите, что 9 превратится в 18 два (2) раза. Таким образом, этот член становится равным 2 ·  1 = 2,

.

Вот очищенное уравнение, за которым следует его решение:

9 х − 15 х = 2
 
−6 x = 2
 
x = 2
−6
 
x = — 1
3

Пример 3.   Решение для x :

½(5 х — 2) = 2 х + 4,

Решение . Это уравнение с дробью. Очистить дроби, умножив обе части на 2:

5 x − 2 = 4 x + 8
 
5 x − 4 x = 8 + 2
 
x = 10.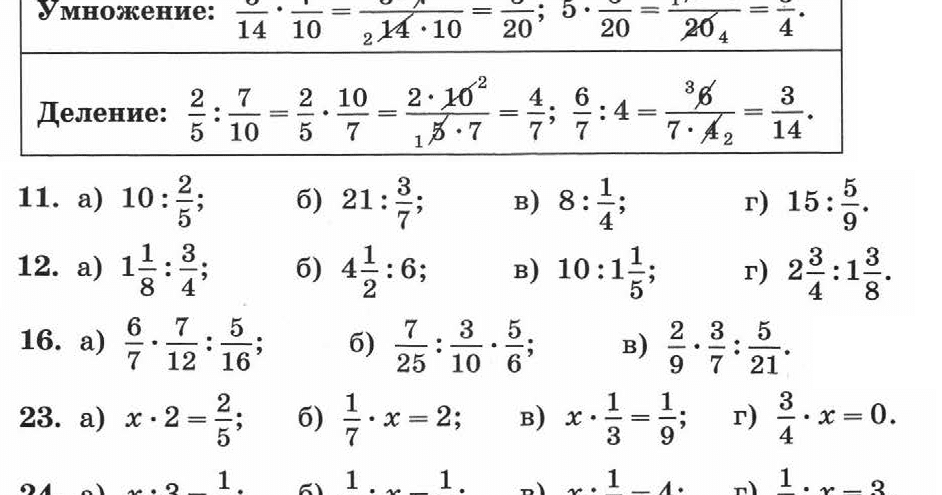

В следующих задачах очистите дроби и решите для x :

Чтобы увидеть каждый ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!

  Проблема 1. х
2		  —  x
5		  =  3
 
       LCM 10. Вот очищенное уравнение и его решение:
 
  5 x − 2 x =  30
 
  3 x =  30
 
  х =  10.

При решении любого уравнения с дробями в следующей строке вы пишете —

5 x − 2 x  =  30

— должно быть , а не дробей.

.
  Задача 2. х
6		  =    1 
12		   +   x
8
 
       LCM 24. Вот очищенное уравнение и его решение:
 
  4 x =   2 + 3 х
 
  4 х − 3 х =   2
 
  х =   2
903:30 16 х − 15 х
  Задача 3. х − 2
5   		   +  х
3		  =  х
2
 
       LCM 30. Вот очищенное уравнение и его решение:
 
  6 (х — 2) + 10 х =  15 x
 
  6 х − 12 + 10 х =  15 x
 
  =  12
 
  х =  12.

Задача 4. Дробь равна дроби.

.
х − 1
4   		  =  х
7
 
       LCM 28. Вот очищенное уравнение и его решение:
 
7( х — 1) =  4 x
 
7 х − 7 =  4 x
 
7 х − 4 х =   7
 
3 x =   7
 
х =   7
3

Мы видим, что когда одна дробь равна одной дроби, уравнение можно очистить путем «перекрестного умножения».

Если  
  а
б 		 =    в
г 		, 
затем  
  объявление  =  до н.э. .

  Задача 5. x − 3
3   		  =  x − 5
   2
 
        Вот очищенное уравнение и его решение:
 
  2( х — 3) =  3( х — 5)
 
  2 х − 6 =  3 х − 15
 
  2 х — 3 х =  − 15 + 6
 
  − x =   −9
 
  х =   9
  Задача 6. х — 3
х — 1		  =  x + 1
x + 2
 
        Вот очищенное уравнение и его решение:
 
  ( х — 3)( х + 2) =  ( х — 1)( х + 1)
 
  х ² − х − 6 =  х ² − 1
 
  − x =  −1 + 6
 
  − x =   5
 
  х =   −5.
  Задача 7. 2 x − 3
9    		  +   x + 1
   2		  =  х − 4
 
       LCM 18. Вот очищенное уравнение и его решение:
 
  4 х — 6 + 9 х + 9 =  18 х − 72
 
  13 х + 3 =  18 х − 72
 
  13 х − 18 х =  − 72 − 3
 
  −5 x =  −75
 
  х =  15.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта