Дополнение | Теория множеств
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
Прежде чем мы определим, что такое дополнение множества, вспомним определения универсального множества и подмножества — эти термины будут часто использоваться в этом уроке. Универсальное множество — это множество всех элементов, которые рассматриваются в конкретной задаче или ситуации.
Допустим, нам нужно найти все целые числа, которые удовлетворяют неравенству . Нам дано универсальное множество целых чисел:
Целые числа, которые удовлетворяют неравенству:
— это подмножество универсального множества
Допустим, у нас есть множество — подмножество некоторого универсального множества . Дополнение — это все остальные элементы из , которые не вошли в .
В нашем примере выше, дополнение для — это множество, содержащее все целые числа, которые не удовлетворяют неравенству: .
Мы можем проиллюстрировать это определение на другом примере.
Тогда дополнением будет множество, содержащее все остальные города, которые не являются миллионниками.
Существуют различные способы обозначения дополнения множества с помощью нотации. Например, можно использовать знак простого числа. Иногда используется надстрочная строчная буква . Над именем исходного множества может стоять черточка или символ подчеркивания. Мы будем использовать .
В этом уроке мы подробно рассмотрим дополнение множества, его определение и свойства.
Что такое дополнение множества?
Простыми словами, дополнение множества — это разность между универсальным множеством и множеством .
Это тождество можно записать так:
В дополнение входят те элементы
из множества
, которые не входят в
.
Условные обозначения
Дополнение любого множества представляется как и т.д. Другими словами, если задано универсальное множество и подмножество универсального множества , то разность универсального множества и подмножества универсального множества является дополнением подмножества, то есть .
Рассмотрим на таком примере:
Найдем дополнение:
Диаграмма
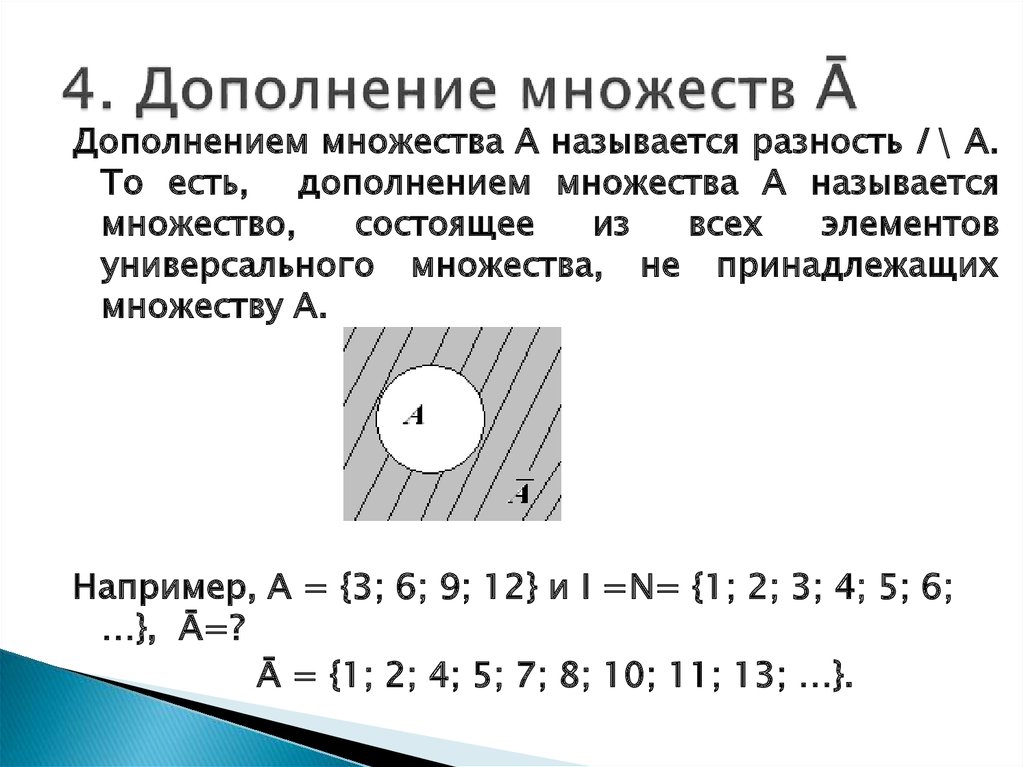
Для лучшего понимания посмотрите на приведенную ниже диаграмму Венна, которая ясно показывает дополнение множества , то есть :
Здесь не является частью множества , и множество также не является частью . и являются подмножествами .
Свойства дополнения множества
Ниже перечислены свойства дополнения множества, которые включают в себя:
Законы дополнения
Закон двойного дополнения
Закон универсального множества
Законы дополнения
Если является подмножеством универсального множества, то также является подмножеством универсального множества.
 Поэтому объединение
и
является универсальным множеством, представленным как
Поэтому объединение
и
является универсальным множеством, представленным какПересечение множеств и дает пустое множество » «, представленное как
Рассмотрим на таком примере:
Если и и
и
Кроме того,
Закон двойного дополнения
Дополнением дополненного множества является исходное множество
Дополнение множества , где само является дополнением , двойное дополнение , таким образом, является самим
В предыдущем примере и , тогда . Дополнение , что равно множеству .
Закон для пустого множества и универсального множества
- Дополнением универсального множества является пустое множество или нулевое множество ( ), а дополнением пустого множества — универсальное множество
Поскольку универсальное множество содержит все элементы, а пустое множество не содержит никаких элементов, следовательно, их дополнения прямо противоположны друг другу, что представляется как И
В примере выше, множество
содержит все элементы множества
, а множество
как универсальное множество содержит все элементы, поэтому
(пустое множество) и
.
Выводы
Дополнением универсального множества является пустое множество или нулевое множество
Множество пересечения содержит элементы, которые являются общими для обоих множеств
Объединение двух множеств — это множество, содержащее все элементы, которые находятся в A или B или в обоих
Самостоятельная работа
Задача №1:
По условию задачи:
Найдите .
Нажмите, чтобы увидеть ответПо условию задачи:
кратно
Следовательно, дополнением множества является:
Ответ:
Задача №2:
Если — универсальное множество, содержащее учеников класса школы совместного обучения, а — множество всех девочек и оно содержит девочек. Найдите количество элементов дополнения множества девочек?
Нажмите, чтобы увидеть ответЕсли множество
содержит всех девочек, то дополнением множества
является множество всех мальчиков. Разность между универсальным множеством и множеством всех девочек является дополнением множества девочек.
Разность между универсальным множеством и множеством всех девочек является дополнением множества девочек.
Таким образом, . Следовательно, дополнение множества содержит мальчиков.
Ответ:
Задача №3
Найдите дополнение множества и множества .
Покажите, что , где и ?
Нажмите, чтобы увидеть ответДополнение множества или содержит элементы, отличные от элементов множества A.
Следовательно, .
Аналогично, .
Найдем . Так содержатся элементы, включенные как в , так и в .
Значит, .
Таким образом, .
Значит, дополнение или .
Следовательно, .
Из и следует, что .
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты.
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
Подписку можно отменить в любой момент.
Получить доступ
130
курсов
1000
упражнений
2000+
часов теории
3200
тестов
Открыть доступ
Курсы программирования для новичков и опытных разработчиков. Начните обучение бесплатно
- 130 курсов, 2000+ часов теории
- 1000 практических заданий в браузере
- 360 000 студентов
Электронная почта *
Отправляя форму, вы принимаете «Соглашение об обработке персональных данных» и условия «Оферты», а также соглашаетесь с «Условиями использования»
Наши выпускники работают в компаниях:
объединение, пересечение, дополнение и различие
Редакция Кодкампа
читать 2 мин
Набор — это набор предметов.
Мы обозначаем набор с помощью заглавной буквы, а элементы в наборе определяем с помощью фигурных скобок. Например, предположим, что у нас есть некоторый набор под названием «A» с элементами 1, 2, 3. Мы запишем это так:
Например, предположим, что у нас есть некоторый набор под названием «A» с элементами 1, 2, 3. Мы запишем это так:
А = {1, 2, 3}
В этом руководстве объясняются наиболее распространенные операции с множествами, используемые в теории вероятностей и статистике.
СоюзОпределение: Объединение множеств A и B — это множество элементов, которые находятся либо в A, либо в B.
Обозначение: А ∪ В
Примеры:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Определение: Пересечение множеств A и B — это множество элементов, которые находятся как в A, так и в B.
Обозначение: А ∩ В
Примеры:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Определение: Дополнением множества A называется множество элементов, которые входят в универсальное множество U, но не входят в A.
Обозначение: A’ или A c
Примеры:
- Если U = {1, 2, 3, 4, 5, 6} и A = {1, 2}, то A c = {3, 4, 5, 6}
- Если U = {1, 2, 3} и A = {1, 2}, то A c = {3}
Определение: Разность множеств А и В — это множество элементов, которые есть в А, но отсутствуют в В.
Обозначение: А – Б
Примеры:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Определение: Симметричная разность множеств A и B — это множество элементов, которые находятся либо в A, либо в B, но не в обоих.
Обозначение: А Δ В
Примеры:
- {1, 2, 3} ∆ {2, 3, 4} = {1, 4}
- {1, 2} ∆ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Определение: Декартово произведение множеств A и B — это множество упорядоченных пар из A и B.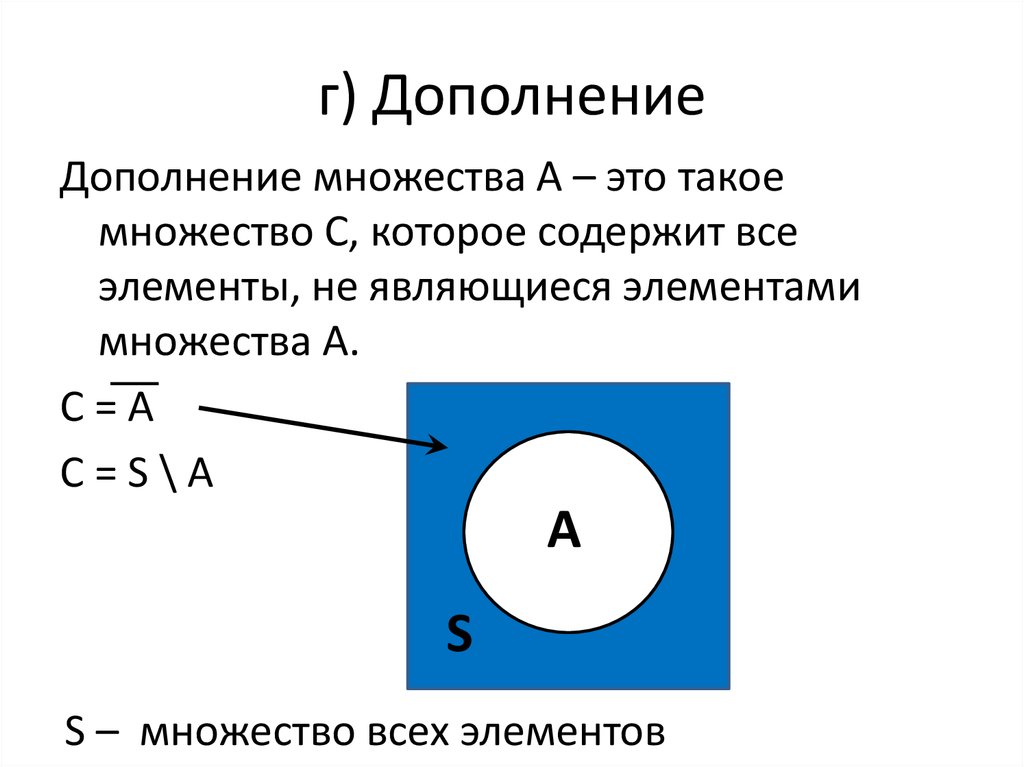
Обозначение: А х В
Примеры:
- Если A = {H, T} и B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
- Если A = {T, H} и B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( Н, 2), (Н, 3)}
Дополнение множества — определение, свойства, примеры
Дополнение множества — это множество, включающее в себя все элементы универсального множества, отсутствующие в данном множестве. Допустим, A — это множество всех монет, которое является подмножеством универсального множества, содержащего все монеты и банкноты, поэтому дополнением множества A является множество банкнот (которое не включает монеты).
В этой статье мы подробно обсудим дополнение множества, его определение вместе со свойствами, решенными примерами и практическими вопросами.
| 1. | Что такое дополнение набора? |
2. | Дополнение набора диаграмм Венна |
| 3. | Свойства дополнения набора |
| 4. | Дополнение к набору примеров |
| 5. | Часто задаваемые вопросы о дополнении набора |
Что такое дополнение набора?
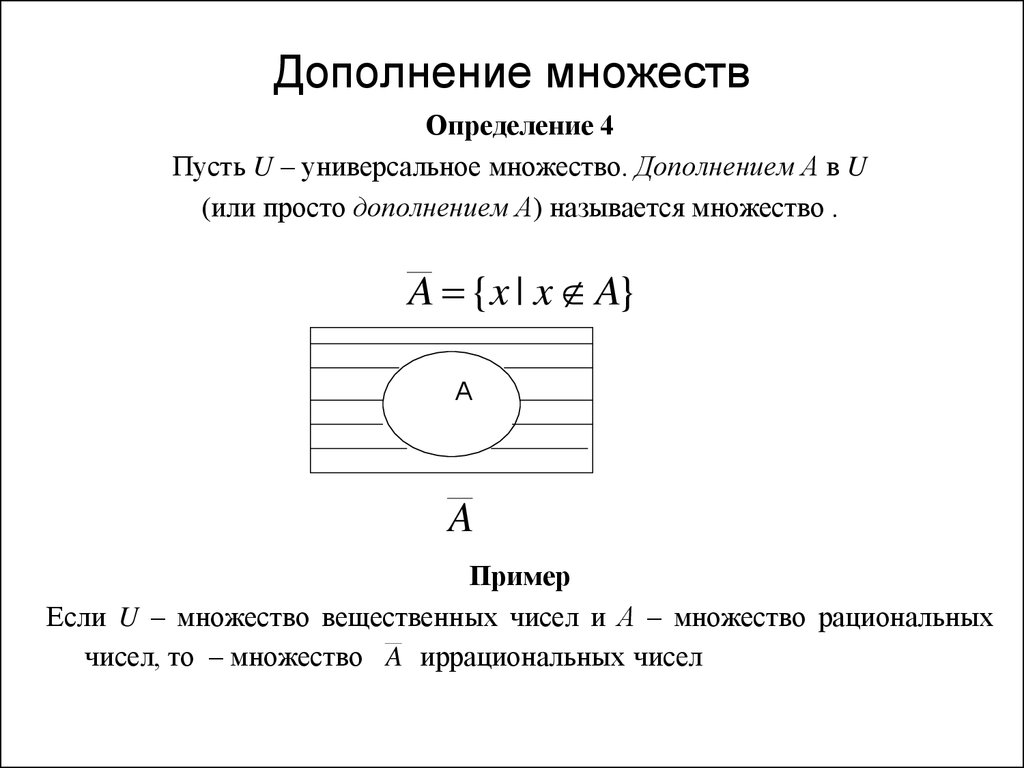
Если универсальное множество (U) имеет подмножество A, то дополнение множества A, представленное как A’, содержит элементы, отличные от элементов множества A. т. е. A’ включает в себя элементы универсального множества, но не элементы множества A. Математически дополнение множества A записывается как A’ = {x ∈ U : x ∉ A}. Другими словами, дополнением множества А является разность универсального множества и множества А, т. е. А’ = U — А.
Дополнение множества Символ
Дополнение любого множества представлено как A’, B’, C’ и т. д. Другими словами, мы можем сказать, что если универсальное множество есть (U) и подмножество универсального множества ( A) задано, то разность между универсальным множеством (U) и подмножеством универсального множества (A) является дополнением подмножества, то есть
- A’ = U — A [OR]
- А’ = {х ∈ U : х ∉ А}
Пример дополнения множества
Процедура нахождения дополнения множества демонстрируется здесь на примере. Если универсальный набор состоит из всех простых чисел до 25 и множества A = {2, 3, 5}, то дополнение множества A содержит элементы, отличные от элементов A.
Если универсальный набор состоит из всех простых чисел до 25 и множества A = {2, 3, 5}, то дополнение множества A содержит элементы, отличные от элементов A.
- Шаг 1: Проверьте наличие универсального набора и набора, для которого необходимо найти дополнение. U = {2, 3, 5, 7, 11, 13, 17, 19, 23}, А = {2, 3, 5}.
- Шаг 2: Вычесть, то есть (U — A). Здесь,
У — А = А’
= { ̶2̶,̶ 3̶,̶ 5̶, 7, 11, 13, 17, 19, 23} — { ̶2̶,̶ 3̶,̶ 5̶}
= {7, 11, 13, 17, 19, 23}
Дополнение набора диаграмм Венна
Для лучшего понимания взгляните на приведенную ниже диаграмму Венна дополнения множества, которая ясно показывает дополнение множества A, то есть A’. Здесь А’ не является частью множества А, и множество А также не является частью А’. т. е. А и А’ — два непересекающихся множества. Кроме того, A и A’ являются подмножествами U.
- Здесь оранжевым цветом показан набор A
- Заштрихованная часть белого цвета показывает дополнение набора A (A’).

Свойства дополнения набора
Ниже приведены свойства дополнения множества, которые включают законы дополнения, закон двойного дополнения, закон пустого множества и универсального множества, а также закон де Моргана.
Законы дополнений
- Если A является подмножеством универсального множества, то A’ также является подмножеством универсального множества, поэтому объединение A и A’ является универсальным множеством, представленным как A ∪ A’ = U
- Пересечение множеств A и A’ дает пустое множество «∅», представленное как A ∩ A’ = ∅
Например, если U = {1, 2, 3, 4, 5} и A = {4, 5}, то A’ = {1, 2, 3}. Теперь заметьте, что A ∪ A’ = U = {1, 2, 3, 4, 5}. Кроме того, A ∩ A’ = ∅
Закон двойного дополнения
- В этом законе дополнением дополняемого множества является исходное множество, (A’)’ = A
- Дополнение множества A′, где само A′ является дополнением A, двойное дополнение A, таким образом, является самим A.

В предыдущем примере U = {1, 2, 3, 4, 5} и A = {4, 5}, тогда A’ = {1, 2, 3}.
Дополнение A’ = (A’)’ = {4, 5}, равное множеству A.
Закон пустого множества и универсальное множество
- Дополнение универсального множества — это пустое множество или нулевое множество (∅) и дополнение к пустому множеству является универсальным множеством.
- Поскольку универсальное множество содержит все элементы, а пустое множество не содержит элементов, следовательно, их дополнение прямо противоположно друг другу, представленному как ∅’ = U И U’ = ∅
В приведенном выше примере набора U = {1, 2, 3, 4, 5} мы можем заметить, что U’ = ∅ (пустое множество) и ∅’ = {1, 2, 3, 4, 5} .
Закон Де Моргана
Вот законы Де Моргана, в которых говорится о дополнении.
- Дополнение объединения двух множеств равно дополнению множеств и их пересечению. (A U B)’ = A’ ∩ B’ (закон союза Де Моргана).
- Дополнение пересечения двух множеств равно дополнению множеств и их объединению.
 (A ∩ B)’ = A’ UB’ (закон пересечения Де Моргана).
(A ∩ B)’ = A’ UB’ (закон пересечения Де Моргана).
Вот пример для доказательства закона Де Моргана, U = {1, 2, 3, 4, 5} и A = {4, 5} и B = {1, 2}. Таким образом,
Закон Союза Де Моргана: (AU B) = {1, 2, 4, 5} и (AU B)’ = {3} и, таким образом, A’ ∩ B’ = {1, 2, 3} ∩ {3, 4, 5} = {3}. Таким образом, (A U B)’ = A’ ∩ B’ = {3}.
Закон пересечения де Моргана: (A ∩ B) = ∅ (пусто), (A ∩ B)’ = {1, 2, 3, 4, 5} и, таким образом, A’ U B’ = {1, 2, 3 } U {3, 4, 5} = {1, 2, 3, 4, 5}. Таким образом, (A ∩ B)’ = A’ UB’
Важные замечания о дополнении множества:
- Дополнение множества A обозначается A’ и получается вычитанием A из универсального множества U, т. е. A’ = U — A.
- Множество и его дополнение всегда не пересекаются.
- Дополнением универсального набора является пустой набор или нулевой набор.
☛ Связанные темы:
- Наборы Formula
- Диаграмма Венна Формула
- Установить нотацию построителя
Часто задаваемые вопросы о дополнении набора
Что такое дополнение набора?
Дополнение множества A определяется как множество, содержащее элементы, присутствующие в универсальном множестве, но не в множестве A. Например, множество U = {2, 4, 6, 8, 10, 12} и множество A = {4, 6, 8}, то дополнение множества A, A′ = {2, 10, 12}.
Например, множество U = {2, 4, 6, 8, 10, 12} и множество A = {4, 6, 8}, то дополнение множества A, A′ = {2, 10, 12}.
Как найти дополнение к набору?
Если задано универсальное множество (U) и задано другое множество A, содержащее некоторые элементы универсального множества, мы можем найти дополнение множества A, представив его как A’. Элементы, которые не являются частью множества A, но частью множества U, будут элементами множества A’, являющегося дополнением множества A. Здесь A’ = {x ∈ U: x ∉ A}.
Что входит в состав универсального набора?
Универсальный набор содержит все возможные элементы, а нулевой набор вообще не содержит элементов. Таким образом, дополнением универсального множества является нулевое множество.
Каково дополнение набора А, если универсальный набор — это набор букв английского алфавита, а набор А — набор согласных в английском алфавите?
Если универсальное множество состоит из всех алфавитов и множество А содержит все согласные, то дополнением множества А, то есть А’, будет множество гласных английских алфавитов.
Что такое дополнение перекрестка B?
Пересечение B-дополнение есть не что иное, как объединение A-дополнение B-дополнение. (A ∩ B)’ = A’ U B’. Это известно как закон пересечения де Моргана.
Что такое дополнение пересечения множеств?
Дополнением пересечения множеств называется множество элементов, входящих в универсальное множество U, но не входящих в множество пересечений. Например, предположим, что множество U = множество натуральных чисел меньше 10 и элементы множества X = {1, 2, 5, 6}, а множество Y = {1, 3, 4, 5, 6}. Таким образом, пересечение множества X и Y или X ∩ Y = {1, 5, 6} и дополнение (X ∩ Y) или (X ∩ Y)’ = {2, 3, 4, 7, 8, 9}.
Легко доказать, что дополнение пересечения двух множеств равно объединению дополнения каждого из множеств.
Что такое дополнение к пустому набору или нулевому набору?
Пустое множество означает, что в множестве нет элементов, поэтому дополнением к пустому множеству или нулевому множеству является универсальное множество, содержащее все элементы.
Что такое дополнение Union B?
Объединение B-дополнение есть не что иное, как A-дополнение, пересечение B-дополнения. (A U B)’ = A’ ∩ B’. Это известно как закон объединения множеств Де Моргана.
Определение, свойства с примерами и приложениями
Включите JavaScript
Освоение основ: полное руководство по пониманию простых процентов на примерах из реальной жизни
Дополнение множества — это множество, содержащее все элементы, не оригинальный набор. Другими словами, это множество всех элементов, принадлежащих универсальному множеству, но не принадлежащих исходному множеству. Дополнение множества обозначается штрихом (‘)
Дополнение множества примеров: рассмотрим множество четных чисел: {2, 4, 6, 8, 10,12..} Дополнение этого множества, обозначаемое
(четные числа)’, это множество всех элементов, не входящих в множество четных
числа. В этом случае универсальное множество — это множество всех целых чисел, обозначаемое
Z. Следовательно, (четные числа)’ = {1, 3, 5, 7, 9, 11,}, то есть множество всех
нечетные числа.
Следовательно, (четные числа)’ = {1, 3, 5, 7, 9, 11,}, то есть множество всех
нечетные числа.
Другим примером является группа сотрудников, работающих в компания. Дополнением этого множества, обозначаемого (сотрудники)’, является множество всех лица, не работающие в компании. В этом случае универсальный набор множество всех людей, обозначаемое P. Следовательно, (служащие)’ = {студенты, пенсионеры, безработные лица и др.}.
Важно отметить, что комплектация набора зависит на рассматриваемом универсальном множестве. Например, если универсальное множество множество действительных чисел, то дополнение множества натуральных чисел будет включать все числа, кроме натуральных чисел.
Дополнение множества можно также выразить с помощью множества разница. То есть, если А — подмножество универсального множества U, то А’ = U — А. Например, если A = {1, 2, 3} и U = {1, 2, 3, 4, 5}, то A’ = {4, 5}.
Таким образом, дополнение множества является полезной концепцией в
математике и имеет практическое применение в различных областях, включая данные
анализ, теория вероятностей, системы баз данных, сетевая безопасность и набор
теория. Давайте посмотрим на дополнение множества в деталях…..
Давайте посмотрим на дополнение множества в деталях…..
Дополнением множества A, обозначаемого A’, является множество всех элементов универсального множества, не входящих в A. Обозначается A’
Некоторые свойства дополнительных множеств 1) A ∪ A′ = U
2) A ∩ A′ = Φ
3) Закон двойного дополнения: (A′) ′ = A
4) Законы пустого множества и универсального множества Φ′ = U и U′ = Φ.
Пример 1: Если A = {1, 2, 3, 4} и U = {1, 2, 3, 4, 5, 6, 7, 8}, найдите A дополнение (А’).
Решение: A = {1, 2, 3, 4} и универсальный набор = U = {1, 2, 3, 4, 5, 6, 7, 8}
Дополнение множества A содержит элементы, присутствующие в универсальном множестве, но не набор A. Элементы 5, 6, 7, 8.
∴ Дополнение = A’ = { 5, 6, 7, 8}
Пример 2: Если B = { x | x — это книга по алгебре в вашей библиотеке} Найдите B’.
Решение: B’ знак равно { х | x — книга в вашей библиотеке и x ∉ B }
Пример 3: Если A = { 1,
2, 3, 4, 5} и U = N, то найдите A’.
Решение: A = {1, 2, 3, 4, 5}
U = N
⇒ U = {1, 2, 3, 4, 5, 6, 7, 8, 9,10,… }
A’ = { 6, 7, 8, 9, 10, … }
Пример 4: Если A = { x | x кратно 3, x ∉ N}. Находить А’.
Решение: По соглашению x ∉
N в скобках означает, что N является универсальным набором.
N = U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11, …}
A = {x | x кратно 3, x ∉ N }
A = { 3, 6, 9, 12, 15, … }
Итак, A’ = { 1, 2, 4, 5, 7, 8, 10,11, … }
Другой пример дополнения множества можно увидеть на контекст диаграммы Венна. Допустим, у нас есть два набора A = {1, 2, 3, 4} и B = {3, 4, 5, 6}.
Мы можем представить эти наборы с помощью диаграммы Венна следующим образом:
Диаграмма ВеннаНа этой диаграмме площадь внутри круга представляющий A представляет элементы A, а площадь внутри круга представляющий B представляет элементы B. Перекрытие двух кругов представляет элементы, которые есть как в A, так и в B.
Дополнение A — это множество всех элементов, которые
не входят в A, то есть все, что находится за пределами круга, представляющего A. Это
представлен заштрихованной областью (область синего цвета) за пределами круга:
Это
представлен заштрихованной областью (область синего цвета) за пределами круга:
Итак, дополнение A равно:
A’ = {5, 6}
Это представляет элементы, которых нет в A. Это несколько вариантов дополнения a набор, который может быть полезен в разных контекстах. Вот некоторые общие вариации:
Абсолютное дополнение:Абсолютное дополнение множества A, обозначаемое A’, — это множество всех элементов, не принадлежащих A, относительно универсального множества U. То есть A’ = {x ∈ U : x ∉ A}. Например, если A = {1, 2, 3} и U = {1, 2, 3, 4, 5}, то A’ = {4, 5}
Относительное дополнение:Относительное дополнение множества A относительно множества B, обозначаемое B\A, — это множество всех элементов B, которые не принадлежат A. То есть B\A = {x ∈ B : x ∉ A}. Например, если А = {1, 2, 3} и В = {1, 2, 3, 4, 5}, то В\А = {4, 5}.
Дополнение в топологии: В топологии дополнением множества A в топологическом пространстве X, обозначаемым X\A, является множество всех элементов в X, которые не принадлежат A.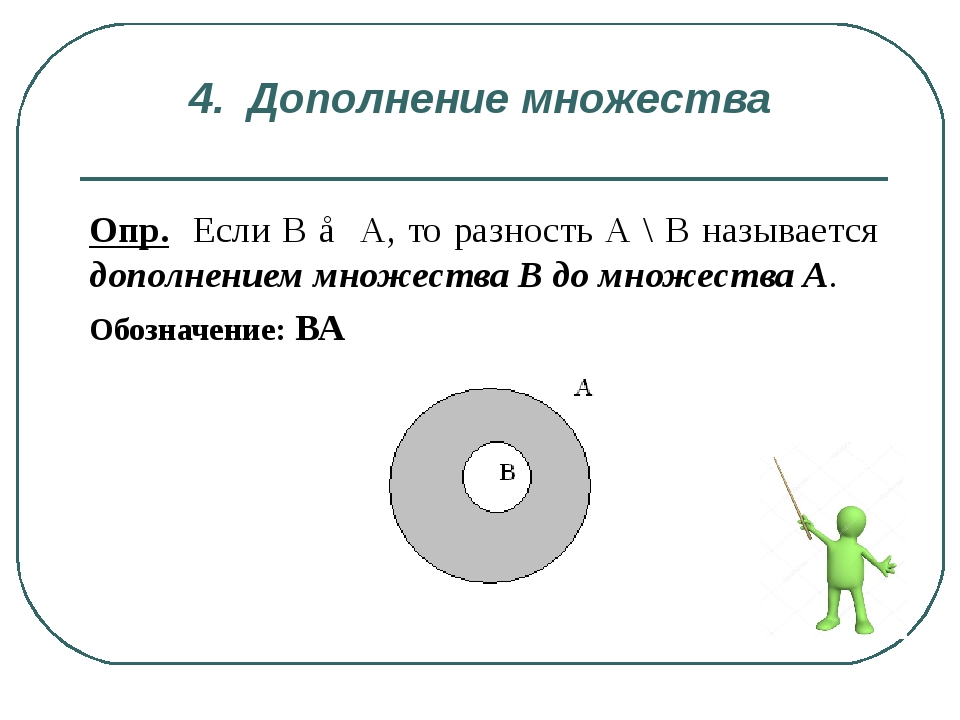 Это отличается от абсолютного дополнения, которое определено относительно универсального множества. Например, если X — множество действительных чисел, а A = (0, 1),
Это отличается от абсолютного дополнения, которое определено относительно универсального множества. Например, если X — множество действительных чисел, а A = (0, 1),
, то X\A = (-∞, 0] U [1, ∞).
Дополнение в булевой алгебре:В булевой алгебре дополнение множества A, обозначаемое À, является уникальным дополнением множества A относительно булевых операций объединения и пересечения. То есть Ā — единственное множество, удовлетворяющее условию A ∪ Ā = U и A ∩ Ā = ∅, где U — универсальное множество. Например, если A = {1, 2, 3} и U = {1, 2, 3, 4, 5}, то Ā = {4, 5}.
Дополнение множества также используется в законе де Моргана
В целом, различные варианты дополнения набора могут быть полезны в различных контекстах, в зависимости от типа набора и используемой математической или теоретической основы.
Дополнение множества имеет несколько практических применений в различных областях Вот несколько примеров:
Анализ данных: или аномалии в структуре данных. Например, дополнение набора нормальных данных может использоваться для идентификации точек данных, выходящих за пределы нормального диапазона, что может указывать на ошибку в данных или необычное явление.
Например, дополнение набора нормальных данных может использоваться для идентификации точек данных, выходящих за пределы нормального диапазона, что может указывать на ошибку в данных или необычное явление.
Поиск информации: При поиске информации дополнение набора может использоваться для поиска документов, которые не содержат определенных ключевых слов или фраз. Например, если пользователь ищет «кошки», но хочет исключить документы, содержащие слово «собаки», дополнение набора документов, содержащих слово «собаки», может использоваться для извлечения только документов, связанных с «кошками».
Компьютерное программирование: В компьютерном программировании дополнение множества может использоваться для выполнения операций над множествами, таких как объединение, пересечение и разность. Например, дополнение набора пользователей, которые уже зарегистрировались для услуги, может использоваться для идентификации потенциальных новых пользователей, которые еще не зарегистрировались.
Генетика: В генетике дополнение набора может использоваться для идентификации генов или генетических признаков, которые не связаны с конкретным состоянием или заболеванием. Например, дополнение набора генов, связанных с раком молочной железы, может быть использовано для идентификации генов, не связанных с заболеванием, что может помочь выявить новые потенциальные мишени для лечения.
В целом, дополнение набора является полезной концепцией, имеющей множество практических применений во многих областях.
Вот несколько важных моментов, которые необходимо изучить и понять о дополнении множества, как в теории, так и на практике Теоретически:
Определение: Комплектация набора определяется как множество всех элементов, не принадлежащих исходному множеству. Обозначается A’ или À, в зависимости от контекста.
Свойства: Дополнение множества имеет несколько важных свойств, таких как закон Де Моргана, который гласит, что дополнение объединения множеств есть пересечение их дополнений, и наоборот.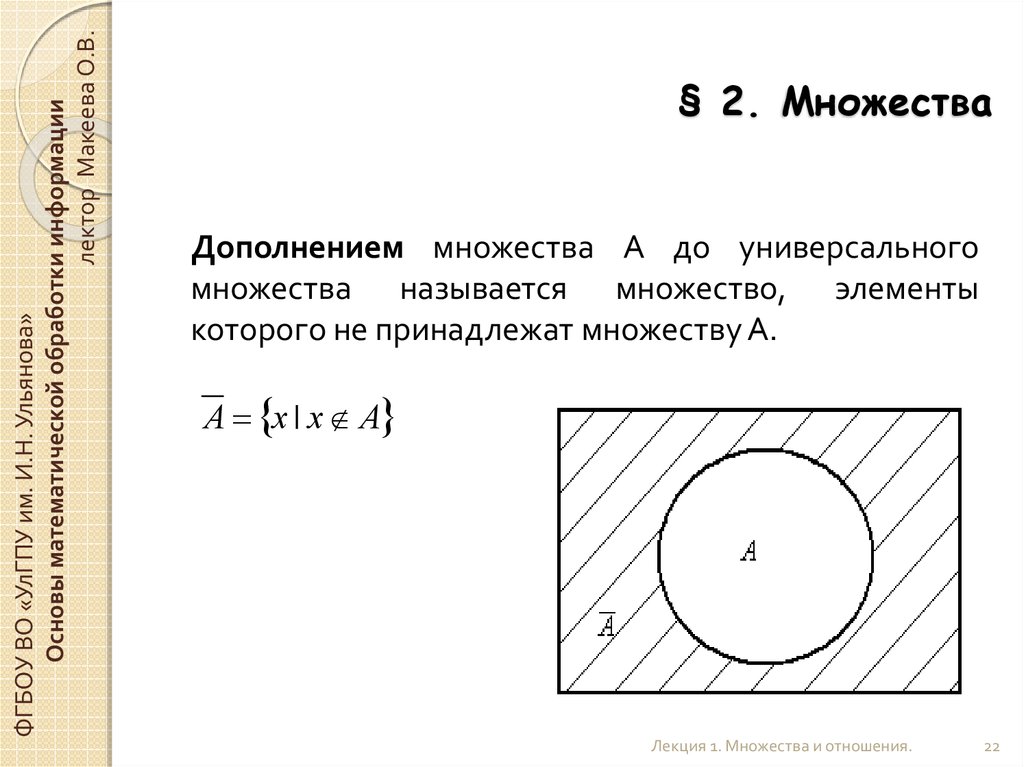 Другие свойства включают тот факт, что дополнение множества является исходным множеством и что дополнение пустого множества является универсальным множеством.
Другие свойства включают тот факт, что дополнение множества является исходным множеством и что дополнение пустого множества является универсальным множеством.
Типы дополнений: Существуют различные типы дополнений в зависимости от контекста. Абсолютное дополнение определяется относительно универсального набора, а относительное дополнение определяется относительно другого набора. Дополнение в топологии определяется в контексте топологического пространства, а дополнение в булевой алгебре определяется относительно булевых операций объединения и пересечения.
На практике:
Вычисление: Чтобы вычислить дополнение множества, вам необходимо идентифицировать элементы, которые не принадлежат множеству, либо путем их явного перечисления, либо с помощью правила или условия. Это может быть сделано с использованием различных методов, в зависимости от конкретного контекста и проблемы.
Приложения: Дополнение к набору имеет множество практических применений в различных областях, таких как теория вероятностей, анализ данных, системы баз данных и сетевая безопасность.

 Поэтому объединение
и
является универсальным множеством, представленным как
Поэтому объединение
и
является универсальным множеством, представленным как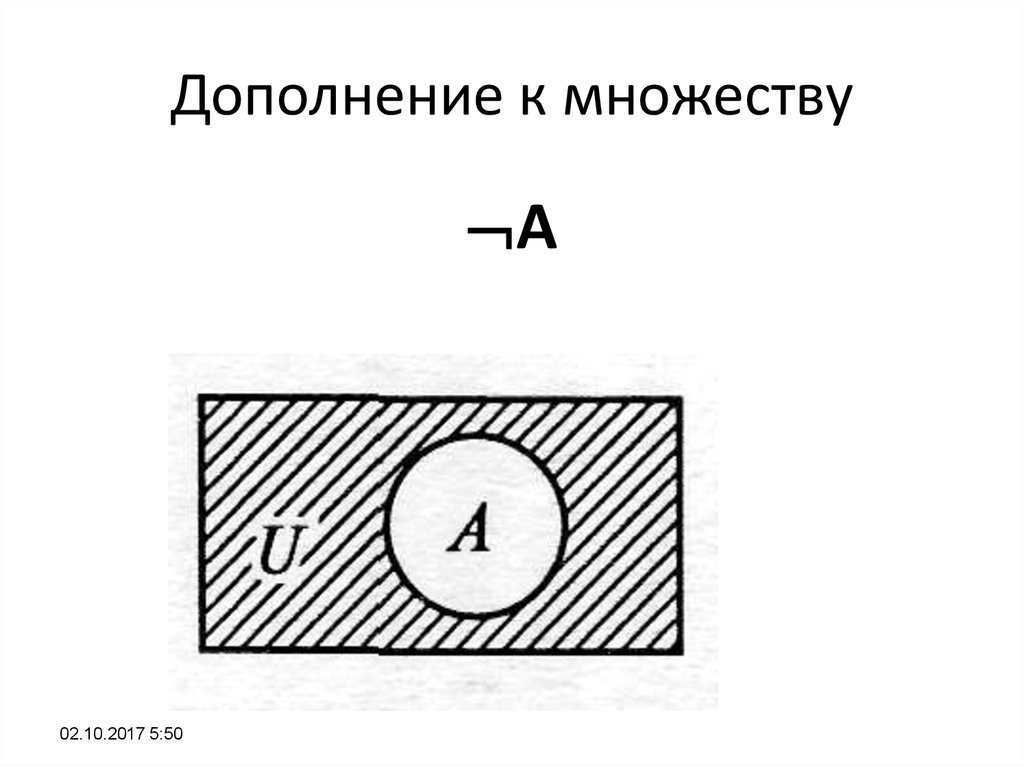

 (A ∩ B)’ = A’ UB’ (закон пересечения Де Моргана).
(A ∩ B)’ = A’ UB’ (закон пересечения Де Моргана).