Пример матрицы — Энциклопедия по экономике
Используя приведенный на рис. 2 пример матрицы воздействий НТП для подсистемы бурения, можно назвать примеры образуемых первичных ячеек НИР [c.37]Типичными примерами матриц, которые могут быть применены для этих целей в нефтеснабжении являются [c.373]
Построение цифровой модели календарного плана при параллельно-последовательном выполнении смежных операций показывается в табл. 42 на примере матрицы времени 3-го случая (табл. 39) II варианта очередности запуска деталей. [c.169]
Последовательное преобразование матрицы А(0) применительно к данному примеру (матрицы а, б, в, г) показано ниже. [c.95]
В табл. 31 приведен пример матрицы РАФУ, построенной по приведенной выше методике. [c.121]
О = 1, m), на пересечении строк и столбцов проставляются количественные оценки показателей. Пример матрицы исходных данных представлен в таблице 2.51. [c.274]
| Таблица 3.6. Пример матрицы отчетности для проекта-примера |
4.6 показан пример матрицы ответственности. Роли в примере указывают вид участия подразделения в работе О — ответственный исполнитель, И — исполнитель, П — приемка работ, К — консультации.
[c.180] X Этап П. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу (табл. 4.15), в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт А, а в соответствующих клетках — кратчайшие расстояния между ними. Для примера матрица принята симметричной Q = Сп, хотя приведенный ниже способ [c.145]
Уравнение (4.4), а также упражнение 5.15.1 утверждают, что у невырожденных матриц ранг локально постоянен. Вырожденные матрицы (точнее, матрицы с рангом, меньшим полного по строкам или столбцам) этим свойством не обладают. Рассмотрим, к примеру, матрицы [c.202]
Особенности выбора наилучшей стратегии лучше всего уяснить на примере матрицы (25) [c.108]
| Рис. 39 ПРИМЕР МАТРИЦЫ БАЛЛОВ |
Матрица полезного результата имеет вид, представленный в табл. 2.4. Найдем значения В, — тахе.-.- [c.79]Рассмотрим пример матрицы ортогонального планирования 2-го порядка для случая k = 3 [c.275]
Построим матрицу загрузок для различных значений числа наладчиков / и количества швейных машину. Элементы такой матрицы обозначим By. Пример матрицы представлен в виде табл. 8.6. Как было показано выше, в оценочном и не совсем верном расчете, поиск оптимальных значений / и у можно начать со значений / = 3 и у = 3, пропустив меньшие значения (/ — число наладчиков, / = 3, 4, 5 у — число арендуемых швейных машин, у = 3,4, 5). [c.307]
Отметим, что в нашем примере матрица входящего сальдо AS(t — 1) является нулевой, т. е. она имеет следующий вид [c.17]
Примеры матриц (и векторов) этого вида приводятся ниже. [c.373]
| Таблица 4. Пример матрицы ключевых результатов |
Матрица цен имеет тот же вид, но мы ее повторили на рис. 2.5, а.
[c.166]Рис, 4-10. Пример матрицы распределения ответственности по проекту конверсии программного [c.127]
Пример. Матрица А А неотрицательно определена для любой матрицы А. В самом деле, для любого вектора х [c.500]
В этом примере матрица А имеет размерность 4 х 4, а элементы матрицы вычисляются по определенной формуле. Показан вывод всей матрицы, а также некоторых ее элементов. [c.168]
Рассмотрим пример. Матрица парных коэффициентов корреляции признаков (выше главной диагонали) представлена в следующей таблице [c.42] Каждый эксперт получает неполную матрицу, на осях абсцисс и ординат которой расположены сравниваемые параметры (рис. 2 — пример матрицы для случая пяти параметров). Заполняются только те клетки, которые находятся справа от нисходящей диагностики. [c.37]
Пример матрицы для определения групп продукта [c.62]
| Рисунок 17. Пример матрицы 2×2 |
Таблица 12. Пример матрицы ответственности |
Вероятность прямо влияет на определение ожидаемого значения — центральной концепции платежной матрицы. Ожидаемое значение альтернативы или варианта стратегии — это сумма возможных значений, умноженных на соответствующие вероятности. К примеру, если вы считаете, что вложение средств (как стратегия действий) в киоск для торговли мороженым с вероятностью 0,5 обеспечит вам годовую прибыль 5000 долл., с вероятностью 0,2 — 10 000 долл. и с вероятностью 0,3 — 3000 долл., то ожидаемое значение составит [c.237]
Продемонстрируем матричный способ построения модели на примере формирования матрицы для технологического комплекса с постоянными параметрами (табл. 24.1), включающего два производства (рис.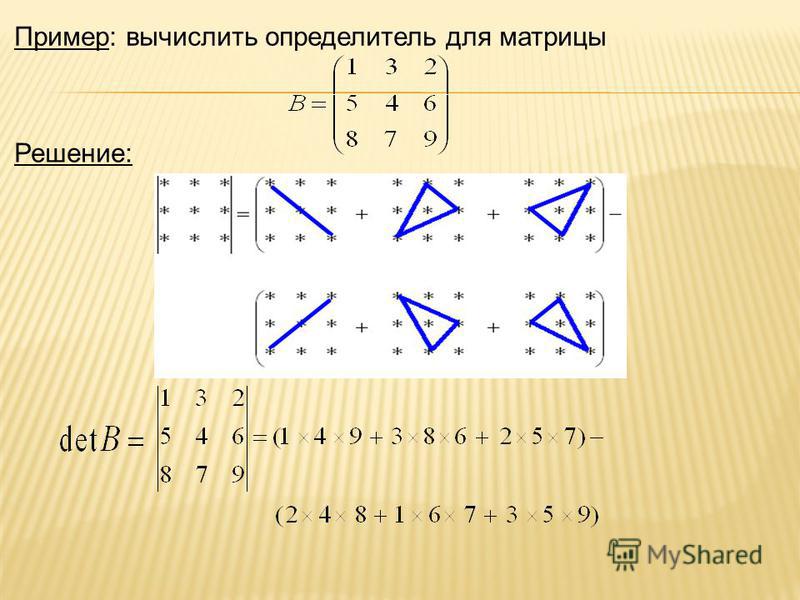
24.2). Практическая трудность здесь может состоять Е том, что эти производства не только выпускают готовые продукты, но и обмениваются между собой материальными потоками. Матричная развертка технологии в данном случае весьма наглядна п помогает не запутаться в нумерации многочисленных возвратных материальных потоков.
[c.415]
Первое из указанных требований означает, что предназначенная к использованию в практике планирования модель (далее для краткости эти модели называются плановыми) должна быть ориентирована на решение конкретной планово-экономической задачи, предусмотренной существующей или проектируемой методологией планирования. Это диктует необходимость трансформации многих известных экономико-математических моделей. Так, например, классическая модель межотраслевого баланса позволяет рассчитывать сбалансированные объемы выпусков продукции при заданной матрице коэффициентов прямых затрат и известном конечном продукте. Однако на практике такая задача может возникнуть лишь на завершающем этапе работы над планом, когда уже -рассмотрены вопросы технической политики в отраслях и приняты соответствующие решения (а значит, известна матрица плановых коэффициентов прямых затрат), изучены и обоснованы объем и структура капитальных вложений, товарооборота, экспорта и импорта (а значит, известен конечный продукт).
Приведем пример. Значительная часть матрицы технологических коэффициентов планового межотраслевого баланса может формироваться (и в результате внедрения первой очереди АСПР в определенной мере уже формируется) по данным централизованных расчетов потребности в материальных ресурсах, выполняемых на ЭВМ. Это существенно снижает затраты труда плановых работников на выполнение наиболее трудоемкой процедуры построения межотраслевых моделей —процедуры формирования исходной информации.
Рассмотрим морфологический ящик на примере матрицы для часов, приведенной в работе немецких маркетологов Е.
Дихтля и X. Хершгена (рис. 2.6). [c.90]
Для экспериментальной проверки указанных методов по достигаемым результатам и затратам времени на выполнение расчетов были взяты 15 примеров матриц операционных затрат времени на обработку партий деталей с однонаправленными технологическими маршрутами 1. В числе этих примеров одиннадцать матриц размером i X / = 6 X 12 и четыре матрицы 7 X 12. По технологическому процессу при обработке отдельных деталей занято от 7 до 11 станков. Характер матриц аналогичен приведенному в табл. 36 2. [c.185]
В табл. 4.6показан пример матрицы ответственности. Роли в примере указывают на вид участия подразделения в работе О — Ответственный исполнитель, И — Исполнитель, П — Приемка работ, К — Консультации. [c.297]
Теория жизненного цикла товара (ЖЦТ) получила широкое распространение в учебной литературе по маркетингу. В каждом учебнике ей посвящена как минимум отдельная глава, а число научных статей, описывающих жизнь товаров, не поддается учету.
Она оказала влияние и на используемые маркетологами популярные методы планирования (к примеру, матрица БКГ или портфельный метод M Kinsey).
[c.178]
Приведем два примера матриц Гессе для матричных функций. Во-первых, рассмотрим матричную функцию от п х 1 вектора х [c.251]
Применительно к рассматриваемому примеру матрица смежностей для прадерева (рис. 4.6) представлена на стр. 146—147. [c.145]
Второй пример матрицы создан под влиянием работ Л. Хольбе-ка-Ханссена. Матрица состоит из более детальных 6 х 6 ячеек. Она устанавливает следующие сектора собственную организационную структуру фирмы, ее потребителей, сбытовиков, конкурентов, поставщиков и, наконец, социальную среду. Эта матрица определяет также 6 уровней, а именно экономический, технический, социологический, психологический, биологический и геофизический. Как мы видим, обе матрицы имеют много общего. Основное различие состоит в том, что матрица 6×6 может дать возможность для более детального анализа участников рынка и их характеристик.
[c.162]
Это неполный пример матрицы оценки риска, использованной а проекте Информационные Системы , занимающемся переходом от системы Windows Olfi e-97 к системе Windows-2000, Проектная команда выявила риски, такие, как зависание системы после установки, жалобы конечных пользователей на изменение и сопротивление им и плохую работу оборудования. Помимо оценки вероятности, серьезности и времени события, проектная команда также оценивала свою способность вовремя определить тот момент, когда соответствующее событие действительно будет иметь место, чтобы смягчить его последствия, Обратите внимание, что команда считает высокой степень трудности обнаружения события, связанного с зависанием системы, так как системы рушатся без предупреждения, а отказ пользователя получил среднюю оценку, так как растущее недовольство и сопротивление можно заметить задолго до того, как оно приобретет угрожающие размеры. [c.166]
Положительные матрицы очевидно строго коположительны. Однако, как показывают примеры, матрицы вида
[c.
24]
Матрица плотности
Н.В. Никитин
Матрица плотности
Часть 1. КВАНТОВАЯ МЕХАНИКА ЧИСТЫХ СОСТОЯНИЙ
Постулаты квантовой механики (для чистых состояний)
Теорема о невозможности клонирования произвольного чистого состояния
Первооткрыватели «No-cloning theorem»
Совместное клонирование ортогональных состояний
Теорема о невозможности уничтожения копии произвольного чистого
состояния
Люди, доказавшие «No-deleting theorem»
Правила суперотбора
Часть 2. МАТРИЦА ПЛОТНОСТИ: ОСНОВНЫЕ СВОЙСТВА
Смешанные состояния
Матрица плотности чистого состояния
Как строить матрицу плотности чистого состояния |ψ>?
Матрица плотности смешанного состояния
Примеры матриц плотности
«Отцы» матрицы плотности
Неоднозначность разложения матрицы плотности смешанного состояния на
чистые
Нерелятивистская матрица плотности спина s = 1/2
Теорема Глизона (1957 г.
)
Количественное сравнение квантовых состояний
Как найти F1(А, В)?
Как найти DTr{А, В)?
Пример вычисления F1(А, В)
и DTr{А, В)
Пример вычисления остальных степеней совпадения и метрик
Матрица плотности составной системы
Запутанные состояния
Квантовое происхождение вероятностей Wℓ
Клонирование помогает запутанности?
Матрица плотности и постулаты квантовой механики
Факторизация матрицы плотности
Разложение Шмидта
Число Шмидта и запутанные состояния
Разложение Шмидта для трех и более подсистем
Состояния Белла (the Bell states)
Необходимое условие сепарабельности А.Переса
А.Перес и клан Городецких
Состояние Вернера и критерий сепарабельности Переса
Редукционное условие сепарабельности
Состояние Вернера и редукционный критерий
Часть 3. ФОРМУЛА ФОН НЕЙМАНА И ЕЕ СЛЕДСТВИЯ
Условная матрица плотности и формула фон Неймана
Редукция матрицы плотности и парадокс друга Вигнера
Проекционный постулат М.
Борна и проекционный постулат Дирака — фон
Неймана
Постулат о среднем значении операторов
Модель измерения по фон Нейману
Локальность нерелятивистской квантовой механики на макроскопическом
уровне и теорема Эберхарда
Суперпозиция или смесь!
Альтернатива принципу суперпозиции
Часть 4. ЭВОЛЮЦИЯ КВАНТОВОЙ СИСТЕМЫ ВО ВРЕМЕНИ
Эволюция матрицы плотности во времени. Квантовое
уравнение Лиувилля (уравнение фон Неймана)
Решение квантового уравнения Лиувилля
Важный частный случай
Уравнение Блоха
Обобщенная формула фон Неймана
Квантовый парадокс Зенона
Производная оператора по времени для смешанных состояний
Квантовое уравнение Лиувилля в координатном представлении
Матрица плотности свободной частицы
Часть 5. ОПИСАНИЕ ОТКРЫТЫХ КВАНТОВЫХ СИСТЕМ
Распад нестабильной микросистемы
Квантовое уравнение Лиувилля для открытых систем
Эволюция матрицы плотности открытых квантовых систем. Общий подход
Операторы Крауса и представление Крауса для матрицы плотности
открытой квантовой системы
Уравнение Линдблада
Как работает уравнением Линдблада.
Простой пример
Уравнением Линдблада для наблюдаемых в представлении Гейзенберга
Релаксационное уравнение для частицы в термостате
Часть 6. ОСНОВЫ КЛАССИЧЕСКОЙ ТЕОРИИ ИНФОРМАЦИИ
Классическая энтропия. Биты и наты
Энтропия и информация
Декогеренция и парадокс кота Шредингера
Граница между мирами
Ограничения на величину шенноновской энтропии
Двоичная энтропия
Неравенство Йенсена и вогнутость энтропии Шеннона
Классическая относительная энтропия и неравенство Гиббса
Классическая совместная энтропия и субаддитивность
Условная вероятность и теорема Байеса
Классическая условная энтропия
Доказательство субаддитивности
Классическая взаимная информация
Наглядная связь между различными энтропиями и взаимной информацией
Сильная субаддитивность
Часть 7. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ ИНФОРМАЦИИ
Квантовая энтропия (энтропия фон Неймана)
Ограничения на величину энтропии фон Неймана
Энтропия чистого состояния
Гипотеза о скрытых параметрах
Тример вычисления энтропии смешанного состояния
Сравнение квантовой и классической энтропии
Квантовая относительная энтропия и неравенство Клейна
Квантовая совместная энтропия и субаддитивность
Свойство субаддитивности для состояния Вернера
Субаддитивность и второе начало термодинамики
Квантовая взаимная информация
Неравенство треугольника (неравенство Араки-Либа)
Вогнутость квантовой энтропии
Теорема о невозможности клонирования произвольного смешанного
состояния
Часть 8.
НЕРАВЕНСТВА БЕЛЛА И КОРРЕЛЯЦИИ В КВАНТОВОЙ
ТЕОРИИОдновременная измеримость и неизмеримость
Понятие об элементах физической реальности
Неравенств Белла. Историческая справка
Неравенств Белла. Основная идея
Простой вывод CHSH-неравенства
Вывод CHSH-неравенства из условия неотрицательности совместных
вероятностей
Граница Цирельсона
Запутанные состояния вступают в игру
А теперь — пресловутая нелокальность!
CHSH-неравенство и сепарабельные состояния
Носки профессора Бертлмана, запутанность и CHSH-неравенство
Видео лекций
Матрица плотности. Вводный курс
Лекция 1
Лекция 2
Лекция 3
Обратная связь с автором
Мне очень хотелось сделать интересный и современный курс,
который
бы показал студентам красоту и глубину квантовой теории. Удалось это
или нет, судить слушателям и читателям (почти уверен, что курс будет
гулять «по интернетам»).
Очевидно, что написать столько текста и не
сделать ни одной ошибки в формулах или опечатки в словах абсолютно
невозможно. Поэтому у меня просьба, если кто найдет ошибку, опечатку
или, упаси боже, «дырку» в доказательстве какого-либо утверждения,
свяжитесь пожалуйста с автором по e-mail и сообщите ему о своей
находке. Вознаграждение не предлагаю. 🙂
Если у кого-то возникнут пожелания, какие еще интересные
вопросы можно было бы включить в курс, я с удовольствием рассмотрю
эти предложения (но не обещаю, что приму).
e-mail для связи [email protected],
в теме письма просьба указать «Обсуждение лекций по матрице
плотности», чтобы мне было легче находить соответствующие сообщения.
P.S. Работы, опровергающие квантовую физику и теорию
относительности, не рассматриваю. Дискуссии на эти темы не веду.
Свойства с примерами и специальными матрицами
Матрицы — форма множественного числа матрицы, которая символизирует прямоугольный массив или таблицу, в которой числа/элементы организованы в строки и столбцы.
Матрицы могут содержать любое количество столбцов и строк. Прямоугольный массив из m × n чисел (действительных или комплексных) в кадре из m горизонтальных строк (называемых строками ) и n вертикальных линий (называемых столбцами ) называется матрицей, имеющей порядка m на n и записывается в виде матрицы m × n, как показано ниже.
\(A=\left[\begin{matrix}a_{11}&a_{12}&……&a_{1n}\\a_{21}&a_{22}&……&a_{2n}\\ .& .&.&.\\ .&.&.&.\\a_{m1}&a_{m2}&……&a_{mn}\end{matrix}\right] \)
\(\text{Здесь число }a_{11},a_{12\ },\dots..\ \text{etc) известны как элементы матрицы A} \)
Пример матрицы:
\(B=\begin{bmatrix} 2&3&6\\3&4&5\\6&5&9\end{bmatrix}_{3\times3} \)
Приведенная выше матрица B имеет порядок 3 × 3. Следовательно, всего 9элементы в матрице. Здесь горизонтальный массив идентифицируется как строки, а вертикальный массив распознается как столбцы.
Матрицы доступны во всех размерах, но, как правило, их форма остается неизменной.
Размер матрицы называется ее размерностью, которая представляет собой общее количество строк и столбцов в назначенной матрице. Над матрицами могут выполняться различные операции, такие как сложение матриц, вычитание матриц, скалярное умножение матриц, умножение матриц, транспонирование матриц и т. д. Существуют различные типы матриц в зависимости от количества компонентов и организации элементов в матрицах.
В линейной алгебре существует множество типов матриц. Все типы матриц различаются по компонентам, порядку и определенному набору условий. Различные типы матриц: матрица-строка, матрица-столбец, одноэлементная матрица, прямоугольная матрица, квадратная матрица, единичная матрица, нулевая матрица, диагональная матрица и т. д. Существуют также некоторые специальные матрицы.
Какие бывают типы матриц?В линейной алгебре существуют различные типы матриц. Все типы матриц различаются по компонентам, порядку и определенному набору условий. Различные типы матриц с примерами приведены ниже:
1.
Матрица-строка: Любая матрица, состоящая из одной строки и n столбцов, называется матрицей-строкой.
т. е. \(A=\left[a_{11}\dots..a_{1n}\right]_{1\times n} \)
Пример матрицы строк:
\(P=\begin{bmatrix }\ 1&-3&17\end{bmatrix} \)
2. Матрица-столбец: Любая матрица, имеющая m строк и один столбец, называется матрицей-столбцом.
т.е. \(A=\begin{bmatrix}a_{11}\\\vdots\\a_{m1}\end{bmatrix}_{m\times1}\)
Пример матрицы столбца:
\(Q=\begin{bmatrix}2\\3\\7\end{bmatrix}\)
3. Нулевая матрица или нулевая матрица: Любая матрица, в которой все компоненты равны нулю, называется нулевой матрицей. Она также распознается как нулевая матрица и обозначается O. нулевая матрица порядка 3 x 3.
4. Одноэлементная матрица: Любая матрица называется одноэлементной, если матрица имеет только один элемент.
т. е. \(A=\left[a_{ij}\right]_{ m\times n}\) является одноэлементной матрицей, если m = n = 1.
Пример одноэлементной матрицы:
\(\left [4\right],\left[7\right],\left[b\right]\) являются примерами одноэлементной матрицы.
5. Квадратная матрица: Любая матрица, в которой количество строк равно количеству столбцов, скажем «A», называется квадратной матрицей порядка n.
т. е. \(A=\left[a_{ij}\right]_{ m\times n}\) объявляется квадратной матрицей порядка n, если m = n.
Пример квадратной матрицы:
\(B=\begin{bmatrix}2&3&6\\3&4&5\\6&5&9\end{bmatrix}\)
6. Прямоугольная матрица: Матрица идентифицируется как прямоугольная, если количество строк не совпадает с количеством столбцов.
Пример прямоугольной матрицы:
\(B=\begin{bmatrix}2&3&6&-1\\3&4&5&5\\6&5&9&-1\end{bmatrix}\)
Здесь мы видим, что есть четыре столбца и три строки в эта матрица, поэтому B является прямоугольной матрицей.
7. Горизонтальная матрица: Матрица порядка m x n называется горизонтальной матрицей, если n > m.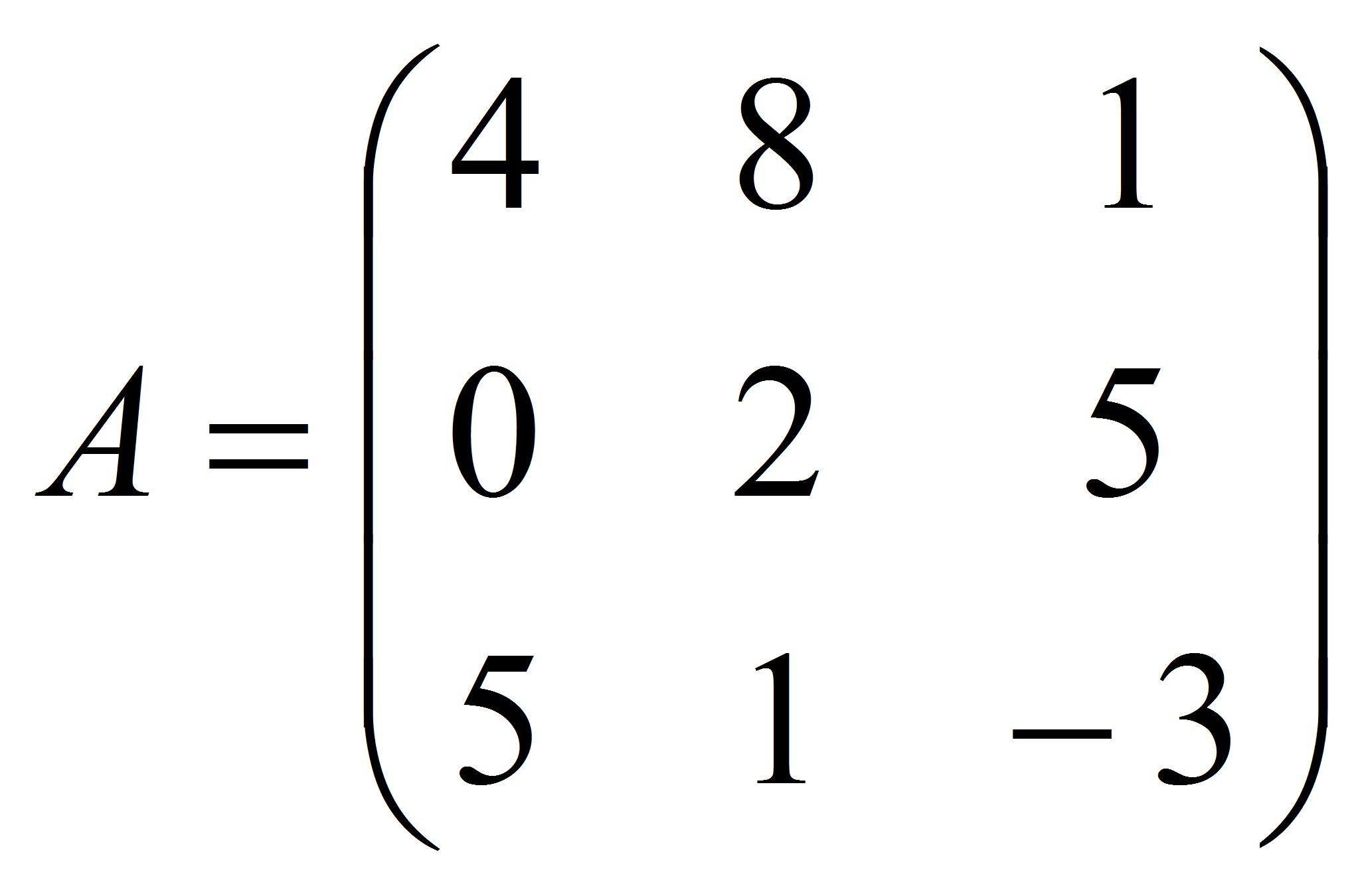
То есть, если количество столбцов больше, чем количество строк в горизонтальной матрице.
\(B=\begin{bmatrix}1&2&3&4\\4&3&2&1\end{bmatrix}\)
8. Вертикальная матрица: Матрица порядка m x n называется вертикальной, если m > n. То есть, если количество строк больше, чем количество столбцов в вертикальной матрице.
\(B=\begin{bmatrix}1&1\\2&5\\3&6\\2&4\end{bmatrix}\)
9. Диагональная матрица: Любая квадратная матрица, в которой все компоненты равны нулю, за исключением компонентов в главная диагональ называется диагональной матрицей.
Т.е. \(A=\left[a_{ij}\right]_{n\times n}\) является диагональной матрицей, если \(a_{ij}=0\) для i не равно j.
Пример диагональной матрицы:
\(B=\begin{bmatrix}2&\ 0&\ \ 0\\0&\ 1&\ \ 0\\0&\ 0&-2\end{bmatrix}_{3\times3}\ )
\(P=\begin{bmatrix}1&0&0&0\\0&5&0&0\\0&\ 0&2&0\\0&0&0&4\end{bmatrix}\)
Здесь мы можем понять, что кроме диагональных элементов все остальные элементы равны до нуля.
Следовательно, вышеупомянутый тип матрицы в математике является диагональной матрицей.
10. Прямоугольные диагональные матрицы: Прямоугольная диагональная матрица — это тип матрицы, которая также имеет одну ведущую диагональ с числами, а остальные записи — нули. Ведущая диагональ выбирается из самого большого квадрата в неквадратной матрице.
\(\begin{bmatrix}1&0&0&0&0\\0&4&0&0&0\\0&0&7&0&0\end{bmatrix}\)
11. Скалярная матрица: Диагональная матрица, в которой все главные диагональные компоненты равны, называется скалярной матрицей.
Пример скалярной матрицы:
\(B=\begin{bmatrix}2&\ 0&\ 0\\0&\ 2&\ 0\\0&\ 0&\ 2\end{bmatrix}_{3\times3}\)
\(B=\begin{bmatrix}-5&\ 0&\ 0\\0&\ -5&\ 0\\0&\ 0&-5\end{bmatrix}_{3\times3}\)
12. Единичная матрица или единичная матрица: Диагональная матрица, в которой все главные диагональные компоненты равны 1, называется единичной матрицей. Она также признается единичной матрицей.
Единичная матрица порядка n обозначается I или \(I_{n}\).
Примеры матрицы идентичности:
\(I_2=\begin{bmatrix}1&\ \ 0\\0&\ \ 1\end{bmatrix}\)
\(B=\begin{bmatrix}1&0&0\\0&1&0\ \0&0&1\end{bmatrix}_{3\times3}\)
Подробнее об определителях
Специальные типы матрицСуществуют некоторые специальные типы матриц, которые применяются в передовых математических расчетах и компьютерных технологиях:
1. Вырожденная и невырожденная матрица: Любая квадратная матрица, определитель которой равен нулю называется сингулярной матрицей, а любая матрица, определитель которой не равен нулю, называется невырожденной матрицей.
Пример сингулярной матрицы:
\(B=\begin{bmatrix}1&\ 1&1\\1&1&1\\1&1&1\end{bmatrix}\left|B\right|=\begin{vmatrix}1&1&1\\1&1&1\\ 1&1&1\конец{vmatrix}=1\влево(1-1\вправо)-1\влево(1-1\вправо)+1\влево(1-1\вправо)\влево|B\вправо|=0+0 +0=0\)
Пример невырожденной матрицы:
\(B=\begin{bmatrix}2&\ 1&1\\1&2&1\\1&1&1\end{bmatrix}\left|B\right|=\begin{vmatrix}2&1&1\\1&2&1 \\1&1&1\end{vmatrix}=2\влево(2-1\вправо)-1\влево(1-1\вправо)+1\влево(1-2\вправо)\влево|B\вправо|=2 -0-1=1\)
Любая квадратная матрица называется треугольной матрицей , если элементы выше или ниже главной диагонали равны нулю.
Существует 2 типа треугольных матриц, как показано ниже:
2. Верхнетреугольная матрица: Любая квадратная матрица \(A=\left[a_{ij}\right]_{n\times n}\) называется верхнетреугольной матрицей, если \(a_{ij} =0\) ∀ i > j.
Пример верхней треугольной матрицы:
\(B=\begin{bmatrix}2&\ 3&\ \ 4\\0&\ 1&\ \ 5\\0&\ 0&-2\end{bmatrix}_{3\times3} \)
3. Нижняя треугольная матрица: Любая квадратная матрица, например \(A=\left[a_{ij}\right]_{n\times n}\), называется нижней треугольной матрицей, если \(a_{ ij}=0\) ∀ i < j. 9{’} (транспонировать A) \)тогда A называется кососимметричной матрицей.
Пример кососимметричной матрицы:
\(Q=\begin{bmatrix}\ 0&\ \ 3\\-3&\ \ 0\end{bmatrix}\)
Характеристики симметричных и кососимметричных матриц
- Для кососимметричной матрицы A все ее диагональные элементы равны нулю. то есть \(a_{ii\left(i=j\right)}=0\) ∀ i и j.
- Нулевая матрица / Нулевая матрица является как симметричной, так и кососимметричной матрицей.
- A+B и AB также являются симметричными матрицами. 9{\ тета} \).
\(Q=\begin{bmatrix}0&\ -2+i\\2-i&\ \ \ \ \ 0\end{bmatrix}\)
Подробнее о матрице преобразования
Типы матриц в табличной формеТипы матриц с примерами приведены в табличной форме ниже:
Важные замечания по типам матрицТип матриц MATRIX. A=\left[a_{ij}\right]_{1\times n}\) \(P=\begin{bmatrix}\ 1&-3&17\end{bmatrix}\) Матрица столбцов \(A=\left[a_{ij}\right]_{m\times1} \) \(Q=\begin{bmatrix}2\\3\\7\end{bmatrix}\) Нулевая или нулевая матрица \(A=\left[a_{ij}\right ]_{m\times n}\text{где}a_{ij}=0\) \(B=\begin{bmatrix}0&0&0\0&0&0\0&0&0\end{bmatrix}_{3\times3}\) Одноэлементная матрица \(A=\left[a_{ij}\right]_{m\times n}\text{где }m=n=1\) \(\left[4\right],\left[7\right],\left[b\right]\) Горизонтальная матрица \(A=\left[a_{ij}\right ]_{m\times n}\text{ где }n\gt m\) \(B=\begin{bmatrix}1&2&3&4\\4&3&2&1\end{bmatrix}\) Вертикальная матрица \ (A=\left[a_{ij}\right]_{m\times n}\text{, где }m>n\) \(B=\begin{bmatrix}1&1\\2&5\\3&6\\ 2&4\end{bmatrix}\) Квадратная матрица \(A=\left[a_{ij}\right]_{m\times n}\text{где}m=n\) \(B=\begin{bmatrix}2&3&6\\3&4&5\\ 6&5&9\end{bmatrix}\) Диагональная матрица \(A=\left[a_{ij}\right]_{n\times n}\text{где} a_{ij}=0\text { for } i\ne j\) \(P=\begin{bmatrix}1&0&0&0\\0&5&0&0\\0&\ 0&2&0\\0&0&0&4\end{bmatrix}\) Скалярная матрица \(A =\left[a_{ij}\right]_{n\times n}\text{ где }a_{ij}=\begin{Bmatrix}0&i\ne j\\k&i=j\end{Bmatrix}\) Здесь k — константа.
\(B=\begin{bmatrix}-5&\ 0&\ 0\\0&\ -5&\ 0\\0&\ 0&-5\end{bmatrix}_{3\times3}\) Идентичность или единичная матрица \(A=\left[a_{ij}\right]_{n\times n}\text{, где }a_{ij}=\begin{Bmatrix}0&i\ne j\\1&i= j\end{Bmatrix}\) \(B=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}_{3\times3}\) Равная матрица \(A =\left[a_{ij}\right]_{m\times n}\text{ и }B=\left[b_{ij}\right]_{r\times s}\text{ где}a_{ij }=b_{ij},\ m=r,\text{ и } n=s\) \(A=\begin{bmatrix}2&-5\\2&\ 4\end{bmatrix},\ B=\begin{bmatrix}2&-5\\2&\ 4\end{bmatrix}\) Здесь A и B — равные матрицы.
Верхняя треугольная матрица \(A=\left[a_{ij}\right]_{n\times n}\text{ for }a_{ij}=0\ ∀\ i>j\) \(B=\begin{bmatrix}2&\ 3&\ \ 4\\0&\ 1&\ \ 5\\0&\ 0&-2\end{bmatrix}_{3\times3}\) Нижний Треугольная матрица \(A=\left[a_{ij}\right]_{n\times n}\text{ for }a_{ij}=0\ ∀\ i \(B=\begin{bmatrix}2&\ 0&\ \ 0\\3&\ 1&\ \ 0\\4&\ 5&-2\end{bmatrix}_{3\times3}\) Единственное число Матрица \(\left|A\right|=0\) \(B=\begin{bmatrix}1&\ 1&1\\1&1&1\\1&1&1\end{bmatrix}\) Несингулярный Матрица \(\left|A\right|\ne 0\) \(B=\begin{bmatrix}2&\ 1&1\\1&2&1\\1&1&1\end{bmatrix}\) Симметричные матрицы 9{m} = O\), где O — нулевая матрица порядка n. – - Для матричных продуктов матрицы должны быть совместимы. Это утверждает, что две матрицы A и B совместимы, если количество столбцов в A= количеству строк в B.
- Если мы умножаем матрицу на скалярное значение, то это распознается как скалярное умножение.
- Чтобы матрица была симметричной, она должна быть квадратной, т. е. иметь одинаковое количество строк и столбцов.
- Если m=n, матрица считается квадратной.
- Если m \ne n, матрица считается прямоугольной.
- Здесь m обозначает количество строк, а n обозначает количество столбцов.
- Диагональная матрица, в которой все главные диагональные компоненты равны 1, называется единичной матрицей. Она также распознается как единичная матрица, тогда как единичная матрица порядка n обозначается \(I\) или \(I_n\).
- Единичная матрица, нулевая матрица или нулевая матрица, а также скалярная матрица являются примерами диагональной матрицы, поскольку во всех них неглавным диагональным элементам присваивается нуль.
Мы надеемся, что приведенная выше статья о типах матриц поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о типах матрицВ.1 Каковы различные типы матриц?
Ответ 1 Существуют различные типы матриц: матрица-строка, матрица-столбец, одноэлементная матрица, прямоугольная матрица, квадратная матрица, единичная матрица, нулевая матрица, диагональная матрица и т. д.
Q.2 Можно ли добавлять матрицы разных размеров?
Ответ 2 Для выполнения сложения или вычитания матриц они должны иметь одинаковый размер или размерность. Если сложение или разность двух матриц, имеющих разные размеры или размерности, не определены.
Q.3 Каков порядок матрицы?
Ответ 3 Говорят, что матрица с m строк и n столбцов имеет порядок m x n.
Q.4 Что такое транспонирование матрицы?
Ответ 4 Можно определить транспонирование матрицы путем переключения строк в столбцы и столбцов в строки для предоставленной матрицы, т.е. строки и столбцы меняются местами.
В.5 Что такое матрицы?
Ответ 5 Матрицы — форма множественного числа матрицы, которая символизирует прямоугольный массив или таблицу, в которой числа/элементы организованы в строки и столбцы. Матрицы могут содержать любое количество столбцов и строк.
Скачать публикацию в формате PDFЧитать больше сообщений
Алкены: формула, структура, типы, получение, свойства, использование алкенов0284 Теорема Байеса: определение, связанные термины, формула, доказательство и применение здесь! Величина: знание определения, величины действительного числа и векторы с примерами Режим: определение, формулы, типы и примеры решения Матрица — определение и примеры
3 90
сущ. , множественное число: матрицы или матрицы
[ˈmeɪtɹɪks]
Определение: основная среда или вещество, занимающее пространства, например, в тканях, агрегатах клеток или внутри митохондрий.Содержание
Тела живых организмов представляют собой организованные структуры. Они организованы в иерархию систем органов, органов, тканей и клеток. Самая основная единица — это ячейка . Но задумывались ли вы когда-нибудь, как клетки удерживаются вместе? Должна же быть какая-то среда, которая удерживает эти клетки вместе? Что это такое?
Кроме того, все клеточные органеллы эукариотических клеток, такие как ядро, аппарат Гольджи, митохондрии, хлоропласты (у растений) и т. д., также имеют некоторые собственные четко определенные внутренние структуры. Как внутренние структуры, такие как ДНК, тилакоиды (в хлоропластах), кристы (в митохондриях), хроматин (в ядре) организованы и удерживаются на месте?
Что держит все на своих местах? Кроме того, соединительные ткани, такие как кости и хрящи, также имеют среду вместо цитоплазмы.
Что это? Ответом на все эти вопросы и запросы, поднятые выше, является «МАТРИЦА».Определение матрицы
Биологическое определение:
Матрица – это основная, неживая среда или вещество ткани, занимающее свободные пространства между клетками. В частности, его называют внеклеточным матриксом. Матрикс может также относиться к тому, что находится внутри органеллы, в частности, к митохондриальному матриксу . Этимология: от латинского «mātrix», что означает «плотина» или «матка», от «māter», что означает «мать».
Matrix — форма единственного числа, тогда как термин «матрицы » — форма множественного числа. В биологических структурах примерами матриц являются следующие:
- Внеклеточный матрикс
- Органеллярная матрица
Внеклеточный матрикс — это матрикс, который заполняет пространство между клетками в организме живого организма.
Когда мы говорим «клеточный матрикс» , мы обычно имеем в виду внеклеточный матрикс; клеточная матрица — «матрица между ячейками» .Термин «матрица» в биологии также обычно используется для обозначения желеобразной структуры в соединительных тканях, таких как хрящевая и костная ткани. Матрица в соединительной ткани помогает в правильном функционировании этих тканей, например, помогая защитным функциям костей и гладких поверхностей суставов через хрящ. На вопрос, что такое матрикс в анатомии, можно объяснить на примере костно-хрящевого матрикса.
Органеллярная матрица (ядерный матрикс, митохондриальный матрикс, пластидный матрикс, хлоропластный матрикс, матрикс Гольджи) представляет собой матрикс, который удерживает внутренние структуры этих органелл на месте. Это вещество, в которое встроены, организованы и удерживаются вместе различные клетки или клеточные органеллы. Итак, когда в биологии просят дать определение матрицы, можно объяснить, что это основное вещество или среда, в которую встроены клетки или клеточные компоненты.
В медицине матрикс определяется как межклеточное вещество любой биологической ткани, будь то твердое вещество, такое как кость или хрящ, или жидкое, такое как кровь.
Теперь, когда мы знаем определение матрицы в биологии и медицине, давайте теперь узнаем их соответствующие функции.
Функция матрицы
Различные функции и роли матриц в биологии перечислены ниже. Но сначала давайте взглянем на иллюстрацию ниже, чтобы понять природу различных матриц.
Рисунок 1. Природа матрицы варьируется в зависимости от назначения и роли в различных организмах и частях тела. Источник изображения: Аканкша Саксена из биологии в Интернете.- Твердый матрикс: Внеклеточный матрикс, который находится вне клеток и удерживает их вместе, представляет собой твердый матрикс. Его также можно назвать «межклеточным матриксом» , так как он находится между клетками. Он секретируется клетками и заполняет пустующие пространства, тем самым обеспечивая защиту клеток.
Рисунок 2: Обратите внимание на ВКМ (внеклеточный матрикс) снаружи клетки. Источник изображения: Пул, Дж. Дж. А., и Мостасо-Гвидолин, Л. Б. (2021).
- Жидкая/Жидкая матрица: Матрица крови представляет собой жидкую матрицу. Его еще называют « плазма ». Это почти 90-92% воды и около 6-8% белков, таких как фибриногены, глобулины, альбумины, и т. д. Эта жидкая матрица помогает почти во всех важных процессах от доставки питательных веществ, гормонов, и т. д. к частям тела, которые нуждаются их к удалению метаболических отходов.
- Желеобразный матрикс: Соединительнотканный матрикс костей и хрящей имеет желеобразную природу. Это помогает кости в защите жизненно важных органов тела. Он также помогает хрящам в формировании гладких суставов. Костный матрикс минерализован и хранит множество важных факторов роста, таких как IGF (инсулиноподобные факторы роста), TGF (трансформирующий фактор роста), и т. д.
Рисунок 3: Минерализованный костный матрикс по своей природе желеобразен и служит резервуаром для многих важных факторов роста. Источник изображения: Мохан С. и Бэйлинк Д.Дж. (1991)
- Желатиновая матрица: Многие многоклеточные организмы, такие как Volvox spp. имеют желеобразную матрицу, в которую встроены как их зародышевые, так и соматические клетки.
Рис. 4. Желатиновая матрица многоклеточных видов Volvox включает как соматические, так и зародышевые клетки. Volvox – это зеленая водоросль (Kingdom-Plantae). Изображение предоставлено: Дэвид Кирк.- Купер Г. М. (2000).
Примеры матриц
В биологическом мире есть несколько примеров матриц. Во-первых, взгляните на иллюстрацию ниже, чтобы понять классификацию.
Рисунок 5: Различные типы матриц в теле живых организмов. Источник изображения: Аканкша Саксена из биологии в Интернете.Матрицы тканей
Все эукариотические клетки имеют организацию в виде тканей .
Материал между клетками в тканях называется тканевой матрицей 9.0617 . В зависимости от типа клеток существуют различные типы тканевых матриц. Давайте посмотрим на них один за другим.Внеклеточный матрикс (ECM)
- Все клетки секретируют специальные гликопротеины (GP), составляющие ECM.
- Коллаген, который образует самые прочные волокна вне биологических клеток, является наиболее распространенным GP в большинстве клеток животных.
- Протеогликаны образуют очень плотную переплетенную сеть, в которую встроены GP.
- Много раз мы наблюдали образование крупных протеогликановых комплексов. Это сборка из сотен протеогликанов, нековалентно присоединенных к одной длинной молекуле полисахарида.
- Фибронектин : тип гликопротеина внеклеточного матрикса, который помогает прикреплять клетки к внеклеточному матриксу.
- Все клетки имеют рецепторные белки клеточной поверхности, называемые «интегринами ». Они находятся на клеточной мембране.
- Гликопротеины внеклеточного матрикса, такие как фибронектин, связываются с интегринами.
- Интегрины имеют 2 стороны: одна сторона обращена к ВКМ, которая связывается с гликопротеинами ВКМ, а другая сторона обращена к цитоплазме и связывается с микрофиламентами цитоскелета. Следовательно, интегрины способны передавать сигналы между ECM и цитоскелетом. Это помогает уравновешивать и преобразовывать изменения, происходящие снаружи и внутри клетки.
- ролей:
- ВКМ может влиять на активность генов в ядре
- ECM играет роль в механической сигнализации. (Каскад через гликопротеины, полисахариды, интегрины и микрофиламенты цитоскелета ВКМ)
- ВКМ играет роль в координации поведения клеток в ткани.
Костный матрикс
Поскольку костная ткань по своей природе очень твердая, ее матрикс является твердым и способствует обеспечению жесткости по своей природе.
Компонент органической матрицы состоит из коллагена, а компонент неорганической матрицы состоит из минералов. Поскольку коллаген является гибким по своей природе, это помогает предотвратить случаи переломов. Напротив, неорганические минеральные компоненты помогают обеспечить стадию минерализации, которая упрочняет матрицу.Хрящевой матрикс
Хрящевой матрикс «гибкий» или «желеобразный» по своей природе. Это связано с наличием «Агрегирующая соль сульфата хондроитина ГАГ» или «Агрекан» . Эта соль придает гибкость и податливость хрящевой матрице. Соль хондроитина богата сульфатами, которые помогают хрящу сопротивляться сжатию и, таким образом, помогают сгибаться и предотвращать поломку.
Рисунок 6. Агрекан или хондроитинсульфат помогают обеспечить гибкость хрящевой матрицы. Хрящевой матрикс обладает способностью впитывать много воды из-за свойств аггрекана. Источник изображения: Университет Лидса.Субклеточные матриксы
Внутри клетки есть несколько различных органелл.
У них также есть матрица, такая как митохондриальная матрица , ядерная матрица и пластидная матрица . Митохондриальный матрикс
Митохондриальный матрикс представляет собой пространство, заключенное во внутренней мембране (ВМ) митохондрий. Производство НАДН в цикле Кребса происходит в митохондриальном матриксе. Кроме того, АТФ-синтаза, расположенная на внутренней мембране митохондрий, производит АТФ на стороне матрицы (в матрице). Многие метаболиты переходят из межмембранного пространства в матрикс и наоборот. Из общего количества митохондриальных белков две трети принадлежат матриксу митохондрий.
Рисунок 7: Митохондрии имеют митохондриальный матрикс, который содержит гранулы матрикса, многочисленные ферменты, играющие ключевую роль в реакциях окислительного метаболизма, несколько копий митохондриальной ДНК, тРНК, выступающие внутрь АТФ-синтазы и рибосомы. Источник: Kelvinsong, лицензия CC.Ядерный матрикс
Представляет собой сеть ядерных волокон, подобно элементам цитоскелета внутри клетки.
Рисунок 8: Модель состава и структуры ядерного матрикса. Источник изображения: Джеффри Никерсон. Он выполняет важную функцию расшифровки генетической информации внутри клетки.Матрица Гольджи
Для правильного функционирования аппарата Гольджи существует сеть белков, которые собирают и формируют матрицу Гольджи. Семейство белков было названо « golgins ». Также во время митоза аппарат Гольджи должен распадаться на везикулы. Это происходит с помощью фосфорилирования множества белков матрикса Гольджи.
Матрица (среда)
Термин «матрица» часто используется вместо среды, означая среду, в которой можно выращивать живые организмы, такие как бактерии, грибы, и т. д.
Попробуйте ответить на приведенный ниже тест, чтобы проверить, что вы уже узнали о матрице.
Викторина
Выберите лучший ответ.
1.
, множественное число: матрицы или матрицы 
Что это? Ответом на все эти вопросы и запросы, поднятые выше, является «МАТРИЦА».
Когда мы говорим «клеточный матрикс» , мы обычно имеем в виду внеклеточный матрикс; клеточная матрица — «матрица между ячейками» .
д. 
Материал между клетками в тканях называется тканевой матрицей 9.0617 . В зависимости от типа клеток существуют различные типы тканевых матриц. Давайте посмотрим на них один за другим.
Они находятся на клеточной мембране.
Компонент органической матрицы состоит из коллагена, а компонент неорганической матрицы состоит из минералов. Поскольку коллаген является гибким по своей природе, это помогает предотвратить случаи переломов. Напротив, неорганические минеральные компоненты помогают обеспечить стадию минерализации, которая упрочняет матрицу.
У них также есть матрица, такая как митохондриальная матрица , ядерная матрица и пластидная матрица . 
Он выполняет важную функцию расшифровки генетической информации внутри клетки.