Примеры множества и подмножества: определение, способ задания, примеры; подмножество и булеан

Новости — Костромской автотранспортный колледж

Новости

Форма входа

Пароль

Запомнить меня

• Регистрация
• Забыли логин?
• Забыли пароль?

Версия для слабовидящих

Подробности

Опубликовано 30 Сентябрь 2022

ОГБПОУ «Костромской автотранспортный колледж» продлевает прием документов на 2022-2023 учебный год по следующим образовательным программам:

Подробнее…

Подробности

Опубликовано 26 Сентябрь 2022

«С Днем среднего профессионального образования!» — такими теплыми словами впервые начнется праздничный концерт во Дворце творчества 01.

10.2022 года. День среднего профессионального образования, объявленный Президентом страны 2 октября, должен коснуться каждого студента, преподавателя колледжа, мастера производственного обучения.

Подробнее…

Подробности

Опубликовано 29 Август 2022

График проведения 1 сентября 2022 г.

1 курс
11.30-12.00 — линейка
12.00-12.45 — классный час

2, 3, 4, 5 курс
8.40-9.40 — 1 пара
9.50-10.50 — 2 пара, согласно расписания
11.00-11.30 — классный час
11.30-12.00 — линейка

 

Подробности

Опубликовано 16 Август 2022

ОГБПОУ «Костромской автотранспортный колледж» продлевает прием документов на 2022-2023 учебный год по следующим образовательным программам:

Подробнее. ..

Подробности

Опубликовано 15 Август 2022

Торжественно и празднично Кострома отмечает 78-ю годовщину образования Костромской области. Не остались в стороне студенты и преподаватели нашего колледжа.

Подробнее…

1. Окончание учебного года в КАТК
2. Награждения участников IV Всероссийской летней Спартакиады «Юность России»
3. Свидетельства «Слесарь по ремонту автомобилей 1 разряда» вручены учащимся 8 и 9 классов
4. Фестиваль культур народов Костромской области
5. Олимпиада по математике

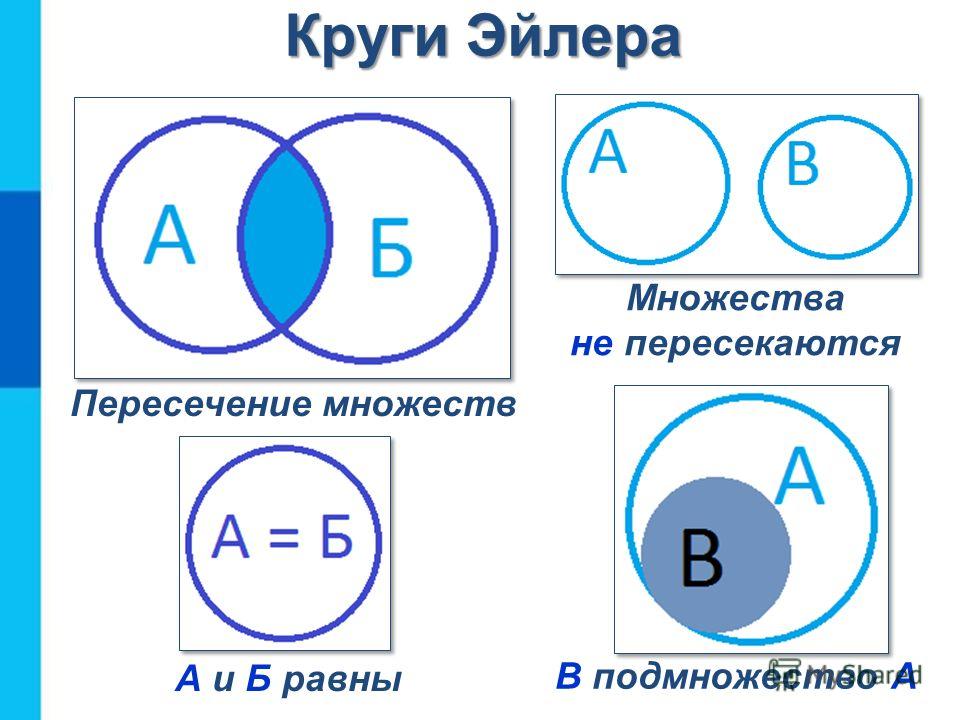
1.2. Множество и подмножество

Определение 1.2. Множество называютподмножеством множества , если каждый элемент множестваявляется элементом.

Определение 1.3. Отношение между множеством и подмножеством называют отношением включения.

Если множество является подмножеством множества , то говорят, чтовключено в иливключает в себя .

Слова «включено» и «не включено» обозначаются символами: и. Предложениеможет быть прочитано любым из следующих способов: «множествовключено во множество», «множествовключает в себя множество», «множествоявляется подмножеством множества».

Обратим внимание на то, что в определении 1.2 не сказано, имеются ли во множестве элементы, не принадлежащие. Возможны два случая: (1)содержит элементы, не принадлежащие, (2)не содержит элементов, не принадлежащих.

В первом случае множество в некотором смысле «больше» множества, так как кроме всех элементов, входящих в, имеет еще какие-то элементы. В этом случаеназываютправильной частью множества , а отношение междуи– отношением строгого включения.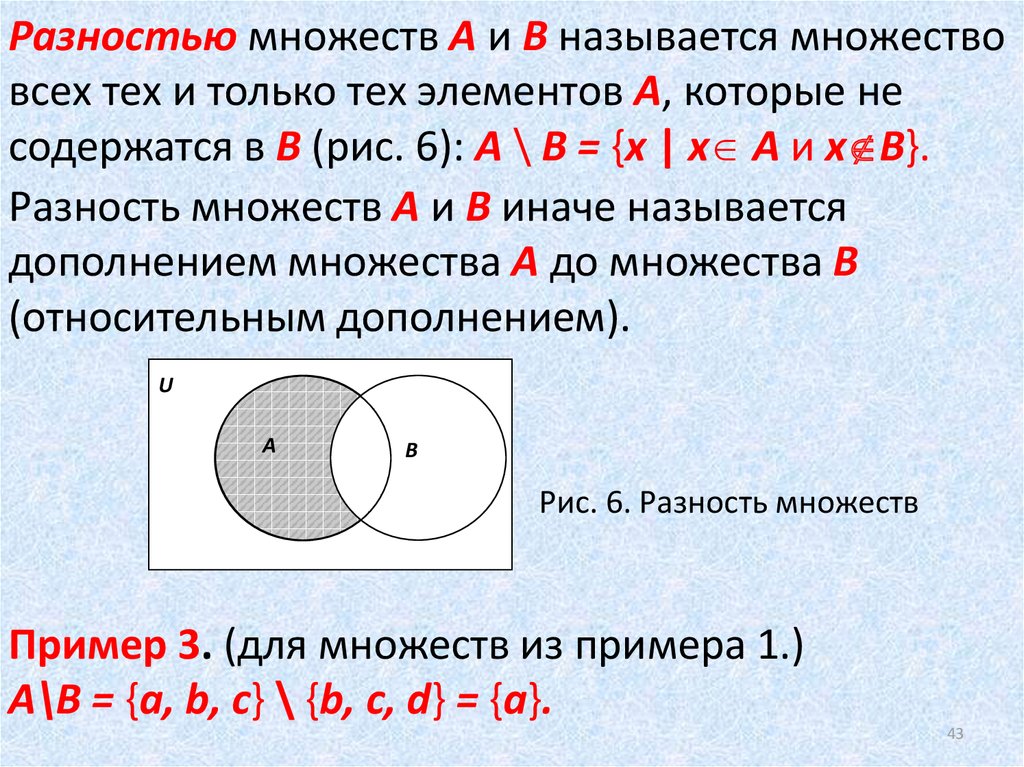 Знак строгого включения «». Предложениеможно читать «строго включено в», или «является правильной частью».

Во втором случае, когда исостоят из одних и тех же элементов, их называютравными множествами =, а отношение между ними –отношением равенства. В случае равенства множеств, справедливы оба включения: и. Поскольку любое множестворавно самому себе, то оно является подмножеством самого себя:.

Таким образом, утверждение истинно для тех множеств, которые либо являются правильной частью, либо равны. Аналогично нестрогое числовое неравенство:, справедливо для всех значений переменной, которые меньшеили равны.

Диаграммы Эйлера-Венна, иллюстрирующие отношение включения, показаны на рис. 1.2.

Пусть – универсальное множество, множестваизаданы своими характеристическими функциямии(), причемявляется подмножеством. По смыслу характеристической функции, очевидно, что при любых значениях аргумента значение характеристической функции подмножества не превосходит значений характеристической функции множества:

.

(1.2)

Характеристические функции равных множеств равны при любом значении :. Если множествоявляется правильной частью множества, то между характеристическими функциями этих множества имеет место строгое неравенство:.

Верны также и обратные утверждения:

1. Если для любого справедливо, то.

2. Если для любого справедливо, то.

Определение 1.4. Множество всех подмножеств множества называютбулеаном множества .

Применяются обозначения: P(A). В этих обозначениях определение 1.4 можно записать так: P(A)=.

Рассмотрим несколько примеров.

Примеры.

1). Запишем булеан множества – =, содержащего два элемента.

P(A)=. Булеан содержит 4=2²элемента.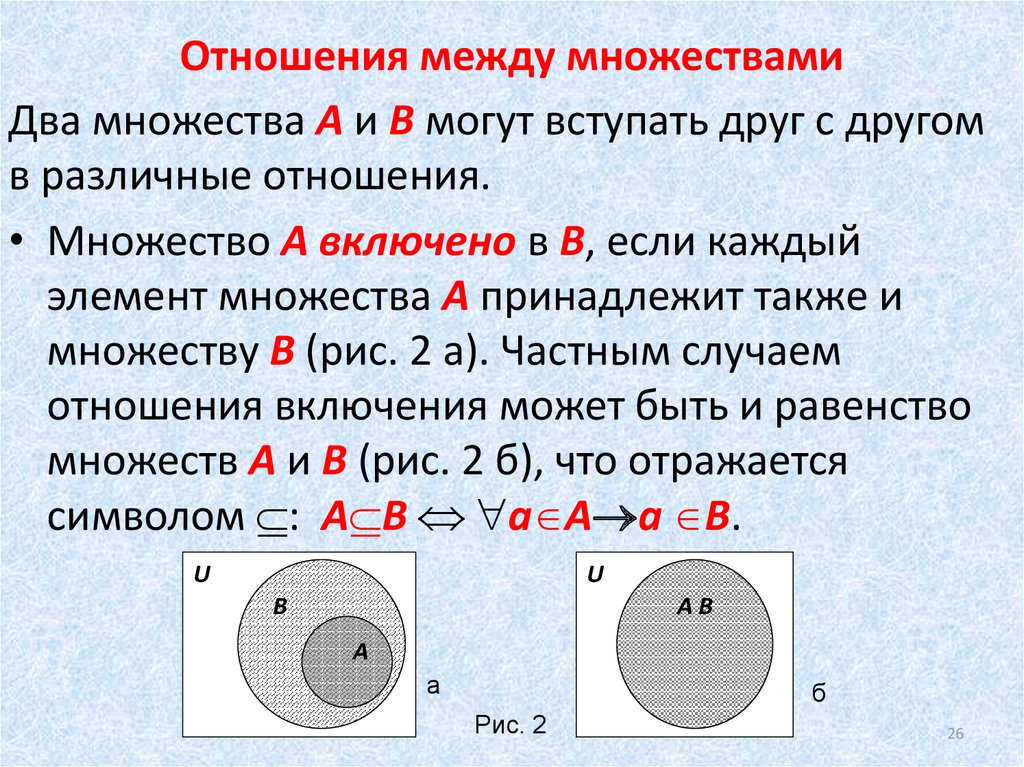

Составим таблицу элементов булеана и характеристических функций подмножеств множества .

Подмножества множества	Значения характеристических функций подмножеств
	Элементы множества
	0	0
	0	1
	1	0
	1	1

Обратим внимание на то, что любое из подмножеств множества (любой элемент булеана) имеет свой двоичный номер, составленный из значений характеристических функций подмножества на каждом из элементов множества. В данном примере множествосодержит два элемента, следовательно двоичные номера – это всевозможные двумерные двоичные векторы. Таких векторов 4, следовательно и число подмножеств двухэлементного множества тоже равно четырем.

Изобразим схематически отношение включения между подмножествами множества (рис. 1.3).

Все подмножества множества разбиты на три уровня (рис.1.3). На нулевом уровне находится «наименьшее» – пустое множество с характеристической функцией (00). Это множество является подмножеством всех элементов булеана. На первом уровне располагаются два одноэлементных множества. Ни одно из них не является подмножеством другого множества этого же уровня. В таком случае говорят, что множестванесравнимыдруг с другом. На втором уровне расположено «наибольшее» множество, совпадающее с самим множеством.

Двигаясь по диаграмме снизу вверх, получаем последовательность включений множеств. Существует два пути движения по диаграмме: (1) , (2). Движение по первому пути дает последовательность включений, по второму –.

2). Пусть множество =содержит три элемента.

Составим таблицу элементов булеана и их характеристических функций, а также диаграмму отношений включения между его элементами.

Подмножества множества	Значения характеристических функций подмножеств
	Элементы множества
	0	0	0
	0	0	1
	0	1	0
	0	1	1
	1	0	0
	1	0	1
	1	1	0
	1	1	1

Число подмножеств с добавлением элемента удвоилось: булеан трехэлементного множества содержит 8=42=2³подмножеств.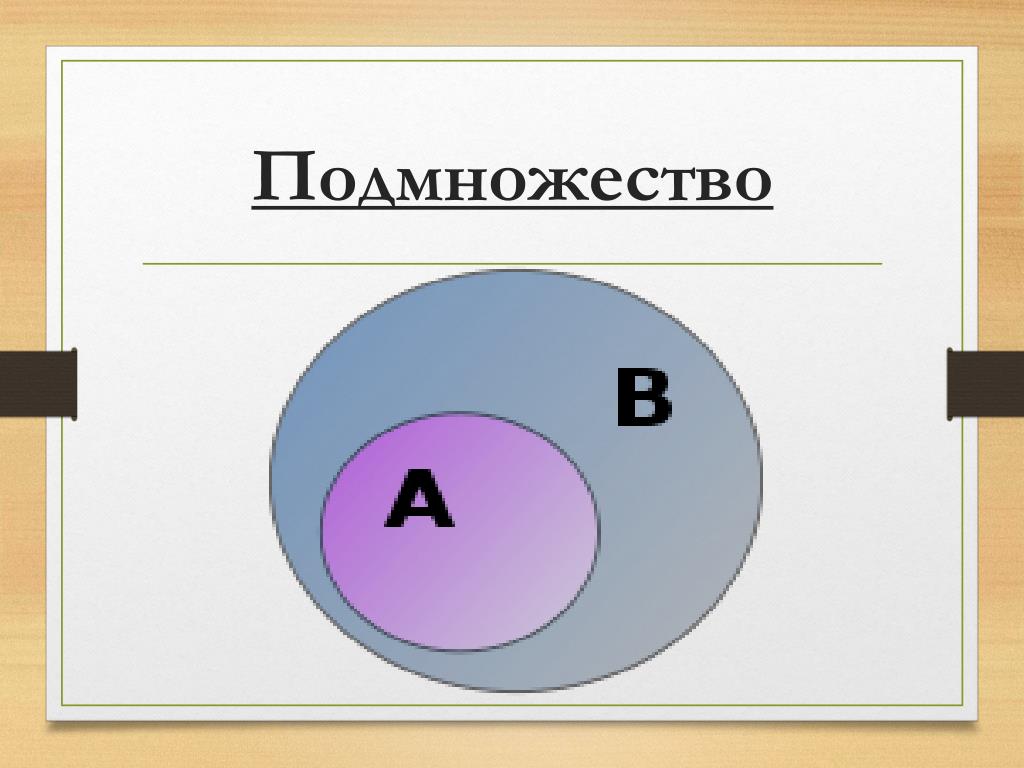

Диаграмма отношений включения представлена на рис. 1.4.

Все подмножества множества разбиты на четыре уровня (см. рис.1.4). Множества одного уровня несравнимы между собой по отношению включения, но двигаясь по любому пути диаграммы, получаем последовательную цепочку включений.

Интересным является вопрос: сколько всего путей существует в диаграмме? Ответить на него достаточно просто, построив так называемое «дерево путей» (рис. 1.5).

Как видно из рис.1.5, существует 6 цепочек включений подмножеств, причем каждая состоит из четырех включений

;;

;;

;.

Отметим, что двоичные векторы играют в теории множеств весьма существенную роль. Они использовались при нумерации областей на диаграммах Эйлера-Венна (см. разд. 1.1). В этом параграфе с их помощью кодируются элементы булеанов множеств. Между элементами булеана множества , содержащего n элементов, и n-мерными двоичными векторами существует взаимно однозначное соответствие, т.е. каждому подмножеству множествасоответствует определенный n-мерный двоичный вектор, и наоборот – каждому n-мерному двоичному вектору соответствует единственное подмножество множества.

Отношению включения множеств соответствует отношение «меньше или равно» во множестве двоичных векторов.

Определение1.5. Говорят, что двоичный вектор меньше или равен двоичному вектору, если каждая координата вектора не больше одноименной координаты вектора.

В буквенной форме определение 1.5 имеет следующий вид:

(1.3)

Рассматривая n-мерные двоичные векторы как числа в двоичной системе счисления, можно утверждать, что всего таких векторов существует 2ⁿ, а следовательно любое n-элементное множество содержит 2ⁿ подмножеств.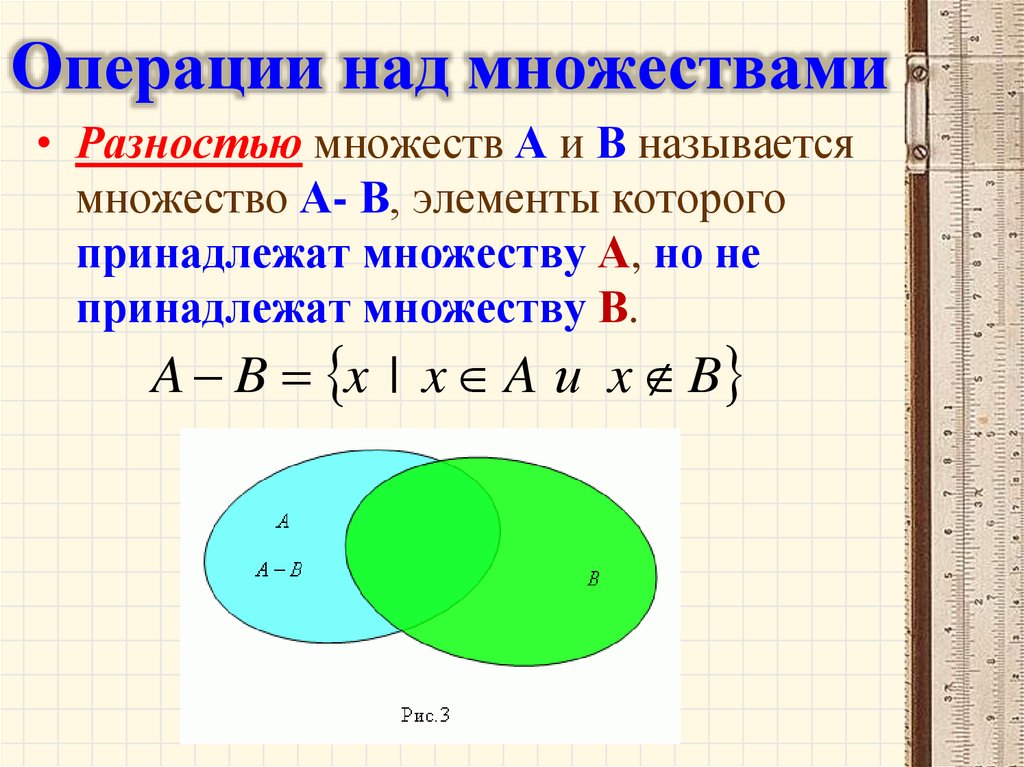 Поэтому булеан множества называют такжемножеством-степенью и, кроме обозначенияP(A), применяют также обозначение 2^A: 2^A=P(A)=.

Знакомство с множествами и подмножествами

В сегодняшней статье мы рассмотрим небольшое введение в множества и подмножества: какие существуют типы, как они выражаются… Все с некоторыми примерами, которые очень легко понять. Для этого вместо чисел мы будем использовать такие элементы, как фрукты, животные, дети…

Первое, что мы должны знать, это , что такое множество.  Мы можем определить его как набор объектов, который мы называем элементами , которые имеют некоторые общие характеристики.

Наборы могут содержать элементы любого типа: цифры, буквы, предметы, люди… Например, этот набор содержит фрукты:

НАБОР

Классификация наборов:

Набор можно классифицировать по количество элементов, которые он имеет. Это:

• Конечное: , если у него есть коллекция, которую можно подсчитать, даже если это может быть трудно сделать. Например, набор фруктов включает в себя все виды фруктов, которые существуют в мире. Несмотря на то, что это может быть трудно, можно сосчитать все виды фруктов в мире, поэтому оно конечно.
• Бесконечно: , если у него есть коллекция, которая никогда не может закончить подсчет. Например, множество всех четных чисел (которые бесконечны) является бесконечным множеством.

Отношения между множествами:

По отношению между собой множества могут быть:

• Непересекающиеся множества: те множества, которые не имеют ни одного общего элемента.

Например, множества фруктов и животных не пересекаются, потому что нет ни плода, который мог бы быть животным, ни животного, которое могло бы быть плодом:

РАЗЪЕДИНЕННЫЕ МНОЖЕСТВА

• Равные множества:   бывает, когда все элементы одного множества принадлежат другому.

Например, набор красных фруктов и набор желтых фруктов являются равными наборами фруктов, поскольку все красные фрукты являются фруктами, и все желтые фрукты также являются фруктами.

ПОДМНОЖЕСТВА

Множество живых существ очень велико: оно имеет множество подмножеств. Например:

• Растения — это подмножество живых существ.
• Животные — это подмножество живых существ.
• Люди являются подмножеством животных.

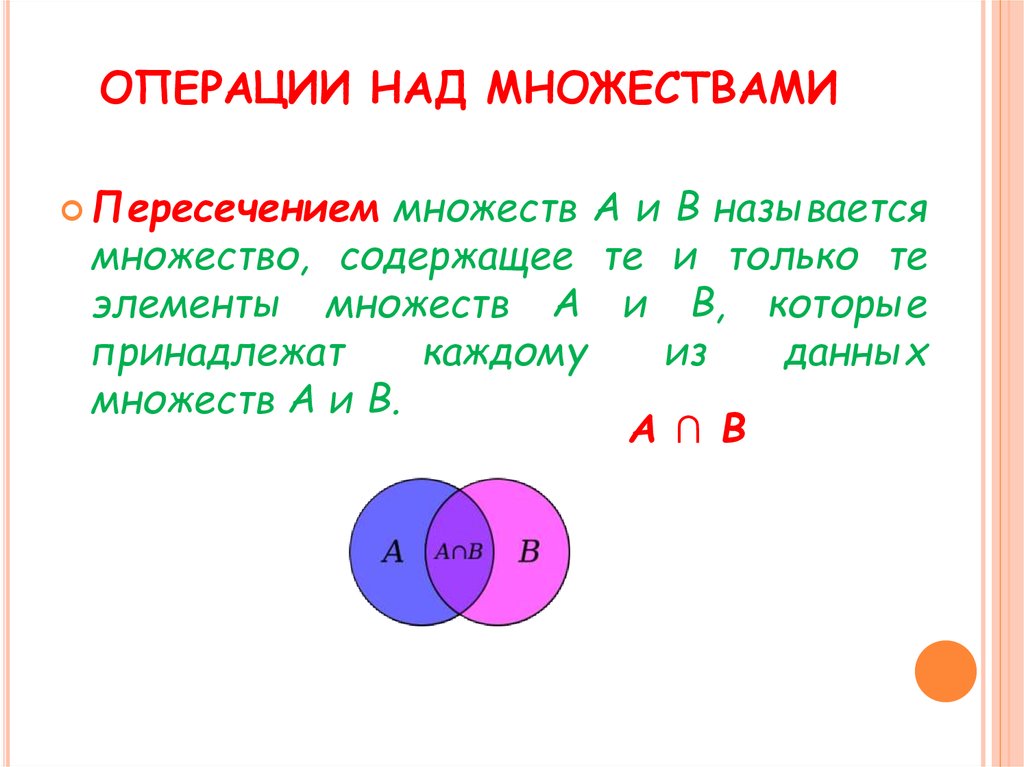
Пересечение подмножеств: иногда разные наборы отличаются друг от друга, но имеют некоторые общие элементы. Затем определяется область пересечения, содержащая все общие элементы.

Например, у нас есть группа девушек и группа людей, которые носят очки. Поскольку есть девушки, которые носят очки, они составляют часть пересечения двух наборов:

ПЕРЕКРЕСТОК

Что вы думаете об этом посте? Помогло ли это вам лучше понять множества и подмножества?

Если вы хотите попрактиковаться в этих наборах упражнений и многом другом, зарегистрируйтесь и попробуйте бесплатную пробную версию Smartick.

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

Подмножества — определение и примеры

В ходе нашего предыдущего обсуждения мы узнали, что множество — это набор отдельных элементов. Итак, что произойдет, если мы вынесем некоторые элементы из этого набора и сформируем подгруппу. Имеет ли смысл эта подгруппа? Будет ли он обладать какими-то уникальными свойствами? Как мы можем это назвать? На все эти вопросы можно ответить с помощью концепции подмножеств.

В этой статье мы попытаемся ответить на эти вопросы по отдельности, так что давайте приступим.

Разделение набора приводит к образованию меньших наборов, называемых подмножествами.

Темы, которые мы рассмотрим в этой статье:

• Что такое подмножество?
• Как представить подмножество?
• Свойства подмножества
• Примеры
• Практические задачи

 

Что такое подмножество?

Подмножество, как следует из названия, является поднабором любого множества. Предположим, что у нас есть два множества, X и Y. Математически говоря, X будет подмножеством Y тогда и только тогда, когда все элементы X присутствуют в Y. Мы также можем сказать, что X содержится в Y. Это отношение называется включением или включением X в Y. 

Чтобы лучше понять это, представьте, что у вас есть множество A, такое что A включает в себя названия всех городов в вашей стране. В этом случае множество B, состоящее из названий городов вашей провинции, будет подмножеством A. Это потому, что все города в вашей провинции также должны быть городами вашей страны; следовательно, B является подмножеством A.

В любом наборе существует только определенное количество различных или уникальных подмножеств, поэтому остальные избыточны и повторяются.

Подмножество может быть классифицировано следующим образом:

1. Правильная подмножество
2. Неправильное подмножество

Давайте решаем некоторые примеры подразделения:

Пример 1 2009 9

Определите, является ли A — это B. следующее:

1. A = {набор всех четных чисел}, B = {набор целых чисел}
2. A = {1, 2, 3}, B = {1, 2, 3, 4, 5, 6, 7, 8, 9}
3. A = {все письменные принадлежности в канцелярском магазине}, B = { ручки}
4. A = {седан}, B = {все автомобили}

Решение

(i) Набор четных чисел задается как:

     A = {0, 2, 4, 6, …}

    Аналогично множество целых чисел задается как:

B = {0, 1, 2, 3, …}

      Совершенно ясно, что элементы A принадлежат множеству B. Таким образом, A является подмножеством B

(ii) Из анализа двух наборов A и B ясно, что элементы A принадлежат множеству B. Таким образом, A является подмножеством B

(iii) Набор A включает в себя ручки, карандаши, блокноты, маркеры и т. д. Тогда как множество B включает только ручки. Таким образом, мы не можем сказать, что все элементы A находятся в B, что является условием для того, чтобы A было подмножеством B. В этом случае B является подмножеством A, но A не является подмножеством B.

(iv) Набор B включает в себя все типы автомобилей; седаны, хэтчбеки, пикапы и т.д. А, А — набор седанов. Таким образом, все элементы A включены в B. Следовательно, A является подмножеством B.

Типы подмножеств

Ранее мы упоминали, что существует два типа подмножеств . Так что же это за типы? Давайте сделаем обзор.

Правильное подмножество

Любое множество A считается правильным подмножеством B, если в B есть хотя бы один элемент, которого нет в A.

Другими словами, если A и B равны неравны и все элементы A присутствуют в B, то A является правильным подмножеством B. 

Также называется строгим подмножеством.

Давайте рассмотрим пример:

Пример 2

1. Является ли A правильным подмножеством B, когда A = {1, 2, 3, 8} и B = {1, 2, 3, 8}?
2. Является ли A правильным подмножеством B, если A = {1, 2} и B = {1, 5, 6, 7}?

Решение

1. Нет, A не является правильным подмножеством B, так как оба равны, и B не имеет уникального элемента, которого нет в A.
2. Нет, A не является правильным подмножеством. Это даже не подмножество, поскольку 2 отсутствует в B.

Неверное подмножество

Рассмотрим два набора, A и B; A является неправильным подмножеством B, если оно содержит все элементы B. Любое множество является неправильным подмножеством самого себя.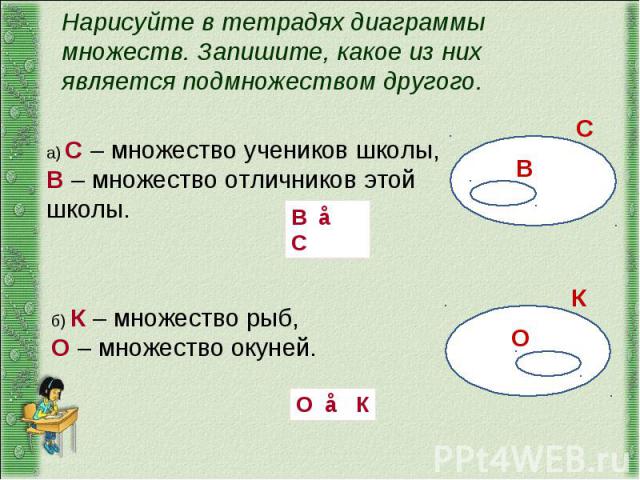

Как представлять подмножества?

Мы ознакомились с тем, что такое подмножество, теперь посмотрим, как его представить. Подмножество, как и любое другое множество, записывается так, чтобы его элементы были заключены в фигурные скобки. Но его представление — другое дело. Поскольку подмножество является частью множества, оно записывается с помощью интуитивно понятного символа ⊆, который читается как 9.0008 ‘является подмножеством’ :

Итак, рассмотрим два множества, A и B: 

Если A является подмножеством B, то мы запишем это как:

A ⊆ B

Если A не является подмножеством B, мы запишем его как:

A ⊈ B

Некоторые математики также используют символ ⊂ для обозначения правильного подмножества. Таким образом, мы можем также записать приведенные выше утверждения следующим образом:

Если A является правильным подмножеством B, то мы представляем его как:

 A ⊂ B.  

мы пишем это как:

 A ⊄ B

Чтобы понять разницу между ⊆ и ⊂, можно подумать о знаках неравенства ≤ и <. Для любых двух чисел a и b, если a ≤ b, то a может быть равно или не равно b. Наоборот, если мы имеем a < b, то a меньше, чем b.

Символы  ⊆  и ⊂ одинаковы; для A ⊆ B A может быть равно B, но для A ⊂ B , A никогда не равно B; следовательно, это правильное подмножество.

Разница между правильным подмножеством и надмножеством

Частой причиной путаницы среди студентов, впервые изучающих теорию множеств, является различие между правильным подмножеством и надмножеством. Итак, попробуем разобраться с этим недоразумением.

Как обсуждалось ранее, A является правильным подмножеством B, если B имеет по крайней мере один элемент, не присутствующий в A. Это обозначается символом «⊂», который показывает, что A является правильным подмножеством B. Это также называется строгое подмножество.

Принимая во внимание, что B будет надмножеством A тогда и только тогда, когда все элементы, присутствующие в A, являются частью B, что примерно означает, что B больше по размеру, чем A. Если A является правильным подмножеством B, то B является надмножеством A. Символ, используемый для обозначения отношения надмножества, — «⊇».

Следующий пример может помочь нам лучше понять это.

Пример 3

Объясните, почему A = {2, 4, 5, 7, 8} является надмножеством B = {2, 4, 5}.

Решение

Чтобы A было надмножеством B, оно должно иметь все элементы, присутствующие в множестве B. Как видно из данной информации, A имеет элементы, равные B, тогда как B является правильным подмножеством A ; следовательно, A является надмножеством B.

Записывается как:

A ⊇ B

Представление подмножеств с помощью диаграмм Венна

Для понимания отношений между различными множествами диаграмма Венна является наиболее подходящим инструментом для визуализации логических связей между определенными множествами. Они широко используются для представления множеств, что более важно, конечных множеств. Диаграмма Венна обозначает множества как области внутри круглого объекта с элементами как точки внутри области.

Поскольку подмножества обычно включают два множества, мы можем легко использовать диаграмму Венна, чтобы объяснить и визуализировать их. Цифра выглядит следующим образом:

Предположим, мы установили A = {1, 5, 9} и установили B = {1, 5, 9, 12, 15, 2, 3}.

Представление множеств A и B на диаграмме Венна выглядит следующим образом:

Как видно из диаграммы A, окруженная областью, обозначенной ее множеством, является частью области B. Каждая область имеет свои элементы, обозначенные как точки внутри область.

Давайте решим другой пример, используя диаграмму Венна.

Пример 4

С помощью диаграммы Венна покажите, что B = {1, 5, 9, 12, 15, 2, 3} является надмножеством A = {1, 5, 9}.

Решение

Поскольку B будет надмножеством A, когда все его существующие элементы являются подгруппой элементов B, мы должны решить это, используя диаграмму Венна.

Диаграмма Венна выглядит следующим образом:

Как мы видим, существует полностью перекрывающаяся область A и B с запасной областью B, поэтому B является надмножеством A.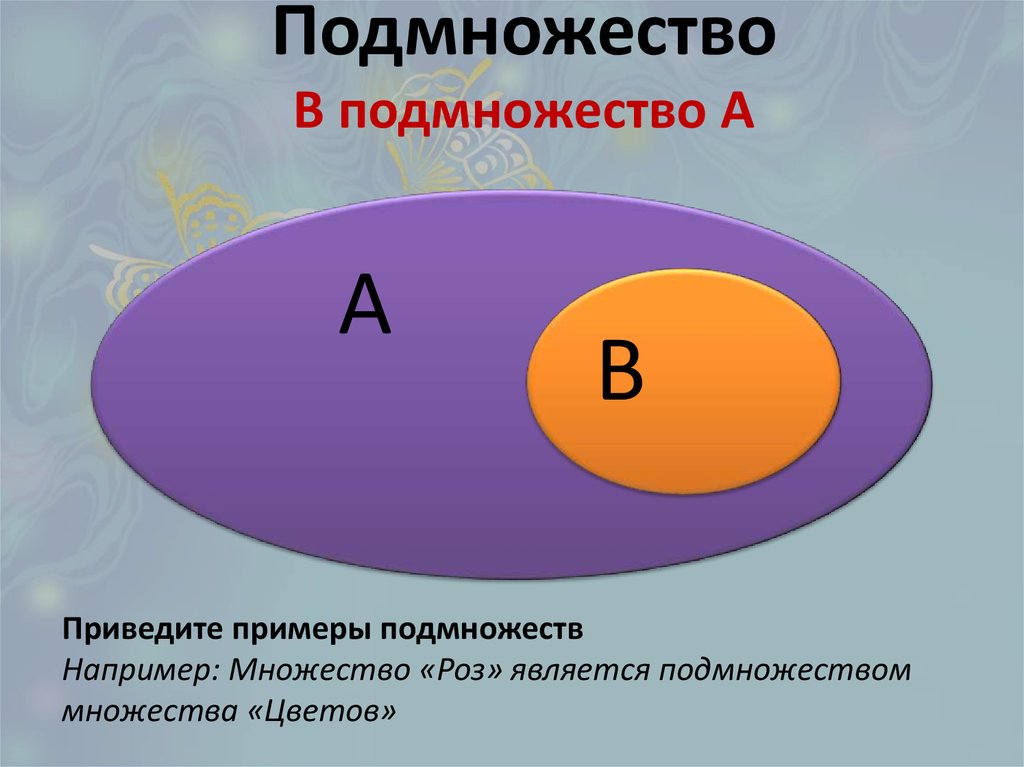

Свойства подмножеств

Подмножества — одно из самых фундаментальных понятий в области множеств. Подчеркивая важность подмножеств, необходимо оценить свойства подмножеств. Ниже приведены некоторые из наиболее важных свойств подмножеств.

Подмножество самого себя:

Каждое множество считается подмножеством самого себя.

Независимо от того, имеем ли мы конечное или бесконечное множество, само множество будет считаться подмножеством самого себя. Это происходит безоговорочно. Всякий раз, когда мы перечисляем подмножества любого данного множества, мы всегда будем включать само множество в качестве его подмножества.

Но в случае правильных подмножеств мы пропустим сам набор, чтобы сделать подмножество равным набору.

Например, для конечного множества A = {2,5} все возможные подмножества:

 A = Ⲫ, A = {2}, A = {5}, A = {5}, A = { 2, 5}

Как видите, мы включили подмножество с теми же элементами, что и исходный набор, чтобы удовлетворить свойству.

Как упоминалось ранее, это относится не только к конечным множествам; бесконечные множества следуют тому же свойству.

Пустой набор является подмножеством:

Пустой набор является подмножеством каждого набора.

Допустим, мы рассматриваем множество A, которое может быть конечным или бесконечным. Мы можем вычислить все возможные подмножества A; среди этих подмножеств мы будем включать нулевое/пустое множество.

Например, рассмотрим конечное множество A = {1, 2}, поэтому все возможные подмножества этого множества:

A = Ⲫ, A = {1}, A = {2}, A = {1, 2}

Как видите, мы включили пустое подмножество в наш список подмножеств, чтобы удовлетворить свойству:

Ⲫ ⊂ A

В случае бесконечных множеств можно применить тот же принцип. Не имеет значения, является ли множество конечным или бесконечным; пустой набор всегда будет подмножеством данного набора.

Давайте рассмотрим пример, чтобы лучше применить это.

Пример 5

Рассмотрим множество X = {2, 5, 8}. Перечислите все его возможные подмножества.

Решение

Чтобы решить этот пример, мы рассмотрим указанное выше свойство.

Список всех подмножеств множества X:

Ⲫ, {2}, {5}, {8}, {2, 5}, {5, 8}, {2, 8}

Пустое множество также является подмножеством из-за следующего соотношения:

Ⲫ ⊂ X

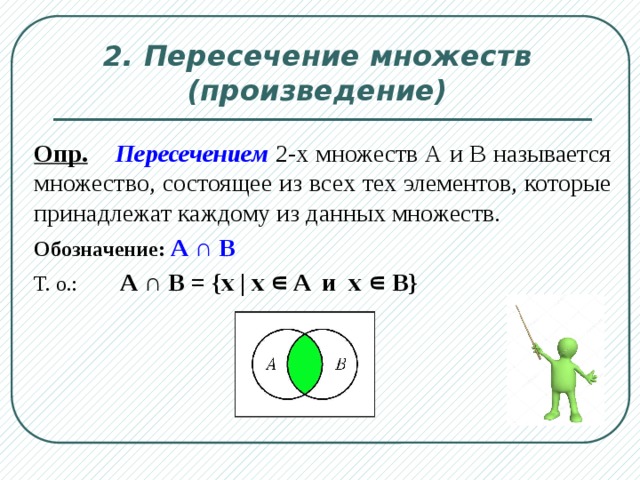
Пересечение двух множеств

Множество A будет подмножеством множества B тогда и только тогда, когда пересечение A и B равно A. 

Для заданного конечного или бесконечного множества A , чтобы оно было подмножеством любого конечного/бесконечного множества B, их пересечение всегда должно быть равно множеству A. Это одно из условий того, чтобы множество A было подмножеством множества B. Если это условие не выполняется, то мы можем легко сказать, что множество A не является подмножеством множества B.

Мы можем обозначить это как:

A ⊂ B 🡪 A ∩ B = A

Давайте рассмотрим пример, чтобы применить это лучше.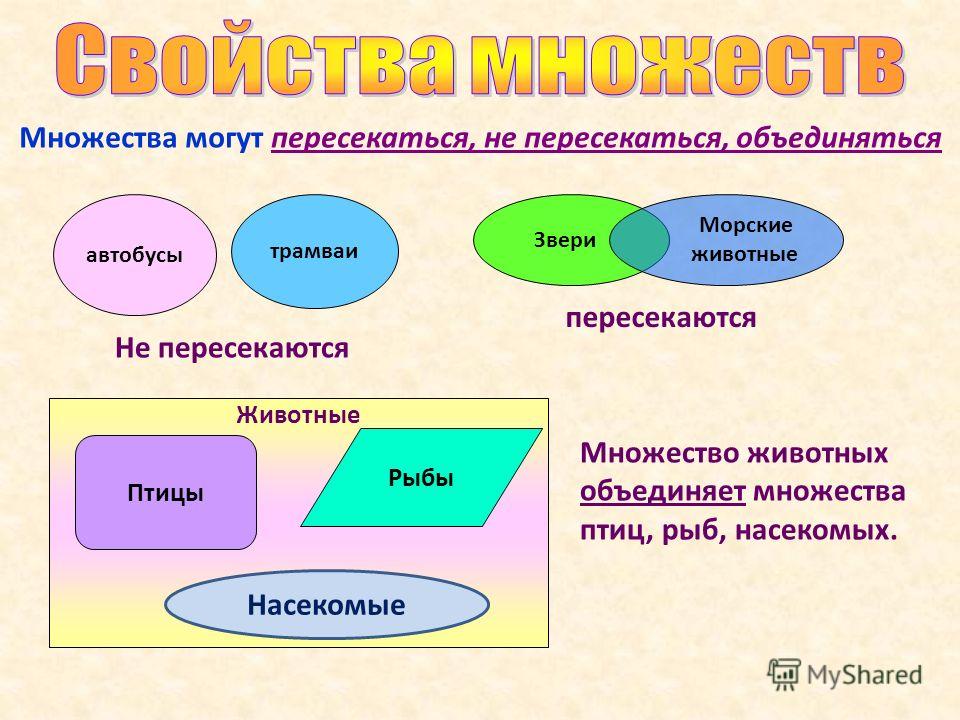

Пример 6 

Рассмотрим множество X = {2, 5, 8} и Y = {2, 4, 5, 6, 7, 8}. Является ли X подмножеством Y?

Решение

Чтобы решить этот пример, мы рассмотрим указанное выше свойство.

X∩Y = {2, 5, 8}

Поскольку это равно X, следовательно, X является подмножеством Y.

Объединение двух множеств:

Чтобы любое множество A было подмножеством множества B, их объединение должно быть равно множеству B.

быть подмножеством любого конечного/бесконечного множества B, их объединение всегда должно быть равно множеству B. Это одно из условий для того, чтобы множество A было подмножеством множества B. Если это условие не выполняется, то мы можем легко сказать что множество A не является подмножеством множества B.

Мы можем обозначить это как:

A ⊂ B 🡪 A ∪ B = B

Давайте посмотрим на пример для применения этого лучшего

Пример 7

Рассмотрим набор x = {2, .