Примеры множество и подмножество: Множества и подмножества, число, мощность, примеры, урок и презентация по алгебре, 9 класс

Содержание

Математический анализ. (Виленкин)

Виленкин Н.Я., Шварцбурд С.И. Математический анализ. Учебное пособие для IX—X классов средних школ с математической специализацией. M., Просвещение, 1969 г.

Учебное пособие для школ с математической специализацией, снабженное большим количеством задач и упражнений. Как и вышедшая ранее (1968 г.) книга «Алгебра» того же авторского коллектива, может быть использована преподавателями и учащимися общеобразовательной школы.

8. Вычитание множеств.
9. Отображение множеств.
10. Краткие исторические сведения.
Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
§ 1. Тождественные преобразования многочленов
2. Целые рациональные выражения и функции.
3. Степень с натуральным показателем и ее свойства.
4. Многочлены.
5. Умножение многочленов.
6. Числовые кольца и поля.
7. Кольцо многочленов над данным числовым полем.
8. Бином Ньютона.
§ 2. Деление многочленов. Корни многочленов
2. Теорема Безу. Схема Горнера.
3. Корни многочлена.
4. Интерполяционные формулы.
5. Кратные корни.
6. Многочлены второй степени.
7. Многочлены с целыми коэффициентами.
8. Краткие исторические сведения.
Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
§ 1. Общая теория уравнений
2. Область допустимых значений.
3. Уравнения.
4. Совокупности уравнений.
5. Преобразования уравнений.
6. Теоремы о равносильности уравнений.
§ 2. Уравнения с одним неизвестным

Метод разложения на множители.
3. Метод введения нового неизвестного.
4. Биквадратные уравнения.
5. Возвратные уравнения 3-й и 4-й степеней.
§ 3. Функциональные неравенства
2. Равносильные неравенства.
3. Доказательство неравенств.
4. Линейные неравенства.
5. Решение неравенств второй степени.
6. Решение алгебраических неравенств высших степеней.
7. Краткие исторические сведения.
Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
§ 1. Степени с целым показателем
2. Степень с нулевым показателем.
3. Степень с целым отрицательным показателем.
§ 2. Корни. Степени с рациональными показателями
2. Степени с рациональными показателями.
3. Свойства степеней с рациональными показателями.
§ 3. Иррациональные алгебраические выражения
2. Одночленные иррациональные выражения.
3. Сокращение показателей и приведение корней к общему показателю.
4. Извлечение корня из произведения и степени.
5. Вынесение алгебраических выражений из-под корня и внесение их под корень.

6. Возведение корня в степень.
7. Извлечение корня из корня.
8. Подобные корни.
9. Сложение и вычитание корней.
10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
11. Преобразование выражений вида …
12. Смешанные задачи на преобразование иррациональных выражений.
§ 4. Иррациональные уравнения и неравенства
2. Сведение иррациональных уравнений к рациональным.
3. Уединение радикала.
4. Введение нового неизвестного.
5. Особые случаи решения иррациональных уравнений.
6. Иррациональные неравенства.
7. Краткие историчесие сведения.
Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ

§ 1. Системы алгебраических уравнений
2. Системы уравнений.
3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
4. Совокупность уравнений.
5. Равносильные системы уравнений.
6. Метод подстановки.
7. Метод алгебраического сложения уравнений.

8. Метод введения новых неизвестных.
9. Системы однородных уравнений.
10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
§ 2. Системы линейных уравнений
2. Теоремы о равносильности систем линейных уравнений.
3. Пример решения системы линейных уравнений методом Гаусса.
4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
5. Решение обобщенно-треугольной системы линейных уравнений.
6. Системы однородных линейных уравнений.
§ 3. Симметрические многочлены и их приложения к решению систем уравнений
2. Выражение степенных сумм
3. Основная теорема о симметрических многочленах от двух переменных.
4. Системы симметрических алгебраических уравнений.
5. Применение симметрических многочленов к решению иррациональных уравнений.
§ 4. Неравенства с многими переменными
2. Среднее арифметическое и среднее геометрическое трех чисел.
3. Неравенство Коши (двумерный вариант).
4. Задачи на наибольшие и наименьшие значения.

§ 5. Решение неравенств
2. Неравенства с двумя переменными.
3. Задание областей неравенствами и системами неравенств.
4. Понятие о линейном программировании.
5. Краткие исторические сведения.
Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
§ 1. Комплексные числа в алгебраической форме
2. Комплексные числа.
3. Сложение комплексных чисел; умножение на действительные числа.
4. Умножение комплексных чисел.
5. Квадратные уравнения с действительными коэффициентами.

6. Деление комплексных чисел.
7. Сопряженные комплексные числа.
8. Извлечение квадратных корней из комплексных чисел.
§ 2. Тригонометрическая форма комплексных чисел
2. Полярная система координат.
3. Тригонометрическая форма комплексного числа.
4. Умножение и деление комплексных чисел в тригонометрической форме.
5. Возведение комплексных чисел в степень. Формула Муавра.
6. Извлечение корня из комплексного числа.
7. Функции комплексного переменного и преобразования комплексной плоскости.

§ 3. Некоторые виды алгебраических уравнений
2. Двучленные уравнения.
3. Корни из единицы и построение правильных многоугольников.
4. Трехчленные уравнения.
§ 4. Основная теорема алгебры многочленов и ее следствия
2. Многочлены с действительными коэффициентами.
3. Разложение на множители многочленов с действительными коэффициентами.

4. Краткие исторические сведения.
Глава VI. ЦЕПНЫЕ ДРОБИ
§ 1. Конечные цепные дроби
2. Пример цепной дроби.
3. Определение цепной дроби.
4. Представление рациональных чисел в виде конечной цепной дроби.
5. Подходящие дроби.
6. Свойства подходящих дробей.
8. Подходящие дроби и календарь.
9. Приближение цепной дроби подходящими дробями.
§ 2. Бесконечные цепные дроби
2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
3. Цепные дроби как вычислительный инструмент.
4. Краткие исторические сведения.
Глава VII. КОМБИНАТОРИКА
§ 1. Комбинаторные задачи
§ 2.

Комбинаторные задачи. Продолжение
§ 3. Определения и формулы
§ 4. Соединения с повторениями
§ 5. Комбинаторные задачи. Окончание
§ 6. Бином Ньютона и его обобщения
§ 7. Краткие исторические сведения
Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

§ 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
§ 3. Примеры вычисления вероятностей
§ 4. Полная вероятность. Формула Байеса
§ 5. Повторение испытаний
§ 6. Примеры вычисления вероятностей. Окончание
§ 7. Краткие исторические сведения

Страница 21. Урок 7 — ГДЗ Математика 3 класс. Петерсон. Учебник часть 1

Главная
ГДЗ
org/ListItem»> 3 класс

Математика
Петерсон. Учебник
Страница 21. Урок 7. Часть 1

Вернуться к содержанию учебника

Вопрос

Задание № 3. Определи по диаграмме, какое из множеств является подмножеством другого.

Ответ

Вопрос

Задание № 4. Определи, какое из указанных двух множеств является подмножеством другого.

Сделай записи и нарисуй диаграммы Эйлера-Венна.

а) В — множество учеников некоторой школы,

С — множество отличников этой школы.

б) D — множество девочек некоторого класса,

Е — множество всех учеников этого класса.

в) К — множество рыб,

О — множество окуней.

г) N — множество натуральных чисел,

М — множество чётных чисел.

Ответ

Вопрос

Задание № 5. Определи, какое из множеств М = {а; b; ; ; +} и К = {b; } является подмножеством другого. Докажи. Запиши с помощью знака ⊂и прочитай разными способами.

б) Нарисуй диаграмму Эйлера-Венна множеств М и К и отметь на ней элементы этих множеств.

Ответ

Вопрос

Задание № 6. Придумай примеры множества и его подмножества.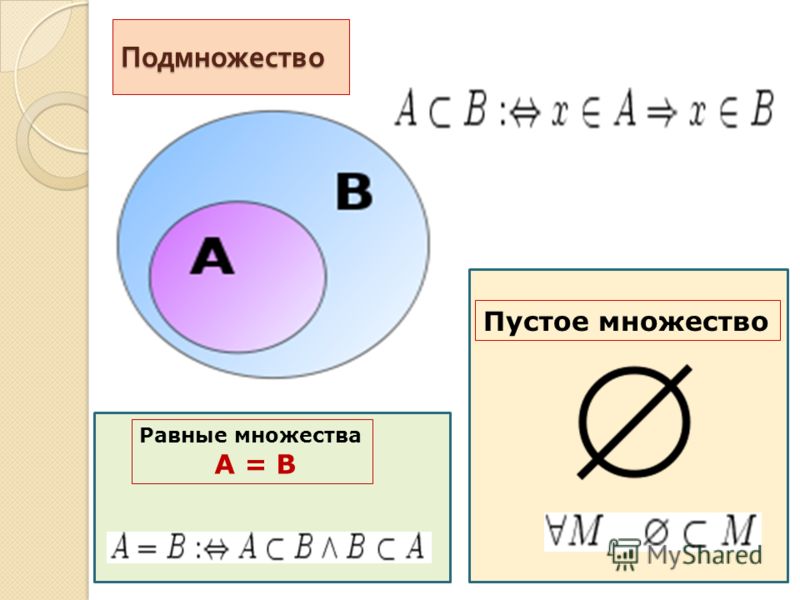 Нарисуй диаграмму Эйлера-Венна.

Ответ

Вопрос

Задание № 7. Квадрат разбит на части. Назови каждый элемент множества получившихся геометрических фигур.

Ответ

Вернуться к содержанию учебника

Правильное подмножество множества

Множество X называется правильным подмножеством множества Y, если X ⊆ Y и X ≠ Y.

В символе мы пишем X ⊂ Y.

Обозначение чтения:

Читать X ⊂ Y, поскольку «X является правильным подмножеством Y».

Это показано на рисунке ниже.

Пример 1 :

Пусть A = {1, 2, 3, 4, 5} и B = {5, 3, 4, 2, 1}. Определите, является ли B правильным подмножеством A.

Решение:

Если B является правильным подмножеством A, каждый элемент B также должен быть элементом A, а также B не должен быть равен A.

В заданных множествах A и B каждый элемент B также является элементом A. Но B равен A.

Следовательно, B является подмножеством A, но не собственным подмножеством.

Пример 2 :

Пусть A = {1, 2, 3, 4, 5} и B = {1, 2, 5}. Определите, является ли B правильным подмножеством A.

Решение:

В для заданных множеств A и B каждый элемент B также является элементом A.

А также But B не равно A.

Следовательно, B является правильным подмножеством A. подмножества A.

Решение:

Пусть данное множество содержит n элементов.

Тогда формула для нахождения количества правильных подмножеств:

= 2 ⁿ — 1

Значение n для заданного множества A равно 5.

Поскольку множество A = {1, 2, 3, 4, 5} содержит пять элементов.

Количество правильных подмножеств = 2 ⁵ — 1

= 32 — 1

= 31

Следовательно, количество правильных подмножеств A равно 31.

Подмножество множества

A множество X 900 подмножество множества Y, если каждый элемент X также является элементом Y.

В символе мы пишем

x ⊆ y

Обозначение чтения:

Читаем ⊆ как «X является подмножеством Y» или «X является содержится в Y».

Читается ⊈ как «X не является подмножеством Y» или «X не содержится в Y».

Набор мощностей

Набор всех подмножеств A называется набором мощностей множества A.

Обозначение чтения:

Набор мощностей A обозначается P(A).

Надмножество

Множество X называется правильным подмножеством множества Y, если X ⊆ Y и X ≠ Y.

В символе мы пишем X ⊂ Y.

Здесь

Y называется надмножеством of X

Формула для нахождения количества подмножеств

Если заданное множество A содержит n элементов, мы можем использовать следующую формулу для нахождения количества подмножеств.

Количество подмножеств = 2 ⁿ

Формула для нахождения количества подмножеств:

Количество подмножеств = 2 ⁿ — 1

Мощность набора

Мы уже знаем, что все множества Подмножества множества A называются набором мощности множества A и обозначаются P(A).

Если A содержит n элементов, то формула для мощности множества A равна

n[P(A)] = 2 ⁿ

Примечание:

Мощность набора мощности A и количество подмножеств A совпадают.

Нулевой набор является подмножеством или правильным подмножеством

Нулевой набор является правильным подмножеством для любого набора, который содержит хотя бы один элемент.

Например, рассмотрим множество A = {1}.

Имеет два подмножества. Это { } и {1}.

Здесь нулевое множество является правильным подмножеством A. Поскольку нулевое множество не равно A.

Если нулевое множество является надмножеством

Если нулевое множество является надмножеством, то оно имеет только одно подмножество. То есть { }.

Точнее, нулевой набор является единственным подмножеством самого себя. Но это не правильное подмножество.

Потому что { } = { }.

Таким образом, набор, который содержит только одно подмножество, называется нулевым набором.

Пожалуйста, отправьте свой отзыв на [email protected]

Мы всегда ценим ваши отзывы.

Определение:Подмножество — ProofWiki

Содержание

1 Определение
- 1.1 Диаграмма Эйлера
- 1.2 Суперсет
2 Подмножество класса
- 2.1 Отношение подмножества
3 Также известен как
4 Обозначение
5 примеров
- 5.1 Британцы — подмножество людей
- 5.2 Подмножество алфавита
- 5.3 Целые числа являются подмножеством действительных чисел
- 5.4 Начальный сегмент является подмножеством целых чисел
- 5.5 Четные числа образуют подмножество целых чисел
6 См. также
7 Историческая справка
8 источников

Определение

Пусть $S$ и $T$ — множества.

$S$ является подмножеством $T$ тогда и только тогда, когда все элементы $S$ также являются элементами $T$.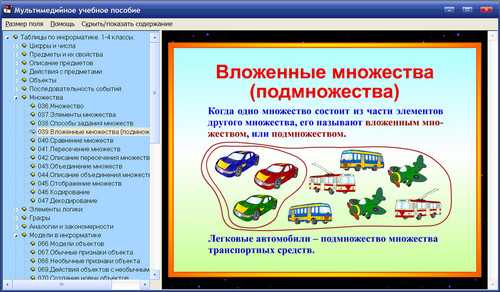

Обозначается:

$S \subseteq T$

То есть:

$S \subseteq T \iff \forall x: \paren {x \in S \implis x \in T}$

Если не все элементы $S$ также являются элементами $T$, тогда $S$ не подмножество $T$:

$S \nsubseteq T$ означает $\neg \paren {S \subseteq T}$

Диаграмма Эйлера

Утверждение, что $T$ является подмножеством $S$, можно проиллюстрировать на следующей диаграмме Эйлера .

Надмножество

Если $S$ является подмножеством $T$, то $T$ является надмножеством надмножества $S$.

Это можно выразить с помощью обозначения $T \supseteq S$.

Это можно интерпретировать как $T$ включает $S$ или (реже) $T$ содержит $S$ .

Таким образом, $S \subseteq T$ и $T \supseteq S$ означают одно и то же.

Множество $S$ является подмножеством класса $T$ тогда и только тогда, когда оно является подклассом $T$.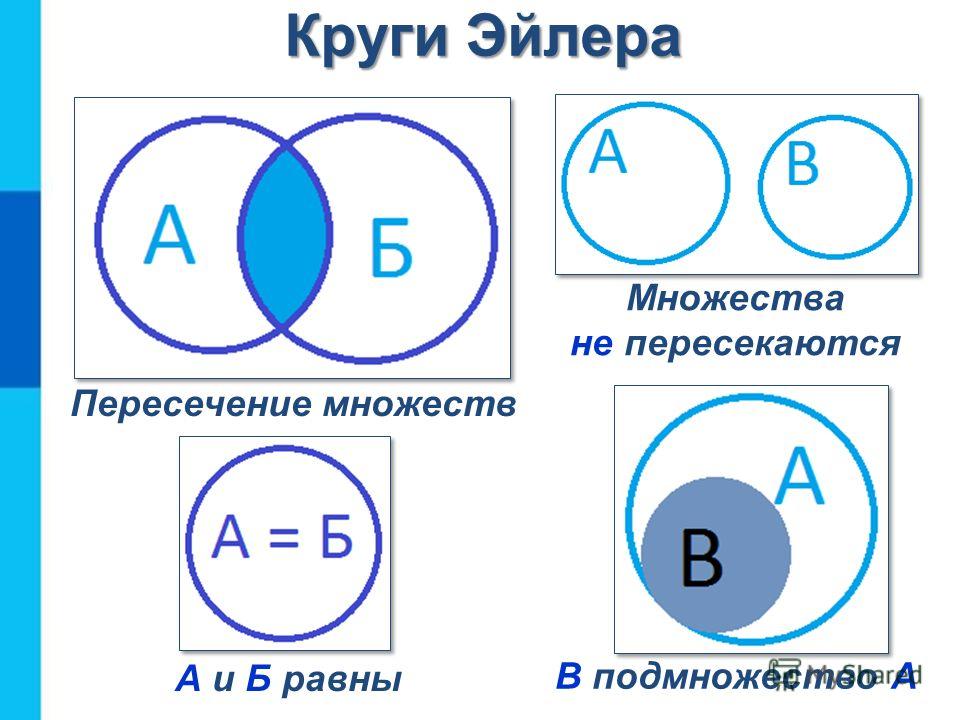

Альтернативно, множество $S$ является подмножеством класса $T$ тогда и только тогда, когда каждый элемент $S$ также является элементом $T$.

Отношение подмножества

Отношение подмножества , обозначаемое $\subseteq$, представляет собой класс всех упорядоченных пар $\tuple {x, y}$, таких что $x$ является подмножеством $y$.

Также известен как

Когда эта концепция была впервые предложена Георгом Кантором, он использовал термины часть и частичный агрегат для этой концепции.

$S \subseteq T$ можно также прочитать как:

$S$ содержится в $T$, или $T$ содержит $S$

$S$ включен в $T$, или $T$ включает $S$

Термин слабо включает или слабо содержит 9Иногда здесь можно увидеть 0206, чтобы отличить от строгое включение .

Следовательно, $\subseteq$ также называют отношением включения или (реже) отношением включения .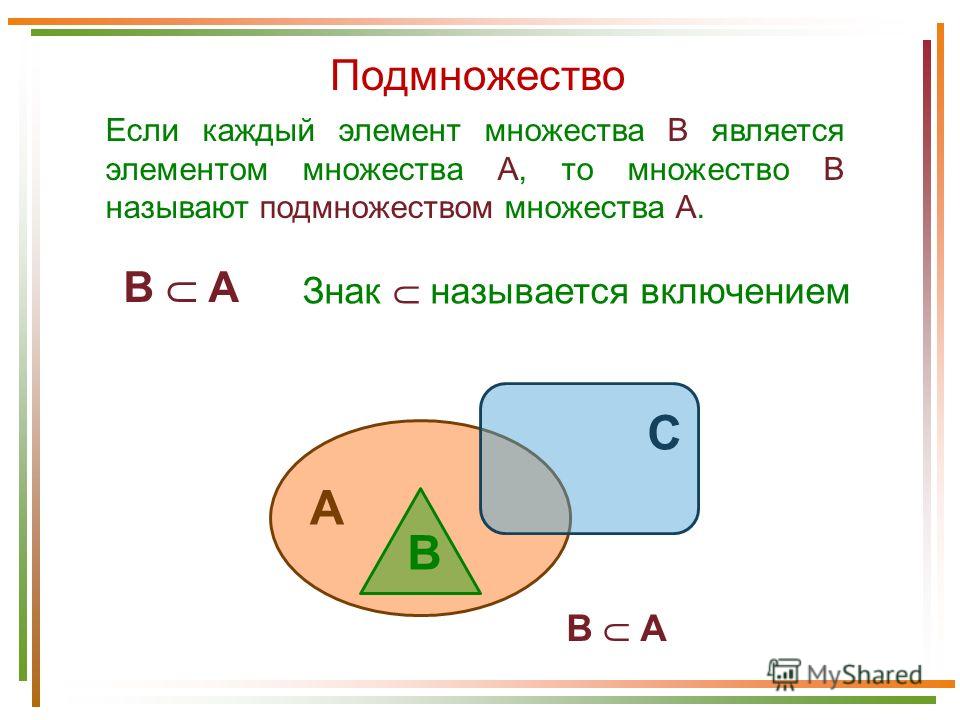

Термин слабо включает или слабо содержит , иногда можно увидеть здесь, чтобы отличить его от строгого включения .

Остерегайтесь этого использования: $T$ содержит $S$ также может быть интерпретировано как $S$ является элементом $T$ . Таковы возможности неправильного толкования, что обязательно добавлено дополнительное объяснение, чтобы было ясно, имеете ли вы в виду подмножество или элемент. Обычный способ сделать это — добавить к фразе «как подмножество».

Мы также описываем эту ситуацию, говоря, что $E$ — это , содержащее в $F$, или что $E$ — это , содержащее в $F$, хотя последней терминологии лучше избегать.
— 1975: Т.С. Blyth: Теория множеств и абстрактная алгебра

это редкость и сомнительная ценность.

Обозначение в литературе концепции подмножества может сбивать с толку.

Для $\mathsf{Pr} \infty \mathsf{fWiki}$ соглашение следующее:

$\subseteq$ используется для общего подмножества

$\subsetneq$ или $\subsetneqq$ используется для понятия правильного подмножества .

Обозначение $\subset$ устарело в $\mathsf{Pr} \infty \mathsf{fWiki}$ на том основании, что оно может означать и то, и другое.

Британцы — подмножество людей

Пусть $B$ обозначает множество британцев.

Пусть $P$ обозначает множество людей.

Тогда $B$ является правильным подмножеством $P$:

$B \subsetneq P$

Подмножество алфавита

Пусть $S$ обозначает заглавные буквы (английского) алфавита:

$S = \set {A, B, C, D, \dotsc, Z}$

Тогда $\set {A, B, C}$ является подмножеством $S$:

$\set {A, B, C} \subseteq S$

Целые числа являются подмножеством действительных чисел

Множество целых чисел $\Z$ является правильным подмножеством множества действительных чисел $\R$ :

$\Z \subsetneq \R$ 9*_{\le n} \subsetneq \Z$

Четные числа образуют подмножество целых чисел

Множество четных целых чисел образует подмножество множества целых чисел $\Z$.

См. также

Определение: правильное подмножество

Обратите внимание на разницу между:

элемент: $x\in T$

и:

a подмножество : $S \subseteq T$.

Результаты по подмножествам можно найти здесь .

Понятие подмножества, включения множества , было сформулировано Лейбницем в его первоначальной концепции символической логики.

Источники

1915: Георг Кантор: Вклад в создание теории трансфинитных чисел … (предыдущая) … (следующая): Первая статья: $\S 1$: Концепция власти или Кардинальный номер
1951: Дж. К. Беркилл: Интеграл Лебега … (предыдущий) … (следующий): Глава $\text {I}$: Наборы точек: $1 \cdot 1$. Алгебра множеств
1951: Натан Джейкобсон: Лекции по абстрактной алгебре: Том $\text { I }$: Основные понятия … (предыдущий) … (следующий): Введение $\S 1$: Операции над множествами
1955: Джон Л. Келли: Общая топология … (предыдущая) … (следующая): Глава $0$: Подмножества и дополнения; Союз и пересечение
1959: Э. М. Паттерсон: Топология (2-е изд.) … (предыдущее) … (следующее): Глава $\text {II}$: Топологические пространства: $\S 8$. Обозначения и определения теории множеств
1960: Пол Р. Халмос: Наивная теория множеств … (предыдущая) … (следующая): $\S 1$: аксиома расширения
1961: Джон Г. Хокинг и Гейл С. Янг: Топология … (предыдущая) … (следующая): Заметка о теоретико-множественных концепциях
1963: Джордж Ф. Симмонс: Введение в топологию и современный анализ … (предыдущий) … (следующий): $\S 1$: множества и включение множеств
1964: У.Э. Deskins: Абстрактная алгебра … (предыдущая) … (следующая): $\S 1.1$: Определение $1.1$
1964: Стивен А. Гаал: Топология множества точек … (предыдущая) … (следующая): Введение в теорию множеств: $1$. Элементарные операции над множествами
1964: Вальтер Рудин: Основы математического анализа (2-е изд.) … (предыдущее) … (следующее): Глава $2$: Элементы теории множеств: конечные, счетные и несчетные множества: $2,2$. Определение
1964: Уильям К. Смит: Пределы и непрерывность … (предыдущая) … (следующая): $\S 2.1$: множества
1965: А.М. Артурс: Теория вероятностей … (предыдущая) … (следующая): Глава $1$: Теория множеств: $1.2$: Множества и подмножества
1965: Клод Берж и А. Гуила-Ури: Программирование, игры и транспортные сети … (предыдущий) … (следующий): $1$. Предварительные идеи; множества, векторные пространства: $1.1$. Наборы
1965: Дж.А. Зеленый: наборов и групп … (предыдущий) … (следующий): $\S 1.2$. Подмножества
1965: Сет Уорнер: Современная алгебра … (предыдущая) … (следующая): Глава $\text I$: Алгебраические структуры: $\S 1$: Язык теории множеств
1966: Ричард А. Дин: Элементы абстрактной алгебры … (предыдущая) … (следующая): $\S 0,2$. Наборы
1967: Джордж Маккарти: Топология: введение в приложения к топологическим группам … (предыдущая) … (следующая): Введение: теоретико-множественная нотация
1968: А.Н. Колмогоров и С.В. Фомин: Введение в реальный анализ … (предыдущий) … (следующий): $1$ Теория множеств: $1$. Наборы и функции: $1.1$: Основные определения
1968: Ян Д. Макдональд: Теория групп … (предыдущая) … (следующая): Приложение: Элементарная теория множеств и чисел
1970: Авнер Фридман: Основы современного анализа … (предыдущий) … (следующий): $\S 1.1$: Кольца и алгебры
1971: Аллан Кларк: Элементы абстрактной алгебры … (предыдущая) … (следующая): Глава $1$: Обозначения и терминология теории множеств: $\S 3$
1971: Роберт Х. Касриэль: Топология бакалавриата … (предыдущий) … (следующий): $\S 1. 3$: Подмножества: Определение $3.1$
1971: Патрик Дж. Мерфи и Альберт Ф. Кемпф: Новая математика стала проще (2-е изд.) … (предыдущее) … (следующее): Глава $1$: Множества: Подмножества: Определение: $1,6$
1971: Гайси Такеути и Уилсон М. Заринг: Введение в аксиоматическую теорию множеств : $\S 5,9$
1972: А. Г. Хаусон: Справочник терминов, используемых в алгебре и анализе … (предыдущий) … (следующий): $\S 2$: Множества и функции: Множества
1974: Мюррей Р. Шпигель: Теория и проблемы расширенного исчисления (изд. SI) … (предыдущая) … (следующая): Глава $1$: Числа: Множества
1975: Т.С. Блит: Теория множеств и абстрактная алгебра … (предыдущая) … (следующая): $\S 1$. наборы; включение; перекресток; союз; дополнение; системы счисления
1975: Берт Мендельсон: Введение в топологию (3-е изд.) … (предыдущее) … (следующее): Глава $1$: Теория множеств: $\S 2$: Множества и подмножества
1975: В. А. Сазерленд: Введение в метрические и топологические пространства … (предыдущий) … (следующий): Обозначения и терминология
1977: К.Г. Бинмор: Математический анализ: простой подход … (предыдущий) … (следующий): $\S 1$: Действительные числа: $\S 1.1$: Набор обозначений
1977: Гэри Чартранд: Введение в теорию графов … (предыдущая) … (следующая): Приложение $\text{A}.1$: Множества и подмножества
1978: Джон С. Роуз: Курс теории групп … (предыдущий) … (следующий): $0$: некоторые соглашения и некоторые основные факты
1978: Томас А. Уайтлоу: Введение в абстрактную алгебру … (предыдущая) … (следующая): $\S 6$: подмножества
1979: Джон Э. Хопкрофт и Джеффри Д. Ульман: Введение в теорию автоматов, языки и вычисления … (предыдущая) … (следующая): Глава $1$: Предварительные сведения: $1.4$ Система обозначений
1981: Г. де Барра: Теория мер и интеграция . .. (предыдущая) … (следующая): Глава $1$: Предварительные сведения: $1.1$ Теория множеств
1981: Мюррей Р. Шпигель: Теория и проблемы комплексных переменных (изд. SI) … (предыдущая) … (следующая): $1$: Комплексные числа: наборы точек: $14.$
1982: П.М. Кон: Алгебра Том 1 (2-е изд.) … (предыдущая) … (следующая): Глава $1$: Множества и отображения: $\S 1.2$: Множества
1986: Джеффри Гриммет и Доминик Уэлш: Вероятность: Введение … (предыдущая) … (следующая): $1$: События и вероятности: $1,2$: Исходы и события
1989: Эфраим Дж. Боровски и Джонатан М. Борвейн: Математический словарь … (предыдущий) … (следующий): Запись: включение
1989: Эфраим Дж. Боровски и Джонатан М. Борвейн: Математический словарь … (предыдущий) … (следующий): Запись: подмножество или подкласс
1991: Ричард С. Миллман и Джордж Д. Паркер: Геометрия: метрический подход с моделями (2-е изд. ) … (следующее): $\S 1.2$: множества и отношения эквивалентности
1993: Кит Девлин: Радость множеств: основы современной теории множеств (2-е изд.) … (предыдущее) … (следующее): $\S 1$: Наивная теория множеств: $\S 1.1 $: Что такое набор?
1993: Ричард Дж. Трюдо: Введение в теорию графов … (предыдущая) … (следующая): $2$. Графики: Наборы: Определение $3$
1996: Х. Джером Кейслер и Джоэл Роббин: Математическая логика и вычислимость … (предыдущий) … (следующий): Приложение $\text A$: Множества и функции: $\text{A}.1$ : Наборы
1998: Дэвид Нельсон: Математический словарь Penguin (2-е изд.) … (предыдущее) … (следующее): Запись: включение
1999: Андраш Хайнал и Питер Гамбургер: Теория множеств … (предыдущая) … (следующая): $1$. Обозначения, условные обозначения: $5$: Определение $1.1$
2000: Джеймс Р. Манкрес: Топология (2-е изд.) … (предыдущее) . .. (следующее): $1$: Теория множеств и логика: $\S 1$: Основные понятия
2002: Томас Джех: Теория множеств (3-е изд.) … (предыдущее) … (следующее): Глава $1$: Power Set
2008: Пол Халмос и Стивен Гивант: Введение в булевы алгебры … (предыдущий) … (следующий): Приложение $\text{A}$: Теория множеств: множества и подмножества
2008: Дэвид Джойнер: Приключения в теории групп (2-е изд.) … (предыдущее) … (следующее): Глава $1$: Элементарно, мой дорогой Ватсон: $\S 1.2$: Элементы, мой дорогой Ватсон
2008: Дэвид Нельсон: Математический словарь Penguin (4-е изд.) … (предыдущее) … (следующее): Ввод: включение
2010: Раймонд М. Смаллиан и Мелвин Фитинг: Теория множеств и проблема континуума (пересмотренное издание) … (предыдущая) … (следующая): Глава $1$: Общие сведения: $\S 3$ A несчетное множество
2012: М. Бен-Ари: Mathematical Logic for Computer Science (3-е изд.
No related posts.