Примеры модули математика: Модуль числа — урок. Математика, 6 класс.

Модуль числа – определение, примеры (6 класс, математика)

4.7

Средняя оценка: 4.7

Всего получено оценок: 318.

Обновлено 11 Января, 2021

4.7

Средняя оценка: 4.7

Всего получено оценок: 318.

Обновлено 11 Января, 2021

Понятие модуля числа часто вызывает у учеников страх и непонимание. На самом деле, ничего сложного из себя эта тема в математике 6 класса не представляет. Чтобы разобраться в вопросе подробнее, проговорим основные моменты понятия темы модуля.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Числовая прямая

Начинать изучение модуля нужно с понятия числовой прямой и вектора. Числовая прямая – это прямая, на которой отмечено направление движения, точка 0 (начало отсчета) и указан размер единичного отрезка

На числовой прямой можно отметить любое из действительных чисел. Вне зависимости от подмножества, величины числа и его дробной части.

Прямая бесконечна, а потому вмещает в себя абсолютно любые числа, кроме комплексных.

Числовую прямую часто использую для сравнения разного рода чисел. Если отметить на прямой два числа, то число, лежащее правее будет больше, а левее – меньше.

Вектор – это направленный отрезок. Это значит, что у вектора две характеристики: направление и размер самого отрезка. Векторы можно складывать между собой по правилу многоугольника или параллелограмма и умножать с помощью специальной формулы.

Любое число, отмеченное на числовой прямой, создает вектор, соответствующий этому числу. Направление вектора указывается с помощью знака числа. Положительные числа сонаправлены с числовой прямой, отрицательные – направлены противоположно.

Модуль

Если каждое число можно отметить на числовой прямой, то каждому числу соответствует свой вектор.
У вектора три возможных состояния:

• Положительное число и вектор, сонаправленный с числовой прямой.
• Отрицательное число и вектор, направленный в противоположную числовой прямой сторону.
• Число ноль или ноль-вектор – это вектора без направления.

Модулем зовется размер отрезка вектора. То есть, если к числу ставится знак модуль, то у вектора убирается параметр направления. В геометрии это необходимо для нахождения произведений векторов и вообще любых алгебраических действий с векторами. В примере не получится прописать и учесть направление, поэтому и был придуман модуль.

В алгебре модуль числа означает, что в вычислениях берется только размер отрезка без учета направления. На практике это значит, что модуль превращает:

• Положительное число в положительное.
• Отрицательное число в положительное.
• Ноль в ноль.

Возникает вопрос, а почему отрицательное число становится положительным? Знак минус это просто указание направления вектора. Не больше и не меньше. А знак модуль убирает параметр направления.

Разве может быть размер отрезка отрицательным? Конечно, нет. Поэтому модуль отрицательного числа всегда число положительное.

Почему модуль нуля это ноль? Потому что вектор нуля это точка. А какие размеры могут быть у точки? Правильно – никаких. Поэтому модуль числа ноль это ноль.

Что мы узнали?

Мы дали определение модуля числа. Поговорили о числовой прямой и векторе. Узнали, что каждому числу соответствует свое значение на числовой прямой. Отрезок от точки нуля до точки числа на числовой прямой представляет собой вектор этого числа. Сказали о том, что длина этого отрезка и есть модуль. Рассказали, что модуль не может быть отрицательным, потому что длина отрезка не бывает отрицательной. Отдельно поговорили о модуле числа ноль. Сказали, что вектор числа ноль это точка, а точка не может иметь размеров. Поэтому модуль нуля равен нулю.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Максим Чепурко

  10/10

• Артём Вековцов

  10/10

• Гриша Клопов

  10/10

• Илья Зюба

  5/10

Оценка статьи

4. 7

Средняя оценка: 4.7

Всего получено оценок: 318.

---

А какая ваша оценка?

Что такое модуль действительного числа: определение, примеры, график, интерпретация

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Что такое модуль действительного числа

В данной публикации мы рассмотрим определение, геометрическую интерпретацию, график функции и примеры модуля положительного/отрицательного числа и нуля.

• Определение модуля числа
• Геометрическая интерпретация модуля
• График функции с модулем
• Пример задачи

Определение модуля числа

Модуль действительного числа (иногда называется абсолютной величиной) – это величина, равная ему же, если число положительное или равная противоположному, если оно отрицательное.

Модуль числа a обозначается вертикальными черточками с обеих сторон от него – |a|.

Противоположное число отличается от исходного знаком. Например, для числа 5 противоположным является -5. При этом ноль является противоположным самому себе, т.е. |0| = 0.

Геометрическая интерпретация модуля

Модуль числа a – это расстояние от начала координат (O) до точки A на координатной оси, которая соответствует числу a, т.е. |a| = OA.

|-4| = |4| = 4

График функции с модулем

График четной функции y = |х| выглядит следующим образом:

• y = x при x>0
• y = -x при x<0
• y=0 при x=0
• область определения: (−∞;+∞)
• область значений: [0;+∞).
• в точке x=0 график “ломается”.

Пример задачи

Чему равняются следующие модули |3|, |-7|, |12,4| и |-0,87|.

Решение:
Согласно приведенному выше определению:

• |3| = 3
• |-7| = 7
• |12,4| = 12,4
• |-0,87| = 0,87

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

абстрактная алгебра — Примеры модулей (базис и образующие)

$\begingroup$

Я должен привести примеры для таких модулей, что

$1. $ Существует линейно независимый набор с большим количеством элементов, чем набор образующих.

$2.$ Существует линейно независимое множество с той же мощностью, что и у базы, но не является базой.

$3.$ Существует генератор с той же мощностью, что и базис, но не является базисом.

$4.$ Модуль конечно порожден и имеет не конечно порожденный подмодуль. 9²}$ и рассмотрим набор векторов $\{v_1,v_2,\dots\}$, где каждый $v_i$ имеет только рациональные элементы. Я не знаю, как действовать формально, чтобы сделать доказательство. Вторая идея: $\mathbb{Z}$ как $\mathbb{Z}-$модуль имеет базис $\{1\}$, а множество {2,3} линейно независимо и имеет большее число элементов.

$(2)$ $\mathbb{Z}$ как $\mathbb{Z}-$модуль имеет в основе множество $\{1\}$, а множество $\{2\}$ имеет тот же кардинал, что и $\{1\}$, но не является базисом, потому что он порождает только четные элементы.

$(3)$ Моим кандидатом было векторное пространство $\{f:f:\mathbb{R}\to\mathbb{R}\}$ над $\mathbb{Q}$, но я не смог доказать Это.

$(4)$ Если бы $M$ был циклическим $R-$модулем, где $R$ — кольцо полиномов переменных $x_1,x_2,\dots$ и коэффициентов в поле $\mathbb{K}$. Множество $\{x_1,x_2,\dots\}$ порождает подмодуль, но не может быть порождено конечным множеством.

• абстрактная алгебра
• модули
• проверка решения

$\endgroup$

2

$\begingroup$

Для (1), если вы вспомните линейную алгебру, вы вспомните, что вы не можете сделать это в векторном пространстве. Итак, хорошо, что это кажется неправильным! Но это не так. Простейшие примеры здесь некоммутативны: например, в кольце линейных операторов на бесконечномерном векторном пространстве с базисом $e_1,e_2,…$ (как левый модуль над собой) операторы $(e_i\mapsto e_{2i})$ и $(e_i\mapsto e_{2i+1})$ линейно независимы, хотя само кольцо, конечно, является циклическим левым модулем.

$\{2,3\}$ не является линейно независимым над $\mathbb{Z},$, поскольку $3\times 2+(-2)\times 3=0$. Вы правы в (2). Ваше массивное векторное пространство в (3) будет работать, как оказалось, потому что все пространство имеет одинаковую мощность в качестве основы, но это, возможно, не самый простой пример. Просто подумайте о любом бесконечномерном векторном пространстве. (4) тоже верно.

РЕДАКТИРОВАТЬ : Мой пример для (1) обратный. Нам нужно либо рассматривать эти два оператора как линейно независимые для структуры модуля right , либо операторы $(e_{2i+1}\mapsto e_i, e_{2i}\mapsto 0)$ и $(e_{ 2i}\mapsto e_i,e_{2i+1}\mapsto 0)$ как линейно независимые слева. Я объясню первый выбор. Итак, пусть $A$ — кольцо линейных операторов в вещественном векторном пространстве, натянутое на $(e_i)_{i\in \mathbb{N}}$. Кольцевые операции здесь аналогичны матричным операциям в конечномерном случае. Пусть $T_e$ — оператор, определенный на основе $e_i\mapsto e_{2i}$ и $T_o$, аналогично $e_i\mapsto e_{2i+1}$.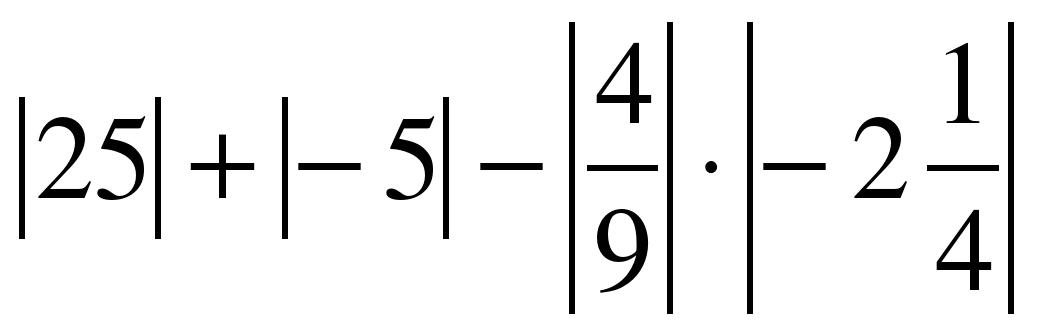

Я утверждаю, что $T_e$ и $T_o$ линейно независимы для правой структуры $A$-модуля на $A$, заданной правым умножением. В самом деле, предположим, что $U,V\in A$ и $T_eU+T_oV=0$. Если $Ue_i=\sum u_{ij}e_j$, то $T_eU e_i=\sum u_{ij}e_{2j}$ и аналогично, если $Ve_i=\sum v_{ij} e_j$, то $T_o Ve_i=\sum v_ {ij}e_{2j+1}$.

Если вы думаете об элементах $A$ как о «матрицах $\mathbb{N}\times\mathbb{N}$», то это просто говорит о том, что четные строки $T_e U$ являются строками $U$ и нечетные строки $T_e U$ равны $0$, и аналогично для $T_o V$ (отсюда названия $T_e$ и $T_o$.) Таким образом, в сумме $T_eU+T_oV$ никакие элементы не могут компенсировать друг друга. — мы разделили единую матрицу пополам, чтобы получить всю информацию из $U$ и $V$ в нее! Таким образом, эта сумма может обратиться в нуль только в том случае, если $U$ и $V$ равны нулю, а $T_e$ и $T_o$ линейно независимы, как утверждается. Заметьте, что нет ничего особенного в том, что я выбрал здесь $2$: я могу легко получить любое конечное число линейно независимых элементов или даже счетное число, в основном только потому, что есть разложение $\mathbb{N}$ на счетное число копий сам.

И все это делается в бесплатном модуле $A$, который может быть сгенерирован одним элементом!

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

абстрактная алгебра — Пример модуля для нематематиков

Задавать вопрос

спросил 9 лет, 4 месяца назад

Изменено 9 лет, 4 месяца назад

Просмотрено 241 раз

$\begingroup$

Я ищу нетривиальный ¹ пример модуля, который был бы понятен не математику. т.е. Я ищу примеры модулей, которые можно встретить в «реальном мире».

Самое близкое, что я могу придумать, это векторные пространства, но я бы предпочел пример, который является , а не векторным пространством (то есть таким, где кольцо модуля на самом деле не является полем).

(Если бы этот вопрос касался групп, а не модулей, хорошим ответом была бы группа вращений куба или группа перестановок трех объектов. Конечно, большинство нематематиков не стали бы истолковывать такие вращения и перестановки как «группу «теоретически», но идеи будут для них «узнаваемы», по крайней мере, в том смысле, который я имею в виду. На самом деле популярные описания теории групп часто обращаются к таким группам как к первым примерам, представляемым читателям, не владеющим математикой. )

---

_{¹ Здесь я использую нетривиальное в специальном, нестандартном смысле. Под «нетривиальным модулем» я подразумеваю не модуль с более чем одним элементом, а тот, который не является просто кольцом. (Например, кольцо целых чисел $\mathbb{Z}$ можно рассматривать и как модуль, причем $\mathbb{Z}$ играет и роль кольца, и абелеву группу, которые входят в определение модуля. Этот «модуль» $\mathbb{Z}$, безусловно, знаком нематематикам, но он входит в число тех, которые я пытаюсь исключить с помощью квалификатора «нетривиальный».) Если есть лучшее имя для таких » нетривиальные» модули, пожалуйста, дайте мне знать.}

• абстрактная алгебра
• примеры-контрпримеры

$\endgroup$

2

$\begingroup$

Если у кого-то есть пять четвертинок, их можно рассматривать как $\mathbb{F}_2S_5$-модули, действующие путем перестановки и перестановки (здесь мы предполагаем, что все четверти начинаются как решки, и что добавление двух элементов модуля соответствует взятию все хвосты, переворачивая столько, сколько вам нужно, чтобы получить первый элемент, а затем переворачивая столько, сколько вам нужно, чтобы получить второй элемент, давая вам третий элемент Таким образом, добавление любого элемента к самому себе повторяет ту же самую последовательность переворотов дважды, поэтому возвращается к решке).

Модули группового кольца повсюду. Молекулы с нетривиальной группой симметрии имеют уравнения движения/колебаний, инвариантные относительно групповых колец, где группа является группой симметрии.