2 3 4
5 6 7 8 9 | Актуализация знаний Актуализация знаний Самоопределение к деятельности Открытие нового знания Физкультминутка
Закрепление изученного материала Рефлексия Подведение итогов урока Домашнее задание | Подготовка к работе на уроке, разминка Постановка темы и задачи урока Составить таблицу умножения на 6, научиться применять таблицу умножение Закрепить новые знания, научиться использовать их на практике Выявить уровень усвоения новых знаний у учеников Выявить уровень усвоения новых знаний у учеников Объяснение домашнего задания ученикам | Устный счёт. а) -Дайте полную характеристику числа 24. — А в таблице умножения встречается число 24? — Посмотрите на ваши таблички. Сколько раз в изученной нами части встречается число 24? — Назовите в каких случаях. Запишите эти выражения на доске. — Составьте все возможные выражения из данных -Какие правила использовали? б) Среди данных чисел назовите числа, кратные 4, 5. 9, 8, 15, 2, 10, 17, 20, 16, 30, 12, 45. -Какие числа остались лишними? Почему? в) Решение задач. • В пяти коробках лежит по 4 игрушки. Сколько всего игрушек лежит в этих коробках? • Двадцать игрушек разложили в пять коробок поровну. Сколько игрушек положили в каждую коробку? • Двадцать игрушек разложили по четыре игрушек в коробку. Сколько понадобилось коробок? – Как называются такие задачи? • У бабушки в хозяйстве 15 кур и 7гусей. На сколько гусей больше, чем кур?
— А теперь я предлагаю Вам решить примеры. 3х9= 4х8= 5х7= 7х5= 8х4= 9х3= -Какое правило здесь используется? -А почему мы смогли решить эти примеры? -Посмотрите внимательно ещё раз на данный столбик примеров и скажите, а какого примера не хватает в столбике? -Как вы думаете, почему я его пропустила? Чего побоялась? — Сформулируйте тему и задачи урока. 1. Составление таблицы умножения и деления с числом 6 — Как найти значение произведения 6 х 6? — На сколько больше будет каждое следующее произведение? — Составьте таблицу умножения числа 6 самостоятельно. — Как умножить на 6? — Составьте таблицу умножения на 6. — Каким правилом воспользуемся для составления таблицы деления с числом 6? — Составьте таблицу деления с числом 6. Составление таблицы умножения на 6 (работа в группах) — Давайте проверим, как Вы справились.
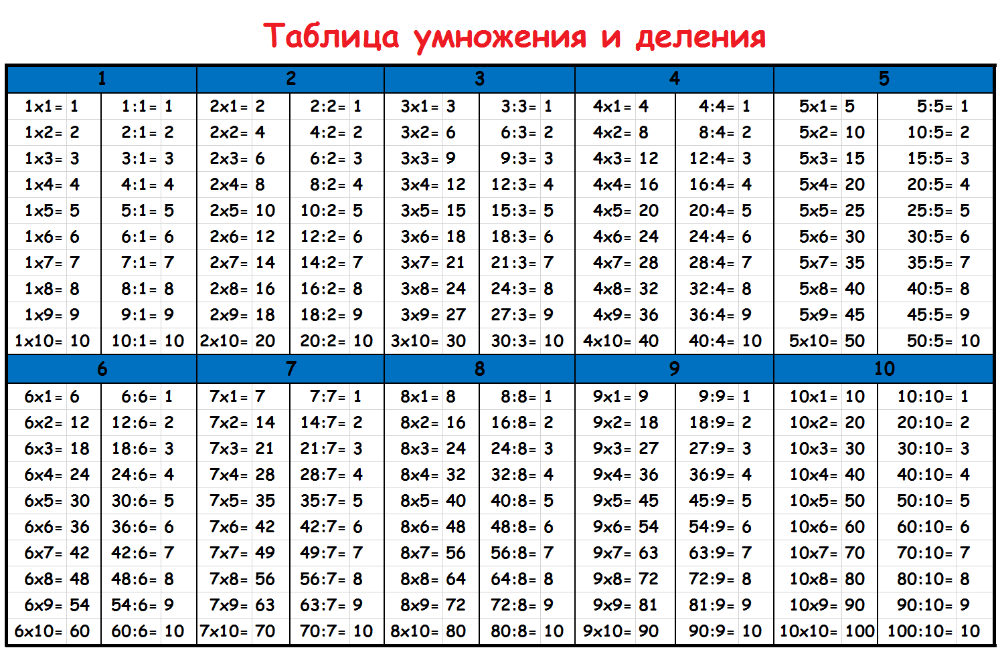
Заполните квадратную таблицу умножения новой строчкой с числом 6
— Мы составили таблицу умножения и деления с числом 6. -А теперь ребята давайте поищем закономерности, ключики к лучшему запоминанию таблицы. -Посмотрите внимательно и скажите, что интересного вы увидели? Закономерности:
на 6 (сверху вниз, а снизу вверх уменьшается на 6)
Работа по учебнику № 1 (с. 44) (Устное выполнение по цепочке.)
Танцевальные упражнения под музыку «Барбарики»
№6 (с. 44). Самостоятельное выполнение. Один ученик работает на откидной доске.
— Решите выражения, расшифруйте слово. 12: 6= 0 48:6= м 6х7= е 6х9= л 24:6= ц 5х6= д
— А теперь я хочу, чтобы вы оценили свою работу на уроке. Поднимите: Зелёную карточку- если всё легко понял и можешь научить другого. жёлтый – если понял, но было нелегко. красный- кому было трудно, нужна помощью. — Какие цели были поставлены на урок? — Смогли мы выполнить задачу урока? — Что нового вы узнали сегодня на уроке? — Что вам показалось трудным? — За что можете себя похвалить? Учебник: № 2, 5 (с. 44). Во втором номере вам надо решить выражения, а в пятом номере дополнить условие и поставить вопрос так, чтобы задача решалась двумя действиями. Если остались вопросы, задавайте их мне. Спасибо за урок, до свидания! | Словесные: диалог Практические: решение примеров и задач Словесные: диалог, беседа Практические: решение примеров Словесные: беседа, диалог, фронтальный опрос. Практические: составление таблицы умножения, самостоятельная работа. Словесные: беседа, диалог. Практические: решение задач, выражений. Словесные: диалог Словесные: фронтальный опрос Словесные: беседа |
-24-двузначное, чётное, в нём 2 д. и 4 ед. Соседи числа 21 и 23. -да -2 раза — 3 х 8; 4 х 6 3 х 8=24 4 х 6=24 8 х 3=24 6 х 4= 24 24 : 3 = 8 24 : 4 = 6 24 : 8 = 3 24 : 6 = 4 -Переместительное свойство умножения; при делении целого на часть получается другая часть. — Кратные 4 — (8, 12, 16, 20) Кратные 5 — (10, 15, 20, 30,45) -9, 2, 17 -20 -4 -5 -Обратные — 15-7=8 — 12:4=3 — 27 — 32 — 35 — 35 — 32 — 27 — таблица умножения — потому что мы уже изучили таблицу умножения до 5 — 6 х 6 -Мы не изучали таблицу умножения на 6 -Составление таблицы умножения и деления на 6. Составить, записать таблицу умножения на 6 и научиться её использовать. 6 + 6 + 6 + 6 + 6 + + 6 = 36 или 6х5 + 6 = 36. — на 6 -Можно переставить слагаемые местами -Если произведение разделить на один из множителей, то получится другой множитель. — 36, 42, 48, 54, 42, 48, 54, 6, 7, 8, 9, 6, 6, 6. -Запомнить и научиться применять таблицу 6х2=12 6х3=18 6х4=24 6х5=30 6х6=36 6х7=42 6х8=48 6х9=54 1)18, 30,42, 54, 60, 6. 2)2, 4, 8, 7, 10, 1. Выполняют физкультминутку
Было — 50 кг. Израсходовали — ?, 2 • 6 (кг). Осталось — ? 1)6*12=12 (кг) – израсходовали сахара. 2)50-12=38 (кг) – сахара осталось. Ответ: 38 кг. Выполняют задание на карточках. -Получилось слово «молодец». Поднимают карточки Отвечают на вопросы Слушают объяснения домашнего задания. | К-1 – выражать в речи свои мысли и действия; К-2 – строить понятные для партнёра высказывания, учитывающие, что партнёр видит и знает, а что нет; Л-2 — учебно-познавательный интерес к новому материалу и способам решения новой учебной задачи. К-4 – использовать речь для регуляции своего действия; Р-1 – принимать учебную задачу, соответствующую этапу обучения; Р-2– планировать своё действие в соответствии с поставленной задачей и условиями её реализации, в том числе во внутреннем плане. К -9 – воспринимать различные точки зрения; К -11 – понимать необходимость использования правил; К -12 – использовать простые речевые средства; Л-2 — учебно-познавательный интерес к новому материалу и способам решения новой учебной задачи. К -13 – контролировать свои действия в классе. Р-13 – проговаривать вслух последовательность производимых действий, составляющих основу осваиваемой деятельности; Л-1 — внутренняя позиция школьника на уровне положительного отношения к школе; Л-2 — учебно-познавательный интерес к новому материалу и способам решения новой учебной задачи; Л-3- готовность целенаправленно использовать знания, умения и навыки в учебной деятельности и в повседневной жизни. Р-1 – принимать учебную задачу, соответствующую этапу обучения. К-1 – выражать в речи свои мысли и действия; К-2 – строить понятные для партнёра высказывания, учитывающие, что партнёр видит и знает, а что нет; Р-11 – самостоятельно адекватно оценивать правильность выполнения действия и вносить необходимые коррективы в исполнение как по ходу его реализации, так и в конце действия. |
Поставьте задачу на следующий этап урока.
Тем, кто испытывает затруднения, учитель дает карточку-помощницу с краткой записью.
Умножение и деление целых чисел на однозначное число. 6-й класс
- Павлова Валентина Ивановна, учитель математики
Разделы: Математика, Конкурс «Презентация к уроку»
Класс: 6
Презентация к уроку
Загрузить презентацию (13 МБ)
Цели урока: совершенствовать вычислительные
навыки, формировать умение решать задачи,
развивать мышление, способствовать развитию
самостоятельности, математическую речь,
воспитывать интерес к математике,
дисциплинированность, ответственное отношение к
труду.
Оборудование: компьютерный класс, монгольская игра, сигнальные карточки.
Ход урока
I. Орг. момент.
Включение в деловой ритм. Настрой на урок.
— Число, классная работа.
— Сообщение темы урока, слайд №2
Постановка целей урока:
- решать задачи и примеры на умножение и деление,
- работать на уроке в основном самостоятельно, поэтому будьте внимательны.
II. Устные упражнения.
— Как называются числа при умножении?
— Как называются числа при делении?
Задание по таблице умножения. Слайд №4
Задание на мышление. Слайд №5
Повторение алгоритма деления и умножения вместе с детьми.
— Запишите пример в тетради. Слайд №6, №7.
III. Формирование умений и навыков.
1. Решение и проверка задачи. Слайд № 8
Предварительная проверка задачи с помощью сигнальных карточек
(сигнальные карточки с цифрами: 1, 2, 3, 4 и знаками
действия: +,-,х,:).
— Покажите сколько вопросов в задаче?
— Какой знак действия в первом вопросе? Почему?
— Какой знак действия во втором действии? Почему?
— Исправьте ошибки в задаче. Слайд № 9.
Работа над условием задачи.
— Какой ещё вопрос можно поставить к данной задаче?
— Запишите в тетрадь с решением.
(На сколько лет дольше может прожить дуб, чем ель?) И др.
— Рассказ о пользе деревьев. Слайды № 10-11
IV. Физкультминутка. Слайд № 12. (под пение птиц)
Вместе по лесу идём
Не спешим, не отстаём
Вот выходим мы на луг
Тысяча цветов вокруг
Вот ромашка, василёк
Медуница кашка клевер
Расстилается ковёр
И направо и налево
К верху руки потянули
Позвоночник растянулиОтдохнуть вы все успели
И на место тихо сели.
2. Решение примеров самостоятельно по
вариантам.
Работа в парах.
— Решив примеры, вы узнаете о птице, которая приносит пользу.
Слайды № 13
(Слово написано наоборот)
— Рассказ о кукушке (пение кукушки) Слайд №14
V. Монгольская игра.
Сложить из геометрических фигур птиц, животных (заяц, лиса и др.).
Предложить сложить по образцу или придумать самим.
— Какие геометрические фигуры перед вами?
— Покажите прямоугольник.
— Покажите треугольник.
— Какие виды треугольников вы знаете по видам углов?
— Какие треугольники вы знаете по длинам сторон?
VI. Домашнее задание. Слайд №15.
Итог урока. Слайд № 16
— Ребята, закройте глаза представьте, что вы в лесу, послушайте пение птиц, отдохните, наберитесь сил к следующему уроку.
Обратные операции: умножение и деление
Что такое обратные операции?
Обратные операции — это два разных типа вычислений, оказывающих противоположное влияние друг на друга.
Например, вычитание — операция, обратная сложению, а деление — операция, обратная умножению.
В математике слово «инверсия» означает «противоположное».
Обратные операции можно использовать для отмены исходной операции. Это приводит к возврату значения, с которого мы начали до первого вычисления.
Например, мы можем начать с числа 5, а затем умножить его на 4.
5 × 4 = 20. Мы начали с 5, но теперь их 20.
Чтобы вернуться от 20 к 5, мы используем обратную операцию.
20 ÷ 4 = 5. Мы можем вернуться от 20 к 5, разделив на 4.
Мы говорим, что умножение на 4 — это операция, обратная делению на 4.
Умножение 5 на 4 дало 20.
Разделив 20 на 4, мы вернулись к 5.
Умножение и деление являются примерами обратных операций.
Что такое обратное умножению?
Обратным умножением является деление. Если вы умножите на заданное число, а затем разделите на то же число, вы получите то же число, с которого начали.
Деление имеет эффект, противоположный умножению.
Например, здесь 3 × 2 = 6.
Мы начали с числа 3.
Мы умножили его на 2, чтобы увеличить от 3 до 6.
Для возврата от 6 к 3 необходимо использовать обратную операцию.
Противоположностью умножения на 2 является деление на 2.
Делим 6 на 2, чтобы вернуться к исходному числу 3.
Деление имело обратный эффект по отношению к умножению, выполненному в исходном расчете.
Деление и умножение обратны только в том случае, если деление и умножение на одно и то же число. В этом примере мы умножили и разделили на 2.
Что такое обратное делению?
Обратное деление — умножение. Если вы разделите на заданное число, а затем умножите на то же число, вы получите то же число, с которого начали. Умножение имеет эффект, противоположный делению.
Например, вот 10 ÷ 2 = 5.
Мы начали с числа 10.
Мы разделили его на 2, чтобы уменьшить 10 до 5.
Чтобы вернуться от 5 к нашему исходному числу 10, мы должны использовать обратную операцию.
Мы можем умножить 5 на 2, чтобы вернуться к исходному числу 10. 5 × 2 = 10.
Деление на 2 и умножение на 2 являются обратными операциями. Умножение на 2 привело к отмене деления на 2.
Как записать умножение в виде деления
Чтобы записать умножение как деление, выполните следующие действия:
- Запишите ответ умножения в начале деления перед знаком деления.
- Запишите два умножаемых числа после знака деления и после знака равенства соответственно.
- Два числа на втором шаге можно записать в любом порядке, чтобы образовать два разных предложения с делением.
Например, вот 7 × 8 = 56. Запишем это умножение как деление.
Каждое умножение можно переписать как деление, используя те же числа, но в другом порядке.
Если вы знаете ответ на данное умножение, вы можете сразу использовать его для создания деления без выполнения каких-либо вычислений.
Просто переставьте числа.
Первый шаг — написать ответ на умножение в начале предложения деления. Результат умножения теперь равен числу, на которое оно делится.
56 — это ответ на умножение 7 × 8 = 56. Мы начнем наше деление с 56.
Следующим шагом будет запись умножаемых чисел в предложении умножения после знака деления и после знака равенства в любом порядке.
Умножаются два числа: 7 и 8. Мы напишем 7 после знака деления и 8 после знака равенства.
Преобразуем умножение 7 × 8 = 56 в деление 56 ÷ 7 = 8. Используемые числа те же, но они записаны в другом порядке.
В то время как 56 должно идти в начале деления, два других числа 7 и 8 могут быть записаны в любом порядке. Для каждого умножения можно записать два разных деления.
На этот раз мы напишем эти два числа в другом порядке.
Преобразуем умножение 7×8=56 в деление 56÷8=7.
7 × 8 = 56 можно записать как 56 ÷ 7 = 8 или 56 ÷ 8 = 7.
Как записать деление как умножение
Чтобы записать деление как умножение, выполните следующие действия:
- Запишите делимое число как ответ в конце умножения.
- Запишите оставшиеся два числа в предложении деления, умноженные вместе в предложении умножения.
- Два числа из второго шага можно записать в любом порядке, чтобы получились два разных предложения умножения.
Например, вот 18 ÷ 6 = 3
Первый шаг — записать делимое число в начале деления как ответ в конце умножения.
18 — это число, которое нужно разделить. Это сформирует ответ в конце умножения.
Следующим шагом будет запись оставшихся двух чисел из деления, умноженных вместе, в предложении умножения.
Два других числа в делении — это 6 и 3.
Мы можем записать 18 ÷ 6 = 3 как 6 × 3 = 18.
Мы также можем записать 18 ÷ 6 = 3 как 3 × 6 = 18. Неважно, в каком порядке умножаются два числа.
Каждое предложение деления может быть записано как два разных предложения умножения.
18 ÷ 6 = 3 можно записать как 6 × 3 = 18 или 3 × 6 = 18.
6. Умножение и деление дробей
Вспомните следующие факты дроби:
Умножение дробей
При умножении на дробь умножить числители и умножить знаменатели:
`2/3xx 5/7=(2xx5)/(3xx7)=10/21`
Если можете, сначала упростите .
В этом примере мы можем отменить `13` и `39` дать `1/3`:
`\cancel{13}/24xx 12/\cancel{39}=1/24 xx 12/3`
Затем отмените «12» на «24», чтобы получить «1/2»:
`1/\отмена{24} хх \отмена{12}/3=1/2 хх 1/3`
Теперь мы умножаем вершины и основания, чтобы получить:
`1/2 х х 1/3 = 1/6`
Деление дробей
Когда разделить на дробь, инвертировать и умножить:
`3/5-:2/7=3/5xx7/2=(3xx7)/(5xx2)` `=21/10` `=2 1/10`
(я умножил на обратную величину 2/7, что равно 7/2).
Когда мы делаем то же самое с алгебраическими выражениями,
не забудьте УПРОСТИТЬ СНАЧАЛА , чтобы проблему было легко решить
выполнять.
Пример 1
Упростить 92`
Упражнения
Упростить:
(1) `5/16-:25/13`
Ответить
Этот включает инвертирование «25/13», чтобы получить «13/25», а затем умножение на это «13/25».
`5/16 -: 25/13=5/16xx13/25`
Затем мы отменяем 5 сверху и 25 снизу, чтобы получить «1/5».
`=1/16 xx 13/5`
`=13/80`
Последняя строка просто:
92− 16)` и получить `(3x + 4)(3x − 4)`, используя разность квадратов, которую мы изучили ранее.`((3x+4)(3x-4))/(x+1)xx1/(4-3x)`
Далее мы используем следующий полезный прием:
`(4 − 3x) = −(3x − 4)`
(Чтобы понять, почему это работает, просто умножьте правую часть.)
`((3x+4)(3x-4))/(x+1)xx1/-(3x-4)`
После отмены у нас остается коэффициент (−1) от сокращенной дроби, и этот минус для удобства помещается впереди.