Непрерывность функции
Непрерывность функции Math Task
|
1.Непрерывность функции.
|
|||||||||||||||||||||||||||||
| 7 8 9 10 11 12 13 14 15 | |||||||||||||||||||||||||||||
1. Непрерывность функции.
|
|||||||||||||||||||||||||||||
|
Функция f(x) называется непрерывной в точке х0, если она имеет конечный предел в этой точке. И этот предел равен значению функции в данной точке. |
|||||||||||||||||||||||||||||
|
Если функция непрерывна в точке, следовательно на графике это изображается непрерывной линией. Отсюда следует, что если дать независимой переменной х приращение равное нулю (Δх=0), то приращение функции также будет равно нулю. (рис.1) |
Рис. 1 |
||||||||||||||||||||||||||||
|
Отсюда можно сделать вывод, что если независимая переменная х будет стремиться к х0, то функция будет стремиться к f(x0). |
|||||||||||||||||||||||||||||
| Таким образом, если не выполняется данное условие, то точка х0 называется точкой разрыва и функция прерывается в данной точке. | |||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Пример. |
|||||||||||||||||||||||||||||
| 7 8 9 10 11 12 13 14 15 | |||||||||||||||||||||||||||||
www. mathtask.ru |
||
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
| Справочник по математике | Элементы математического анализа | Производная функции |
| Приращение аргумента и приращение функции. Производная как предел отношения приращений |
| Непрерывность функции |
Приращение аргумента и приращение функции. Производная как предел отношения приращений
В разделе «Секущая графика функции.
Касательная к графику функции. Производная функции. Геометрический смысл производной» нашего справочника приведено определение производной функции y = f (x) в точке x0 (в том случае, если она существует) как числа, к которому стремится отношение
| (1) |
при x1 → x0 . Коротко это принято записывать так:
| (2) |
Заметим, что существование производной функции y = f (x) и значение производной зависят от выбора точки x0 . Поэтому производная функции сама является функцией точки x0 .
Если в формуле (2) заменить x0 на x , а разность x1 – x0 обозначить символом Δx, то эта формула примет вид
| (3) |
Определение 1.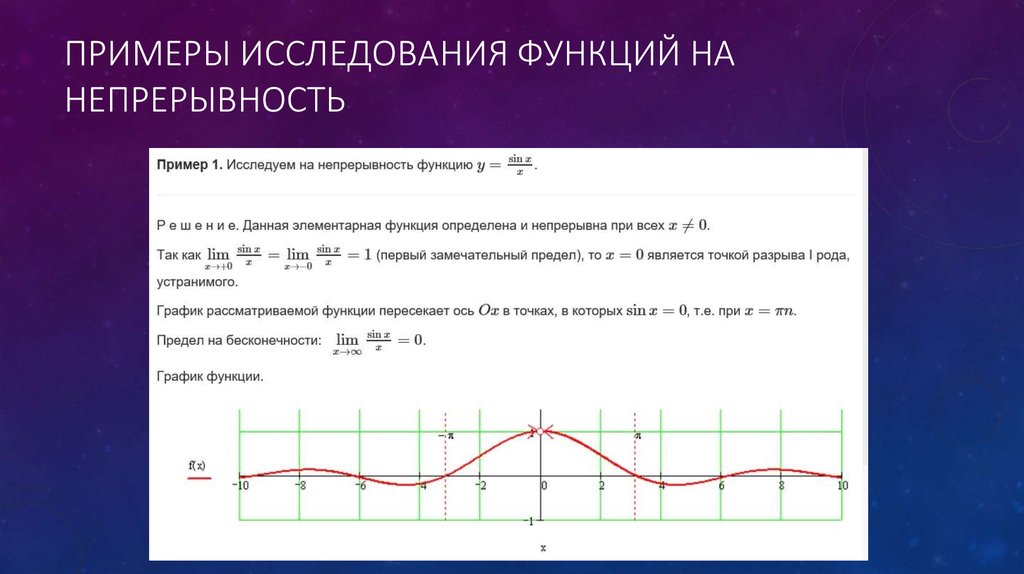
Переменную Δx называют приращением аргумента, а разность
f (x + Δx) – f (x)
называют приращением функции f (x) в точке x , соответствующим приращению аргумента Δx, и обозначают Δf .
Таким образом,
| Δf = f (x + Δx) – f (x) | (4) |
Используя определения приращения аргумента и приращения функции, формулу (3) можно переписать так:
| (5) |
В соответствии с этой формулой производную функции f (x) в точке x называют пределом отношения приращения функции к приращению аргумента в точке x , когда приращение аргумента стремится к нулю.
Пример 1.
Вывести формулу для производной функции y = x 2 .
Решение. Из формулы (3) получаем:
Ответ.
Непрерывность функции
Определение 2. Функцию y = f (x) называют непрерывной в точке x0 , если выполнено равенство
| (6) |
Другими словами, функция f (x) непрерывна в точке x0 тогда и только тогда, когда выполнено равенство
| (7) |
Пример 2. Доказать, что функция y = x3 непрерывна в любой точке x , где .
Решение. Выберем произвольную точку x, где , и воспользуемся формулой сокращенного умножения «куб суммы»:
Соотношение (7) выполнено, что и завершает решение примера 2.
Пример 3. Доказать, что функция
| (8) |
разрывна (не является непрерывной) в точке x = 0 .
Решение. Поскольку в точке x = 0
причем
то соотношение (7) в точке x = 0 не выполняется. Таким образом, функция (8) является разрывной в точке x = 0 .
Доказано.
Для наглядности приведем график функции (8) (рис. 1).
Рис.1
Замечание. Если в точке x = x0 у функции f (x) существует производная, то функция f (x) непрерывна в точке x0 .
Обратное утверждение, вообще говоря, неверно: если функция f (x) непрерывна в точке x0 , то отсюда вовсе не следует, что в этой точке у функции должна существовать производная.
Примером является функция f (x) = |x| (модуль x), которая непрерывна в точке x = 0 , но у нее не существует производной в этой точке.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Непрерывность функции в точке
Непрерывность функции в точкеСуществует много типов функций и форм: периодические функции, определенные по частям, возрастающие, убывающие, полые, выпуклые… Но между всеми ними мы можем классифицировать их еще по двум элементарным наборам: непрерывные и не непрерывные функции.
Обычно говорят, что функция непрерывна, если ее можно нарисовать, не поднимая карандаша роли, и, следовательно, нарисовать ее всего за одну черту. 9-}x=2 \end{массив} $$$ и если мы вычислим функцию в $$x=2$$, мы получим, что $$f(2)=0$$, таким образом, функция не является непрерывной в точке $$x=2$$.
Похожие темы
- Свойство Дарбу (теорема о промежуточном значении)
- Прерывание функций: Предотвратимый, Прыжок и Существенный разрыв
- Теорема Больцано
Решенные задачи непрерывности функции в точке
Посмотреть проблемыТеория математики в твоем мобильном
Download it for freeContinuous Functions and Discontinuities
Continuous Functions and Discontinuities- About
- Statistics
- Number Theory
- Java
- Data Structures
- Cornerstones
- Исчисление
Интуитивные понятия и терминология
Возвращаясь к нашему интуитивному понятию предела, вспомним, что мы говорили, что если не знать, что делает функция при определенном значении $x$ (как показано на графике ниже, когда $x=2$), предел можно считать в качестве «ожидания» высоты функции при этом значении $x$ — в предположении, что вблизи этого значения $x$ график функции можно нарисовать одним непрерывным росчерком пера.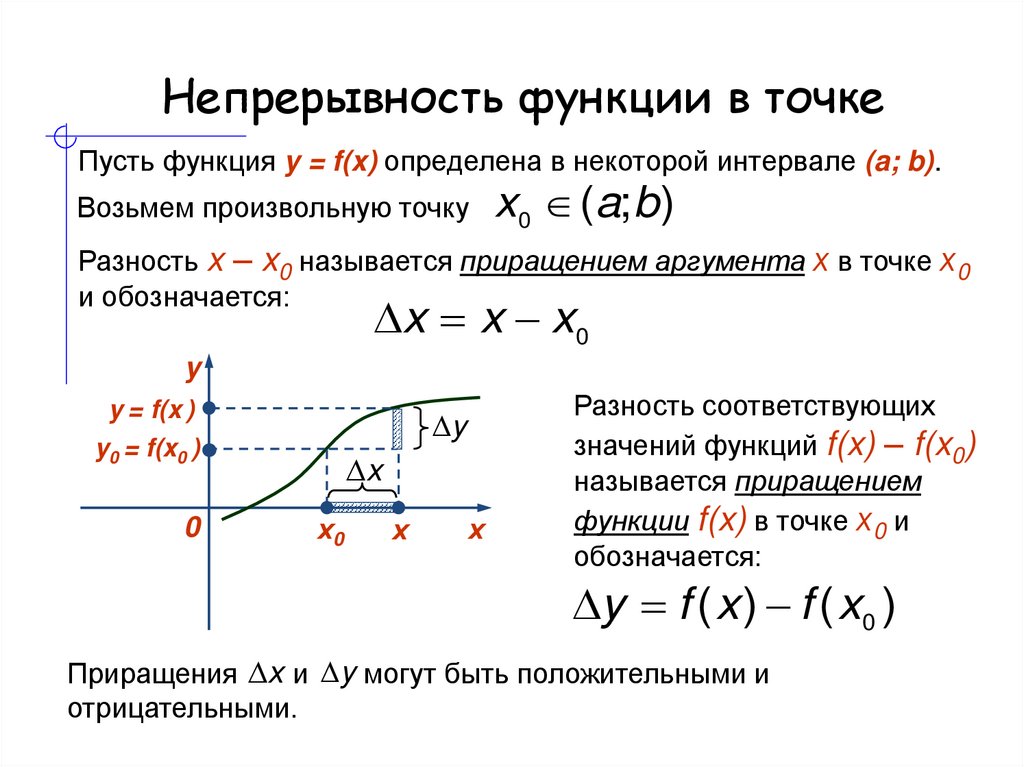
Как мы видели, это ожидание, даже если оно существует, не обязательно должно согласовываться с фактическим поведением функции при рассматриваемом значении $x$. То есть не обязательно, чтобы $\lim_{x \rightarrow c} f(x) = f(c)$. Рассмотрим еще раз следующие три функции.
В первом примере фактическое значение $f(2)$ совпадает с нашим «ожидаемым значением», $\lim_{x \rightarrow 2} f(x)$. Также обратите внимание, что в первом примере функция может быть нарисована одним непрерывным росчерком пера (во всяком случае, около $x=2$).
Во втором случае $f(2)$ даже не существует ($x=2$ не находится в области определения второй функции), поэтому она никак не может совпадать с нашим «ожидаемым значением», $\lim_{ х \rightarrow 2} f(x)$.
Кроме того, может показаться, что рисование этой функции требует, чтобы мы на мгновение оторвали перо от бумаги в точке $x=2$, учитывая наличие там «дыры». Таким образом, мы не можем нарисовать эту функцию одним непрерывным штрихом.
Аналогично, в третьем примере $f(2)$ существует, но отличается по значению от $\lim_{x \rightarrow 2} f(x)$. Это снова приводит к «дыре» в функции, из-за которой мы поднимаем перо, когда пытаемся нарисовать эту функцию. Следовательно, мы не можем нарисовать эту функцию вблизи $x=2$ одним непрерывным штрихом.
Точно так же, если мы посмотрим на три функции, где $\lim_{x \rightarrow c} f(x)$ не существует, мы увидим в каждом случае функции, которые нельзя нарисовать одним непрерывным росчерком пера вокруг $х=с$. ( По общему признанию, за последней функцией может быть сложнее следить, но, конечно, вы должны согласиться с тем, что рисовать эту функцию вокруг $x=0$ сложно! )
| $$y=f(x), \quad c=2$$ | $$y=g(x), \quad c=1$$ | $$y=h(x), \quad c=0$$ |
Конечно, если $\lim_{x \rightarrow c} f(x)$ не существует, мы не можем иметь $\lim_{x \rightarrow c} f(x) = f(c)$.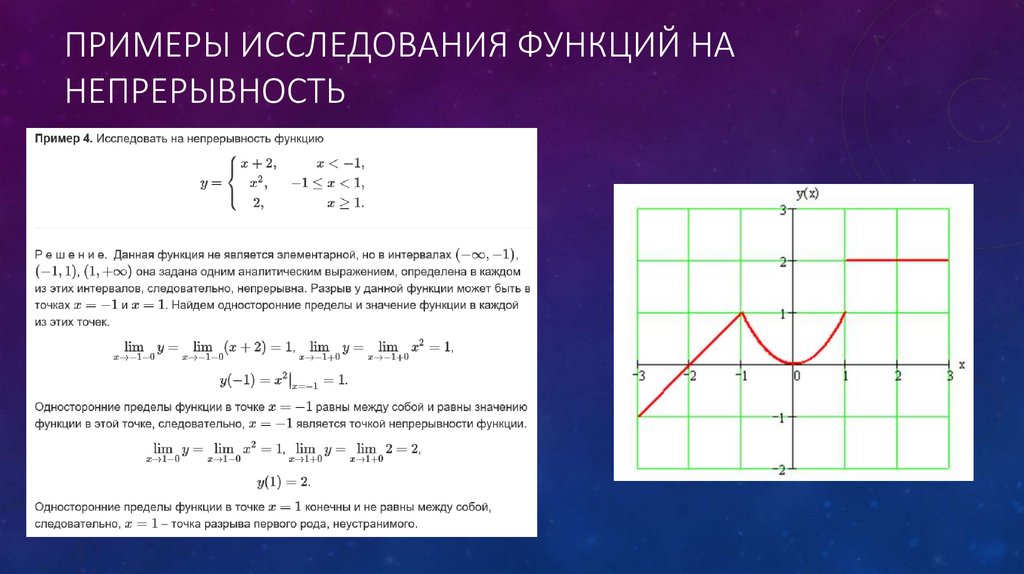
Таким образом, из этих примеров может показаться, что мы можем нарисовать график $y=f(x)$ около некоторого $x=c$ одним непрерывным штрихом только в том случае, если происходят три вещи:
$\lim_{x \rightarrow c} f(x)$ существует,
$f(c)$ существует (т. е. $c$ находится в области определения $f(x)$), и
- 9+} f(x)$ ВСЕ существуют и совпадают по значению.
Существует множество вариаций на тему, когда речь заходит о словоблудии, используемой в разговоре о непрерывных функциях. Например:
Мы говорим, что функция непрерывна всюду , если она непрерывна при каждом действительном значении $c$.
Мы также можем сказать, что функция непрерывна в своей области определения , если она непрерывна при каждом действительном значении $c$, попадающем в область определения рассматриваемой функции. 9-} f(x) = f(c)}$.
Обратите внимание, что функции могут быть прерывистыми по-разному (все, кроме одного из приведенных выше маленьких рисунков, в какой-то момент были прерывистыми).
Если $\lim_{x \rightarrow c} f(x)$ существует, но по какой-то другой причине не является непрерывным в точке $x=c$ (т. е. либо $f(c)$ не существует, либо не равно значение этого предела), мы говорим, что $f(x)$ имеет устранимый разрыв при $x=c$ .
Можно думать о функциях с устранимыми разрывами как о функциях, непрерывность которых легко «починить» в определенном смысле. То есть, если просто определить (или переопределить) значение функции при $x=c$, разрыв можно устранить. Следующие два графика имеют устранимые разрывы при $x=2$. 92-1 &\textrm{if} x \neq 2\\ 1 & \textrm{если} х = 2 \end{массив} \right.$$
Как видно выше, устранимые разрывы представляются графически как « отверстий » в функциях.
Конечно, если $\lim_{x \rightarrow c} f(x)$ не существует, то определения или переопределения значения $f(x)$ при $x=c$ будет недостаточно для устранения разрыва. Мы говорим в этой ситуации, что $f(x)$ имеет неустранимых разрывов в точке $x=c$}.
9+} f(x)$ (см. график D ниже) Мы говорим, что имеем вертикальную асимптоту , когда $\lim_{x \rightarrow c} f(x)$ или один из связанных с ней односторонних пределов не существует, поскольку он бесконечен. (см. диаграмму E ниже)
9+} f(x)$ (см. график D ниже)Какие функции являются непрерывными?
Примеров непрерывных функций множество. Например, рассмотрим полиномиальную функцию $p(x)$. Мы знаем, что область определения $p(x)$ — это множество всех вещественных чисел. Это в сочетании с одним из наших предельных законов, «$\lim_{x \rightarrow c} p(x) = p(c)$ всякий раз, когда $p(x)$ является полиномиальной функцией», говорит нам, что $\lim_{ x \rightarrow c} p(x)$ и $p(x)$ существуют и совпадают по значению для каждого действительного числа $c$. Таким образом, все полиномиальные функции непрерывны всюду (т.