Тест для подготовке к огэ 9 класс, первое задание: «Обыкновенные дроби»
Тест для подготовке к огэ 9 класс, первое задание: «Обыкновенные дроби»| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Учебно-дидактические материалы
▪КИМ
Материал опубликовал
2
#6 класс #7 класс #8 класс #9 класс #Математика #ФГОС #Учебно-дидактические материалы #КИМ #Учитель-предметник #Школьное образование
Задания для подготовке к ГИА 9 класс.
Первое задание.
Обыкновенные дроби
Ответом к каждому заданию является конечная десятичная дробь или целое число.
Вариант 1 | Вариант 2 |
Найдите значение выражения: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) | Найдите значение выражения: 1) 2) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) |
Вариант 3 | Вариант 4 |
Найдите значение выражения: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) | Найдите значение выражения: 1) 2) 3) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) |
Ответы:
Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
1) -2 2) 5,9 3) -0,3 4) 126 5) 58,4 6) 3,25 7) 0,6 8) 0,9 9) 0,24 10) 0,9 11) 4,5 12) 1,35 | 1) -2 2) 0,33 3) -0,375 4) 17,5 5) -8,75 6) 3,9 7) 1,25 8) 2,1 9) -0,6 10) 0,6 11) 3,3 12) 0,3 | 1) -3 2) 2,7 3) -0,55 4) 16,8 5) 11,75 6) 1,17) 0,9 8) 1,9 9) -0,1 10) 0,45 11) 0,32 12) 0,7 | 1)-1 2) 3,85 3) -0,35 4) 264 5) 79,2 6) 5,75 7) 0,75 8) 1,6 9) -0,62 10) 10,5 11) 8,75 12) 1,25 |
Опубликовано
Чтобы написать комментарий необходимо авторизоваться.
Десятичные дроби
Вопросы занятия:
· повторить понятие «десятичные дроби», правила их записи;
· повторить способы представления обыкновенной дроби в виде десятичной;
· вспомнить правила сравнения десятичных дробей;
· правила округления десятичных дробей;
· повторить порядок выполнения действий над десятичными дробями.
Материал урока
Дробь, у которой знаменатель равен разрядной единице,
то есть десяти, ста, тысяче и так далее можно записать особым способом, в виде
десятичной дроби. При этом сначала пишут целую часть, а затем после запятой
записывают числитель.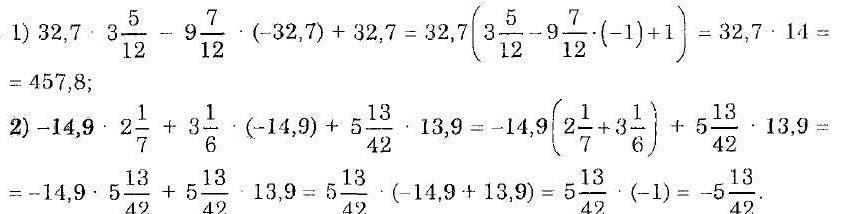
Особое внимание нужно обращать на то, что количество
знаков после запятой соответствует числу нулей разрядной единицы, стоящей в
знаменателе.
Видим, что в записи любой десятичной дроби присутствует и целая, и дробная части. Напомним разряды целой и дробной частей десятичной дроби. У целой части выделяют разряд единиц, разряд десятков, разряд сотен, разряд тысяч и так далее. Теперь назовём разряды дробной части: разряд десятых, разряд сотых, разряд тысячных, разряд десятитысячных и так далее.
Вы помните, что в конце дробной части десятичной дроби можно дописывать и отбрасывать нули, при этом значение дроби не изменится. Это удобно использовать при выполнении действий над десятичными дробями и при сравнении десятичных дробей.
Прежде чем приступить к повторению этих вопросов, напомним правила записи десятичных дробей.
Пример.
Как обыкновенные дроби с разрядной единицей в знаменателе
мы записали в виде десятичных, так и, наоборот, десятичные можно записывать в
виде обыкновенных.
Пример.
Теперь поговорим о сравнении. Десятичные дроби сравнивают поразрядно, начиная со старшего разряда (слева направо).
Пример.
Далее давайте вспомним правила сложения и вычитания десятичных дробей. Эти действия выполняют по тем же правилам, что и для целых чисел, только при записи столбцов вычисления запятую записывают под запятой и у результата её ставят в том же месте.
А теперь напомним правило умножения десятичных дробей. При этом вычисления производят как с обычными числами, не взирая на запятую, а затем у результата запятую ставят так, чтобы число знаков после запятой равнялось сумме знаков после запятой у множителей.
Причём, если в произведении меньше цифр, чем нужно отделить запятой, то слева нужно дописать необходимое число нулей.
Обратите внимание, вычисления выполнены также, как и над целыми числами.
Ещё стоит вспомнить два случая умножения десятичных
дробей на разрядную единицу.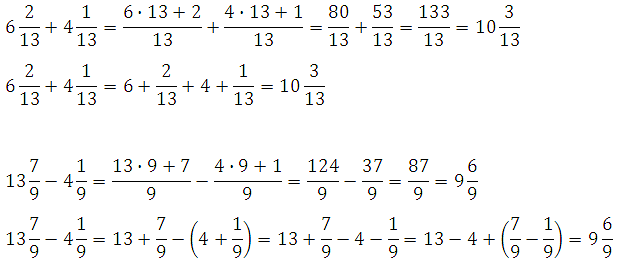
При умножении десятичной дроби на 10, 100, 1000 и так далее, запятую у дроби переносят вправо на количество нулей в разрядной единице.
А при умножении десятичной дроби на одну десятую, одну сотую, одну тысячную и так далее, запятую у дроби переносят влево на количество цифр после запятой в разрядной единице.
Рассмотрим конкретный пример деления десятичной дроби на число.
При делении десятичной дроби на другую десятичную дробь нужно перенести запятые в делимом и делителе на число десятичных знаков в делителе, то есть сделать делитель целым числом.
При делении десятичной дроби на 10, 100, 1000 и так далее, запятую у дроби переносят влево на количество нулей в разрядной единице
А при делении десятичной дроби на одну десятую, одну
сотую, одну тысячную и так далее, запятую у дроби переносят вправо на
количество цифр после запятой в разрядной единице.
Часто можно встретить задания, в которых нужно работать с обыкновенными и десятичными дробями одновременно. Поэтому стоит напомнить способы представления обыкновенной дроби в виде десятичной.
Так мы с вами показали, что обыкновенную дробь можно представить, как в виде конечной десятичной дроби, так и в виде бесконечной периодической десятичной дроби.
Как видите не всегда обыкновенную дробь можно представить в виде конечной десятичной. Поэтому стоит напомнить, что обыкновенную несократимую дробь можно перевести в конечную десятичную, если разложение знаменателя на простые множители содержит только цифры 2 и 5.
Далее вспомним правило округления десятичной дроби.
Определение.
Округлить число — это значит заменить его «круглым числом» с нулями на конце или с укороченной дробной частью в зависимости от того, до какого разряда производится округление.
Подчеркнув цифру округляемого разряда, обращаем
внимание на ту, которая стоит справа.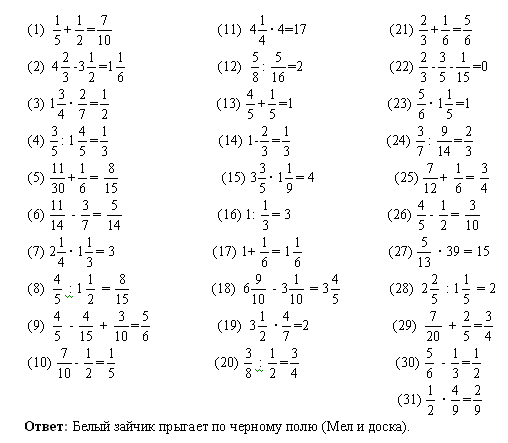
Если это 0, 1, 2, 3 или 4, то подчёркнутую цифру оставляем той же.
Если это 5, 6, 7, 8 или 9, то подчёркнутую цифру увеличиваем на единицу.
Цифры справа от округляемого разряда, стоящие после запятой отбрасываем. А те, которые стоят до запятой, заменяем нулями.
Далее выполним задание, где нужно найти значения выражений, содержащих как обыкновенные, так и десятичные дроби.
Пример
Итоги урока
В подведении итогов урока напомним все его основные моменты.
Мы вспомнили, что за дроби называют десятичными, и повторили правила их записи. Напомнили способы представления обыкновенной дроби в виде десятичной.
А также повторили правила сравнения десятичных дробей, правила их округления и правила выполнения арифметических действий над десятичными дробями.
Что я узнал о дробях 9 класса
11 октября 2018 г.
- Отображение отрицательных дробей в числовой строке
- Сравнение дробей
- Сложение и вычитание отрицательных дробей
- Умножение и деление отрицательных дробей
Давайте начнем с основ.
.. Чтобы отображать отрицательные дроби, вам нужно всегда помнить; отрицательные числа находятся левее нуля, и чем левее, тем меньше число. Положительные числа располагаются справа от нуля, и чем правее, тем больше число. Вы также должны были научиться складывать, вычитать, умножать и делить целые числа, прежде чем изучать следующее.
Шаг 1 (Знаменатели):
Простой способ находить дроби в числовой прямой — это знать, что представляет собой знаменатель. Знаменатель соответствует количеству шагов между одним целым числом и следующим (на сколько частей «Разделить» или «Разбить» строку перед следующим целым числом). Совет: Полезный способ отслеживать — рисовать «пузыри или шишки», чтобы подсчитывать шаги в знаменателе.
Напр.
Шаг 2 Нахождение числителя:
Чтобы найти числитель на числовой прямой; Посмотрите на числитель дробей и посчитайте количество пробелов/шагов (начиная с нуля) в отрицательном или положительном направлении в зависимости от вашей дроби.
Сравнение дробей может быть очень простым, но может быть и сложным. При сравнении всегда хочется быть осторожным и обращать внимание на отрицательные числа. Чтобы показать, какой из них больше или меньше, мы используем такие символы, как <, > или =.
Шаг 1:
При работе с дробями вы часто сталкиваетесь со смешанной числовой дробью или неправильной дробью. Для сравнения дробей лучше работать с неправильными дробями, если это возможно, потому что вы можете четко видеть различия в размере/количестве.
Сравнивать дроби означает смотреть на две дроби и выяснять, какая из них больше. Чтобы сравнить дроби, все, что вам нужно сделать, это сделать так, чтобы у них был один и тот же знаменатель, а затем посмотреть, у какой дроби больший числитель.
Первое, что вы хотите сделать, это превратить обе дроби в неправильные дроби, если они уже не являются таковыми. Вы делаете это, умножая целые числа на знаменатель, а затем добавляя числитель.
Напр.
Шаг 2:
Отсюда вы найдете общий знаменатель обеих дробей. (Можно просто умножить одно на другое).
Шаг 3:
Как только обе дроби будут иметь общий знаменатель, станет ясно, какая дробь больше, а какая наименьшая. Не забывайте следить за любыми отрицательными символами, так как они могут изменить ответ. Теперь на этом этапе вы можете использовать <, > или =.
Пример сложения (правила применяются как к сложению, так и к вычитанию) :
+
Шаг 1:
Когда добавляет дробей, вы всегда хотите начать с того, что обе дроби станут неправильными. Вы делаете это, умножая целые числа на знаменатель, а затем добавляя числитель.
Напр.
Шаг 2:
Теперь вам нужно найти общий знаменатель. Самый простой способ сделать это — умножить их друг на друга.
Напр.
Шаг 3: перетягивание каната:
Это ваш последний шаг.
Теперь вы хотите добавить (или вычесть) числители (оставив Демонизаторы одинаковыми). Совет: давайте воспользуемся сценарием «Перетягивание каната», а числа — это «люди». Чем больше людей (общее количество), которые появятся на любом из них, выиграет.
напр.
Итак, ответ для этого примера (добавление): $latex \frac{-9}{15}.
Умножение и деление дробей:
Умножение :
х
Шаг 1:
Умножать дроби очень просто. Для начала вам нужно убедиться, что обе ваши дроби являются неправильными дробями, если они еще не являются таковыми. Для этого нужно умножить целые числа на знаменатель, а затем добавить числитель.
Шаг 2:
Умножение дробей очень просто. Вы умножаете числитель на числитель, а знаменатель на знаменатель.
Напр.
Шаг 3:
Отсюда вы можете упростить. Вы делаете это, разделив числитель и знаменатель на одно и то же делимое число.
Напр.
Разделение :
÷
Шаг 1: Для начала вам нужно убедиться, что обе ваши дроби являются неправильными дробями, если они уже не являются таковыми. Для этого нужно умножить целые числа на знаменатель, а затем добавить числитель.
Напр.
Шаг 2:
Теперь умножьте на обратное (это означает перевернуть одну дробь и умножить ее). (Применение навыков умножения сверху)
Напр.
Шаг 4:
Отсюда вы можете упростить. Вы делаете это, разделив числитель и знаменатель на одно и то же делимое число.
Напр.
Критерии:
Объясни и покажи как отрицательные дроби:
- а) отображается в числовой строке
- б) как вы сравниваете дроби
- c) сложение и вычитание дробей (где хотя бы одна из них является отрицательной)
- г) умножение и деление дробей (где хотя бы одна из них отрицательная)
- до : среда, 17 октября — тег: дроби
*Все изображения были созданы Эмили из Word и скриншотов*
двухшаговых уравнений с дробями — Pre-Algebra
Все ресурсы Pre-Algebra
11 Диагностические тесты 177 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Pre-Algebra Help » Алгебраические уравнения » Двухшаговые уравнения » Двухшаговые уравнения с дробями
Решите для :
Возможные ответы:
Правильный ответ:
Объяснение:
Цель состоит в том, чтобы изолировать переменную с одной стороны.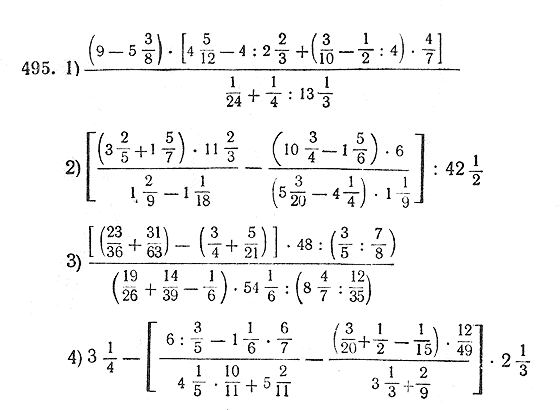
Subtract from each side of the equation:
Multiply both sides by :
Report an Error
Solve for :
Possible Answers:
Correct answer:
Объяснение:
Цель состоит в том, чтобы изолировать переменную в одну сторону.
Сначала преобразуйте смешанные номера в неправильные фракции:
Вычитание с обеих сторон:
Умножьте каждую сторону на обратно
Сообщить об ошибке9 Объяснение:
Шаг 1: Добавить в обе стороны:
Шаг 2: Добавить в . Помните, что при сложении дробей необходимо найти общий знаменатель. Общий знаменатель для и . становится, когда вы умножаете и числитель, и знаменатель на .
Точно так же становится, когда вы умножаете и числитель, и знаменатель на .
Шаг 3: Умножьте обе стороны уравнения на взаимного из :
Шаг 4: Упрощайте фракцию, разделяя нумеров и деноминатор на 9019 -основной коэффициент GCF). GCF и составляет:
Сообщить об ошибке
Решить для:
Возможные ответы: 7
3
Объяснение:
Вы пытаетесь изолировать .
Чтобы сделать это, вы должны сначала вычесть обе стороны на 2, чтобы получить
Затем это становится одношаговой задачей, где вы умножаете обе части на 2, чтобы получить
Сообщить об ошибке
Решите для x:
Возможные ответы:
Правильный ответ:
Объяснение:
После выделения x важно найти наименьший общий знаменатель, чтобы можно было сложить две дроби, с которыми вы работаете.
Шаг 1. Выделите x и приведите дроби к общему знаменателю
Шаг 2. Найдите x
Сообщите об ошибке
Найдите .
Возможные ответы:
Правильный ответ:
Объяснение:
Перекрестное умножение — это сокращенный способ умножения на знаменатели обеих частей уравнения. В разбивке это работает так:
Четверки в левой части уравнения сокращаются.
Теперь сделайте то же самое со знаменателем справа.
Буквы справа отменяются.
Это просто результат удаления знаменателей, а затем их умножения на противоположные стороны, то есть перекрестного умножения.
Теперь, чтобы закончить решение для , упростите обе части.
Затем извлеките квадратный корень, чтобы закончить.
Отчет о ошибке
Решение для:
Возможные ответы:
Правильный ответ:
.
Правильный ответ:
66:
. Объяснение:
Сообщить об ошибке
Решить проблему .
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, вы хотите оставить все термины с x с одной стороны, а все остальные термины с другой. Для этого мы можем вычесть 4/3 с обеих сторон.
Теперь у нас есть
Теперь мы можем умножить обе части на обратную величину 2/5, что равно 5/2, чтобы найти только x.
Отчет о ошибке
Решение для :
Возможные ответы:
Правильный ответ:
Объяснение:
Объяснение:
Цель состоит в том, чтобы изолировать переменную с одной стороны.