Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь .
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
 Найти значение выражения .
Найти значение выражения .Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3.
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2.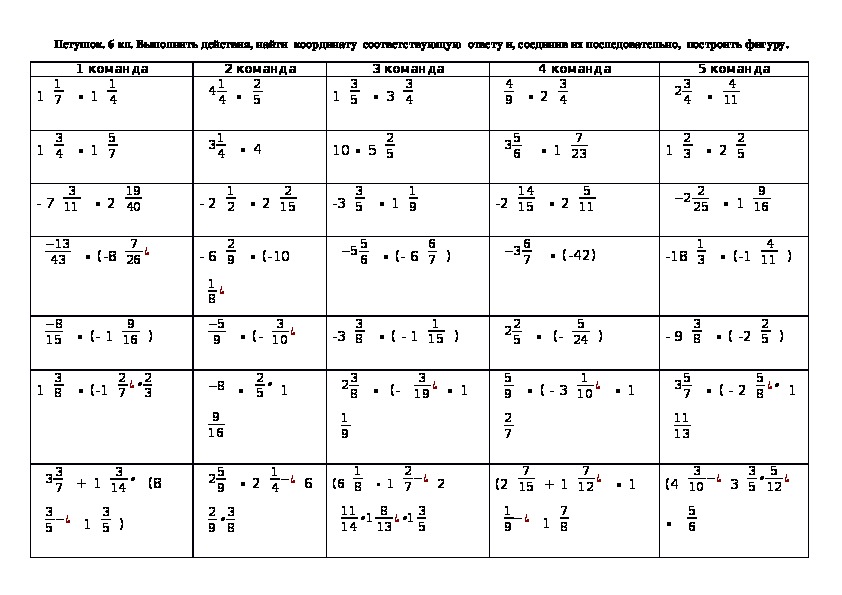 То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражение
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Задание 11. Найдите значение выражения:
Решение:
Задание 12. Найдите значение выражения:
Решение:
Задание 13. Найдите значение выражения:
Решение:
Задание 14. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Математика: уроки, тесты, задания.
 Математика: уроки, тесты, задания.
Математика: уроки, тесты, задания.
-
-
Сравнение предметов
-
Точка, прямая линия, кривая и отрезок
-
Особенности многоугольников
-
Пространственные и временные представления
-
Объединение предметов в группы и пары
-
Сравнение (больше, меньше, столько же)
-
Знаки сравнения и знаки действий
-
-
-
Нумерация.
 Сколько? От 1 до 5
Сколько? От 1 до 5
-
Примеры на сложение и вычитание от 1 до 5
-
Сравнение чисел от 1 до 5
-
Текстовые задачи (от 1 до 5)
-
Задачи на смекалку (от 1 до 5)
-
-
-
Примеры на сумму
-
Текстовые задачи (сумма)
-
-
Переместительный закон сложения
-
-
Примеры на разность
-
Текстовые задачи (разность)
-
-
Таблица сложения.
 Числа от 1 до 9
Числа от 1 до 9
-
-
Нумерация. Сколько? От 0 до 10
-
Примеры от 0 до 10
-
Сравнение чисел от 0 до 10 и выражений
-
Текстовые задачи (от 0 до 10)
-
Задачи на смекалку (от 0 до 10)
-
-
Увеличить/уменьшить на…
-
-
Мера длины — сантиметр
-
Мера длины — дециметр
-
-
На сколько больше? На сколько меньше?
-
-
Счёт десятками
-
Счёт круглых чисел
-
-
-
Нумерация.
 Сколько? От 11 до 20
Сколько? От 11 до 20
-
Примеры от 11 до 20
-
Сравнения чисел от 11 до 20
-
Текстовые задачи (от 11 до 20)
-
Задачи на смекалку (от 11 до 20)
-
-
Числа от 20 до 100.
 Нумерация. Числа и цифры
Нумерация. Числа и цифры
-
-
Сочетательный закон сложения. Скобки
-
Таблица сложения. Числа от 0 до 18
-
Вычитаем сумму из числа
-
Правила сложения и вычитания чисел в пределах 20 с переходом через десяток
-
Сложение и вычитание чисел в пределах 100 без перехода через десяток
-
Правила сложения и вычитания чисел в пределах 100 с переходом через десяток
-
Правила сложения и вычитания чисел в пределах 100
-
-
-
Находим периметр
-
Решение задач в два действия
-
-
-
Мера длины — метр
-
Килограмм
-
Литр
-
-
-
Уравнение (сумма)
-
Уравнение (разность)
-
-
-
Понятие умножения
-
Переместительный закон умножения
-
Умножение на 2 (таблица)
-
Умножение на 3 (таблица)
-
Умножение на 4 (таблица)
-
Умножение на 5 (таблица)
-
-
Деление
-
Чётные и нечётные числа
-
-
Выражения без скобок
-
Выражения со скобками
-
-
-
Узнаём о луче
-
Фигура угол и его характеристики
-
Характеристики прямого, тупого и острого углов
-
-
-
Увеличить на.
 .. Увеличить в… Уменьшить на… Уменьшить в…
.. Увеличить в… Уменьшить на… Уменьшить в…
-
Больше на… Больше в… Меньше на… Меньше в…
-
-
-
Умножение на 6 (таблица)
-
Умножение на 7 (таблица)
-
Умножение на 8 (таблица)
-
Умножение на 9 (таблица)
-
-
-
Нахождение неизвестного множителя
-
Нахождение неизвестного делимого
-
Нахождение неизвестного делителя
-
-
-
Свойства ломаной линии
-
Треугольники.
 Виды треугольников
Виды треугольников
-
-
-
Умножение и деление на 0, 1, 10. Деление числа на само себя
-
Выполняем умножение и деление круглого числа на однозначное число
-
Правила деления круглого числа на круглое число
-
-
-
Умножаем сумму на число
-
Умножаем двузначное число на однозначное число
-
-
-
Правила деления суммы на число
-
Правила деления двузначного числа на однозначное
-
Правила деления двузначного числа на двузначное
-
Правила деления с остатком
-
-
-
Находим долю от числа
-
Сравниваем доли
-
Находим число по доле
-
-
-
Трёхзначные числа.
 Нумерация
Нумерация
-
Сложение и вычитание трёхзначных чисел
-
Выполняем умножение и деление трёхзначного числа на однозначное число
-
Связь между величинами
-
-
Календарь
-
-
Нумерация
-
Правила сложения и вычитания многозначных чисел
-
Правила сочетательного закона умножения
-
Умножаем и делим числа на 10, 100, 1000
-
Круглые числа (умножение и деление)
-
-
-
Единицы измерения времени (час, минута, сутки)
-
Миллиметр
-
Километр
-
-
-
Нахождение площади фигуры, прямоугольника
-
Единицы измерения площади
-
-
-
Умножение на однозначное число.
 Распределительный закон умножения относительно сложения
Распределительный закон умножения относительно сложения
-
Умножаем круглое число на однозначное число
-
Выполняем умножение на круглое число
-
Выполняем умножение круглых чисел
-
Выполняем умножение на двузначное число
-
Выполняем умножение на трёхзначное число
-
-
-
Деление многозначного числа на однозначное число
-
Деление круглого многозначного числа на однозначное
-
Деление многозначного числа на 10, 100, 1000 с остатком
-
Деление многозначного числа с остатком на однозначное число
-
Выполняем деление трёхзначного числа на двузначное число
-
Деление с остатком трёхзначного числа на двузначное число
-
Деление многозначного числа на двузначное число
-
Деление с остатком на двузначное число
-
Выполняем деление на трёхзначное число
-
Деление с остатком на трёхзначное число
-
Деление круглого многозначного числа на круглое число
-
-
-
Единицы времени.
 Минута. Секунда
Минута. Секунда
-
Единицы массы и площади. Гектар. Центнер. Тонна
-
-
-
Понятие дроби
-
Сравниваем дроби
-
Дроби.
 Нахождение части числа
Нахождение части числа
-
Дроби. Нахождение числа по его части
-
-
-
Решение задач на нахождение скорости, времени, расстояния
-
Решение задач на нахождение работы, времени, производительности
-
Решение задач на нахождение цены, количества, стоимости
-
-
-
Десятичная система счисления.
 Римская нумерация
Римская нумерация
-
Числовые и буквенные выражения
-
Начальные геометрические понятия: прямая, отрезок, луч, ломаная, прямоугольник
-
Определение координатного луча
-
Округление чисел.
 Прикидка и оценка результатов вычислений
Прикидка и оценка результатов вычислений
-
Законы арифметических действий. Вычисления с многозначными числами
-
Решение текстовых задач арифметическим способом
-
Формулы. Уравнения. Упрощение выражений
-
Математический язык и математическая модель
-
-
-
Деление с остатком.
 Понятие обыкновенной дроби
Понятие обыкновенной дроби
-
Основное свойство дроби. Сокращение и расширение дробей
-
Правильные и неправильные дроби. Смешанные числа. Понятие, запись и чтение
-
Сравнение обыкновенных дробей
-
Сложение и вычитание обыкновенных дробей и смешанных чисел
-
Умножение и деление обыкновенной дроби на натуральное число
-
Нахождение части от целого и числа по его части
-
Геометрические понятия: окружность и круг
-
-
-
Угол.
 Измерение углов
Измерение углов
-
Биссектриса угла. Свойство биссектрисы угла
-
Треугольник. Площадь треугольника
-
Свойство углов треугольника. Размеры объектов окружающего мира (масштаб)
-
Расстояния между двумя точками.
 Масштаб. Виды масштаба
Масштаб. Виды масштаба
-
Перпендикулярность прямых. Расстояние от точки до прямой. Серединный перпендикуляр
-
-
-
Понятие десятичной дроби. Представление десятичной дроби в виде обыкновенной дроби и наоборот
-
Десятичные дроби.
 Сравнение
Сравнение
-
Десятичные дроби. Сложение и вычитание
-
Десятичные дроби. Умножение
-
Степень с натуральным показателем
-
Десятичные дроби.
 Среднее арифметическое, деление на натуральное число
Среднее арифметическое, деление на натуральное число
-
Десятичные дроби. Деление на десятичную дробь
-
Проценты. Задачи на проценты: нахождение процента от величины и величины по её проценту
-
-
-
Прямоугольный параллелепипед.
 Определение, свойства
Определение, свойства
-
Прямоугольный параллелепипед. Развёртка
-
Прямоугольный параллелепипед. Объём
-
-
-
Делимость натуральных чисел
-
Признаки делимости на 2, 3, 5, 9, 10
-
Простые и составные числа.
 Разложение натурального числа на простые множители
Разложение натурального числа на простые множители
-
Наибольший общий делитель и наименьшее общее кратное
-
-
-
Положительные и отрицательные числа. Определение координатной прямой
-
Противоположные числа.
 Модуль числа. Целые и рациональные числа
Модуль числа. Целые и рациональные числа
-
Сравнение рациональных чисел
-
Сложение рациональных чисел с помощью координатной прямой
-
Алгебраическая сумма. Свойства
-
Алгебраическая сумма рациональных чисел с одинаковыми знаками
-
Алгебраическая сумма рациональных чисел с разными знаками
-
Умножение и деление рациональных чисел
-
Умножение и деление обыкновенных дробей
-
Дробные выражения
-
Координаты.
 Координатная плоскость, координаты точки
Координатная плоскость, координаты точки
-
-
-
Отношение двух чисел
-
Пропорция. Основное свойство пропорции
-
Прямая и обратная пропорциональность
-
Решение задач с помощью пропорций
-
Разные задачи
-
-
-
Упрощение выражений, раскрытие скобок
-
Решение линейных уравнений
-
Этапы решения линейных уравнений
-
-
-
Начальные понятия и факты курса геометрии
-
Параллельность прямых
-
Центральная и осевая симметрия
-
Окружность и круг.
 Число Пи. Длина окружности. Площадь круга
Число Пи. Длина окружности. Площадь круга
-
Наглядные представления о шаре, сфере. Формулы площади поверхности сферы и объёма шара
-
-
Коллекция интерактивных моделей
Тема дроби 5 класс, суть дроби, сложение, вычитание, деление, умножение, примеры с объяснениями.
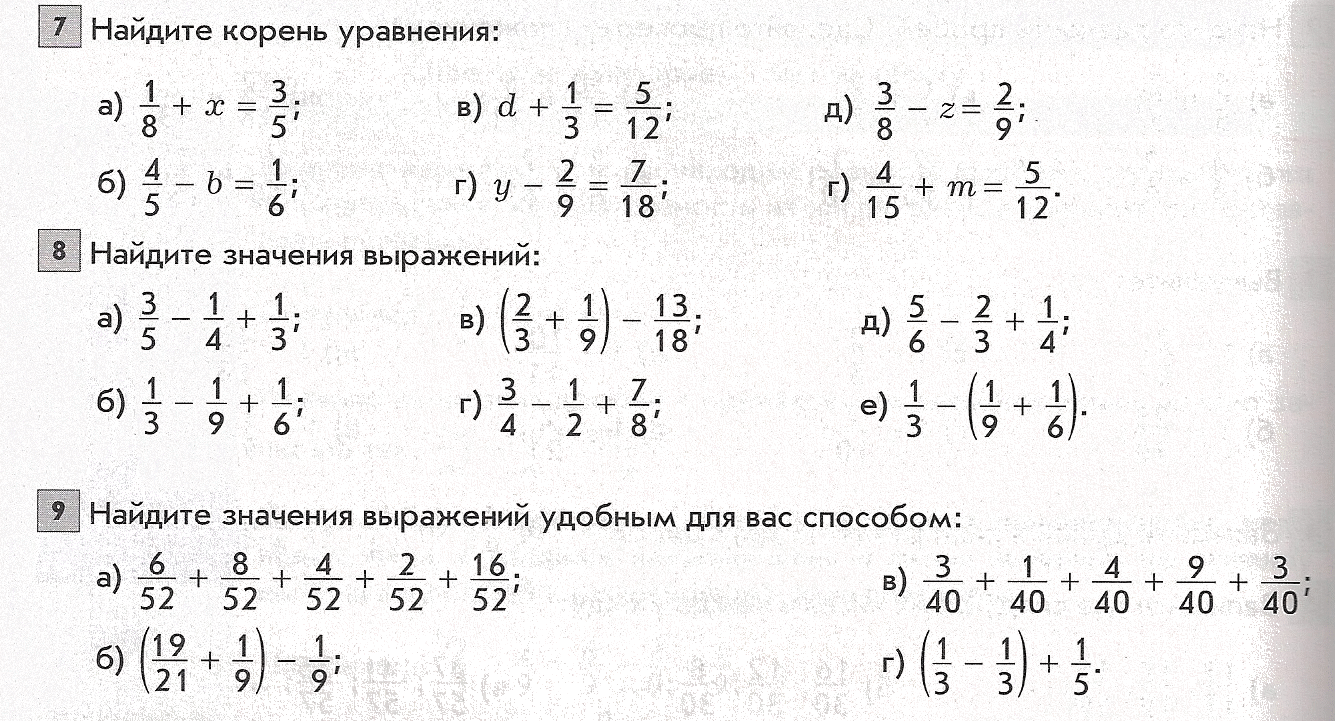 Как понять дроби
Как понять дробиПрактически каждый пятиклассник после первого знакомства с обыкновенными дробями находится в небольшом шоке. Мало того, что нужно еще понять суть дроби, так с ними еще придется выполнять арифметические действия. После этого маленькие ученики будут систематически допрашивать своего учителя, разузнавать когда же эти дроби кончатся.
Содержание статьи
Чтобы избежать подобных ситуаций, достаточно всего лишь как можно проще объяснить детям эту нелегкую тему, а лучше в игровой форме.
Суть дроби
Перед тем, как узнать что такое дробь, ребенок должен познакомиться с понятием доля. Здесь лучше всего подойдет ассоциативный метод.
Представьте целый торт, который поделили на несколько равных частей, допустим на четыре. Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.
Доли бывают разные, потому что, целое можно поделить на совершенно разное количество частей. Чем больше долей в целом, тем они меньше, и наоборот.
Чем больше долей в целом, тем они меньше, и наоборот.
Чтобы доли можно было обозначить, придумали такое математическое понятие, как обыкновенная дробь. Дробь позволит нам записать столько долей, сколько потребуется.
Составными частями дроби являются числитель и знаменатель, которые разделены дробной чертой либо наклонной чертой. Многие дети не понимают их смысла, поэтому и суть дроби им не понятна. Дробная черта обозначает деление, здесь нет ничего сложного.
Знаменатель принято записывать снизу, под дробной чертой или справа от накл.черты. Он показывает количество долей целого. Числитель, он записывается сверху над дробной чертой или слева от накл.черты, определяет сколько долей взяли.К примеру дробь 4/7. В данном случае 7-это знаменатель, показывает, что есть всего 7 долей, а числитель 4 указывает на то, что из семи долей взяли четыре.
Основные доли и их запись в дробях:
Помимо обыкновеной, существует еще и десятичная дробь.
Действия с дробями 5 класс
В пятом классе учатся выполнять все арифметические действия с дробями.
Все действия с дробями выполняются по правилам, и надеяться на то, что не выучив правило все получится само сабой не стоит. Поэтому не стоит пренебрегать устной частью домашнего задания по математике.
Мы уже поняли, что запись десятичной и обыкновенной дроби различны, следовательно и арифметические действия будут выполняться по-разному. Действия с обыкновенными дробями зависят от тех чисел, которые стоят в знаменателе, а в десятичной-после запятой справа.
Для дробей, у которых знаменатели одинаковые, алгоритм сложения и вычитания очень прост. Действия выполняем только с числителями.
Пример:
Для дробей с разными знаменателями нужно найти Наименьший Общий Знаменатель ( НОЗ). Это то число, которое будет делиться без остатка на все знаменатели, и будет наименьшим из таких чисел, если их несколько.
Пример:
Для сложения либо вычитания десятичных дробей, нужно записать их в столбик, запятая под запятой, и уравнить количество десятичных знаков если это требуется.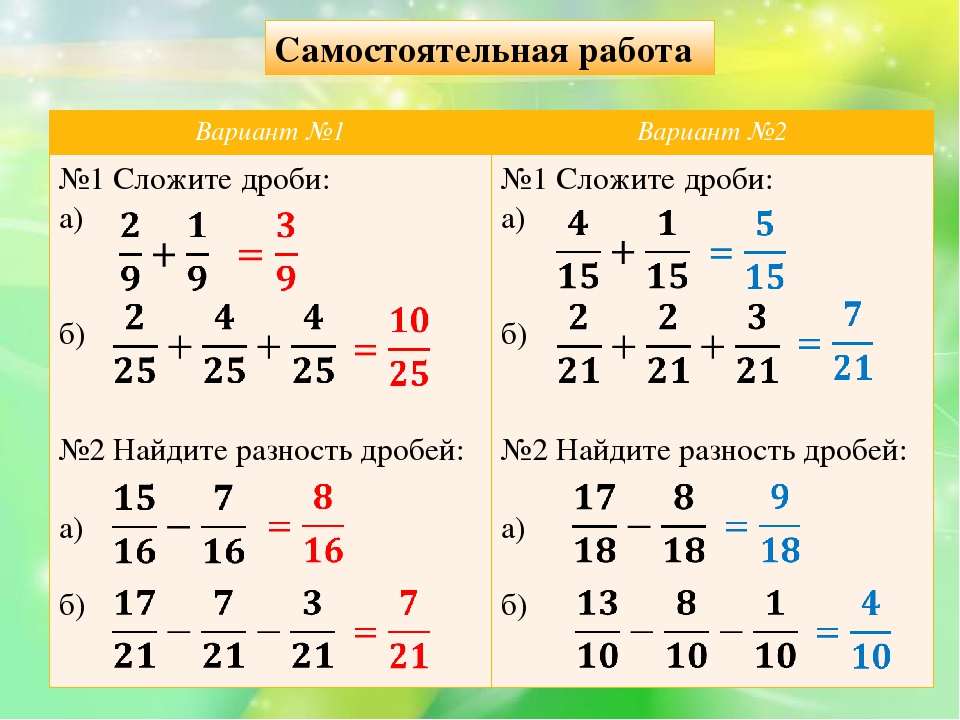
Пример:
Чтобы перемножить обыкновенные дроби просто найди произведение числителей и знаменателей. Очень простое правило.
Пример:
Деление выполняется по следующему алгоритму:
- Делимое записать без изменения
- Деление превратить в умножение
- Делитель перевернуть (записать обратную дробь делителю)
- Выполнить умножение
Пример:
Сложение дробей, объяснение
Давайте более подробно разберем, как складывать обыкновенные и десятичные дроби.
Как видно на изображении выше, у дроби одна третья и две третьих общий знаменатель три. Значит требуется сложить только числители единицу и два, а знаменатель оставить без изменения. В итоге получается сумма три третьих. Такой ответ, когда числитель и знаменатель дроби равны, можно записать как 1, так как 3:3 = 1.
Требуется найти сумму дробей две третьих и две девятых. В этом случае знаменатели различны, 3 и 9. Чтобы выполнить сложение, нужно подобрать общий. Есть очень простой способ. Выбираем наибольший знаменатель, это 9. Проверяем делится ли он на 3. Так как 9:3 = 3 без остатка, следовательно 9 подходит как общий знаменатель.
Есть очень простой способ. Выбираем наибольший знаменатель, это 9. Проверяем делится ли он на 3. Так как 9:3 = 3 без остатка, следовательно 9 подходит как общий знаменатель.
Следующим шагом находим дополнительные множители для каждого числителя. Для этого общий знаменатель 9 делим поочередно на знаменатель каждой дроби, полученные числа и будут допол. множ. Для первой дроби: 9:3 = 3, дописываем к числителю первой дроби 3. Для второй дроби: 9:9 = 1, единицу можно не дописывать, так как при умножении на нее получится то же самое число.
Теперь умножаем числители на их дополнительные множители и складываем результаты. Полученная сумма дробь восемь девятых.
Сложение десятичных дробей выполняется по тому же правилу, что и сложение натуральных чисел. В столбик, разряд записывается под разрядом. Единственное отличие в том, что в десятичных дробях нужно правильно поставить запятую в результате. Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз.
Найдем сумму дробей 38, 251 и 1, 56. Чтобы было удобнее выполнять действия, мы уровняли количество десятичных знаков справа, добавив 0.
Складываем дроби не обращая внимания на запятую. А в полученной сумме просто опускаем запятую вниз. Ответ: 39, 811.
Вычитание дробей, объяснение
Чтобы найти разность дробей две третьих и одна третья, нужно вычислить разность числителей 2-1 = 1, а знаменатель оставить без изменения. В ответе получаем разность одну третью.Найдем разность дробей пять шестых и семь десятых. Находим общий знаменатель. Используем способ подбора, из 6 и 10 наибольший 10. Проверяем: 10 : 6 без остатка не делится. Добавляем еще 10, получается 20:6, тоже без остатка не делится. Снова увеличиваем на 10, получили 30:6 = 5. Общий знаменатель 30. Так же НОЗ можно найти по таблице умножения.
Находим дополнительные множители. 30:6 = 5 — для первой дроби. 30:10 = 3 — для второй. Перемножаем числители и их доп.множ. Получаем уменьшаемое 25/30 и вычитаемое 21/30. Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.
Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.
В результате получилась разность 4/30. Дробь сократимая. Разделим ее на 2. В ответе 2/15.
Деление десятичных дробей 5 класс
В этой теме рассматривается два варианта действий:
Умножение десятичных дробей 5 класс
Вспомните, как вы умножаете натуральные числа, точно таким же способом и находят произведение десятичных дробей. Сначала разберемся, как умножить десятичную дробь на натуральное число. Для этого:
При умножении десятичной дроби на десятичную, действуем точно также.Смешанные дроби 5 класс
Пятиклашки любят называть такие дроби не смешанные, а <<смешные>>, наверное так легче запомнить. Смешанные дроби называются так от того, что они получились путем соединения целого натурального числа и обыкновенной дроби.
Смешанная дробь состоит из целой и дробной части.
При чтении таких дробей сначала называют целую часть, затем дробную: одна целая две третьих, две целых одна пятая, три целых две пятых, четыре целых три четвертых.
Как же они получаются, эти смешанные дроби? Все довольно просто. Когда мы получаем в ответе неправильную дробь ( дробь у которой числитель больше знаменателя), мы ее должны всегда переводить в смешанную. Достаточно разделить числитель на знаменатель. Это действие называется выделением целой части:
Перевести смешанную дробь обратно в неправильную тоже несложно:
Примеры с десятичными дробями 5 класс с объяснением
Много вопросов у детей вызывают примеры на несколько действий. Разберем пару таких примеров.
Пример 1.
( 0,4 · 8,25 — 2,025 ) : 0,5 =
Первым действием находим произведение чисел 8,25 и 0,4. Выполняем умножение по правилу. В ответе отсчитываем справа налево три знака и ставим запятую.Второе действие находится там же в скобках, это разность. От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой.
Третье действие-деление. Полученную разность во втором действии делим на 0,5. Запятая переносится на один знак. Результат 2,55.
Результат 2,55.
Ответ: 2,55.
Пример 2.
( 0, 93 + 0, 07 ) : ( 0, 93 — 0, 805 ) =
Первое действие сумма в скобках.Складываем в столбик, помним, что запятая под запятой. Получаем ответ 1,00.
Второе действие разность из второй скобки. Так как у уменьшаемого меньше знаков после запятой, чем у вычитаемого, добавляем недостающий. Результат вычитания 0 ,125.
Третьим действие делим сумму на разность. Запятая переносится на три знака. Получилось деление 1000 на 125.
Ответ: 8.
Примеры с обыкновенными дробями с разными знаменателями 5 класс с объяснением
В первом примере находим сумму дробей 5/8 и 3/7. Общим знаменателем будет число 56. Находим дополнительные множ., разделим 56:8 = 7 и 56:7 = 8. Дописываем их к первой и второй дроби соответственно. Перемножаем числители и их множители, получаем сумму дробей 35/56 и 24/56. Получили сумму 59/56. Дробь неправильная, переводим ее в смешанное число.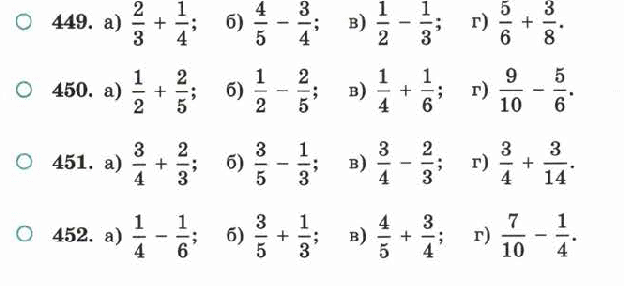 Остальные примеры решаются аналогично.
Остальные примеры решаются аналогично.
Примеры с дробями 5 класс для тренировки
Для удобства переведите смешанные дроби в неправильные и выполняйте действия.
Как научить ребенка легко решать дроби с помощью лего
С помощью такого конструктора можно не только хорошо развивать воображение ребенка, но и объяснить наглядно в игровой форме, что такое доля и дробь.
На картинке ниже показано, что одна часть с восемью кружками это целое. Значит, взяв пазл с четырьмя кружками, получается половина, или 1/2. На картинке наглядно показано, как решать примеры с лего, если считать кружки на деталях.
Вы можете построить башенки из определенного количества частей и подписать каждую из них, как на картинке ниже. Например возьмем башенку из семи частей. Каждая часть зеленого конструктора будет 1/7. Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.
Чтобы получать пятерки по математике не забывайте учить правила и отрабатывать их на практике.
Электронный справочник по математике для школьников арифметика сложение вычитание умножение деление дробей действия со смешанными числами
Действия с дробями и смешанными числами
Содержание
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями получается дробь с тем же знаменателем, а её числитель равен сумме (разности) числителей рассматриваемых дробей.
Например,
При сложении (вычитании) дробей с разными знаменателями предварительно нужно привести их к общему знаменателю. Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным.
Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным.
Например,
(в уголках сверху здесь обозначены дополнительные множители).
Умножение и деление дробей
При умножении дробей получается дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Например,
Деление дробей осуществляется в соответствии со следующим правилом:
Иногда это правило формулируют так: для того, чтобы разделить первую дробь на вторую, нужно первую дробь умножить на перевернутую вторую.
В частности,
Действия со смешанными числами
Для того, чтобы избежать ошибок при выполнении арифметических действий со смешанными числами, рекомендуется сначала обратить смешанные числа в неправильные дроби, затем выполнить нужные арифметические действия, а потом, если это требуется, обратить результат в смешанное число.
ПРИМЕР. Найти сумму, разность, произведение и частное смешанных чисел
и
РЕШЕНИЕ. Преобразуем эти числа в неправильные дроби:
Далее получаем:
Действия с дробями: правила, примеры, решения
Данная статья рассматривает действия над дробями. Будут сформированы и обоснованы правила сложения, вычитания, умножения, деления или возведения в степень дробей вида AB, где A и B могут быть числами, числовыми выражениями или выражениями с переменными. В заключении будут рассмотрены примеры решения с подробным описанием.
Правила выполнения действий с числовыми дробями общего вида
Числовые дроби общего вида имеют числитель и знаменатель, в которых имеются натуральные числа или числовые выражения. Если рассмотреть такие дроби, как 35, 2,84, 1+2·34·(5-2), 34+782,3-0,8, 12·2, π1-23+π, 20,5ln 3, то видно, что числитель и знаменатель может иметь не только числа, но и выражения различного плана.
Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:
- При вычитании дробей с одинаковыми знаменателями складываются только числители, а знаменатель остается прежним, а именно: ad±cd=a±cd, значения a, c и d≠0 являются некоторыми числами или числовыми выражениями.
- При сложении или вычитании дроби при разных знаменателях, необходимо произвести приведение к общему, после чего произвести сложение или вычитание полученных дробей с одинаковыми показателями. Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.
- При умножении дробей выполняется действие с числителями, после чего со знаменателями, тогда получим ab·cd=a·cb·d, где a, b≠0, c, d≠0 выступают в роли действительных чисел.
- При делении дроби на дробь первую умножаем на вторую обратную, то есть производим замену местами числителя и знаменателя: ab:cd=ab·dc.

Обоснование правил
Определение 2Существуют следующие математические моменты, на которые следует опираться при вычислении:
- дробная черта означает знак деления;
- деление на число рассматривается как умножение на его обратное значение;
- применение свойства действий с действительными числами;
- применение основного свойства дроби и числовых неравенств.
С их помощью можно производить преобразования вида:
ad±cd=a·d-1±c·d-1=a±c·d-1=a±cd;ab±cd=a·pb·p±c·rd·r=a·ps±c·es=a·p±c·rs;ab·cd=a·db·d·b·cb·d=a·d·a·d-1·b·c·b·d-1==a·d·b·c·b·d-1·b·d-1=a·d·b·cb·d·b·d-1==(a·c)·(b·d)-1=a·cb·d
Примеры
В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.
Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.
Пример 1Даны дроби 82,7 и 12,7, то по правилу необходимо числитель сложить, а знаменатель переписать.
Решение
Тогда получаем дробь вида 8+12,7. После выполнения сложения получаем дробь вида 8+12,7=92,7=9027=313. Значит, 82,7+12,7=8+12,7=92,7=9027=313.
Ответ: 82,7+12,7=313
Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:
82,7+12,7=8027+1027=9027=313
Пример 2Произведем вычитание из 1-23·log23·log25+1 дроби вида 233·log23·log25+1.
Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что
1-23·log23·log25+1-233·log23·log25+1=1-2-233·log23·log25+1
Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.
Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.
Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.
Пример 3Рассмотрим на примере сложения дробей 235+1 и 12.
Решение
В данном случае общим знаменателем выступает произведение знаменателей. Тогда получаем, что 2·35+1. Тогда при выставлении дополнительных множителей имеем, что к первой дроби он равен 2, а ко второй 35+1. После перемножения дроби приводятся к виду 42·35+1. Общее приведение 12 будет иметь вид 35+12·35+1. Полученные дробные выражения складываем и получаем, что
235+1+12=2·22·35+1+1·35+12·35+1==42·35+1+35+12·35+1=4+35+12·35+1=5+352·35+1
Ответ: 235+1+12=5+352·35+1
Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет. В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.
Пример 4Рассмотрим на примере 16·215 и 14·235, когда их произведение будет равно 6·215·4·235=24·245. Тогда в качестве общего знаменателя берем 12·235.
Тогда в качестве общего знаменателя берем 12·235.
Рассмотрим примеры умножений дробей общего вида.
Пример 5Для этого необходимо произвести умножение 2+16 и 2·53·2+1.
Решение
Следую правилу, необходимо переписать и в виде знаменателя написать произведение числителей. Получаем, что 2+16·2·53·2+12+1·2·56·3·2+1. Когда дробь будет умножена, можно производить сокращения для ее упрощения. Тогда 5·332+1:1093=5·332+1·9310.
Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:
5·332+1:1093=5·332+1·9310
После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что
5·332+1:1093=5·33·9310·2+1=5·210·2+1=32·2+1==3·2-12·2+1·2-1=3·2-12·22-12=3·2-12
Ответ: 5·332+1:1093=3·2-12
Данный пункт применим, когда число или числовое выражение может быть представлено в виде дроби, имеющую знаменатель, равный 1, тогда и действие с такой дробью рассматривается отдельным пунктом. Например, выражение 16·74-1·3 видно, что корень из 3 может быть заменен другим 31 выражением. Тогда эта запись будет выглядеть как умножение двух дробей вида 16·74-1·3=16·74-1·31.
Например, выражение 16·74-1·3 видно, что корень из 3 может быть заменен другим 31 выражением. Тогда эта запись будет выглядеть как умножение двух дробей вида 16·74-1·3=16·74-1·31.
Выполнение действие с дробями, содержащими переменные
Правила, рассмотренные в первой статье , применимы для действий с дробями, содержащими переменные. Рассмотрим правило вычитания, когда знаменатели одинаковые.
Необходимо доказать, что A, C и D (D не равное нулю) могут быть любыми выражениями, причем равенство AD±CD=A±CD равноценно с его областью допустимых значений.
Необходимо взять набор переменных ОДЗ. Тогда А, С, D должны принимать соответственные значения a0, c0 и d0. Подстановка вида AD±CD приводит разность вида a0d0±c0d0, где по правилу сложения получаем формулу вида a0±c0d0. Если подставить выражение A±CD, тогда получаем ту же дробь вида a0±c0d0. Отсюда делаем вывод, что выбранное значение, удовлетворяющее ОДЗ, A±CD и AD±CD считаются равными.
При любом значении переменных данные выражения будут равны, то есть их называют тождественно равными. Значит это выражение считается доказываемым равенством вида AD±CD=A±CD.
Значит это выражение считается доказываемым равенством вида AD±CD=A±CD.
Примеры сложения и вычитания дробей с переменными
Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это незаметно, так как необходимо выполнять некоторые преобразования. Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 6Вычислить:1) x2+1x+x-2-5-xx+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2), x-1x-1+xx+1.
Решение
- Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x2+1x+x-2-5-xx+x-2=x2+1-5-xx+x-2.
 После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2 - Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель:lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg2x+4+4x·(lg x+2)
Сложение было выполнено. Видно, что можно произвести сокращение дроби. Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (lg x+2)2из формул сокращенного умножения. Тогда получаем, что
lg2x+4+2·lg xx·(lg x+2)=(lg x+2)2x·(lg x+2)=lg x+2x - Заданные дроби вида x-1x-1+xx+1 с разными знаменателями. После преобразования можно перейти к сложению.
Рассмотрим двоякий способ решения.
Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида
x-1x-1=x-1(x-1)·x+1=1x+1
Значит, x-1x-1+xx+1=1x+1+xx+1=1+xx+1.
В таком случае необходимо избавляться от иррациональности в знаменателе.
Получим:
1+xx+1=1+x·x-1x+1·x-1=x-1+x·x-xx-1
Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x-1. Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда
x-1x-1+xx+1=x-1x-1+x·x-1x+1·x-1==x-1x-1+x·x-xx-1=x-1+x·x-xx-1
Ответ: 1) x2+1x+x-2-5-xx+x-2=x2+x-4x+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg x+2x, 3)x-1x-1+xx+1=x-1+x·x-xx-1.
В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей с добавлением дополниетльных множителей к числителям.
Пример 7Вычислить значения дробей: 1) x3+1×7+2·2, 2) x+1x·ln2(x+1)·(2x-4)-sin xx5·ln(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x
Решение
- Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3·x7+2·2, тогда к первой дроби x7+2·2 выбирают как дополнительный множитель, а 3 ко второй.
 При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2 - Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться произведение вида x5·ln2x+1·2x-4. Отсюда x4 является дополнительным множителем к первой дроби, а ln(x+1) ко второй. После чего производим вычитание и получаем, что:
x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x+1·x4x5·ln2(x+1)·2x-4-sin x·lnx+1×5·ln2(x+1)·(2x-4)==x+1·x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)=x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4) - Данный пример имеет смысл при работе со знаменателями дробями. Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
После чего получаем, что
1cos2x-x+1cos2x+2·cos x·x+x==1cos x-x·cos x+x+1cos x+x2==cos x+xcos x-x·cos x+x2+cos x-xcos x-x·cos x+x2==cos x+x+cos x-xcos x-x·cos x+x2=2·cos xcos x-x·cos x+x2
Ответ:
1) x3+1×7+2·2=x·x7+2·2·x+33·x7+2·2, 2) x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x=2·cos xcos x-x·cos x+x2.
Примеры умножения дробей с переменными
При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.
Пример 8Произвести умножение дробей x+2·xx2·ln x2·ln x+1 и 3·x213·x+1-2sin2·x-x.
Решение
Необходимо выполнить умножение. Получаем, что
x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)==x-2·x·3·x213·x+1-2×2·ln x2·ln x+1·sin (2·x-x)
Число 3 переносится на первое место для удобства подсчетов, причем можно произвести сокращение дроби на x2, тогда получим выражение вида
3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x)
Ответ: x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)=3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x).
Деление
Деление у дробей аналогично умножению, так как первую дробь умножают на вторую обратную. Если взять к примеру дробь x+2·xx2·ln x2·ln x+1 и разделить на 3·x213·x+1-2sin2·x-x, тогда это можно записать таким образом, как
x+2·xx2·ln x2·ln x+1:3·x213·x+1-2sin(2·x-x), после чего заменить произведением вида x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)
Возведение в степень
Перейдем к рассмотрению действия с дробями общего вида с возведением в степень. Если имеется степень с натуральным показателем, тогда действие рассматривают как умножение одинаковых дробей. Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:
Если имеется степень с натуральным показателем, тогда действие рассматривают как умножение одинаковых дробей. Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:
x0,7-π·ln3x-2-5x+12,5==x0,7-π·ln3x-2-52,5x+12,5
Порядок выполнения действий с дробями
Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.
Пример 9Вычислить 1-xcos x-1cos x·1+1x.
Решение
Так как имеем одинаковый знаменатель, то 1-xcos x и 1cos x, но производить вычитания по правилу нельзя, сначала выполняются действия в скобках, после чего умножение, а потом сложение. Тогда при вычислении получаем, что
Тогда при вычислении получаем, что
1+1x=11+1x=xx+1x=x+1x
При подстановке выражения в исходное получаем, что 1-xcos x-1cos x·x+1x. При умножении дробей имеем: 1cos x·x+1x=x+1cos x·x. Произведя все подстановки, получим 1-xcos x-x+1cos x·x. Теперь необходимо работать с дробями, которые имеют разные знаменатели. Получим:
x·1-xcos x·x-x+1cos x·x=x·1-x-1+xcos x·x==x-x-x-1cos x·x=-x+1cos x·x
Ответ: 1-xcos x-1cos x·1+1x=-x+1cos x·x.
Сложение, вычитание, умножение и деление десятичных дробей
Сложение и вычитание десятичных дробей аналогично сложению и вычитанию натуральных чисел, но с определенными условиями.
Правило. Сложение и вычитание десятичных дробей производится по разрядам целой и дробной части как натуральных чисел.
При письменном сложении и вычитании десятичных дробей запятая, отделяющая целую часть от дробной, должна находиться у слагаемых и суммы или у уменьшаемого, вычитаемого и разности в одном столбце (запятая под запятой от записи условия до конца вычисления).
Примеры.
Сложение и вычитание десятичных дробей в строку:
243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651
843,217 — 700,628 = (800 — 700) + 40 + 3 + (0,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + (1,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + (0,11 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589
Сложение и вычитание десятичных дробей в столбик:
Сложение десятичных дробей требует верхней дополнительной строки для записи чисел, когда сумма разряда переходит через десяток. Вычитание десятичных дробей требует верхней дополнительной строки для того, чтобы отметить разряд, в котором одалживается 1.
Если справа от слагаемого или уменьшаемого не хватает разрядов дробной части, то справа в дробной части можно дописывать столько нулей (увеличивать разрядность дробной части), сколько разрядов в другом слагаемом или уменьшаемом.
Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма разрядов множителей — это количество разрядов после запятой у множителей, вместе взятых).
Пример:
При умножении десятичных дробей в столбик первая справа значащая цифра подписывается под первой справа значащей цифрой, как и в натуральных числах:
Запись умножения десятичных дробей в столбик:
Запись деления десятичных дробей в столбик:
Подчеркнутые знаки — это знаки, за которые переносится запятая, потому что делитель должен быть целым числом.
Правило. При делении дробей делитель десятичной дроби увеличивается на столько разрядов, сколько разрядов в дробной его части. Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.
При делении дробей делитель десятичной дроби увеличивается на столько разрядов, сколько разрядов в дробной его части. Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.
Для десятичных дробей, как и для натуральных чисел, сохраняется правило: на ноль десятичную дробь делить нельзя!
Урок 65. деление дробей — Математика — 5 класс
Математика
5 класс
Урок № 65
Деление дробей
Перечень рассматриваемых вопросов:
– правило деления обыкновенных дробей;
– деление дроби на натуральное число.
Тезаурус
Частное двух дробей – это дробь, которая при умножении на делитель даёт делимое.
Периметр – сумма длин всех сторон плоской геометрической фигуры.
Обязательная литература:
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС. / С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017, стр. 272.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС. / С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017, стр. 272.
Теоретический материал для самостоятельного изучения
Сегодня мы с вами познакомимся с последним, четвёртым арифметическим действием над обыкновенными дробями – делением.
Частным двух дробей называют дробь, которая при умножении на делитель даёт делимое.
Проверим правило, умножив частное на делитель:
Действительно, если умножить частное на делитель, мы получим делимое.
Например, две третьих разделим на четыре пятых. Заменим деление умножением, а делитель четыре пятых на обратную дробь – пять четвёртых. Сократим два и четыре, получим дробь пять шестых.
Пять седьмых разделим на семь пятых. Умножим делимое на дробь, обратную делителю. Получим двадцать пять сорок девятых.
Решим задачу.
Кусок ткани длиной 4 метра разделили на несколько равных частей длиной метра. Сколько таких частей получилось?
Сколько таких частей получилось?
Решение. Итак, представим натуральное число четыре в виде обыкновенной дроби – четыре первых, и применим правило деления двух обыкновенных дробей. Чтобы узнать, сколько частей ткани получилось, разделим четыре метра ткани на одну часть длиной метра.
Ответ: 32 части ткани.
Чтобы разделить дробь на натуральное число, можно её знаменатель умножить на это число.
Например, разделим шесть одиннадцатых на пять. Применяя правило деления дроби на натуральное число, получаем, что знаменатель, равный одиннадцати, нужно умножить на натуральное число пять. Получаем:
Отметим, что число 0, делённое на любую отличную от нуля дробь, даёт 0.
Делить на нуль нельзя!
Для любых двух натуральных чисел p и q всегда есть их частное – дробь .
Черту в записи дроби можно рассматривать как знак деления числителя на знаменатель. Поэтому иногда говорят не «три пятых», а «три, делённое на пять»:
Итак, ещё раз повторим алгоритм деления обыкновенных дробей:
1) заменяем деление умножением;
2) «переворачиваем» делитель;
3) применяем правило умножения обыкновенных дробей.
Разбор решения заданий тренировочного модуля
№ 1. Вычислите значение выражения .
Сначала определим порядок действий:
- вычитание, т. к. оно находится в скобках;
- деление;
- умножение;
- сложение.
Ответ: .
№ 2. Найдите частное
Решение: разделим дроби, применив правило деления дробей и сократим полученный результат. Получаем:
Ответ: .
Операции с дробями — математика 5-го класса
Сложение дробейДроби — это части целого. Сложив две дроби, вы получите целое. Например, если у вас есть половина файла cookie и одна треть файла cookie, вы приближаетесь к созданию целого файла cookie. Чтобы сложить эти дроби вместе, каждую дробь необходимо разбить на одинаковое количество частей. Ниже приведены некоторые стратегии, которые помогут вам сложить дроби.
Стратегия: Площадь или прямоугольная модель для отображения сложения дробей
Шаг 1: Нарисуйте каждую дробь (одну с горизонтальным разделением, а другую с вертикальным разделением)
Шаг 2: Нарисуйте пунктирные линии в каждой дроби так, чтобы у них был общий знаменатель.
Шаг 3: Подсчитайте все закрашенные части и начертите сумму дробей
Пример 1:
Пример 2:
Стратегия: Найти общее Знаменатель и сложите
Шаг 1. Посмотрите на дроби
Шаг 2. Подумайте, как сделать так, чтобы каждая дробь имела общий знаменатель (Общий коэффициент)
Шаг 3: Перепишите дроби в их эквивалентную дробь с теми же знаменателями
Шаг 4: Найдите сумму дробей
Шаг 5: Запишите сумму дроби в младших числах
Сложение дробей со смешанными числами
Стратегия 1:
Шаг 1: Сначала сложите целые числа
Шаг 2: Затем сложите дробные части (используйте приведенные выше стратегии)
Шаг 3: Посмотрите на сумму и при необходимости перепишите дробь
Мы знаем, что это также эквивалентно 4 и 1 / 2
Вот еще один пример:
Стратегия: Используйте неправильные дроби для сложения дробных частей
Шаг 1: Преобразуйте их в неправильные дроби
Шаг 2: Найдите общие знаменатели
Шаг 3 : Найдите сумму дробей
Шаг 4: Выложите сумму дробей в младших членах
Затем не забудьте преобразовать неправильное число в смешанное число:
Вычитание дробей
Дроби являются частями весь. При вычитании дробей вы убираете часть дроби. Например, если у вас есть половина файла cookie, а вы передали треть файла cookie, у вас останется меньше половины того, что у вас есть. У вас останется одна шестая часть оставшегося файла cookie.
При вычитании дробей вы убираете часть дроби. Например, если у вас есть половина файла cookie, а вы передали треть файла cookie, у вас останется меньше половины того, что у вас есть. У вас останется одна шестая часть оставшегося файла cookie.
Для решения задач вычитания можно использовать многие из тех же стратегий, что и для задач сложения.
Умножение дробей
Когда мы умножаем дроби, мы думаем о слове «Of».Например:
Что такое 1/2 от 20 или 1/4 от 100. Мы часто можем думать, что, умножая дроби, мы делим их на целое число.
Давайте посмотрим на некоторые закономерности:
Когда оба фактора меньше, чем значение 1, произведение меньше, чем оба фактора.
Примеры:
1/2 x 1/4 —— Подумайте: 1/4 от 1/2 или 1/2 от 1/4
Таким образом, ответ 1/8 (продукт меньше, чем 1/2 и 1/4)
Вот еще один:
2/7 x 3/5 —— это как думать, что мне нужно 3 / 5 из 2/7 — 6/35 меньше обоих факторов.
Глядя на модели, мы видим, что есть шаги, которые можно предпринять, чтобы добраться до продукта.
* Умножить числители
* Умножить знаменатели
* Упростить дробь до наименьших членов (преобразовать в смешанное число)
Когда один множитель больше единицы, а один меньше единицы, мы получаем произведение, которое находится между обоими этих факторов.
Примеры:
1 и 2/3 x 1/2
В этом случае нам нужно подумать.(То же самое, если мы думаем, что 23 x 2 = (20 x 2) + (3 x 2)
1 x 1/2 = 1/2
2/3 x 1/2 = (1/2 из 2 / 3) равно 2/6 или 1/3
1/2 + 1/3 = 3/6 + 2/6 = 5/6
Мы знаем, что 5/6 больше 1/2, но меньше 1 и 2/3
Когда оба фактора больше одного, наш продукт будет больше, чем оба этих фактора.
Пример:
2 1/2 x 1 2/3 (два смешанные числа)
На данный момент имеет смысл сделать их неправильными дробями.
2 1/2 = 5/2
1 2/3 = 5/3
5/2 x 5/3 = 25/6 = 4 и 1/6 (произведение больше обоих факторов)
Когда один из факторов равен 1, тогда продукт всегда будет другим фактором. (ИДЕНТИЧНОСТЬ СВОЙСТВА УМНОЖЕНИЯ)
2/3 x 1 = 2/3
242/2313 x 1 = ?????
Когда один из факторов равен 0, продукт всегда будет НУЛЬ (НУЛЕВОЙ СВОЙСТВА УМНОЖЕНИЯ)
2/3 x 0 = 0
1/5 x 0 = 0
Введение в арифметические операции | Безграничная алгебра
Основные операции
Основными арифметическими операциями с действительными числами являются сложение, вычитание, умножение и деление.
Цели обучения
Вычисление суммы, разницы, произведения и частного положительных целых чисел
Ключевые выводы
Ключевые моменты
- Основными арифметическими операциями с действительными числами являются сложение, вычитание, умножение и деление.

- Основными арифметическими свойствами являются коммутативные, ассоциативные и дистрибутивные свойства.
Ключевые термины
- ассоциативный : ссылка на математическую операцию, которая дает один и тот же результат независимо от группировки элементов.
- коммутативный : ссылка на двоичную операцию, в которой изменение порядка операндов не меняет результат (например, сложение и умножение).
- произведение : результат умножения двух величин.
- частное : результат деления одного количества на другое.
- сумма : результат сложения двух величин.
- разница : результат вычитания одной величины из другой.
Четыре арифметических операции
Дополнение
Сложение — это самая основная операция в арифметике. В простейшей форме сложение объединяет две величины в одну, или , сумма . Например, предположим, что у вас есть группа из 2 ящиков и еще одна группа из 3 ящиков. Если вы объедините обе группы вместе, у вас получится одна группа из 5 ящиков. Чтобы представить эту идею в математических терминах:
Например, предположим, что у вас есть группа из 2 ящиков и еще одна группа из 3 ящиков. Если вы объедините обе группы вместе, у вас получится одна группа из 5 ящиков. Чтобы представить эту идею в математических терминах:
[латекс] 2 + 3 = 5 [/ латекс]
Вычитание
Вычитание противоположно сложению.Вместо того, чтобы складывать количества вместе, мы удаляем одно количество из другого, чтобы найти разницу в между ними. Продолжая предыдущий пример, предположим, что вы начинаете с группы из 5 блоков. Если вы затем удалите 3 поля из этой группы, у вас останутся 2 поля. Математически:
[латекс] 5-3 = 2 [/ латекс]
Умножение
Умножение также объединяет несколько величин в одну величину, которая называется продуктом . Фактически, умножение можно рассматривать как объединение множества сложений.В частности, произведение [latex] x [/ latex] и [latex] y [/ latex] является результатом сложения [latex] x [/ latex] вместе [latex] y [/ latex] раз. Например, один из способов подсчета четырех групп по две коробки — сложить группы вместе:
Например, один из способов подсчета четырех групп по две коробки — сложить группы вместе:
[латекс] 2 + 2 + 2 + 2 = 8 [/ латекс]
Однако есть еще один способ посчитать коробки — это умножить количество:
[латекс] 2 \ cdot 4 = 8 [/ латекс]
Обратите внимание, что оба метода дают один и тот же результат — 8, но во многих случаях, особенно когда у вас есть большие количества или много групп, умножение может быть намного быстрее.
Дивизия
Деление — это величина, обратная умножению. Вместо того, чтобы умножать количества вместе, чтобы получить большее значение, вы разделяете количество на меньшее значение, называемое частным . Опять же, возвращаясь к примеру с блоком, разделение группы из 8 блоков на 4 равные группы приводит к получению 4 групп по 2 блока:
[латекс] 8 \ div 4 = 2 [/ латекс]
Основные арифметические свойства
Коммутационная собственность
Свойство коммутативности описывает уравнения, в которых порядок чисел не влияет на результат. Сложение и умножение — это коммутативные операции:
Сложение и умножение — это коммутативные операции:
- [латекс] 2 + 3 = 3 + 2 = 5 [/ латекс]
- [латекс] 5 \ cdot 2 = 2 \ cdot 5 = 10 [/ латекс]
Однако вычитание и деление не коммутативны.
Ассоциативная собственность
Ассоциативное свойство описывает уравнения, в которых группировка чисел не влияет на результат. Как и в случае с коммутативностью, сложение и умножение являются ассоциативными операциями:
- [латекс] (2 + 3) + 6 = 2 + (3 + 6) = 11 [/ латекс]
- [латекс] (4 \ cdot 1) \ cdot 2 = 4 \ cdot (1 \ cdot 2) = 8 [/ латекс]
Еще раз, вычитание и деление не ассоциативны.
Распределительная собственность
Свойство распределения можно использовать, когда сумма двух величин затем умножается на третье количество.
- [латекс] (2 + 4) \ cdot 3 = 2 \ cdot 3 + 4 \ cdot 3 = 18 [/ латекс]
Отрицательные числа
Арифметические операции могут выполняться с отрицательными числами в соответствии с определенными правилами.
Цели обучения
Вычисление суммы, разницы, произведения и частного отрицательных целых чисел
Ключевые выводы
Ключевые моменты
- Сложение двух отрицательных чисел дает отрицательное значение; сложение положительного и отрицательного числа дает число, имеющее тот же знак, что и число большей величины.
- Вычитание положительного числа дает тот же результат, что и добавление отрицательного числа равной величины, а вычитание отрицательного числа дает тот же результат, что и добавление положительного числа.
- Произведение одного положительного числа и одного отрицательного числа отрицательно, а произведение двух отрицательных чисел положительно.
- Частное одного положительного числа и одного отрицательного числа отрицательно, а частное двух отрицательных чисел положительно.
Четыре операции
Дополнение
Сложение двух отрицательных чисел очень похоже на сложение двух положительных чисел. Например:
Например:
[латекс] (- 3) + (−5) = −8 [/ латекс]
Основополагающий принцип заключается в том, что два долга — отрицательные числа — могут быть объединены в один долг большей величины.
При сложении положительных и отрицательных чисел другой способ записать отрицательные числа — вычесть положительные величины. Например:
[латекс] 8 + (−3) = 8 — 3 = 5 [/ латекс]
Здесь кредит 8 сочетается с задолженностью 3, что дает общий кредит 5.Однако, если отрицательное число имеет большую величину, результат будет отрицательным:
[латекс] (- 8) + 3 = 3 — 8 = −5 [/ латекс]
Аналогично:
[латекс] (- 2) + 7 = 7 — 2 = 5 [/ латекс]
Здесь долг 2 сочетается с кредитом 7. Кредит имеет большую величину, чем долг, поэтому результат положительный. Но если кредит меньше долга, результат будет отрицательным:
[латекс] 2 + (−7) = 2-7 = −5 [/ латекс]
Вычитание
Вычитание положительных чисел друг из друга может дать отрицательный ответ. Например, вычитая 8 из 5:
Например, вычитая 8 из 5:
[латекс] 5-8 = −3 [/ латекс]
Вычитание положительного числа обычно аналогично сложению отрицательного числа. То есть:
[латекс] 5 — 8 = 5 + (−8) = −3 [/ латекс]
и
[латекс] (- 3) — 5 = (−3) + (−5) = −8 [/ латекс]
Аналогично, при вычитании отрицательного числа дает тот же результат, что и при добавлении положительного числа из этого числа. Идея здесь в том, что , потеряв долг, — это то же самое, что получит кредит.Следовательно:
[латекс] 3 — (−5) = 3 + 5 = 8 [/ латекс]
и
[латекс] (- 5) — (−8) = (−5) + 8 = 3 [/ латекс]
Умножение
При умножении положительных и отрицательных чисел знак произведения определяется по следующим правилам:
- Произведение двух положительных чисел положительно. Произведение одного положительного числа и одного отрицательного числа отрицательно.
- Произведение двух отрицательных чисел положительно.

Например:
[латекс] (- 2) × 3 = −6 [/ латекс]
Это просто потому, что сложение −2 три раза дает −6:
[латекс] (- 2) × 3 = (−2) + (−2) + (−2) = −6 [/ латекс]
Однако
[латекс] (- 2) × (−3) = 6 [/ латекс]
Снова идея заключается в том, что потеря долга — это то же самое, что и получение кредита. В этом случае потерять два долга по три в каждом — это то же самое, что получить кредит в шесть раз:
[латекс] \ left (−2 \ text {долги} \ right) \ times \ left (−3 \ text {each} \ right) = +6 \ text {кредит} [/ latex]
Дивизия
Знаковые правила деления такие же, как и для умножения.
- Разделение двух положительных чисел дает положительное число.
- Разделение одного положительного числа и одного отрицательного числа дает отрицательное число.
- Разделение двух отрицательных чисел дает положительное число.
Если у делимого и делителя один и тот же знак, то есть результат всегда положительный. Например:
Например:
[латекс] 8 ÷ (−2) = −4 [/ латекс]
и
[латекс] (- 8) ÷ 2 = −4 [/ латекс]
но
[латекс] (- 8) ÷ (−2) = 4 [/ латекс].
Дополнительные соображения
Основные свойства сложения (коммутативность, ассоциативность и дистрибутивность) также применимы к отрицательным числам. Например, следующее уравнение демонстрирует свойство распределения:
[латекс] -3 (2 + 5) = (-3) \ cdot 2 + (-3) \ cdot 5 [/ латекс]
Фракции
Дробь представляет собой часть целого и состоит из целого числителя и ненулевого целого знаменателя.
Цели обучения
Вычислить результат операций с дробями
Ключевые выводы
Ключевые моменты
- Для сложения и вычитания дробей требуется «одинаковые количества» — общий знаменатель.Чтобы сложить или вычесть дроби, содержащие различающиеся количества (например, прибавление четвертей к третям), необходимо преобразовать все суммы в одинаковые количества.

- Умножение дробей требует умножения числителей друг на друга, а затем знаменателей друг на друга. Быстрый путь — использовать стратегию отмены, которая уменьшает числа до минимально возможных значений перед умножением.
- При делении на дроби первое число умножается на величину, обратную второму числу.
Ключевые термины
- числитель : Число, которое находится над чертой дроби и представляет собой часть целого числа.
- обратная : дробь, перевернутая так, что числитель и знаменатель поменялись местами.
- знаменатель : Число под чертой дроби и представляет собой целое число.
- дробь : отношение двух чисел — числителя и знаменателя — обычно записываемых одно над другим и разделенных горизонтальной чертой.
Дробь представляет собой часть целого. Обычная дробь, например [латекс] \ frac {1} {2} [/ latex], [latex] \ frac {8} {5} [/ latex] или [latex] \ frac {3} {4} [/ latex], состоит из целого числителя (верхнее число) и ненулевого целого знаменателя (нижнее число). Числитель представляет определенное количество равных частей целого, а знаменатель указывает, сколько из этих частей необходимо, чтобы составить одно целое. Пример можно увидеть на следующем рисунке, на котором торт разделен на четвертинки:
Числитель представляет определенное количество равных частей целого, а знаменатель указывает, сколько из этих частей необходимо, чтобы составить одно целое. Пример можно увидеть на следующем рисунке, на котором торт разделен на четвертинки:
Четверти торта: Торт с удаленной четвертью.Показаны остальные три четверти. Пунктирными линиями обозначены места, где торт можно разрезать, чтобы разделить его на равные части. Каждая оставшаяся четверть торта обозначается дробью [латекс] \ frac {1} {4} [/ latex].
Дополнение
Добавление одинаковых количеств
Первое правило сложения дробей — начать с добавления дробей, которые содержат одинаковые знаменатели, например, кратные четверти или четверти. Четверть представлена дробью [латекс] \ frac {1} {4} [/ latex], где числитель 1 представляет одну четверть, а знаменатель 4 представляет количество четвертей, необходимое для создания целого , или один доллар.
Представьте себе, что один карман содержит две четвертинки, а другой карман — три четверти. Всего пять кварталов. Поскольку четыре четверти эквивалентны одному (доллару), это можно представить следующим образом:
Всего пять кварталов. Поскольку четыре четверти эквивалентны одному (доллару), это можно представить следующим образом:
[латекс] \ displaystyle \ frac {2} {4} + \ frac {3} {4} = \ frac {5} {4} = 1 \ frac {1} {4} [/ latex]
Добавление отличных количеств
Чтобы добавить дроби, которые содержат знаменатели в отличие от (например, четверти и трети), необходимо сначала преобразовать все суммы в одинаковые величины, что означает, что все дроби должны иметь общий знаменатель.Один простой способ найти знаменатель, который даст вам одинаковые количества, — это просто перемножить два знаменателя дробей. (Важно помнить, что каждый числитель также должен быть умножен на то же значение, на которое умножается его знаменатель, чтобы дробь представляла то же отношение.)
Например, чтобы прибавить четверти к третям, оба типа дробей преобразуются в двенадцатые:
[латекс] \ displaystyle \ frac {1} {3} + \ frac {1} {4} = \ frac {1 \ cdot 4} {3 \ cdot4} + \ frac {1 \ cdot3} {4 \ cdot3} = \ frac {4} {12} + \ frac {3} {12} = \ frac {7} {12} [/ latex]
Этот метод можно алгебраически выразить следующим образом:
[латекс] \ displaystyle \ frac {a} {b} + \ frac {c} {d} = \ frac {ad + cb} {bd} [/ latex]
Этот метод работает всегда. Однако иногда есть более быстрый способ — использовать меньший знаменатель или наименьший общий знаменатель. Например, чтобы добавить [latex] \ frac {3} {4} [/ latex] к [latex] \ frac {5} {12} [/ latex], знаменатель 48 (произведение 4 и 12, два знаменатели), но можно использовать и меньший знаменатель 12 (наименьшее общее кратное 4 и 12).
Однако иногда есть более быстрый способ — использовать меньший знаменатель или наименьший общий знаменатель. Например, чтобы добавить [latex] \ frac {3} {4} [/ latex] к [latex] \ frac {5} {12} [/ latex], знаменатель 48 (произведение 4 и 12, два знаменатели), но можно использовать и меньший знаменатель 12 (наименьшее общее кратное 4 и 12).
Сложение дробей к целым числам
Что делать, если к целому числу прибавляется дробная часть? Просто начните с записи целого числа в виде дроби (напомним, что целое число имеет знаменатель [латекс] 1 [/ латекс]), а затем продолжайте описанный выше процесс сложения дробей.
Вычитание
Процесс вычитания дробей, по сути, такой же, как и процесс их сложения. Найдите общий знаменатель и замените каждую дробь на эквивалентную дробь, используя этот общий знаменатель. Затем вычтите числители. Например:
[латекс] \ displaystyle \ frac {2} {3} — \ frac {1} {2} = \ frac {2 \ cdot 2} {3 \ cdot2} — \ frac {1 \ cdot3} {2 \ cdot3} = \ frac {4} {6} — \ frac {3} {6} = \ frac {1} {6} [/ latex]
Чтобы вычесть дробь из целого числа или вычесть целое число из дроби, перепишите целое число как дробь, а затем выполните описанный выше процесс вычитания дробей.
Умножение
В отличие от сложения и вычитания, при умножении знаменатели не обязательно должны быть одинаковыми. Чтобы умножить дроби, просто умножьте числители друг на друга, а знаменатели друг на друга. Например:
[латекс] \ displaystyle \ frac {2} {3} \ cdot \ frac {3} {4} = \ frac {6} {12} [/ latex]
Если какой-либо числитель и знаменатель имеют общий множитель, дроби могут быть уменьшены до наименьшего значения до или после умножения. Например, полученная дробь может быть уменьшена до [latex] \ frac {1} {2} [/ latex], потому что числитель и знаменатель делят множитель 6.В качестве альтернативы дроби в исходном уравнении можно было бы уменьшить, как показано ниже, потому что 2 и 4 имеют общий множитель 2, а 3 и 3 имеют общий множитель 3:
[латекс] \ displaystyle \ frac {2} {3} \ cdot \ frac {3} {4} = \ frac {1} {1} \ cdot \ frac {1} {2} = \ frac {1} { 2} [/ латекс]
Чтобы умножить дробь на целое число, просто умножьте это число на числитель дроби:
[латекс] \ displaystyle \ frac {3} {4} \ cdot 5 = \ frac {15} {4} [/ latex]
Обычная ситуация, когда умножение дробей бывает полезным, — это во время готовки. Что, если кто-то захочет «половину» рецепта печенья, для которого требуется [латекс] \ frac {1} {2} [/ latex] чашки шоколадной стружки? Чтобы найти необходимое количество шоколадной крошки, умножьте [латекс] \ frac {1} {2} \ cdot \ frac {1} {2} [/ latex]. В результате получается [латекс] \ frac {1} {4} [/ latex], поэтому правильное количество шоколадной стружки составляет [латекс] \ frac {1} {4} [/ latex] чашки.
Что, если кто-то захочет «половину» рецепта печенья, для которого требуется [латекс] \ frac {1} {2} [/ latex] чашки шоколадной стружки? Чтобы найти необходимое количество шоколадной крошки, умножьте [латекс] \ frac {1} {2} \ cdot \ frac {1} {2} [/ latex]. В результате получается [латекс] \ frac {1} {4} [/ latex], поэтому правильное количество шоколадной стружки составляет [латекс] \ frac {1} {4} [/ latex] чашки.
Дивизия
Процесс деления числа на дробь влечет за собой умножение числа на обратную величину дроби.Обратная величина — это просто дробь, перевернутая так, что числитель и знаменатель меняются местами. Например:
[латекс] \ displaystyle \ frac {1} {2} \ div \ frac {3} {4} = \ frac {1} {2} \ cdot \ frac {4} {3} = \ frac {4} { 6} = \ frac {2} {3} [/ latex]
Чтобы разделить дробь на целое число, либо разделите числитель дроби на целое число (если оно делится просто):
[латекс] \ displaystyle \ frac {10} {3} \ div 5 = \ frac {10 \ div 2} {3} = \ frac {2} {3} [/ latex]
или умножьте знаменатель дроби на целое число:
[латекс] \ displaystyle \ frac {10} {3} \ div 5 = \ displaystyle \ frac {10} {3 \ cdot5} = \ frac {10} {15} = \ frac {2} {3} [/ латекс]
Сложные фракции
Комплексная дробь — это дробь, в которой числитель, знаменатель или оба являются дробями, которые могут содержать переменные, константы или и то, и другое.
Цели обучения
Упростить сложные дроби
Ключевые выводы
Ключевые моменты
- Сложные дроби включают такие числа, как [latex] \ frac {\ left (\ frac {8} {15} \ right)} {\ left (\ frac {2} {3} \ right)} [/ latex] и [латекс] \ frac {3} {1- \ frac {2} {5}} [/ latex], где числитель, знаменатель или оба включают дроби.
- Прежде чем решать сложные рациональные выражения, полезно их максимально упростить.
- «Метод комбинирования-деления» для упрощения сложных дробей влечет за собой (1) объединение членов в числителе, (2) объединение членов в знаменателе и, наконец, (3) деление числителя на знаменатель.
Ключевые термины
- комплексная дробь : отношение, в котором числитель, знаменатель или оба сами являются дробями.
Комплексная дробь, также называемая комплексным рациональным выражением, — это дробь, в которой числитель, знаменатель или оба являются дробями. Например, [латекс] \ frac {\ left (\ frac {8} {15} \ right)} {\ left (\ frac {2} {3} \ right)} [/ latex] и [latex] \ frac {3} {1- \ frac {2} {5}} [/ latex] — сложные дроби. При работе с уравнениями, которые включают сложные дроби, полезно упростить сложную дробь перед тем, как решать уравнение.
Например, [латекс] \ frac {\ left (\ frac {8} {15} \ right)} {\ left (\ frac {2} {3} \ right)} [/ latex] и [latex] \ frac {3} {1- \ frac {2} {5}} [/ latex] — сложные дроби. При работе с уравнениями, которые включают сложные дроби, полезно упростить сложную дробь перед тем, как решать уравнение.
Процесс упрощения сложных дробей, известный как «метод комбинирования-деления», выглядит следующим образом:
- Объедините члены в числителе.
- Объедините члены в знаменателе.
- Разделите числитель на знаменатель.
Пример 1
Давайте применим этот метод к первой сложной дроби, представленной выше:
[латекс] \ displaystyle {\ frac {\ left (\ frac {8} {15} \ right)} {\ left (\ frac {2} {3} \ right)}} [/ латекс]
Поскольку нет терминов, которые можно объединить или упростить ни в числителе, ни в знаменателе, мы перейдем к шагу 3, разделив числитель на знаменатель:
[латекс] \ displaystyle {\ frac {\ left (\ frac {8} {15} \ right)} {\ left (\ frac {2} {3} \ right)} = \ frac {8} {15} \ div \ frac {2} {3}} [/ латекс]
Из предыдущих разделов мы знаем, что деление на дробь аналогично умножению на обратную величину этой дроби.Поэтому мы используем метод сокращения, чтобы максимально упростить числа, а затем умножаем его на упрощенную обратную величину делителя или знаменателя дроби:
[латекс] \ displaystyle {{\ frac 8 {15}} \ cdot {\ frac 32} = {\ frac 4 {5}} \ cdot {\ frac 11} = {\ frac 4 {5}}} [/ латекс]
Следовательно, комплексная дробь [латекс] \ frac {\ left (\ frac {8} {15} \ right)} {\ left (\ frac {2} {3} \ right)} [/ latex] упрощается до [ латекс] \ frac {4} {5} [/ латекс].
Пример 2
Давайте попробуем другой пример:
[латекс] \ displaystyle {\ frac {\ left (\ dfrac {1} {2} + \ dfrac {2} {3} \ right)} {\ left (\ dfrac {2} {3} \ cdot \ dfrac {3} {4} \ right)}} [/ латекс]
Начните с шага 1 описанного выше метода комбинирования-деления: объедините члены в числителе.Вы обнаружите, что общий знаменатель двух дробей в числителе равен 6, а затем вы можете сложить эти два члена вместе, чтобы получить один член дроби в числителе большей дроби:
[латекс] \ displaystyle \ frac {\ left (\ dfrac {1} {2} + \ dfrac {2} {3} \ right)} {\ left (\ dfrac {2} {3} \ cdot \ dfrac { 3} {4} \ right)} = \ dfrac {\ left (\ dfrac {3} {6} + \ dfrac {4} {6} \ right)} {\ left (\ dfrac {2} {3} \ cdot \ dfrac {3} {4} \ right)} = \ dfrac {\ left (\ dfrac {7} {6} \ right)} {\ left (\ dfrac {2} {3} \ cdot \ dfrac {3 } {4} \ right)} [/ латекс]
Перейдем к шагу 2: объединим члены в знаменателе.Для этого мы умножаем дроби в знаменателе вместе и упрощаем результат, сокращая его до наименьших членов:
[латекс] \ dfrac {\ left (\ dfrac {7} {6} \ right)} {\ left (\ dfrac {2} {3} \ cdot \ dfrac {3} {4} \ right)} = \ dfrac {\ left (\ dfrac {7} {6} \ right)} {\ left (\ dfrac {6} {12} \ right)} = \ dfrac {\ left (\ dfrac {7} {6} \ right )} {\ left (\ dfrac {1} {2} \ right)} [/ latex]
Перейдем к шагу 3: разделим числитель на знаменатель. Напомним, что деление на дробь аналогично умножению на обратную величину этой дроби:
[латекс] \ frac {\ left (\ dfrac {7} {6} \ right)} {\ left (\ dfrac {1} {2} \ right)} = {\ dfrac {7} {6}} \ cdot {\ dfrac {2} {1}} = \ dfrac {14} {6} [/ latex]
Наконец, упростим полученную дробь:
[латекс] \ displaystyle \ frac {14} {6} = 2 \ frac {2} {6} [/ latex]
Следовательно, в итоге:
[латекс] \ frac {\ left (\ dfrac {1} {2} + \ dfrac {2} {3} \ right)} {\ left (\ dfrac {2} {3} \ cdot \ dfrac {3} {4} \ right)} = 2 \ dfrac {2} {6} [/ latex]
Введение в экспоненты
Экспоненциальная форма, записанная [latex] b ^ n [/ latex], представляет собой умножение базового [latex] b [/ latex] на сам [latex] n [/ latex] раз. 5 = 3 \ cdot 3 \ cdot 3 \ cdot 3 \ cdot 3 = 243 [/ латекс]
Показатели 0 и 1
Любое число, возведенное в степень [латекс] 1 [/ латекс], является самим числом.0 = 1 [/ латекс].
Порядок действий
Порядок операций — это подход к оценке выражений, включающих несколько арифметических операций.
Цели обучения
Различие между правильным и неправильным использованием порядка операций
Ключевые выводы
Ключевые моменты
- Порядок операций предотвращает двусмысленность математических выражений.
- Порядок операций следующий: 1) упростить члены в круглых или квадратных скобках, 2) упростить показатели и корни, 3) выполнить умножение и деление, 4) выполнить сложение и вычитание.
- Умножение и деление имеют равный приоритет, равно как и сложение и вычитание. Это означает, что операции умножения и деления (а также операции сложения и вычитания) могут выполняться в том порядке, в котором они появляются в выражении.
- Полезный мнемоник для запоминания порядка действий — PEMDAS, иногда расширяемый до «Прошу прощения, моя дорогая тетя Салли».
Ключевые термины
- математическая операция : действие или процедура, которая создает новое значение из одного или нескольких входных значений.
Порядок операций — это способ вычисления выражений, которые включают более одной арифметической операции. Эти правила говорят вам, как вам следует упростить или решить выражение или уравнение таким образом, чтобы получить правильный результат.
Например, когда вы встретите выражение [латекс] 4 + 2 \ cdot 3 [/ latex], как вы поступите?
Один вариант:
[латекс] \ begin {align} \ displaystyle 4 + 2 \ cdot3 & = (4 + 2) \ cdot 3 \\ & = 6 \ cdot 3 \\ & = 18 \ end {align} [/ latex]
Другой вариант:
[латекс] \ begin {align} \ displaystyle 4 + 2 \ cdot 3 & = 4+ (2 \ cdot 3) \\ & = 4 + 6 \\ & = 10 \ end {align} [/ latex]
Какой порядок действий правильный?
Чтобы иметь возможность общаться с помощью математических выражений, у нас должен быть согласованный порядок операций, чтобы каждое выражение было однозначным.Например, для приведенного выше выражения все математики согласятся, что правильный ответ — 10.
Порядок операций, используемых в математике, науке, технике и многих языках программирования, следующий:
- Упростите термины в круглых или квадратных скобках
- Упростить экспоненты и корни
- Выполнить умножение и деление
- Выполнить сложение и вычитание
Эти правила означают, что в математическом выражении сначала должна выполняться операция, занимающая наивысшее место в списке.3 \\ & = 6-5 + 8 \\ & = 1 + 8 \\ & = 9 \ end {align} [/ latex]
Примечание о равной приоритетности
Поскольку умножение и деление имеют равный приоритет, может быть полезно думать о делении на число как о умножении на обратную величину этого числа. Таким образом, [латекс] 3 \ div 4 = 3 \ cdot \ frac {1} {4} [/ latex]. Другими словами, частное 3 и 4 равно произведению 3 и [латекс] \ frac {1} {4} [/ latex].
Точно так же, поскольку сложение и вычитание имеют равный приоритет, мы можем думать о вычитании числа как о сложении отрицательного числа.Таким образом [латекс] 3−4 = 3 + (- 4) [/ латекс]. Другими словами, разница 3 и 4 равна сумме положительных трех и отрицательных четырех.
При таком понимании представьте [латекс] 1−3 + 7 [/ latex] как сумму 1, минус 3 и 7, а затем сложите эти термины вместе. Теперь, когда вы изменили структуру операций, любой заказ будет работать:
- [латекс] (1-3) + 7 = -2 + 7 = 5 [/ латекс]
- [латекс] (7−3) + 1 = 4 + 1 = 5 [/ латекс]
Важно сохранять отрицательный знак с любым отрицательным числом (здесь 3).
Мнемоника
В США аббревиатура PEMDAS является распространенным мнемоническим символом для запоминания порядка операций. Это означает круглые скобки, экспоненты, умножение, деление, сложение и вычитание. PEMDAS часто расширяется до «Прошу прощения, моя дорогая тетя Салли».
Эта мнемоника может вводить в заблуждение, однако, поскольку «MD» подразумевает, что умножение должно выполняться перед делением, а «AS» — это сложение перед вычитанием, а не признание их равного приоритета.Чтобы проиллюстрировать, почему это проблема, рассмотрим следующее:
[латекс] 10-3 + 2 [/ латекс]
Это выражение правильно упрощается до 9. Однако, если вы сначала сложите 2 и 3, чтобы получить 5, и , а затем выполнил вычитание, вы получили бы 5 в качестве окончательного ответа, что неверно. Чтобы избежать этой ошибки, лучше всего рассматривать эту проблему как сумму положительных десяти, отрицательных трех и положительных двух.
[латекс] 10 + (- 3) +2 [/ латекс]
Чтобы полностью избежать этой путаницы, альтернативный способ записи мнемоники:
-P
E
MD
КАК
Или, просто как PEMA, где учат, что умножение и деление по своей сути имеют один и тот же приоритет, а сложение и вычитание по своей сути имеют одинаковый приоритет.Эта мнемоника проясняет эквивалентность умножения и деления, а также сложения и вычитания.
Сложение, вычитание, умножение и деление целых чисел
Цели обучения
- Используйте сложение, вычитание, умножение и деление при вычислении целочисленных выражений
Работа с целыми числами и выполнение основных вычислений — основа всей математики. Предположим, вы помните, как выполнять сложение, вычитание, умножение и деление одной цифры.Для выполнения этих расчетов у вас часто будет под рукой калькулятор, но быстрое освежение знаний поможет вам лучше понять, как работать с числами, чтобы сложные уравнения были менее сложными.
Дополнение
пример
Добавьте: [латекс] 28 + 61 [/ латекс]
Решение
Чтобы сложить числа, состоящие из более чем одной цифры, часто проще записать числа в вертикальном направлении в столбцы.
| Напишите числа так, чтобы цифры единиц и десятков располагались вертикально. | [латекс] \ begin {array} {c} \ hfill 28 \\ \\ \ hfill \ underset {\ text {____}} {+ 61} \ end {array} [/ latex] |
| Затем добавьте цифры в каждое разрядное значение. Складываем единицы: [латекс] 8 + 1 = 9 [/ латекс] Складываем десятки: [латекс] 2 + 6 = 8 [/ латекс] | [латекс] \ begin {array} {c} \ hfill 28 \\ \\ \ hfill \ underset {\ text {____}} {+ 61} \\ \ hfill 89 \ end {array} [/ latex] |
В предыдущем примере сумма единиц и сумма десятков были меньше [латекс] 10 [/ латекс].Но что будет, если сумма [латекс] 10 [/ латекс] или больше? Давайте воспользуемся нашей моделью base- [latex] 10 [/ latex], чтобы выяснить это.
На рисунке ниже снова показано добавление [латекса] 17 [/ латекса] и [латекса] 26 [/ латекса].
Когда мы складываем те, [latex] 7 + 6 [/ latex], мы получаем [latex] 13 [/ latex]. Поскольку у нас больше, чем [латекс] 10 [/ латекс], мы можем обменять [латекс] 10 [/ латекс] на десять [латекс] 1 [/ латекс]. Теперь у нас есть [латексные] 4 [/ латексные] десятки и [латексные] 3 [/ латексные] десятки.Не используя модель, мы показываем это как маленький красный [латекс] 1 [/ латекс] над цифрами в разряде десятков.
Когда сумма в столбце значений разряда больше [latex] 9 [/ latex], мы переносимся в следующий столбец слева. Перенос — это то же самое, что перегруппировка путем обмена. Например, [латекс] 10 [/ латекс] единиц за [латекс] 1 [/ латекс] десятку или [латекс] 10 [/ латекс] десяток за [латекс] 1 [/ латекс] сотню.
Сложить целые числа
- Напишите числа так, чтобы каждое разрядное значение располагалось вертикально.
- Добавьте цифры в каждое разрядное значение. Работайте справа налево, начиная с единиц. Если сумма в разряде больше [latex] 9 [/ latex], переносится к следующему разряду.
- Продолжайте добавлять каждое разрядное значение справа налево, добавляя каждое разрядное значение и перенося, если необходимо.
пример
Добавьте: [латекс] 43 + 69 [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы цифры выстраивались вертикально. | [латекс] \ begin {array} {c} \ hfill 43 \\ \\ \ hfill \ underset {\ text {____}} {+ 69} \ end {array} [/ latex] |
| Добавьте цифры в каждом месте. Складываем единицы: [латекс] 3 + 9 = 12 [/ латекс] | |
| Запишите [латекс] 2 [/ латекс] в разрядах единиц суммы. Добавьте [latex] 1 [/ latex] десятку к разряду десятков. | [латекс] \ begin {массив} {c} \ hfill \ stackrel {1} {4} 3 \\ \ hfill \ underset {\ text {____}} {+ 69} \\ \ hfill 2 \ end {array} [/ латекс] |
| Теперь сложите десятки: [латекс] 1 + 4 + 6 = 11 [/ латекс] Запишите 11 в сумме. | [латекс] \ begin {array} {c} \ hfill \ stackrel {1} {4} 3 \\ \ hfill \ underset {\ text {____}} {+ 69} \\ \ hfill 112 \ end {array} [/ латекс] |
Если слагаемые содержат разное количество цифр, будьте осторожны, чтобы выровнять соответствующие разрядные значения, начиная с единиц и двигаясь влево.
пример
Добавить: [латекс] 1,683 + 479 [/ латекс].
Покажи ответРешение
| Напишите числа так, чтобы цифры выстраивались вертикально. | [латекс] \ begin {array} {c} \ hfill 1,683 \\ \\ \ hfill \ underset {\ text {______}} {+ 479} \ end {array} [/ latex] |
| Сложите цифры в каждом значении разряда. | |
| Складываем единицы: [латекс] 3 + 9 = 12 [/ латекс]. Напишите [latex] 2 [/ latex] в разряде единиц суммы и перенесите [latex] 1 [/ latex] десять в разряды десятков. | [латекс] \ begin {array} {c} \ hfill 1,6 \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ text {______}} {+ 479} \\ \ hfill 2 \ end {array} [/ latex] |
| Складываем десятки: [латекс] 1 + 7 + 8 = 16 [/ латекс] Напишите [латекс] 6 [/ латекс] в разряде десятков и отнесите [латекс] 1 [/ латекс] сотню к разряду сотен. | [латекс] \ begin {array} {c} \ hfill 1, \ stackrel {1} {6} \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ text {______}} {+ 479} \\ \ hfill 62 \ end {array} [/ latex] |
| Складываем сотни: [латекс] 1 + 6 + 4 = 11 [/ латекс] Напишите [латекс] 1 [/ латекс] в разряде сотен и перенесите [латекс] 1 [/ латекс] тысячу в разряды тысяч. | [латекс] \ begin {array} {c} \ hfill \ stackrel {1} {1}, \ stackrel {1} {6} \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ текст {______}} {+ 479} \\ \ hfill 162 \ end {array} [/ latex] |
| Сложите тысячи [латекс] 1 + 1 = 2 [/ латекс]. Напишите [латекс] 2 [/ латекс] в разряде тысяч суммы. | [латекс] \ begin {array} {c} \ hfill \ stackrel {1} {1}, \ stackrel {1} {6} \ stackrel {1} {8} 3 \\ \\ \ hfill \ underset {\ текст {______}} {+ 479} \\ \ hfill 2,162 \ end {array} [/ latex] |
Посмотрите видео ниже, чтобы увидеть еще один пример того, как сложить три целых числа, выровняв разряды.
Вычитание
Сложение и вычитание — обратные операции. Сложение отменяет вычитание, а вычитание отменяет сложение.
Мы знаем [латекс] 7 — 3 = 4 [/ latex], потому что [latex] 4 + 3 = 7 [/ latex]. Знание всех фактов сложения чисел поможет при вычитании. Затем мы можем проверить вычитание, добавив. В приведенных выше примерах наши вычитания можно проверить сложением.
| [латекс] 7-3 = 4 [/ латекс] | потому что | [латекс] 4 + 3 = 7 [/ латекс] |
| [латекс] 13-8 = 5 [/ латекс] | потому что | [латекс] 5 + 8 = 13 [/ латекс] |
| [латекс] 43-26 = 17 [/ латекс] | потому что | [латекс] 17 + 26 = 43 [/ латекс] |
Для вычитания чисел, состоящих из более чем одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения.Выровняйте цифры по разряду, а затем вычтите каждый столбец, начиная с единиц, а затем двигаясь влево.
Упражнение
Вычтите и проверьте, добавив: [латекс] 89 — 61 [/ латекс].
Покажи ответРешение
| Напишите числа так, чтобы цифры единиц и десятков располагались вертикально. | [латекс] \ begin {array} {c} \ hfill 89 \\ \ hfill \ underset {\ text {____}} {- 61} \ end {array} [/ latex] |
| Вычтите цифры в каждом значении разряда. Вычтите единицы: [латекс] 9 — 1 = 8 [/ латекс] Вычтите десятки: [латекс] 8–6 = 2 [/ латекс] | [латекс] \ begin {array} {c} \ hfill 89 \\ \ hfill \ underset {\ text {____}} {- 61} \\ \ hfill 28 \ end {array} [/ latex] |
| Проверить с помощью дополнения. [латекс] \ begin {массив} {c} \ hfill 28 \\ \ hfill \ underset {\ text {____}} {+ 61} \\ \ hfill 89 \ end {array} \ quad \ checkmark [/ latex] |
Наш ответ правильный.
Вычесть целые числа
- Напишите числа так, чтобы каждое разрядное значение располагалось вертикально.
- Вычтите цифры в каждом значении разряда. Работайте справа налево, начиная с единиц. Если цифра вверху меньше цифры внизу, при необходимости заимствуйте.
- Продолжайте вычитать каждое разрядное значение справа налево, при необходимости заимствуя.
- Проверить добавлением.
упражнение
Вычтите: [латекс] 43 — 26 [/ латекс].
В приведенном выше примере, если мы моделируем вычитание [latex] 26 [/ latex] из [latex] 43 [/ latex], мы бы заменили [latex] 1 [/ latex] десять на [latex] 10 [/ latex]. .Когда мы делаем это без моделей, мы говорим, что заимствуем [latex] 1 [/ latex] из разряда десятков и добавляем [latex] 10 [/ latex] в разряды единиц.
Упражнение
Вычтите и проверьте, добавив: [латекс] 207 — 64 [/ латекс].
Упражнение
Вычтите и проверьте, добавив: [латекс] 2,162 — 479 [/ латекс].
Покажи ответРешение
Наш ответ правильный.
Посмотрите видео ниже, чтобы увидеть еще один пример вычитания целых чисел путем выравнивания значений разряда.
Умножение
Чтобы умножать без использования моделей, вам необходимо знать все факты однозначного умножения. Убедитесь, что вы хорошо их знаете, прежде чем переходить к этому разделу. В таблице ниже показаны факты умножения.
Каждое поле показывает произведение числа в левом столбце и числа в верхнем ряду. Если вы не уверены в продукте, смоделируйте его. Важно, чтобы вы запомнили любые числовые факты, которых вы еще не знаете, чтобы вы были готовы умножать большие числа.
| [латекс] x [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 1 [/ латекс] | [латекс] 2 [/ латекс] | [латекс] 3 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 5 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 7 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 9 [/ латекс] |
|---|---|---|---|---|---|---|---|---|---|---|
| [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 0 [/ латекс] |
| [латекс] 1 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 1 [/ латекс] | [латекс] 2 [/ латекс] | [латекс] 3 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 5 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 7 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 9 [/ латекс] |
| [латекс] 2 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 2 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 10 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 14 [/ латекс] | [латекс] 16 [/ латекс] | [латекс] 18 [/ латекс] |
| [латекс] 3 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 3 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 9 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 15 [/ латекс] | [латекс] 18 [/ латекс] | [латекс] 21 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 27 [/ латекс] |
| [латекс] 4 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 16 [/ латекс] | [латекс] 20 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 28 [/ латекс] | [латекс] 32 [/ латекс] | [латекс] 36 [/ латекс] |
| [латекс] 5 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 5 [/ латекс] | [латекс] 10 [/ латекс] | [латекс] 15 [/ латекс] | [латекс] 20 [/ латекс] | [латекс] 25 [/ латекс] | [латекс] 30 [/ латекс] | [латекс] 35 [/ латекс] | [латекс] 40 [/ латекс] | [латекс] 45 [/ латекс] |
| [латекс] 6 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 12 [/ латекс] | [латекс] 18 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 30 [/ латекс] | [латекс] 36 [/ латекс] | [латекс] 42 [/ латекс] | [латекс] 48 [/ латекс] | [латекс] 54 [/ латекс] |
| [латекс] 7 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 7 [/ латекс] | [латекс] 14 [/ латекс] | [латекс] 21 [/ латекс] | [латекс] 28 [/ латекс] | [латекс] 35 [/ латекс] | [латекс] 42 [/ латекс] | [латекс] 49 [/ латекс] | [латекс] 56 [/ латекс] | [латекс] 63 [/ латекс] |
| [латекс] 8 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 8 [/ латекс] | [латекс] 16 [/ латекс] | [латекс] 24 [/ латекс] | [латекс] 32 [/ латекс] | [латекс] 40 [/ латекс] | [латекс] 48 [/ латекс] | [латекс] 56 [/ латекс] | [латекс] 64 [/ латекс] | [латекс] 72 [/ латекс] |
| [латекс] 9 [/ латекс] | [латекс] 0 [/ латекс] | [латекс] 9 [/ латекс] | [латекс] 18 [/ латекс] | [латекс] 27 [/ латекс] | [латекс] 36 [/ латекс] | [латекс] 45 [/ латекс] | [латекс] 54 [/ латекс] | [латекс] 63 [/ латекс] | [латекс] 72 [/ латекс] | [латекс] 81 [/ латекс] |
Мы знаем, что изменение порядка сложения не меняет суммы.Мы видели, что [латекс] 8 + 9 = 17 [/ латекс] то же самое, что [латекс] 9 + 8 = 17 [/ латекс].
Верно ли это и для умножения? Давайте посмотрим на несколько пар факторов.
[латекс] 4 \ cdot 7 = 28 \ quad 7 \ cdot 4 = 28 [/ латекс]
[латекс] 9 \ cdot 7 = 63 \ quad 7 \ cdot 9 = 63 [/ латекс]
[латекс] 8 \ cdot 9 = 72 \ quad 9 \ cdot 8 = 72 [/ латекс]
При обратном порядке факторов продукт не изменяется. Это называется коммутативным свойством умножения.
Коммутативное свойство умножения
Изменение порядка факторов не меняет их произведения.
[латекс] a \ cdot b = b \ cdot a [/ латекс]
пример
Умножить:
[латекс] 8 \ cdot 7 [/ латекс]
[латекс] 7 \ cdot 8 [/ латекс]
Решение:
| 1. | [латекс] 8 \ cdot 7 [/ латекс] |
| Умножить. | [латекс] 56 [/ латекс] |
| 2. | [латекс] 7 \ cdot 8 [/ латекс] |
| Умножить. | [латекс] 56 [/ латекс] |
Изменение порядка факторов не приводит к изменению продукта.
Чтобы умножать числа, состоящие более чем из одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения и вычитания.
[латекс] \ begin {array} {c} \ hfill 27 \\ \ hfill \ underset {\ text {___}} {\ times 3} \ end {array} [/ latex]
Начнем с умножения [латекс] 3 [/ латекс] на [латекс] 7 [/ латекс].
[латекс] 3 \ раз 7 = 21 [/ латекс]
Мы пишем [латекс] 1 [/ латекс] на единицах товара. Переносим [latex] 2 [/ latex] десятки, написав [latex] 2 [/ latex] над разрядами десятков.
Затем мы умножаем [latex] 3 [/ latex] на [latex] 2 [/ latex] и добавляем [latex] 2 [/ latex] над разрядами десятков к продукту. Итак, [латекс] 3 \ times 2 = 6 [/ латекс], и [латекс] 6 + 2 = 8 [/ латекс]. Напишите [латекс] 8 [/ латекс] в разряде десятков продукта.
Изделие [латекс] 81 [/ латекс].
Когда мы умножаем два числа на разное количество цифр, обычно проще написать меньшее число внизу. Можно было бы написать и по-другому, но с этим проще работать.
пример
Умножение: [латекс] 15 \ cdot 4 [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы цифры [латекс] 5 [/ латекс] и [латекс] 4 [/ латекс] выстроились вертикально. | [латекс] \ begin {array} {c} \ hfill 15 \\ \ hfill \ underset {\ text {_____}} {\ times 4} \ end {array} [/ latex] |
| Умножьте [латекс] 4 [/ латекс] на цифру в разряде единиц [латекс] 15 [/ латекс]. [латекс] 4 \ cdot 5 = 20 [/ латекс]. | |
| Напишите [латекс] 0 [/ латекс] в единицах изделия и несите [латекс] 2 [/ латекс] десятки. | [латекс] \ begin {массив} {c} \ hfill \ stackrel {2} {1} 5 \\ \ hfill \ underset {\ text {_____}} {\ times 4} \\ \ hfill 0 \ end {массив } [/ latex] |
| Умножьте [латекс] 4 [/ латекс] на цифру в разряде десятков [латекс] 15 [/ латекс]. [латекс] 4 \ cdot 1 = 4 [/ латекс]. Добавьте [латекс] 2 [/ латекс] десятки, которые мы несли. [латекс] 4 + 2 = 6 [/ латекс]. | |
| Напишите [латекс] 6 [/ латекс] в разряде десятков продукта. | [латекс] \ begin {array} {c} \ hfill \ stackrel {2} {1} 5 \\ \ hfill \ underset {\ text {_____}} {\ times 4} \\ \ hfill 60 \ end {массив } [/ latex] |
пример
Умножение: [латекс] 286 \ cdot 5 [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы цифры [латекс] 5 [/ латекс] и [латекс] 6 [/ латекс] выстроились вертикально. | [латекс] \ begin {array} {c} \ hfill 286 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \ end {array} [/ latex] |
| Умножьте [латекс] 5 [/ латекс] на цифру в разряде единиц [латекс] 286 [/ латекс]. [латекс] 5 \ cdot 6 = 30 [/ латекс] | |
| Напишите [латекс] 0 [/ латекс] на месте единицы продукта и перенесите [латекс] 3 [/ латекс] в разряд десятков. Умножьте [латекс] 5 [/ латекс] на цифру в десятки раз [латекс] 286 [/ латекс]. [латекс] 5 \ cdot 8 = 40 [/ латекс] | [латекс] \ begin {массив} {} \\ \ hfill 2 \ stackrel {3} {8} 6 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \\ \ hfill 0 \ end {array} [/ latex] |
| Добавьте [латекс] 3 [/ латекс] десятки, которые мы принесли, чтобы получить [латекс] 40 + 3 = 43 [/ латекс]. Напишите [латекс] 3 [/ латекс] в разряде десятков продукта и отнесите [латекс] 4 [/ латекс] к разряду сотен. | [латекс] \ begin {array} {c} \ hfill \ stackrel {4} {2} \ stackrel {3} {8} 6 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \ \ \ hfill 30 \ end {array} [/ latex] |
| Умножьте [латекс] 5 [/ латекс] на цифру в разряде сотен [латекс] 286 [/ латекс]. [латекс] 5 \ cdot 2 = 10 [/ латекс]. Добавьте [латекс] 4 [/ латекс] сотни, которые мы принесли, чтобы получить [латекс] 10 + 4 = 14 [/ латекс]. Напишите [латекс] 4 [/ латекс] в разряде сотен продукта и [латекс] 1 [/ латекс] в разряде тысяч. | [латекс] \ begin {array} {c} \ hfill \ stackrel {4} {2} \ stackrel {3} {8} 6 \\ \ hfill \ underset {\ text {_____}} {\ times 5} \ \ \ hfill 1,430 \ end {array} [/ latex] |
Когда мы умножаем на число, состоящее из двух или более цифр, мы умножаем на каждую из цифр отдельно, работая справа налево. Каждое отдельное произведение цифр называется частичным произведением.Когда мы пишем частичные продукты, мы должны убедиться, что выровнены значения позиций.
Умножение целых чисел
- Напишите числа так, чтобы каждое разрядное значение располагалось вертикально.
- Умножьте цифры в каждом значении разряда.
- Работайте справа налево, начиная с единиц в нижнем ряду.
- Умножьте нижнее число на цифру единиц в верхнем числе, затем на цифру десятков и так далее.
- Если продукт в разряде больше, чем [латекс] 9 [/ латекс], переходить к следующему разряду.
- Напишите частичные продукты, выровняв цифры в позиционных значениях с числами, указанными выше.
- Повторите эти действия для разряда десятков в нижнем числе, разряда сотен и так далее.
- Вставляйте ноль в качестве заполнителя с каждым дополнительным частичным продуктом.
- Работайте справа налево, начиная с единиц в нижнем ряду.
- Добавьте частичные продукты.
пример
Умножение: [латекс] 62 \ влево (87 \ вправо) [/ латекс]
Покажи ответРешение
| Напишите числа так, чтобы каждое место было расположено вертикально. | |
| Начните с умножения 7 на 62. Умножьте 7 на цифру 62 в разряде единиц. [латекс] 7 \ cdot 2 = 14 [/ латекс]. Напишите 4 в разряде единиц продукта и перенесите 1 в разряды десятков. | |
| Умножьте 7 на цифру в разряде десятков 62. [латекс] 7 \ cdot 6 = 42 [/ латекс]. Добавьте 1 десятку, которую мы несли. [латекс] 42 + 1 = 43 [/ латекс] латекс]. Запишите 3 в разряде десятков произведения и 4 в разрядах сотен. | |
| Первый частичный продукт — [латекс] 434 [/ латекс]. | |
| Теперь напишите [latex] 0 [/ latex] под [latex] 4 [/ latex] в месте единиц следующего частичного продукта в качестве заполнителя, так как теперь мы умножаем цифру на разряды десятков [latex ] 87 [/ латекс] [латекс] 62 [/ латекс]. Умножить [латекс] 8 [/ латекс] на цифру в разряде единиц [латекс] 62 [/ латекс] [латекс] 8 \ cdot 2 = 16 [/ латекс]. Напишите [латекс] 6 [/ латекс] на следующем месте продукта, то есть на разряде десятков.Отнесите [латекс] 1 [/ латекс] к разряду десятков. | |
| Умножьте [latex] 8 [/ latex] на [latex] 6 [/ latex], цифру в десятках [latex] 62 [/ latex], затем добавьте [latex] 1 [/ latex] десять. повезли получить [латекс] 49 [/ латекс]. Напишите [латекс] 9 [/ латекс] в разряде сотен продукта и [латекс] 4 [/ латекс] в разряде тысяч. | |
| Второй частичный продукт [латекс] 4960 [/ латекс]. Добавьте частичные продукты. |
Продукт [латекс] 5,394 [/ латекс].
Если имеется три или более факторов, мы умножаем первые два, а затем умножаем их произведение на следующий коэффициент. Например:
| для умножения | [латекс] 8 \ cdot 3 \ cdot 2 [/ латекс] |
| первое умножение [латекс] 8 \ cdot 3 [/ латекс] | [латекс] 24 \ cdot 2 [/ латекс] |
| , затем умножьте [латекс] 24 \ cdot 2 [/ latex] | [латекс] 48 [/ латекс] |
В видео ниже мы суммируем концепции, представленные на этой странице, включая свойство умножения нуля, свойство идентичности умножения и свойство коммутативности умножения.м
Дивизия
Мы сказали, что сложение и вычитание — обратные операции, потому что одно отменяет другое. Точно так же деление — это операция, обратная умножению. Мы знаем [латекс] 12 \ div 4 = 3 [/ latex], потому что [латекс] 3 \ cdot 4 = 12 [/ latex]. При делении очень важно знать все факты о числах умножения.
Мы проверяем наш ответ на деление, умножая частное на делитель, чтобы определить, равно ли оно дивиденду.Мы знаем, что [latex] 24 \ div 8 = 3 [/ latex] правильно, потому что [latex] 3 \ cdot 8 = 24 [/ latex].
пример
Разделить. Затем проверьте умножением.
- [латекс] 42 \ div 6 [/ латекс]
- [латекс] \ frac {72} {9} [/ латекс]
- [латекс] 7 \ overline {) 63} [/ латекс]
Решение:
| 1. | |
| [латекс] 42 \ div 6 [/ латекс] | |
| Разделите [латекс] 42 [/ латекс] на [латекс] 6 [/ латекс]. | [латекс] 7 [/ латекс] |
| Проверить умножением. [латекс] 7 \ cdot 6 [/ латекс] | |
| [латекс] 42 \ квадратик \ галочка [/ латекс] |
| 2. | |
| [латекс] \ frac {72} {9} [/ латекс] | |
| Разделите [латекс] 72 [/ латекс] на [латекс] 9 [/ латекс]. | [латекс] 8 [/ латекс] |
| Проверить умножением. [латекс] 8 \ cdot 9 [/ латекс] | |
| [латекс] 72 \ квадратик \ галочка [/ латекс] |
| 3. | |
| [латекс] 7 \ overline {) 63} [/ латекс] | |
| Разделите [латекс] 63 [/ латекс] на [латекс] 7 [/ латекс]. | [латекс] 9 [/ латекс] |
| Проверить умножением. [латекс] 9 \ cdot 7 [/ латекс] | |
| [латекс] 63 \ квадратик \ галочка [/ латекс] |
Каково частное при делении числа на само себя?
[латекс] \ frac {15} {15} = 1 \ text {потому что} 1 \ cdot 15 = 15 [/ латекс]
Разделение любого числа [латекс] \ text {(кроме 0)} [/ latex] на само по себе дает частное [латекс] 1 [/ latex].Кроме того, любое число, деленное на [latex] 1 [/ latex], дает частное от числа. Эти две идеи изложены в разделе «Свойства единицы».
Подразделение недвижимости одного
| Любое число (кроме 0), разделенное само по себе, равно единице. | [латекс] a \ div a = 1 [/ латекс] |
| Любое число, разделенное на единицу, является одним и тем же числом. | [латекс] a \ div 1 = a [/ латекс] |
пример
Разделить. Затем проверьте умножением:
- [латекс] 11 \ div 11 [/ латекс]
- [латекс] \ frac {19} {1} [/ латекс]
Решение:
| 1. | |
| [латекс] 11 \ div 11 [/ латекс] | |
| Число, разделенное само по себе, — [латекс] 1 [/ латекс]. | [латекс] 1 [/ латекс] |
| Проверить умножением. [латекс] 1 \ cdot 11 [/ латекс] | |
| [латекс] 11 \ квадратик \ галочка [/ латекс] |
| 2. | |
| [латекс] \ frac {19} {1} [/ латекс] | |
| Число, деленное на [латекс] 1 [/ латекс], равно самому себе. | [латекс] 19 [/ латекс] |
| Проверить умножением. [латекс] 19 \ cdot 1 [/ латекс] | |
| [латекс] 19 \ квадратик \ галочка [/ латекс] |
Предположим, у нас есть [latex] \ text {\ $ 0} [/ latex], и мы хотим разделить его между [latex] 3 [/ latex] людьми. Сколько получит каждый человек? Каждый получит [латекс] \ текст {\ $ 0} [/ латекс]. Ноль разделенный на любое число — [латекс] 0 [/ латекс].
Теперь предположим, что мы хотим разделить [latex] \ text {\ $ 10} [/ latex] на [latex] 0 [/ latex].Это означает, что нам нужно найти число, которое мы умножим на [latex] 0 [/ latex], чтобы получить [latex] 10 [/ latex]. Этого не может произойти, потому что [латекс] 0 [/ латекс] умноженное на любое число равно [латекс] 0 [/ латекс]. Деление на ноль называется undefined .
Эти две идеи составляют свойство деления нуля.
Подразделение недвижимости Zero
| Нуль, деленный на любое число, будет [латекс] 0 [/ латекс]. | [латекс] 0 \ div a = 0 [/ латекс] |
| Деление числа на ноль не определено. | [латекс] a \ div 0 [/ латекс] undefined |
Другой способ объяснить, почему деление на ноль не определено, — это помнить, что деление на самом деле является повторным вычитанием. Сколько раз мы можем убрать [latex] 0 [/ latex] из [latex] 10? [/ Latex] Поскольку вычитание [latex] 0 [/ latex] никогда не изменит общую сумму, мы никогда не получим ответа. Таким образом, мы не можем разделить число на [латекс] 0 [/ латекс].
пример
Разделить. Проверить умножением:
- [латекс] 0 \ div 3 [/ латекс]
- [латекс] \ frac {10} {0} [/ латекс]
Решение
| 1. | |
| [латекс] 0 \ div 3 [/ латекс] | |
| Ноль, деленный на любое число, равняется нулю. | [латекс] 0 [/ латекс] |
| Проверить умножением. [латекс] 0 \ cdot 3 [/ латекс] | |
| [латекс] 0 \ четырехугольник \ галочка [/ латекс] |
| 2. | |
| [латекс] 10/0 [/ латекс] | |
| Деление на ноль не определено. | undefined |
Когда делитель или делимое состоит более чем из одной цифры, обычно проще использовать нотацию [latex] 4 \ overline {) 12} [/ latex]. Этот процесс называется длинным делением. Давайте поработаем над процессом, разделив [латекс] 78 [/ латекс] на [латекс] 3 [/ латекс].
| Разделите первую цифру делимого, [латекс] 7 [/ латекс], на делитель, [латекс] 3 [/ латекс]. | |
| Делитель [латекс] 3 [/ латекс] может входить в [латекс] 7 [/ латекс] два раза, так как [латекс] 2 \ times 3 = 6 [/ латекс].Напишите [латекс] 2 [/ латекс] над [латексом] 7 [/ латекс] в частном. | |
| Умножьте [латекс] 2 [/ латекс] в частном на [латекс] 2 [/ латекс] и запишите произведение [латекс] 6 [/ латекс] под [латекс] 7 [/ латекс]. | |
| Вычтите это произведение из первой цифры дивиденда. Вычтите [латекс] 7 — 6 [/ латекс]. Напишите разницу, 1, под первой цифрой делимого. | |
| Опустите следующую цифру делимого.Сбиваем [латекс] 8 [/ латекс]. | |
| Разделите [латекс] 18 [/ латекс] на делитель, [латекс] 3 [/ латекс]. Делитель [латекс] 3 [/ латекс] переходит в [латекс] 18 [/ латекс] шесть раз. | |
| Напишите [латекс] 6 [/ латекс] в частном над [латексом] 8 [/ латексом]. | |
| Умножьте [латекс] 6 [/ латекс] в частном на делитель и запишите произведение [латекс] 18 [/ латекс] под делимым. Вычтите [латекс] 18 [/ латекс] из [латекс] 18 [/ латекс]. |
Мы будем повторять процесс до тех пор, пока в дивиденде не останется цифр, которые нужно уменьшить. В этой задаче больше нет цифр, которые нужно сбивать, поэтому деление закончено.
[латекс] \ text {So} 78 \ div 3 = 26 [/ латекс].
Проверьте, умножив частное на делитель, чтобы получить дивиденд. Умножьте [латекс] 26 \ на 3 [/ латекс], чтобы убедиться, что продукт равен дивиденду, [латекс] 78 [/ латекс].
[латекс] \ begin {array} {c} \ hfill \ stackrel {1} {2} 6 \\ \ hfill \ underset {\ text {___}} {\ times 3} \\ \ hfill 78 \ end {массив } [/ латекс]
Да, поэтому наш ответ правильный.[латекс] \ галочка [/ латекс]
Деление целых чисел
- Разделите первую цифру делимого на делитель. Если делитель больше, чем первая цифра делимого, разделите первые две цифры делимого на делитель и т. Д.
- Напишите частное над дивидендом.
- Умножьте частное на делитель и запишите произведение под делимым.
- Вычтите этот продукт из дивиденда.
- Введите следующую цифру делимого.
- Повторяйте действия с шага 1 до тех пор, пока в делимом не останется цифр, которые нужно уменьшить.
- Проверьте, умножив частное на делитель.
На видео ниже мы показываем еще один пример использования деления в столбик.
пример
Разделить [латекс] 2,596 \ div 4 [/ латекс]. Проверить умножением:
Покажи ответРешение
Это равняется дивиденду, поэтому наш ответ правильный.
пример
Разделите [латекс] 4,506 \ div 6 [/ латекс].Проверить умножением:
Покажи ответРешение
Это равняется дивиденду, поэтому наш ответ правильный.
Посмотрите это видео, чтобы увидеть еще один пример того, как использовать длинное деление для деления четырехзначного целого числа на двузначное целое число.
Пока все проблемы с разделением решаются равномерно. Например, если бы у нас было [латексное] 24 [/ латексное] печенье и мы хотели бы сделать пакеты из [латексного] 8 [/ латексного] печенья, у нас были бы [латексные] 3 [/ латексные] пакеты.Но что, если бы было печенье [latex] 28 [/ latex], и мы хотели бы сделать пакеты из [latex] 8? [/ Latex] Начнем с файлов cookie [latex] 28 [/ latex].
Попробуйте разместить файлы cookie группами по восемь штук.
Остались [latex] 3 [/ latex] группы из восьми файлов cookie и [latex] 4 [/ latex] файлов cookie. Мы вызываем оставшиеся файлы cookie [latex] 4 [/ latex] и показываем их, записывая R4 рядом с [latex] 3 [/ latex]. (R означает остаток.)
Чтобы проверить это деление, мы умножаем [latex] 3 [/ latex] на [latex] 8 [/ latex], чтобы получить [latex] 24 [/ latex], а затем складываем остаток [latex] 4 [/ latex].
[латекс] \ begin {array} {c} \ hfill 3 \\ \ hfill \ underset {\ text {___}} {\ times 8} \\ \ hfill 24 \\ \ hfill \ underset {\ text {___} } {+ 4} \\ \ hfill 28 \ end {array} [/ latex]
пример
Разделить [латекс] 1,439 \ div 4 [/ латекс]. Проверить умножением.
Покажи ответРешение
Итак [латекс] 1,439 \ div 4 [/ latex] — это [латекс] 359 [/ latex] с остатком [латекс] 3 [/ latex]. Наш ответ правильный.
пример
Разделите, а затем проверьте умножением: [латекс] 1,461 \ div 13 [/ латекс].
Покажи ответРешение
Наш ответ правильный.
Посмотрите видео ниже, чтобы увидеть еще один пример того, как использовать длинное деление для деления целых чисел, когда есть остаток.
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Математика для 5-х классов — Блок 5: Умножение и деление дробей
Сводка по установке
В 5 классе 5 класса учащиеся продолжают изучение операций с дробями, углубляя свое понимание умножения дробей с 4 класса и знакомя их с делением на дроби.
Учащиеся очень рано начали изучать дроби, как описано в разделе «Краткое содержание раздела 4». Однако ученики начали знакомиться с умножением дробей только в 4 классе, когда они научились умножать дробь на целое число, интерпретируя это как повторное сложение. Например, $$ {4 \ times {2 \ over3}} $$ рассматривается как 4 копии 2 третей. Это понимание основано на понимании умножения как равных групп (3.OA.1). Однако в 4-м классе ученики также развили понимание мультипликативного сравнения (4.OA.1), что будет иметь особое значение для новых способов интерпретации учащимися умножения дробей в этом модуле.
Раздел начинается с того, что учащиеся развивают новое понимание дробей как деления. Раньше они думали о дробях как о разделах целого равного размера, но здесь они развивают понимание дроби как самой операции и представляют проблемы деления как дроби (5.NF.3). Теперь студенты видят, что остатки можно интерпретировать еще по-другому, а именно делить на делитель, чтобы получить частное со смешанными числами.Затем учащиеся развивают новое понимание умножения дробей как дробных частей набора определенного размера (5.NF.4), что представляет собой новую интерпретацию мультипликативного сравнения. Студенты используют это понимание для разработки общих методов умножения дробей на целые числа и дроби, включая смешанные числа. На протяжении этой работы студенты развивают понимание умножения как шкалы (5.NF.5), «важной возможности для студентов рассуждать абстрактно» (MP.2), как отмечается в Progressions (Progressions for the Common Core State Standards in Mathematics, Число и операции — Дроби, 3-5, стр.14). Затем учащиеся изучают деление единичной дроби на целое число и целого числа на единичную дробь (5.NF.7), подготавливая учащихся к делению дробями во всех случаях в 6 классе (6.NS.1). Затем студенты также решают множество задач со словами, видя, что стратегии, которые они использовали для решения задач со словами с целыми числами, все еще применимы, но особое внимание следует уделять обсуждаемому целому (5.NF.6, MP.4), а также писать и решать выражения, содержащие дроби, как способ поддержки основной работы (5.OA.1, 5.OA.2). Наконец, учащиеся создают линейные графики для отображения набора данных измерений в долях единицы и решения задач, связанных с информацией, представленной на линейных графиках (5.MD.2), поддерживающем кластерном стандарте, который поддерживает основную работу этого и предыдущего модуля. использования всех четырех операций с дробями (5.NF).
В Блоке 6 студенты научатся умножать и делить десятичные дроби, полагаясь на свое понимание этих операций с дробями, разработанное для этого в этом блоке. В 6 классе ученики сталкиваются с оставшимися случаями дробного деления (6.NS.1). «Работа с дробями и умножением — это строительный блок для работы с отношениями. В 6 и 7 классах учащиеся используют свое понимание целых и частей, чтобы рассуждать о соотношениях двух величин, составляя и анализируя таблицы эквивалентных соотношений, и отображая пары из этих таблиц в координатной плоскости. Эти таблицы и графики представляют собой пропорциональные отношения, которые учащиеся рассматривают как функции в 8-м классе »(NF Progression, стр. 20). Студенты в дальнейшем будут полагаться на эту оперативную беглость на протяжении всей оставшейся части своей математической карьеры, от дробных коэффициентов в функциях до связи между иррациональными числами и неповторяющимися десятичными знаками.
Темп: 27 учебных дней (24 урока, 2 гибких дня, 1 оценочный день)
Чтобы узнать, как изменить темп на 2020-2021 учебный год в связи с закрытием школ, см. Наши Рекомендуемые корректировки объема и очередности 5-го класса.
Решение задач умножением и делением дробей и смешанных чисел
Задачи на дробные слова с помощью интерактивных упражнений
Пример 1. Если для изготовления платья требуется 5/6 ярдов ткани, то сколько ярдов потребуется для изготовления 8 платьев?
Анализ: Чтобы решить эту проблему, мы преобразуем целое число в неправильную дробь.Затем мы умножим две дроби.
Решение:
Ответ: Для изготовления 8 платьев потребуется 6 и 2/3 ярда ткани.
Пример 2: У Рене была коробка кексов, половину которой она отдала своему другу Хуану. Хуан отдал 3/4 своей доли своей подруге Елене. Какая дробная часть оригинальной коробки кексов досталась Елене?
Анализ: Чтобы решить эту проблему, мы умножим эти две дроби.
Решение:
Ответ: Елене досталось 3/8 оригинальной коробки кексов.
Пример 3: Класс математики Нины имеет длину 6 и 4/5 метра и ширину 1 и 3/8 метра. Какая площадь классной комнаты?
Анализ: Чтобы решить эту проблему, мы умножим эти смешанные числа. Но сначала мы должны преобразовать каждое смешанное число в неправильную дробь.
Решение:
Ответ: Площадь аудитории 9 и 7/20 квадратных метров.
Пример 4: Плитка шоколада имеет длину 3/4 дюйма. Если он разделен на части длиной 3/8 дюйма, то сколько это частей?
Анализ: Чтобы решить эту задачу, мы разделим первую дробь на вторую.
Решение:
Ответ: 2 шт.
Пример 5. У электрика есть кусок провода длиной 4 и 3/8 сантиметра. Она делит проволоку на кусочки длиной 1 и 2/3 сантиметра. Сколько у нее штук?
Анализ: Чтобы решить эту проблему, мы разделим первое смешанное число на второе.
Решение:
Ответ: У электрика 2 и 5/8 куска провода.
Пример 6: На складе 1 и 3/10 метров ленты. Если они разделят ленту на куски длиной 5/8 метров, то сколько кусков у них получится?
Анализ: Чтобы решить эту проблему, мы разделим первое смешанное число на второе. Сначала мы преобразуем каждое смешанное число в неправильную дробь.
Решение:
Ответ: На складе будет 2 и 2/25 кусков ленты.
Резюме: В этом уроке мы узнали, как решать задачи со словами, связанные с умножением и делением дробей и смешанных чисел.
Упражнения
Указания: вычтите смешанные числа в каждом упражнении ниже. Обязательно упростите ваш результат, если необходимо. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
Примечание. Чтобы написать смешанное число четыре и две трети, введите в форму 4, пробел и затем 2/3.
| 1. | Одна партия печенья содержит 1 и 3/4 стакана растопленного шоколада. Сколько чашек растопленного шоколада нужно для изготовления 8 партий печенья? |
| 2. | Тодд выпил 5/8 банки сока объемом 24 унции. Лайла выпила на треть меньше сока, чем Тодд. Сколько унций выпила Лила? |
| 3. | Прямоугольный коврик имеет длину 3 и 2/3 фута и ширину 2 и 3/4 фута. Какова площадь коврика? |
| 4. | У Джанет 5 и 3/4 сантиметра лакричника. Она делит лакрицу на кусочки длиной 1 и 7/8 сантиметра. Сколько кусочков солодки у нее будет? |
| 5. | Кусок дерева длиной 15 футов.Сколько 3/4 фута можно вырезать из него? |
Важные математические навыки для пятиклассников
Хотите помочь своему пятикласснику освоить математику? Вот некоторые из навыков, которые ваш пятиклассник будет изучать в классе.
Сложение, вычитание, умножение и деление
Многозначные целые числа
Быстро и точно умножайте многозначные целые числа. Разделите целые числа (до четырех цифр) на двузначные числа.
Пример:
Решить 4,824 ÷ 12 =?
Объясните или проиллюстрируйте, как вы решили эту проблему.
Совет: выделите реальные примеры использования математики.
По мере того, как математика, которую они изучают, становится более сложной и менее очевидно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревога. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять, как в реальной жизни применяются концепции, которые ребенок изучает в школе.Составление бюджета на школьные принадлежности или их ежемесячное пособие — один из способов практиковать сложение и вычитание. Попросите их помочь вам с приготовлением или выпечкой, чтобы показать, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.
Связанные
Понимание разряда
Расширьте понимание разряда: в многозначном числе цифра в одном месте представляет 1⁄10 того, что она представляет в месте слева от него, и в 10 раз больше как он изображен справа от него.
Сравнение десятичных знаков
Чтение, запись и сравнение десятичных знаков с разрядами тысячных, используя символы> (больше чем) и <(меньше чем). Например:
- Прочтите это десятичное число: 23,002.
- Запишите две и шестьдесят две тысячные в виде десятичного числа.
- Какой знак подтверждает это утверждение: 5,389 _? _ 5,420
- Исследователь измеряет количество бактерий, выросших на образцах неохлажденных продуктов. Ваш ребенок насчитывает 73.343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий к наименьшему. Объясните или проиллюстрируйте, как вы приводите эти образцы в порядок.
Связанные
Десятичные доли до сотых
Сложение, вычитание, умножение и деление десятичных долей до сотых.
Совет: потренируйтесь в вычислениях с использованием десятичных знаков.
Свяжите работу с десятичными знаками, которую ваш ребенок делает в классе, с реальным миром, поощряя их делать покупки по выгодным ценам.Попросите их разделить стоимость товаров, упакованных оптом, на количество отдельных товаров, чтобы определить стоимость каждого товара. Итак, сколько вы платите за рулон бумажного полотенца или за банку газировки при покупке оптом? Или попросите ребенка подсчитать, сколько вы сэкономите на каждом товаре, если цены со скидкой предполагают оптовые скидки.
Показатели степени
Разберитесь, что такое показатель степени. Например, «2» в 10² указывает, сколько раз нужно умножить число само на себя. 10² можно читать как «10 в степени 2», «10 в степени 2» или «10 в квадрате» и означает 10 x 10 или 100.10³ (или «10 в третьей степени» или «10 в кубе») означает 10 x 10 x 10, или 1000.
Дроби
Решение задач со словами
Решение задач со словами, включающих сложение и вычитание дробей.
Пример:
Ученики пятого класса собирают пазл из 600 деталей. Они начали вчера и собрали 100 частей — всего одну шестую (1⁄6) головоломки. Сегодня их собрано 400 штук. Какая часть головоломки завершена? Нарисуйте картинку И запишите математику, чтобы показать, как вы решили задачу.
Совет: выделите реальные примеры использования математики.
По мере того, как математика, которую они изучают, становится более сложной и менее очевидно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревога. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять, как в реальной жизни применяются концепции, которые он изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — один из способов для нее практиковать сложение и вычитание.Если вы попросите ее помочь вам с приготовлением или выпечкой, это покажет ей, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.
Нахождение общего знаменателя
Решите задачи со словами, включающие сложение и вычитание дробей с разными знаменателями (нижние числа), преобразовывая их в дроби с одинаковым знаменателем, называемые общим знаменателем.
Пример:
Самая высокая девочка в пятом классе имеет рост 51 7⁄8 дюйма.Самый высокий мальчик в пятом классе имеет рост 49 1⁄2 дюйма. Какая разница в их росте?
После вечеринки остались две чашки лимонада. В одной миске 1⁄3 галлона. В другом — 1⁄2 галлона лимонада. Друг говорит, что не стоит пытаться объединить их в 1-галлонный контейнер, потому что лимонад вытечет наверх. Вы согласны? Почему или почему нет?
Умножение дробей
Решайте задачи со словами, включающие умножение дробей на другие дроби и умножение дробей на смешанные числа (целое число и дробь, например 11⁄4 или 21⁄2).
Пример:
- В оркестре средней школы 1⁄3 учащихся-музыкантов играют на струнных инструментах. Из учеников, играющих на струнных инструментах, 3⁄4 играют на скрипке. Какая часть оркестра играет на скрипке?
- Утром во время экскурсии в яблоневый сад пятиклассники собрали 4⁄5 бушеля яблок. После обеда в полдень они собрали в 2,5 раза больше яблок. Уместятся ли все яблоки, собранные ими днем, в ящик на 2 бушеля? Откуда вы знаете?
Совет: потренируйтесь использовать дроби.
Помогите своему ребенку познакомиться с дробями, попросив его масштабировать рецепты для вашей семьи. Пусть они начнут с того, что сократят или удвоят рецепт. Когда они почувствуют себя комфортно, попросите их преобразовать его на 1 1/2, что позволит рецепту, который должен накормить семью из четырех человек, работать на семью из шести человек.
Дроби единицы деления
Разделите дроби единицы (дроби с 1 в числителе или верхним числом) на целые числа. Разделите целые числа на единичные дроби.
Пример:
Если три человека разделят ½ фунта шоколада поровну, сколько шоколада получит каждый? Объясните или проиллюстрируйте, как вы решили эту проблему.
Умножение на дроби
Помните, что умножение числа на дробь меньше 1 даст ответ меньше числа — например: 12 x ¾ = 9. Умножение числа на дробь больше 1 даст результат в ответе больше числа — например: 12 x 2 ½ = 30.
Измерения и данные
Преобразование единиц и дробей
Преобразование единиц и долей единиц в одной системе измерения.
Пример:
Сколько минут составляет 1⁄5 часа? Объясните или проиллюстрируйте, как вы решили эту проблему.
Проблемы многоступенчатого преобразования единиц измерения
Решайте многоступенчатые проблемы со словами, используя преобразование стандартных единиц измерения разного размера.
Пример:
У меня 75 см ленты.Для выполнения проекта мне нужно в семь раз больше ленты. Сколько еще метров ленты мне нужно?
Объясните или проиллюстрируйте, как вы решили эту проблему.
Использование линейного графика
Решайте проблемы, используя информацию (в единицах дроби), представленную на линейном графике.
Геометрия
Объем
Под объемом понимается измерение пространства внутри трехмерной или твердой фигуры. Используйте формулы длина x ширина x высота или основание x высота , чтобы измерить объем трехмерного или твердого объекта с прямоугольными сторонами, например куба.Измеряйте объем для решения реальных проблем.
Пример:
Прямоугольный контейнер для мороженого имеет длину 8 дюймов и высоту 4 дюйма. Каков объем контейнера, выраженный в кубических дюймах?
Советы, которые помогут вашему пятикласснику в уроке математики, можно найти на нашей странице с советами по математике для пятого класса.
Ресурсы Parent Toolkit были разработаны NBC News Learn с помощью профильных экспертов и соответствуют Общим основным государственным стандартам.
Сначала умножить или сложить? Порядок обучения правилам действий
Когда ученики 3-х классов и выше учатся складывать, вычитать, умножать, делить и работать с основными числовыми выражениями, они начинают с выполнения операций над двумя числами. Но что происходит, когда выражение требует нескольких операций? Например, вы сначала складываете или умножаете? А как насчет умножения или деления? В этой статье объясняется, в каком порядке выполняются операции, и приводятся примеры, которые вы также можете использовать со студентами.Он также содержит два урока, которые помогут вам представить и развить концепцию.
Ключевой стандарт:
- Выполняйте арифметические операции, включающие сложение, вычитание, умножение и деление в обычном порядке, независимо от того, присутствуют ли скобки или нет. (Оценка 3)
Порядок операций — пример математики, которая очень процедурна. Легко ошибиться, потому что это не столько концепция, которую вы усвоили, а скорее список правил, которые вам нужно запомнить.Но не обманывайтесь, думая, что процедурные навыки не могут быть глубокими! Он может представлять сложные проблемы, подходящие для старших школьников и созревшие для обсуждения в классе:
- Меняется ли правило слева направо, когда умножение подразумевается, а не прописано? (Например, \ (3g \) или \ (8 (12) \) вместо \ (3 \ times g \) или \ (8 \ cdot 12 \).)
- Где факториал попадает в порядок операции?
- Что происходит, когда показатель степени возводится в другой показатель, но скобок нет? (Обратите внимание, что этот урок не включает экспоненты, хотя, если учащиеся готовы, вы можете расширить свой урок, включив их.)
Что первично в порядке работы?
Со временем математики согласовали набор правил, называемый порядком операций , чтобы определить, какую операцию выполнить в первую очередь. Когда выражение включает только четыре основных операции, вот правила:
- Умножайте и делите слева направо.
- Сложить и вычесть слева направо.
При упрощении выражения, такого как \ (12 \ div 4 + 5 \ times 3-6 \), сначала вычислите \ (12 \ div 4 \), поскольку порядок операций требует сначала оценки любого умножения и деления (в зависимости от того, что произойдет первый) слева направо перед вычислением сложения или вычитания.В данном случае это означает сначала вычисление \ (12 \ div 4 \), а затем \ (5 \ times 3 \). После того, как все умножение и деление будут завершены, продолжайте, добавляя или вычитая (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.
| \ (12 \ div 4 + 5 \ times 3-6 \) | |
| \ (3 + 5 \ times 3-6 \) | Потому что \ (12 \ div 4 = 3 \) |
| \ (3 + 15 — 6 \) | Потому что \ (5 \ times 3 = 15 \) |
| \ (18-6 \) | Потому что \ (3 + 15 = 18 \) |
| \ (12 \) | Потому что \ (18-6 = 12 \) |
Рассмотрим в качестве примера другое выражение:
| \ (6 + 4 \ times 7-3 \) | |
| \ (6 + 28-3 \) | Потому что \ (4 \ times 7 = 28 \), что выполняется первым, потому что умножение и деление оцениваются в первую очередь. |
| \ (34-3 \) | Потому что \ (6 + 28 = 34 \) |
| \ (31 \) | Потому что \ (34-3 = 1 \) |
Иногда мы можем захотеть убедиться, что сначала выполняется сложение или вычитание. Группировка символов , таких как скобки , \ (() \), скобки , \ ([] \) или фигурные скобки , \ (\ {\} \), позволяют нам определять порядок, в котором выполняются определенные операции. выполнено.
Порядок операций требует, чтобы операции внутри символов группировки выполнялись перед операциями вне их.Например, предположим, что выражение 6 + 4 заключено в круглые скобки:
| \ ((6 + 4) \ times 7-3 \) | |
| \ (10 \ times 7-3 \) | Потому что \ (6 + 4 = 10 \), что и делается во-первых, потому что он заключен в круглые скобки. |
| \ (70 — 3 \) | Потому что \ (10 \ times 7 = 70 \), и скобок больше нет. |
| \ (67 \) | Потому что \ (70-3 = 67 \) |
Обратите внимание, что выражение имеет совершенно другое значение! Что, если вместо этого мы заключим \ (7 — 3 \) в круглые скобки?
| \ (6 + 4 \ times (7-3) \) | |
| \ (6 + 4 \ times 4 \) | На этот раз \ (7-3 \) находится в скобках, так что мы делаем это в первую очередь. |

 Сколько? От 1 до 5
Сколько? От 1 до 5
 Числа от 1 до 9
Числа от 1 до 9
 Сколько? От 11 до 20
Сколько? От 11 до 20
 Нумерация. Числа и цифры
Нумерация. Числа и цифры
 .. Увеличить в… Уменьшить на… Уменьшить в…
.. Увеличить в… Уменьшить на… Уменьшить в…
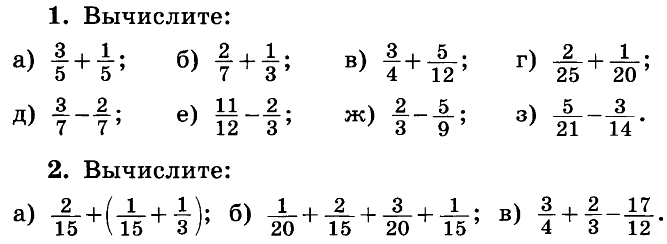 Виды треугольников
Виды треугольников
 Нумерация
Нумерация
 Распределительный закон умножения относительно сложения
Распределительный закон умножения относительно сложения
 Минута. Секунда
Минута. Секунда
 Нахождение части числа
Нахождение части числа
 Римская нумерация
Римская нумерация
 Прикидка и оценка результатов вычислений
Прикидка и оценка результатов вычислений
 Понятие обыкновенной дроби
Понятие обыкновенной дроби
 Измерение углов
Измерение углов
 Масштаб. Виды масштаба
Масштаб. Виды масштаба
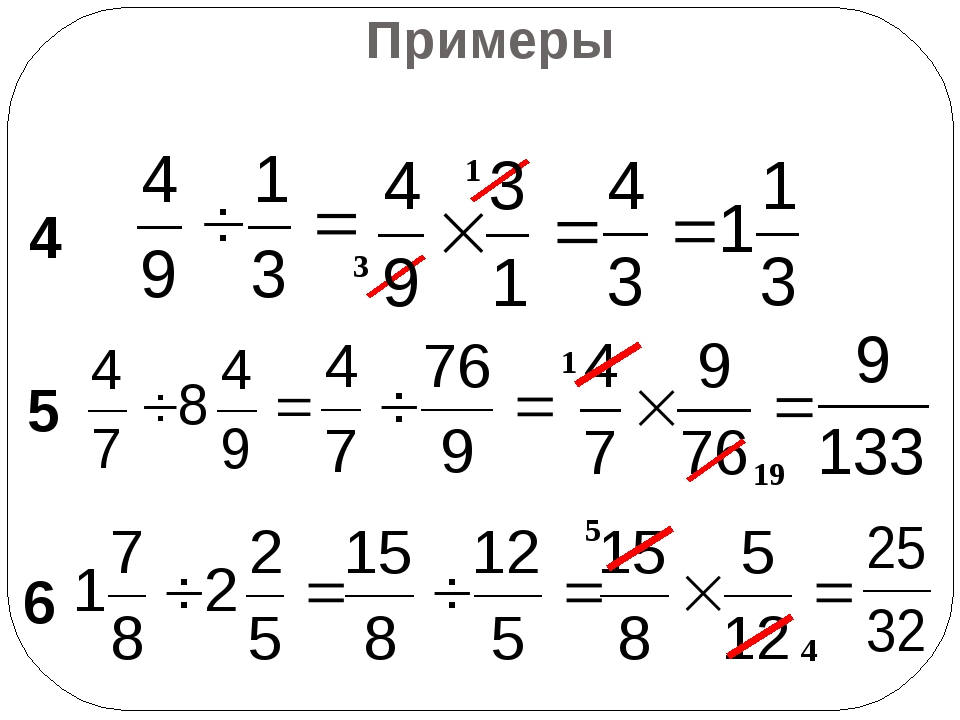 Сравнение
Сравнение
 Среднее арифметическое, деление на натуральное число
Среднее арифметическое, деление на натуральное число
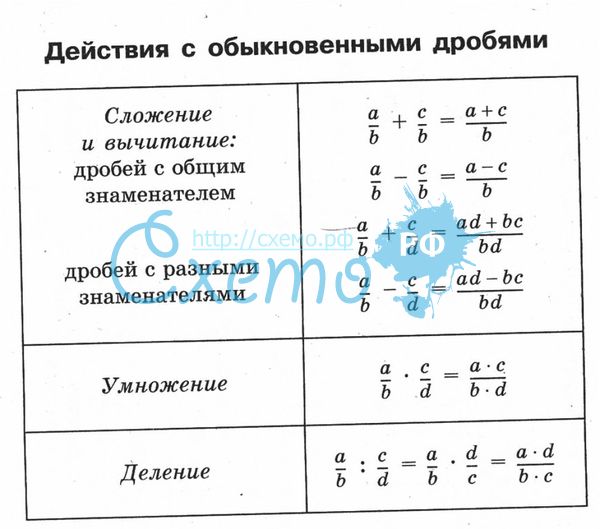 Определение, свойства
Определение, свойства
 Разложение натурального числа на простые множители
Разложение натурального числа на простые множители
 Модуль числа. Целые и рациональные числа
Модуль числа. Целые и рациональные числа
 Координатная плоскость, координаты точки
Координатная плоскость, координаты точки
 Число Пи. Длина окружности. Площадь круга
Число Пи. Длина окружности. Площадь круга

 После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2 При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2

