Примеры с обыкновенными дробями как решать: Примеры и задачи с дробями

Содержание

Порядок действий в примерах без скобок

Порядок действий в примерах без скобок.

Цели урока:

образовательная: учить решать примеры в несколько действий с обыкновенными дробями и смешанными числами по степени их сложности;

развивающая: развивать математическую речь, умение работать с различными видами информации (таблицы, макеты часов, касса дробей, дидактические карточки), математическую речь;

воспитательная: воспитывать активную личность.

Оборудование. Макеты часов, касса дробей, дидактические карточки.

Ход урока.

I. Организационный момент.

Садится только тот, кто правильно прочитает дроби:

1011; 66; 18 17; 188; 165; 23; 83; 1112; 49.

Какая дробь называется правильной?

Какая дробь называется неправильной?

Что показывает знаменатель дроби?

Что показывает числитель дроби?

Учитель. Чем отличается дробь от смешанного числа?

Дети.

Хором: Каждый может за версту

Видеть дробную черту

Над чертой – числитель, знайте

Под чертою – знаменатель.

Дробь такую, непременно

Надо звать обыкновенной.

Словарная работа.

Верста – путевая мера в 500 сажен.

Сажень – мера в 3 аршина.

Аршин – длина всей руки от руки до плеча.

Верста- путевая мера длины, составляющая 1067 км.

II. Проверка домашнего задания.

№322, 2 примера: 1 пример на умножение и 1 пример на деление.

Как называются компоненты при делении?

Как называются компоненты при умножении?

238 х 6 = 198 х 6 = 19х69 = 574 = 14 14

9 16 : 22 = 556Х22 = 512

III. Устный счет.

1. Сколько минут составляет четверть часа? (15 мин)

1 ч = 60 мин

Чтобы найти 14 от 60 мин надо 60 мин : 4 = 15 мин

Чтобы найти часть от числа, надо знаменатель дроби разделить на это число.

Учитель:

1. Покажите на макете часов четверть девятого.

2 .Восемь часов пятнадцать минут.

3. Пятнадцать минут девятого.

Учитель. Секунда, минута, часы – это какая мера измерения? (меры времени)

Воспитательный момент.

Ребята, а вы умеете ценить время?

Ребята, дорожите своим временем.

В сказке “Потерянное время” дети не умели ценить свое время и не успели оглянуться, как быстро состарились.

Загадка.

Две сестрички друг за другом

Пробегают круг за кругом.

Коротышка – только раз

Та, что выше – каждый час. (Минутная и часовая стрелки)

2. У Саши было 4 целых яблока, 4 половинки и 4 четвертинки. Сколько яблок было у Саши? (7 яблок).

3. Назовите 6 дробей, которые непосредственно следуют за дробью 311

4. Назовите 5 дробей. Которые предшествуют дроби 67

5. Масса 14 арбуза равна 3 кг. Чему равна масса всего арбуза?

14 х = 3 кг х = 3 кг х 4

х= 44 х = 12 кг

Число по его доле находится умножением. Данная доля умножается на количество долей.

6. Работа с ребусом: дробь, числитель, знаменатель.

IV. Сообщение темы и цели урока.

Сегодня на уроке мы с вами должны вспомнить все действия с обыкновенными дробями и смешанными числами, решать примеры по порядку действий по степени их сложности. по поря

Повторение пройденной темы.

Учитель.

— Давайте вспомним, как умножить дробь на целое число?

Например: 35 х 2 = 3 х 25 = 65 = 1 15

Чтобы умножить дробь на целое число, надо числитель дроби умножить на целое число, а знаменатель оставить тот же.

— Как разделить дробь на целое число?

Например: 35 : 2 = = 3 5 х 2 = 310

Чтобы разделить дробь на целое число, надо знаменатель дроби умножить на целое число, а числитель оставить без изменения.

— Как умножить смешанное число на целое число?

Например: 2 14 х 5 = 94 х 5 = 9 х 54 = 454 = 11 14

Чтобы умножить смешанное число на целое число, надо записать смешанное число в виде неправильной дроби и умножить ее на целое число.

— Как разделить смешанное число на целое число?

Например: 5 12 : 3 = 112 : 3 = 112 х 3 = 116 = 1 56

Чтобы разделить смешанное число на целое число, надо записать смешанное число в виде неправильной дроби и умножить его на целое число.

V. Работа с учебником.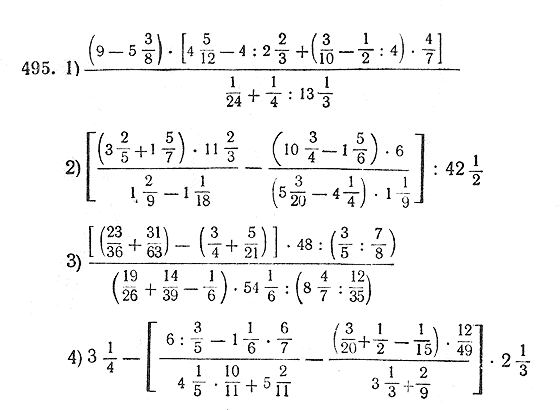

№ 323, страница 115

1. 6 38 : 3 — 58 : 10 = 8 38

2. 6 38 : 3 =

518 х 3 =178 = 2 18

3. 58 : 10 = 508 = 6 28

4. 2 18 + 6 28 = 8 38

Речевая физминутка.

Настольная лампа, зеленый диван.

Сидит на диване Матюшин Иван (Приседают.)

Он пишет … (имитация письма)

Не будем, ребята, мешать.

А только тихонько, (Подходят тихонечко на носочках.)

Заглянем в тетрадь. (Имитация подглядывания.)

В тетрадке написано все по порядку: (Указательным пальцем перечисляют.)

«В семь двадцать встаем, производим зарядку».

(Ноги на ширине плеч, руки перед грудью, кончики пальцев касаются друг друга. На «раз-два» движения рывком, на «три-четыре» — в разные стороны.)

«В семь тридцать, умывшись холодной водой, (Имитация умывания.)

Застелем постель (имитация приведения в порядок постели)

И займемся едой.

Готовим по плану похлебку.

(Имитация помешивания в кастрюле воображаемой ложкой.)

Развесим белье на веревку.(Руки вверх, встряхивают белье, вешают.)

С мамой попрощаемся, (Прощальный жест.)

С друзьями повстречаемся (рукопожатие с соседом)

В школу отправляемся (Шаги на месте.)

За парту садимся (Садятся за парту.)

Воспитательный момент. Ребята, а вы делаете по утрам зарядку? Постель сами застилаете?

Решение примеров.

1. 25 : 8 – 5 38 : 8 = 110

1. 6 25 : 8 = 325 х 8 = 3240 = 45

2. 5 35 : 8 = 285 х 8 = 2840 = 710

3. 45 — 710 = 810 — 710 = 110

Упражнение для рук «Рыбка».

Установить кисть ладонью к себе. Совершать волнообразные движения всей кистью во всех направлениях.(вправо –влево, вперед – назад, вверх – вниз) на длину вытянутой руки.

Упражнение выполнять 15-20 секунд

Упражнение для рук «Осьминог».

Установить кисть на столе, касаясь его подушечками пальцев, запястьем вверх. Пальцы врозь. Движение по столу выполнять каждым пальцем по отдельности. Упражнение делать поочередно правой и левой рукой, затем одновременно двумя руками. Упражнение выполнять 15-20 секунд.

Дыхательное упражнение.

Дуновением открыть изображение геометрических фигур.

Гимнастика для глаз «Филин».

Закрыть глаза и держать закрытыми на счет 1 – 4. Широко раскрыть глаза, посмотреть вдаль и держать открытыми на счет 1 – 6.

Упражнение повторить 4 – 5 раз.

Продолжение решения примеров по порядку действий.

2. 89 : 5 — 49 : 6 =

VII. Итог урока

Услышим скоро мы звонок

Пора заканчивать урок.

Какую тему прошли? Все ли было понятно на уроке?

Выполнение совместных действий над обыкновенными дробями

Елсукова Любовь Ивановна

org/BreadcrumbList»> Разделы: Математика

Тип урока: урок обобщения и систематизации знаний.

Вид урока: смешанный.

Цели урока:

обобщение и систематизация знания по теме;
развитие навыков выполнения действий с обыкновенными дробями;
воспитание чувства ответственности за свои действия, умения сопереживать, потребности оказания помощи товарищу.

Методы обучения: фронтальная работа, самостоятельная работа, работа в парах.

Оборудование:

учебник “Математика 6”, Виленкин Н.Я., карточки-задания, переносная доска.

ХОД УРОКА

1 этап. Организационный момент.

Сегодня на уроке мы должны повторить правила выполнения действий с обыкновенными дробями, показать, как мы умеем применять эти правила при решении конкретных примеров и задач.

2 этап. Актуализация.

Устный счет – математическая зарядка.

На доске записаны примеры с ответами. Если пример выполнен верно – поднять руки вперед, неверно – руки вверх, если выполнен не до конца – встать.

В ходе решения исправить ошибки.

3 этап. Применение.

1. Математический диктант.

Таблица ответов (на переносной доске).

Учащиеся письменно отвечают на вопросы, затем обмениваются тетрадями и проверяют друг у друга, выставляют отметки согласно таблице критериев оценки.

Число верных ответов	4	5	6
Отметка	3	4	5

2. “Отгадай слово”. (Решение примеров, парная работа)

У учащихся на столе карточки с примерами. Ответ примера соответствует букве слова. Если все примеры решены правильно, то с помощью “ключа” можно отгадать слово.

Ключ к ответам.

Задача 1. В русском языке это слово появилось в VIII веке, оно происходит от глагола “дробить” — разбивать, ломать на части.

Карточка 1.

Ответ: ДРОБЬ.

В первых учебниках дроби так и называли “ломаные числа”. Современное обозначение дробей берет начало в Древней Индии. Вначале в записи дробей не использовалась дробная черта. Она появилась лишь в 1202 году. Автором первого европейского учебника, в котором использовалась современная запись дробей итальянский купец и путешественник Кибоначчи Леонардо Пизанский. Название числитель и знаменатель ввел в XIII в. Максим Пеануд-греческий – монах, учитель-математик.

Задача 2. Какую единицу длины впервые ввели купцы. Ее еще называли “локоть”.

Карточка 2.

Ответ: АРШИН.

1 аршин=71 см.

Задача 3. На земном шаре живут птицы – безошибочные “составители” прогноза погоды на лето.

Карточка 3.

Ответ: ФЛАМИНГО.

Фламинго строят гнезда в воде конуса: высокие – к дождливому лету, низкие – к сухому.

3. Фронтальный опрос.

Рассказать правила:

— сложение дробей;
— вычитание дробей;
— умножение дробей и смешанных чисел;
— деление дробей и смешанных чисел;
— нахождение дроби от числа;
— нахождение числа по его дроби.

4. Решение задач-шуток Г. Остера.

(Ответ: 3 мальчика и две девочки; должна родиться одна девочка.)

4 этап. Подведение итогов урока, выставление оценок, постановка домашнего задания.

№№ 669, 673,675(в)

22.02.2005

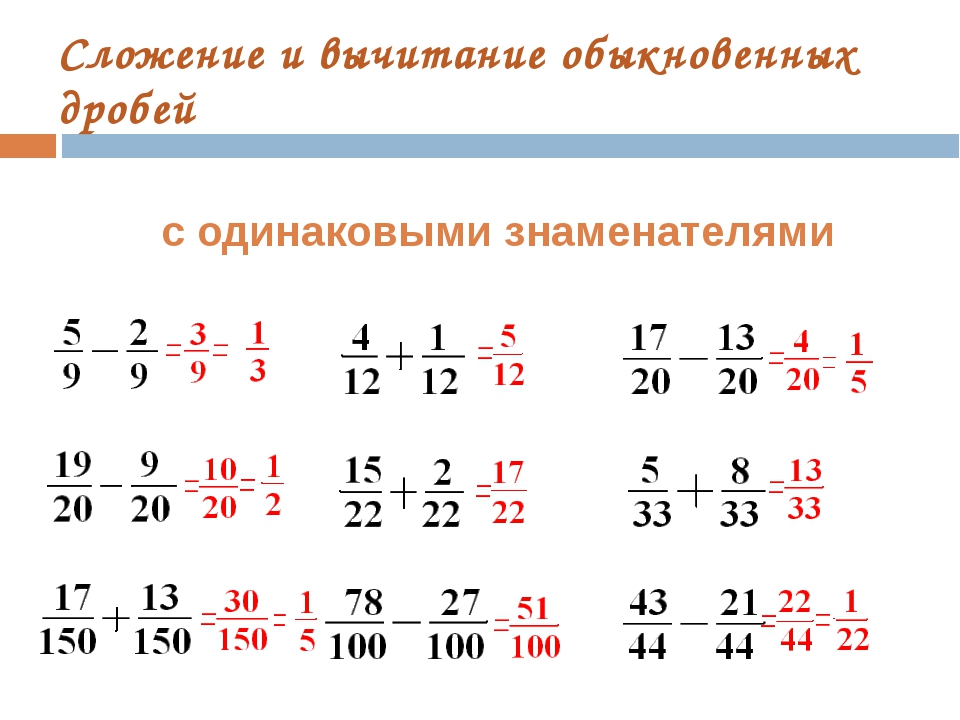
Как складывать дроби с одинаковым знаменателем

Сопутствующие ресурсы: Бум-карты с добавлением фракций, Упражнения с цифровыми фракциями, Учебное пособие для печати,

Что такое общий знаменатель?

Во-первых, давайте убедимся, что мы понимаем различные части дроби: числитель и знаменатель. Числитель — это первое число в верхней части дроби, а знаменатель — второе число в нижней части дроби.

Знаменатель дроби — это число равных частей, на которые разбито целое. Например, если дробь равна 1/6, это означает, что целое было разделено на 6 равных частей, и у вас есть 1 из 6 частей. Если дробь 3/4, это означает, что целое было разделено на 4 равные части, и у вас есть 3 из этих частей.

Когда мы говорим, что дроби имеют общий знаменатель, это означает, что у них одинаковые числа внизу. Когда две дроби имеют общий знаменатель, это означает, что оба целых числа были разделены на одинаковое количество равных частей.

Дроби 5/7 и 2/7 имеют общий знаменатель, потому что у них в знаменателе 7. Это также говорит нам о том, что для обеих дробей целое было разделено на 7 равных частей.

Важно отметить, что когда две дроби имеют общий знаменатель, равные части будут одного размера . Чем больше знаменатель, тем меньше будет каждая часть. Чем меньше знаменатель, тем больше каждая часть. Когда знаменатели одинаковы, куски имеют одинаковый размер.

Каковы знаменатели?

Общие знаменатели также иногда называют «подобными знаменателям». Так что, если вам говорят, что у двух дробей знаменатели , например , это просто означает, что у них одинаковое нижнее число.

Как складывать дроби?

Чтобы складывать дроби, дроби должны иметь общий знаменатель. Нам нужно, чтобы части каждой фракции были одинакового размера, чтобы объединить их вместе.

Допустим, нам нужно сложить 2/7 и 3/7. Эти две дроби имеют одинаковый знаменатель, поэтому равные части, на которые разбито целое, имеют одинаковый размер. Поскольку все части имеют одинаковый размер, мы можем сложить эти две дроби вместе.

Добро пожаловать на уроки математики Кейт!
Учителя, обязательно ознакомьтесь с учебными пособиями и заданиями.

Мы можем добавить 2/7 к 3/7, заполнив дополнительные 2 клетки на диаграмме. Мы видим, что это дает нам сумму 5/7. (2 части плюс еще 3 части равняются 5 частям из 7 всего)

Если вы складываете две дроби с общим знаменателем, вы можете объединить их вместе, сложив вместе числители (верхние числа). Знаменатель всегда будет оставаться одним и тем же, потому что размер равных частей не изменится, когда вы объедините две дроби вместе.

Допустим, у вас есть 1/10 + 6/10. У них одинаковый знаменатель, поэтому их можно объединить вместе. Сложите числители (1 + 6 = 7). Оставьте знаменатель прежним (нижнее число останется 10).

Помните, знаменатель не меняется, потому что размеры фигур остаются прежними. Вы просто подсчитываете общее количество штук, когда складываете две дроби.

Вот визуальный способ взглянуть на ту же проблему:

Добавление дробей Примеры

Попробуйте сложить эти дроби самостоятельно, а затем прокрутите вниз, чтобы убедиться, что вы правы! Если вы сомневаетесь, это может помочь нарисовать картинку, которая поможет вам визуализировать проблему.

Прежде чем складывать дроби, убедитесь, что у них одинаковые знаменатели! Если знаменатели разные, мы не можем их объединить, потому что кусочки не одного размера.

В первой задаче оба знаменателя равны 9, поэтому у них есть общий знаменатель. Мы можем сложить дроби 2/9 и 5/9, сложив числители и сохранив тот же знаменатель. Это дает нам дробь 7/9.

Во второй задаче обе дроби имеют общий знаменатель 5. Это означает, что мы можем сложить числители (1 и 3) и оставить тот же знаменатель (всего 5 частей). Это дает нам сумму 4/5.

Распространенная ошибка при сложении дробей

Распространенная ошибка, которую учащиеся допускают при сложении дробей, заключается в том, что они случайно добавляют и числитель, и знаменатель. Не добавляйте нижние числа! Знаменатель говорит вам, сколько равных частей в целом, это число останется прежним, когда вы сложите дроби.

Видео

Хотите увидеть еще несколько примеров? Посмотрите короткое видео о добавлении дробей ниже.

Практика сложения дробей

Думаете, вы готовы попробовать складывать дроби самостоятельно? Нажмите кнопку СТАРТ ниже, чтобы пройти пробный тест.

Работает на Interact

Готовы научиться складывать и вычитать дроби с разными знаменателями?
Хотите научиться умножать или делить дроби на дроби?

Сравнение дробей — определение, методы, примеры, часто задаваемые вопросы

« Сравнение фракций » относится к определению большей и меньшей фракции в заданном наборе фракций. При сравнении дробей соблюдается набор правил для сравнения числителя и знаменателя дроби, где числитель — это число над дробной чертой, а знаменатель — число под дробной чертой. Мы можем определить большую и меньшую дроби, сравнивая любые две дроби. Дроби можно сравнивать, даже если у них разные числители и знаменатели. Чтобы лучше понять концепцию, давайте рассмотрим различные способы сравнения дробей.

Дробь

Прежде чем перейти к понятию сравнения двух дробей, давайте вспомним, что такое дробь. Дробь определяется как часть целого, состоящая из двух частей: числителя и знаменателя, где числитель — это число над дробной чертой, а знаменатель — число под дробной чертой.

Как сравнить две дроби в числах?

Чтобы определить, какая из двух дробей больше или меньше, нужно их сравнить. В зависимости от числителя, знаменателя и вида дробей существуют разные методы и правила сравнения дробей. Их:

Сравнение фракций с теми же знаменателями
Сравнение фракций с неконтролиными знаменателями
Сравнивая фракции с использованием десятичного метода
Сравнивая фракции
СПОСОБРАЖЕНИЕ СОЗДАНИЯ ФРАКЦИИ ИСПОЛЬЗОВАНИЯ Множество
111111111.
111191191119119.
111111111111. легко найти большую или меньшую дробь, если дроби имеют одинаковые знаменатели. При сравнении дробей проверяйте, совпадают ли знаменатели. Если знаменатели равны, то больше та дробь, у которой числители больше. Дроби равны, если равны числители и знаменатели обеих дробей.
Пример: Сравните: 12.05 и 17.12.
Решение:
Шаг 1: Сначала обратите внимание на знаменатели данных дробей, то есть 5/12 и 17/12. Здесь знаменатели одинаковы для обеих дробей.
Шаг 2: Теперь сравните числители данных дробей. Мы можем заметить, что 17 > 5.
Шаг 3: Мы знаем, что дробь с большим числителем больше. Следовательно, 5/12 < 17/12.
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, мы должны преобразовать их в одинаковые знаменатели, для которых мы должны найти наименьшее общее кратное (НОК) знаменателей. Поскольку знаменатели равны, мы можем легко сравнивать дроби.
Пример: Сравните: 1/4 и 2/3.
Решение:
Шаг 1: Сначала обратите внимание на знаменатели данных дробей, то есть 1/4 и 2/3. Поскольку знаменатели разные, сделайте их равными, найдя НОК 4 и 3. НОК(4,3) = 12,
Шаг 2: Теперь преобразуем данную дробь так, чтобы у них были одинаковые знаменатели. Итак, умножьте первую дробь на 3/3, т. е. 1/4 × 3/3 = 4/12.
Шаг 3: Точно так же умножьте вторую дробь на 4/4, т. е. 2/3 × 4/4 = 8/12. Таким образом, первая дробь становится 4/12, а другая — 8/12.
Шаг 4: Сравните полученные новые дроби, т. е. 4/12 и 8/12. Так как знаменатели одинаковые, сравним числители. Мы можем заметить, что 4 < 8,
Шаг 5: Дробь с большим числителем является большей дробью. Итак, 8/12 > 4/12. Итак, 1/4 > 2/3.
Примечание: Обратите внимание, что если данные дроби имеют одинаковые числители и разные знаменатели, то мы можем легко сравнивать их, глядя на их знаменатели. Дробь, у которой знаменатель меньше, имеет большее значение, а дробь, у которой знаменатель больше, имеет меньшее значение. Например 6/2 > 6/5.
Сравнение дробей десятичным методом
В этом методе можно сравнивать дроби, находя десятичные значения дробей и сравнивая их. Для этого делим числитель на знаменатель, и таким образом дробь преобразуется в десятичную. Наконец, сравните их десятичные значения. Давайте разберемся в этом на примере.
Пример: Сравните 3/5 и 2/4.
Решение:

Шаг 1: Чтобы записать 3/5 и 2/4 десятичными знаками, разделите числитель на знаменатель. Разделите 3 на 5 и 2 на 4.
Шаг 2: Полученные десятичные значения равны 0,6 и 0,5.
Шаг 3: Наконец, сравните десятичные значения. 0,6 > 0,5. Дробь с большим десятичным значением будет больше. Следовательно, 3/5 > 2/4.
Сравнение дробей с помощью визуализации
По сравнению с любым другим методом сравнение дробей с помощью визуализации проще. Сделайте два ящика так, чтобы длина и ширина обоих были одинаковыми. На приведенном ниже рисунке показаны модели А и В, которые представляют собой две фракции. Затем разделите каждую модель на равные части, соответствующие их соответствующим знаменателям. Теперь мы можем легко обнаружить, что 2/6 < 2/4, так как 2/4 покрывает большую заштрихованную область по сравнению с 2/6. Меньшая фракция занимает меньшую площадь того же целого, а большая фракция занимает большую площадь того же целого.

Сравнение дробей методом перекрестного умножения
Чтобы сравнивать дроби методом перекрестного умножения, мы должны умножить числитель одной дроби на знаменатель другой дроби. Давайте разберемся в этом на примере.
Пример: Сравните 3/8 и 4/5.
Обратите внимание на приведенный ниже рисунок, который лучше объясняет концепцию перекрестного умножения.

Шаг 1: Обратите внимание, что когда мы выполняем перекрестное умножение для сравнения двух дробей, мы должны умножить числитель первой дроби на знаменатель второй дроби. Мы должны написать произведение на стороне выбранного числителя. Здесь произведение 3 × 5 = 15, которое мы пишем рядом с первой дробью.
Шаг 2: Аналогично, при умножении числителя второй дроби на знаменатель первой дроби мы должны записать произведение рядом со второй дробью. Здесь произведение 4 × 8 = 32, которое мы запишем возле второй дроби.
Шаг 3: Теперь сравните оба произведения, т. е. 15 и 32. Поскольку 15 < 32, можно легко сравнить соответствующие дроби, т. е. 3/8 < 4/5. Следовательно, 3/8 < 4/5.
Решенные примеры на сравнение дробей
Пример 1: Какая из следующих дробей больше: 6/11 или 8/15?
Решение:
Даны дроби: 6/11 и 8/15
Знаменатели данных дробей различны. Итак, найдите НОК знаменателей, т. е. НОК(11, 15) = 165.
Теперь умножьте 6/11 на 15/15 и 8/15 на 11.
6/11 × 15/15 = 90/165
8/15 × 11/11 = 88/165
Теперь сравните числители, так как знаменатели одинаковы.
Итак, 90 > 88, т. е. 90/165 > 88/165.
Следовательно, 6/11 > 8/15, т. е. 6/11 — большая дробь.
Пример 2: Какая из данных дробей меньше: 13/85 или 21/85?
Решение:
Даны дроби: 13/85 и 21/85.
Знаменатели данных дробей совпадают. Итак, сравните числители данных дробей.
13 < 21.
Итак, 13/85 < 21/85.
Следовательно, 13/85 — меньшая дробь.
Пример 3: Сравните дроби 4/25 и 33/100.
Решение:
Чтобы сравнить данные дроби, найдите их десятичные значения. Итак, делим 4 на 25 и 33 на 100.
4/25 = 0,16
33/100 = 0,33
Из десятичных значений можно сделать вывод, что 0,33 > 0,16. Итак, 33/100 больше, чем 4/25.
Следовательно, 33/100 больше, чем 4/25.
Пример 4: Мрунала попросили доказать равенство данных дробей: 30/90 и 25/75. Можете ли вы доказать данное утверждение, используя метод НОК?
Решение:
Даны дроби: 30/90 и 25/75.
Знаменатели данных дробей различны. Итак, найдите НОК знаменателей, т. е. НОК(90, 75) = 450.
Теперь умножьте 30/90 на 5/5 и 25/75 на 6/6.
30/90 × 5/5 = 150/450
25/75 × 6/6 = 150/450
Теперь сравните числители, так как знаменатели одинаковы.
Итак, 150 = 150, т. е. 150/450 = 150/450.
Таким образом, 30/90 = 25/75, т. е. обе указанные дроби равны.
Значит, доказано.
Пример 5: Какая из следующих дробей больше: 27/41 или 27/67?
Решение:
Даны дроби: 27/41 и 27/67.
Здесь числители обеих дробей одинаковы, но знаменатели разные.
Мы знаем, что дробь с меньшим знаменателем имеет большее значение, а дробь с большим знаменателем имеет меньшее значение.
Здесь 41 < 67.
Итак, 27/41 > 27/67
Следовательно, 27/41 — большая дробь.
Часто задаваемые вопросы о сравнении дробей
Вопрос 1: Что подразумевается под сравнением дробей?
Ответ:
«Сравнение дробей» относится к определению большей и меньшей дроби в заданном наборе дробей. Мы можем определить большую, меньшую или эквивалентную дробь, сравнив любые две дроби. В зависимости от числителя, знаменателя и вида дробей существуют разные методы и правила сравнения дробей.
Вопрос 2: По какому правилу сравнивать дроби с одинаковыми знаменателями?
Ответ:
Если данный набор дробей имеет одинаковый знаменатель, то дробь, числитель которой меньше, является меньшей дробью, а дробь, числитель которой больше, является большей дробью. Если числители равны, то дроби считаются равнозначными дробями. Например, если нам нужно сравнить 2/3 и 5/3, нам просто нужно проверить их числители и сравнить их. Поскольку 2 < 5, значит, 2/3 < 5/3.
Вопрос 3: Каково правило сравнения дробей с одинаковым числителем?
Ответ:
Если данный набор дробей имеет одинаковый числитель, то дробь, у которой знаменатель меньше, является большей дробью, а дробь, у которой знаменатель больше, является меньшей дробью. Например, если нам нужно сравнить 4/3 и 4/9, нам просто нужно проверить их знаменатели и сравнить их. Теперь из 4/3 и 4/9 дробь с меньшим знаменателем равна 4/3. Следовательно, 4/3 является большей частью данных дробей.
Вопрос 4: Что такое эквивалентные дроби?
Ответ:
Равные дроби — это те, которые имеют различные числители и знаменатели, но имеют одинаковые значения при упрощении. Например, 3/12 и 5/20 являются эквивалентными дробями, так как обе они равны 1/4 в упрощенном виде.
Вопрос 5: Как сравнивать дроби с разными знаменателями?
Ответ:
Чтобы сравнить дроби с разными знаменателями, мы должны преобразовать их в одинаковые знаменатели, для которых мы должны найти наименьшее общее кратное (НОК) знаменателей.
No related posts.