Примеры с решением сокращенного умножения: Формулы сокращенного умножения, примеры, тесты

Формулы сокращенного умножения с примерами решения

Содержание:

1. Основные и некоторые дополнительные формулы сокращённого умножения
2. Примеры решения

Основные и некоторые дополнительные формулы сокращённого умножения

Теорема 1. Для любых действительных чиеел справедливы тождества:

.

В последнем тождестве выражение всегда неотрицательно и называется неполным квадратом разности (суммы). Эти тождества называют основными формулами сокращённого умножения. Их доказательство проводится непосредственной проверкой.

Приведём дополнительно ещё несколько формул общего вида

Теорема 2. Для любых действительных чисел и для любых натуральных справедливы тождества:

Каждая из трёх формул доказывается раскрытием скобок в правой части и упрощением сё путём приведения подобных членов. Теорема 3 (квадрат суммы нескольких слагаемых). Для любых действительных чисел справедливо тождество:

Данное тождество доказывается в разделе, посвященном методу математической индукции.

Теорема 4 (куб суммы трёх слагаемых). Для любых действительных чисел справедливо тождество: Тождество доказывается непосредственным раскрытием скобок в правой части с последующим упрощением.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Произведение всех натуральных чисел, начиная с единицы и закапчивая , называется , -факториалом и обозначается т.е. По определению полагают Например, Задачи на факториалы достаточно редко, но всс же встречаются на вступительных экзаменах.

Примеры решения

Пример 1:

Сколькими нулями оканчивается число Рассмотрим решение этой достаточно известной задачи. Предположим, что мы разложили данное большое число на простые множители (в силу основной теоремы арифметики это можно сделать, причём единственным образом): 2000!= 2*’ -3*г • 5*3 •.

..•//’> где показатели степеней некоторые неизвестные нам натуральные числа. Нуль будут давать только произведения пар простых множителей 2 и 5. В этом разложении пятёрок, причём каждое второе число в натуральном ряду чисел кратно двум и только каждое пятое кратно пяти. Следовательно, Поэтому число нулей будет равно . Найдём это число. Среди чисел 1,2,3,…, 1999,2000 каждое пятое делится на 5. Таких чисел штук (квадратные скобки обозначают целую часть). Далее, каждое 25-е число делится ещё на пять, и таких чисел с число делится ещё на пять, и таких пятёрок будет штук. Затем каждое 125-2000 штук. Продолжая 125 этот конечный процесс (начиная с определённого момента целая часть будет обращаться в нуль), получим в результате

Возможно вам будут полезны данные страницы:

Действия со степенями

Действия с корнями

Дифференциал функции

Полный дифференциал функции: пример решения

Пример 2:

Найти значение выражения

Решение. Заметим, что каждое слагаемое в приведённой сумме, кроме последнего, имеет вид где ,7 изменяется от значения 1 (у первого члена суммы) до 2000 (у предпоследнего слагаемого). Поскольку можно представить в виде , то, заменяя каждое из слагаемых (кроме последнего) на соответствующую сумму, получим:

Пример 3:

Вычислить сумму Решение. Воспользуемся тождеством для каждого из слагаемых Тогда имеем

Пример 4:

Решить в целых числах уравнение Решение. Непосредственной проверкой убеждаемся, что при решениями уравнения будут пары чисел Докажем теперь, что при решений пет. Для этого заметим, что оканчивается цифрой всс оканчиваются нулём. Таким образом, при сумма оканчивается цифрой 3, а потому не может равняться квадрату целого числа у (никакой квадрат целого числа не оканчивается на 3). Наряду с понятием обычного, или одинарного, факториала существует понятие двойного факториала. Приведём для любознательных читателей соответствующее определение. Произведение всех натуральных чисел, начиная с единицы и заканчивая п, имеющих одинаковую с чётность, называется двойным -факториалом и обозначается В частности, если а если то По определению полагают Например, Справедливо тождество

Пример 5:

Сколько различных целых делителей имеет число ? Решение. Поскольку то, следовательно, делителями этого числа являются числа вида Таким образом, искомое количество делителей равно Рассмотрим вопрос из области комбинаторики, сколькими способами можно выбрать предметов из различных предметов? Количество таких способов принято обозначать и называть числом сочетаний из по ? Число сочетаний из по можно вычислить по следующей формуле, в написании которой используется понятие факториала:

Например,

Кстати, число в комбинаторике также имеет свой смысл. Количество различных способов, какими можно упорядочить данных предметов, называется числом перестановок из предметов, обозначается и вычисляется по формуле К разряду формул сокращённого умножения принято относить и бином Ньютона. Пусть произвольные действительные числа, любое натуральное число.

Биномом Ньютона называется следующая формула для вычисления (доказывается в разделе 4):

Здесь числа называются биномиальными коэффициентами [1]. Формула бинома Ньютона была известна математикам задолго до Ньютона. Паскаль Блез (1623-1662) французский математик, физик, философ. Эти коэффициенты бывают нужны, например, если при решении какой-либо задачи надо быстро раскрыть, чему равно Например, используя указанное выше свойство треугольника Паскаля, легко вычислить

• 1. Правило симметрии: равноотстоящие от концов биномиального разложения коэффициенты равны между собой, т.е.
• 2. Число членов разложения равно
• 3. Сумма показателей степеней у чисел в каждом члене разложения равна показателю степени бинома
• 4. Сумма коэффициентов всех членов разложения равна
• 5. Правило Паскаля: Формулы сокращённого умножения весьма часто используются при решении всевозможных математических задач, позволяют преобразовать уравнение (неравенство) к более простому для дальнейшего решения виду.

Пример 6:

Сколько времени в течение суток на электронном табло вокзальных часов, которые показывают время в диапазоне от 00:00 до 23:59, присутствует хотя бы одна цифра 3?

Решение. Занумеруем четыре позиции табло слева направо. В 1-й позиции цифра «3» не появляется никогда. Во 2-й позиции цифра «3» присутствует в течение трёх полных часов, начинающихся с 03:00, 13:00, 23:00. Остаётся 21 час, в течение каждого из которых цифра «3» по одному разу занимает 3-ю позицию табло в течение 10 минут, а в течение остальных 50 минут каждого часа 5 раз ровно (03,13,23,43,53) по 1 минуте занимает последнюю, 4-ю позицию табло. В результате общее время присутствия цифры «3» на табло равно 3

Формулы ⚠️ сокращенного умножения: для старших степеней, многочленов

Что такое формулы сокращенного умножения

Формулы сокращенного умножения — это алгебраические тождества, которые используются для упрощенного решения типичных часто встречающихся многочленов. Формулы позволяют возвести в степень сложные выражения быстрее в ряде случаев. Слово «сокращенное» в названии объясняется тем, что при использовании формул частично пропускаются вычисления.

Формулы сокращенного умножения используются для алгебраических выражений и алгебраических дробей, для разложения на множители, решения неравенств и уравнений. Кроме этого с помощью формул можно привести многочлен к стандартному виду без раскрытия скобок.

Доказательство

Формулы сокращенного умножения естественным образом следуют из правила умножения многочлена на многочлен.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Докажем, что (a + b)² = a² + 2ab + b²

(a + b)² тождественно (a + b)(a + b)

Раскроем скобки (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b²

Проделаем то же самое в обратную сторону с квадратом разности

a² − 2ab + b² = (a² − ab) + (-ab + b²)

Вынесем общий множитель за скобки a(a − b) − b(a − b) = (a − b)(a − b) = (a − b)²

Список формул

Формулы квадратов

(a − b)(a + b) = a² − b²

(a + b)² = a² + 2ab + b²

(a − b)² = a² − 2ab + b²

Формулы кубов

(a + b)(a² − ab + b²) = a³ + b³

(a − b)(a² + ab + b²) = a³ − b³

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a − b)³ = a³ − 3a²b + 3ab² − b³

Формулы четвертой степени

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

(a – b)⁴ = a⁴ – 4a³b + 6a²b² – 4ab³ + b⁴

a⁴ – b⁴ = (a – b)(a + b)(a² + b²)

Формула квадрата суммы 

(a + b)² = a² + 2ab + b²

Квадрат суммы выражений a и b равен квадрату первого выражения, прибавить квадрат второго выражения и их удвоенное произведение.  

Формула квадрата разности

(a − b)² = a² − 2ab + b²

Квадрат разности чисел a и b равен сумме квадратов a и b минус их удвоенное произведение.

Формула куба суммы

(a + b)³ = a³ + 3a²b + 3ab² + b³

Куб суммы выражений a и b равен возведенному в третью степень первому выражению плюс утроенное произведение квадрата первого выражения и второго выражения плюс утроенное произведение первого выражения и квадрата второго выражения плюс второе выражение, возведенное в третью степень.

Куб суммы двух выражений

(a + b)³ = a³ + 3a²b + 3ab² + b³

Куб суммы чисел a и b равен сумме кубов этих чисел, утроенного произведения квадрата первого числа и второго и утроенного произведения квадрата второго числа и первого числа.

Формула куба разности

(a − b)³ = a³ − 3a²b + 3ab² − b³

Куб разности выражений a и b равен возведенному в третью степень первому выражению минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус возведенное в третью степень второе выражение.

Формула разности квадратов

a² – b² = (a – b)(a + b)

Разность квадратов чисел a и b равна произведению их разности на их сумму.

Формула суммы кубов

a³ + b³ = (a + b)(a² – ab + b²)

Сумма кубов выражений a и b равна произведению суммы выражений на квадрат их разности.

Формула разности кубов

a³ − b³ = (a − b)(a² + ab + b²)

Разность кубов чисел a и b равна разности чисел умноженной на неполный квадрат их суммы.

Примеры применения формул

Выполним вычисления через упрощение на основе приведенных выше формул. С помощью них мы сократим выражение, что позволит нам решать его намного быстрее и проще.

Пример

Используем формулу квадрата суммы:

(5+3x)² = 5 + (3x)² + 2 ⋅ 5 ⋅ 3x = 25 +9x² +30x

x² + 4xy + 4y² = x² + (2y)² + 2 ⋅ x ⋅ 2y = (x + 2y)²

Пример

Используем формулу разности квадратов:

49x² − 9y² = (7x)² − (3y)² + (7x − 3y)(7x + 3y)

(x +3)² − 16 = (x +3)² — 4² = (x + 3 − 4)(x + 3 + 4) = (x − 1)(x +7)

Пример

Используем формулу квадрата разности:

(1 − 2xy)² = 1² +(2xy)² − 2 ⋅ 1 ⋅ 2xy + 1 + 4x²y² − 4xy

4x² − 4x + 1 = (2x)² + 1 − 2 ⋅ 2x ⋅ 1 = (2x − 1)²

Пример

Используем формулу куба суммы:

(2x + y)³ = (2x)³ + 3 ⋅ (2x)² ⋅ y + 3 ⋅ 2x ⋅ y² +y³ = 8x³ +12x² ⋅ y + 6x ⋅ y² +y³

Пример

Используем формулу куба разности:

(4x − 3y)³ = ((4x)³ − 3 ⋅ (4x)²) ⋅ 3y + 3 ⋅ 4x (3y)² − (3y)³) = 64x³ — 144x² ⋅ y² = 27y³

Пример

Используем формулу сумма кубов:

(3a + 2)(9a² − 6 6a + 4) = (3a)³ + (2)³ = 27a³ + 8

Пример

Используем формулу разности кубов:

(2 − y)(4 + 2y + y²) = (2 − y)(2² + 2y + y²) = 2³ — y³ = 8 − y³

Пример

Рассмотрим пример с дробями: 

\(\frac{8x^3\;-\;z^6}{4x^{2\;}-\;z^4}\)

Необходимо сократить эту дробь. 4)}{(2x\;+\;z)}\)

Что такое PEMDAS? Порядок операций Правила простыми словами

Какое отношение фраза «Пожалуйста, извините, моя дорогая тетя Салли» имеет к математике? Это мнемоника, которая помогает учащимся запомнить PEMDAS — аббревиатуру, описывающую правила порядка операций в математической задаче. Продолжайте читать, чтобы узнать значение PEMDAS, что он означает и почему это важно при правильном решении проблем.

Правила порядка работы PEMDAS

Реклама

PEMDAS Значение

В английском языке вы привыкли читать слева направо. Вы решаете математические задачи аналогичным образом — за исключением нескольких важных шагов. Вот тут-то и появляется PEMDAS. Но что означает PEMDAS? Each letter in the acronym stands for a mathematical operation:

• P arentheses
• E xponents and square roots
• M ultiplication or D ivision
• A ddition or S вычитание

Обратите внимание, что хотя М (умножение) предшествует D (деление), вы не обязательно завершаете умножение до деления. Это же правило применимо к сложению и вычитанию. Вы решаете, какая операция будет первой при чтении слева направо.

Решение задач с помощью PEMDAS

Шаги в PEMDAS указывают порядок, в котором вы решаете математическую задачу.

Например, в уравнении 6 x (9-2) + 5 ² , you can separate the parts like this:

6 x	(9-2)	+	5 2
multiplication	скобки	сложение	показатели степени

5 = 57, 57 ² = 3249), что неверно .

PEMDAS указывает вам работать в следующем порядке:

1. Решить все скобки (P): (9-2) = 7
2. Решить все показатели степени/степени (E): 5 ² = 25
3. Решить все умножение ИЛИ деление (M или D), слева направо: 6 x 7 = 42
4. Решить все сложение ИЛИ вычитание (A или S), слева направо: 42 + 25 = 67

Используя PEMDAS, мы можем определить, что 6 х (9-2) + 5 ² = 67 , что является правильным ответом. Вы можете видеть, какая большая разница, когда вы используете правильный порядок операций!

Пример проблем с использованием PEMDAS

Действительно ли PEMDAS работает в любой ситуации? Взгляните еще на несколько уравнений, в которых PEMDAS необходим, чтобы найти правильный ответ.

8 ³ ÷ (10-8) — 4 ²

Это уравнение включает все порядки операций в PEMDAS, включая два набора показателей. Как и в других шагах PEMDAS, вы решаете эти показатели степени слева направо. Используйте следующие шаги:

1. Решение скобок: 8 ³ ÷ (2) — 4 ²
2. Решение показателей степени: 512 ÷ 2 — 16
3. Решение умножения ИЛИ деление, слева направо сложение, 16 900 Решение слева направо: 240

3(7 х 4) ² + 8(2 х 5)

Когда вы видите число перед скобками, вы умножаете решение скобок на это число. В этом уравнении вы должны умножить (7 x 4) на 3 и (2 x 5) на 8. Но правила PEMDAS указывают, что вам нужно решить скобки (и возвести в квадрат решение первой скобки), прежде чем вы умножить. Получается так:

1. Решение скобок: 3(28) ² + 8(10)
2. Решение показателей степени: 3(784) + 8(10)
3. Решение умножения ИЛИ деления слева направо: 2352 + 80
4. 6 Решение сложение ИЛИ вычитание слева направо: 2432

100 ÷ 5 ² + (20 — (3 x 5))

Некоторые учащиеся впадают в панику, когда видят скобки внутри скобок. Что по этому поводу говорит PEMDAS? Работайте изнутри наружу, то есть решайте самый внутренний набор скобок, а затем работайте с внешними скобками.

1. Решение внутренних скобок: 100 ÷ 5 ² + (20 — (15))
2. Решение внешних скобок: 100 ÷ 5 ² + (5)
3. Решение показателей степени: 100 (6) 5 ÷ 255
4. Решение умножения ИЛИ деления слева направо: 4 + (5)
5. Решение сложения ИЛИ вычитания слева направо:
   9

15 ² + √(27 ^{÷ 3) — (2 x 6) 2 ÷ 2}

Что делать, если в смеси есть квадратный корень? Квадратные корни попадают на тот же шаг, что и показатели степени. Вы решаете их после решения скобок и перед делением или умножением.

1. Решение скобок: 15 ² + √9 — (12) ² ÷ 2
2. Решение показателей степени и квадратного корня, слева направо: 225 + 3 — 144 ÷ 2
3. Решение деления слева на умножение справа: 225 + 3 — 72
4. Решение сложения ИЛИ вычитания, слева направо: 156

10 ³ + 2(25 ² ) ÷ 5(1 ² x 1)

Показатель степени в скобках может привести к путанице. Но помните, правила PEMDAS по-прежнему применяются внутри круглых скобок, поэтому показатели степени стоят перед умножением.

1. Рассчитать показатели степени внутри круглых скобок: 10 ³ + 2(625) ÷ 5(1 x 1)
2. Раскрыть скобки: 10 ³ + 2(625) ÷ 5(1)
3. Рассчитать степени: 1000 + 2(625) ÷ 5(1)
4. Решить умножение ИЛИ деление, слева направо: 1000 + 250
5. Решить сложение ИЛИ вычитание, слева направо: 1250

Получили ли вы ответы? ? Помните, что все операции внутри круглых скобок идут перед любой другой операцией. Если нет круглых скобок или степеней, вы просто пропускаете эти шаги и умножаете или делите слева направо, а затем складываете или вычитаете слева направо.

Реклама

Другие аббревиатуры для порядка операций

Если концепция порядка операций вам знакома, а PEMDAS — нет, возможно, вы привыкли к другому аббревиатору. Другие аббревиатуры для объяснения порядка операций включают в себя:

• Bedmas ( B Рэкетки, E Xponents, D IVision, M Ultiplication, A DDITIO Ракетки B , 9 шт.0014 O RDER, D IVISION, M Ultiplication, A DDITIO A добавление, S вычитание)

Все эти сокращения объясняют один и тот же процесс разными словами. Кажется, что GEMDAS отличается от других, но «группировка» — это другое слово для «круглых скобок» или «квадратных скобок». Он также переключает умножение и деление, но, как мы знаем, вы все равно используете эти операции на одном шаге.

Дополнительные математические сокращения и сокращения

Такие сокращения, как PEMDAS, помогают молодым учащимся (и опытным математикам) запомнить основные этапы решения уравнений с использованием более чем одной операции. Узнайте больше о мнемотехнике и о том, как она помогает нам учиться, с помощью этих полезных примеров мнемоники. Вы также можете освоить общепринятые сокращения для общепринятых единиц измерения, прежде чем приступать к важным понятиям геометрии.

Штатный писатель

Правила использования формул сокращенного умножения

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрат суммы и квадрат разности двух выражений; разность квадратов двух выражений; куб суммы и куб разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, факторизации многочленов и приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть

.

Пусть a, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.

а 2 — b 2 = (а — b) (а + b)

4. сумма куба двух выражений равна кубу первого выражения плюс утроенный квадрат первого выражения умноженное на второе плюс умноженное на три произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрат первого выражения и второго плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.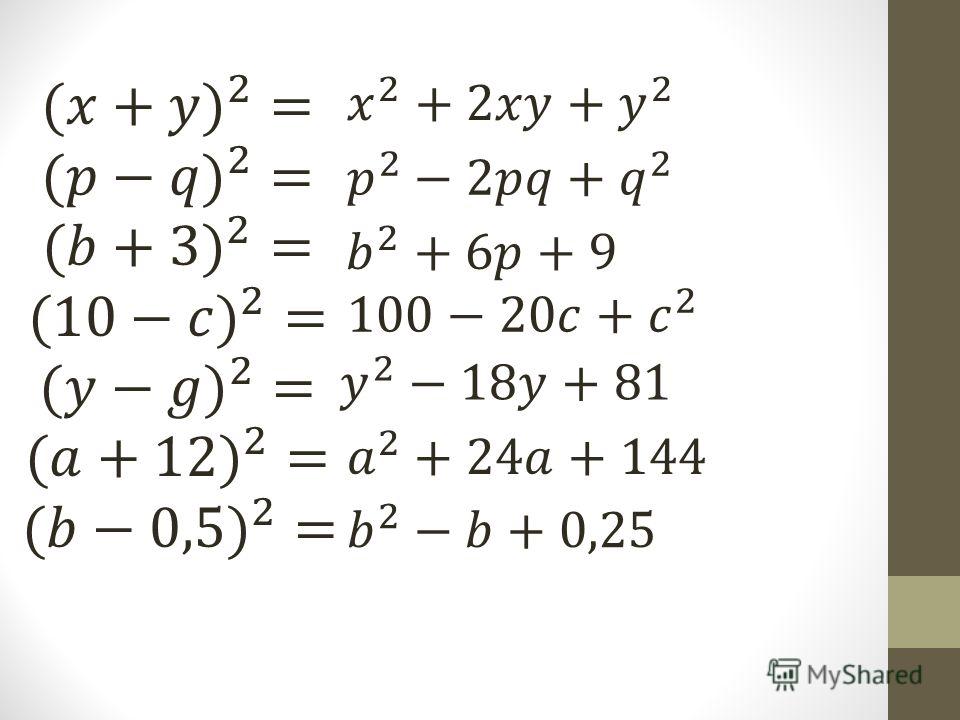

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражений на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения неполным квадратом суммы этих выражений.

а 3 — b 3 = (а — b) (а 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получаем

98 2 = ( 100 — 2) 2 = 100 2 — 2 100 2 + 2 2 = 10000 — 400 + 4 = 9604

получаем

Пример 3

Упростить выражение

(x — y) 2 + (x + y) 2

Используем формулы квадрата суммы и квадрата разности двух выражений

(x — y) 2 + (x + y) 2 = x 2 — 2xy + y 2 + x 2 + 2xy + y 2 = 2x 2 + 2y 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2) 92$. 2$ 92\right)\]

Формулы или правила редуцированного умножения используются в арифметике, а точнее в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами формулы выведены из существующих в алгебре правил умножения нескольких многочленов.

Использование этих формул обеспечивает достаточно быстрое решение различных математических задач, а также помогает упростить выражения. Правила алгебраических преобразований позволяют производить некоторые манипуляции с выражениями, следуя которым можно получить выражение в левой части равенства, которое в правой части, или преобразовать правую часть равенства (чтобы получить выражение в слева после знака равенства).

Формулы сокращенного умножения удобно знать по памяти, так как они часто используются при решении задач и уравнений. Основные формулы, включенные в этот список, и их названия приведены ниже.

квадрат суммы

Чтобы вычислить квадрат суммы, нужно найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения это правило записывается так: (a + c)² = a² + 2ac + c².

Квадрат разности

Для вычисления квадрата разности нужно вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с обратным знаком ) и квадрат второго числа. В виде выражения это правило выглядит так: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел в квадрате равна произведению суммы этих чисел на их разность. В виде выражения это правило выглядит так: а² — с² = (а + с) (а — с).

куб суммы

Чтобы вычислить куб суммы двух слагаемых, нужно вычислить сумму, состоящую из куба первого слагаемого, утроить произведение квадрата первого слагаемого и второго, утроить произведение первого члена на квадрат второго и куб второго члена. В виде выражения это правило выглядит так: (a + c)³ = a³ + 3a²c + 3ac² + c³.

Сумма кубов

Согласно формуле равна произведению суммы этих слагаемых на их неполный квадрат разности.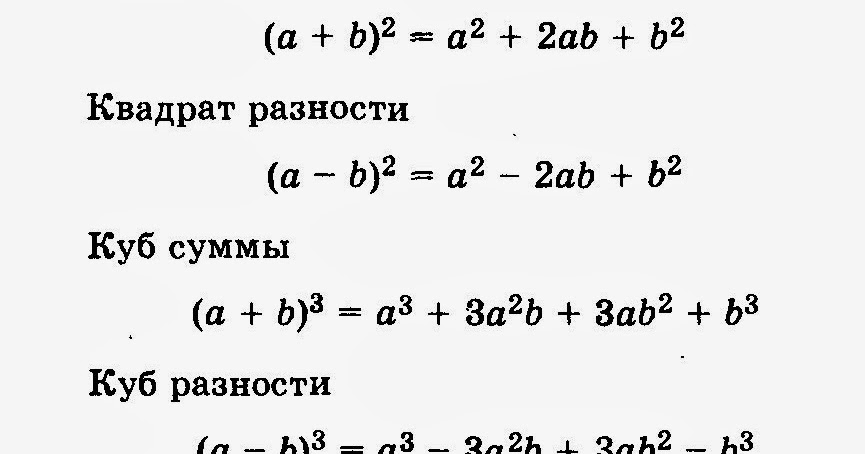 В виде выражения это правило выглядит так: а³ + с³ = (а + с) (а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образуется при сложении двух кубиков. Известны только величины их сторон.

Если значения сторон малы, то легко произвести расчеты.

Если длины сторон выражены громоздкими числами, то в этом случае проще применить формулу «Сумма кубов», что значительно упростит расчеты.

куб разности

Выражение для кубической разности звучит так: как сумму третьей степени первого члена утроить отрицательное произведение квадрата первого члена на второй утроить произведение первого члена на квадрат второго и отрицательный куб второго члена. В виде математического выражения куб разности выглядит так: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов только одним знаком. Таким образом, разность кубов представляет собой формулу, равную произведению разности этих чисел на их неполный квадрат суммы. В виде разность кубов выглядит так: а 3 — с 3 = (а — с) (а 2 + ас + с 2).

Пример. Необходимо рассчитать объем фигуры, который останется после вычитания желтой объемной фигуры, которая также является кубом, из объема синего куба. Известен только размер стороны малого и большого куба.

Если значения сторон небольшие, то расчеты достаточно просты. А если длины сторон выражены значащими числами, то стоит воспользоваться формулой под названием «Разность кубов» (или «Разностный куб»), которая значительно упростит расчеты.

В предыдущих уроках мы рассмотрели два способа разложения полинома на множители: вынесение общего множителя за скобки и метод группировки.

В этом уроке мы рассмотрим другой способ разложения многочлена на множители с использованием формул сокращенного умножения .

Мы рекомендуем писать каждую формулу не менее 12 раз. Для лучшего запоминания запишите все формулы сокращенного умножения для себя на небольшой шпаргалке.

Вспомните, как выглядит формула разности кубов.

а 3 — б 3 = (а — б) (а 2 + аб + б 2)

Формулу разности кубов не очень легко запомнить, поэтому рекомендуем использовать специальный способ ее запоминания.

Важно понимать, что любая формула сокращенного умножения работает и в обратную сторону.

(а — б) (а 2 + аб + б 2) = а 3 — б 3

Рассмотрим пример. Необходимо факторизовать разность кубов.

Обратите внимание, что «27a 3» — это «(3a) 3», а это значит, что в формуле разности кубов вместо «a» используется «3a».

Используем формулу разности кубов. На месте «а 3» имеем «27а 3», а на месте «б 3», как и в формуле, «б 3».

Применение кубической разности в обратном порядке

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов по формуле сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1) (x 2 + x + 1)» напоминает правую часть формулы разности кубов «», только вместо «a» стоит «x», А вместо «б» стоит «1».

Для «(x − 1)(x 2 + x + 1)» используется формула разности кубов в обратном направлении.

Рассмотрим более сложный пример. Требуется упростить произведение многочленов.

Если сравнить «(y 2 − 1)(y 4 + y 2 + 1)» с правой частью формулы разности кубов
« a 3 − b 3 = (a − b)(a 2 + ab + b 2)», то можно понять, что на месте «а» из первой скобки стоит «у 2», а на месте «б» стоит «1».

Формулы сокращенного умножения (FSU) используются для возведения в степень и умножения чисел и выражений. Зачастую эти формулы позволяют производить расчеты более компактно и быстро.

В этой статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательства формул сокращенного умножения.

Впервые тема БСС рассматривается в рамках курса «Алгебра» для 7 класса. Ниже приведены 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
2. формула квадрата разности: а — b 2 = а 2 — 2 а b + b 2
3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
5. формула разности квадратов: а 2 — b 2 = а — b а + b
6. формула суммы кубов: а 3 + b 3 = а + b а 2 — а b + b 2
7. формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2

Буквы a, b, c в этих выражениях могут быть любыми числами, переменными или выражениями. Для удобства использования семь основных формул лучше выучить наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислить, соответственно, квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем умножения их суммы и разности.

Шестая и седьмая формулы — это соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формулу сокращенного умножения иногда также называют тождествами сокращенного умножения. Это неудивительно, так как всякое равенство есть тождество.

При решении практических примеров часто используются формулы сокращенного умножения с переставленными левой и правой частями. Это особенно удобно при разложении многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу БСС еще несколько формул.

Сначала рассмотрим биномиальную формулу Ньютона.

а + б п знак равно С п 0 а п + С п 1 а п — 1 б + С п 2 а п — 2 б 2 + . . + C n n — 1 a b n — 1 + C n n b n

Здесь C n k — биномиальные коэффициенты, стоящие в строке номер n треугольника Паскаля. Биномиальные коэффициенты рассчитываются по формуле:

C nk = n ! к! · (н — к) ! = п (п — 1) (п — 2) . . (п — (к — 1)) к !

Как видите, БСС для квадрата и куба разности и суммы является частным случаем биномиальной формулы Ньютона для n=2 и n=3 соответственно.

Но что, если в сумме, которую нужно возвести в степень, больше двух членов? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

а 1 + а 2 + . . + а п 2 знак равно а 1 2 + а 2 2 + . . + а п 2 + 2 а 1 а 2 + 2 а 1 а 3 + . . + 2 а 1 а п + 2 а 2 а 3 + 2 а 2 а 4 + . . + 2 а 2 а н + 2 а н — 1 а н

Еще одна формула, которая может пригодиться, — это формула разности энных степеней двух членов.

а н — б н = а — б а н — 1 + а н — 2 б + а н — 3 б 2 + . . + a 2 b n — 2 + b n — 1

Эта формула обычно делится на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2

Для нечетных показателей 2m+1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 б 2 + . . + б 2 м

Формулы разности квадратов и разности кубов, как вы уже догадались, являются частными случаями этой формулы для n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на -b.

Как читать формулы сокращенного умножения?

Приведем соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Проще всего это сделать на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

а + б 2 знак равно а 2 + 2 а б + б 2 .

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенному произведению выражений и квадрату второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности а — b 2 = а 2 — 2 а b + b 2 запишем:

квадрат разности двух выражений а и Ь равен сумме квадратов этих выражений минус удвоенное произведение первое и второе выражения.

Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3. Куб суммы двух выражений a и b равен сумме кубов этих выражений, трех произведение квадрата первого выражения на второе и произведение квадрата второго выражения на первое выражение в три раза.

Переходим к чтению формулы разности кубов а — b 3 = а 3 — 3 а 2 b + 3 а b 2 — b 3. Куб разности двух выражений а и b равен кубу первого выражения минус умноженный на три квадрат первого выражения и второго, плюс умноженный на три квадрат второго выражения и первого выражения минус куб второго выражения.

Пятая формула а 2 — b 2 = а — b а + b (разность квадратов) звучит так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называются соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого формулы суммы и разности кубов читаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

БСС Доказательство

Доказать БСС довольно просто. Опираясь на свойства умножения, проведем умножение частей формул, стоящих в скобках.

Например, рассмотрим формулу квадрата разности.

а — b 2 = а 2 — 2 а b + b 2.

Чтобы возвести выражение во вторую степень, выражение надо умножить само на себя.

а — б 2 = а — б а — б.

Раскроем скобки:

а — Ь а — Ь = а 2 — а Ь — Ь а + Ь 2 = а 2 — 2 а Ь + Ь 2.

Формула доказана. Аналогично доказываются остальные ФСО.

Примеры применения ФСО

Целью использования сокращенных формул умножения является быстрое и лаконичное умножение и возведение выражений в степень. Однако это далеко не все возможности ФСО. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСО

Упростим выражение 9 y — (1 + 3 y) 2 .

Примените формулу суммы квадратов и получите:

9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2. ФСО

Сократите дробь 8 x 3 — z 6 4 x 2 — z 4 .

Заметим, что в выражении в числителе стоит разность кубов, а в знаменателе — разность квадратов.

8 х 3 — з 6 4 х 2 — з 4 = 2 х — з (4 х 2 + 2 х з + з 4) 2 х — з 2 х + з.

Уменьшаем и получаем:

8 х 3 — z 6 4 х 2 — z 4 = (4 х 2 + 2 х z + z 4) 2 х + z

Пох также помогают вычислить значения выражений . Главное, уметь замечать, куда наносить формулу. Покажем это на примере.

Возведем в квадрат число 79. Вместо громоздких вычислений запишем:

79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241.

Казалось бы, сложное вычисление было проведено быстро с использованием только формул сокращенного умножения и таблицы умножения.

No related posts.