Примеры со степенями 5 класс математика: Понятие степени с натуральным показателем — урок. Математика, 5 класс.

«Степень числа». Урок математики 5 класс

Дата: _______

Класс: 5

Предмет: математика

Тема: «Степень числа. Квадрат и куб числа».

Цель: ознакомление с понятием степень числа, куб и квадрат числа совершенствование навыков чтения степеней.

Задачи:

1. Образовательные: сформировать понятие степени; научиться: читать и записывать степень; называть компоненты степени; заменять произведение степенью; представлять степень в виде произведения; объяснить, что называется квадратом и кубом числа.

2. Развивающие: развивать логическое мышление, память, внимание.

3. Воспитательные: воспитывать ответственность и аккуратность, интерес к предмету.

Тип урока: урок «открытия» нового знания.

Ход урока

1. Орг. Момент

— Здравствуйте.

— Какие вопросы по контрольной работе?

— С какими проблемами вы столкнулись?

— Сегодня на уроке мы сначала восхитимся нашими умениями вычислять, для этого проведем устный счет.

1. Речевая разминка

-C-

—СТА-, -СТО-, -СТУ-.

Степень

В степень.

1. Актуализация знаний:

Устный счет. “Круговые” примеры.

— Ответ первого выражения является началом в записи следующего.

— Вычислите. Соедините выражения стрелочками.

35+35+35+35+35

51+51+51+51

7*13+37*7

150+270/90

204-104-65

175/25

350-50*4

153/3

— В каких выражениях можно одно действие заменить другим?

— Запишите, полученные выражения.

1. Изучение новой темы:

— На доске записаны выражения. 

2 + 2 + 2 + 2 + 2 и 2 · 2 · 2 · 2 · 2

— Как вы думаете, что общего у них?

— Чем они отличаются?

— Мы с вами уже повторили, как сумму 2 + 2 + 2 + 2 + 2 записать короче.

2 + 2 + 2 + 2 + 2=2 · 5.

— А как вы думаете, можно ли произведение 2 · 2 · 2 · 2 · 2 записать короче?

— Оказывается можно. И вот как: 2 · 2 · 2 · 2 · 2 =2 ⁵.

Тема нашего урока “Степень числа. Квадрат и куб числа”.

— Запись 2⁵ читают “два в пятой степени”. (Запись в тетрадь и проговорить). 

2 – основание степени;

5 – показатель степени;

2 ⁵ – степень.

— Прочитайте выражения, назовите в каждом основание и показатель степени: 

6⁷, 12³, 4¹⁰, 15², 3⁵, 8¹

— Запишем произведения в виде степени:

а) 4 · 4 · 4; б) 3 · 3 · 3; в) 2 · 2 · 2 · 2 · 2 · 2.

Г) 5* 5 д) 7* 7* 7* 7 е)6*6

— Вторую степень числа принято называть иначе.

— Произведение 5 · 5 называют квадратом числа 5 и обозначают 5².

n² = n · n (Чтение правила в учебнике).

— Рассмотрим таблицу квадратов первых десяти натуральных чисел. Как получены числа второй строки?

— Третья степень числа также имеет свое особое название.

— Произведение 7 · 7 · 7 называют кубом числа 7 и обозначают 7³.

n³ = n · n · n (чтение правила в учебнике).

— Рассмотрим таблицу кубов первых десяти натуральных чисел. Как получены числа второй строки?

— Квадрат числа в пределах 10 вычислить легко, это примеры из таблицы умножения, а вот квадрат чисел в пределах 20 помещены на форзаце учебника. Откройте эту таблицу. Чему равен квадрат 11, 12, 13. Для удобства здесь размещена таблица кубов, чтобы не искать ее в учебнике.

— Найдите значения выражений:

3¹ =? 15¹ =? 1¹=?

— Показатель степени 1 обычно не пишут.

1. Физминутка

2. Закрепление изученного материала

№ 653 у доски.

№ 654 4 столбика

2 столбика

3 столбика

1. Итог урока:

Назовите основание степени и показатель степени:

34, 57, 93, 158, 132.

Что такое “квадрат числа”?

Что такое “куб числа”?

Выставляются отметки за урок.

1. Домашнее задание:

С. 101 № 666.

Дата: ______

Класс: 6

Предмет: математика

Тема урока: «Сложение и вычитание рациональных чисел. Длина отрезка на координатной прямой».

Цель: Формирование навыков сложения и вычитания рациональных чисел

Задачи:

1. -закрепить навыки сложения и вычитания положительных и отрицательных чисел, проверить знания учащихся по данной теме;

2. -развивать навыки беглого устного счета, логическое мышление учащихся; развитие воли через задание посильной сложности, развитие интеллекта через заучивание математических терминов;

3. -воспитывать у учащихся интерес к математике и сознательную дисциплину.

Ход урока:

1. Организационный момент.

Думать — коллективно!

Решать — оперативно!

Отвечать — доказательно!

Бороться — старательно!

И открытия нас ждут обязательно!

1 препятствие.

Математика – царица наук,

Арифметика – царица математики

(К.Гаусс)

1.Сформулируйте правило сложения двух отрицательных чисел.

2.Сумма двух отрицательных чисел отрицательное или положительное число?

3.Что больше, сумма двух отрицательных чисел или одно из них?

4. Сформулируйте правило сложения чисел с разными знаками.

5.Если из двух слагаемых больший модуль имеет отрицательное число, то какой знак будет иметь сумма данных чисел?

6.Чему равна сумма противоположных чисел?

7.По какому правилу выполняется вычитание рациональных чисел?

8.Как вычитаются числа с разными знаками?

9. Как вычитаются числа с одинаковыми знаками?

10. Как найти длину отрезка на координатной прямой?

11. Сформулируйте правило раскрытия скобок, перед которыми стоит знак «+».

Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.

+ (+ a) = + a
+ (- a) = — a

12. Сформулируйте правило раскрытия скобок, перед которыми стоит знак «-».

Знак «минус» перед скобками меняет знак числа в скобках на противоположный.

— (+ a) = — a
— (- a) = + a

Правило знаков для чисел

+ (+) = +

+ (-) = —
— (-) = +	— (+) = —

Или выучить простое правило.

2 препятствие.

Тот, кто не знает математики , не может узнать никакой другой науки.

(Роджер Бэкон)

Устный счет.

1) 15 – (- 58) = 4) 28 – 100 = 7) 75 – 90 =

2) – 36 – 24 = 5) – 20 + 6 = 8) – 189 + 64 =

3) -70 + 16= 6) – 75 + 75 = 9) -35 – 28 =

3 препятствие.

Математика – точильный камень способностей.

Работа в тетрадях.

1. Упростите сумму:

-8+х+(-22).

1. Упростите сумму:

-10+а+34.

1. Разность у и 6 равна 12. Найдите у.

1. Решите уравнение: 5-с=12.

1. Найдите длину отрезка с концами в точках с координатами 3 и -7.

4 препятствие.

Математика черпает свою силу в умении исключать все лишнее в процессе мышления. (Э.Мах)

Работа над нестандартными заданиями.

Связь математики с живой природой.

На островах Тихого океана живут черепахи-гиганты. Они такой величины, что дети могут кататься сидя у них на панцире. Название этих черепах мы узнаем после того, как выполним следующее задание:

Решая примеры, определите название этой черепахи.

-42 + 18=

0	Е
-3,91 + 3,91 =	-5	Л
15,3 + (- 2,3) =	19	О
-12 – (-2) =	-24	Д
31 – 12 =	-102,08	С
-48 – 23 =	14	М
-6,1 + 6,1 + 0 =	-71	Х
15 – 20 =	13	Р
-25 – (-5) =	-20	И
-102,08 – 0 =

(Дермохелис)

5. Препятствие.В мире интересного.

Только забавляясь и учимся. (Анатоль Франс)

а).На земном шаре обитают птицы – безошибочные определители прогноза погоды на лето. Название этих птиц зашифровано в примерах, которые нам предстоит решить. (Решаем письменно с комментарием).

Выполните действия.

-379 + 948 =

-0,15	Л
-0,81 + 0,66 =	-1000,7	Н
-7,6 + 19,2 =	-24,3	О
-2,6 – (-1,4) =	-1,2	М
3,2 – 6,28 =	569	Ф
-1408,7 + 408 =	0	Г
-817 + 817 =	-3,08	И
-13,25 – 11,05 =	11,6	А

(Фламинго)

– «Это интересно!»

Фламинго строят из песка гнезда в форме усеченного конуса, в верхнем основании его делают углубления, в которые складывают яйца. Если лето будет дождливым, то гнезда строятся высокими, чтобы их не могла затопить вода, а если засушливым – то более низкими.

б). Самое маленькое государство – Ватикан. Какова его площадь?

– 189 + 233 =?

в). Материк с наибольшим числом границ – Африка. Каково число границ?

– 75 +? = 33

6.Препятствие.

МИР построен на силе ЧИСЕЛ.

(Пифагор)

а).Математические знаки.

1). *6 *8 =-14

2). *29 * 50=+21

б).Какая рыба без чешуи?

1).Щука-5, 2).Сом-7, 3).Карась-9.

–15+у=-8

в).Какое озеро самое красивое?

1).Чудское-2, 20.Ильмень-4, 3).Байкал-6.

m+(-14)=-8

г). Сколько учеников вашего класса пробовали курить?

– 6 + ? = -4

д). Во сколько лет они попробовали курить?

1).– 15 – (-21)= ?

2)? –16= – 8;

7. Препятствие.

Мы с наслаждением познаем математику…

Она восхищает нас, как цветок лотоса.

(Аристотель)

Задание:

Расположите числа в порядке убывания:

— —Р; — И; 6,1 – Ф; 16 –П; -0,2 –Г; 0,2 –А; -0,6 – О.

(ответ: Пифагор)

Пифагор (1- призер Олимпийских Игр, 2- победитель в кулачных боях, 3- “Царица геометрии” – теорема Пифагора)

Самостоятельная работа

Вариант № 1

1.Сравните значения выражений: 3,87 + (-2,63) и 5,29 + (-3,59) (3 б)

2. Вычислите: 5,4 + (- 3,7) + (- 4,2) (3 б)

3. Вычислите: 3,7 – х = -2,3 (3 б)

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: — 6,1 * (- 2,3)* 3,8 = 0 (3 б)

Вариант № 2

1. Сравните значения выражений: — 7,35 +4,54 и -4,68 + 3,46 (3 б)

2. Вычислите: 12,8 + (- 3,5) + (- 7,6) (3 б)

3. Вычислите: х – 3,9 = -2,7 (3 б)

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: 3,9 * 7,4 * (- 9,3) = — 12,8 (3 б)

Проверка самостоятельной работы по образцу.

Вариант № 1

1.Сравните значения выражений: 3,87 + (-2,63)

3. Вычислите: 3,7 – х = -2,3 х = 6

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: — 6,1 — (- 2,3) + 3,8 = 0

Вариант № 2

1.Сравните значения выражений: — 7,35 +4,54

2. Вычислите: 12,8 + (- 3,5) + (- 7,6) = 1,7

3.Вычислите: х – 3,9 = -2,7 х = 1,2

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: 3,9 — 7,4 + (- 9,3) = — 12,8

8.Заключение.

Числа отрицательные – новые для нас
Лишь совсем недавно их узнал наш класс
Сразу поприбавилось всем теперь мороки
Учим – учим правила, готовимся к урокам!

Школьные дни-

Быстры они,

К финишу мчатся как птицы

Помни везде-

Помни всегда,

Что без труда

В учебе побед не добиться!

9. Подведение итогов урока. Выставление оценок.

— Что есть больше всего на свете? – Пространство.

— Что быстрее всего? – Ум.

— Что мудрее всего? – Время.

— Что приятнее всего? – Достичь желаемого.

Слова древнегреческого математика Фалеса.

10.Домашнее задание:

Найти сумму всех целых чисел от – 499 до 501.

Степень числа 5 класс с ответами

Тестовые задания для 5 класса по теме: Степень числа.

Правильный вариант ответа отмечен знаком +

1. Что делают со степенью?

a. возродят -

b. возводят +

c. возят -

d. возражают -

2. (-4)⁴= …

a. -256 -

b. 16 -

c. 256 +

d. -16 -

3. Как записать в виде степени 7×7×7?

a. 7³ +

b. 7² —

c. 7⁴ -

d. 7¹ -

4. Из каких частей состоит степень?

a. логарифма и радикала -

b. ширины и длины -

c. градуса и угла -

d. основания и показателя +

5. Какой результат умножения получится в примере на картинке?

a. 64 -

b. 88 +

c. 72 -

d. 64 -

6. Чему равно любое число в нулевой степени?

a. 1 +

b. 2 -

c. 0 -

d. нет ответа -

7. Какое равенство верное?

a. 8³=10×12 -

b. 9×4=6² +

c. 11² — 65=96 — 7² -

d. 16:1⁹=2²+8 -

8. Сколько всего свойств у степеней?

a. 6 +

b. 8 -

c. 2 -

d. 11 -

9. Какое число является основанием степени в 0,143?

a. 0 -

b. 1 -

c. 3 -

d. 0,14 +

тест 10. Что делают со степенями при делении, если основания одинаковы?

a. суммируются -

b. умножаются -

c. вычитаются +

d. делятся -

11. Как записать по-другому 6^-2?

a. ⅓ -

b. (⅙)² +

c. 3 -

d. 6² -

12. Какой числовой показатель степени нужно вставить при основании 5, если ответ будет равен 125?

a. 3 +

b. 5 -

c. 2 -

d. 6 -

13. Как прочесть 9⁶?

a. девять с шестой степенью -

b. девять шестой степени -

c. девять в шестой степени +

d. девять и шестая степень -

14. Чему равно 4 в кубе?

a. 49 -

b. 64 +

c. 81 -

d. 36 -

15. 4,62= …

a. 16,36 -

b. 10,8 -

c. 18,5 -

d. 21,16 +

16. Какое неравенство составлено неверно?

a. (-3)³>(-4)⁵ -

b. 6²<5³ -

c. 2⁴>4² +

d. 7³<6⁷ -

17. -8²= …

a. -64 +

b. 64 -

c. -16 -

d. 16 -

^{18. При возведении степени в дробь возводятся в степень числитель и …}

a. полученный результат -

b. только числитель -

c. знаменатель +

d. сама степень -

^{19. 122: … =8}

a. 16 -

b. 18 +

c. 20 -

d. 14 -

тест-20. Какой вариант совпадает с ответом в 5²?

a.

√25 +

b. √16 -

c. √81 -

d. √49 -

21. Что в данном примере 3²+6=15 является показателем степени?

a. 6 -

b. 3 -

c. 2 +

d. 15 -

22. Какое число самое наименьшее?

a. 4⁴ -

b. 6² +

c. 8³ -

d. 2⁷ -

23. Чему равен x в примере 11² — x=8²?

a. 60 -

b. 48 -

c. 98 -

d. 57 +

24. Как читается «a²»?

a. a в квадрате +

b. a в двойке -

c. a и два -

d. a вторых -

25. … +11=92

a. 5⁴ -

b. 9²

+

c. 7³ -

d. 2⁶ -

26. Какое число нужно вставить вместо знака вопроса 3,4^?=39,304?

a. 4 -

b. 2 -

c. 1 -

d. 3 +

27. Чем является цифра «5» на картинке?

a. процентом -

b. показателем степени +

c. интегралом -

d. основанием степени -

28. Чему равна площадь квадрата, если его сторона равняется 4 см?

a. 16 см² +

b. 12 см² -

c. 20 см² -

d. 18 см² -

29. Как записать пример 6³×4³ по-другому?

a. 6×4³⁺³ -

b. (6×4)³ +

c. 6

3+3×4 -

d. 6×4+3×3 -

тест_30. 2⁴+20= …

a. 4³ -

b. 1⁹ -

c. 6² +

d. 3⁴ —

Угол 180 градусов — форма, примеры

LearnPracticeDownload

Угол 180 градусов представляет собой прямой угол, поскольку он образует прямую линию. Это ровно половина полного угла (угол 360 градусов). Если говорить о реальном примере угла в 180 градусов, то прекрасным примером является угол между двумя стрелками часов в положении 6 часов. Угол между двумя стрелками часов составляет 180°, потому что они образуют прямую линию.

1.	Что такое угол 180 градусов?
2.	Угол 180 градусов Название
3.	Как нарисовать угол 180 градусов?
4.	Часто задаваемые вопросы об угле 180 градусов

Что такое угол 180 градусов?

Угол 180 градусов — это прямой угол, равный половине оборота. Его также называют углом полуокружности. Прямой угол получается прямой линией. Два плеча угла, составляющие 180 градусов, находятся как раз напротив друг друга из общей вершины. Угол 180 градусов изменяет направление точки. А 9Угол 0 градусов составляет половину угла 180 градусов и известен как прямой угол.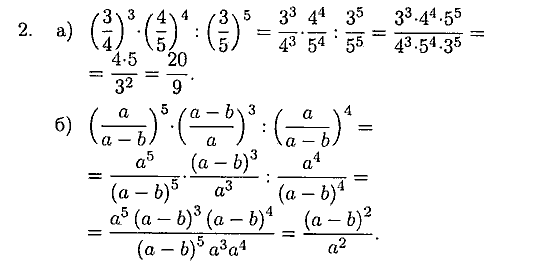 Посмотрите на изображение, приведенное ниже, показывает, как выглядит угол 180 градусов.

На изображении выше лучи AO и OB имеют общую точку O. Лучи AO и OB противоположны друг другу. АВ — прямая линия, образующая угол 180 градусов.

Угол 180 градусов Название

Угол, равный 180 градусам, называется прямым углом . Всякий раз, когда мы строим угол 180 градусов, он всегда образует прямую линию, поэтому он известен как прямой угол. Существуют разные названия углов разных измерений. Например, половина угла 180 градусов, т.е. 9Угол 0 градусов известен как прямой угол в геометрии. Точно так же удвоение 180 градусов, то есть угол в 360 градусов, известен как полный угол. Углы меньше 180 градусов делятся на острые и тупые.

Два угла, которые вместе составляют 180 градусов, называются дополнительными углами. В то время как два или более угла, соединяющиеся вместе в точке на линии, образующей 180 градусов, известны как линейные пары углов.

Как нарисовать угол 180 градусов?

Угол 180 градусов можно нарисовать с помощью транспортира и циркуля.

Построение угла 180 градусов с помощью транспортира

Выполните указанные действия, чтобы построить угол 180 градусов с помощью транспортира:

• Шаг 1: Нарисуйте луч OA.
• Шаг 2: Поместите транспортир в точку O.
• Шаг 3: Во внутреннем круге транспортира найдите отметку 180°, карандашом отметьте точку и назовите ее C.
• Шаг 4: Соедините O и C. Теперь ∠AOC=угол 180 градусов.

Построение угла 180 градусов с помощью циркуля

Выполните указанные действия, чтобы построить угол 180 градусов с помощью циркуля.

• Шаг 1: Нарисуйте прямую линию с помощью линейки и назовите ее AB.
• Шаг 2: Отметьте точку O в любом месте между A и B.
• Шаг 3: Возьмите О за центральную точку, начертите с помощью циркуля дугу любого радиуса, дуга должна проходить слева от точки О вправо от О или наоборот, касаясь линии АВ .
• Шаг 4: Дуга пересекает прямую в двух точках. Отметьте срезы точками C и D.
• Шаг 5: Таким образом, угол COD равен 180 градусам.

Важные примечания

• Угол в 180 градусов также называют прямым углом, полукругом или полукругом.
• Угол 180 градусов можно построить с помощью транспортира или циркуля.

Похожие статьи

Ознакомьтесь с интересными статьями об углах 180 градусов в геометрии.

• Угол 30 градусов
• Угол 60 градусов
• Измерение углов
• 30-60-90 Треугольник

 

Примеры угла 180 градусов

1. Пример 1: Можете ли вы помочь Алексу найти разницу между углом 180° и углом 90°?

   Решение: Угол в 180 градусов представляет собой прямую линию, известную как полуокружность. А 9Угол 0 градусов составляет четверть окружности. 180 градусов образуют прямую линию, а 90 градусов образуют перпендикуляр.

2. Пример 2: Если угол в 180 градусов разделить на две части и один угол равен 70 градусам, то чему равен другой угол?

   Решение:

   Пусть неизвестный угол равен b, а данный угол равен a = 70°.

   a + b = 180°

   70° + b = 180°

   b = 180° — 70° = 110°

   Следовательно, другой угол равен 110°. Это тупой угол.

3. Пример 3: Есть три угла, образующих вместе прямой угол: угол A, угол B и угол C. Если угол A = 30 градусов, угол B = 90 градусов, то какова величина угла C?

   Решение: Мы знаем, что прямой угол равен 180 градусам. Это означает, что угол А + угол В + угол С = 180 градусов.

   30° + 90° + C = 180°

   C = 180° — 90° — 30° = 60°

   Следовательно, угол C равен 60 градусам.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по углу 180 градусов

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об угле 180 градусов

Что такое углы 180 градусов в реальной жизни?

Углы 180° часто встречаются в реальной жизни. В повседневной жизни 180-градусные углы используются инженерами и архитекторами для строительства сооружений, автомагистралей, домов и спортивных сооружений. Плотники делают скамейки, столы и диваны, используя прямые углы.

Как выглядит угол 180 градусов?

180 градусов выглядят как прямая линия, потому что лучи или стороны угла, составляющие 180 градусов, полностью противоположны друг другу. Общая точка, соединяющая прямые, совершает половину оборота, т. е. угол 180 градусов.

Сколько углов 180 градусов требуется, чтобы сделать полный оборот?

Для полного поворота нам нужны два угла по 180 градусов. Угол 360 градусов — это полный оборот или полный оборот. Половина 360 градусов составляет 180 градусов, таким образом, угол в два или два раза больше 180 градусов дает полный поворот.

Как называется угол 180 градусов?

Угол в 180 градусов известен как прямой угол. Стороны угла противоположны друг другу и образуют прямой угол на прямой, проходящей через вершину. Внешний вид угла 180 градусов — это прямая линия.

Угол 180 градусов тупой?

Мера тупого угла больше 90°, но меньше 180°, поэтому угол 180° не является тупым углом. Его называют прямым углом.

Сколько углов 90 градусов составляет угол 180 градусов?

В угле 180 градусов есть два угла по 90 градусов, так как сумма двух углов по 90 градусов равна 180 градусам.

Что такое 180 градусов для треугольника?

Сумма всех внутренних углов треугольника всегда равна 180 градусам. Кроме того, пара внутреннего угла и следующего за ним внешнего угла в треугольнике дает прямой угол, равный 180 градусам.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по 180-градусному углу [PDF]

Рабочие листы по математике и
наглядный учебный план

Common Core Math: Grade 5

All Common Core: Ресурсы по математике 5th Grade

7 Диагностические тесты 225 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 … 196 197 198 199 200 201 202 203 204 205 206 207 Следующая →

Common Core: Справка по математике для 5-го класса » Common Core Math: 5 класс

Прямоугольный треугольник должен иметь угол, равный __________ градусов.

Возможные ответы:

Правильный ответ:

Объяснение:

В прямоугольном треугольнике должен быть прямой угол, равный . Изображение ниже является примером:

Сообщить об ошибке

Как называется двумерная фигура ниже?

Возможные ответы:

Octagon

Pentagon

Heptagon

Hexagon

Правильный ответ:

Пентагон

. Пояснение:

Двумерная фигура, показанная на рисунке, представляет собой пятиугольник. Пятиугольник классифицируется по пяти сторонам, пяти углам и пяти вершинам. У пятиугольника внутренние углы в сумме составляют 540 градусов. Правильные пятиугольники имеют стороны одинаковой длины и внутренние углы 108 градусов.

Сообщить об ошибке

К какому типу относится приведенный ниже треугольник?

Возможные ответы:

Правый треугольник

ЭКОЛИЗАТОРНЫЙ ТРЕУГЛИЯ

СЛОЙНАЯ ТРЕУГЛИЯ

ISOCELES Triangle

Правильный Ответ:

Scalenge Triangle

95. Пояснение:

Этот треугольник является разносторонним, потому что длины всех его сторон различны.

Это не равносторонний треугольник, потому что у равностороннего треугольника все стороны должны быть равны по длине.

Это не равнобедренный треугольник, потому что у равнобедренного треугольника две равные стороны.

Это не прямоугольный треугольник, потому что у прямоугольного треугольника должен быть прямой угол, угол, который измеряет .

Сообщить об ошибке

Разделить: 

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Во-первых, мы хотим использовать блоки с основанием 10 для представления

. Поскольку мы делим на, нам нужно разбить наш на группы

Как видите, у нас есть группы. Таким образом, ответ есть.

Сообщить об ошибке

Разделить:

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Во-первых, мы хотим использовать блоки с основанием десять для представления

. Поскольку мы делим на , нам нужно разделить нашу на группы

. Мы видим, что у нас есть 2 группы по 2, поэтому ответ равен 2. . 

Сообщить об ошибке

Разделить:

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Во-первых, мы хотим использовать блоки с основанием десять для представления 0,2

. Поскольку мы делим 0,2 на 0,2, нам нужно разделить нашу 0,2 на группы 0,2:

Мы можем видеть, что мы есть 1 группа, поэтому наш ответ 1. 

 

Сообщить об ошибке

Разделить: 

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Во-первых, мы хотим использовать блоки с основанием десять для представления 

. Поскольку мы делим на, нам нужно разделить наше на группы:

Как видите, у нас есть группы; таким образом, 

Сообщить об ошибке

Разделить: 

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Во-первых, мы хотим использовать блоки с основанием десять для представления 

. Поскольку мы делим на, нам нужно разделить наше на группы:

Как видите, у нас есть группы; таким образом, 

Сообщить об ошибке

Решите следующее: 

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Во-первых, мы хотим использовать блоки с основанием десять для представления

. Поскольку мы делим на, нам нужно разбить наши на группы

Как видите, у нас есть группы; таким образом,  

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Проблема, которую вам предстоит решить, такова.

 

 это делимое, это то, что разбивается на группы. наш делитель, который является количеством групп, которые вы делаете. Нам нужно разделить  пополам, чтобы увидеть, сколько человек в каждой группе.

 

Первый шаг — поставить десятичную дробь над уравнением на то же место. Он совпадет с десятичной дробью внутри вашего «дома длинного деления».

 

Далее нам нужно использовать или умножить факты, чтобы определить, на что можно умножить, чтобы получить или приблизиться к этому, не переходя.