Приведение кубического уравнения к каноническому виду
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Частное решение.
Настройка.
Подробно4.4. Приведение к каноническому виду уравнения кривой 2-го порядка
Общее уравнение кривой 2-го порядка:(23)
Уравнение (23) можно представить в виде , где – квадратичная форма уравнения кривой, а – линейная функция.
Приведение уравнения кривой (23) к каноническому виду начинается с приведения к каноническому виду соответствующей квадратичной формы . Её матрица Из характеристического уравнения находятся собственные значения и матрицы , при этом , так как . Затем находят соответствующие собственные векторы, которые после нормировки образуют ОНБ .
В новом базисе квадратичная форма примет канонический вид:
. (24)
Переход от ОНБ к ОНБ описывается матрицей , в столбцах которой находятся координаты векторов ОНБ . Связь между координатами и определяется из уравнения т. е.
. (25)
Подставляя зависимости (25) в линейную функцию получим:
Тогда уравнение (23) примет вид:
(26)
Выделяя в (26) полные квадраты, получим каноническое уравнение одной из кривых 2-го порядка. О какой кривой идет речь, можно определить сразу по матрице квадратичной формы. Если , то линия, задаваемая уравнением (23), Эллиптического типа, если – Гиперболического, если – Параболического типа.
Пример 20. Определить тип кривой 2-го порядка и построить её:
Решение. Уравнение кривой представим в виде Где – квадратичная форма, – линейная функция.
Квадратичная форма, соответствующая заданной кривой, Её матрица .
Так как , то кривая параболического типа. Составим характеристическое уравнение и найдём собственные значения матрицы :
Собственные векторы, соответствующие найденным собственным значениям:
Построим ОНБ из собственных векторов:
Матрица перехода Выполним проверку соответствия ориентации ОНБ ориентации ОНБ : , значит, ориентация совпадает. В этом базисе .
Так как то Подставляя эти разложения в линейную часть кривой, получим:
Тогда уравнение кривой примет вид или т. е. где Заданная кривая изображена на рисунке 1.
Рисунок 1
Пример 21. Привести уравнение кривой 2-го порядка к каноническому виду и определить тип кривой:
Решение.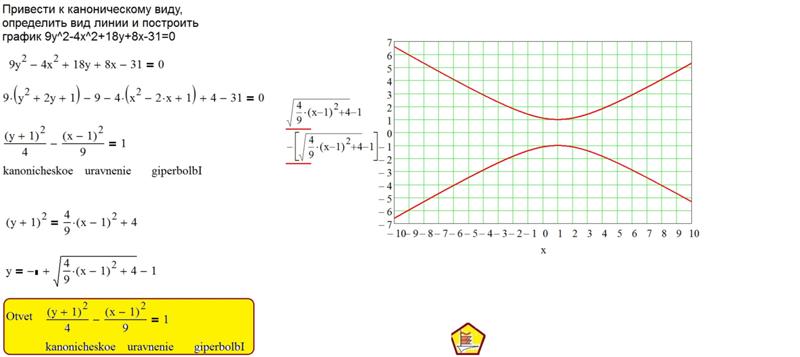
Уравнение кривой представим в виде Где – квадратичная форма, – линейная функция.
В нашем случае , её матрица .
Определим тип кривой. Для этого вычислим Так как То заданная кривая эллиптического типа.
Приведем квадратичную форму к каноническому виду. Для нахождения собственных значений матрицы составим характеристическое уравнение: Т. е. , тогда .
Теперь найдём соответствующие им собственные векторы:
Построим ОНБ: , тогда матрица перехода от ОНБ к ОНБ имеет вид: Так как значит, ориентация ОНБ соответствует ориентации ОНБ .
Матрица заданной квадратичной формы в базисе имеет вид: , а сама квадратичная форма: .
Напомним, что матрица может быть получена в результате преобразования подобия: , где – матрица перехода к новому ОНБ. Координаты и связаны между собой соотношением: т. е. .
Преобразуем линейную часть уравнения кривой:
Теперь можно записать уравнение кривой в координатах :
Таким образом, выполнен первый шаг в преобразовании кривой к каноническому виду, в результате которого в исходном уравнении кривой исчезло слагаемое, содержащее произведение координат и .
Выделим полные квадраты: или . Если то каноническое уравнение заданной кривой 2-го порядка примет вид и задаёт эллипс с полуосями Кривая изображена на рисунке 2.
Рисунок 2
Литература: [3, 6, 7, 15].
| < Предыдущая | Следующая > |
|---|
Нормальная форма Жордана — онлайн-калькулятор канонического приведения матрицы
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Матрица в нормальной форме Жордана
Инструмент для вычисления нормальной формы матрицы Жордана (путем редукции квадратной матрицы Жордана) для получения путем разложения 2 матрицы S и J такие, что M = S . Дж. S̄
Результаты
Матрица нормальной формы Джордана — dCode
Теги: Матрица
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор матриц Джордана
Загрузка.
..
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
См. также: Диагонализация матрицы — Собственные значения матрицы — Собственные векторы матрицы
Ответы на вопросы (FAQ)
Что такое матрица Жордана? (Определение)
Квадратная матрица $M$ размера $n\times n$ диагонализируема тогда и только тогда, когда сумма размерностей ее собственных пространств равна $n$.
Если $ M $ не диагонализируема, то существует почти диагональная матрица $ J $, называемая нормальной формой Жордана, вида $$ \begin{bmatrix} \lambda_i & 1 & \; & \; \\\; & \lambda_i &\ddots & \; \\\; & \; &\ddots&1\\\; & \; & \; & \lambda_i \end{bmatrix} $$
Как рассчитать нормальную форму Жордана для матрицы?
Возьмем $M$ квадратную матрицу размера $n$, которая имеет собственные значения из множества $\lambda_n$.
Пример: $$ M = \begin{bmatrix} 4 & 0 & 0 \\ 0 & 4 & -1 \\ 0 & 1 & 2 \end{bmatrix} \Rightarrow \lambda_n = \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} $$ Здесь $M$ имеет только 2 собственных вектора: $v_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} $et $v_2 = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $, поэтому не диагонализируется, но имеет для Матрица Жордана (каноническая форма) $$ M=\begin{bmatrix} 3 & 0 & 0 \\ 0 & 3 & 1 \\ 0 & 0 & 3 \end{bmatrix} $$
Пример: Альтернатива Метод: вычислить матрицу $S$, найдя третий вектор $v_3$, такой как $(M — 3 I_3) v_3 = k_1 v_1 + k_2 v_2 \Rightarrow v_3 = \begin{pmatrix} 0 \\ 1 \\ 0 \end {pматрица} $.
Итак, $$ S = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 0 \end{bmatrix} $$ и $ M = S . Дж. \bar{S} $ 9{-1} $ (см. степени матрицы).
Исходный код
dCode сохраняет за собой право собственности на исходный код «Матрицы нормальной формы Джордана». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Матрица нормальной формы Джордана», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или алгоритма «Джордан Матрица нормальной формы» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Матрицы нормальной формы Иордании» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Матрица нормальной формы Джордана» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Jordan Normal Form Matrix на dCode.fr [онлайн-сайт], получено 24 октября 2022 г., https://www.dcode.fr/matrix-jordan
Сводка
- Калькулятор матрицы Жордана
- Что такое матрица Жордана? (Определение)
- Как рассчитать нормальную форму Жордана для матрицы?
- Что такое разложение Жордана?
- Что такое редукция Жордана?
- Как вычислить мощность матрицы Жордана?
Similar pages
- Eigenvectors of a Matrix
- Eigenvalues of a Matrix
- Matrix Diagonalization
- Matrix Reduced Row Echelon Form
- Matrix Addition
- Cofactor Matrix
- Transpose of a Matrix
- Список инструментов Dcode
Поддержка
- PayPal
- Patreon
- Подробнее
Форум/Справка
Ключевые слова
Jordan, Matrix, Reding, Decomposition, Norch, Linksosition, Norch, Norch, Norch, Decomposition, Decomposition, Decomposition, Decomposition, Norm.
▲
Нормальная форма Жордана — онлайн-калькулятор матричного канонического приведения
Поиск инструмента
Поиск инструмента в dCode по ключевым словам:Просмотреть полный список инструментов dCode
Матрица в нормальной форме Жордана
Инструмент для вычисления нормальной формы Жордана матрицы (приведением квадратной матрицы по Жордану) для получения путем разложения двух матриц S и J, таких что M = S . Дж. S̄
Результаты
Jordan Normal Form Matrix — dCode
Метки: Matrix
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты оказывают ценную помощь в играх, математике и задачах геокэшинга решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор матриц Джордана
Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
См.
также: Диагонализация матрицы — Собственные значения матрицы — Собственные векторы матрицы
Ответы на вопросы (FAQ)
Что такое матрица Жордана? (Определение)
Квадратная матрица $M$ размера $n\times n$ диагонализируема тогда и только тогда, когда сумма размерностей ее собственных пространств равна $n$.
Если $ M $ не диагонализируема, то существует почти диагональная матрица $ J $, называемая нормальной формой Жордана, вида $$ \begin{bmatrix} \lambda_i & 1 & \; & \; \\\; & \lambda_i &\ddots & \; \\\; & \; &\ddots&1\\\; & \; & \; & \lambda_i \end{bmatrix} $$
Как вычислить нормальную форму Жордана для матрицы?
Возьмем $M$ квадратную матрицу размера $n$, которая имеет собственные значения из множества $\lambda_n$.
Пример: $$ M = \begin{bmatrix} 4 & 0 & 0 \\ 0 & 4 & -1 \\ 0 & 1 & 2 \end{bmatrix} \Rightarrow \lambda_n = \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} $$ Здесь $M$ имеет только 2 собственных вектора: $v_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} $ et $v_2 = \ begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $, поэтому не диагонализируется, но имеет для матрицу Жордана (каноническая форма) $$ M=\begin{bmatrix} 3 & 0 & 0 \\ 0 & 3 & 1 \\ 0 & 0 & 3 \end{bmatrix} $$
Пример: Альтернативный метод: вычислить матрицу $ S $, найдя третий вектор $ v_3 $, такой как $ (M — 3 I_3) v_3 = k_1 v_1 + k_2 v_2 \Rightarrow v_3 = \begin{pmatrix} 0 \ \ 1 \\ 0 \end{pmatrix} $.
Итак, $$ S = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 0 \end{bmatrix} $$ и $ M = S . Дж. \bar{S} $
Что такое разложение Жордана?
Разложение Жордана состоит в получении из матрицы $ M $ матриц $ S $ и $ J $ таких, что $ M = S . Дж. \bar{S} $ 9{-1} $ (см. степени матрицы).
Исходный код
dCode сохраняет за собой право собственности на исходный код «Матрицы нормальной формы Джордана». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Матрица нормальной формы Джордана», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или алгоритма «Джордан Матрица нормальной формы» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Матрицы нормальной формы Иордании» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.