Привести матрицы к ступенчатому виду: Приведение матрицы к ступенчатому виду онлайн

Свойства обратной матрицы — Мегаобучалка

1.Обратная матрица единственна.

Доказательство.Пусть существуют две обратные матрицы: и . Тогда

2. . Это следует из определения.

3. .

Доказательство: и

.

4. .

Доказательство: и

.

5.Если – невырожденная матрица, то – тоже невырожденная.

Доказательство: .

Пример.Найти обратную матрицу для матрицы

.

Найдём определитель матрицы :

,

следовательно, существует обратная матрица.

Вычислим алгебраические дополнения всех элементов матрицы :

; ; ; ; ; ;

; ; ,

тогда

.

Проверка

.

Лекция 5

Понятие линейной зависимости строк матрицы, основные теоремы.

Элементарные преобразования матриц. Ступенчатые матрицы. Приведение матрицы к ступенчатому и единичному виду. Построение обратной матрицы с помощью элементарных преобразований.

Понятие линейной зависимости строк матрицы, основные теоремы

Основная литература: [1], [4].

Элементарные преобразования матриц. Ступенчатые матрицы.

Приведение матрицы к ступенчатому и единичному виду.

Построение обратной матрицы с помощью элементарных преобразований

Определение. Элементарными преобразованиями матрицы называют следующие действия:

1) транспонирование матрицы;

2) умножение всех элементов строки (столбца) матрицы на число, отличное от нуля;

3) изменение порядка строк (столбцов) матрицы;

4) прибавление к каждому элементу строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;

5) отбрасывание нулевой строки (столбца).

Алгоритм приведения матрицы к ступенчатому виду

1) Из всех строк матрицы выбрать такую строку, первый элемент которой равен единице. Если такой строки нет, то получить ее с помощью элементарного преобразования 4. Меняя порядок строк, сделать выбранную строку первой строкой.

2) С помощью элементарного преобразования 4 получить нули во всех строках первого столбца, кроме первой.

3) Из всех строк матрицы, кроме первой, выбрать такую строку, второй элемент которой равен единице. Если такой строки нет, то получить ее с помощью элементарного преобразования 4. Меняя порядок строк, сделать выбранную строку второй строкой.

4) С помощью элементарного преобразования 4 получить нули во всех строках второго столбца, кроме первой и второй.

5) Алгоритм продолжать до тех пор, пока все элементы, лежащие ниже главной диагонали, не обратятся в нуль.

Пример 1.Привести матрицу к ступенчатому виду.

Решение.

.

Рассмотрим ещё один способ нахождения обратной матрицы с использованием элементарных преобразований.

Пример 2. .

Следовательно, .

Лекция 6

Ранг матрицы, определение. Понятие базисного минора матрицы.

алгебра_2_курс_вечерники_осень_2021 | Кафедра высшей алгебры

Лекции и семинары по алгебре на Вечернем отделении, осень 2021

Преподаватель: Куликова О.В.

Вопросы к экзамену

Занятия проходят по субботам с 09:00 до 12:20 в ауд. 16-04, 15-03

Программа курса

1. Системы линейных уравнений, методы их решения.

2. Векторные пространства, линейная зависимость векторов, базис. Ранг системы векторов.

3. Матрицы, операции над ними.

4. Перестановки и подстановки.

5. Определители.

6. Основные алгебраические структуры: группы, кольца, поля.

7. Комплексные числа, «основная теорема алгебры».

8. Вычеты.

9. Теория многочленов: деление с остатком, корни многочленов, разложение на множители.

10. Многочлены от нескольких переменных. Симметрические многочлены.

11. Рациональные дроби.

Литература

1. Э.Б.Винберг. Курс алгебры.

2. А.И.Кострикин. Введение в алгебру. Часть I. Основы алгебры.

3. А.Г.Курош. Курс высшей алгебры.

4. Сборник задач по алгебре под ред. А.И.Кострикина. Часть I. Основы алгебры.

Нумерация задач даётся по «Сборнику задач по алгебре» под ред. А.И.Кострикина, 3-е изд., Москва, Физматлит, 2015. Дополнительные задачи помечены знаком ★.

4 сентября 2021

Лекция 1

Матрицы: определение. Квадратные, диагональные, (главная и побочная диагональ), единичная матрица. Операции сложения и умножения на число. Свойства этих операция.

Определители 2-го и 3-го порядка: определение. Основные свойства (пока только формулировки). Описание метода разложения по строке/по столбцу.

Ведущие элементы (лидеры) строк матрицы. Матрицы ступенчатого вида. Элементарные преобразование над строками. Метод Гаусса приведения матрицы к ступенчатому (и улучшенному ступенчатому) виду.

Семинар

Определители 2-го и 3-го порядка. Вычисление определителей 2-го и 3-го порядка по определению и методом разложения по строке/по столбцу.

Домашнее задание: 9.1 в,г,д, 9.2 б(решить методом разложения по строке/по столбцу),в,д,е, 11.5, 12.1

11 сентября 2021

Лекция 2

Системы линейных алгебраических уравнений (СЛАУ) и их решения: определение и примеры. Совместные и несовместные, определённые и неопределённые СЛАУ. Матрица коэффициентов и расширенная матрица системы.

Элементарные преобразования систем линейных уравнений. Их связь с элементарными преобразованиями над строками расширенной матрицы. Элементарное преобразование приводит к эквивалентной СЛАУ.

Метод Гаусса решения СЛАУ: приведение к ступенчатому (и улучшенному ступенчатому) виду, анализ ступенчатой СЛАУ, главные и свободные неизвестные, общее решение системы.

Общее решение системы. Преимущество улучшенного ступенчатого вида.

Однородные системы линейных уравнений (ОСЛУ), их совместность. ОСЛУ с числом уравнений меньше числа неизвестных имеет ненулевое решение.

Арифметическое векторное пространство. Примеры. Линейная комбинация векторов. Линейная зависимость и линейная независимость системы векторов.

Семинар

1) Метод Гаусса решения СЛАУ. СЛАУ с параметром.

2) Векторное пространство: проверка аксиом. Проверка системы векторов на линейную зависимость.

Домашнее задание:

1) 8.1 б,в,г, 8.2 в,г,з

2) 6.2 б, 6.3 б,д, 6.4, 6.7д, 6.8, 6.9 б,д

18 сентября 2021

Лекция 3

1) Определение векторного подпространства. Примеры.

2) Свойства линейно зависимых и линейно независимых систем.

3) Линейная оболочка системы векторов. Определение множества, порождающего векторное пространство. Основная лемма о линейной зависимости.

4) Определение базиса. Свойства. Всякое конечномерное векторное подпространство обладает базисом. Все базисы конечномерного векторного пространства содержат одно и то же число векторов. Определение размерности векторного пространства. Примеры.

Семинар

Определение векторного пространства.

Домашнее задание:

1) Доказать следствия из аксиом векторного пространства V над R:

• единственность нулевого вектора,

• единственность противоположного вектора,

• λ0=0, λ(-x)=-λx, λ(x-y)=λx-λy, 0x=0, (-1)x=-x, (λ-µ)x=λx-µx, где x,y∈V, λ,µ∈R.

2) 6.8, 6.10

25 сентября 2021

Лекция 4

Всякую линейно независимую систему векторов конечномерного векторного пространства можно дополнить до базиса.

Определение ранга системы векторов. Определение ранга матрицы как ранга системы ее строк. Ранг матрицы не изменяется при элементарных преобразованиях над строками. Ранг матрицы ступенчатого вида равен числу ее ненулевых строк.

Ранг системы столбцов матрицы не меняется при элементарных преобразованиях над строками. Ранг матрицы не изменяется при элементарных преобразованиях над столбцами. Ранг системы строк матрицы равен рангу системы ее столбцов.

Семинар

1) Ранг матрицы.

Домашнее задание:

1) 7.1 (б,к,л) (решить методом ЭП), 7.2 (д,е,з), 7.3, 7.5

2) 6.11

2 октября 2021

Лекция 5

Критерий совместности и определенности СЛАУ в терминах рангов матриц (теорема Кронекера-Капелли)….

Однородные СЛАУ. Свойства решений однородной СЛАУ. Подпространство решений однородной СЛАУ и его базис (ФСР). Теорема о размерности подпространства решений однородной СЛАУ. Связь между множествами решений совместной системы линейных уравнений и соответствующей системы однородных линейных уравнений.

Семинар

1) Алгоритм нахождения базиса и ранга конечной системы векторов и линейных выражений всех векторов системы через найденный базис.

Алгоритм нахождения базиса и размерности линейной оболочки.

2) Нахождение ФСР однородной СЛАУ. Связь между множествами решений совместной системы линейных уравнений и соответствующей системы однородных линейных уравнений.

Домашнее задание:

1) 6.12 (б,г,д), 6.10 (б,д), 6.13, 35.11

2) 8.4 (в,г), 8.1 (в,г), ★7.19, ★8.25

9 октября 2021

Лекция 6

1)Определение перестановки из n элементов. Инверсии и знак перестановки. Свойства перестановок.

2) Формула полного разложения определителя. Примеры определителя 2-го и 3-го порядка. Определитель треугольной матрицы.

3) Определитель как полилинейная кососимметрическая функция. Элементарные преобразования над строками определителя. Вычисление определителя посредством приведения к треугольному виду.

Семинар

1) Перестановки. Инверсии. Знак перестановки.

2) Задачи на формулу полного разложения определителя.

Свойства определителя. Метод Гаусса вычисления определителей.

Домашнее задание:

1)3.5 (б,в,г,д)

2) 10.2, 10.4 г,д, 10.6, 11.1, 11.2, 11.3, 13.1 б.е, 13.2 а, б, з.

16 октября 2021

Лекция 7

Определитель транспонированной матрицы. К какому виду можно привести матрицу с помощью элементарных преобразований, если определитель матрицы равен нулю (отличен от нуля)? Определитель матрицы с углом нулей. Разложение определителя по строке (столбцу). Фальшивое разложение. Определитель Вандермонда.

Семинар

Определители. Разложение по строке (по столбцу). Рекуррентные соотношения.

Домашнее задание: 12.2, 12.3 д,и, 14.1 г-ж, 4.1, 4.2 б

23 октября 2021

Лекция 8

1) Умножение матриц, свойства. Транспонирование матриц, свойства.

2) Связь операций над матрицами и ранга. Ранг суммы матриц. Ранг произведения матриц.

Семинар

1) Умножение матриц, свойства. Транспонирование матриц, свойства.

2) Связь операций над матрицами и ранга. Ранг суммы матриц. Ранг произведения матриц.

Домашнее задание: 17.1 в,ж, 17.2 б, 17.4 а, 17.5а, 7.7, 7.10, 7.11, 7.12,

30 октября 2021

Лекция 9

1) Элементарные матрицы, их связь с элементарными преобразованиями над строками и столбцами матрицы.

2) Определитель произведения матриц.

3) Критерий равенства определителя нулю. Теорема о ранге матрицы (характеризация ранга в терминах миноров).

4) Обратные матрицы. Определение. Свойства

Семинар

1) Определитель произведения матриц.

2) Метод окаймляющих миноров.

3) Обратные матрицы (определение).

Домашнее задание:

1) 15.1, 15.2 (а, б, в),

2) 7.1 (б,з,к) (решить методом окаймляющих миноров),

3) 18.10 (б), ★18.17, 18.18

6 ноября 2021

Лекция 10

1) Критерий существования обратной матрицы. Обоснование метода элементарных преобразований для нахождения обратной матрицы.

2) Матричные уравнения. Правило Крамера.

Семинар

1) Обратные матрицы. Методы вычислений.

2) Матричные уравнения. Правило Крамера.

Домашнее задание:

1) 18.8 (г,ж,з,л), 18.9 (е,ж,л), 18.10 (б), ★17.26

2) 18.3 (а,д,в,г,з,и), 8.6 (б, д)

13 ноября 2021

Лекция 11

1) Бинарные операции. Определение коммутативности, ассоциативности бинарной операции, нейтрального элемента, обратного элемента, обратимого элемента. Примеры. Утверждение об единственности нейтрального элемента. Утверждение об единственности обратного элемента. Определение группоида, полугруппы, моноида, группы. Примеры.

2) Группа преобразований. Группа подстановок (операции над подстановками)

Семинар

1) Бинарные операции. Определение коммутативности, ассоциативности бинарной операции, нейтрального элемента, обратного элемента, обратимого элемента. Определение группоида, полугруппы, моноида, группы.

2) Группа подстановок (операции над подстановками)

Домашнее задание:

1) 54. 1(в, г, д), 54.3, 55.1 (г,д,е)

2) 3.1

20 ноября 2021

Лекция 12

Группа подстановок. Разложение на независимые циклы. Свойства. Умножение на транспозицию. Доказательство утверждения о разложении подстановки в виде произведения транспозиций. Четность. Свойства.

Семинар

Группа подстановок.

Домашнее задание:

3.2, 3.3, 3.4, 3.6, 3.7, 3.8

27 ноября 2021

Лекция 13

1) Определение кольца. Определение коммутативного (ассоциативного, с единицей) кольца. Примеры. Простейшие свойства. Определение обратимых элементов и делителей нуля. Простейшие свойства. Определение поля. Примеры. В поле нет делителей нуля.

2) Кольцо вычетов по модулю n. Утверждение о том, когда кольцо вычетов по модулю n является полем.

3) Мультипликативная группа ассоциативного кольца с единицей.

4) Определение характеристики поля. Свойство характеристики.

Семинар

1) Определение кольца и поля. Делители нуля и обратимые элементы.

Домашнее задание:

1) 63.1 (а-ж), 63.3 (а,б), 63.13 …

4 декабря 2021

Лекция 14

1) Поле комплексных чисел. Операции в алгебраической форме. Свойства. Операции в тригонометрической форме. Утверждение о произведении и делении в тригонометрической форме. Следствие о возведении в степень. Утверждение об извлечении корня из ненулевого комплексного числа.

Семинар

1) Комплексные числа. Операции в алгебраической форме. Операции в тригонометрической форме.

Домашнее задание:

1) 20.1 (б,г,к), 20.3 (а), 20.4 (а), 21.1 (г,и,ф,х), 21.2 (а,б,ж), 22.7 (б,в,п), 23.1 (б), 23.2 (б)

11 декабря 2021

Лекция 15

1) Кольцо многочленов от одной переменной над полем. Степень многочлена. Отсутствие делителей нуля и обратимые элементы в кольце многочленов над полем.

2) Деление с остатком в кольце многочленов над полем. Существование наибольшего общего делителя в кольце многочленов от одной переменной над полем (и в кольце целых чисел) и его представление в виде НОД(f,g)=fu+gv (алгоритм Евклида).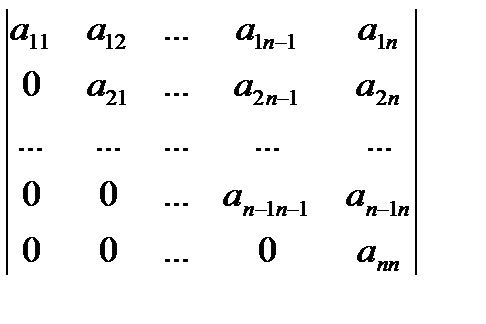

3) Многочлены как функции. Разные многочлены над бесконечным полем задают разные функции.

4) Теорема Безу. Схема Горнера. Корни многочлена, кратность корня. Следствие из теоремы Безу. Число корней многочлена.

5) Формальная производная многочлена от одной переменной. Кратные корни. Понижение кратности при дифференцировании многочленов над полем характеристики 0.

6) Теорема об алгебраической замкнутости поля комплексных чисел (основная теорема алгебры) (б/д). Следствия. Комплексные корни многочленов с вещественными коэффициентами. Разложение многочлена с вещественными коэффициентами на линейные множители и квадратичные множители с отрицательным дискриминантом.

7) Неприводимые многочлены. Неприводимые многочлены над полем комплексных и полем действительных чисел. Факториальность кольца многочленов от одной переменной над полем.

Семинар

1) Деление с остатком в кольце многочленов над полем. Существование наибольшего общего делителя в кольце многочленов от одной переменной над полем (и в кольце целых чисел) и его представление в виде НОД(f,g)=fu+gv (алгоритм Евклида).

2) Многочлены как функции. Корни многочлена, кратность корня. Теорема Безу, следствие о корнях. Схема Горнера. Формальная производная многочлена от одной переменной. Определение кратности корней многочленов над полем характеристики 0 путем дифференцирования.

3) Неприводимые многочлены. Неприводимые многочлены над полем комплексных и полем действительных чисел. Разложение многочлена с комплексными коэффициентами на линейные множители. Разложение многочлена с вещественными коэффициентами на линейные множители и квадратичные множители с отрицательным дискриминантом.

4) Примеры неприводимых многочленов над конечными полями. Разложение на неприводимые над полем вычетов.

Домашнее задание:

1) 25.1, 25.3, 25.7 (а,б)

2) 26.1 (в), 26.2 (в), 26.3 (б), 26.6

3) 27.1 (б,в), 27.2 (б),

4) 28.22 (а,б),

5) многочлены над полем рациональных чисел: 28.1, 28.2, 28.6, 28.8, 28.9 (б)

18 декабря 2021

Лекция 16

1) Кратные неприводимые множители. Отделение кратных множителей.

2) Поле частных. Поле рациональных функций. Простейшие и правильные дроби. Примеры. Теорема о разложении правильной дроби в сумму простейших дробей (б/д).

3) Кольцо многочленов от нескольких переменных. Степень многочлена от нескольких переменных. Одночлены. Однородные многочлены. Лексикографический порядок. Старший член многочлена. Лемма о старшем члене произведения многочленов.

Симметрические многочлены. Лемма о старшем члене симметрического многочлена. Элементарные симметрические многочлены. Лемма об одночлене от симметрических многочленов. Теорема о симметрических многочленах (б/д). Формулы Виета.

Семинар

1) Кратные неприводимые множители. Отделение кратных множителей.

2) Поле рациональных функций. Простейшие и правильные дроби. Разложение правильной дроби в сумму простейших дробей.

3) Кольцо многочленов от нескольких переменных. Лексикографический порядок. Старший член многочлена. Симметрические многочлены. Элементарные симметрические многочлены. Представление симметрического многочлена в виде многочлена от элементарных симметрических многочленов.

4) Формулы Виета.

Домашнее задание:

1) 25.8 (а)

2) 29.1 (в,г,и), 29.2 (в,г), ★(д,е), ★29.3

3) 31.9 (б), 31.10 (б)

4) 31.1 (б), 31.2 (б), 31.21 (б)

Преобразование обычной матрицы в разреженную матрицу в Python | от Самир | Analytics Vidhya

В этой статье мы рассмотрим пошаговую процедуру простого преобразования обычной матрицы в разреженную с помощью Python.

Матрица — это тип структуры данных, похожий на массив, в котором значения хранятся в строках и столбцах. Здесь значения имеют уникальный тип. Имея дело с матрицами (линейной алгеброй) в машинном обучении и НЛП, мы часто слышим о двух типах матриц:0003

• Плотная матрица — Матрица, в которой большинство элементов ненулевые. В этой матрице очень мало нулевых элементов.
• Разреженная матрица — Напротив, матрица, в которой большинство элементов нулевые и очень мало элементов не равны нулю.

Примечание — Не существует как такового критерия того, сколько нулевых значений в матрице определяет необходимость разрежения матрицы.

Представьте, что у вас есть большая матрица с N строки и M столбца, в которых большинство значений являются нулями. Вас просят учитывать только ненулевые элементы, поскольку нулевые элементы не добавляют большой ценности. Определенно, у вас есть ограничения по времени и пространству, поскольку вы имеете дело с очень большой матрицей.

Простой метод здесь состоит в том, чтобы пренебречь всеми 0 и сохранить ненулевые элементы в виде [ row_index , col_index , ненулевое_значение

9 ] 9 .

Подход:

1. Перебрать каждую строку входной матрицы.
2. Перебрать каждое значение каждой строки .
3. Если (значение == 0) → пропустить.
4. Если (значение != 0) → получить номер строки и номер столбца вместе со значением из входной матрицы.
5. Сохранить результат как [ строка , столбец , значение ] для каждой строки и столбца .
6. Стоп.

Допустим, нам дана матрица, большинство элементов которой равны 0 .

 Импорт Numpy As NP 
 из Scipy. Sparse Import CSR_MATRIX 

. Для демонстрации. 0 элемента больше всего.

 >>> mat = np.random.randint(low=0, high=3, size=(5, 5)) 
 >>> print(mat) 
 [[2 2 0 2 0] 
 [2 1 0 0 2] 
 [2 1 0 1 0] 
[0 1 2 0 2] 
 [0 1 2 2 1]] 

С помощью метода csr_matrix() мы можем легко получить разреженную матрицу.

 >>> smat = csr_matrix(mat) 
 >>> print(smat) 
 (0, 0) 2 
 (0, 1) 2 
 (0, 3) 2 
 (1, 0) 2 
 (1 , 1) 1 
 (1, 4) 2 
 (2, 0) 2 
 (2, 1) 1 
 (2, 3) 1 
 (3, 1) 1 
 (3, 2) 2 
 (3, 4) 2 
 (4, 1) 1 
 (4, 2) 2 
 (4, 3) 2 
 (4, 4) 1 

Мы можем думать о словаре на питоне, который представляет собой пару ключа и значения . Приведенный выше вывод представляет собой что-то вроде словаря , где ключи — это расположение индекса (строка, столбец), а значения — фактические ненулевые элементы.

Чтобы реализовать его с нуля, мы можем следовать алгоритмическому подходу, который я объяснил ранее.

  класс  SparseMatrix(): 
  def  __init__(self, arr): 
 self.arr = arr  def  keep_sparsity(self, to_dict=False): 
 sparse_mat = [ 
 [rindx, cindx, val] 
  for  (rindx, row)  в   enumerate 900ar09) 
  для  (cindx, val)  в   перечислить  (строка) 
  если  (val != 0) 
 ]  если  to_dict: 
 sparse_mat) r, c, v)  в  sparse_mat} 
  возврат  sparse_mat 

Приведенный выше класс SparseMatrix() имеет метод keep_sparsity , в котором аргументом по умолчанию to_dict является False . Аргумент to_dict используется для получения вывода в виде словаря или нет.

Создание объекта

 sparse = SparseMatrix(arr=mat) 

Вывод — Список

 >>> smat_c = sparse.retain_sparsity() 
_c >>> print(smat0109 [[0, 0, 2], 
 [0, 1, 2], 
 [0, 3, 2], 
 [1, 0, 2], 
 [1, 1, 1], 
 [1, 4, 2], 
 [2, 0, 2], 
 [2, 1, 1], 
 [2, 3, 1], 
 [3, 1, 1], 
 [3, 2, 2], 
 [3, 4, 2], 
 [4, 1, 1], 
 [4, 2, 2], 
 [4, 3, 2], 
 [4, 4, 1]] 

Выход — словарь

 >>> smat_d = sparse.retain_sparsity(to_dict=True) 
 >>> print(smat_d) 
 {(0, 0): 2, 
 (0, 1): 2, 
 (0, 3) : 2, 
 (1, 0): 2, 
 (1, 1): 1, 
 (1, 4): 2, 
 (2, 0): 2, 
 (2, 1): 1, 
 (2, 3): 1, 
 (3, 1): 1, 
 (3, 2) ): 2, 
 (3, 4): 2, 
 (4, 1): 1, 
 (4, 2): 2, 
 (4, 3): 2, 
 (4, 4): 1} 

• Когда при работе с большими матрицами у нас есть ограничения по объему, часто предпочтительнее преобразовать матрицу в разреженное представление, и это действительно занимает меньше места по сравнению с исходной матрицей.
• На самом деле мы можем проверить место (в байтах), занимаемое исходной матрицей мат и разреженная матрица .

 >>> from sys import getsizeof 
 >>> # проверка пространства исходной матрицы 
 >>> getsizeof(mat) 
 156 
 >>> # проверка пространства разреженной матрицы scipy 
 >>> getsizeof(smat ) 
 24 
 >>> # проверка пользовательской реализации разреженной матрицы 
 >>> getsizeof(smat_c) 
 92 

• Мы можем наблюдать, что scipy 9Метод 0022 занимает меньше места, чем наш пользовательский метод. Это потому, что scipy — это оптимизированная хорошо разработанная библиотека, в основном используемая для различных научных вычислений.
• Всегда лучше использовать библиотечные методы, чем собственный код, для достижения более быстрых результатов с меньшим объемом памяти.

Купи мне кофе

Если тебе понравилась моя статья, ты можешь купить кофе и поддержать меня здесь. Это мотивировало бы меня писать и узнавать больше о том, что я знаю.

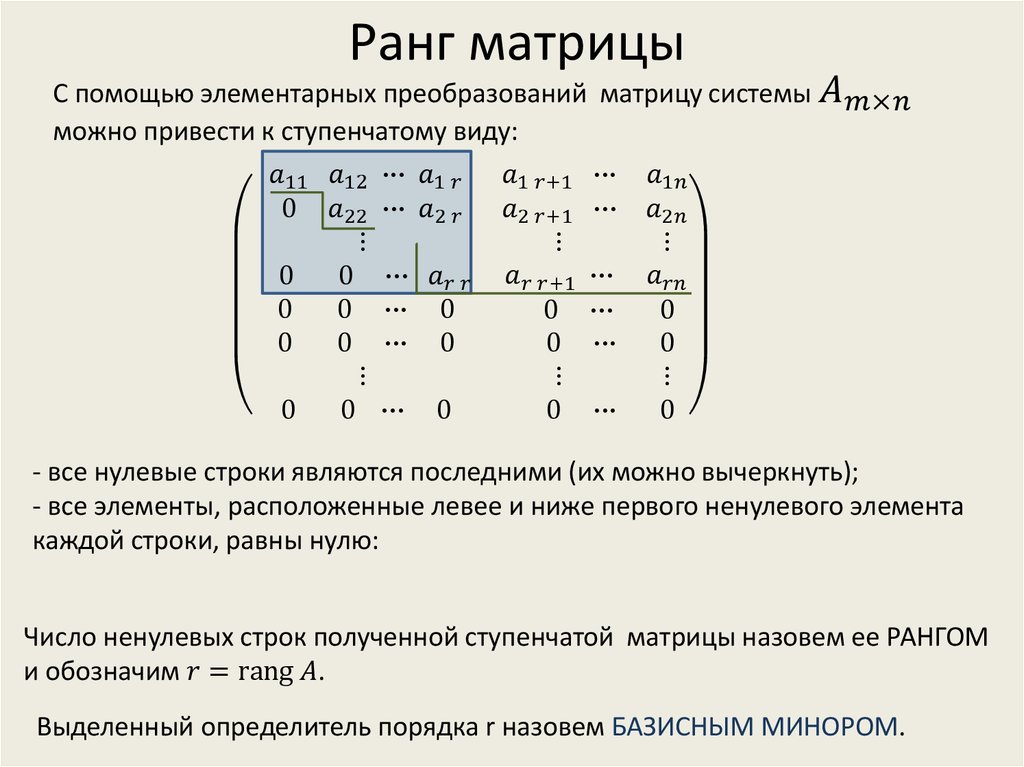
Объяснить эшелонированную форму матрицы

Эшелонная форма матрицы используется для решения линейного уравнения путем преобразования сложной матрицы в простую. Матрица находится в форме Echelon Form , если она удовлетворяет некоторым условиям, которые мы обсудим в этом посте. Мы должны знать, как преобразовать матрицу в Echelon Form и упростить нашу матрицу для дальнейших операций линейной алгебры.

Что такое форма эшелона

Матрица находится в форме эшелона, если она удовлетворяет следующим условиям:

• Первый ненулевой элемент в строке равен 1. Эта запись называется сводной или ведущей записью.

• Каждая опорная точка в столбце является правой стороной опорной колонки в предыдущей строке.

• Строка со всеми нулями должна быть ниже строк, содержащих ненулевой элемент.

Этот процесс преобразования матрицы в форму эхолона известен как процесс исключения Гаусса . Если вы применяете исключение Гаусса к строкам, то это Row Echelon Form 9.0009, а если применяется к столбцам, то это форма Column Echelon Form . Можно сказать, что инверсия формы эшелона строк является формой эшелона столбцов.

Сокращенная форма эшелона строк

Это специальная форма матрицы формы эшелона строк. Таким образом, эшелонированная форма строки является уменьшенной формой эшелона строки, если она удовлетворяет следующему условию:

• Сводная или ведущая запись 1 в строке будет единственным ненулевым значением в ее столбцах. Таким образом, все остальные значения в том же столбце будут иметь нулевое значение.

Итак, обратите внимание, что все остальные значения равны нулю в том же столбце, в котором ведущая единица (выделена красным).

Каждая матрица имеет уникальную форму уменьшенного ряда строк и помогает легко решать линейную систему.

Преобразование в эшелонированную форму строк

Мы можем преобразовать любую матрицу в форму эшелонирования строк, применяя несколько элементарных операций. Существует 3 основных элементарных операции , как описано ниже:

• Замена двух строк или столбцов

8

9

10

11

R1 <> R2

8

10

110003

• Умножение каждого значения в рядо

(2R 1  –> R 1 )

• Умножить каждое значение в строке или столбце на ненулевое значение и прибавить к другой строке.

(-2R 1  + R 2  –> R 2 )

Этот процесс известен как процесс исключения Гаусса . Дальнейшее преобразование эшелонированной формы строк в уменьшенную форму эшелона строк известно как процесс Gauss-Jordan Elimination . Оба процесса очень полезны для решения системы линейных уравнений. Давайте разберемся в этом на примере дуновения.

Решение линейных уравнений

Рассмотрим два линейных уравнения и найдем значения x и y методом исключения Гаусса.

X + Y = 2 и X+ 2Y = 3

Шаг 1 – Создайте матрицу коэффициентов. Это матрица, в которой каждая строка представляет собой уравнение, а значения столбцов представляют собой значения коэффициентов для каждой переменной.

Шаг 2 – Создайте постоянную матрицу. Это матрица-столбец, где каждое значение представляет собой решение уравнения.

Шаг 3 – Создайте расширенную матрицу, которая представляет собой комбинированную форму матрицы коэффициентов и матрицы констант.

Шаг 4 – Преобразуйте эту расширенную матрицу в эшелонированную форму из строк , используя элементарные операции.

(R2 – R1 -> R2)

обратите внимание, что результирующая матрица имеет форму эшелона строк, поэтому теперь перепишите матрицу в виде уравнений.

1*X+1*Y = 2 и 0*X + 1*Y = 1

Таким образом, Y=1 согласно второму уравнению и подставьте это значение в первое уравнение, чтобы найти значение X.